[1]
Open Cascade SAS. Open cascade technology [EB/OL]. (2023-01-01)[2023-04-15]. https://www.opencascade.com/.
[本文引用: 1]
[2]
SCHÖBERL J NETGEN An advancing front 2D/3D-mesh generator based on abstract rules
[J]. Computing and Visualization in Science 1997 , 1 (1 ): 41 - 52
DOI:10.1007/s007910050004
[本文引用: 2]
[3]
GEUZAINE C, REMACLE J F Gmsh: a 3-D finite element mesh generator with built-in pre-and post-processing facilities
[J]. International Journal for Numerical Methods in Engineering 2009 , 79 (11 ): 1309 - 1331
DOI:10.1002/nme.2579
[本文引用: 1]
[5]
JU T Robust repair of polygonal models
[J]. ACM Transactions on Graphics 2004 , 23 (3 ): 888 - 895
DOI:10.1145/1015706.1015815
[6]
王骁, 雷娜, 罗钟铉 基于局部的全自动网格修复算法
[J]. 计算机辅助设计与图形学学报 , 2022 , 34 (19179 ): 1391 - 1401
[本文引用: 1]
WANG Xiao, LEI Na, LUO Zhongxuan An automatic surface-based mesh repairing algorithm
[J]. Journal of Computer-Aided Design and Computer Graphics 2022 , 34 (19179 ): 1391 - 1401
[本文引用: 1]
[7]
CENTIN M, PEZZOTTI N, SIGNORONI A Poisson-driven seamless completion of triangular meshes
[J]. Computer Aided Geometric Design 2015 , 35 : 42 - 55
[本文引用: 1]
[8]
ALLIEZ P, UCELLI G, GOTSMAN C, et al. Recent advances in remeshing of surfaces [M]// DE FLORIANI L, SPAGNUOLO M. Shape analysis and structuring . Berlin: Springer , 2008: 53-82.
[本文引用: 1]
[9]
BOTSCH M, KOBBELT L, PAULY M, et al. Polygon mesh processing [M]. Boca Raton: CRC Press, 2010: 85-150.
[10]
KHAN D, PLOPSKI A, FUJIMOTO Y, et al Surface remeshing: a systematic literature review of methods and research directions
[J]. IEEE Transactions on Visualization and Computer Graphics 2020 , 28 (3 ): 1680 - 1713
[本文引用: 1]
[11]
HARTMANN E A marching method for the triangulation of surfaces
[J]. The Visual Computer 1998 , 14 (3 ): 95 - 108
DOI:10.1007/s003710050126
[本文引用: 1]
[13]
ZHONG Z, GUO X, WANG W, et al Particle-based anisotropic surface meshing
[J]. ACM Transactions on Graphics 2013 , 32 (4 ): 1 - 14
[本文引用: 1]
[14]
SHIMADA K, GOSSARD D C Automatic triangular mesh generation of trimmed parametric surfaces for finite element analysis
[J]. Computer Aided Geometric Design 1998 , 15 (3 ): 199 - 222
DOI:10.1016/S0167-8396(97)00037-X
[本文引用: 1]
[15]
PEYRÉ G, COHEN L. Surface segmentation using geodesic centroidal tessellation [C]// Proceedings of 2nd International Symposium on 3D Data Processing, Visualization and Transmission . Thessaloniki: IEEE, 2004: 995-1002.
[本文引用: 1]
[16]
VALETTE S, CHASSERY J M, PROST R Generic remeshing of 3D triangular meshes with metric-dependent discrete Voronoi diagrams
[J]. IEEE Transactions on Visualization and Computer Graphics 2008 , 14 (2 ): 369 - 381
DOI:10.1109/TVCG.2007.70430
[17]
YAN D M, LÉVY B, LIU Y, et al Isotropic remeshing with fast and exact computation of restricted Voronoi diagram
[J]. Computer Graphics Forum 2009 , 28 (5 ): 1445 - 1454
DOI:10.1111/j.1467-8659.2009.01521.x
[本文引用: 1]
[18]
DU Q, WANG D Anisotropic centroidal Voronoi tessellations and their applications
[J]. SIAM Journal on Scientific Computing 2005 , 26 (3 ): 737 - 761
DOI:10.1137/S1064827503428527
[本文引用: 1]
[19]
LABELLE F, SHEWCHUK J R. Anisotropic Voronoi diagrams and guaranteed-quality anisotropic mesh generation [C]// Proceedings of the 19th Annual Symposium on Computational Geometry . New York: ACM, 2003: 191- 200.
[本文引用: 1]
[21]
GU X, YAU S T. Global conformal surface parameterization [C]// Proceedings of the 2003 Eurographics/ACM SIGGRAPH Symposium on Geometry Processing . Goslar: ACM, 2003: 127-137.
[本文引用: 1]
[22]
LIU L, YE C, NI R, et al Progressive parameterizations
[J]. ACM Transactions on Graphics 2018 , 37 (4 ): 1 - 12
[23]
SU K, LEI N, CHEN W, et al Curvature adaptive surface remeshing by sampling normal cycle
[J]. Computer-Aided Design 2019 , 111 : 1 - 12
DOI:10.1016/j.cad.2019.01.004
[本文引用: 1]
[24]
BÉCHET E, CUILLIERE J C, TROCHU F Generation of a finite element MESH from stereolithography (STL) files
[J]. Computer-Aided Design 2002 , 34 (1 ): 1 - 17
DOI:10.1016/S0010-4485(00)00146-9
[本文引用: 1]
[25]
AUBRY R, KARAMETE B K, MESTREAU E L, et al A three-dimensional parametric mesher with surface boundary-layer capability
[J]. Journal of Computational Physics 2014 , 270 : 161 - 181
DOI:10.1016/j.jcp.2014.03.057
[26]
GUO J, DING F, JIA X, et al Automatic and high-quality surface mesh generation for CAD models
[J]. Computer-Aided Design 2019 , 109 : 49 - 59
DOI:10.1016/j.cad.2018.12.005
[本文引用: 1]
[27]
尤磊, 申则宇, 张立强, 等 CAD 模型三角网格优化算 法
[J]. 计算机辅助设计与图形学学报 , 2019 , 31 (6 ): 878 - 885
DOI:10.3724/SP.J.1089.2019.17393
[本文引用: 1]
YOU Lei, SHEN Zeyu, ZHANG Liqiang, et al A mesh optimization algorithm for CAD models
[J]. Journal of Computer-Aided Design and Computer Graphics 2019 , 31 (6 ): 878 - 885
DOI:10.3724/SP.J.1089.2019.17393
[本文引用: 1]
[28]
SHEWCHUK J R. What is a good linear element? interpolation, conditioning, and quality measures [C]// Proceedings of the International Meshing Roundtable . Ithaca: SIAM, 2002: 115-126.
[本文引用: 1]
[29]
FREY P J, BOROUCHAKI H Geometric surface mesh optimization
[J]. Computing and Visualization in Science 1998 , 1 (3 ): 113 - 121
DOI:10.1007/s007910050011
[本文引用: 1]
[30]
BOTSCH M, BOMMES D, VOGEL C, et al. GPU-based tolerance volumes for mesh processing [C]// Proceedings of the Pacific Conference on Computer Graphics and Applications . Goslar: IEEE, 2004: 237-243.
[本文引用: 1]
[31]
MANDAD M, COHEN-STEINER D, ALLIEZ P Isotopic approximation within a tolerance volume
[J]. ACM Transactions on Graphics 2015 , 34 (4 ): 1 - 12
[本文引用: 1]
[32]
WANG B, SCHNEIDER T, HU Y, et al Exact and efficient polyhedral envelope containment check
[J]. ACM Transactions on Graphics 2020 , 39 (4 ): 114
[本文引用: 1]
[33]
HU K, YAN D M, BOMMES D, et al Error-bounded and feature preserving surface remeshing with minimal angle improvement
[J]. IEEE Transactions on Visualization and Computer Graphics 2016 , 23 (12 ): 2560 - 2573
[本文引用: 1]
[34]
YANG Y, ZHANG W X, LIU Y, et al Error-bounded compatible remeshing
[J]. ACM Transactions on Graphics 2020 , 39 (4 ): 1 - 15
[本文引用: 1]
[35]
ZHANG W X, WANG Q, GUO J P, et al Constrained remeshing using evolutionary vertex optimization
[J]. Computer Graphics Forum 2022 , 41 (2 ): 237 - 247
DOI:10.1111/cgf.14471
[本文引用: 1]
[36]
MEYER M, DESBRUN M, SCHRÖDER P, et al. Discrete differential-geometry operators for triangulated 2-manifolds [C]// Visualization and Mathematics III . Berlin: Springer, 2003: 35-57.
[本文引用: 1]
1
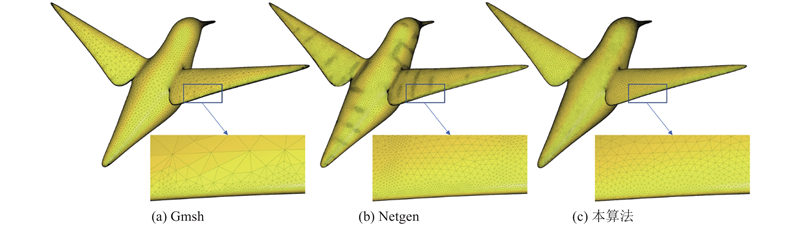
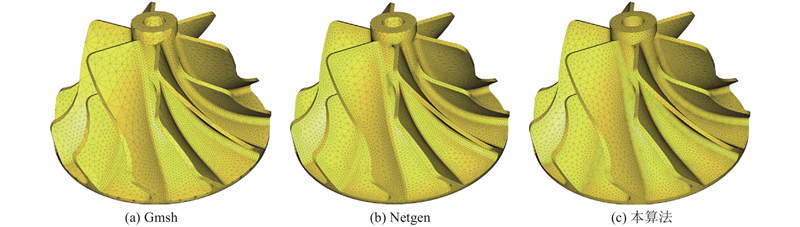
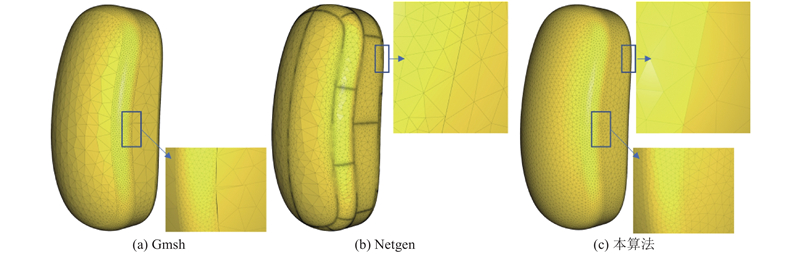
... 边界表示(boundary representation)的参数曲面模型在计算机辅助设计(computer aided design, CAD) 系统中十分常见,从边界表示模型生成网格是数值模拟、快速成型、计算流体力学、可视化等众多领域关注的重点问题. 目前的主流 CAD 软件如Open Cascade[1 ] 、NetGen[2 ] 、 Gmesh[3 ] 等在网格生成过程中会产生错误的网格结构,如退化三角形、网格缝隙、相交面片等,并且无法控制生成网格的误差. 尽管可以使用网格修复技术修复错误的网格结构,但修复结果往往存在较大的误差. ...
NETGEN An advancing front 2D/3D-mesh generator based on abstract rules
2
1997
... 边界表示(boundary representation)的参数曲面模型在计算机辅助设计(computer aided design, CAD) 系统中十分常见,从边界表示模型生成网格是数值模拟、快速成型、计算流体力学、可视化等众多领域关注的重点问题. 目前的主流 CAD 软件如Open Cascade[1 ] 、NetGen[2 ] 、 Gmesh[3 ] 等在网格生成过程中会产生错误的网格结构,如退化三角形、网格缝隙、相交面片等,并且无法控制生成网格的误差. 尽管可以使用网格修复技术修复错误的网格结构,但修复结果往往存在较大的误差. ...
... 直接法利用曲面的曲率、法向和到曲面的投影点等几何信息,直接在三维空间中生成网格. 直接法的相关工作包括基于栅格的网格生成法 [11 ] 、波前推进法 [2 ,12 ] 、基于粒子的网格生成法 [13 ] 、气泡堆积法 [14 ] 、基于 Delaunay 三角剖分的网格生成法[15 -17 ] 等. 直接法的难点包括计算网格点到参数曲面的投影或直线与参数曲面的交点. 在参数曲面上,这些算法的效率和精度较低,比不上隐式曲面. 如果先将曲面隐式化,又会引入累积误差. ...
Gmsh: a 3-D finite element mesh generator with built-in pre-and post-processing facilities
1
2009
... 边界表示(boundary representation)的参数曲面模型在计算机辅助设计(computer aided design, CAD) 系统中十分常见,从边界表示模型生成网格是数值模拟、快速成型、计算流体力学、可视化等众多领域关注的重点问题. 目前的主流 CAD 软件如Open Cascade[1 ] 、NetGen[2 ] 、 Gmesh[3 ] 等在网格生成过程中会产生错误的网格结构,如退化三角形、网格缝隙、相交面片等,并且无法控制生成网格的误差. 尽管可以使用网格修复技术修复错误的网格结构,但修复结果往往存在较大的误差. ...
A lightweight approach to repairing digitized polygon meshes
1
2010
... 网格生成产生错误结构的原因之一是边界表示模型不水密. 边界表示模型上2个面片的共边是在2个参数曲面的参数域上分别存储的,因此会受到计算机截断误差的影响产生缝隙. 另外,设计误差、布尔运算求交误差、不同 CAD 软件的不同精度要求导致的误差等都会破坏模型的水密性. 网格生成算法必须对模型的重合边和重合点进行特殊处理. 修复模型的水密性通常采取以下2种手段. 1)通过局部网格编辑操作,填补、合并网格上的缝隙[4 -6 ] ,该类方法仅适用于缝合间距较小的缝隙,无法识别在几何上互相重合的网格边. 2)通过全局重构建模型的隐式曲面,离散化该曲面来生成水密网格[7 ] ,该方法能够保证输出水密网格,但会模糊网格的尖点、硬边界、薄板等重要特征,导致生成网格模型存在较大的误差. 此外,可以对边界进行配对采样,保证网格的水密性,但现有的边界线采样方案多数仅考虑曲线精度的需求,没有综合考虑相邻2个曲面的精度需求. 本文通过对参数曲面边界线进行配对采样和配对优化来解决生成网格不水密和精度不可控的问题,并在采样时的目标边长计算策略中引入曲面精度估计项,以满足相邻面片的精度需求. ...
Robust repair of polygonal models
0
2004
基于局部的全自动网格修复算法
1
2022
... 网格生成产生错误结构的原因之一是边界表示模型不水密. 边界表示模型上2个面片的共边是在2个参数曲面的参数域上分别存储的,因此会受到计算机截断误差的影响产生缝隙. 另外,设计误差、布尔运算求交误差、不同 CAD 软件的不同精度要求导致的误差等都会破坏模型的水密性. 网格生成算法必须对模型的重合边和重合点进行特殊处理. 修复模型的水密性通常采取以下2种手段. 1)通过局部网格编辑操作,填补、合并网格上的缝隙[4 -6 ] ,该类方法仅适用于缝合间距较小的缝隙,无法识别在几何上互相重合的网格边. 2)通过全局重构建模型的隐式曲面,离散化该曲面来生成水密网格[7 ] ,该方法能够保证输出水密网格,但会模糊网格的尖点、硬边界、薄板等重要特征,导致生成网格模型存在较大的误差. 此外,可以对边界进行配对采样,保证网格的水密性,但现有的边界线采样方案多数仅考虑曲线精度的需求,没有综合考虑相邻2个曲面的精度需求. 本文通过对参数曲面边界线进行配对采样和配对优化来解决生成网格不水密和精度不可控的问题,并在采样时的目标边长计算策略中引入曲面精度估计项,以满足相邻面片的精度需求. ...
基于局部的全自动网格修复算法
1
2022
... 网格生成产生错误结构的原因之一是边界表示模型不水密. 边界表示模型上2个面片的共边是在2个参数曲面的参数域上分别存储的,因此会受到计算机截断误差的影响产生缝隙. 另外,设计误差、布尔运算求交误差、不同 CAD 软件的不同精度要求导致的误差等都会破坏模型的水密性. 网格生成算法必须对模型的重合边和重合点进行特殊处理. 修复模型的水密性通常采取以下2种手段. 1)通过局部网格编辑操作,填补、合并网格上的缝隙[4 -6 ] ,该类方法仅适用于缝合间距较小的缝隙,无法识别在几何上互相重合的网格边. 2)通过全局重构建模型的隐式曲面,离散化该曲面来生成水密网格[7 ] ,该方法能够保证输出水密网格,但会模糊网格的尖点、硬边界、薄板等重要特征,导致生成网格模型存在较大的误差. 此外,可以对边界进行配对采样,保证网格的水密性,但现有的边界线采样方案多数仅考虑曲线精度的需求,没有综合考虑相邻2个曲面的精度需求. 本文通过对参数曲面边界线进行配对采样和配对优化来解决生成网格不水密和精度不可控的问题,并在采样时的目标边长计算策略中引入曲面精度估计项,以满足相邻面片的精度需求. ...
Poisson-driven seamless completion of triangular meshes
1
2015
... 网格生成产生错误结构的原因之一是边界表示模型不水密. 边界表示模型上2个面片的共边是在2个参数曲面的参数域上分别存储的,因此会受到计算机截断误差的影响产生缝隙. 另外,设计误差、布尔运算求交误差、不同 CAD 软件的不同精度要求导致的误差等都会破坏模型的水密性. 网格生成算法必须对模型的重合边和重合点进行特殊处理. 修复模型的水密性通常采取以下2种手段. 1)通过局部网格编辑操作,填补、合并网格上的缝隙[4 -6 ] ,该类方法仅适用于缝合间距较小的缝隙,无法识别在几何上互相重合的网格边. 2)通过全局重构建模型的隐式曲面,离散化该曲面来生成水密网格[7 ] ,该方法能够保证输出水密网格,但会模糊网格的尖点、硬边界、薄板等重要特征,导致生成网格模型存在较大的误差. 此外,可以对边界进行配对采样,保证网格的水密性,但现有的边界线采样方案多数仅考虑曲线精度的需求,没有综合考虑相邻2个曲面的精度需求. 本文通过对参数曲面边界线进行配对采样和配对优化来解决生成网格不水密和精度不可控的问题,并在采样时的目标边长计算策略中引入曲面精度估计项,以满足相邻面片的精度需求. ...
1
... 网格生成的相关工作可以参考文献[8 ~10 ]. 现有的参数曲面三角网格生成算法可以分为映射法、直接法和混合法3类. ...
Surface remeshing: a systematic literature review of methods and research directions
1
2020
... 网格生成的相关工作可以参考文献[8 ~10 ]. 现有的参数曲面三角网格生成算法可以分为映射法、直接法和混合法3类. ...
A marching method for the triangulation of surfaces
1
1998
... 直接法利用曲面的曲率、法向和到曲面的投影点等几何信息,直接在三维空间中生成网格. 直接法的相关工作包括基于栅格的网格生成法 [11 ] 、波前推进法 [2 ,12 ] 、基于粒子的网格生成法 [13 ] 、气泡堆积法 [14 ] 、基于 Delaunay 三角剖分的网格生成法[15 -17 ] 等. 直接法的难点包括计算网格点到参数曲面的投影或直线与参数曲面的交点. 在参数曲面上,这些算法的效率和精度较低,比不上隐式曲面. 如果先将曲面隐式化,又会引入累积误差. ...
An adaptive method for the automatic triangulation of 3D parametric surfaces
1
1998
... 直接法利用曲面的曲率、法向和到曲面的投影点等几何信息,直接在三维空间中生成网格. 直接法的相关工作包括基于栅格的网格生成法 [11 ] 、波前推进法 [2 ,12 ] 、基于粒子的网格生成法 [13 ] 、气泡堆积法 [14 ] 、基于 Delaunay 三角剖分的网格生成法[15 -17 ] 等. 直接法的难点包括计算网格点到参数曲面的投影或直线与参数曲面的交点. 在参数曲面上,这些算法的效率和精度较低,比不上隐式曲面. 如果先将曲面隐式化,又会引入累积误差. ...
Particle-based anisotropic surface meshing
1
2013
... 直接法利用曲面的曲率、法向和到曲面的投影点等几何信息,直接在三维空间中生成网格. 直接法的相关工作包括基于栅格的网格生成法 [11 ] 、波前推进法 [2 ,12 ] 、基于粒子的网格生成法 [13 ] 、气泡堆积法 [14 ] 、基于 Delaunay 三角剖分的网格生成法[15 -17 ] 等. 直接法的难点包括计算网格点到参数曲面的投影或直线与参数曲面的交点. 在参数曲面上,这些算法的效率和精度较低,比不上隐式曲面. 如果先将曲面隐式化,又会引入累积误差. ...
Automatic triangular mesh generation of trimmed parametric surfaces for finite element analysis
1
1998
... 直接法利用曲面的曲率、法向和到曲面的投影点等几何信息,直接在三维空间中生成网格. 直接法的相关工作包括基于栅格的网格生成法 [11 ] 、波前推进法 [2 ,12 ] 、基于粒子的网格生成法 [13 ] 、气泡堆积法 [14 ] 、基于 Delaunay 三角剖分的网格生成法[15 -17 ] 等. 直接法的难点包括计算网格点到参数曲面的投影或直线与参数曲面的交点. 在参数曲面上,这些算法的效率和精度较低,比不上隐式曲面. 如果先将曲面隐式化,又会引入累积误差. ...
1
... 直接法利用曲面的曲率、法向和到曲面的投影点等几何信息,直接在三维空间中生成网格. 直接法的相关工作包括基于栅格的网格生成法 [11 ] 、波前推进法 [2 ,12 ] 、基于粒子的网格生成法 [13 ] 、气泡堆积法 [14 ] 、基于 Delaunay 三角剖分的网格生成法[15 -17 ] 等. 直接法的难点包括计算网格点到参数曲面的投影或直线与参数曲面的交点. 在参数曲面上,这些算法的效率和精度较低,比不上隐式曲面. 如果先将曲面隐式化,又会引入累积误差. ...
Generic remeshing of 3D triangular meshes with metric-dependent discrete Voronoi diagrams
0
2008
Isotropic remeshing with fast and exact computation of restricted Voronoi diagram
1
2009
... 直接法利用曲面的曲率、法向和到曲面的投影点等几何信息,直接在三维空间中生成网格. 直接法的相关工作包括基于栅格的网格生成法 [11 ] 、波前推进法 [2 ,12 ] 、基于粒子的网格生成法 [13 ] 、气泡堆积法 [14 ] 、基于 Delaunay 三角剖分的网格生成法[15 -17 ] 等. 直接法的难点包括计算网格点到参数曲面的投影或直线与参数曲面的交点. 在参数曲面上,这些算法的效率和精度较低,比不上隐式曲面. 如果先将曲面隐式化,又会引入累积误差. ...
Anisotropic centroidal Voronoi tessellations and their applications
1
2005
... 映射法利用曲面参数域上的黎曼度量来生成网格[18 -19 ] . 映射法用映射距离代替投影距离来估算网格精度. 对于参数曲面$S( \cdot ):{\bf{R}^2} \to {\bf{R}^3}$ $a$ $a$ $A、B、C$ $a$ $(\alpha ,\beta ,\gamma ) \in {\bf{R}^3}$ $A、B、C$ $ {{\boldsymbol{u}}_A}、{{\boldsymbol{u}}_B}、{{\boldsymbol{u}}_C} \in {\bf{R}^2} $ $S(\alpha {{\boldsymbol{u}}_A}+\beta {{\boldsymbol{u}}_B}+\gamma {{\boldsymbol{u}}_C})$ $a$ 图1 所示,粗折线表示生成的折线(或网格面),细曲线表示原曲线(或曲面). 直接法将折线上的$ab$ $bc$ ${a_1}{b_1}$ ${b_2}{c_1}$ ${b_1}{b_2}$ $ab$ $bc$ ${a_1}{b_1}$ ${b_1}{c_1}$ [20 ] 基于映射法度量,生成高精度的网格. 当参数曲面的映射存在较大的扭曲和拉伸时,可以利用重新参数化方法进行解决[21 -23 ] . ...
1
... 映射法利用曲面参数域上的黎曼度量来生成网格[18 -19 ] . 映射法用映射距离代替投影距离来估算网格精度. 对于参数曲面$S( \cdot ):{\bf{R}^2} \to {\bf{R}^3}$ $a$ $a$ $A、B、C$ $a$ $(\alpha ,\beta ,\gamma ) \in {\bf{R}^3}$ $A、B、C$ $ {{\boldsymbol{u}}_A}、{{\boldsymbol{u}}_B}、{{\boldsymbol{u}}_C} \in {\bf{R}^2} $ $S(\alpha {{\boldsymbol{u}}_A}+\beta {{\boldsymbol{u}}_B}+\gamma {{\boldsymbol{u}}_C})$ $a$ 图1 所示,粗折线表示生成的折线(或网格面),细曲线表示原曲线(或曲面). 直接法将折线上的$ab$ $bc$ ${a_1}{b_1}$ ${b_2}{c_1}$ ${b_1}{b_2}$ $ab$ $bc$ ${a_1}{b_1}$ ${b_1}{c_1}$ [20 ] 基于映射法度量,生成高精度的网格. 当参数曲面的映射存在较大的扭曲和拉伸时,可以利用重新参数化方法进行解决[21 -23 ] . ...
Triangulation of trimmed surfaces in parametric space
1
1992
... 映射法利用曲面参数域上的黎曼度量来生成网格[18 -19 ] . 映射法用映射距离代替投影距离来估算网格精度. 对于参数曲面$S( \cdot ):{\bf{R}^2} \to {\bf{R}^3}$ $a$ $a$ $A、B、C$ $a$ $(\alpha ,\beta ,\gamma ) \in {\bf{R}^3}$ $A、B、C$ $ {{\boldsymbol{u}}_A}、{{\boldsymbol{u}}_B}、{{\boldsymbol{u}}_C} \in {\bf{R}^2} $ $S(\alpha {{\boldsymbol{u}}_A}+\beta {{\boldsymbol{u}}_B}+\gamma {{\boldsymbol{u}}_C})$ $a$ 图1 所示,粗折线表示生成的折线(或网格面),细曲线表示原曲线(或曲面). 直接法将折线上的$ab$ $bc$ ${a_1}{b_1}$ ${b_2}{c_1}$ ${b_1}{b_2}$ $ab$ $bc$ ${a_1}{b_1}$ ${b_1}{c_1}$ [20 ] 基于映射法度量,生成高精度的网格. 当参数曲面的映射存在较大的扭曲和拉伸时,可以利用重新参数化方法进行解决[21 -23 ] . ...
1
... 映射法利用曲面参数域上的黎曼度量来生成网格[18 -19 ] . 映射法用映射距离代替投影距离来估算网格精度. 对于参数曲面$S( \cdot ):{\bf{R}^2} \to {\bf{R}^3}$ $a$ $a$ $A、B、C$ $a$ $(\alpha ,\beta ,\gamma ) \in {\bf{R}^3}$ $A、B、C$ $ {{\boldsymbol{u}}_A}、{{\boldsymbol{u}}_B}、{{\boldsymbol{u}}_C} \in {\bf{R}^2} $ $S(\alpha {{\boldsymbol{u}}_A}+\beta {{\boldsymbol{u}}_B}+\gamma {{\boldsymbol{u}}_C})$ $a$ 图1 所示,粗折线表示生成的折线(或网格面),细曲线表示原曲线(或曲面). 直接法将折线上的$ab$ $bc$ ${a_1}{b_1}$ ${b_2}{c_1}$ ${b_1}{b_2}$ $ab$ $bc$ ${a_1}{b_1}$ ${b_1}{c_1}$ [20 ] 基于映射法度量,生成高精度的网格. 当参数曲面的映射存在较大的扭曲和拉伸时,可以利用重新参数化方法进行解决[21 -23 ] . ...
Progressive parameterizations
0
2018
Curvature adaptive surface remeshing by sampling normal cycle
1
2019
... 映射法利用曲面参数域上的黎曼度量来生成网格[18 -19 ] . 映射法用映射距离代替投影距离来估算网格精度. 对于参数曲面$S( \cdot ):{\bf{R}^2} \to {\bf{R}^3}$ $a$ $a$ $A、B、C$ $a$ $(\alpha ,\beta ,\gamma ) \in {\bf{R}^3}$ $A、B、C$ $ {{\boldsymbol{u}}_A}、{{\boldsymbol{u}}_B}、{{\boldsymbol{u}}_C} \in {\bf{R}^2} $ $S(\alpha {{\boldsymbol{u}}_A}+\beta {{\boldsymbol{u}}_B}+\gamma {{\boldsymbol{u}}_C})$ $a$ 图1 所示,粗折线表示生成的折线(或网格面),细曲线表示原曲线(或曲面). 直接法将折线上的$ab$ $bc$ ${a_1}{b_1}$ ${b_2}{c_1}$ ${b_1}{b_2}$ $ab$ $bc$ ${a_1}{b_1}$ ${b_1}{c_1}$ [20 ] 基于映射法度量,生成高精度的网格. 当参数曲面的映射存在较大的扭曲和拉伸时,可以利用重新参数化方法进行解决[21 -23 ] . ...
Generation of a finite element MESH from stereolithography (STL) files
1
2002
... 混合法综合考虑上述方法的优缺点,共同利用 三维几何和二维参数域信息来生成高质量网格. 多 数综合网格生成法[24 -27 ] 通过映射法生成高精度三角网格或低分辨率三角网格,利用三维几何信息进行质量优化. 这些方案中多数没有考虑网格模型的水密性,特别地,Guo等[26 ] 通过对边界进行均匀采样,保证初始网格的水密性,但这种非自适应采样方案容易导致过高的网格分辨率. 在精度方面,现有的多数综合网格生成法不直接计算网格误差,而是利用逼近论中的相关结论进行精度优化. Shewchuk[28 ] 利用曲面的各向异性,生成给定三角形数量下曲面的最优三角网格逼近. Frey等[29 ] 利用三角形边长、三角形面片的插值误差与曲率的关系,控制生成网格的误差. 这些方法可以用于改善网格的误差与分辨率,但不能完全保证生成网格的精度. 此外,也有一些方法从隐式曲面或网格曲面出发,以误差为硬约束进行网格优化. Botsch等[30 ] 通过估计网格曲面的有符号距离场来生成误差包络,利用该包络实现控制误差的快速网格优化,避免了多个网格优化过程的误差累积效应. Mandad等[31 ] 通过对误差包络进行自适应采样,以生成拓扑正确且满足误差的网格. Wang等[32 ] 提出判定线段是否位于误差包络内的精确快速算法. 从参数曲面生成误差包络,可能会丢失特征边,甚至导致拓扑错误. Hu等[33 ] 基于网格局部编辑操作,设计保证精度的网格重新生成算法,该方法中基于贪心算法设计的角度优化流程能够有效地提高角度质量,但超参数较多,设置不当,会造成算法陷入死循环. Yang等[34 ] 利用参数化方法生成满足误差的相容网格,在保证精度的前提下优化网格分辨率. Zhang等[35 ] 通过遗传变异算法来进行精度、角度和数量的优化,利用该算法能够显著地优化三角网格的角度,但参数设置较复杂,计算更耗时. ...
A three-dimensional parametric mesher with surface boundary-layer capability
0
2014
Automatic and high-quality surface mesh generation for CAD models
1
2019
... 混合法综合考虑上述方法的优缺点,共同利用 三维几何和二维参数域信息来生成高质量网格. 多 数综合网格生成法[24 -27 ] 通过映射法生成高精度三角网格或低分辨率三角网格,利用三维几何信息进行质量优化. 这些方案中多数没有考虑网格模型的水密性,特别地,Guo等[26 ] 通过对边界进行均匀采样,保证初始网格的水密性,但这种非自适应采样方案容易导致过高的网格分辨率. 在精度方面,现有的多数综合网格生成法不直接计算网格误差,而是利用逼近论中的相关结论进行精度优化. Shewchuk[28 ] 利用曲面的各向异性,生成给定三角形数量下曲面的最优三角网格逼近. Frey等[29 ] 利用三角形边长、三角形面片的插值误差与曲率的关系,控制生成网格的误差. 这些方法可以用于改善网格的误差与分辨率,但不能完全保证生成网格的精度. 此外,也有一些方法从隐式曲面或网格曲面出发,以误差为硬约束进行网格优化. Botsch等[30 ] 通过估计网格曲面的有符号距离场来生成误差包络,利用该包络实现控制误差的快速网格优化,避免了多个网格优化过程的误差累积效应. Mandad等[31 ] 通过对误差包络进行自适应采样,以生成拓扑正确且满足误差的网格. Wang等[32 ] 提出判定线段是否位于误差包络内的精确快速算法. 从参数曲面生成误差包络,可能会丢失特征边,甚至导致拓扑错误. Hu等[33 ] 基于网格局部编辑操作,设计保证精度的网格重新生成算法,该方法中基于贪心算法设计的角度优化流程能够有效地提高角度质量,但超参数较多,设置不当,会造成算法陷入死循环. Yang等[34 ] 利用参数化方法生成满足误差的相容网格,在保证精度的前提下优化网格分辨率. Zhang等[35 ] 通过遗传变异算法来进行精度、角度和数量的优化,利用该算法能够显著地优化三角网格的角度,但参数设置较复杂,计算更耗时. ...
CAD 模型三角网格优化算 法
1
2019
... 混合法综合考虑上述方法的优缺点,共同利用 三维几何和二维参数域信息来生成高质量网格. 多 数综合网格生成法[24 -27 ] 通过映射法生成高精度三角网格或低分辨率三角网格,利用三维几何信息进行质量优化. 这些方案中多数没有考虑网格模型的水密性,特别地,Guo等[26 ] 通过对边界进行均匀采样,保证初始网格的水密性,但这种非自适应采样方案容易导致过高的网格分辨率. 在精度方面,现有的多数综合网格生成法不直接计算网格误差,而是利用逼近论中的相关结论进行精度优化. Shewchuk[28 ] 利用曲面的各向异性,生成给定三角形数量下曲面的最优三角网格逼近. Frey等[29 ] 利用三角形边长、三角形面片的插值误差与曲率的关系,控制生成网格的误差. 这些方法可以用于改善网格的误差与分辨率,但不能完全保证生成网格的精度. 此外,也有一些方法从隐式曲面或网格曲面出发,以误差为硬约束进行网格优化. Botsch等[30 ] 通过估计网格曲面的有符号距离场来生成误差包络,利用该包络实现控制误差的快速网格优化,避免了多个网格优化过程的误差累积效应. Mandad等[31 ] 通过对误差包络进行自适应采样,以生成拓扑正确且满足误差的网格. Wang等[32 ] 提出判定线段是否位于误差包络内的精确快速算法. 从参数曲面生成误差包络,可能会丢失特征边,甚至导致拓扑错误. Hu等[33 ] 基于网格局部编辑操作,设计保证精度的网格重新生成算法,该方法中基于贪心算法设计的角度优化流程能够有效地提高角度质量,但超参数较多,设置不当,会造成算法陷入死循环. Yang等[34 ] 利用参数化方法生成满足误差的相容网格,在保证精度的前提下优化网格分辨率. Zhang等[35 ] 通过遗传变异算法来进行精度、角度和数量的优化,利用该算法能够显著地优化三角网格的角度,但参数设置较复杂,计算更耗时. ...
CAD 模型三角网格优化算 法
1
2019
... 混合法综合考虑上述方法的优缺点,共同利用 三维几何和二维参数域信息来生成高质量网格. 多 数综合网格生成法[24 -27 ] 通过映射法生成高精度三角网格或低分辨率三角网格,利用三维几何信息进行质量优化. 这些方案中多数没有考虑网格模型的水密性,特别地,Guo等[26 ] 通过对边界进行均匀采样,保证初始网格的水密性,但这种非自适应采样方案容易导致过高的网格分辨率. 在精度方面,现有的多数综合网格生成法不直接计算网格误差,而是利用逼近论中的相关结论进行精度优化. Shewchuk[28 ] 利用曲面的各向异性,生成给定三角形数量下曲面的最优三角网格逼近. Frey等[29 ] 利用三角形边长、三角形面片的插值误差与曲率的关系,控制生成网格的误差. 这些方法可以用于改善网格的误差与分辨率,但不能完全保证生成网格的精度. 此外,也有一些方法从隐式曲面或网格曲面出发,以误差为硬约束进行网格优化. Botsch等[30 ] 通过估计网格曲面的有符号距离场来生成误差包络,利用该包络实现控制误差的快速网格优化,避免了多个网格优化过程的误差累积效应. Mandad等[31 ] 通过对误差包络进行自适应采样,以生成拓扑正确且满足误差的网格. Wang等[32 ] 提出判定线段是否位于误差包络内的精确快速算法. 从参数曲面生成误差包络,可能会丢失特征边,甚至导致拓扑错误. Hu等[33 ] 基于网格局部编辑操作,设计保证精度的网格重新生成算法,该方法中基于贪心算法设计的角度优化流程能够有效地提高角度质量,但超参数较多,设置不当,会造成算法陷入死循环. Yang等[34 ] 利用参数化方法生成满足误差的相容网格,在保证精度的前提下优化网格分辨率. Zhang等[35 ] 通过遗传变异算法来进行精度、角度和数量的优化,利用该算法能够显著地优化三角网格的角度,但参数设置较复杂,计算更耗时. ...
1
... 混合法综合考虑上述方法的优缺点,共同利用 三维几何和二维参数域信息来生成高质量网格. 多 数综合网格生成法[24 -27 ] 通过映射法生成高精度三角网格或低分辨率三角网格,利用三维几何信息进行质量优化. 这些方案中多数没有考虑网格模型的水密性,特别地,Guo等[26 ] 通过对边界进行均匀采样,保证初始网格的水密性,但这种非自适应采样方案容易导致过高的网格分辨率. 在精度方面,现有的多数综合网格生成法不直接计算网格误差,而是利用逼近论中的相关结论进行精度优化. Shewchuk[28 ] 利用曲面的各向异性,生成给定三角形数量下曲面的最优三角网格逼近. Frey等[29 ] 利用三角形边长、三角形面片的插值误差与曲率的关系,控制生成网格的误差. 这些方法可以用于改善网格的误差与分辨率,但不能完全保证生成网格的精度. 此外,也有一些方法从隐式曲面或网格曲面出发,以误差为硬约束进行网格优化. Botsch等[30 ] 通过估计网格曲面的有符号距离场来生成误差包络,利用该包络实现控制误差的快速网格优化,避免了多个网格优化过程的误差累积效应. Mandad等[31 ] 通过对误差包络进行自适应采样,以生成拓扑正确且满足误差的网格. Wang等[32 ] 提出判定线段是否位于误差包络内的精确快速算法. 从参数曲面生成误差包络,可能会丢失特征边,甚至导致拓扑错误. Hu等[33 ] 基于网格局部编辑操作,设计保证精度的网格重新生成算法,该方法中基于贪心算法设计的角度优化流程能够有效地提高角度质量,但超参数较多,设置不当,会造成算法陷入死循环. Yang等[34 ] 利用参数化方法生成满足误差的相容网格,在保证精度的前提下优化网格分辨率. Zhang等[35 ] 通过遗传变异算法来进行精度、角度和数量的优化,利用该算法能够显著地优化三角网格的角度,但参数设置较复杂,计算更耗时. ...
Geometric surface mesh optimization
1
1998
... 混合法综合考虑上述方法的优缺点,共同利用 三维几何和二维参数域信息来生成高质量网格. 多 数综合网格生成法[24 -27 ] 通过映射法生成高精度三角网格或低分辨率三角网格,利用三维几何信息进行质量优化. 这些方案中多数没有考虑网格模型的水密性,特别地,Guo等[26 ] 通过对边界进行均匀采样,保证初始网格的水密性,但这种非自适应采样方案容易导致过高的网格分辨率. 在精度方面,现有的多数综合网格生成法不直接计算网格误差,而是利用逼近论中的相关结论进行精度优化. Shewchuk[28 ] 利用曲面的各向异性,生成给定三角形数量下曲面的最优三角网格逼近. Frey等[29 ] 利用三角形边长、三角形面片的插值误差与曲率的关系,控制生成网格的误差. 这些方法可以用于改善网格的误差与分辨率,但不能完全保证生成网格的精度. 此外,也有一些方法从隐式曲面或网格曲面出发,以误差为硬约束进行网格优化. Botsch等[30 ] 通过估计网格曲面的有符号距离场来生成误差包络,利用该包络实现控制误差的快速网格优化,避免了多个网格优化过程的误差累积效应. Mandad等[31 ] 通过对误差包络进行自适应采样,以生成拓扑正确且满足误差的网格. Wang等[32 ] 提出判定线段是否位于误差包络内的精确快速算法. 从参数曲面生成误差包络,可能会丢失特征边,甚至导致拓扑错误. Hu等[33 ] 基于网格局部编辑操作,设计保证精度的网格重新生成算法,该方法中基于贪心算法设计的角度优化流程能够有效地提高角度质量,但超参数较多,设置不当,会造成算法陷入死循环. Yang等[34 ] 利用参数化方法生成满足误差的相容网格,在保证精度的前提下优化网格分辨率. Zhang等[35 ] 通过遗传变异算法来进行精度、角度和数量的优化,利用该算法能够显著地优化三角网格的角度,但参数设置较复杂,计算更耗时. ...
1
... 混合法综合考虑上述方法的优缺点,共同利用 三维几何和二维参数域信息来生成高质量网格. 多 数综合网格生成法[24 -27 ] 通过映射法生成高精度三角网格或低分辨率三角网格,利用三维几何信息进行质量优化. 这些方案中多数没有考虑网格模型的水密性,特别地,Guo等[26 ] 通过对边界进行均匀采样,保证初始网格的水密性,但这种非自适应采样方案容易导致过高的网格分辨率. 在精度方面,现有的多数综合网格生成法不直接计算网格误差,而是利用逼近论中的相关结论进行精度优化. Shewchuk[28 ] 利用曲面的各向异性,生成给定三角形数量下曲面的最优三角网格逼近. Frey等[29 ] 利用三角形边长、三角形面片的插值误差与曲率的关系,控制生成网格的误差. 这些方法可以用于改善网格的误差与分辨率,但不能完全保证生成网格的精度. 此外,也有一些方法从隐式曲面或网格曲面出发,以误差为硬约束进行网格优化. Botsch等[30 ] 通过估计网格曲面的有符号距离场来生成误差包络,利用该包络实现控制误差的快速网格优化,避免了多个网格优化过程的误差累积效应. Mandad等[31 ] 通过对误差包络进行自适应采样,以生成拓扑正确且满足误差的网格. Wang等[32 ] 提出判定线段是否位于误差包络内的精确快速算法. 从参数曲面生成误差包络,可能会丢失特征边,甚至导致拓扑错误. Hu等[33 ] 基于网格局部编辑操作,设计保证精度的网格重新生成算法,该方法中基于贪心算法设计的角度优化流程能够有效地提高角度质量,但超参数较多,设置不当,会造成算法陷入死循环. Yang等[34 ] 利用参数化方法生成满足误差的相容网格,在保证精度的前提下优化网格分辨率. Zhang等[35 ] 通过遗传变异算法来进行精度、角度和数量的优化,利用该算法能够显著地优化三角网格的角度,但参数设置较复杂,计算更耗时. ...
Isotopic approximation within a tolerance volume
1
2015
... 混合法综合考虑上述方法的优缺点,共同利用 三维几何和二维参数域信息来生成高质量网格. 多 数综合网格生成法[24 -27 ] 通过映射法生成高精度三角网格或低分辨率三角网格,利用三维几何信息进行质量优化. 这些方案中多数没有考虑网格模型的水密性,特别地,Guo等[26 ] 通过对边界进行均匀采样,保证初始网格的水密性,但这种非自适应采样方案容易导致过高的网格分辨率. 在精度方面,现有的多数综合网格生成法不直接计算网格误差,而是利用逼近论中的相关结论进行精度优化. Shewchuk[28 ] 利用曲面的各向异性,生成给定三角形数量下曲面的最优三角网格逼近. Frey等[29 ] 利用三角形边长、三角形面片的插值误差与曲率的关系,控制生成网格的误差. 这些方法可以用于改善网格的误差与分辨率,但不能完全保证生成网格的精度. 此外,也有一些方法从隐式曲面或网格曲面出发,以误差为硬约束进行网格优化. Botsch等[30 ] 通过估计网格曲面的有符号距离场来生成误差包络,利用该包络实现控制误差的快速网格优化,避免了多个网格优化过程的误差累积效应. Mandad等[31 ] 通过对误差包络进行自适应采样,以生成拓扑正确且满足误差的网格. Wang等[32 ] 提出判定线段是否位于误差包络内的精确快速算法. 从参数曲面生成误差包络,可能会丢失特征边,甚至导致拓扑错误. Hu等[33 ] 基于网格局部编辑操作,设计保证精度的网格重新生成算法,该方法中基于贪心算法设计的角度优化流程能够有效地提高角度质量,但超参数较多,设置不当,会造成算法陷入死循环. Yang等[34 ] 利用参数化方法生成满足误差的相容网格,在保证精度的前提下优化网格分辨率. Zhang等[35 ] 通过遗传变异算法来进行精度、角度和数量的优化,利用该算法能够显著地优化三角网格的角度,但参数设置较复杂,计算更耗时. ...
Exact and efficient polyhedral envelope containment check
1
2020
... 混合法综合考虑上述方法的优缺点,共同利用 三维几何和二维参数域信息来生成高质量网格. 多 数综合网格生成法[24 -27 ] 通过映射法生成高精度三角网格或低分辨率三角网格,利用三维几何信息进行质量优化. 这些方案中多数没有考虑网格模型的水密性,特别地,Guo等[26 ] 通过对边界进行均匀采样,保证初始网格的水密性,但这种非自适应采样方案容易导致过高的网格分辨率. 在精度方面,现有的多数综合网格生成法不直接计算网格误差,而是利用逼近论中的相关结论进行精度优化. Shewchuk[28 ] 利用曲面的各向异性,生成给定三角形数量下曲面的最优三角网格逼近. Frey等[29 ] 利用三角形边长、三角形面片的插值误差与曲率的关系,控制生成网格的误差. 这些方法可以用于改善网格的误差与分辨率,但不能完全保证生成网格的精度. 此外,也有一些方法从隐式曲面或网格曲面出发,以误差为硬约束进行网格优化. Botsch等[30 ] 通过估计网格曲面的有符号距离场来生成误差包络,利用该包络实现控制误差的快速网格优化,避免了多个网格优化过程的误差累积效应. Mandad等[31 ] 通过对误差包络进行自适应采样,以生成拓扑正确且满足误差的网格. Wang等[32 ] 提出判定线段是否位于误差包络内的精确快速算法. 从参数曲面生成误差包络,可能会丢失特征边,甚至导致拓扑错误. Hu等[33 ] 基于网格局部编辑操作,设计保证精度的网格重新生成算法,该方法中基于贪心算法设计的角度优化流程能够有效地提高角度质量,但超参数较多,设置不当,会造成算法陷入死循环. Yang等[34 ] 利用参数化方法生成满足误差的相容网格,在保证精度的前提下优化网格分辨率. Zhang等[35 ] 通过遗传变异算法来进行精度、角度和数量的优化,利用该算法能够显著地优化三角网格的角度,但参数设置较复杂,计算更耗时. ...
Error-bounded and feature preserving surface remeshing with minimal angle improvement
1
2016
... 混合法综合考虑上述方法的优缺点,共同利用 三维几何和二维参数域信息来生成高质量网格. 多 数综合网格生成法[24 -27 ] 通过映射法生成高精度三角网格或低分辨率三角网格,利用三维几何信息进行质量优化. 这些方案中多数没有考虑网格模型的水密性,特别地,Guo等[26 ] 通过对边界进行均匀采样,保证初始网格的水密性,但这种非自适应采样方案容易导致过高的网格分辨率. 在精度方面,现有的多数综合网格生成法不直接计算网格误差,而是利用逼近论中的相关结论进行精度优化. Shewchuk[28 ] 利用曲面的各向异性,生成给定三角形数量下曲面的最优三角网格逼近. Frey等[29 ] 利用三角形边长、三角形面片的插值误差与曲率的关系,控制生成网格的误差. 这些方法可以用于改善网格的误差与分辨率,但不能完全保证生成网格的精度. 此外,也有一些方法从隐式曲面或网格曲面出发,以误差为硬约束进行网格优化. Botsch等[30 ] 通过估计网格曲面的有符号距离场来生成误差包络,利用该包络实现控制误差的快速网格优化,避免了多个网格优化过程的误差累积效应. Mandad等[31 ] 通过对误差包络进行自适应采样,以生成拓扑正确且满足误差的网格. Wang等[32 ] 提出判定线段是否位于误差包络内的精确快速算法. 从参数曲面生成误差包络,可能会丢失特征边,甚至导致拓扑错误. Hu等[33 ] 基于网格局部编辑操作,设计保证精度的网格重新生成算法,该方法中基于贪心算法设计的角度优化流程能够有效地提高角度质量,但超参数较多,设置不当,会造成算法陷入死循环. Yang等[34 ] 利用参数化方法生成满足误差的相容网格,在保证精度的前提下优化网格分辨率. Zhang等[35 ] 通过遗传变异算法来进行精度、角度和数量的优化,利用该算法能够显著地优化三角网格的角度,但参数设置较复杂,计算更耗时. ...
Error-bounded compatible remeshing
1
2020
... 混合法综合考虑上述方法的优缺点,共同利用 三维几何和二维参数域信息来生成高质量网格. 多 数综合网格生成法[24 -27 ] 通过映射法生成高精度三角网格或低分辨率三角网格,利用三维几何信息进行质量优化. 这些方案中多数没有考虑网格模型的水密性,特别地,Guo等[26 ] 通过对边界进行均匀采样,保证初始网格的水密性,但这种非自适应采样方案容易导致过高的网格分辨率. 在精度方面,现有的多数综合网格生成法不直接计算网格误差,而是利用逼近论中的相关结论进行精度优化. Shewchuk[28 ] 利用曲面的各向异性,生成给定三角形数量下曲面的最优三角网格逼近. Frey等[29 ] 利用三角形边长、三角形面片的插值误差与曲率的关系,控制生成网格的误差. 这些方法可以用于改善网格的误差与分辨率,但不能完全保证生成网格的精度. 此外,也有一些方法从隐式曲面或网格曲面出发,以误差为硬约束进行网格优化. Botsch等[30 ] 通过估计网格曲面的有符号距离场来生成误差包络,利用该包络实现控制误差的快速网格优化,避免了多个网格优化过程的误差累积效应. Mandad等[31 ] 通过对误差包络进行自适应采样,以生成拓扑正确且满足误差的网格. Wang等[32 ] 提出判定线段是否位于误差包络内的精确快速算法. 从参数曲面生成误差包络,可能会丢失特征边,甚至导致拓扑错误. Hu等[33 ] 基于网格局部编辑操作,设计保证精度的网格重新生成算法,该方法中基于贪心算法设计的角度优化流程能够有效地提高角度质量,但超参数较多,设置不当,会造成算法陷入死循环. Yang等[34 ] 利用参数化方法生成满足误差的相容网格,在保证精度的前提下优化网格分辨率. Zhang等[35 ] 通过遗传变异算法来进行精度、角度和数量的优化,利用该算法能够显著地优化三角网格的角度,但参数设置较复杂,计算更耗时. ...
Constrained remeshing using evolutionary vertex optimization
1
2022
... 混合法综合考虑上述方法的优缺点,共同利用 三维几何和二维参数域信息来生成高质量网格. 多 数综合网格生成法[24 -27 ] 通过映射法生成高精度三角网格或低分辨率三角网格,利用三维几何信息进行质量优化. 这些方案中多数没有考虑网格模型的水密性,特别地,Guo等[26 ] 通过对边界进行均匀采样,保证初始网格的水密性,但这种非自适应采样方案容易导致过高的网格分辨率. 在精度方面,现有的多数综合网格生成法不直接计算网格误差,而是利用逼近论中的相关结论进行精度优化. Shewchuk[28 ] 利用曲面的各向异性,生成给定三角形数量下曲面的最优三角网格逼近. Frey等[29 ] 利用三角形边长、三角形面片的插值误差与曲率的关系,控制生成网格的误差. 这些方法可以用于改善网格的误差与分辨率,但不能完全保证生成网格的精度. 此外,也有一些方法从隐式曲面或网格曲面出发,以误差为硬约束进行网格优化. Botsch等[30 ] 通过估计网格曲面的有符号距离场来生成误差包络,利用该包络实现控制误差的快速网格优化,避免了多个网格优化过程的误差累积效应. Mandad等[31 ] 通过对误差包络进行自适应采样,以生成拓扑正确且满足误差的网格. Wang等[32 ] 提出判定线段是否位于误差包络内的精确快速算法. 从参数曲面生成误差包络,可能会丢失特征边,甚至导致拓扑错误. Hu等[33 ] 基于网格局部编辑操作,设计保证精度的网格重新生成算法,该方法中基于贪心算法设计的角度优化流程能够有效地提高角度质量,但超参数较多,设置不当,会造成算法陷入死循环. Yang等[34 ] 利用参数化方法生成满足误差的相容网格,在保证精度的前提下优化网格分辨率. Zhang等[35 ] 通过遗传变异算法来进行精度、角度和数量的优化,利用该算法能够显著地优化三角网格的角度,但参数设置较复杂,计算更耗时. ...
1
... 网格上的最小曲率半径可以通过网格的平均曲率与高斯曲率求出[36 ] . ...