吊弦作为接触网悬挂系统中使用数量最多的部件之一，连接接触线与承力索并将接触线的荷载与振动传递给承力索. 随着列车运行速度和行车密度的提升，由于安装不恰当、长期列车运行中机械振动、与其他零部件摩擦等因素的影响，吊弦线断裂、松弛、散股等事故时有发生，接触网吊弦改善受流、受力的性能不能实现，反而容易造成弓网故障，给铁路运营带来安全隐患^[1]. 为了确保高铁供电设备运行安全，提升供电系统安全保障能力，构建了高速铁路供电安全检测监测系统（6C系统）. 其中，接触网悬挂状态检测监测系统（4C系统）对吊弦、腕臂、接触线等部件进行高分辨率成像，通过智能检测系统并辅助人工逐张判别接触网零部件状态，形成维修建议，指导接触网检修. 但是，面对4C装置采集到的海量接触网图像，当前4C系统智能化检测能力接近饱和并且人工判别的方式存在工作量大、时效性差的问题，因此，亟须提升4C系统的智能化检测能力.

近年来，深度学习在目标检测领域取得了重大进步，深度学习算法被广泛应用于吊弦缺陷检测任务中，包括RefineDet网络^[2]、FCOS网络^[3]、Faster-RCNN网络^[4]等. 上述网络需要大量带标注样本进行训练，然而在实际工程领域中缺陷样本难以获取. 因此，在少样本，甚至零样本条件下实现对吊弦缺陷的识别，对深度学习技术在实际接触网检修任务中的应用具有重要意义.

Larochelle等^[5]提出零样本学习（zero-shot learning，ZSL）概念，目前，主要有3大类研究方法：基于属性预测方法、基于特征映射方法、基于特征生成方法. Lampert等^[6] 采用属性作为中间层构建图像到标签之间的关联，首先基于专家标注的属性计算属性层和标签之间的关联概率，其次计算图像特征与属性层的关联概率，最后将最大概率的标签作为图像的预测标签. 但是，该方法的分类效果很大程度上倚仗于属性标注的维度和品质，增加了应用中的时间和人工成本. Frome等^[7]利用Word2Vec^[8]技术将标签嵌入语义空间，首先将图像提取的视觉特征映射到语义空间，然后在语义空间中寻找相似度最高的语义特征作为该图像的语义描述，其对应的标签作为该图像的预测标签. 但是，这些语义词向量中不可避免地存在一定的冗余信息和噪声，影响了类别间距离结构信息的有效表达. Kingma等^[9]通过变分自编码机将输入语义特征编码为隐空间中的概率分布，再对隐空间进行采样和解码重建，从而生成对应类的视觉特征，但由于语义描述和视觉表达差异性问题，利用语义生成的视觉特征质量低，难以代表该类别.

为了解决上述问题，本研究提出基于组合零样本学习(compositional zero-shot learning, CZSL)的接触网吊弦线缺陷识别方法. 该方法主要思路如下：通过ResNet-50网络提取图像视觉特征；使用训练的Word2Vec词向量作为组合标签图的节点特征，通过图卷积网络为标签组合图各节点聚合其相关节点的特征表示，增强各组合标签节点的语义特征，消除人工标注属性和单纯语义信息嵌入的弊端；在兼容性学习框架中构建组合标签语义特征和图像视觉特征之间的相似度函数，并计算两者之间的相似度得分，通过交叉熵损失实现对缺陷吊弦图像的识别.

组合学习是指将2个，甚至多个简单概念结合为一个复杂的概念. 在计算机视觉领域中，Hoffman等^[10-11]认为视觉系统可以通过学习简单概念进而学习复杂概念. Misra等^[12]受成分识别理论的启发，将属性视觉分类器和目标视觉分类器组合后得到新的复杂视觉分类器，例如：红色(属性)+酒(对象)=红酒. 组合已知视觉概念的分类器，并应用这个模型来识别具有未知概念组合的物体. 与零样本不同的是，组合零样本学习主要将已学习的简单概念组合为复杂的不可见类概念并进行学习，已有的研究包括TMN^[13]、AttOp^[14]、SymNet^[15]等. Purushwkakam等^[13]提出任务驱动的模块化网络，将识别任务分解，然后通过组合产生未知类分类器，通过计算图像与“属性-对象”对之间的兼容性分数，为正确的三元组匹配高分，实现零样本分类. Nagarajan等^[14]学习视觉映射函数f(x)和“属性-对象”映射函数g(p)，并在语义空间中计算两者之间的欧氏距离，以达到分类目的.

图卷积网络(graph convolutional network, GCN)^[16]是能够直接作用于图并且利用其结构信息的卷积神经网络，可使图中各节点之间相互传递信息并增强节点自身的特征信息表示^[17]. 给定图G={V, E, A}，其中，V、E、 $ {\boldsymbol{A}} \in {{{\bf{R}}}^{K \times K}} $分别表示图的节点集合、边集合和邻接矩阵. GCN通过如下公式对输入特征 $ {{\boldsymbol{H}}^{(l)}} \in {{\bf{R}}^{K \times d}} $和邻接矩阵 $ {\boldsymbol{A}} \in {{\bf{R}}^{K \times K}} $进行学习：

(1) $ {{\boldsymbol{H}}}^{(l\text{+1})}=\sigma ({\tilde{{\boldsymbol{D}}}}^{-1/2}+\tilde{{\boldsymbol{A}}}{\tilde{{\boldsymbol{D}}}}^{-1/2}{{\boldsymbol{H}}}^{(l)}{{\boldsymbol{W}}}^{(l)}) . $

式中： $ {{\boldsymbol{H}}^{(l+1)}} $为第l+1层的特征矩阵； $ {\tilde{\boldsymbol A}} $为标准化前添加自连接的邻接矩阵， $ {\tilde{\boldsymbol A}} = {\boldsymbol{A}}+{\boldsymbol{I}} $， $ {\boldsymbol{I}} $为单位矩阵； $ {\tilde{\boldsymbol D}} $为 $ {\tilde{\boldsymbol A}} $的度矩阵； $ \sigma $为非线性激活函数； ${{\boldsymbol{W}}}^{(l)} $为第l层的权重矩阵.

本研究提出的CZSL方法框架如图1所示，训练阶段如图1(a) 所示，主要包括3个模块. 1) 视觉特征提取模块. 使用ResNet-50网络，将训练集中的可见类样本转换为向量表示，并将其对应的类别标签一起输入到兼容性学习框架中，用以在测试阶段对可见类样本进行分类. 2)图卷积模块. 通过构建标签组合图使得算法可以发现标签之间相互作用和依赖关系，并将与节点名称相对应的词向量作为节点的特征表示. GCN在标签组合图上执行信息传递和节点更新的过程，并将更新的节点特征向量传递到下一层. 通过多次迭代，GCN可以捕获标签组合图中复杂的、非线性的关系，并且使用这些关系来优化组合标签特征表示G， 提高模型的分类准确性. 3)兼容性学习模块. 通过相似度函数计算图像视觉特征F和组合标签特征表示G之间的相似度得分，为图像分配正确的组合标签.

测试阶段如图1 ( b) 所示，使用预训练的ResNet-50网络提取测试图像的视觉特征，利用相似度函数计算测试图像视觉特征与组合标签语义特征之间的相似度，将测试图像分配给具有最高相似度得分的类别.

CZSL的任务可以描述为 $ {{T}} = \{ (x,y)|x \in {{X}}, y \in {{{Y}}_{\text{s}}}\} $，其中，T表示训练集；x表示集合X中的图像；y表示图像x对应的标签，属于可见类标签集合Y_s，y=(s, o)是由状态标签 $ s \in {{S}} $和对象标签 $ o \in {{O}} $组成的元组，S和O分别表示状态标签和对象标签的集合. CZSL的最终目标是预测一组新的不可见类标签 $ {{{Y}}_{\text{u}}} $，并通过相似度函数为不可见类图像匹配组合标签 $ y' \in {{{Y}}_{\text{u}}} $，其中 $ {{{Y}}_{\text{s}}} \cap {{{Y}}_{\text{u}}} = \varnothing $.

在CZSL中，状态标签和对象标签的组合是通过建立图来实现的. 算法会通过解析数据集中的标签信息，自动确定所有可能的组合标签，并创建相应的节点和边. 因此，本研究将s、o、y作为图的节点，互相影响的节点之间通过一条无向边连接，构建标签组合图，如图2所示. 标签组合图总共包括10个节点，其中3个状态标签节点由第1行蓝色节点表示，2个对象标签节点由第2行绿色节点表示，5个组合标签节点由第3行黄色节点表示. 每一个组合标签 $ y = (s,o) \in Y $定义了状态标签s、对象标签o以及两者组合标签y之间的依赖关系，其中 $ Y = {Y_{\text{s}}} \cup {Y_{\text{u}}} $.

将组合标签图中的节点按照从左向右、从上到下的顺序从0开始编号. 若节点i和节点j之间存在无向边连接，则A_ij=1，若不存在无向边连接，则A_ij=0. 将A_ij作为标签组合图邻接矩阵 $ {\boldsymbol{A}} \in {{\bf{R}}^{10 \times 10}} $的元素：

(2) $ {\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {{A_{00}}}&{{A_{01}}}& \cdots &{{A_{09}}} \\ {{A_{10}}}&{{A_{11}}}&{...}&{{A_{19}}} \\ \vdots & \vdots & & \vdots \\ {{A_{90}}}&{{A_{91}}}& \cdots &{{A_{99}}} \end{array}} \right] . $

一般情况下，为了在对图节点信息进行聚合时，不丢失自身节点信息，通常给网络中的节点增加自连接，此时邻接矩阵表示为 $ {\tilde{\boldsymbol A}} = {\boldsymbol{A}}+{\boldsymbol{I}} $. 但是，此操作对节点自身及其相邻近节点的特征信息赋予了相同的权重，这将造成节点特征信息中自身成分占比过低的问题，为此，Gao等^[18]提出相应的改进措施：

(3) $ {\tilde{\boldsymbol A}} = {\boldsymbol{A}}+\alpha {\boldsymbol{I}} . $

式中：α为常数. 此改进措施使得GCN在信息聚合过程中，给节点自身信息赋予更大的权重，从而使节点自身信息更具有辨识性.

GCN是对图定义的邻域中的节点特征进行操作的，因此在得到标签组合图的邻接矩阵之后，须为每个节点嵌入合适的特征表示. 本研究针对铁路接触网吊弦缺陷识别任务，搜集相关文本语料，并利用Word2Vec模型，训练得到d维Word2Vec英文词向量，将非结构化文本分词嵌入词向量空间中，转化为具有语义信息的数值. 相比于手动定义属性，词向量具有更好的可扩展性和通用性. 标签组合图中的每个状态标签节点和对象标签节点的特征表示由与其相对应的状态标签或对象标签名称相关联的词嵌入来表示. 组合标签节点的初始特征表示通过平均对应状态标签节点和对象标签节点的特征表示得出. 由此，本研究通过为标签组合图添加词嵌入，在语义空间上初步实现了组合性.

d维Word2Vec词向量在图卷积模块中不仅提供了标签组合图节点初始特征向量，还通过节点之间的语义相似度来指导图卷积网络优化节点特征向量. 具体来说，在优化过程中，GCN将每个节点的特征向量作为输入，并将其与相邻节点的特征向量进行卷积操作. 卷积层的参数是通过反向传播来学习的，以最小化节点特征向量与它们的邻居之间的差异. 这样，在每次迭代中，GCN会将每个节点的特征向量更新为与其相邻节点的特征向量更加接近的向量.

如图1(a)所示，将标签组合图中的节点特征作为GCN的输入，使用图卷积网络从每个节点自身以及所连接的相邻节点中聚合信息. 图卷积网络的计算如下：

(4) $ \left. \begin{array}{l} {{\boldsymbol{H}}^{(l+1)}} = \sigma (\hat {\boldsymbol{A}}{{\boldsymbol{H}}^{(l)}}{{\boldsymbol{\theta}} ^l}), \\ \hat {\boldsymbol{A}} = {{\tilde {\boldsymbol{D}}}^{ - 1/2}}\tilde {\boldsymbol{A}}{{\tilde {\boldsymbol{D}}}^{ - 1/2}} , \\ \tilde {\boldsymbol{A}} = {\boldsymbol{A}}+{\boldsymbol{I}} , \\ {{\boldsymbol{H}}^{(0)}} = {\boldsymbol{E}}. \\ \end{array} \right\} $

式中： $ \sigma $为非线性激活函数ReLU； $ {\hat{\boldsymbol A}} $为标准化后的邻接矩阵； $ {{{\boldsymbol{\theta}} }^l} $为权值矩阵， ${{\boldsymbol{\theta }}^l} \in {{{\bf{R}}}^{10 \times d}}$；E为标签组合图的节点特征矩阵， ${\boldsymbol{E}} \in {{{\bf{R}}}^{10 \times d}}$； D为A的度矩阵.

相比于Frome等^[7-8], CZSL将词向量嵌入标签组合图后，使用GCN可以从复杂的文本关系中学习语义信息，并捕捉对象之间的关系，能够更好地处理对象之间的复杂关系，学习到更准确、更全面的语义信息、提高模型的性能和泛化能力.

目前，针对图卷积网络的研究主要集中于一阶谱图卷积，然而随着图卷积网络层数的增加，节点特征所表示的信息将会被稀释，进而极大降低了距离较大节点之间的可区分性，即过度平滑现象^[17]. 因此，须通过对比实验确定最佳的图卷积网络层数.

在得到图像的视觉特征和组合标签的语义特征后，构建两者之间的相似度函数，计算图像x、状态表示y、对象o之间的相似度得分，为图像x匹配与其取得最高相似度分数的组合标签y=(s, o)，即正确的三元组(x, s, o)将会获得更高的相似度分数. 相似度函数如下：

(5) $ f(x, s, o)=\boldsymbol{F}(x, \boldsymbol{W}) \cdot \boldsymbol{G}(s, o, \boldsymbol{\theta}). $

式中： $ {{\boldsymbol{F}}}{\text{(}}x,{{\boldsymbol{W}}}{\text{)}} $为利用ResNet-50网络提取的视觉特征， $ {{\boldsymbol{G}}}(s,o,{{\boldsymbol{\theta}} }) $为输出组合标签节点的特征表示，W和 $\boldsymbol{\theta} $分别为F和G的可学习权重.

兼容性学习框架的分类损失采用二值交叉熵损失. 在多分类问题中，神经网络最后一层全连接层的原始输出只是每一类的得分向量. 因此，通过softmax函数将网络输出转化为概率值，softmax函数如下：

(6) $ {p_i} = {{\rm{softmax}}} \;(f({x_i},y)) = \frac{{\exp\; f({x_i},y)}}{{\displaystyle \sum\limits_{j = 1}^{\left| {{Y_{\text{s}}}} \right|} {\exp\; f({x_i},y')} }} . $

式中: y为图像x_i的真实标签, $ y = ({s_i},{o_i}) $； $ y' $为可见类标签集合Y_s中任意一个标签, $ y' = ({s_j},{o_j}) $; p_i为输入值 $ f({x_i},y) $属于 $ f({x_i},y') $的概率.

采用交叉熵损失函数作为评价兼容性学习框架分类准确率的指标，搜寻最正确的三元组(x, s, o)并为其赋予更高的相似度得分，从而实现图像分类. 损失函数为

(7) $ \mathop {\min }\limits_{{\boldsymbol{W}},\;{\boldsymbol{\theta }}} \;\left\{ - \frac{1}{{\left| T \right|}}\sum\limits_{i = 1}^{\left| T \right|} {\ln\; {p_i}} \right\} . $

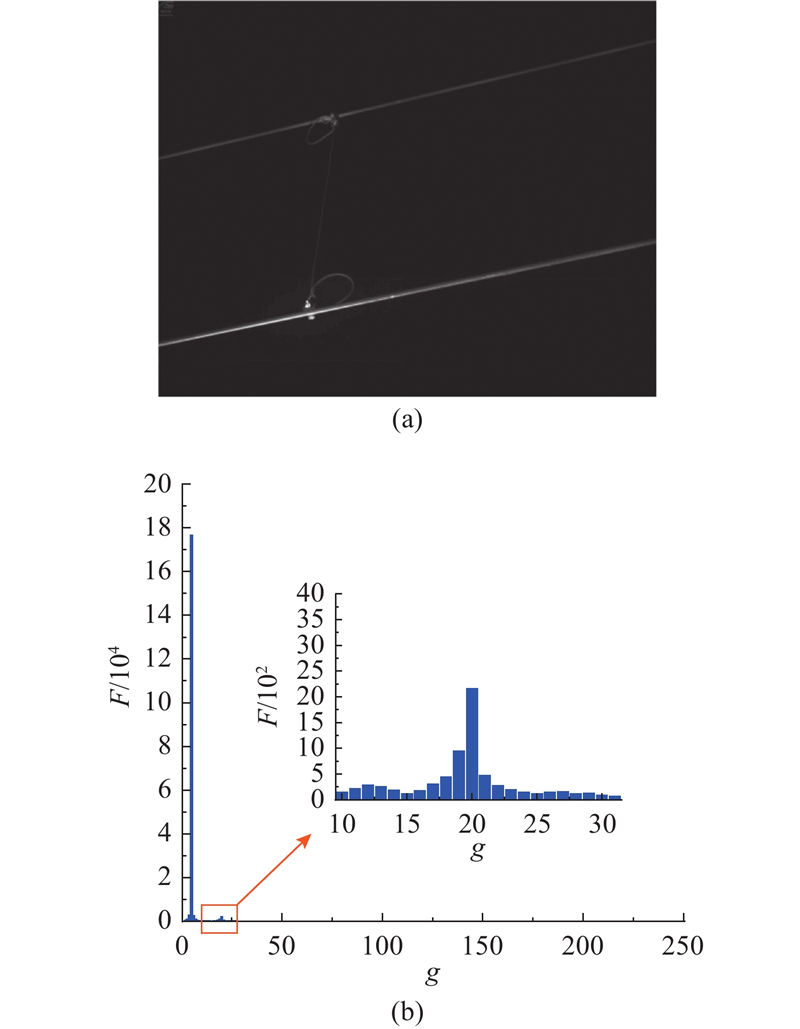
所提方法的关键是利用标签组合图中状态标签节点、对象标签节点以及其组合标签节点之间的依赖关系，强制将相关知识从可见类迁移到不可见类. 实验所用数据集包括接触网悬挂状态检测监测装置(4C装置)采集的接触网吊弦图像和人工拍摄的钢绞线图像. 在训练过程中，将正常吊弦、松弛绞线、断裂绞线作为可见类样本用来学习状态标签和对象标签的视觉特征和语义关系，从而学习如何将它们组合成新的组合标签，即断裂吊弦和松弛吊弦. 接触网吊弦线由直径为4 mm的铜合金绞线制成，其视觉特征与各种绞线极为相似，因此选择将松弛绞线和断裂绞线作为可见类样本. 由于高铁接触网巡检在夜间进行，虽然4C检测车车顶安装了补光装置，但是4C装置拍摄的巡检图像基本上都是低照度图像；由于检测车高速运行，所拍摄的接触网吊弦图像对比度不足，吊弦主体与背景灰度值相近，不易进行待检测对象特征提取，进而影响后续模型检测精度.

采用限制对比度自适应直方图均衡化(contrast limited adaptive histogram equalization, CLAHE)算法^[19]进行接触网吊弦图像增强，前后对比如图3、4所示. 图中，g表示灰度值，F表示像素点频数. 可以看出，如果吊弦图像直方图分布情况单一，灰度值较低，吊弦图像的对比较差，并且细节模糊，难以通过肉眼清晰辨别吊弦主体的边缘. 在使用CLAHE算法对原始吊弦图像增强后，图像灰度值整体提高，背景与吊弦主体的灰度值分布出现较明显的差异，同时图像层次分明、细节清晰可辨.

在训练过程中将7000张图像分为训练集、验证集和测试集，训练集中包括3种可见类样本，验证集和测试集包括3种可见类样本和2种不可见类样本. 本研究实验数据集不同类型图像数量N如表1所示.

本实验使用的评价指标包括类平均准确度和调谐平均准确度. 在广义零样本学习(generalized ZSL，GZSL)^[20]中，类平均准确度是零样本学习领域最常用的评价指标，该指标先对每个类统计类内的分类准确度，再通过计算均值得到类平均准确度. 为了能够更合理地评价模型的整体分类性能，在GSZL实验条件下，同时采用调谐平均准确度^[21]进行评估. 调谐平均准确度表达式如下：

(8) $ H = 2 \times \frac{{{{\rm{Ac}}}{{{\rm{c}}}^{\text{s}}} \times {{\rm{Ac}}}{{{\rm{c}}}^{\text{u}}}}}{{{{\rm{Ac}}}{{{\rm{c}}}^{\text{s}}}+{{\rm{Ac}}}{{{\rm{c}}}^{\text{u}}}}} . $

式中：Acc^s为可见类样本的类平均准确度，Acc^u为不可见类样本的类平均准确度.

为了验证本研究算法的有效性，在pytorch深度学习框架下进行实验，硬件配置如下：操作系统为Windows10，处理器(CPU)为AMD R7 5800H，显卡(GPU)为8 G内存的NVIDIA GeForce RTX3050Ti.

在算法训练过程中，将图像的尺寸调整为512像素×512像素，视觉特征提取采用在ImageNet数据集上预训练的ResNet-50主干网络，其参数见表2. ResNet-50主干网络最开始有一个卷积核为7×7的卷积层，随后有4个Block，每个里面分别包括3、4、6、3个Bottleneck，每个Bottleneck包括卷积核为1×1和3×3的卷积层，最后经过平均池化层、全连接层和Softmax层计算并输出类别概率^[22]. 训练批量大小为32，ResNet-50网络学习率为5×10⁻⁶. 状态标签和对象标签的特征表示采用具有300维的Word2vec词向量，组合标签的词向量为对应状态标签和对象标签词向量的平均值. GCN层数为2层，GCN学习率为5×10⁻⁵，2层图卷积网络之间采用非线性函数ReLU作为激活函数，随机失活dropout为0.5，训练轮次为500次.

在标签组合图的邻接矩阵中，自连接权重控制着每个节点与自己相连的边的权重. 如果自连接权重设置太大，会导致节点的自身特征占据极大比例，可能会导致模型过拟合. 反之，如果自连接权重过小，则无法充分利用节点自身的信息，而导致特征稀疏，性能下降. 为了确定α取值对算法检测准确率的影响，在不同α取值的条件下对CZSL进行训练，训练结果如表3所示. 可以看出，当α=2时，CZSL对可见类样本和不可见类样本的类平均检测准确率均达到最高. 因此，为邻接矩阵添加自连接时，设置α=2.

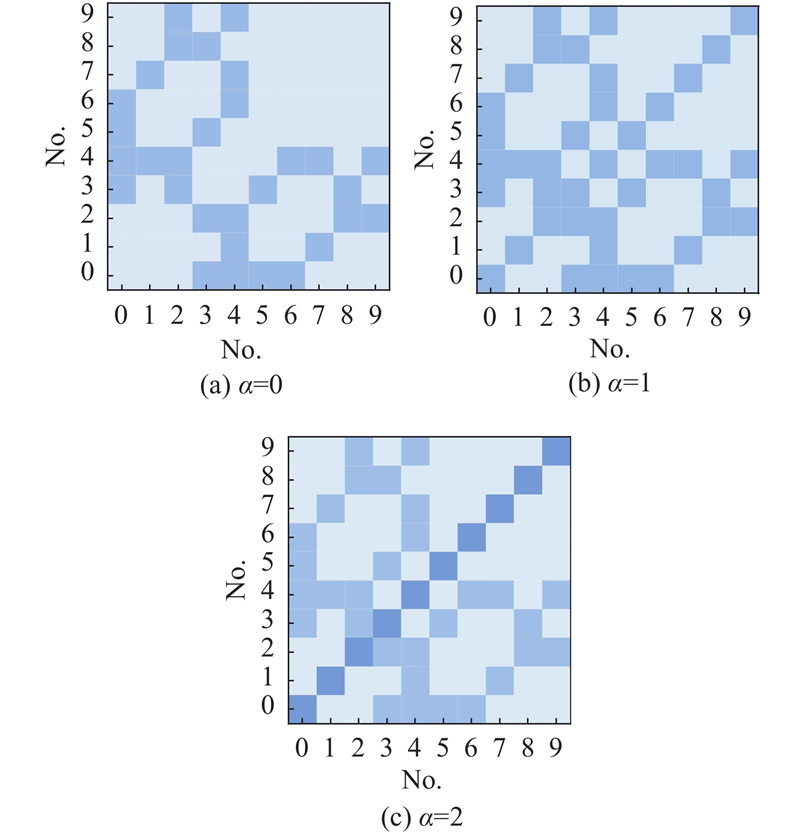
如图5所示为α=0，1，2时，本研究数据集对应的邻接矩阵可视化图. 图中，No.为标签组合图中的节点编号，图中元素对应2个节点之间的连接权重，颜色越深表示自连接关系越显著.可以看出，在使用增强节点自身信息的邻接矩阵后，节点自身信息更为突出.

为了确定图卷积网络层数对算法检测准确率的影响，在不同GCN层数L的条件下对CZSL进行训练，训练结果如表4所示.可以看出，当L=2时，CZSL对可见类样本和不可见类样本的类平均检测准确率均达到最高. 因此，设置图卷积模块中的图卷积网络层数L=2.

为了验证不同视觉特征提取网络对CZSL算法检测效果的影响，分别采用ResNet-18、ResNet-50、ResNet-101、Vgg-16作为算法的视觉特征提取网络. 对比实验结果如表5所示. 表中，M为参数量，t为平均耗时. 可以看出，当采用ResNet-101作为CZSL的视觉特征提取网络时，算法取得了最高的检测准确率，但相比于ResNet-50需要较大的平均耗时，并且检测准确率提升较小；当采用ResNet-18作为CZSL的视觉特征提取网络时，虽然取得了最快的检测速度，但相比于ResNet-50，检测准确率有较大差距. 因此，CZSL算法在综合考虑检测准确率和检测速度的前提下，采用ResNet-50网络作为视觉特征提取网络.

为了验证CZSL算法的检测效果，使用相同的训练数据和训练参数分别训练LE+^[12] 、TMN^[13]、AttOp^[14]、SymNet^[15]4种算法作为对比试验. 对比试验结果如表6所示. 表中，H为调谐平均准确度.可以看出，CZSL对可见类样本的类平均检测准确率为93.5%，对不可见类样本的类平均检测准确率为86.5%，调谐平均准确度为89.9%. CZSL的整体性能均优于其他4种组合零样本学习算法. LE+需要可用的上下文信息来合成对象. 如果缺乏必要的上下文，可能很难实现准确的零样本学习. TMN高度依赖于任务特定数据的可用性，这些数据可能并不总是容易获得或易于访问. AttOp在处理复杂和微妙的对象属性时可能不太有效. SymNet受到所组合的对象、可用的群组和对称性信息质量的限制，可能不适用于学习不具有明显对称性或群组属性的组合关系. 4种对比算法均存在局限性和潜在缺点，在本研究任务要求下，CZSL相比于其他4种算法表现出了更好的检测性能.

为了进一步直观地显示出对比实验的实验效果，绘制对比实验训练过程中的损失曲线，如图6所示. 图中，Loss为损失. 可以看出，CZSL算法的稳定性优于其他算法， 在0~50轮迭代期间快速收敛，当训练到300轮时，训练损失值趋于稳定，直至训练结束.

如表7所示为对比试验中不同算法的参数量和平均耗时. CZSL相比于AttOp、LE+、SymNet在网络参数量未大幅增加的情况下，取得了最高的检测准确率.

综上所述，在接触网吊弦线缺陷识别任务中，CZSL相比于其他4种对比算法表现出了更加优异的检测性能.

选取测试集中具有代表性的不同状态吊弦图像做定性分析. 检测效果如图7所示. 当Top-1预测标签与真实标签相同时，则识别正确.可以看出，第1、2、3列分别为断裂吊弦、松弛吊弦和正常吊弦，Top-1预测标签与真实标签相同，均识别正确. 第4列为松弛吊弦， Top-1预测标签为正常吊弦；第5列为断裂吊弦，Top-1预测标签为正常吊弦.

对于第4、5列吊弦缺陷识别错误的原因从3方面进行分析. 1）从图像角度分析，第4列图像中的吊弦松弛部位位于吊弦线下部，且松弛幅度非常小；第5列图像中的吊弦线断裂部位位于上部载流环钳压管处，吊弦线下垂导致4C装置未完整拍摄到吊弦线. 2）从词向量角度分析，由于铁路接触网吊弦缺陷识别领域的相关文献较少，在训练词向量时文本语料不够丰富，词向量质量下降，进一步影响标签组合图中节点特征表示的准确性，从而使得CZSL在计算相似度时性能下降. 3）从算法角度分析，在综合考虑算法参数量大小和检测准确率的基础上，CZSL采用ResNet-50网络作为视觉特征提取网络. 然而，对于第4列图像中肉眼较难分辨的缺陷，ResNet-50的视觉特征提取能力不足以提取更深层次的特征信息，从而对算法的检测准确率产生一定程度的影响.

（1）本研究利用预训练的Word2Vec词向量作为标签组合图节点的特征表示并采用GCN充分学习状态标签节点、对象标签节点以及组合标签节点三者之间的相互作用和依赖关系，获得更优的组合标签节点的特征表示. 采用ResNet-50作为图像视觉特征提取网络. 最后，通过相似度函数计算图像视觉特征和组合标签节点的特征表示之间的相似度，为不可见类图像匹配正确的组合标签 $ y' $.

（2）仿真实验结果表明，CZSL在广义零样本实验条件下，对可见类样本的类平均检测准确率为93.5%，对不可见类样本即松弛吊弦和断裂吊弦2类缺陷样本的类平均检测准确率为86.5%.

（3）本研究对象仅为接触网吊弦线断裂、松弛2种故障，后续的工作将对接触网吊弦线的其他缺陷进行研究.