随着三维扫描技术的飞速发展,三维点云数据模型已成为几何模型的通用表示形式,并广泛应用于计算机可视化、逆向工程、三维重建等领域. 近年来,国内外学者对三维点云分割方法的研究主要分为2类:基于深度学习[1]和基于点云聚类[2]. 基于深度学习的点云分割方法利用数据集对模型进行训练,得到包含点云空间的局部到全局特征的参数模型,并使用训练好的模型进行点云级分割,但训练过程对算力要求较高. 聚类是一种无监督无训练过程的机器学习算法,通过最大化类内元素相似性,最小化类间元素相似程度划分类别,因其算法简单、模型易修改的特点已经成为点云数据处理的关键步骤之一. 基于点云聚类的方法主要有具有噪声的基于密度的聚类方法[3](density-based spatial clustering of applications with noise,DBSCAN)、模糊C-均值聚类[4](fuzzy C-means,FCM)和K均值聚类[5](K-means clustering ,KMC)等. DBSCAN按点的密度大小进行聚类,耗时较长,计算量大;FCM容易受到初始参数的影响,且不适用于处理高维数据集;KMC简单易实现,收敛较快,但在三维点云数据处理时,对聚类中心较敏感,易陷入局部最优,需要优化改进. 近年来利用群智能优化算法[6]解决上述聚类算法的不足成为新的研究热点. 黄鹤等[7]提出的引入改进飞蛾扑火的K均值交叉迭代聚类算法( improved moth-flame optimization- K-means clustering ,IMFO-KMC)利用最大最小距离积法初始化聚类中心,降低了KMC算法对初始聚类中心的敏感性;Wan等[8]提出基于忆阻混沌麻雀搜索算法的K-means聚类算法,有效提高了大数据分析效率,应用价值较高. 秃鹰搜索 (bald eagle search,BES)算法是Alsattar等[9]提出的新型元启发式群体智能算法,模拟秃鹰捕猎的过程,具有精度高、适应性强的特点,适用于优化聚类. 因此,本研究提出基于疯狂捕猎的柯西反向秃鹰搜索算法(quasi-oppositional bald eagle search algorithm base on crazy-hunting,QO-BESCH)的K均值互补迭代聚类优化算法,并应用于三维点云聚类中,有效提高点云聚类精度.
1. 基于体元初始聚类中心选择模型的KMC初始化
传统KMC初始聚类中心选取的随机性较大,影响聚类精度. 为了改善点云聚类性能,根据“肘部原则”确定K并构建基于体元密度的初始聚类中心选择模型,提升初始化聚类中心质量.
1.1. 传统KMC聚类
在传统KMC聚类中,假设样本数据集的表达式为S={S1, S2,···, Sn}. 聚类任务是将含有n个数据的S,根据准则划分为互不相交的K类,用表达式P={P1, P2,···, PK}表示,其中1<K≤n. 具体步骤如下:1)根据经验或者按一定规则指定K大小,然后采用随机初始化得到KMC的K个聚类中心;2)把样本数据集S中的n个数据,划分到距离其最近的聚类中心所在的类簇;3)在划分完成后,重新计算每一个类簇中所有数据的平均值,以此数据点作为该类簇新的聚类中心;4)迭代更新,将S中数据按照步骤3)不断更新聚类中心,直到其不再发生变化,迭代结束.
KMC的聚类准则为欧氏距离,数据与聚类中心的欧氏距离越小表示数据与聚类中心的相似度越高,聚类效果越好. 样本数据集合中的某一数据Si,与聚类中心cj之间的欧氏距离表达式如下:
综上,传统KMC易受聚类中心随机选取的影响. 因此,提出基于体元初始聚类中心选择模型的KMC初始化方法,提升初始化聚类中心质量.
1.2. 基于点云体元密度选择初始化聚类中心
根据“肘部原则”确定K,构建点云立方体元(包围盒)模型,在考虑密度特征的条件下计算近似均匀分布的点云初始聚类中心. 具体步骤如下.
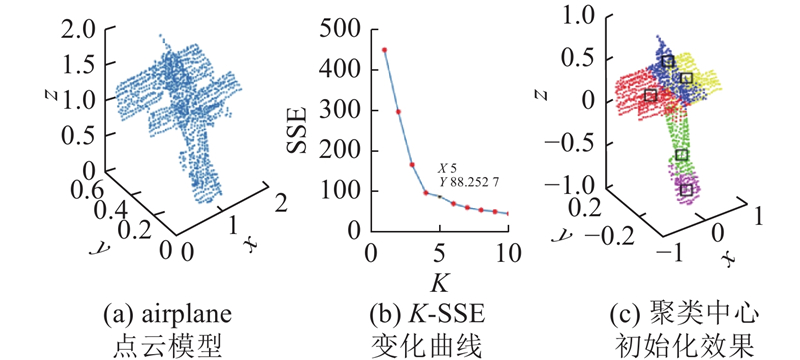
1)根据手肘法确定K,指标是误差平方和(sum of squared errors,SSE). 选取不同K,将对应损失函数画成折线,然后选择折线由陡峭降低转为平缓降低的拐点如手肘,确定最佳K. SSE表达式如下:
式中:Ci为第i个簇,p为Ci中的样本点,ci为Ci的类簇中心. 聚类误差平方和SSE反映了聚类效果.
2)计算点云范围,即获取点云的立方体包围盒. 设点云P={Pi| Pi ϵR3, i=1,2,···, n}在X、Y、Z坐标方向对应的最大值和最小值分别为xmax、ymax、zmax和xmin、ymin、zmin,则其三边长度Lx、Ly、Lz表达式为
3)计算点云体元包围盒大小. 由式(3)得到点云体积V=LxLyLz,假设生成M个体元,M的大小一般取100,体元包围盒边长表达式为
在X、Y、Z 坐标方向体元数量nx、ny、nz的表达式为
4)任取体元b,坐标用(x,y,z)表示,坐标取值范围为
5)计算落入体元b(x,y,z)范围内点的数量Nb(x,y,z),b(x,y,z)的点云密度表达式为
6)计算密度最大的前K个体元的重心,作为初始聚类中心. 聚类中心坐标表达式为
图 1
2. BES改进优化策略
2.1. BES算法
秃鹰是机会主义觅食者,擅长在飞行中捕猎鲑鱼. 在捕食过程中,首先在水面上空搜索猎物,在特定方向降落,选择某个区域开始搜索. 之后直接进入特定区域不断搜索,直到看到猎物. 一旦秃鹰发现猎物,即开始狩猎行为的最后阶段,逐渐下降并变换动作,高速接近后从水中捕获猎物. BES算法模拟了秃鹰捕食猎物的行为,分为选择区域、搜索和俯冲捕获3个阶段,构成一个协同序列,其数学模型如下.
1)选择区域阶段:秃鹰在搜索空间识别并选择最佳(食物数量最多)区域捕获猎物,数学模型描述为
式中:α为秃鹰位置控制参数,取值范围为(1.5, 2.0);r为随机数,取值范围为(0, 1.0);pbest为当前秃鹰最好的搜索位置;pmean为综合先后2次秃鹰更新位置的平均值;pi为种群中第i只秃鹰的位置;pi,new为更新后种群中第i只秃鹰的位置.
2)搜索阶段:秃鹰在搜索空间内搜索猎物,并在螺旋空间中按不同的方向移动,逐渐加大搜索范围. 螺旋飞行数学模型利用极坐标方程进行位置更新,该行为数学模型描述为
式中:θ(i)和r(i)分别为螺旋方程的极角与极径;ɑc和Rc为控制螺旋轨迹的参数,变化范围分别为(0, 5.0)和(0.5, 2.0);rand为(0, 1.0)的随机数;x(i)与y(i)表示极坐标中秃鹰位置,x(i)与y(i)取值范围均为(−1.0, 1.0). 秃鹰位置更新公式为
式中:pi+1为第i+1只秃鹰的位置.
3)俯冲捕获阶段:秃鹰从搜索空间的最佳位置快速俯冲飞向目标猎物,种群其他个体也同时向最佳位置移动并攻击猎物,运动状态用极坐标方程描述如下:
俯冲中秃鹰位置更新公式为
式中:
2.2. QO-BESCH算法
2.2.1. 疯狂捕猎机制
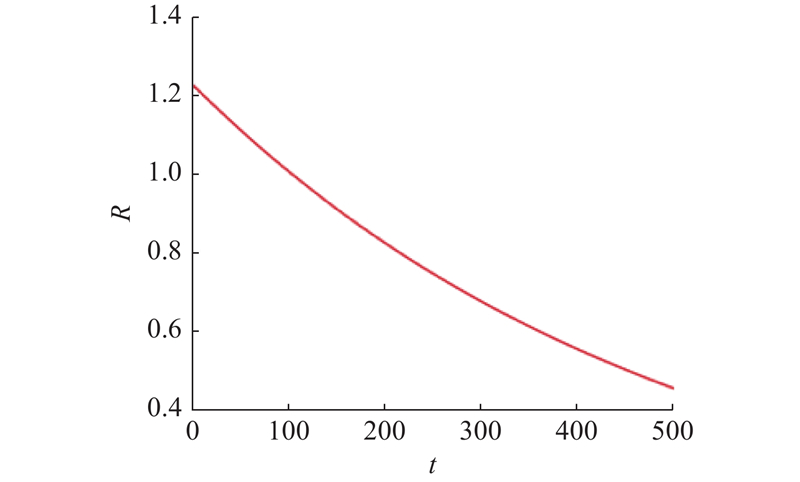
在BES俯冲捕获阶段,种群全部个体同时向“最佳”位置移动并攻击猎物,导致抓捕成功率低,影响算法搜索效率. 为了进一步提高全局能力,提出疯狂捕猎机制,设计逃逸因子R,其变化曲线如图2所示. 据此将秃鹰的攻击形式分为随机捕获、迂回包围和猛冲攻击,改善了耗时耗能的无差别单一攻击形式,能在较大程度上提升寻优性能.
图 2
如图2所示,在迭代初期猎物R较高,秃鹰采取迂回包围方式逐渐接近猎物伺机捕获;随着迭代时间增长,R逐渐衰减,在迭代中后期选取2/3的秃鹰以最快速度猛冲捕获猎物,其余秃鹰向猎物发起带有一定随机性的攻击行为. 该机制能在保证搜索范围最大程度合理的情况下,较快地完成探索最佳位置,有效避免算法陷入局部最优,提高寻优效率和收敛速度. 新的捕获阶段更新公式修订为
式中:χ为平衡搜索策略的质量函数,ω为运动形态参数,t为迭代次数, im为最大迭代次数,N为种群数量.
2.2.2. 融合动态自适应控制算子和柯西反向策略
BES在选择和搜索空间阶段,随机参数α与r控制的种群更新方式使得种群选择搜索空间时过早收敛,导致选定解空间中最优解质量差,影响后期算法的寻优精度. 因此,设计融合动态自适应控制算子和柯西反向策略. 在选择阶段,全局和局部寻优两者之间的平衡,是由α与r的综合作用决定的,若这2个参数值保持固定,会影响算法性能. 动态自适应控制算子在迭代前期值较大,有利于全局探索增加种群多样性;中后期逐渐衰减,向最优位置开发,充分挖掘其寻优潜能. 动态自适应控制算子在迭代的初期值较大,有利于增加种群多样性,从而促进全局探索能力;而在中后期算子逐渐减小,以便更好地向最优位置进行开发,充分挖掘其潜在的寻优性能. 算子表达式为
式中:Lmax=2.5,Lmin=2.0,t为当前迭代次数.
柯西反向策略[10]通过对问题当前解在解空间内进行反向学习,找到对应的柯西反向解,增加寻找最优解的概率. 首先,将此策略应用于选择阶段,能扩张探索空间,优化选择阶段种群质量;同时,在搜索阶段过程中采用柯西反向跳转方式,生成当前种群的反向种群,有利于跳出局部最优,加快算法的收敛速度. 假设在d维空间内,第i只秃鹰的位置为Pi=x(x1,x2,···,xd),其中xiϵ[ui,li],i=1, 2,···, d,ui和li为第i只秃鹰在各个维度的上边界和下边界. Pi的柯西反向点Qi定义为
在选择阶段种群更新后,选取适应度较高的n/2个秃鹰个体,并通过柯西反向对立学习获取其对立位置,修订新的更新公式:
式中:
同时,引入跳转率J,若搜索阶段rand [0,1]≤J [0,1],则为当前种群生成对应的柯西反向种群.
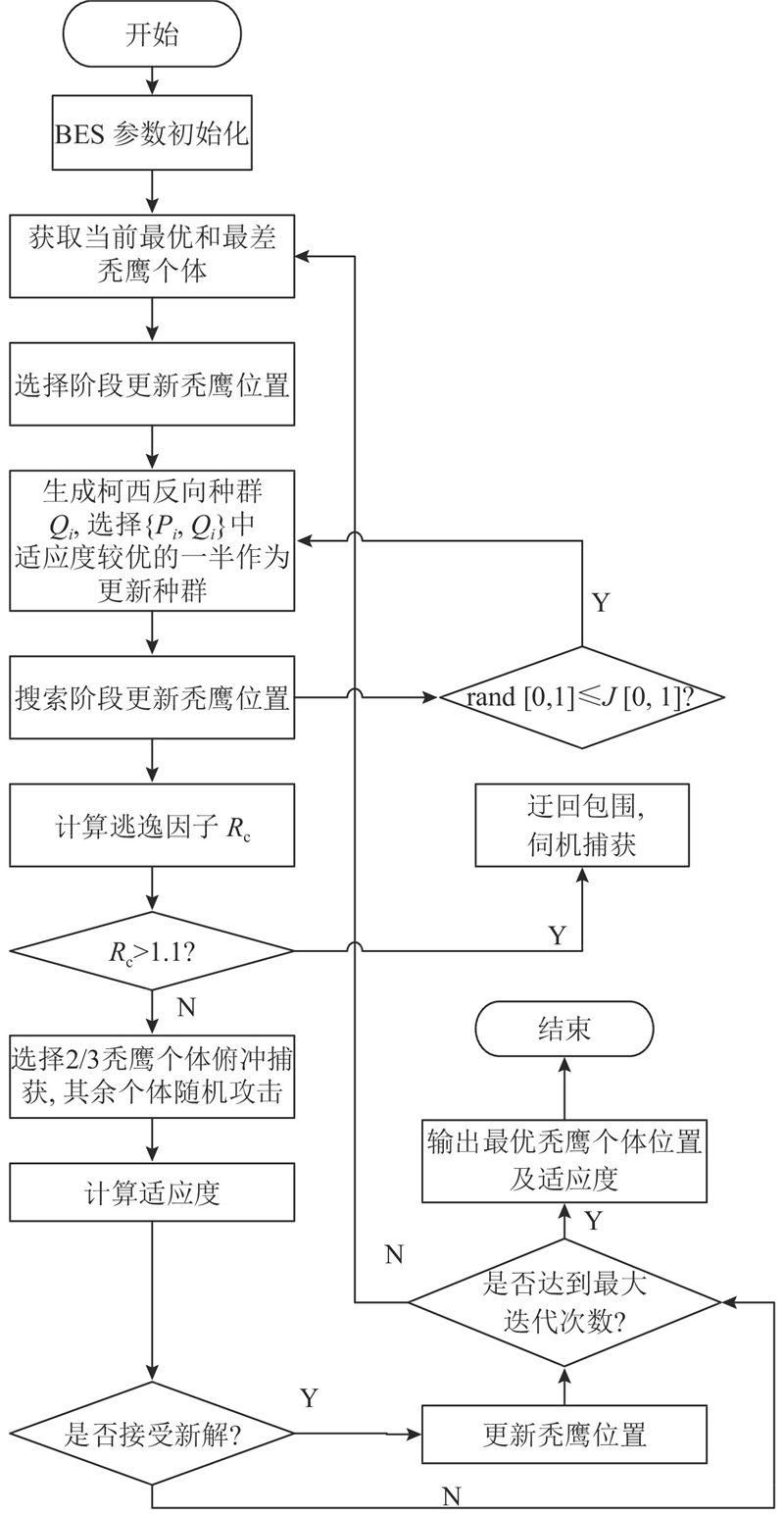
QO-BESCH算法流程图如图3所示.
图 3
2.3. 优化策略的测试
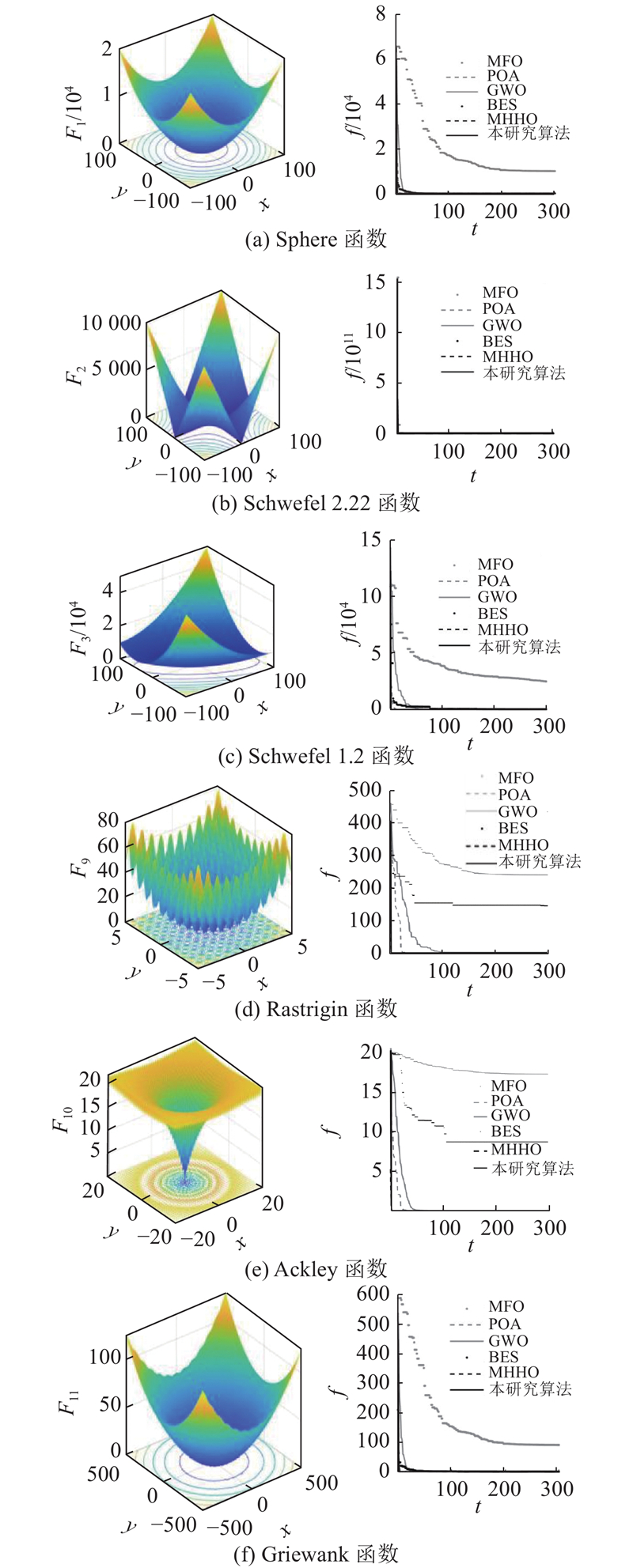
为了测试QO-BESCH的算法性能,选取飞蛾扑火[11] (moth-flame optimization,MFO)算法、鹈鹕优化算法[12] (pelican optimization algorithm,POA)、灰狼优化[13] (grey wolf optimizer, GWO)算法、基于多策略改进的哈里斯鹰优化[14] (multi-strategy Harris hawks optimization,MHHO)算法和秃鹰优化算法[10]5种群体智能算法进行对比. 实验硬件仿真平台为12th Gen Intel(R) Core(TM) i7-12700H 2.30 GHz 16.0 GB内存的计算机,软件平台为Matlab R2020b. 设置种群规模为50,迭代次数为300. 为了验证所提算法的有效性,选取6种具有代表性的测试函数进行性能评价. 各功能测试函数和三维参数空间如表1和图4所示. 图中,f为最优适应度;F1~F3为单峰值函数,用来测试收敛精度;F9~F11为多峰值函数,用来测试寻优能力,维度均为30. 在测试过程中,各个测试函数分别运行30次,得到如图4所示的适应度收敛曲线. 均值(Mean)与标准差(Std)如表2所示.
表 1 功能测试函数
Tab.1
| 函数 | 表达式 | 取值范围 |
| Sphere | | [−100,100]n |
| Schwefel 2.22 | | |
| Schwefel 1.2 | | [−100,100]n |
| Rastrigin | | [−5.12,5.12]n |
| Ackley | | [−32,32]n |
| Griewank | | |
图 4
表 2 各算法在测试函数上的均值和标准差性能对比
Tab.2
| 函数 | 算法 | Mean | Std |
| F1 | MFO | 3.025×103 | 4.308×103 |
| POA | 4.54×10−20 | 1.033×10−19 | |
| GWO | 5.42×10−5 | 1.23×10−4 | |
| BES | 8.77×10−1 | 1.993 953 | |
| MHHO | 4.90×10−79 | 1.114×10−78 | |
| 本研究算法 | 4.36×10−89 | 9.918×10−89 | |
| F2 | MFO | 5.98×10−10 | 1.360 |
| POA | 1.81×10−1 | 4.08×10−1 | |
| GWO | 1.41×10−28 | 3.197×10−28 | |
| BES | 4.96×10−1 | 3.227×10−1 | |
| MHHO | 1.31×101 | 1.908 5 | |
| 本研究算法 | 3.72×10−40 | 8.449×10−40 | |
| F3 | MFO | 2.148×103 | 1.3511×104 |
| POA | 2.30×10−19 | 5.23×10−19 | |
| GWO | 1.19×101 | 2.55×101 | |
| BES | 1.15×103 | 8.496×102 | |
| MHHO | 3.74×10−76 | 8.51×10−76 | |
| 本研究算法 | 9.28×10−112 | 2.1×10−111 | |
| F9 | MFO | 1.699×102 | 4.73×101 |
| POA | 0.00 | 0.00 | |
| GWO | 9.12 | 1.2×101 | |
| BES | 1.67×102 | 3.7×101 | |
| MHHO | 0.00 | 0.00 | |
| 本研究算法 | 0.00 | 0.00 | |
| F10 | MFO | 3.15×10−6 | 1.95×101 |
| POA | 1.25×10−1 | 1.27×10−1 | |
| GWO | 2.51×10−9 | 3.82×10−9 | |
| BES | 1.58 | 1.620 | |
| MHHO | 0.00 | 0.00 | |
| 本研究算法 | 0.00 | 0.00 | |
| F11 | MFO | 1.420 | 1.813 |
| POA | 4.59×10−2 | 9.375×10−2 | |
| GWO | 2.67×10−10 | 6.08×10−10 | |
| BES | 0.00 | 0.00 | |
| MHHO | −5.69×10−12 | 0.00 | |
| 本研究算法 | 0.00 | 0.00 |
将Mean这一性能指标进行Wilcoxon秩和检验实验,如表3所示. 表中,“+”、“−”和“=”分别表示,按照显著性水平, QO-BESCH的性能指标劣于、优于和近似于其他对比算法.
表 3 5种算法的Wilcoxon秩和检验
Tab.3
| 算法 | 测试函数 | |||||
| F1 | F2 | F3 | F9 | F10 | F11 | |
| MFO | − | − | − | − | − | − |
| POA | − | − | − | − | − | − |
| GWO | − | − | − | − | − | − |
| BES | − | − | − | − | − | = |
| MHHO | − | − | − | = | = | + |
由表2和图4可以看出,QO-BESCH在求解各函数时均表现出较优异的性能,不仅收敛速度快,能很快找到最优解,而且算法稳定性强. 由表3可以看出,QO-BESCH的性能在大多数测试函数上优于其他对比算法,只有在个别函数上近似或劣于BES和MHHO,这里根据No Free Lunch定理,并不能期望算法在所有测试函数都有最好的表现. 在F1~F3单峰测试函数中,本研究算法均取得最优均值和方差. 其中,F1为常用的单峰测试函数,本研究算法相较于BES,性能显著提升约178个量级. 在F9、F10测试函数中,本研究算法与多策略融合改进的MHHO算法寻优效果趋于一致,均能快速得到最优值. 其中,F9为较复杂的多峰测试函数,在测试过程中多数优化算法无法找到最优值或易陷入局部极值,尤其MFO对于F9的求解结果与实际最优解相差较大. 而本研究算法迭代约10次就能找到最优值,说明QO-BESCH在复杂交错环境中的寻优能力较强. 因此,6种函数的测试证明本研究算法可以提升原有BES的全局寻优能力,改进后的综合性能优于其他5种算法.
以上实验结果表明,QO-BESCH在测试函数上具有更强的竞争力,且收敛速度更高. 这里,QO-BESCH的高收敛性来源于设计的疯狂捕猎机制,后期根据猎物情况让秃鹰个体选择最适宜的捕猎方式更新位置,可以快速收敛到最佳值. 此外,本研究设计的融合动态自适应控制算子和柯西反向策略保证了全局选择阶段拥有较好的选择解空间的探索能力,算法一旦在选择和搜索阶段陷入局部最优,能快速跳出局部极值点,保证捕猎的成功率. 相比其他5种算法,QO-BESCH优势明显,效果更好.
3. 基于QO-BESCH的K均值互补迭代优化
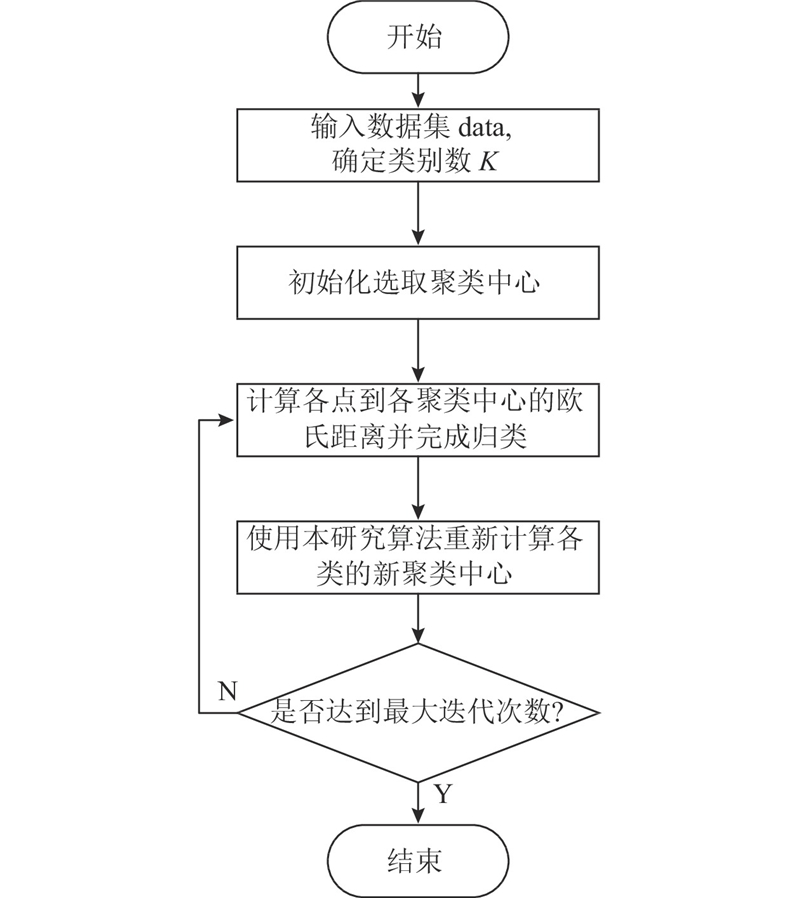
3.1. 算法步骤
结合QO-BESCH与KMC聚类算法的特点,提出基于疯狂捕猎的柯西反向秃鹰搜索算法的K均值互补迭代聚类优化算法(QO-BESCH-KMC). 利用QO-BESCH优化聚类中心,须引入数据的分类信息,在每个类别的秃鹰种群中通过QO-BESCH进行寻优操作,得到新的聚类中心. 利用类内平均距离定义QO-BESCH的种群适应度函数:
式中:d(xj,Cj)为种群到聚类中心的距离,
图 5
3.2. QO-BESCH-KMC性能测试及评价
表 4 UCI标准数据集特征
Tab.4
| 数据集 | Sam | dim | K | sam |
| Aggregation | 788 | 2 | 7 | 170、34、273、102、 130、45、34 |
| Iris | 150 | 4 | 3 | 50、50、50 |
| Cancer | 683 | 9 | 2 | 444、239 |
| Vowel | 871 | 3 | 6 | 72、89、172、 151、207、180 |
图 6
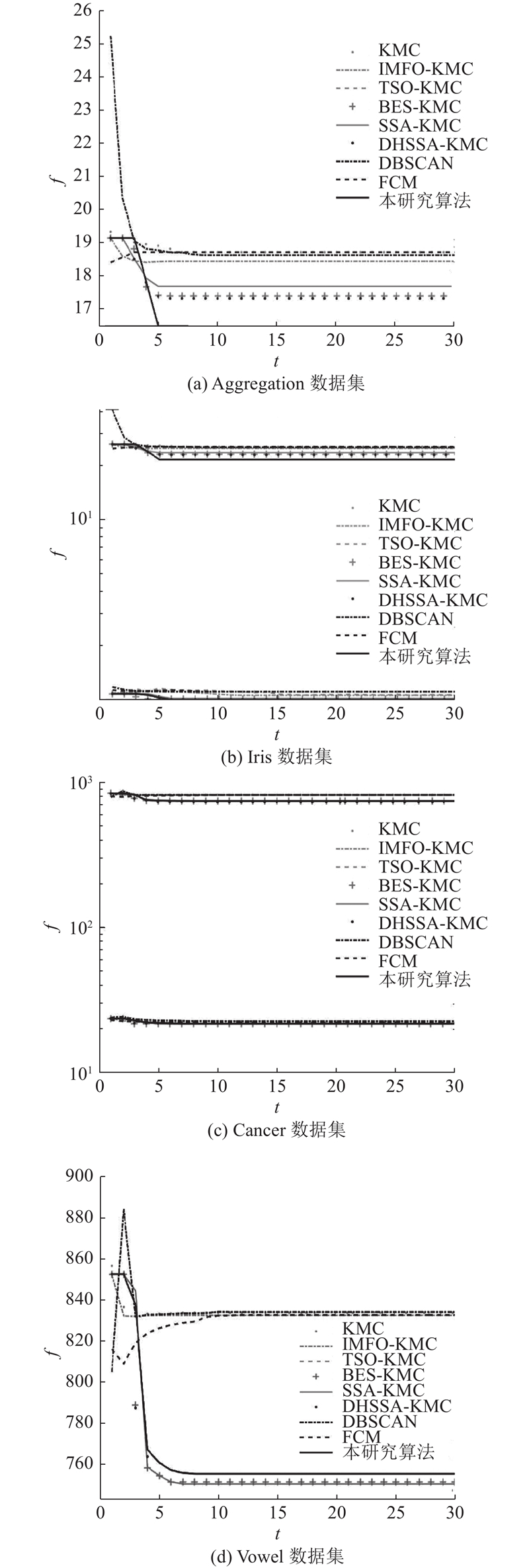
图 6 各聚类算法在不同数据集上的适应度变化曲线
Fig.6 Fitness curves of clustering algorithms on different data sets
表 5 各算法对4个数据集的评价指标
Tab.5
| 数据集 | 算法 | ACC/% | rand_index/% | ARI/% |
| Aggregation | KMC | 90.86 | 92.50 | 76.32 |
| IMFO-KMC | 90.99 | 91.28 | 72.31 | |
| TSO-KMC | 90.99 | 91.28 | 72.31 | |
| BES-KMC | 90.36 | 93.13 | 78.43 | |
| SSA-KMC | 87.94 | 92.45 | 76.20 | |
| DHSSA-KMC | 90.36 | 93.74 | 82.71 | |
| DBSCAN | 69.80 | 91.74 | 63.79 | |
| FCM | 79.18 | 92.73 | 72.43 | |
| 本研究算法 | 91.11 | 94.43 | 80.61 | |
| Iris | KMC | 90.00 | 77.24 | 40.88 |
| IMFO-KMC | 90.67 | 77.67 | 42.00 | |
| TSO-KMC | 90.37 | 77.34 | 41.11 | |
| BES-KMC | 91.33 | 80.63 | 52.86 | |
| SSA-KMC | 90.33 | 80.30 | 51.72 | |
| DHSSA-KMC | 91.20 | 80.44 | 52.68 | |
| DBSCAN | 89.33 | 77.97 | 43.02 | |
| FCM | 68.00 | 77.66 | 46.38 | |
| 本研究算法 | 92.67 | 81.61 | 53.11 | |
| Cancer | KMC | 96.78 | 85.72 | 71.72 |
| IMFO-KMC | 95.22 | 85.82 | 71.93 | |
| TSO-KMC | 95.90 | 82.12 | 65.00 | |
| BES-KMC | 96.49 | 85.36 | 71.01 | |
| SSA-KMC | 96.34 | 85.13 | 70.54 | |
| DHSSA-KMC | 96.63 | 85.58 | 71.44 | |
| DBSCAN | 94.06 | 82.39 | 62.65 | |
| FCM | 75.26 | 63.67 | 53.63 | |
| 本研究算法 | 96.90 | 85.32 | 71.96 | |
| Vowel | KMC | 59.70 | 80.47 | 34.56 |
| IMFO-KMC | 60.05 | 81.58 | 33.93 | |
| TSO-KMC | 62.34 | 81.97 | 31.89 | |
| BES-KMC | 57.75 | 78.24 | 30.29 | |
| SSA-KMC | 55.68 | 77.78 | 28.64 | |
| DHSSA-KMC | 56.95 | 78.20 | 29.63 | |
| DBSCAN | 58.44 | 80.16 | 32.26 | |
| FCM | 56.75 | 72.87 | 30.11 | |
| 本研究算法 | 60.28 | 82.23 | 35.60 |
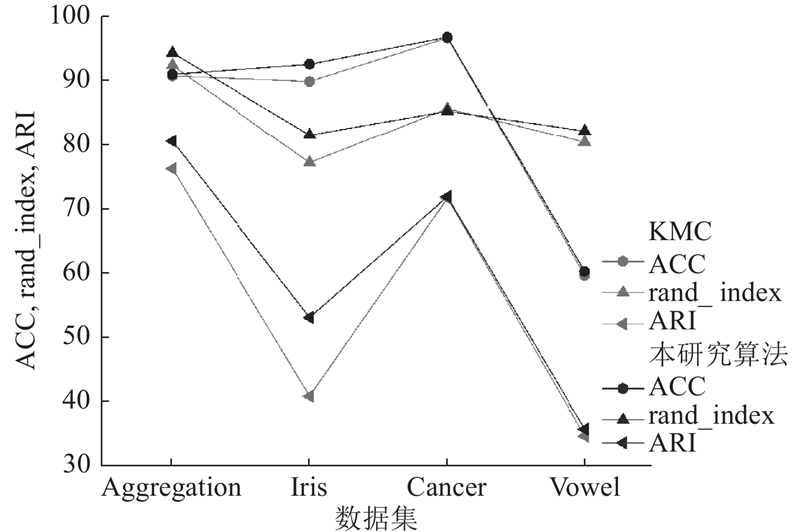
由图6可以看出,相比于KMC、其他5种基于群智能优化的KMC、FCM以及DBSCAN算法,本研究算法在低维数据集Aggregation、Vowel和高维数据集Iris、Cancer上的适应度曲线收敛值均优于其他8种算法的. 在低维Vowel数据集上,收敛速度刚开始较慢,但在迭代约12次时就跳出局部最优,收敛到全局最优位置. 在高维数据集Cancer上,本研究算法兼具迭代速度快和寻优效率高的特点,聚类效果显著提升. 由表5可以看出,在Aggregation数据集上,测得的ACC和rand_index分别高于其他算法0.12%~21.31%和0.69%~3.15%,ARI比DHSSA-KMC的降低2.10%,但整体性能最优;在Iris和Cancer数据集上,QO-BESCH-KMC各项指标相较于其他算法均有不同程度的提升,在聚类准确度、精确度和聚类结果上与真实情况较吻合;在Vowel数据集上,本研究算法兰德系数分别高于其他算法0.26%~4.45%,ARI分别高于其他算法1.04%~6.96%,相较于其他算法在各项指标上均具有明显优势.
综上,FCM、DBSCAN和KMC的稳定性相对较差、精度较低;基于其他群体智能算法优化的KMC互补迭代算法相比原KMC算法稳定性和精度都略有提升,而QO-BESCH-KMC设计了疯狂捕猎机制,引入了动态自适应控制算子和柯西反向策略,较高地提升了寻找聚类中心的成功率,显著提升了聚类准确度和精度,同时适应度变化较平稳.
3.3. QO-BESCH-KMC有效性测试
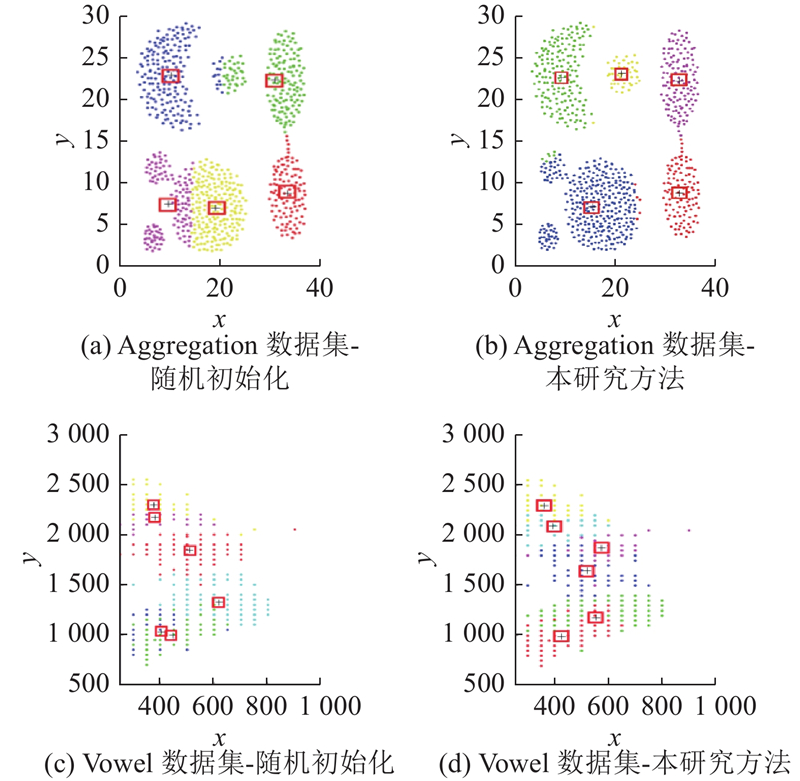
为了验证改进算法的有效性,消融实验分为3部分,分别对基于点云体元密度选择初始化聚类中心与随机初始化聚类中心、改进的秃鹰搜索算法与原秃鹰搜索算法以及传统KMC算法与QO-BESCH-KMC进行实验对比.
图 7
2)改进策略有效性测试. 利用上述UCI标准测试集中的Aggregation、Iris、Cancer、Vowel对本研究改进策略进行测试,将完全未改进算法记为BES-KMC ,将只引入动态自适应控制算子的算法记作BES-KMC1,将只引入柯西反向策略的算法记作BES-KMC2, 将只引入疯狂捕食策略的算法记为BES-KMC3,测试对比结果如图8所示.可以看出,BES-KMC1、BES-KMC2与BES-KMC3收敛曲线均优于原始的BES-KMC算法,表明引入动态自适应控制算子和柯西反向策略、疯狂捕猎机制都可以增加算法的收敛精度和稳定性;对于Aggregation数据集,BES-KMC1、BES-KMC2均可以跳出局部最优值,证明引入动态自适应控制算子和柯西反向策略可以避免函数求解时陷入局部最优,而BES-KMC3的收敛曲线更为平滑,收敛速度快,证明了引入疯狂捕食策略的有效性. 在算法前期,动态自适应控制算子和柯西反向策略可以保证秃鹰个体搜索过程中的全局性,在算法后期,通过疯狂捕食策略可以加速个体向最优解收敛. 因此,各个改进策略都可以有效提高算法的寻优能力,QO-BESCH-KMC的收敛精度和均匀性都有所提升.
图 8
图 9
图 9 本研究算法与KMC算法各评价指标对比
Fig.9 Comparison of evaluation indexes between proposed algorithm and KMC algorithm
4. 基于QO-BESCH优化的K均值互补迭代三维点云聚类
部分三维点云数据庞大复杂,若直接聚类处理,时间复杂度会大幅上升,因此,利用PCL点云库官网的体素滤波法处理.pcd格式点云文件,再通过QO-BESCH-KMC实现三维点云数据聚类分割.
4.1. PCL点云库体素滤波器处理
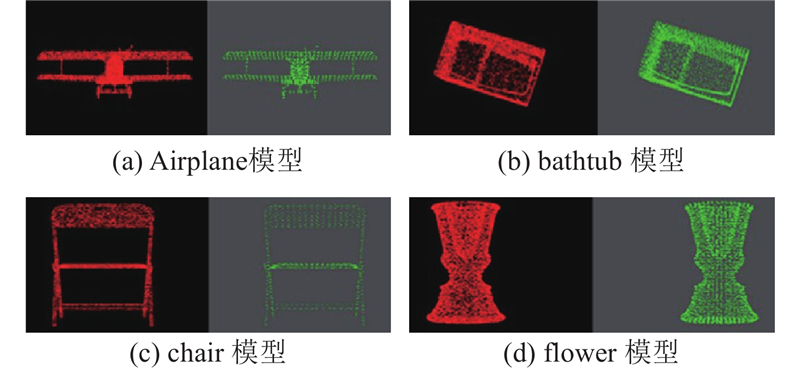
PCL点云库的体素滤波器是下采样的滤波器,在减少点云数据的同时保存点云的形状特征,为下一步聚类处理做准备. 为了满足PCL点云库配置要求,该实验在软件平台Visual Studio 2017和PCL1.8.1进行仿真测试,硬件平台与第3节所用平台保持一致. 实验采用的ModelNet40是由3D-CAD模型对象表示的含丰富注释的大型部件存储库,在点云分割任务中被广泛应用. 为了测试滤波效果,选取9个模型进行测试,结果如表6所示. 表中,nb、na分别为滤波前、后点云个数. 可以看出,体素滤波后的点云个数明显减少. 如图10所示为表6滤波前后对比图,选取4个模型展示,可以看出,各模型点云数据的稀疏稠密程度分布与原始的三维点云数据趋于一致,说明能更好地保存点云模型的细节特征,有利于下一步聚类操作.
表 6 体素滤波器滤波结果
Tab.6
| 模型 | nb | na |
| airplane | 10000 | 1435 |
| bathtub | 10000 | 3271 |
| bottle | 10000 | 1560 |
| bowl | 10000 | 5865 |
| chair | 10000 | 752 |
| curtain | 10000 | 1216 |
| lamp | 10000 | 1921 |
| flower_pot | 10000 | 2517 |
| desk | 10000 | 1990 |
图 10
4.2. 基于QO-BESCH优化的K均值互补迭代三维点云聚类
根据肘部原则指定类簇数K并根据体元密度初始化聚类中心;采用QO-BESCH-KMC不断迭代更新得到较优的K个聚类中心;根据欧氏距离划分三维点云数据为K个类簇.
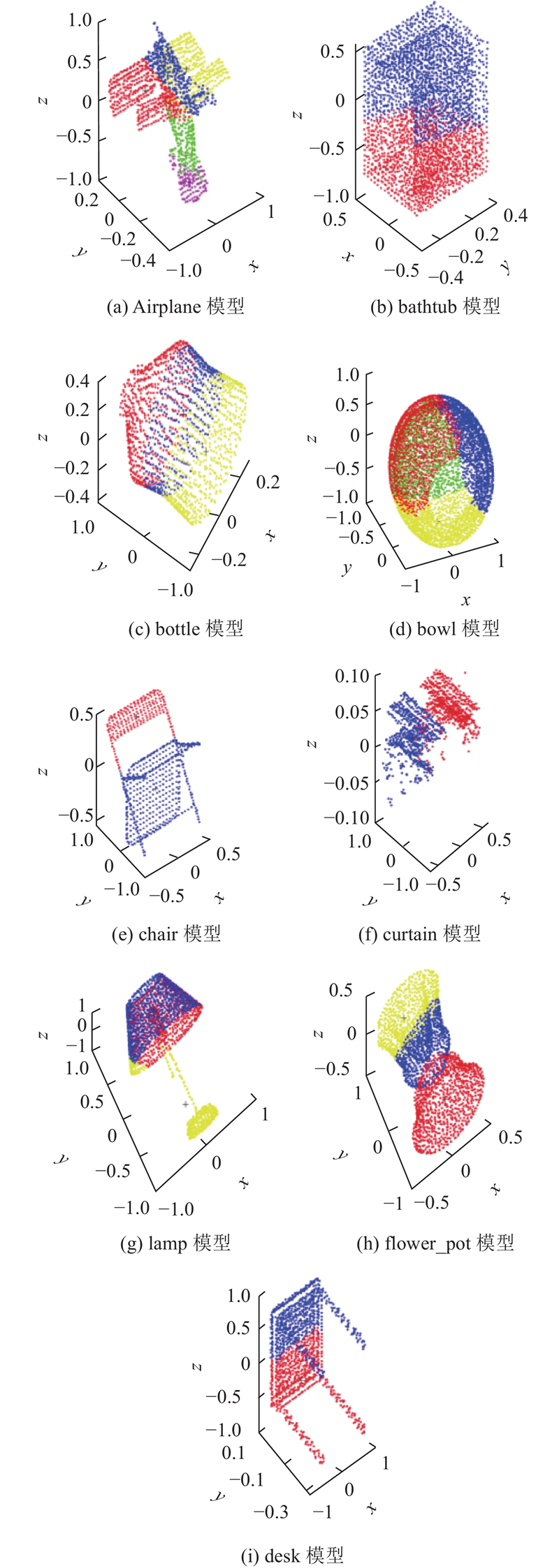
为了验证聚类效果,将QO-BESCH-KMC与KMC、BES-KMC、FCM和DBSCAN算法进行实验对比. 设定各算法实验迭代次数为20,内嵌群体智能算法迭代次数均为100,实验点云模型为4.1节中滤波后的9个模型,聚类结果如图11所示. 为了评价各算法的整体性能,分别使用表示类内紧密性的Scat指数和类间密度的Dens指数评价策略进行测评,指标越小表示聚类效果越好. 此外,将算法耗时作为评价指标,各算法的聚类性能评价结果如表7所示. 表中,tc为时耗,各实验数据由30次独立实验求均值得到. 可以看出,QO-BESCH-KMC在大部分模型中获得了最优的Scat指数和Dens指数,寻优性能最好,仅在curtain点云模型中效果较差. 当Scat指数和Dens指数这2个指标之和达到最小时,聚类一定为最优聚类,QO-BESCH-KMC在不同数据集上能够得到最好的Scat和Dens值的成功率为88.8%,进一步表明了本研究算法聚类效果的有效性. KMC的耗时与FCM、DBSCAN的大致耗时排序为FCM> DBSCAN > KMC,这与算法本身特性相关. FCM在不同模型上比KMC、DBSCAN的耗时多0.967~5.147 s,但相较于这2种算法,FCM的Scat和Dens之和仅在bowl模型中比其他2种算法降低了77.032 9,可见其精确度并无明显提升. KMC在速度最优的同时,兼具与这2种算法相当的精确度,因此选取KMC进行优化改进. 本研究算法与KMC、BES-KMC相比,因算法复杂度的不断提升以及群体智能依赖迭代次数以提高寻优精度,计算量大,数据更加细腻,因此速度稍慢. 耗时排序为本研究算法>BES-KMC>KMC,本研究算法在不同模型上比这2种算法耗时多1.028~5.543 s,本研究算法以稍高的时耗获得更优的聚类效果,但其Scat和Dens之和在不同模型上降低了24.024 6~90.549 5,精度显著提升,算法整体在精度上具有优势. 由图11可以看出QO-BESCH-KMC在各个模型上均取得了较理想的分割结果,几乎无欠分割和混分割现象,且可以看出明显部位的细分割. Airplane模型被划分为5部分,分别为头部、中部、尾部、左翼和右翼;bottle模型被清晰地划分为瓶颈、瓶身、瓶底3部分;curtain模型粗划分为左帘和右帘,同一颜色划分区域内的点云拥有相似的特征 ,有利于为后期的识别或更多扩展做好基础工作,能够满足实际应用. 同时,bowl模型虽得到较为清晰的分割,但分割效果存在一定改进之处.
表 7 不同算法对9个点云模型聚类的评价指标
Tab.7
| 模型 | 算法 | Scat | Dens | tc/s | 模型 | 算法 | Scat | Dens | tc/s | 模型 | 算法 | Scat | Dens | tc/s | ||
| Airplane | KMC | 0.271 4 | 164 | 2.62 | bowl | KMC | 0.271 4 | 164 | 2.62 | lamp | KMC | 0.813 7 | 373 | 2.99 | ||
| BES-KMC | 0.263 3 | 161 | 4.74 | BES-KMC | 0.263 3 | 161 | 4.74 | BES-KMC | 0.329 4 | 317 | 4.01 | |||||
| DBSCAN | 0.271 2 | 219 | 2.56 | DBSCAN | 0.271 2 | 219 | 2.60 | DBSCAN | 0.322 5 | 577 | 2.46 | |||||
| FCM | 0.265 2 | 202 | 4.45 | FCM | 0.265 2 | 202 | 4.45 | FCM | 0.852 2 | 544 | 3.99 | |||||
| 本研究算法 | 0.206 3 | 124 | 4.80 | 本研究算法 | 0.206 3 | 124 | 4.80 | 本研究算法 | 0.264 2 | 283 | 4.02 | |||||
| bathtub | KMC | 0.518 2 | 321 | 2.98 | chair | KMC | 0.412 7 | 116 | 1.30 | flower_pot | KMC | 0.171 4 | 212 | 3.33 | ||
| BES-KMC | 0.544 2 | 310 | 4.01 | BES-KMC | 0.410 5 | 122 | 2.40 | BES-KMC | 0.166 6 | 199 | 5.37 | |||||
| DBSCAN | 0.517 7 | 344 | 2.65 | DBSCAN | 0.410 2 | 129 | 0.93 | DBSCAN | 0.167 0 | 103 | 2.83 | |||||
| FCM | 0.560 3 | 425 | 3.92 | FCM | 0.461 7 | 163 | 2.27 | FCM | 0.165 6 | 206 | 5.29 | |||||
| 本研究算法 | 0.517 7 | 309 | 4.14 | 本研究算法 | 0.388 9 | 106 | 2.63 | 本研究算法 | 0.169 8 | 215 | 5.42 | |||||
| bottle | KMC | 0.293 6 | 222 | 2.62 | curtain | KMC | 0.771 8 | 314 | 2.38 | desk | KMC | 0.1960 | 190 | 2.55 | ||
| BES-KMC | 0.269 6 | 156 | 4.84 | BES-KMC | 0.7680 | 367 | 4.45 | BES-KMC | 0.1860 | 165 | 4.56 | |||||
| DBSCAN | 0.293 6 | 134 | 2.42 | DBSCAN | 0.7680 | 324 | 2.38 | DBSCAN | 0.1860 | 165 | 2.42 | |||||
| FCM | 0.253 5 | 166 | 4.74 | FCM | 0.790 6 | 524 | 4.40 | FCM | 0.182 8 | 212 | 4.48 | |||||
| 本研究算法 | 0.263 6 | 141 | 4.86 | 本研究算法 | 0.756 4 | 312 | 4.61 | 本研究算法 | 0.144 4 | 114 | 4.58 |
图 11
图 11 本研究算法在不同数据集上的聚类分割效果
Fig.11 Clustering segmentation effect of proposed algorithm on different data sets
5. 结 语
提出基于QO-BESCH的K均值互补迭代聚类优化方法. 在BES中设计疯狂捕猎机制,提升寻找聚类中心的成功率;引入动态自适应控制算子和柯西反向策略跳出局部最优,提高全局搜索能力;将QO-BESCH与KMC算法互补迭代聚类,提高鲁棒性和聚类精度. 将QO-BESCH-KMC应用于ModelNet40点云数据集聚类,在定性和定量上证明了算法的优越性,应用价值明显.
本研究采用手肘法确定K,但此方法在效率方面有待改进;本研究算法一定程度上耗时较多,但聚类精度大大提升,今后将在提升算法精度的同时关注效率.
参考文献
基于深度学习的点云分割研究进展分析
[J].DOI:10.11999/JEIT210972 [本文引用: 1]
Analysis on the progress of point cloud segmentation based on deep learning
[J].DOI:10.11999/JEIT210972 [本文引用: 1]
应用于无人驾驶车辆的点云聚类算法研究进展
[J].DOI:10.16507/j.issn.1006-6055.2020.12.025 [本文引用: 1]
Research progress of point cloud clustering algorithm applied to driverless vehicles
[J].DOI:10.16507/j.issn.1006-6055.2020.12.025 [本文引用: 1]
Improved CNN-based indoor localization by using RGB images and DBSCAN algorithm
[J].DOI:10.3390/s22239531 [本文引用: 1]
Application of FCM clustering algorithm in digital library management system
[J].DOI:10.3390/electronics11233916 [本文引用: 1]
基于改进自适应k均值聚类的三维点云骨架提取的研究
[J].DOI:10.16383/j.aas.c200284 [本文引用: 1]
Research on 3D point cloud skeleton extraction based on improved adaptive k-means clustering
[J].DOI:10.16383/j.aas.c200284 [本文引用: 1]
引入改进蝠鲼觅食优化算法的水下无人航行器三维路径规划
[J].
Underwater UAV 3D path planning with improved manta ray foraging optimization algorithm
[J].
引入改进飞蛾扑火的K均值交叉迭代聚类算法
[J].DOI:10.7652/xjtuxb202009003 [本文引用: 1]
Introducing an improved K-means cross iterative clustering algorithm
[J].DOI:10.7652/xjtuxb202009003 [本文引用: 1]
K-means clustering algorithm based on memristive chaotic system and sparrow search algorithm
[J].DOI:10.3390/sym14102029 [本文引用: 2]
Novel meta-heuristic bald eagle search optimisation algorithm
[J].
一种基于交叉选择的柯西反向鲸鱼优化算法
[J].DOI:10.11809/bqzbgcxb2020.08.026 [本文引用: 2]
A Cauchy inverse whale optimization algorithm based on cross selection
[J].DOI:10.11809/bqzbgcxb2020.08.026 [本文引用: 2]
Moth-flame optimization algorithm for efficient cluster head selection in wireless sensor networks
[J].
Pelican optimization algorithm: a novel nature-inspired algorithm for engineering applications
[J].DOI:10.3390/s22030855 [本文引用: 1]
A novel clustering algorithm by clubbing GHFCM and GWO for microarray gene data
[J].
多策略改进哈里斯鹰优化算法
[J].DOI:10.19304/j.cnki.issn1000-7180.2021.07.004 [本文引用: 1]
Multi strategy improved Harris Hawk optimization algorithm
[J].DOI:10.19304/j.cnki.issn1000-7180.2021.07.004 [本文引用: 1]
DHSSA优化的K均值互补迭代车型信息数据聚类
[J].DOI:10.19562/j.chinasae.qcgc.2022.05.006 [本文引用: 1]
DHSSA optimized K-means complementary iterative model information data clustering
[J].DOI:10.19562/j.chinasae.qcgc.2022.05.006 [本文引用: 1]