目前电池SOC预测方法主要包括模型实验法和数据驱动法. 在模型实验法中,来鑫等[7]提出一种基于粒子群优化算法的OCV曲线优化方法,相比传统HPPC测试法具有更高的全局精度. 罗勇等[8]根据电池组充放电实验,得出不同电池参数的电池容量修正因子,提出带容量修正的安时积分法. 寇发荣等[9]利用人工蜂群算法和随机森林优化算法分别实现电池模型参数辨识和SOC估计. 孙国强等[10]以磷酸铁锂电池为研究对象,提出一种基于分数阶阻抗模型的锂电池SOC估计方法. 孙金磊等[11]提出基于FFLRS-EKF联合算法的电池SOC估计方法,利用FFLRS修正电池模型,通过EKF算法修正电池模型估计的SOC. Schwunk等[12]基于较好参数的综合性电池模型,利用粒子滤波描述电池的外部特性,显著提升SOC的预测精度. 模型实验法在测量实验的基础上建立电池模型,一定程度上能表征电池内、外部特性,但是预测精度依赖于电池模型实验的准确性. 模型实验法偏重于电池内部机理及物理特征[13-14],现有研究未考虑电动公交车在实际行驶过程中的电池状态、车辆行驶状态、行驶工况因素.
数据驱动法仅依靠系统输入与输出间的映射关系即可建立SOC预测模型,无需针对不同电池工作环境来建立不同参数的电池模型. 赵轩等[15]提出基于广义生长剪枝径向基函数神经网络的多参数纯电动客车蓄电池的SOC预测模型. 鲍伟等[16]基于电动公交车稀疏采样数据,采用支持向量机算法与贝叶斯优化方法来建立电池SOC预测方法. 电池荷电状态包含时间特征,可将其视为特殊的时间序列[17]. 在深度神经网络架构中,循环神经网络被广泛应用于时间序列预测[18-19],在时间序列预测上较为突出. Chemali等[20]在未使用任何电池模型、滤波器等推理系统的情况下,利用LSTM-RNN预测电池SOC. 现有电池SOC时间序列预测算法难以处理高维数据,且在长序列预测需求下,模型预测精度有待提升.
结合电池状态、车辆行驶状态、行驶工况对SOC的影响,本研究提出一种电动公交车电池荷电状态的序列到序列(sequence to sequence,Seq2Seq)预测模型. 在深度学习框架下,构建WN-Seq2Seq模型分析高维输入特征与预测SOC序列的关系,为电动公交车能耗控制策略、安全管理提供合理且可靠的参数决策支持.
1. 数据来源与特征分析
1.1. 数据采集及内容
表 1 电动公交车的实际行驶数据样例
Tab.1
| 数据名称 | 数值 |
| 采样时间 | 2021−03−22 12:29:58 |
| 经度/(°) | 120.113 67 |
| 纬度/(°) | 30.296 56 |
| 车速/(km·h−1) | 11.796 875 |
| 电机转速/(r·min−1) | 1 435.0 |
| 总行驶里程/km | 113 709.3 |
| 电池组总电流/A | 289.6 |
| 电池组总电压/V | 494.0 |
| 电池组平均温度/℃ | 21.5 |
| SOC/% | 69.8 |
式中:
1.2. 特征分析
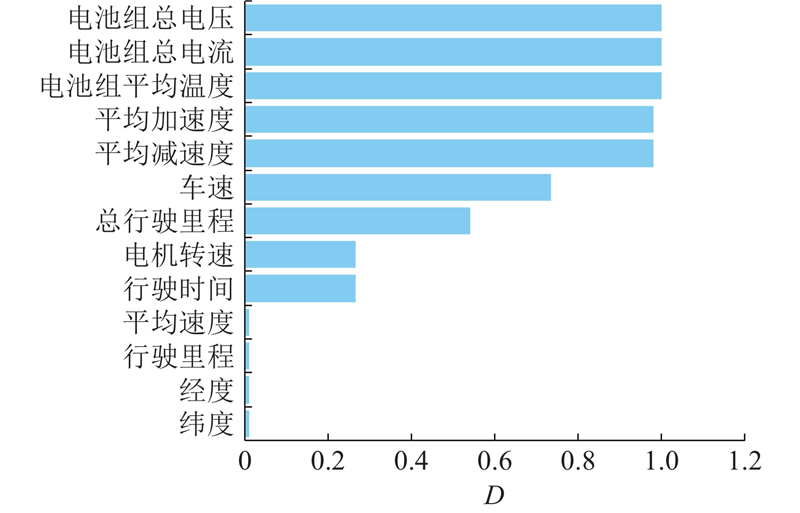
单一的影响因素无法充分反应电池在实际运行中的特性,因此传统电池SOC预测方法将电池状态(电压、电流、电池温度特征)作为输入. 电动公交车作为完整的电力系统,在实际行驶过程中电池也受车辆行驶状态、行驶工况等因素影响. 本研究基于电动公交车的实际行驶数据,在电池状态基础上引入车辆行驶状态和行驶工况,建立多维度、多场景的电池数据库,提升电动公交车电池SOC预测模型在实际运行场景的准确性及鲁棒性.
电池状态包括SOC、电池组总电流、电池组总电压、电池组平均温度. 电池组的电流、电压与SOC明显相关;电池温度也会影响电池组内部的化学反应;同时SOC在时间序列上呈高度自相关性. 在预测
表 2 电动公交车电池的SOC影响因素特征表
Tab.2
| 类型 | 特征名称 |
| 电池状态 | SOC/% |
| 电池组总电压/V | |
| 电池组总电流/A | |
| 电池组平均温度/℃ | |
| 车辆行驶状态 | 车速/(km·h−1) |
| 电机转速/(r·min−1) | |
| 总行驶里程/km | |
| 经度/(°) | |
| 纬度/(°) | |
| 行驶工况 | 平均加速度/(m·s−1) |
| 平均减速度/(m·s−1) | |
| 平均速度/(m·s−1) | |
| 行驶里程/km | |
| 行驶时间/s |
图 1
表 3 SOC预测模型的输入特征
Tab.3
| 特征分类 | 输入特征 |
| 电池状态 | SOC/% |
| 电池组总电压/V | |
| 电池组总电流/A | |
| 电池组平均温度/℃ | |
| 车辆行驶状态 | 车速/(km·h−1) |
| 总行驶里程/km | |
| 行驶工况 | 平均加速度/(m·s−1) |
| 平均减速度/(m·s−1) |
2. 电动公交车电池SOC预测
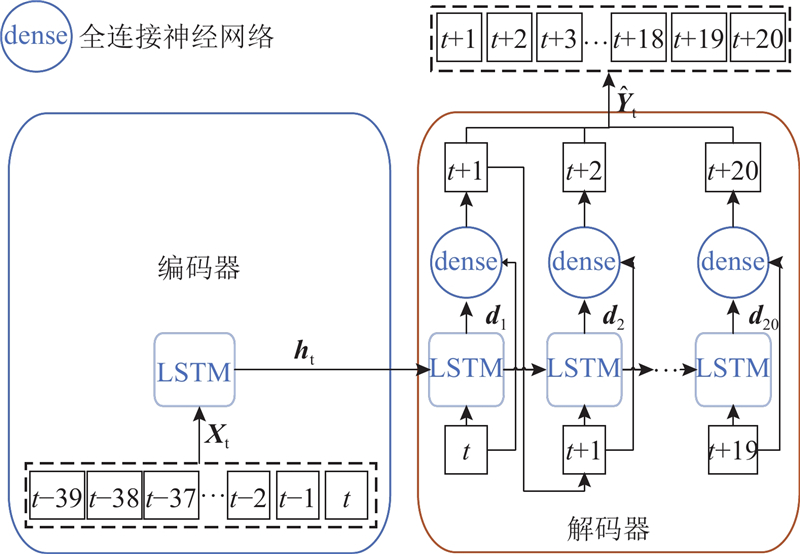
2.1. Seq2Seq模型
Seq2Seq的编码器-解码器模型将
图 2
2.2. WN-Seq2Seq模型
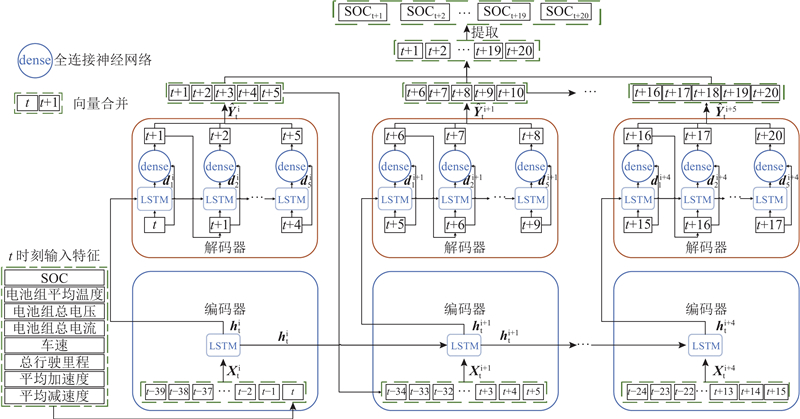
在Seq2Seq的编码器-解码器模型结构上融合WaveNet循环结构,将未来时间段的复杂预测序列拆分为多个简单的局部序列. 根据输入序列循环使用单个编码器-解码器结构预测各局部序列,同时在各编码器间传递记忆信息,提高循环预测过程中高维输入序列与局部预测序列的长期记忆信息传递能力,从而提高模型的预测精度.
WN-Seq2Seq模型在Seq2Seq的编码器-解码器结构基础上融合WaveNet循环结构,将长度为
图 3
图 3 WN-Seq2Seq的编码器-解码器模型结构
Fig.3 Encoder-decoder model structure of WN-Seq2Seq
式中:
第
式中:
每个
WN-Seq2Seq模型循环调用单个编码器-解码器最终获得预测序列长度为
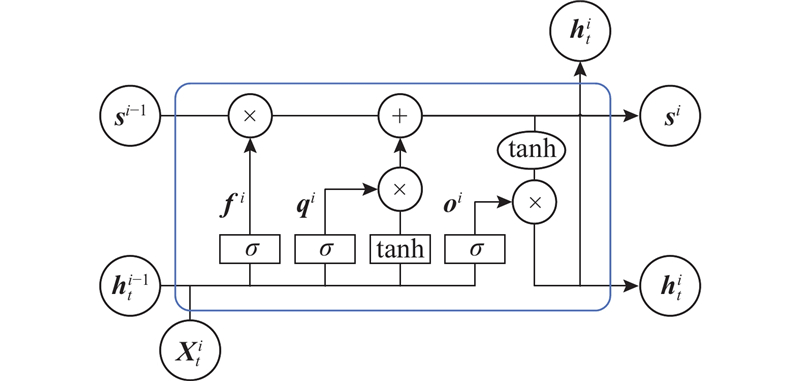
2.3. 编码器
将
图 4
编码器的更新过程为
式中:
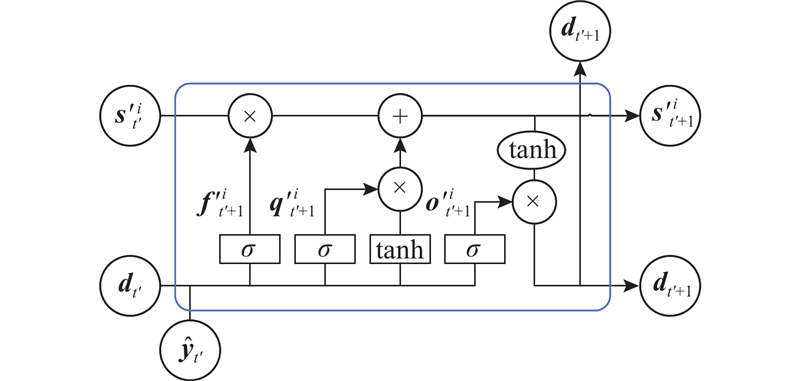
2.4. 解码器
为了得到预测序列
图 5
解码器的更新过程为
式中:
最后通过全连接网络dense将解码器预测的隐层状态
式中:
3. 实验验证与结果分析
3.1. 数据来源与实验设置
实验数据来源于杭州市公交公司的比亚迪商用车智能服务系统中4辆电动公交车实际行驶数据(SOC、电池组电压、电池组电流、电池组平均温度、平均加速度、平均减速度、车速、总行驶里程),各车行驶路线为290路、193路、4B路、188路. 数据采样时间为2021−3−1—2022−2−29,数据采样频率为0.3 Hz,有效数据总量共420万条. 将3辆电动公交车(290路、4B路、188路)4个季节不同月份的实际行驶数据作为训练集进行模型训练. 一辆公交车(193路)4个月的实际行驶数据(1月、4月、7月、10月)作为模型测试集,验证WN-Seq2Seq模型的预测效果,训练集的数据量为2 656 467条,测试集的数据量为199 961条. 对原始电动公交车进行实际行驶数据预处理. 预处理内容包括异常值处理、缺失值补全和归一化. 异常值处理方法为3
实验基于PyTorch深度学习框架搭建WN-Seq2Seq模型,硬件配置为:Ryzen 7 4800H CPU,RTX 2060,16 GB内存. WN-Seq2Seq模型训练采用余弦退火和自适应矩估计(adaptive moment estimation,Adam)[23]优化器,训练的学习率从0.001开始,选择均方误差作为训练损失函数,输入序列步长
3.2. 各模型预测结果与分析
验证WN-Seq2Seq模型预测电动公交车电池SOC的准确性、可靠性及鲁棒性. 将该模型与传统时间序列预测模型进行对比,并分析在不同隐层状态维度的预测结果. 对比分析隐层状态维度对WN-Seq2Seq预测结果的影响,实验结果如表4所示. 随着LSTM隐层状态维度增加,预测准确度也在提升,也使模型参数增多,引发过拟合的现象. 对比实验结果,当维度从32增加到64时,预测精度有所增长,模型预测误差降低16%,但是从64增加到128时预测精度略有下降. 由此说明简单的增加隐层状态维度无法显著增加WN-Seq2Seq模型的预测精度.
表 4 不同隐层状态维度WN-Seq2Seq预测的评价结果
Tab.4
| 隐层状态维度 | MSE/% | MAE/% | MAPE/% |
| 32 | 0.609 | 0.575 | 0.765 |
| 64 | 0.505 | 0.479 | 0.656 |
| 128 | 0.508 | 0.484 | 0.663 |
表 5 各模型预测的结果评价值和计算时间
Tab.5
| 模型名称 | MSE/% | MAE/% | MAPE/% | MCT/s |
| LSTM | 1.163 | 0.709 | 0.960 | 0.001 |
| BILSTM | 1.090 | 0.657 | 0.886 | 0.002 |
| Seq2Seq | 0.698 | 0.549 | 0.757 | 0.012 |
| WN-Seq2Seq | 0.505 | 0.479 | 0.656 | 0.017 |
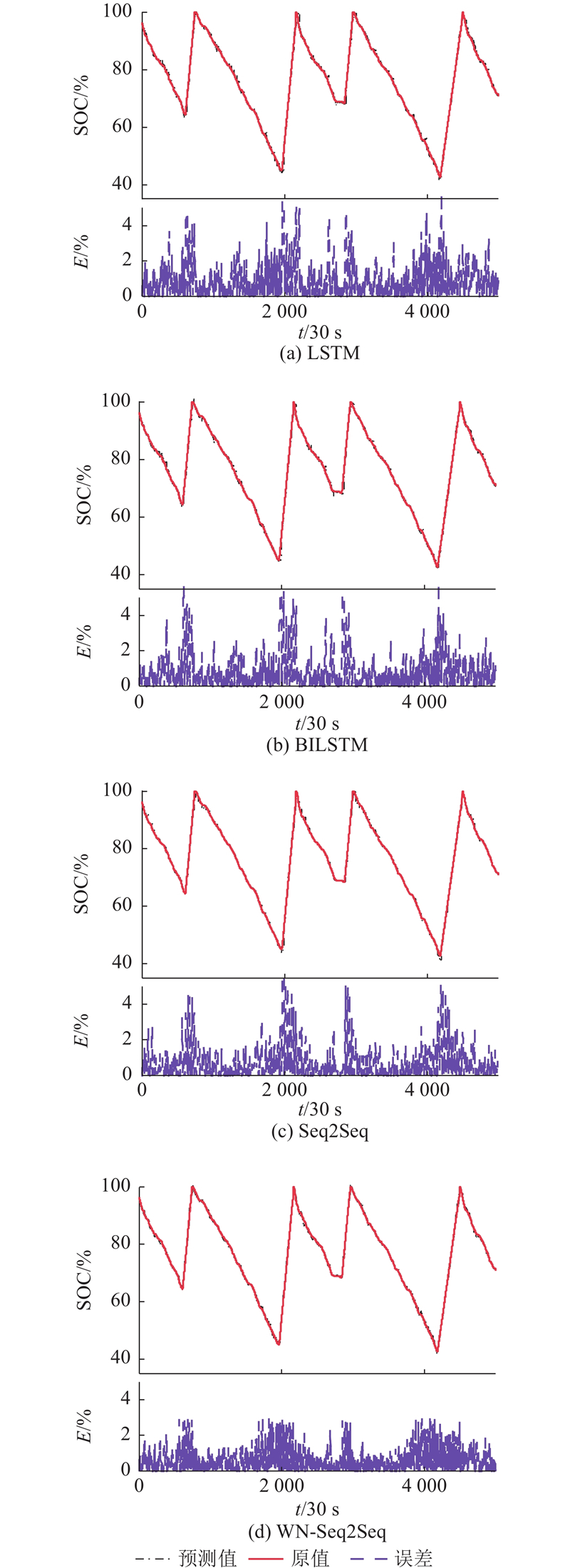
图 6
图 6 不同模型预测SOC曲线与误差的对比
Fig.6 Comparison of SOC curves and errors predicted by different models
WN-Seq2Seq模型的算计时间为0.017 s,相比其他模型慢了0.005~0.016 s. 由于数据采集频率为0.3 Hz,WN-Seq2Seq模型计算时间满足实际需求. 从图6中可以看出,预测过程中所有模型在充电和放电的切换过程中误差E都有所增大,随后在充电和放电的过程中逐渐稳定. 相比传统时间序列预测模型,WN-Seq2Seq在充放电切换过程时的预测误差变化相对较小. 在充放电过程中,传统时间序列预测模型捕捉SOC值突变的能力和真实值的预估能力较差,预测过程中易出现自偏离现象,而WN-Seq2Seq模型在预测过程中能够有效对自偏离现象进行调整,从而提高预测真实SOC值的能力.
3.3. 各特征预测结果与分析
分析模型引入不同特征的预测效果,展开消融实验. WN-Seq2Seq模型加入不同特征后评价指标如表6所示. 在电池状态的基础上分别引入车辆行驶状态或行驶工况,模型预测精度和稳定性都有所提升. 加入车辆行驶状态和行驶工况,模型预测效果显著提高,评价指标MSE、MAE、MAPE分别为0.505%、0.479%和0.656%,相比其他特征类别MAE与MAPE降低了9%~20%,MSE降低了20%~21%. 电动公交车在实际行驶过程中,车辆行驶状态及行驶工况对电池SOC有一定程度影响. 引入的车辆行驶状态和行驶工况有效地提升模型预测预测准确性及稳定性,引入车辆行驶状态和行驶工况后模型计算时间为0.017 s,与其他特征类别的模型计算时间差距较小.
表 6 不同特征类别WN-Seq2Seq预测的评价结果
Tab.6
| 特征类别 | MSE/% | MAE/% | MAPE/% | MCT/s | 特征类别 | MSE/% | MAE/% | MAPE/% | MCT/s | |
| 电池状态 | 0.683 0 | 0.599 0 | 0.817 0 | 0.014 5 | 电池状态+行驶工况 | 0.562 0 | 0.534 0 | 0.723 0 | 0.016 0 | |
| 电池状态+车辆 行驶状态 | 0.546 0 | 0.529 0 | 0.721 0 | 0.014 9 | 电池状态+车辆行驶 状态+行驶工况 | 0.505 0 | 0.479 0 | 0.656 0 | 0.017 0 |
3.4. 单个充放电周期内预测结果与分析
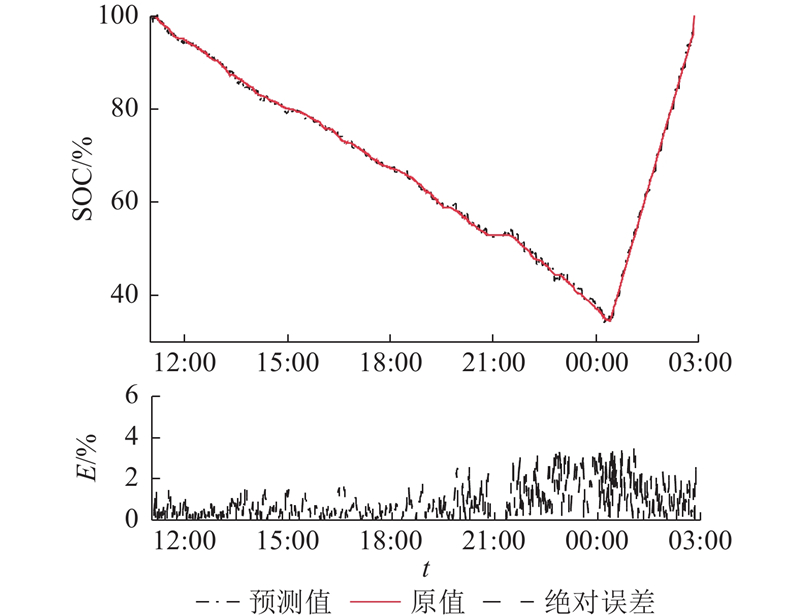
分析WN-Seq2Seq模型在单个充放电周期内的预测效果,结果如图7所示. 模型在放电过程预测的效果明显优于充电过程,主要原因是放电阶段车辆行驶状态特征与工况特征提高了模型的预测效果,而在充电阶段车辆处于静止状态,车辆行驶特征与工况特征未发挥作用. 同时当SOC低于50%时,SOC的下降的速率加快增加了模型预测的难度从而导致模型预测精度有所下降.
图 7
图 7 单个充放电周期内WN-Seq2Seq的预测曲线与误差
Fig.7 Prediction curve and error of WN-Seq2Seq in single charge-discharge cycle
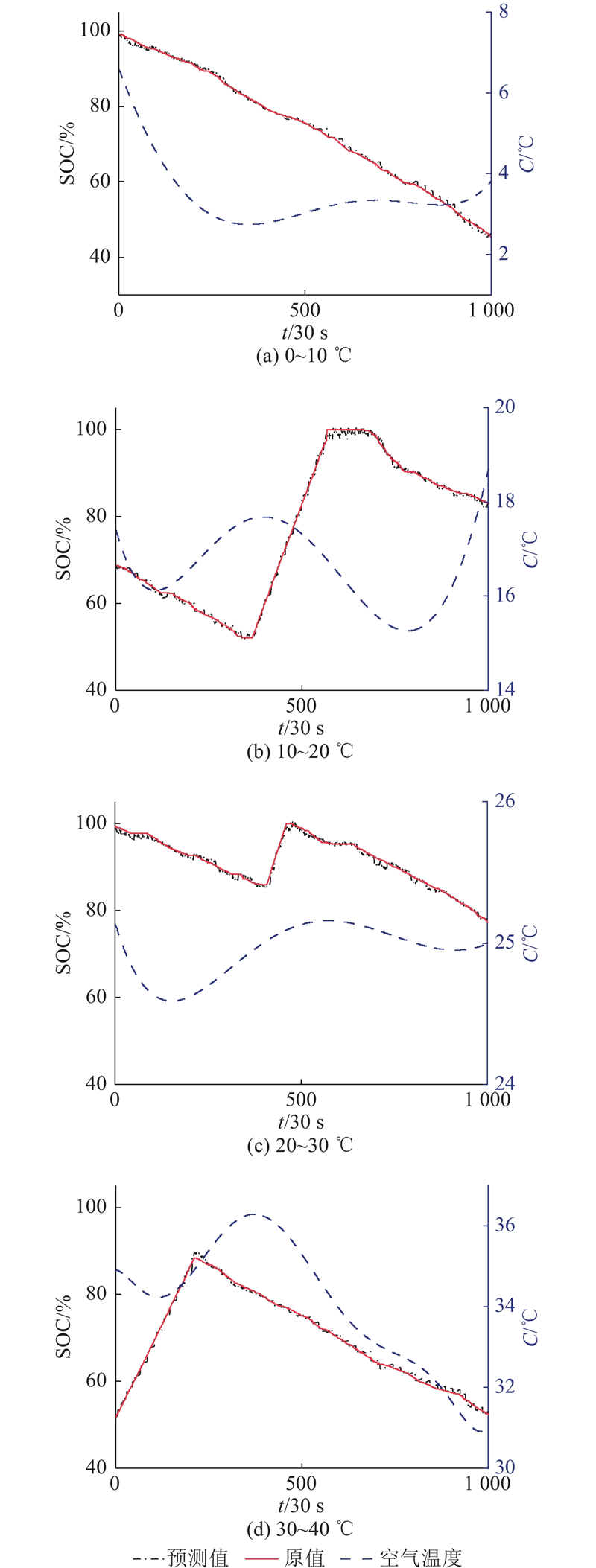
3.5. 各温度区间模型预测结果与分析
表 7 不同温度区间WN-Seq2Seq预测的评价结果
Tab.7
| 温度区间/℃ | MSE/% | MAE/% | MAPE/% |
| 0~10 | 0.489 | 0.464 | 0.709 |
| 10~20 | 0.549 | 0.499 | 0.659 |
| 20~30 | 0.524 | 0.496 | 0.588 |
| 30~40 | 0.469 | 0.461 | 0.687 |
图 8
图 8 不同温度区间WN-Seq2Seq预测SOC曲线的对比
Fig.8 Comparison of WN-Seq2Seq predicted SOC curves in different temperature ranges
4. 结 论
(1)为了充分考虑电动公交车电池在实际驾驶场景中的影响因素,在电池状态的基础上引入车辆行驶状态和行驶工况预测电池SOC,实验结果表明加入特征后模型预测精度有所提高.
(2)融合Seq2Seq与WaveNet循环结构,建立WN-Seq2Seq模型. 实验结果表明,相比传统时间序列预测模型WN-Seq2Seq模型的预测准确性和稳定性更优.
(3)不同温度下电池实际容量具有差异性,分析WN-Seq2Seq在不同温度区间的预测效果,结果表明模型在各温度区间下都具有优秀的预测效果.
(4)所提的电动公交车电池荷电状态WN-Seq2Seq预测方法能将预测的SOC与BMS实际上传的SOC进行相互佐证,对电池管理系统在线诊断意义重大. 发现电池能耗规律为电动公交车能量控制策略、安全管理提供科学的参数决策支持.
参考文献
A review of electric bus vehicles research topics–methods and trends
[J].DOI:10.1016/j.rser.2022.112211 [本文引用: 1]
一种联合锂电池健康和荷电状态的新模型
[J].
A new model of jointed states of charge and health for lithium batteries
[J].
基于EMB的纯电动汽车制动能量回收优化控制策略研究
[J].
Research on optimization control strategy for braking energy recovery of a battery electric vehicle based on EMB system
[J].
Online synthesis of an optimal battery state-of-charge reference trajectory for a plug-in hybrid electric city bus
[J].
电动汽车直流充电桩自动化测试平台的设计与应用
[J].
Development and application of automated test platform for DC charging piles of electric vehicles
[J].
锂离子电池荷电状态估算方法及其应用场景综述
[J].
Review on estimation methods for state of charge of lithiumion battery and their application
[J].
基于SOC-OCV优化曲线与EKF的锂离子电池荷电状态全局估计
[J].
An overall estimation of state-of-charge based on SOC-OCV optimization curve and EKF for lithiumion battery
[J].
基于容量修正的安时积分SOC估算方法研究
[J].
Study on battery SOC estimation by ampere hour intergral method with capacity correction
[J].
基于ABC-RFEKF算法的锂电池SOC估计
[J].
Lithium battery SOC estimation base on an ABC-RFEKF algorithm
[J].
基于分数阶阻抗模型的磷酸铁锂电池荷电状态估计
[J].
State of charge estimation of LiFePO4 battery based on fractional-order impedance model
[J].
基于FFRLS-EKF联合算法的锂离子电池荷电状态估计方法
[J].
State of charge estimation for Lithiumion battery based on FFRLS-EKF joint algorithm
[J].
Particle filter for state of charge and state of health estimation for lithium-iron phosphate batterie
[J].DOI:10.1016/j.jpowsour.2012.10.058 [本文引用: 1]
Fuzzy energy management strategy for a hybrid electric vehicle based on driving cycle recognition
[J].DOI:10.1007/s12239-012-0119-z [本文引用: 1]
基于GGAP-RBF神经网络的多参数纯电动客车蓄电池荷电状态预测
[J].
Multiple parameters state-of-charge estimation of battery for pure electric bus based on GGAP-RBF neural network
[J].
基于稀疏采样数据的电动公交车电池SOC预测方法研究
[J].
Study on battery SOC prediction method for electric bus based on sparsely sampled data
[J].
SeqST-GAN: Seq2Seq generative adversarial nets for multi-step urban crowd flow prediction
[J].
Long short term memory
[J].DOI:10.1162/neco.1997.9.8.1735 [本文引用: 1]
Long short termmemory networks for accurate state-of-charge estimation of Li-ion batteries
[J].
Kalman filter for onboard state of charge estimation and peak power capability analysis of lithium-ion batteries
[J].DOI:10.1016/j.jpowsour.2016.08.065 [本文引用: 1]
基于数据驱动的电动汽车动力电池SOC预测
[J].
A data-driven SOC prediction scheme for traction battery in electric vehicles
[J].