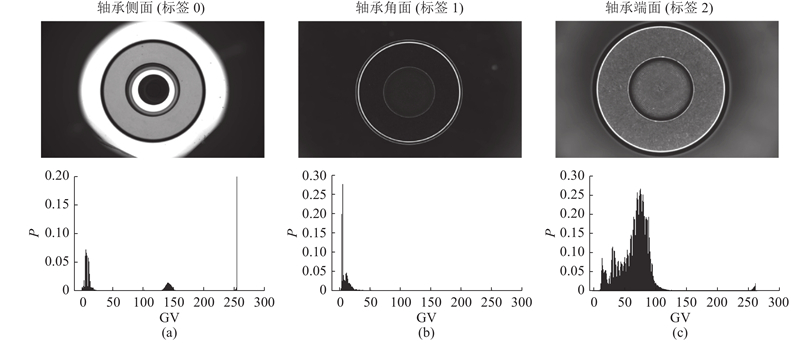
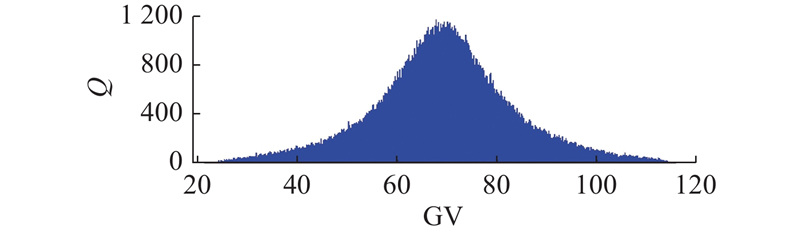
由于轴承滚子各个表面图像像素分布差异较大,且轴承表面样本采集存在一定难度,须先人工擦拭滚子各表面,再通过采集设备逐一采集,人力成本耗费较大,比较贴合实际工业生产中样本采集现状. 以轴承滚子表面灰度图像数据增强为例,验证所提方法的有效性,原始样本灰度图像均通过CCD工业相机采集获得,样本图像分为3类,分别为轴承滚子侧面、倒角、端面灰度图像,数据集中3类表面图像数量分别为351、468、471,总计1290. 输入判别器的图像需要降采样,输入生成器的是二维噪声. 首先将维度为(1 920, 1 200, 1)的原始图像裁剪为(1 920, 1 184, 1),然后用卷积核数量为1的单层卷积层对裁剪后图像数据进行降采样,分别降采样为(480, 296, 1)和(240, 148, 1),并将滚子侧面、倒角、端面图像标签记为0、1、2. 维度为(240, 148, 1)的图像用于训练WGAN-GP网络,维度为(480, 296, 1)的图像作为训练SRCNN模型的高分辨率图像,训练好的生成对抗网络生成的800张维度为(240, 148, 1)的图像作为训练SRCNN模型的低分辨率图像,其中侧面、端面、倒角面图像分别为200、300、300张.
[1]
康守强, 胡明武, 王玉静, 等 基于特征迁移学习的变工况下滚动轴承故障诊断方法
[J]. 中国电机工程学报 , 2019 , 39 (3 ): 764 - 772
DOI:10.13334/J.0258-8013.PCSEE.180130
[本文引用: 1]
KANG Shou-qiang, HU Ming-wu, WANG Yu-jing, et al Fault diagnosis method of a rolling bearing under variable working conditions based on feature transfer learning
[J]. Proceedings of the CSEE , 2019 , 39 (3 ): 764 - 772
DOI:10.13334/J.0258-8013.PCSEE.180130
[本文引用: 1]
[2]
肖雄, 肖宇雄, 张勇军, 等 基于二维灰度图的数据增强方法在电机轴承故障诊断的应用研究
[J]. 中国电机工程学报 , 2021 , 41 (2 ): 738 - 749
DOI:10.13334/j.0258-8013.pcsee.200834
[本文引用: 1]
XIAO Xiong, XIAO Yu-xiong, ZHANG Yong-jun, et al Research on the application of the data augmentation method based on 2D gray pixel images in the fault diagnosis of motor bearing
[J]. Proceedings of the CSEE , 2021 , 41 (2 ): 738 - 749
DOI:10.13334/j.0258-8013.pcsee.200834
[本文引用: 1]
[3]
PAN S J, YANG Q A survey on transfer learning
[J]. IEEE Transactions on Knowledge and Data Engineering , 2009 , 22 (10 ): 1345 - 1359
[本文引用: 1]
[4]
SALAKHUTDINOV R, LAROCHELLE H. Efficient learning of deep Boltzmann machines [C]// Proceedings of the 13th International Conference on Artificial Intelligence and Statistics . Sardinia: JMLR, 2010: 693-700.
[本文引用: 1]
[5]
BENGIO Y, LAUFER E, ALAIN G, et al. Deep generative stochastic networks trainable by backprop [C]// International Conference on Machine Learning . Beijing: PMLR, 2014: 226-234.
[本文引用: 1]
[6]
KINGMA D P, WELLING M. Auto-encoding variational bayes [EB/OL]. [2013-12-20]. https://arxiv.org/abs/1312.6114.
[本文引用: 1]
[7]
VANDEN OORD A, KALCHBRENNER N, ESPEHOLT L, et al. Conditional image generation with pixel-cnn decoders [C]// 30th Conference on Neural Information Processing Systems . Barcelona: CA, 2016: 4797-4805.
[本文引用: 1]
[8]
VAN OORD A, KALCHBRENNER N, KAVUKCUOGLU K. Pixel recurrent neural networks [C]// International Conference on Machine Learning . New York: JMLR, 2016: 1747-1756.
[本文引用: 1]
[9]
GOODFELLOW I, POUGET-ABADIE J, MIRZA M, et al Generative adversarial networks
[J]. Communications of the ACM , 2020 , 63 (11 ): 139 - 144
DOI:10.1145/3422622
[本文引用: 1]
[10]
MIRZA M, OSINDERO S. Conditional generative adversarial nets [EB/OL]. [2014-11-06]. https://arxiv.org/abs/1411.1784.
[本文引用: 1]
[11]
RADFORD A, METZ L, CHINTALA S. Unsupervised representation learning with deep convolutional generative adversarial networks [EB/OL]. [2015-11-19]. https://arxiv.org/abs/1511.06434.
[本文引用: 1]
[12]
ARJOVSKY M, CHINTALA S, BOTTOU L. Wasserstein generative adversarial networks [C]// International Conference on Machine Learning . Sydney: PMLR, 2017: 214-223.
[本文引用: 2]
[13]
GULRAJANI I, AHMED F, ARJOVSKY M, et al. Improved training of wasserstein gans [EB/OL]. [2017-03-31]. https://arxiv.org/abs/1704.00028.
[本文引用: 1]
[14]
BERTHELOT D, SCHUMM T, METZ L. Boundary equilibrium generative adversarial networks [EB/OL]. [2017-03-21]. https://arxiv.org/abs/1703.10717.
[本文引用: 1]
[15]
KARRAS T, AILA T, LAINE S, et al. Progressive growing of gans for improved quality, stability, and variation [C]// International Conference on Learning Representations . Vancouver: JMLR, 2018: 26.
[本文引用: 1]
[16]
KARRAS T, LAINE S, AILA T. A style-based generator architecture for generative adversarial networks [C]// CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019: 4396-4405.
[本文引用: 1]
[17]
KARRAS T, LAINE S, AITTALA M, et al. Analyzing and improving the image quality of style GAN [C]// CVF Conference on Computer Vision and Pattern Recognition . Seattle: IEEE, 2020: 8107-8116.
[18]
KARRAS T, AITTALA M, LAINE S, et al Alias-free generative adversarial networks
[J]. Advances in Neural Information Processing Systems , 2021 , 34 : 852 - 863
[本文引用: 1]
[19]
DONG C, LOY C C, HE K, et al Image super-resolution using deep convolutional networks
[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2015 , 38 (2 ): 295 - 307
[本文引用: 1]
[20]
DEON A F, MENYAEV Y A Twister generator of random normal numbers by box-muller model
[J]. International Journal of Trends in Computer Science , 2020 , 16 (1 ): 1 - 13
[本文引用: 1]
[22]
ARJOVSKY M, BOTTOU L. Towards principled methods for training generative adversarial networks [EB/OL]. [2017-01-17]. https://arxiv.org/abs/1701.04862.
[本文引用: 1]
[23]
LYE A, CICIRELLO A, PATELLI E Sampling methods for solving bayesian model updating problems: a tutorial
[J]. Mechanical Systems and Signal Processing , 2021 , 159 : 107760
DOI:10.1016/j.ymssp.2021.107760
[本文引用: 1]
基于特征迁移学习的变工况下滚动轴承故障诊断方法
1
2019
... 现代零件加工质量检测和设备故障诊断方法逐渐智能化,在各类机器学习和数据挖掘算法中,原始工业数据显得极为重要. 性能良好的算法需要海量且优质的数据支撑,仅用少量数据驱动的模型很难具备较好的泛化能力. 不过,多数情况下难以获取大量的工业数据集,例如变工况条件下标定完整的轴承振动数据集[1 ] . ...
基于特征迁移学习的变工况下滚动轴承故障诊断方法
1
2019
... 现代零件加工质量检测和设备故障诊断方法逐渐智能化,在各类机器学习和数据挖掘算法中,原始工业数据显得极为重要. 性能良好的算法需要海量且优质的数据支撑,仅用少量数据驱动的模型很难具备较好的泛化能力. 不过,多数情况下难以获取大量的工业数据集,例如变工况条件下标定完整的轴承振动数据集[1 ] . ...
基于二维灰度图的数据增强方法在电机轴承故障诊断的应用研究
1
2021
... 在图像处理领域,针对工业数据不足的问题,现有的数据增强方法包括对原始图像进行几何变换、随机调整亮度和对比度、添加各类噪声等操作,然而这些方法不能使训练样本的多样性产生质变[2 ] . 迁移学习[3 ] 可以大幅减少人工标定成本,但是迁移学习模型难以改变其网络结构,且灵活性较差,当训练集和测试集数据分布差异过大时,模型易发生崩溃. 随着生成模型的发展,逐渐出现基于深度玻尔兹曼机(deep Boltzmann machine, DBM)[4 ] 、生成随机网络(generative stochastic network, GSN)[5 ] 、变分自编码器(variational auto-encoding, VAE)[6 ] 、像素递归神经网络(pixel recurrent neural networks, PixelRNN)、像素卷积神经网络(pixel convolution neural networks, PixelCNN)[7 -8 ] 和生产式对抗网络(generative adversarial networks, GAN)等数据增强方法. 与VAE相比,GAN不存在偏置,能够更好地拟合真实样本分布;与DBM、GSN和PixelRNN/CNN相比,GAN可一次性生成样本,而不用反复计算马尔可夫链或通过逐个生成像素的方式生成样本. GAN以其良好的图像质量和快速的运行速度,成为了当前数据增强方法的主流研究方向之一. ...
基于二维灰度图的数据增强方法在电机轴承故障诊断的应用研究
1
2021
... 在图像处理领域,针对工业数据不足的问题,现有的数据增强方法包括对原始图像进行几何变换、随机调整亮度和对比度、添加各类噪声等操作,然而这些方法不能使训练样本的多样性产生质变[2 ] . 迁移学习[3 ] 可以大幅减少人工标定成本,但是迁移学习模型难以改变其网络结构,且灵活性较差,当训练集和测试集数据分布差异过大时,模型易发生崩溃. 随着生成模型的发展,逐渐出现基于深度玻尔兹曼机(deep Boltzmann machine, DBM)[4 ] 、生成随机网络(generative stochastic network, GSN)[5 ] 、变分自编码器(variational auto-encoding, VAE)[6 ] 、像素递归神经网络(pixel recurrent neural networks, PixelRNN)、像素卷积神经网络(pixel convolution neural networks, PixelCNN)[7 -8 ] 和生产式对抗网络(generative adversarial networks, GAN)等数据增强方法. 与VAE相比,GAN不存在偏置,能够更好地拟合真实样本分布;与DBM、GSN和PixelRNN/CNN相比,GAN可一次性生成样本,而不用反复计算马尔可夫链或通过逐个生成像素的方式生成样本. GAN以其良好的图像质量和快速的运行速度,成为了当前数据增强方法的主流研究方向之一. ...
A survey on transfer learning
1
2009
... 在图像处理领域,针对工业数据不足的问题,现有的数据增强方法包括对原始图像进行几何变换、随机调整亮度和对比度、添加各类噪声等操作,然而这些方法不能使训练样本的多样性产生质变[2 ] . 迁移学习[3 ] 可以大幅减少人工标定成本,但是迁移学习模型难以改变其网络结构,且灵活性较差,当训练集和测试集数据分布差异过大时,模型易发生崩溃. 随着生成模型的发展,逐渐出现基于深度玻尔兹曼机(deep Boltzmann machine, DBM)[4 ] 、生成随机网络(generative stochastic network, GSN)[5 ] 、变分自编码器(variational auto-encoding, VAE)[6 ] 、像素递归神经网络(pixel recurrent neural networks, PixelRNN)、像素卷积神经网络(pixel convolution neural networks, PixelCNN)[7 -8 ] 和生产式对抗网络(generative adversarial networks, GAN)等数据增强方法. 与VAE相比,GAN不存在偏置,能够更好地拟合真实样本分布;与DBM、GSN和PixelRNN/CNN相比,GAN可一次性生成样本,而不用反复计算马尔可夫链或通过逐个生成像素的方式生成样本. GAN以其良好的图像质量和快速的运行速度,成为了当前数据增强方法的主流研究方向之一. ...
1
... 在图像处理领域,针对工业数据不足的问题,现有的数据增强方法包括对原始图像进行几何变换、随机调整亮度和对比度、添加各类噪声等操作,然而这些方法不能使训练样本的多样性产生质变[2 ] . 迁移学习[3 ] 可以大幅减少人工标定成本,但是迁移学习模型难以改变其网络结构,且灵活性较差,当训练集和测试集数据分布差异过大时,模型易发生崩溃. 随着生成模型的发展,逐渐出现基于深度玻尔兹曼机(deep Boltzmann machine, DBM)[4 ] 、生成随机网络(generative stochastic network, GSN)[5 ] 、变分自编码器(variational auto-encoding, VAE)[6 ] 、像素递归神经网络(pixel recurrent neural networks, PixelRNN)、像素卷积神经网络(pixel convolution neural networks, PixelCNN)[7 -8 ] 和生产式对抗网络(generative adversarial networks, GAN)等数据增强方法. 与VAE相比,GAN不存在偏置,能够更好地拟合真实样本分布;与DBM、GSN和PixelRNN/CNN相比,GAN可一次性生成样本,而不用反复计算马尔可夫链或通过逐个生成像素的方式生成样本. GAN以其良好的图像质量和快速的运行速度,成为了当前数据增强方法的主流研究方向之一. ...
1
... 在图像处理领域,针对工业数据不足的问题,现有的数据增强方法包括对原始图像进行几何变换、随机调整亮度和对比度、添加各类噪声等操作,然而这些方法不能使训练样本的多样性产生质变[2 ] . 迁移学习[3 ] 可以大幅减少人工标定成本,但是迁移学习模型难以改变其网络结构,且灵活性较差,当训练集和测试集数据分布差异过大时,模型易发生崩溃. 随着生成模型的发展,逐渐出现基于深度玻尔兹曼机(deep Boltzmann machine, DBM)[4 ] 、生成随机网络(generative stochastic network, GSN)[5 ] 、变分自编码器(variational auto-encoding, VAE)[6 ] 、像素递归神经网络(pixel recurrent neural networks, PixelRNN)、像素卷积神经网络(pixel convolution neural networks, PixelCNN)[7 -8 ] 和生产式对抗网络(generative adversarial networks, GAN)等数据增强方法. 与VAE相比,GAN不存在偏置,能够更好地拟合真实样本分布;与DBM、GSN和PixelRNN/CNN相比,GAN可一次性生成样本,而不用反复计算马尔可夫链或通过逐个生成像素的方式生成样本. GAN以其良好的图像质量和快速的运行速度,成为了当前数据增强方法的主流研究方向之一. ...
1
... 在图像处理领域,针对工业数据不足的问题,现有的数据增强方法包括对原始图像进行几何变换、随机调整亮度和对比度、添加各类噪声等操作,然而这些方法不能使训练样本的多样性产生质变[2 ] . 迁移学习[3 ] 可以大幅减少人工标定成本,但是迁移学习模型难以改变其网络结构,且灵活性较差,当训练集和测试集数据分布差异过大时,模型易发生崩溃. 随着生成模型的发展,逐渐出现基于深度玻尔兹曼机(deep Boltzmann machine, DBM)[4 ] 、生成随机网络(generative stochastic network, GSN)[5 ] 、变分自编码器(variational auto-encoding, VAE)[6 ] 、像素递归神经网络(pixel recurrent neural networks, PixelRNN)、像素卷积神经网络(pixel convolution neural networks, PixelCNN)[7 -8 ] 和生产式对抗网络(generative adversarial networks, GAN)等数据增强方法. 与VAE相比,GAN不存在偏置,能够更好地拟合真实样本分布;与DBM、GSN和PixelRNN/CNN相比,GAN可一次性生成样本,而不用反复计算马尔可夫链或通过逐个生成像素的方式生成样本. GAN以其良好的图像质量和快速的运行速度,成为了当前数据增强方法的主流研究方向之一. ...
1
... 在图像处理领域,针对工业数据不足的问题,现有的数据增强方法包括对原始图像进行几何变换、随机调整亮度和对比度、添加各类噪声等操作,然而这些方法不能使训练样本的多样性产生质变[2 ] . 迁移学习[3 ] 可以大幅减少人工标定成本,但是迁移学习模型难以改变其网络结构,且灵活性较差,当训练集和测试集数据分布差异过大时,模型易发生崩溃. 随着生成模型的发展,逐渐出现基于深度玻尔兹曼机(deep Boltzmann machine, DBM)[4 ] 、生成随机网络(generative stochastic network, GSN)[5 ] 、变分自编码器(variational auto-encoding, VAE)[6 ] 、像素递归神经网络(pixel recurrent neural networks, PixelRNN)、像素卷积神经网络(pixel convolution neural networks, PixelCNN)[7 -8 ] 和生产式对抗网络(generative adversarial networks, GAN)等数据增强方法. 与VAE相比,GAN不存在偏置,能够更好地拟合真实样本分布;与DBM、GSN和PixelRNN/CNN相比,GAN可一次性生成样本,而不用反复计算马尔可夫链或通过逐个生成像素的方式生成样本. GAN以其良好的图像质量和快速的运行速度,成为了当前数据增强方法的主流研究方向之一. ...
1
... 在图像处理领域,针对工业数据不足的问题,现有的数据增强方法包括对原始图像进行几何变换、随机调整亮度和对比度、添加各类噪声等操作,然而这些方法不能使训练样本的多样性产生质变[2 ] . 迁移学习[3 ] 可以大幅减少人工标定成本,但是迁移学习模型难以改变其网络结构,且灵活性较差,当训练集和测试集数据分布差异过大时,模型易发生崩溃. 随着生成模型的发展,逐渐出现基于深度玻尔兹曼机(deep Boltzmann machine, DBM)[4 ] 、生成随机网络(generative stochastic network, GSN)[5 ] 、变分自编码器(variational auto-encoding, VAE)[6 ] 、像素递归神经网络(pixel recurrent neural networks, PixelRNN)、像素卷积神经网络(pixel convolution neural networks, PixelCNN)[7 -8 ] 和生产式对抗网络(generative adversarial networks, GAN)等数据增强方法. 与VAE相比,GAN不存在偏置,能够更好地拟合真实样本分布;与DBM、GSN和PixelRNN/CNN相比,GAN可一次性生成样本,而不用反复计算马尔可夫链或通过逐个生成像素的方式生成样本. GAN以其良好的图像质量和快速的运行速度,成为了当前数据增强方法的主流研究方向之一. ...
Generative adversarial networks
1
2020
... 基于生成器与判别器零和博弈的思想,Goodfellow等[9 ] 提出生成式对抗神经网络,并将其应用于手写数字和人脸图像生成. Mirza等[10 ] 将标签信息输入到GAN的生成器和判别器中,提出条件生成对抗网络(conditional generative adversarial nets, CGAN),通过引入条件信息实现GAN的训练过程可控. Radford等[11 ] 将深度神经网络(deep neural networks,DNN)引入GAN,并用全局池化层替换全连接层,提出深度卷积生成对抗网络(deep convolutional generative adversarial networks,DCGAN). 为了稳定GAN的训练,Arjovsky等[12 ] 提出沃瑟斯坦生成对抗网络(Wasserstein GAN,WGAN). Gulrajani等[13 ] 提出带梯度惩罚项的沃瑟斯坦生成对抗网络(Wasserstein GAN with gradient penalty,WGAN-GP). 传统GAN方法生成的图像数据较为模糊,为了生成高分辨率的图像数据,Berthelot等[14 ] 基于自编码器提出边界均衡生成式对抗网络(boundary equilibrium generative adversarial networks, BEGAN). Karras等[15 ] 提出PG-GAN,通过渐进训练的方式增大生成图像的空间分辨率. Karras等[16 -18 ] 借鉴风格迁移网络并通过修改渐进层输入,提出StyleGAN系列对抗网络,实现对隐空间的解耦. 图像超分辨率重建可以利用低分辨率图像经过训练得到高分辨率图像,Dong等[19 ] 将深层卷积网络应用于图像超分辨率重建提出超分辨率卷积神经网络(super-resolution convolutional neural network, SRCNN). 相比通过GAN方法得到高分辨率图像,图像超分辨率重建技术模型结构更简单,且训练过程更稳定. ...
1
... 基于生成器与判别器零和博弈的思想,Goodfellow等[9 ] 提出生成式对抗神经网络,并将其应用于手写数字和人脸图像生成. Mirza等[10 ] 将标签信息输入到GAN的生成器和判别器中,提出条件生成对抗网络(conditional generative adversarial nets, CGAN),通过引入条件信息实现GAN的训练过程可控. Radford等[11 ] 将深度神经网络(deep neural networks,DNN)引入GAN,并用全局池化层替换全连接层,提出深度卷积生成对抗网络(deep convolutional generative adversarial networks,DCGAN). 为了稳定GAN的训练,Arjovsky等[12 ] 提出沃瑟斯坦生成对抗网络(Wasserstein GAN,WGAN). Gulrajani等[13 ] 提出带梯度惩罚项的沃瑟斯坦生成对抗网络(Wasserstein GAN with gradient penalty,WGAN-GP). 传统GAN方法生成的图像数据较为模糊,为了生成高分辨率的图像数据,Berthelot等[14 ] 基于自编码器提出边界均衡生成式对抗网络(boundary equilibrium generative adversarial networks, BEGAN). Karras等[15 ] 提出PG-GAN,通过渐进训练的方式增大生成图像的空间分辨率. Karras等[16 -18 ] 借鉴风格迁移网络并通过修改渐进层输入,提出StyleGAN系列对抗网络,实现对隐空间的解耦. 图像超分辨率重建可以利用低分辨率图像经过训练得到高分辨率图像,Dong等[19 ] 将深层卷积网络应用于图像超分辨率重建提出超分辨率卷积神经网络(super-resolution convolutional neural network, SRCNN). 相比通过GAN方法得到高分辨率图像,图像超分辨率重建技术模型结构更简单,且训练过程更稳定. ...
1
... 基于生成器与判别器零和博弈的思想,Goodfellow等[9 ] 提出生成式对抗神经网络,并将其应用于手写数字和人脸图像生成. Mirza等[10 ] 将标签信息输入到GAN的生成器和判别器中,提出条件生成对抗网络(conditional generative adversarial nets, CGAN),通过引入条件信息实现GAN的训练过程可控. Radford等[11 ] 将深度神经网络(deep neural networks,DNN)引入GAN,并用全局池化层替换全连接层,提出深度卷积生成对抗网络(deep convolutional generative adversarial networks,DCGAN). 为了稳定GAN的训练,Arjovsky等[12 ] 提出沃瑟斯坦生成对抗网络(Wasserstein GAN,WGAN). Gulrajani等[13 ] 提出带梯度惩罚项的沃瑟斯坦生成对抗网络(Wasserstein GAN with gradient penalty,WGAN-GP). 传统GAN方法生成的图像数据较为模糊,为了生成高分辨率的图像数据,Berthelot等[14 ] 基于自编码器提出边界均衡生成式对抗网络(boundary equilibrium generative adversarial networks, BEGAN). Karras等[15 ] 提出PG-GAN,通过渐进训练的方式增大生成图像的空间分辨率. Karras等[16 -18 ] 借鉴风格迁移网络并通过修改渐进层输入,提出StyleGAN系列对抗网络,实现对隐空间的解耦. 图像超分辨率重建可以利用低分辨率图像经过训练得到高分辨率图像,Dong等[19 ] 将深层卷积网络应用于图像超分辨率重建提出超分辨率卷积神经网络(super-resolution convolutional neural network, SRCNN). 相比通过GAN方法得到高分辨率图像,图像超分辨率重建技术模型结构更简单,且训练过程更稳定. ...
2
... 基于生成器与判别器零和博弈的思想,Goodfellow等[9 ] 提出生成式对抗神经网络,并将其应用于手写数字和人脸图像生成. Mirza等[10 ] 将标签信息输入到GAN的生成器和判别器中,提出条件生成对抗网络(conditional generative adversarial nets, CGAN),通过引入条件信息实现GAN的训练过程可控. Radford等[11 ] 将深度神经网络(deep neural networks,DNN)引入GAN,并用全局池化层替换全连接层,提出深度卷积生成对抗网络(deep convolutional generative adversarial networks,DCGAN). 为了稳定GAN的训练,Arjovsky等[12 ] 提出沃瑟斯坦生成对抗网络(Wasserstein GAN,WGAN). Gulrajani等[13 ] 提出带梯度惩罚项的沃瑟斯坦生成对抗网络(Wasserstein GAN with gradient penalty,WGAN-GP). 传统GAN方法生成的图像数据较为模糊,为了生成高分辨率的图像数据,Berthelot等[14 ] 基于自编码器提出边界均衡生成式对抗网络(boundary equilibrium generative adversarial networks, BEGAN). Karras等[15 ] 提出PG-GAN,通过渐进训练的方式增大生成图像的空间分辨率. Karras等[16 -18 ] 借鉴风格迁移网络并通过修改渐进层输入,提出StyleGAN系列对抗网络,实现对隐空间的解耦. 图像超分辨率重建可以利用低分辨率图像经过训练得到高分辨率图像,Dong等[19 ] 将深层卷积网络应用于图像超分辨率重建提出超分辨率卷积神经网络(super-resolution convolutional neural network, SRCNN). 相比通过GAN方法得到高分辨率图像,图像超分辨率重建技术模型结构更简单,且训练过程更稳定. ...
... 生成器随机初始化后的生成分布很难与真实分布有不可忽略的重叠,因此WGAN用Wasserstein距离作为等价优化的距离衡量,进而同时解决稳定训练和进程指标的问题[12 ] . Wasserstein距离计算公式为 ...
1
... 基于生成器与判别器零和博弈的思想,Goodfellow等[9 ] 提出生成式对抗神经网络,并将其应用于手写数字和人脸图像生成. Mirza等[10 ] 将标签信息输入到GAN的生成器和判别器中,提出条件生成对抗网络(conditional generative adversarial nets, CGAN),通过引入条件信息实现GAN的训练过程可控. Radford等[11 ] 将深度神经网络(deep neural networks,DNN)引入GAN,并用全局池化层替换全连接层,提出深度卷积生成对抗网络(deep convolutional generative adversarial networks,DCGAN). 为了稳定GAN的训练,Arjovsky等[12 ] 提出沃瑟斯坦生成对抗网络(Wasserstein GAN,WGAN). Gulrajani等[13 ] 提出带梯度惩罚项的沃瑟斯坦生成对抗网络(Wasserstein GAN with gradient penalty,WGAN-GP). 传统GAN方法生成的图像数据较为模糊,为了生成高分辨率的图像数据,Berthelot等[14 ] 基于自编码器提出边界均衡生成式对抗网络(boundary equilibrium generative adversarial networks, BEGAN). Karras等[15 ] 提出PG-GAN,通过渐进训练的方式增大生成图像的空间分辨率. Karras等[16 -18 ] 借鉴风格迁移网络并通过修改渐进层输入,提出StyleGAN系列对抗网络,实现对隐空间的解耦. 图像超分辨率重建可以利用低分辨率图像经过训练得到高分辨率图像,Dong等[19 ] 将深层卷积网络应用于图像超分辨率重建提出超分辨率卷积神经网络(super-resolution convolutional neural network, SRCNN). 相比通过GAN方法得到高分辨率图像,图像超分辨率重建技术模型结构更简单,且训练过程更稳定. ...
1
... 基于生成器与判别器零和博弈的思想,Goodfellow等[9 ] 提出生成式对抗神经网络,并将其应用于手写数字和人脸图像生成. Mirza等[10 ] 将标签信息输入到GAN的生成器和判别器中,提出条件生成对抗网络(conditional generative adversarial nets, CGAN),通过引入条件信息实现GAN的训练过程可控. Radford等[11 ] 将深度神经网络(deep neural networks,DNN)引入GAN,并用全局池化层替换全连接层,提出深度卷积生成对抗网络(deep convolutional generative adversarial networks,DCGAN). 为了稳定GAN的训练,Arjovsky等[12 ] 提出沃瑟斯坦生成对抗网络(Wasserstein GAN,WGAN). Gulrajani等[13 ] 提出带梯度惩罚项的沃瑟斯坦生成对抗网络(Wasserstein GAN with gradient penalty,WGAN-GP). 传统GAN方法生成的图像数据较为模糊,为了生成高分辨率的图像数据,Berthelot等[14 ] 基于自编码器提出边界均衡生成式对抗网络(boundary equilibrium generative adversarial networks, BEGAN). Karras等[15 ] 提出PG-GAN,通过渐进训练的方式增大生成图像的空间分辨率. Karras等[16 -18 ] 借鉴风格迁移网络并通过修改渐进层输入,提出StyleGAN系列对抗网络,实现对隐空间的解耦. 图像超分辨率重建可以利用低分辨率图像经过训练得到高分辨率图像,Dong等[19 ] 将深层卷积网络应用于图像超分辨率重建提出超分辨率卷积神经网络(super-resolution convolutional neural network, SRCNN). 相比通过GAN方法得到高分辨率图像,图像超分辨率重建技术模型结构更简单,且训练过程更稳定. ...
1
... 基于生成器与判别器零和博弈的思想,Goodfellow等[9 ] 提出生成式对抗神经网络,并将其应用于手写数字和人脸图像生成. Mirza等[10 ] 将标签信息输入到GAN的生成器和判别器中,提出条件生成对抗网络(conditional generative adversarial nets, CGAN),通过引入条件信息实现GAN的训练过程可控. Radford等[11 ] 将深度神经网络(deep neural networks,DNN)引入GAN,并用全局池化层替换全连接层,提出深度卷积生成对抗网络(deep convolutional generative adversarial networks,DCGAN). 为了稳定GAN的训练,Arjovsky等[12 ] 提出沃瑟斯坦生成对抗网络(Wasserstein GAN,WGAN). Gulrajani等[13 ] 提出带梯度惩罚项的沃瑟斯坦生成对抗网络(Wasserstein GAN with gradient penalty,WGAN-GP). 传统GAN方法生成的图像数据较为模糊,为了生成高分辨率的图像数据,Berthelot等[14 ] 基于自编码器提出边界均衡生成式对抗网络(boundary equilibrium generative adversarial networks, BEGAN). Karras等[15 ] 提出PG-GAN,通过渐进训练的方式增大生成图像的空间分辨率. Karras等[16 -18 ] 借鉴风格迁移网络并通过修改渐进层输入,提出StyleGAN系列对抗网络,实现对隐空间的解耦. 图像超分辨率重建可以利用低分辨率图像经过训练得到高分辨率图像,Dong等[19 ] 将深层卷积网络应用于图像超分辨率重建提出超分辨率卷积神经网络(super-resolution convolutional neural network, SRCNN). 相比通过GAN方法得到高分辨率图像,图像超分辨率重建技术模型结构更简单,且训练过程更稳定. ...
1
... 基于生成器与判别器零和博弈的思想,Goodfellow等[9 ] 提出生成式对抗神经网络,并将其应用于手写数字和人脸图像生成. Mirza等[10 ] 将标签信息输入到GAN的生成器和判别器中,提出条件生成对抗网络(conditional generative adversarial nets, CGAN),通过引入条件信息实现GAN的训练过程可控. Radford等[11 ] 将深度神经网络(deep neural networks,DNN)引入GAN,并用全局池化层替换全连接层,提出深度卷积生成对抗网络(deep convolutional generative adversarial networks,DCGAN). 为了稳定GAN的训练,Arjovsky等[12 ] 提出沃瑟斯坦生成对抗网络(Wasserstein GAN,WGAN). Gulrajani等[13 ] 提出带梯度惩罚项的沃瑟斯坦生成对抗网络(Wasserstein GAN with gradient penalty,WGAN-GP). 传统GAN方法生成的图像数据较为模糊,为了生成高分辨率的图像数据,Berthelot等[14 ] 基于自编码器提出边界均衡生成式对抗网络(boundary equilibrium generative adversarial networks, BEGAN). Karras等[15 ] 提出PG-GAN,通过渐进训练的方式增大生成图像的空间分辨率. Karras等[16 -18 ] 借鉴风格迁移网络并通过修改渐进层输入,提出StyleGAN系列对抗网络,实现对隐空间的解耦. 图像超分辨率重建可以利用低分辨率图像经过训练得到高分辨率图像,Dong等[19 ] 将深层卷积网络应用于图像超分辨率重建提出超分辨率卷积神经网络(super-resolution convolutional neural network, SRCNN). 相比通过GAN方法得到高分辨率图像,图像超分辨率重建技术模型结构更简单,且训练过程更稳定. ...
Alias-free generative adversarial networks
1
2021
... 基于生成器与判别器零和博弈的思想,Goodfellow等[9 ] 提出生成式对抗神经网络,并将其应用于手写数字和人脸图像生成. Mirza等[10 ] 将标签信息输入到GAN的生成器和判别器中,提出条件生成对抗网络(conditional generative adversarial nets, CGAN),通过引入条件信息实现GAN的训练过程可控. Radford等[11 ] 将深度神经网络(deep neural networks,DNN)引入GAN,并用全局池化层替换全连接层,提出深度卷积生成对抗网络(deep convolutional generative adversarial networks,DCGAN). 为了稳定GAN的训练,Arjovsky等[12 ] 提出沃瑟斯坦生成对抗网络(Wasserstein GAN,WGAN). Gulrajani等[13 ] 提出带梯度惩罚项的沃瑟斯坦生成对抗网络(Wasserstein GAN with gradient penalty,WGAN-GP). 传统GAN方法生成的图像数据较为模糊,为了生成高分辨率的图像数据,Berthelot等[14 ] 基于自编码器提出边界均衡生成式对抗网络(boundary equilibrium generative adversarial networks, BEGAN). Karras等[15 ] 提出PG-GAN,通过渐进训练的方式增大生成图像的空间分辨率. Karras等[16 -18 ] 借鉴风格迁移网络并通过修改渐进层输入,提出StyleGAN系列对抗网络,实现对隐空间的解耦. 图像超分辨率重建可以利用低分辨率图像经过训练得到高分辨率图像,Dong等[19 ] 将深层卷积网络应用于图像超分辨率重建提出超分辨率卷积神经网络(super-resolution convolutional neural network, SRCNN). 相比通过GAN方法得到高分辨率图像,图像超分辨率重建技术模型结构更简单,且训练过程更稳定. ...
Image super-resolution using deep convolutional networks
1
2015
... 基于生成器与判别器零和博弈的思想,Goodfellow等[9 ] 提出生成式对抗神经网络,并将其应用于手写数字和人脸图像生成. Mirza等[10 ] 将标签信息输入到GAN的生成器和判别器中,提出条件生成对抗网络(conditional generative adversarial nets, CGAN),通过引入条件信息实现GAN的训练过程可控. Radford等[11 ] 将深度神经网络(deep neural networks,DNN)引入GAN,并用全局池化层替换全连接层,提出深度卷积生成对抗网络(deep convolutional generative adversarial networks,DCGAN). 为了稳定GAN的训练,Arjovsky等[12 ] 提出沃瑟斯坦生成对抗网络(Wasserstein GAN,WGAN). Gulrajani等[13 ] 提出带梯度惩罚项的沃瑟斯坦生成对抗网络(Wasserstein GAN with gradient penalty,WGAN-GP). 传统GAN方法生成的图像数据较为模糊,为了生成高分辨率的图像数据,Berthelot等[14 ] 基于自编码器提出边界均衡生成式对抗网络(boundary equilibrium generative adversarial networks, BEGAN). Karras等[15 ] 提出PG-GAN,通过渐进训练的方式增大生成图像的空间分辨率. Karras等[16 -18 ] 借鉴风格迁移网络并通过修改渐进层输入,提出StyleGAN系列对抗网络,实现对隐空间的解耦. 图像超分辨率重建可以利用低分辨率图像经过训练得到高分辨率图像,Dong等[19 ] 将深层卷积网络应用于图像超分辨率重建提出超分辨率卷积神经网络(super-resolution convolutional neural network, SRCNN). 相比通过GAN方法得到高分辨率图像,图像超分辨率重建技术模型结构更简单,且训练过程更稳定. ...
Twister generator of random normal numbers by box-muller model
1
2020
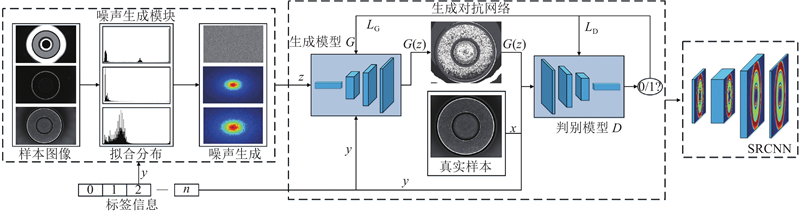
... 综上所述,现有图像数据增强方法存在以下问题:1)基于传统GAN方法直接建立向高分辨率图像的映射网络,网络难以工作. 2)图像超分辨率重建技术是在已知低分辨率图像的基础上生成高分辨率图像,模型无法自主生成低分辨率图像. 3)目前基于GAN的模型对于噪声的输入都极为随意,在多数情况下都是直接输入一维随机噪声,导致输入的噪声和样本原始分布差异较大. 网络可训练参数量过多,会影响模型收敛速度. 4)现有的渐进式训练方法能够生成高分辨率图像,但是也带来了训练速度缓慢的问题. 针对上述问题,本研究提出基于分布拟合对抗神经网络的图像数据增强方法. 通过最大似然估计拟合原始样本数据空间分布;根据Box-Muller和马尔科夫链蒙特卡洛(Markov chain Monte Carlo, MCMC)采样算法[20 ] 生成符合原始样本空间分布的随机噪声;结合带条件信息的WGAN-GP和SRCNN提出新的图像数据增强方法,并利用轴承滚子表面缺陷检测数据验证所提方法的可行性和优越性. ...
基于隐变量后验生成对抗网络的不平衡学习
1
2021
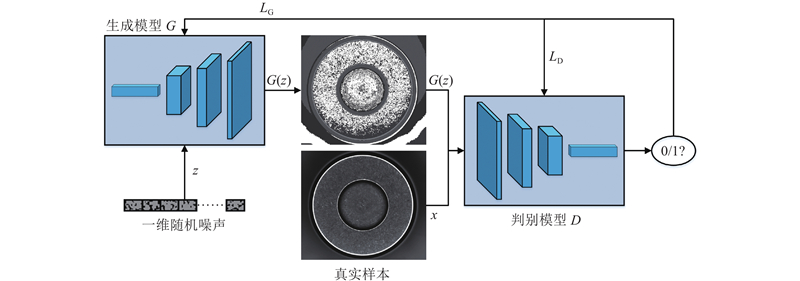
... GAN由生成模型(G )和判别模型(D )2个部分构成,生成模型输入随机噪声 $z $ $G(z) $ $x $ $G(z) $ x .生成模型的目的是最大化 $D(G(z)) $ $G(z) $ $D(G(z)) $ $G(z) $ [21 ] .GAN的目标函数为 ...
基于隐变量后验生成对抗网络的不平衡学习
1
2021
... GAN由生成模型(G )和判别模型(D )2个部分构成,生成模型输入随机噪声 $z $ $G(z) $ $x $ $G(z) $ x .生成模型的目的是最大化 $D(G(z)) $ $G(z) $ $D(G(z)) $ $G(z) $ [21 ] .GAN的目标函数为 ...
1
... 上述2个模型能够生成新的样本,但是都难以训练. 原始GAN和CGAN在训练过程中容易产生模式崩溃和梯度消失问题,并且生成器和判别器的损失值无法反馈模型收敛信息[22 ] . 一维随机噪声长度较长,会导致全连接层参数过多,造成模型参数冗余,严重影响训练效率. ...
Sampling methods for solving bayesian model updating problems: a tutorial
1
2021
... 对于目标分布的累积分布函数或关于 $R$ $ \theta $ [23 ] . MH算法是MCMC采样算法中常用的一种,通过构建马尔可夫链,找到满足细致平稳条件的状态转移矩阵使马尔可夫链趋于平稳分布,算法流程如图4 所示. ...