[1]
李响, 任尊松, 王子 基于梯形轨枕轨道振动特性的钢轨波磨研究
[J]. 铁道学报 , 2020 , 42 (10 ): 38 - 44
[本文引用: 1]
LI Xiang, REN Zun-song, WANG Zi Study on rail corrugation of ladder-type sleeper track based on vibration characteristics
[J]. Journal of the China Railway Society , 2020 , 42 (10 ): 38 - 44
[本文引用: 1]
[2]
彭华, 汤雪扬, 蔡小培, 等 基于轨道振动特征的地铁钢轨波磨成因研究
[J]. 铁道工程学报 , 2021 , 38 (11 ): 41 - 46+66
[本文引用: 2]
PENG Hua, TANG Xue-yang, CAI Xiao-pei, et al Research on causes of metro rail corrugation based on track vibration characteristics
[J]. Journal of Railway Engineering Society , 2021 , 38 (11 ): 41 - 46+66
[本文引用: 2]
[3]
PENG H, YAO Y F, CAI X P, et al Field measurement analysis and control measures evaluation of metro vehicle noise caused by rail corrugation
[J]. Applied Sciences , 2021 , 11 (23 ): 11190
DOI:10.3390/app112311190
[本文引用: 1]
[4]
谢清林. 基于数据与模型双重驱动的地铁钢轨波浪形磨耗识别方法初探[D]. 成都: 西南交通大学, 2021.
[本文引用: 1]
XIE Qing-lin. A preliminary study on rail corrugation detection method of metro lines based on data–model dual drive [D]. Chengdu: Southwest Jiaotong University, 2021.
[本文引用: 1]
[5]
王少锋, 许玉德, 周宇, 等 城市轨道交通曲线钢轨波磨检测与评价方法研究
[J]. 城市轨道交通研究 , 2011 , (10 ): 56 - 60
[本文引用: 1]
WANG Shao-feng, XU Yu-de, ZHOU Yu, et al Detection and evaluation of curve corrugation of urban mass transit
[J]. Urban Mass Transit , 2011 , (10 ): 56 - 60
[本文引用: 1]
[7]
罗林, 张格明, 吴旺青, 等. 轮轨系统轨道平顺状态的控制[M]. 北京: 中国铁道出版社, 2006: 115-135.
[本文引用: 1]
[8]
陈亮. 基于弦测法的钢轨波磨动态检测关键技术研究[D]. 长沙: 湖南大学, 2019.
CHEN Liang. Research on key issue of rail corrugation dynamic measurement based on chord measurement method [D]. Changsha: Hunan University, 2019.
[9]
魏珲, 刘宏立, 马子骥, 等 基于组合弦测的钢轨波磨广域测量方法
[J]. 西北大学学报: 自然科学版 , 2018 , 48 (2 ): 199 - 208
[本文引用: 1]
WEI Hun, LIU Hong-li, MA Zi-ji, et al A wide-area measurement method of rail corrugation based on the combination-chord system
[J]. Journal of Northwest University: Natural Science Edition , 2018 , 48 (2 ): 199 - 208
[本文引用: 1]
[10]
GRASSIE S L Measurement of railhead longitudinal profiles: a comparison of different techniques
[J]. Wear , 1996 , 191 (1/2 ): 245 - 251
[本文引用: 1]
[11]
徐金辉, 王平, 汪力, 等 轨道高低不平顺敏感波长的分布特征及其影响因素的研究
[J]. 铁道学报 , 2015 , 37 (7 ): 72 - 78
[本文引用: 1]
XU Jin-hui, WANG Ping, WANG Li, et al Research on the distribution characteristics and influence factors of sensitive wavelength of track vertical profile irregularity
[J]. Journal of the China Railway Society , 2015 , 37 (7 ): 72 - 78
[本文引用: 1]
[12]
周富强, 张广军, 朱奎义, 等. 钢轨磨耗激光视觉动态测量装置及测量方法: 200510123725. 0[P]. 2006-05-24.
[本文引用: 1]
[13]
王文健, 刘启跃, 王衡禹, 等. 钢轨波浪形磨损激光测量设备: 201220116237. 2[P]. 2012-11-07.
[14]
李清勇, 章华燕, 任盛伟, 等 基于钢轨图像频域特征的钢轨波磨检测方法
[J]. 中国铁道科学 , 2016 , 37 (1 ): 24 - 30
LI Qing-yong, ZHANG Hua-yan, REN Sheng-wei, et al detection method for rail corrugation based on rail image feature in frequency domain
[J]. China Railway Science , 2016 , 37 (1 ): 24 - 30
[15]
马子骥, 董艳茹, 刘宏立, 等 基于多线结构光视觉的钢轨波磨动态测量方法
[J]. 仪器仪表学报 , 2018 , 39 (6 ): 189 - 197
[本文引用: 1]
MA Zi-ji, DONG Yan-ru, LIU Hong-li, et al Rail corrugation dynamic measurement method based on multi-line structured-light vision
[J]. Chinese Journal of Scientific Instrument , 2018 , 39 (6 ): 189 - 197
[本文引用: 1]
[16]
HOPKINS B M, TAHERI S. Broken rail prediction and detection using wavelets and artificial neural networks [C]// Proceedings of the ASME/ASCE/IEEE 2011 Joint Rail Conference . Pueblo: [s.n.], 2011: 77-84.
[本文引用: 1]
[17]
HOPKINS B M, TAHERI S. Track health monitoring using wavelets [C]// Proceedings of the ASME 2010 Rail Transportation Division Fall Technical Conference . Roanoke: [s.n.], 2010: 9-15.
[本文引用: 1]
[18]
GOMES R, BATISTA A, ORTIGUEIRA M D, et al A tool for the detection and quantification of rail corrugation
[J]. Theoretical and Experimental Chemistry , 2010 , 46 (3 ): 153 - 157
DOI:10.1007/s11237-010-9132-3
[本文引用: 1]
[20]
KOJIMA T, TSUNASHIMA H, MATSUMOTO A. Fault detection of railway track by multi-resolution analysis [M]// ALLAN J, RUMSEY A F, SCIUTTO G, et al. Computers in Railways X . [S.l.]: WIT Press, 2006, 88: 955-964.
[本文引用: 1]
[21]
谢清林, 陶功权, 刘孟奇, 等 数学形态学滤波在钢轨波磨波长识别中的应用
[J]. 中南大学学报: 自然科学版 , 2021 , 52 (5 ): 1724 - 1732
[本文引用: 1]
XIE Qing-lin, TAO gong-quan, LIU meng-qi, et al Application of mathematical morphology filter in recognition of rail corrugation wavelength
[J]. Journal of Central South University: Science and Technology , 2021 , 52 (5 ): 1724 - 1732
[本文引用: 1]
[22]
周成, 高建敏 基于三维轮轨瞬态动力学模型的钢轨波磨不平顺动力影响与识别
[J]. 铁道科学与工程学报 , 2020 , 17 (4 ): 841 - 848
[本文引用: 1]
ZHOU cheng, GAO Jian-min Dynamic effect and identification of rail corrugation irregularity based on the three-dimensional wheel-rail transient dynamic model
[J]. Journal of Railway Science and Engineering , 2020 , 17 (4 ): 841 - 848
[本文引用: 1]
[23]
田中博文, 蔡千华 钢轨波磨的车上监视方法
[J]. 国外铁道车辆 , 2017 , 54 (1 ): 31 - 36
[本文引用: 1]
TANAKA Hirofumi, CAI Qian-hua The on-vehicle supervision method for rail corrugation
[J]. Foreign Rolling Stock , 2017 , 54 (1 ): 31 - 36
[本文引用: 1]
[24]
郭建强, 朱雷威, 刘晓龙, 等 地铁司机室噪声与钢轨波磨关系的试验与仿真研究
[J]. 机械工程学报 , 2019 , 55 (16 ): 141 - 147
DOI:10.3901/JME.2019.16.141
[本文引用: 1]
GUO Jian-qiang, ZHU Lei-wei, LIU Xiao-long, et al Experimental and simulation study on the relationship between interior noise of metro cab and rail corrugation
[J]. Journal of Mechanical Engineering , 2019 , 55 (16 ): 141 - 147
DOI:10.3901/JME.2019.16.141
[本文引用: 1]
[25]
冯陈程, 刘晓龙, 李伟, 等 短波长钢轨波磨对地铁车辆车内噪声的影响
[J]. 噪声与振动控制 , 2018 , 38 (6 ): 113 - 117
[本文引用: 1]
FENG Chen-cheng, LIU Xiao-long, Li Wei, et al Influence of short pitch rail corrugation on interior noise of metro vehicles
[J]. Noise and Vibration Control , 2018 , 38 (6 ): 113 - 117
[本文引用: 1]
[26]
江航, 尚春阳, 高瑞鹏 基于EMD和神经网络的轮轨故障噪声诊断识别方法研究
[J]. 振动与冲击 , 2014 , 33 (17 ): 34 - 38
[本文引用: 1]
JIANG Hang, SHANG Chun-yang, GAO Rui-peng Wheel /rail fault noise diagnosis method based on EMD and neural network
[J]. Journal of Vibration and Shock , 2014 , 33 (17 ): 34 - 38
[本文引用: 1]
[27]
周志青, 胡茑庆, 黄玉, 等. 基于支持向量机的轨道波磨检测方法研究[C]// 第十三届全国振动理论及应用学术会议论文集. 西安: [s.n.], 2019: 193−197.
[本文引用: 1]
ZHOU Zhi-qing, HU Niao-qing, HUANG Yu, et al. Research on rail corrugation detection method based on support vector machine [C]// Proceedings of the 13th National Conference on Vibration Theory and Applications . Xi'an: [s.n.], 2019: 193-197.
[本文引用: 1]
[28]
赵立强. 基于列车振动信息的钢轨波磨状态检测与识别研究[D]. 北京: 北京交通大学, 2021.
[本文引用: 1]
ZHAO Li-qiang. Research on detection and recognition of rail corrugation based on train vibration information [D]. Beijing: Beijing Jiaotong University, 2021.
[本文引用: 1]
[29]
张珍珍. 基于时频分析与数据挖掘的钢轨波磨检测[D]. 北京: 华北电力大学, 2021.
[本文引用: 1]
ZHANG Zhen-zhen. Detection of rail corrugation based on time-frequency analysis and data mining [D]. Beijing: North China Electric Power University, 2021.
[本文引用: 1]
[30]
肖炳环, 刘金朝, 牛留斌, 等 基于 WPD-ASTFT 和 SVM 重载铁路钢轨波磨诊断方法
[J]. 铁道车辆 , 2021 , 59 (6 ): 31 - 35+48
[本文引用: 1]
XIAO Bing-huan, LIU Jin-zhao, NIU Liu-bin, et al Diagnosis method of rail corrugation for heavy haul railway based on WPD-ASTFT and SVM
[J]. Railway Vehicles , 2021 , 59 (6 ): 31 - 35+48
[本文引用: 1]
[31]
谢清林, 陶功权, 温泽峰 基于一维卷积神经网络的地铁 钢轨波磨识别方法
[J]. 中南大学学报: 自然科学版 , 2021 , 52 (4 ): 1371 - 1379
[本文引用: 1]
XIE Qing-lin, TAO Gong-quan, WEN Ze-feng Detection method of metro rail corrugation based on 1-dimensional convolutional neural network
[J]. Journal of Central South University: Science and Technology , 2021 , 52 (4 ): 1371 - 1379
[本文引用: 1]
[32]
谢乐, 衡熙丹, 刘洋, 等 基于线性判别分析和分步机器学习的变压器故障诊断
[J]. 浙江大学学报: 工学版 , 2020 , 54 (11 ): 2266 - 2272
[本文引用: 1]
XIE Le, HENG Xi-dan, LIU Yang, et al Transformer fault diagnosis based on linear discriminant analysis and step-by-step machine learning
[J]. Journal of Zhejiang University: Engineering Science , 2020 , 54 (11 ): 2266 - 2272
[本文引用: 1]
[33]
陈之毅, 黄鹏飞 基于概率神经网络的地铁车站易损性分析
[J]. 同济大学学报: 自然科学版 , 2021 , 49 (6 ): 791 - 798+756
[本文引用: 1]
CHEN Zhi-yi, HUANG Peng-fei Fragility analysis of a subway station based on probability artificial neural network
[J]. Journal of Tongji University: Natural Science , 2021 , 49 (6 ): 791 - 798+756
[本文引用: 1]
[34]
冯建鑫, 王雅雷, 王强, 等 基于改进粒子群算法的快速反射镜自抗扰控制
[J]. 系统工程与电子技术 , 2021 , 43 (12 ): 3675 - 3682
[本文引用: 1]
FENG Jin-xin, WANG Ya-lei, WANG Qiang, et al Fast reflector self-anti-disturbance control based on improved particle swarm algorithm
[J]. Systems Engineering and Electronics Technology , 2021 , 43 (12 ): 3675 - 3682
[本文引用: 1]
[35]
陈昆弘, 刘小峰 基于循环相关和LPSO算法的自适应MCKD方法的滚动轴承早期故障特征提取
[J]. 振动与冲击 , 2017 , 36 (22 ): 80 - 85+157
[本文引用: 1]
CHEN Kun-hong, LIU Xiao-feng Incipient fault diagnosis of rolling element bearing based on adaptive maximum correlated kurtosis deconvolution
[J]. Journal of Vibration and Shock , 2017 , 36 (22 ): 80 - 85+157
[本文引用: 1]
[36]
陈秋莲, 郑以君, 蒋环宇, 等 基于神经网络改进粒子群算法的动态路径规划
[J]. 华中科技大学学报: 自然科学版 , 2021 , 49 (2 ): 51 - 55
[本文引用: 1]
CHEN Qiu-lian, ZHENG Yi-jun, JIANG Huan-yu, et al Improved particle swarm optimization algorithm based on neural network for dynamic path planning
[J]. Journal of Huazhong University of Science and Technology: Natural Science Edition , 2021 , 49 (2 ): 51 - 55
[本文引用: 1]
[37]
全国声学标准化技术委员会. 声学 轨道车辆内部噪声测量: GB/T 3449—2011 [S]. 北京: 中国标准出版社, 2011.
[本文引用: 2]
[38]
European Committee for Standardization. Acoustics-railway applications-measurement of noise emitted by railbound vehicles: ISO3095: 2013 [S]. London: British Standards Institution, 2013.
[本文引用: 2]
[39]
刘泽鹏. 基于经验模态分解和优化概率神经网络的变压器励磁涌流识别研究[D]. 北京: 华北电力大学, 2021.
[本文引用: 1]
LIU Ze-peng. Research on transformer magnetizing inrush current identification based on empirical mode decomposition and optimal probability [D]. Beijing: North China Electric Power University, 2021.
[本文引用: 1]
[40]
尉雅晨. 改进粒子群算法研究及其在柔性车间调度问题中的应用[D]. 兰州: 兰州理工大学, 2020.
[本文引用: 1]
WEI Ya-chen. Research on improved particle swarm optimization and its application in flexible job shop scheduling [D]. Lanzhou: Lanzhou University of Technology, 2020.
[本文引用: 1]
[41]
严阳. 粒子群算法的改进及其在非线性问题中的应用[D]. 广州: 华南理工大学, 2010.
[本文引用: 1]
YAN Yang. The improved of particle swarm optimization and its application in solving nonlinear problem [D]. Guangzhou: South China University of Technology, 2010.
[本文引用: 1]
基于梯形轨枕轨道振动特性的钢轨波磨研究
1
2020
... 钢轨波浪形磨耗(简称钢轨波磨)是地铁线路中常见的轨道病害[1 -2 ] ,也是缩短车辆及轨道零部件服役寿命的主要原因之一,对地铁运营的安全性和旅客乘车的舒适性有严重影响[3 ] . 地铁运营部门须定期打磨钢轨波磨地段,因此如何准确高效识别钢轨波磨是铁路行业的热点问题. ...
基于梯形轨枕轨道振动特性的钢轨波磨研究
1
2020
... 钢轨波浪形磨耗(简称钢轨波磨)是地铁线路中常见的轨道病害[1 -2 ] ,也是缩短车辆及轨道零部件服役寿命的主要原因之一,对地铁运营的安全性和旅客乘车的舒适性有严重影响[3 ] . 地铁运营部门须定期打磨钢轨波磨地段,因此如何准确高效识别钢轨波磨是铁路行业的热点问题. ...
基于轨道振动特征的地铁钢轨波磨成因研究
2
2021
... 钢轨波浪形磨耗(简称钢轨波磨)是地铁线路中常见的轨道病害[1 -2 ] ,也是缩短车辆及轨道零部件服役寿命的主要原因之一,对地铁运营的安全性和旅客乘车的舒适性有严重影响[3 ] . 地铁运营部门须定期打磨钢轨波磨地段,因此如何准确高效识别钢轨波磨是铁路行业的热点问题. ...
... 根据彭华等[2 ] 的研究结果,地铁车辆内部的噪声主要来源于轮轨振动激励,钢轨波磨引起的轮轨激励频率计算式为 ...
基于轨道振动特征的地铁钢轨波磨成因研究
2
2021
... 钢轨波浪形磨耗(简称钢轨波磨)是地铁线路中常见的轨道病害[1 -2 ] ,也是缩短车辆及轨道零部件服役寿命的主要原因之一,对地铁运营的安全性和旅客乘车的舒适性有严重影响[3 ] . 地铁运营部门须定期打磨钢轨波磨地段,因此如何准确高效识别钢轨波磨是铁路行业的热点问题. ...
... 根据彭华等[2 ] 的研究结果,地铁车辆内部的噪声主要来源于轮轨振动激励,钢轨波磨引起的轮轨激励频率计算式为 ...
Field measurement analysis and control measures evaluation of metro vehicle noise caused by rail corrugation
1
2021
... 钢轨波浪形磨耗(简称钢轨波磨)是地铁线路中常见的轨道病害[1 -2 ] ,也是缩短车辆及轨道零部件服役寿命的主要原因之一,对地铁运营的安全性和旅客乘车的舒适性有严重影响[3 ] . 地铁运营部门须定期打磨钢轨波磨地段,因此如何准确高效识别钢轨波磨是铁路行业的热点问题. ...
1
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
1
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
城市轨道交通曲线钢轨波磨检测与评价方法研究
1
2011
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
城市轨道交通曲线钢轨波磨检测与评价方法研究
1
2011
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
Rail corrugation: advances in measurement, understanding and treatment
1
2005
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
1
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
基于组合弦测的钢轨波磨广域测量方法
1
2018
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
基于组合弦测的钢轨波磨广域测量方法
1
2018
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
Measurement of railhead longitudinal profiles: a comparison of different techniques
1
1996
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
轨道高低不平顺敏感波长的分布特征及其影响因素的研究
1
2015
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
轨道高低不平顺敏感波长的分布特征及其影响因素的研究
1
2015
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
1
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
基于钢轨图像频域特征的钢轨波磨检测方法
0
2016
基于钢轨图像频域特征的钢轨波磨检测方法
0
2016
基于多线结构光视觉的钢轨波磨动态测量方法
1
2018
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
基于多线结构光视觉的钢轨波磨动态测量方法
1
2018
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
1
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
1
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
A tool for the detection and quantification of rail corrugation
1
2010
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
Urban rail track condition monitoring on in-service vehicle acceleration measurements
1
2016
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
1
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
数学形态学滤波在钢轨波磨波长识别中的应用
1
2021
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
数学形态学滤波在钢轨波磨波长识别中的应用
1
2021
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
基于三维轮轨瞬态动力学模型的钢轨波磨不平顺动力影响与识别
1
2020
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
基于三维轮轨瞬态动力学模型的钢轨波磨不平顺动力影响与识别
1
2020
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
钢轨波磨的车上监视方法
1
2017
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
钢轨波磨的车上监视方法
1
2017
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
地铁司机室噪声与钢轨波磨关系的试验与仿真研究
1
2019
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
地铁司机室噪声与钢轨波磨关系的试验与仿真研究
1
2019
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
短波长钢轨波磨对地铁车辆车内噪声的影响
1
2018
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
短波长钢轨波磨对地铁车辆车内噪声的影响
1
2018
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
基于EMD和神经网络的轮轨故障噪声诊断识别方法研究
1
2014
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
基于EMD和神经网络的轮轨故障噪声诊断识别方法研究
1
2014
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
1
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
1
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
1
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
1
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
1
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
1
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
基于 WPD-ASTFT 和 SVM 重载铁路钢轨波磨诊断方法
1
2021
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
基于 WPD-ASTFT 和 SVM 重载铁路钢轨波磨诊断方法
1
2021
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
基于一维卷积神经网络的地铁 钢轨波磨识别方法
1
2021
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
基于一维卷积神经网络的地铁 钢轨波磨识别方法
1
2021
... 钢轨波磨检测方法[4 ] 按原理分为人工检测法、弦测法、惯性基准法、机器视觉方法. 人工检测法须使用波磨检测尺[5 ] 或波磨检测小车[6 ] 测量现场钢轨波磨,不适用于钢轨波磨的大规模检测. 由于弦测法的参考基准随钢轨高低不平顺变化而变化,造成传递函数 (测量值与实际值之比)不恒为1,不可避免地存在误差[7 -9 ] . 惯性基准法无法排除车轮故障的影响,并且由于采用高通滤波器,车速较低时的测量误差相对较大[10 -11 ] . 机器视觉法依赖高精度的光电及摄像设备以及复杂的图像后处理技术,虽测量精度较高,但其应用成本昂贵[12 -15 ] . 钢轨波磨会引起车辆系统产生明显动态响应,因此基于车辆动态响应的钢轨波磨检测也受到众多专家学者的关注. Hopkins 等[16 -17 ] 利用小波变换处理轴箱加速度数据,实现钢轨波磨的检测. Gomes 等[18 ] 基于1/3倍频程和小波包对轴箱加速度进行分析,提取了钢轨短波不平顺. Wei 等[19 ] 提出轨面不平顺对转向架和车体位移的频率响应函数,并在上海地铁1号线验证了检测系统的有效性. Kojima 等[20 ] 采用小波变换的多分辨率分析法处理车体垂向振动加速度,发现与钢轨波磨相关的频率位于第3层细节分量. 谢清林[21 -22 ] 等基于钢轨波磨工况下的轴箱加速度数据,实现了钢轨波磨波长和波深的检测. 除在车辆部件上安装加速度或位移传感器外,还可利用车内噪声来检测钢轨波磨[23 ] . 郭建强等[24 ] 发现钢轨波磨的激励频率与司机室噪声的显著频率一致. 冯陈程等[25 ] 发现车内噪声的主频为400~700 Hz,与波长为30~50 mm的钢轨波磨激励频率基本一致. 除了传统检测方法外,机器学习方法也被应用于钢轨波磨检测领域. 江航等[26 ] 以轮轨噪声各层本征模态分量的能量和峭度作为BP神经网络的输入特征,用于区分正常钢轨和波磨钢轨,识别率达到93.82%. 周志青等[27 ] 以轴箱加速度信号各频带的功率和峭度作为特征向量,提出基于支持向量机的钢轨波磨识别方法,准确率为94.67%. 赵立强[28 ] 基于车体振动加速度数据,分别通过贝叶斯分类器和深度卷积神经网络识别波磨钢轨,准确率分别为92.00%、96.00%. 张珍珍[29 ] 基于轴箱加速度数据,通过小波包结合支持向量机方法识别钢轨波磨,准确率达到98.10%. 肖炳环等[30 ] 基于轴箱加速度数据,采用WPD-ASTFT和支持向量机提出重载铁路钢轨波磨诊断方法,准确率超过93%. 谢清林等[31 ] 利用轴箱加速度,提出基于卷积神经网络的地铁钢轨波磨识别方法,准确率达到99.20%. ...
基于线性判别分析和分步机器学习的变压器故障诊断
1
2020
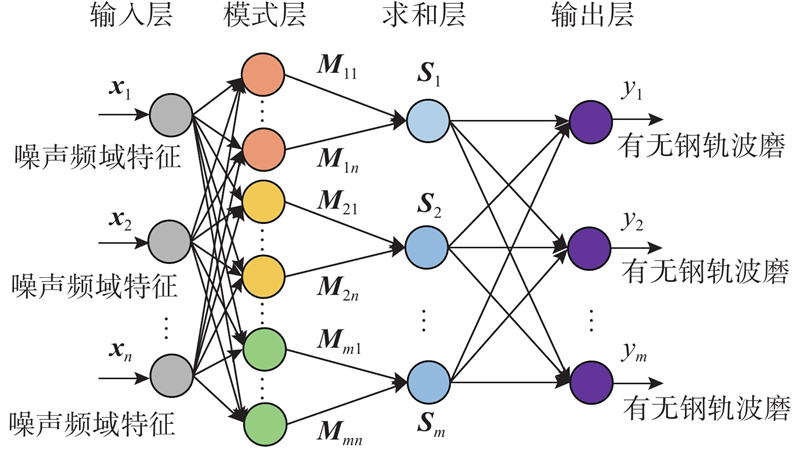
... 既有研究多采用车体部件的振动响应(大部分为轴箱加速度)来区分波磨钢轨和正常钢轨. 加速度传感器在轴箱上的安装位置有限,且安装轴箱加速度的检测列车相对较少,导致轴箱加速度数据的获取难度较大. 车内噪声的数据获取相对容易,声压传感器在车厢内的可安装位置较多,安装方便. 对于车内噪声数据和钢轨波磨的研究主要集中于定性或定量分析两者的关系,基于车内噪声数据特征对波磨钢轨和正常钢轨进行分类的研究较少. 概率神经网络(probabilistic neural network, PNN)采用贝叶斯决策理论,广泛应用于模式分类,但网络中平滑因子的大小会对分类准确率产生极大影响[32 -33 ] . 本研究1)采用粒子群优化算法对传统概率神经网络模型中的平滑因子进行寻优,提出改进的基于概率神经网络的识别算法:粒子概率神经网络(particle probabilistic neural network,PPNN)算法,以提高模式分类的准确率;2)采集轨面粗糙度及其对应的车内噪声数据,分析轨面粗糙度与车内噪声的联系,明确与钢轨波磨相关的车内噪声特征,并将车内噪声特征输入粒子概率神经网络算法,完成钢轨波磨的识别. ...
基于线性判别分析和分步机器学习的变压器故障诊断
1
2020
... 既有研究多采用车体部件的振动响应(大部分为轴箱加速度)来区分波磨钢轨和正常钢轨. 加速度传感器在轴箱上的安装位置有限,且安装轴箱加速度的检测列车相对较少,导致轴箱加速度数据的获取难度较大. 车内噪声的数据获取相对容易,声压传感器在车厢内的可安装位置较多,安装方便. 对于车内噪声数据和钢轨波磨的研究主要集中于定性或定量分析两者的关系,基于车内噪声数据特征对波磨钢轨和正常钢轨进行分类的研究较少. 概率神经网络(probabilistic neural network, PNN)采用贝叶斯决策理论,广泛应用于模式分类,但网络中平滑因子的大小会对分类准确率产生极大影响[32 -33 ] . 本研究1)采用粒子群优化算法对传统概率神经网络模型中的平滑因子进行寻优,提出改进的基于概率神经网络的识别算法:粒子概率神经网络(particle probabilistic neural network,PPNN)算法,以提高模式分类的准确率;2)采集轨面粗糙度及其对应的车内噪声数据,分析轨面粗糙度与车内噪声的联系,明确与钢轨波磨相关的车内噪声特征,并将车内噪声特征输入粒子概率神经网络算法,完成钢轨波磨的识别. ...
基于概率神经网络的地铁车站易损性分析
1
2021
... 既有研究多采用车体部件的振动响应(大部分为轴箱加速度)来区分波磨钢轨和正常钢轨. 加速度传感器在轴箱上的安装位置有限,且安装轴箱加速度的检测列车相对较少,导致轴箱加速度数据的获取难度较大. 车内噪声的数据获取相对容易,声压传感器在车厢内的可安装位置较多,安装方便. 对于车内噪声数据和钢轨波磨的研究主要集中于定性或定量分析两者的关系,基于车内噪声数据特征对波磨钢轨和正常钢轨进行分类的研究较少. 概率神经网络(probabilistic neural network, PNN)采用贝叶斯决策理论,广泛应用于模式分类,但网络中平滑因子的大小会对分类准确率产生极大影响[32 -33 ] . 本研究1)采用粒子群优化算法对传统概率神经网络模型中的平滑因子进行寻优,提出改进的基于概率神经网络的识别算法:粒子概率神经网络(particle probabilistic neural network,PPNN)算法,以提高模式分类的准确率;2)采集轨面粗糙度及其对应的车内噪声数据,分析轨面粗糙度与车内噪声的联系,明确与钢轨波磨相关的车内噪声特征,并将车内噪声特征输入粒子概率神经网络算法,完成钢轨波磨的识别. ...
基于概率神经网络的地铁车站易损性分析
1
2021
... 既有研究多采用车体部件的振动响应(大部分为轴箱加速度)来区分波磨钢轨和正常钢轨. 加速度传感器在轴箱上的安装位置有限,且安装轴箱加速度的检测列车相对较少,导致轴箱加速度数据的获取难度较大. 车内噪声的数据获取相对容易,声压传感器在车厢内的可安装位置较多,安装方便. 对于车内噪声数据和钢轨波磨的研究主要集中于定性或定量分析两者的关系,基于车内噪声数据特征对波磨钢轨和正常钢轨进行分类的研究较少. 概率神经网络(probabilistic neural network, PNN)采用贝叶斯决策理论,广泛应用于模式分类,但网络中平滑因子的大小会对分类准确率产生极大影响[32 -33 ] . 本研究1)采用粒子群优化算法对传统概率神经网络模型中的平滑因子进行寻优,提出改进的基于概率神经网络的识别算法:粒子概率神经网络(particle probabilistic neural network,PPNN)算法,以提高模式分类的准确率;2)采集轨面粗糙度及其对应的车内噪声数据,分析轨面粗糙度与车内噪声的联系,明确与钢轨波磨相关的车内噪声特征,并将车内噪声特征输入粒子概率神经网络算法,完成钢轨波磨的识别. ...
基于改进粒子群算法的快速反射镜自抗扰控制
1
2021
... 式中:t 为当前种群进化次数;p ij p gj $ \omega $ c 1 、c 2 均为学习因子,通常取2.0[34 ] ;r 1j 、r 2j 为[0, 1]的随机数. PPNN无法避免粒子群优化算法存在的“早熟”问题,为了提高PPNN的全局搜索能力和搜索效率,选用凹函数递减惯性权值[35 ] :使得算法在初始阶段保持较大的惯性权值,保证全局搜索,避免陷入局部最优,迭代后期惯性权值应较小,使得算法更快达到收敛. 凹函数递减惯性权值的计算式为 ...
基于改进粒子群算法的快速反射镜自抗扰控制
1
2021
... 式中:t 为当前种群进化次数;p ij p gj $ \omega $ c 1 、c 2 均为学习因子,通常取2.0[34 ] ;r 1j 、r 2j 为[0, 1]的随机数. PPNN无法避免粒子群优化算法存在的“早熟”问题,为了提高PPNN的全局搜索能力和搜索效率,选用凹函数递减惯性权值[35 ] :使得算法在初始阶段保持较大的惯性权值,保证全局搜索,避免陷入局部最优,迭代后期惯性权值应较小,使得算法更快达到收敛. 凹函数递减惯性权值的计算式为 ...
基于循环相关和LPSO算法的自适应MCKD方法的滚动轴承早期故障特征提取
1
2017
... 式中:t 为当前种群进化次数;p ij p gj $ \omega $ c 1 、c 2 均为学习因子,通常取2.0[34 ] ;r 1j 、r 2j 为[0, 1]的随机数. PPNN无法避免粒子群优化算法存在的“早熟”问题,为了提高PPNN的全局搜索能力和搜索效率,选用凹函数递减惯性权值[35 ] :使得算法在初始阶段保持较大的惯性权值,保证全局搜索,避免陷入局部最优,迭代后期惯性权值应较小,使得算法更快达到收敛. 凹函数递减惯性权值的计算式为 ...
基于循环相关和LPSO算法的自适应MCKD方法的滚动轴承早期故障特征提取
1
2017
... 式中:t 为当前种群进化次数;p ij p gj $ \omega $ c 1 、c 2 均为学习因子,通常取2.0[34 ] ;r 1j 、r 2j 为[0, 1]的随机数. PPNN无法避免粒子群优化算法存在的“早熟”问题,为了提高PPNN的全局搜索能力和搜索效率,选用凹函数递减惯性权值[35 ] :使得算法在初始阶段保持较大的惯性权值,保证全局搜索,避免陷入局部最优,迭代后期惯性权值应较小,使得算法更快达到收敛. 凹函数递减惯性权值的计算式为 ...
基于神经网络改进粒子群算法的动态路径规划
1
2021
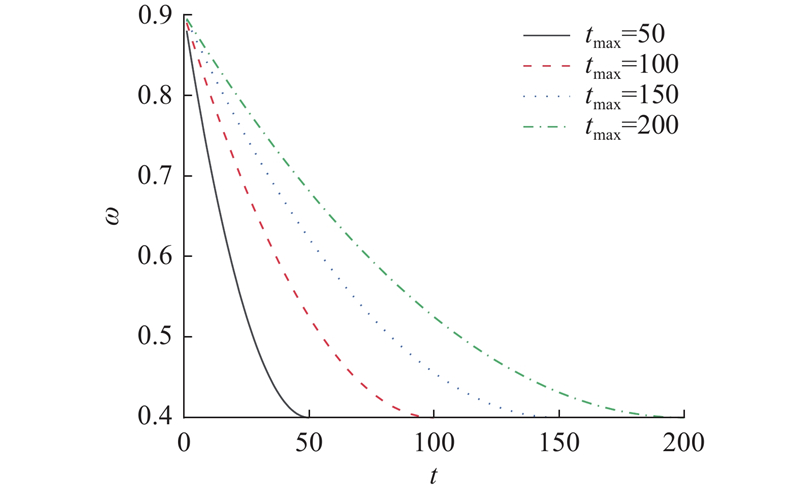
... 式中: $ {\omega _{\max }} $ $ {\omega _{\min }} $ $ {t_{\max }} $ [36 ] . 如图2 所示为种群进化最大次数分别为50、100、150、200的速度更新惯性权值. ...
基于神经网络改进粒子群算法的动态路径规划
1
2021
... 式中: $ {\omega _{\max }} $ $ {\omega _{\min }} $ $ {t_{\max }} $ [36 ] . 如图2 所示为种群进化最大次数分别为50、100、150、200的速度更新惯性权值. ...
2
... 根据文献[37 ],在该条线路开展上下行全程的车内噪声测试,测量前检查测试车辆的走行部,确定并无如踏面失圆的故障. 如图5 所示为车内噪声测试所用仪器:1)声压传感器,作用是感应车内噪声的声压变化,布置于车辆地板之上1.2 m处,采样频率设置为51.2 kHz;2)风罩,作用是屏蔽空气流动产生的干扰噪声;3)声压采集仪,作用是接受声压传感器传递的信号,并记录声压;4)三脚支架,作用是固定测试仪器. ...
... 车内噪声数据集的划分按照以下步骤进行:1)噪声测试时,以相邻2个车站为一个测试单元,得到相邻站间的车内噪声,并与地铁运营公司提供的列车运行图进行比对,明确车内噪声与地铁线路里程的关系;钢轨波磨测试时,也以相邻2个车站为1个测试单元,得到相邻站间的钢轨表面粗糙度,并与地铁线路设计图纸进行比对,明确钢轨表面粗糙度与地铁线路里程的关系;基于以上两者,即可得到钢轨表面粗糙度与车内噪声的匹配关系. 2)根据文献[38 ],分析钢轨表面粗糙度,若某一特定波长的钢轨表面粗糙度超过ISO3095限值6 dB,或连续3个特定波长的钢轨粗糙度超过ISO3095限值3 dB,则可认为是波磨超限,否则为无波磨或轻微波磨. 3)根据文献[37 ],对于匀速行驶的列车,最短的测量时间T 不能小于5 s,因此选取的每组车内噪声的时间长度均为5 s. 基于以上原则,得到无波磨或轻微波磨区段的噪声数据233组,其中训练集数据163组,测试集数据70组;波磨超限区段的噪声数据235组,其中训练集数据164组,测试集数据71组. PPNN中超参数的选择将直接影响钢轨波磨的识别准确率,因此对训练集采用10折交叉验证的方式进行划分,即将训练集平均划分为10份,利用其中9份作为超参数寻优过程中的训练集,其余1份作为验证集,如此重复10次,得到最高的波磨识别准确率对应的超参数. 得到最优超参数后,采用训练集(原始数据集的70%)对模型进行训练,采用测试集(原始数据集的30%)对模型进行测试,最终以测试集得到的钢轨波磨识别准确率作为PPNN的评价指标. ...
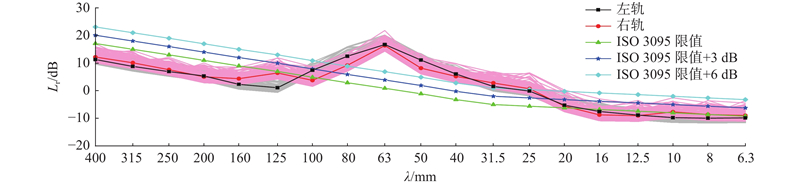
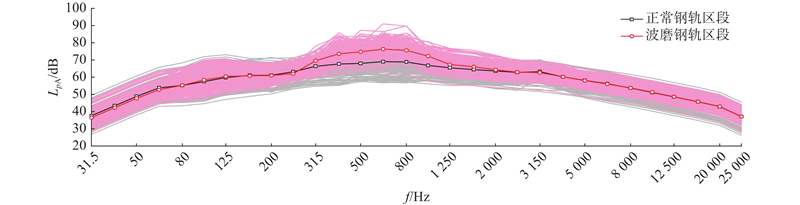
2
... 钢轨波磨测量仪测得的轨面不平顺数据是与线路长度相关的随机过程,由不同波长、幅值和相位的钢轨表面不平顺叠加而成,应采用随机过程理论的统计参数进行分析. 根据文献[38 ]计算钢轨表面的粗糙度级,对钢轨波磨进行评价. ...
... 车内噪声数据集的划分按照以下步骤进行:1)噪声测试时,以相邻2个车站为一个测试单元,得到相邻站间的车内噪声,并与地铁运营公司提供的列车运行图进行比对,明确车内噪声与地铁线路里程的关系;钢轨波磨测试时,也以相邻2个车站为1个测试单元,得到相邻站间的钢轨表面粗糙度,并与地铁线路设计图纸进行比对,明确钢轨表面粗糙度与地铁线路里程的关系;基于以上两者,即可得到钢轨表面粗糙度与车内噪声的匹配关系. 2)根据文献[38 ],分析钢轨表面粗糙度,若某一特定波长的钢轨表面粗糙度超过ISO3095限值6 dB,或连续3个特定波长的钢轨粗糙度超过ISO3095限值3 dB,则可认为是波磨超限,否则为无波磨或轻微波磨. 3)根据文献[37 ],对于匀速行驶的列车,最短的测量时间T 不能小于5 s,因此选取的每组车内噪声的时间长度均为5 s. 基于以上原则,得到无波磨或轻微波磨区段的噪声数据233组,其中训练集数据163组,测试集数据70组;波磨超限区段的噪声数据235组,其中训练集数据164组,测试集数据71组. PPNN中超参数的选择将直接影响钢轨波磨的识别准确率,因此对训练集采用10折交叉验证的方式进行划分,即将训练集平均划分为10份,利用其中9份作为超参数寻优过程中的训练集,其余1份作为验证集,如此重复10次,得到最高的波磨识别准确率对应的超参数. 得到最优超参数后,采用训练集(原始数据集的70%)对模型进行训练,采用测试集(原始数据集的30%)对模型进行测试,最终以测试集得到的钢轨波磨识别准确率作为PPNN的评价指标. ...
1
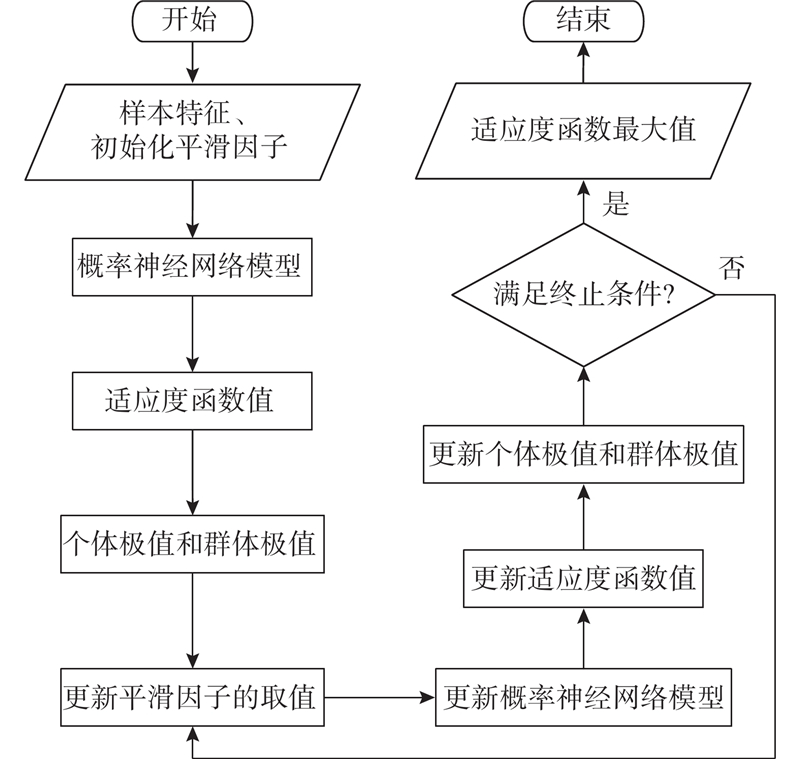
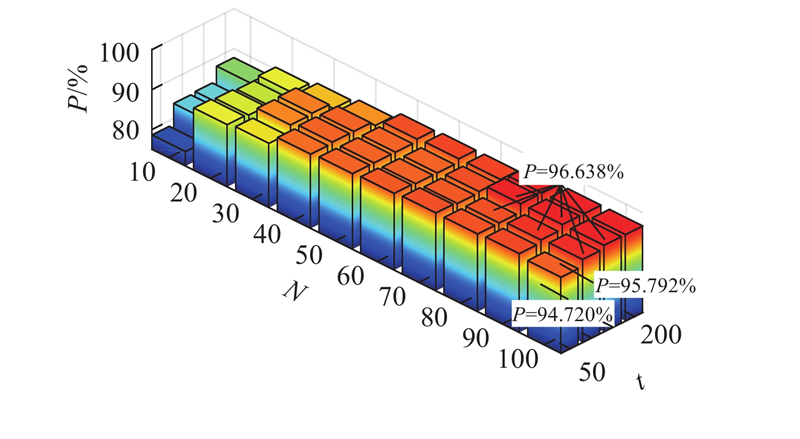
... PPNN中种群规模以及种群进化次数对算法识别钢轨波磨的能力有重要影响,针对粒子群优化算法容易出现的“早熟”问题,研究者进行了不同程度的改进,但算法的最优参数还需要从具体应用出发. 为了提高PPNN的性能,对不同种群规模以及不同种群进化次数的PPNN进行研究. 采用10折交叉验证结果的平均值,可以避免参数优化过程中训练集和验证集的选择对结果的影响;为了避免PPNN中速度更新公式中随机参数对识别结果的影响,对训练集和验证集进行10次10折交叉验证,以10次10折交叉验证结果的平均值作为不同超参数下PPNN算法识别能力的评价指标. 根据文献[39 ],概率神经网络中的平滑因子一般取值为0.1. 为了保证平滑因子的搜索空间足够大,算法中粒子空间位置的上限为0.1×1 000=100,下限为0.1/1 000=0.000 1. 对于种群规模,一般取 20~40 个粒子就能解决大多数问题,对于一些特定的或复杂的问题,粒子个数有时可以取到100[40 -41 ] . 为了保证能够选取到最优的种群规模N ,将种群规模设置为10,20,30,···,100. 种群的最大进化次数一般根据具体问题来确定,在本研究中种群进化次数设置为50、100、150、200次. ...
1
... PPNN中种群规模以及种群进化次数对算法识别钢轨波磨的能力有重要影响,针对粒子群优化算法容易出现的“早熟”问题,研究者进行了不同程度的改进,但算法的最优参数还需要从具体应用出发. 为了提高PPNN的性能,对不同种群规模以及不同种群进化次数的PPNN进行研究. 采用10折交叉验证结果的平均值,可以避免参数优化过程中训练集和验证集的选择对结果的影响;为了避免PPNN中速度更新公式中随机参数对识别结果的影响,对训练集和验证集进行10次10折交叉验证,以10次10折交叉验证结果的平均值作为不同超参数下PPNN算法识别能力的评价指标. 根据文献[39 ],概率神经网络中的平滑因子一般取值为0.1. 为了保证平滑因子的搜索空间足够大,算法中粒子空间位置的上限为0.1×1 000=100,下限为0.1/1 000=0.000 1. 对于种群规模,一般取 20~40 个粒子就能解决大多数问题,对于一些特定的或复杂的问题,粒子个数有时可以取到100[40 -41 ] . 为了保证能够选取到最优的种群规模N ,将种群规模设置为10,20,30,···,100. 种群的最大进化次数一般根据具体问题来确定,在本研究中种群进化次数设置为50、100、150、200次. ...
1
... PPNN中种群规模以及种群进化次数对算法识别钢轨波磨的能力有重要影响,针对粒子群优化算法容易出现的“早熟”问题,研究者进行了不同程度的改进,但算法的最优参数还需要从具体应用出发. 为了提高PPNN的性能,对不同种群规模以及不同种群进化次数的PPNN进行研究. 采用10折交叉验证结果的平均值,可以避免参数优化过程中训练集和验证集的选择对结果的影响;为了避免PPNN中速度更新公式中随机参数对识别结果的影响,对训练集和验证集进行10次10折交叉验证,以10次10折交叉验证结果的平均值作为不同超参数下PPNN算法识别能力的评价指标. 根据文献[39 ],概率神经网络中的平滑因子一般取值为0.1. 为了保证平滑因子的搜索空间足够大,算法中粒子空间位置的上限为0.1×1 000=100,下限为0.1/1 000=0.000 1. 对于种群规模,一般取 20~40 个粒子就能解决大多数问题,对于一些特定的或复杂的问题,粒子个数有时可以取到100[40 -41 ] . 为了保证能够选取到最优的种群规模N ,将种群规模设置为10,20,30,···,100. 种群的最大进化次数一般根据具体问题来确定,在本研究中种群进化次数设置为50、100、150、200次. ...
1
... PPNN中种群规模以及种群进化次数对算法识别钢轨波磨的能力有重要影响,针对粒子群优化算法容易出现的“早熟”问题,研究者进行了不同程度的改进,但算法的最优参数还需要从具体应用出发. 为了提高PPNN的性能,对不同种群规模以及不同种群进化次数的PPNN进行研究. 采用10折交叉验证结果的平均值,可以避免参数优化过程中训练集和验证集的选择对结果的影响;为了避免PPNN中速度更新公式中随机参数对识别结果的影响,对训练集和验证集进行10次10折交叉验证,以10次10折交叉验证结果的平均值作为不同超参数下PPNN算法识别能力的评价指标. 根据文献[39 ],概率神经网络中的平滑因子一般取值为0.1. 为了保证平滑因子的搜索空间足够大,算法中粒子空间位置的上限为0.1×1 000=100,下限为0.1/1 000=0.000 1. 对于种群规模,一般取 20~40 个粒子就能解决大多数问题,对于一些特定的或复杂的问题,粒子个数有时可以取到100[40 -41 ] . 为了保证能够选取到最优的种群规模N ,将种群规模设置为10,20,30,···,100. 种群的最大进化次数一般根据具体问题来确定,在本研究中种群进化次数设置为50、100、150、200次. ...
1
... PPNN中种群规模以及种群进化次数对算法识别钢轨波磨的能力有重要影响,针对粒子群优化算法容易出现的“早熟”问题,研究者进行了不同程度的改进,但算法的最优参数还需要从具体应用出发. 为了提高PPNN的性能,对不同种群规模以及不同种群进化次数的PPNN进行研究. 采用10折交叉验证结果的平均值,可以避免参数优化过程中训练集和验证集的选择对结果的影响;为了避免PPNN中速度更新公式中随机参数对识别结果的影响,对训练集和验证集进行10次10折交叉验证,以10次10折交叉验证结果的平均值作为不同超参数下PPNN算法识别能力的评价指标. 根据文献[39 ],概率神经网络中的平滑因子一般取值为0.1. 为了保证平滑因子的搜索空间足够大,算法中粒子空间位置的上限为0.1×1 000=100,下限为0.1/1 000=0.000 1. 对于种群规模,一般取 20~40 个粒子就能解决大多数问题,对于一些特定的或复杂的问题,粒子个数有时可以取到100[40 -41 ] . 为了保证能够选取到最优的种群规模N ,将种群规模设置为10,20,30,···,100. 种群的最大进化次数一般根据具体问题来确定,在本研究中种群进化次数设置为50、100、150、200次. ...
1
... PPNN中种群规模以及种群进化次数对算法识别钢轨波磨的能力有重要影响,针对粒子群优化算法容易出现的“早熟”问题,研究者进行了不同程度的改进,但算法的最优参数还需要从具体应用出发. 为了提高PPNN的性能,对不同种群规模以及不同种群进化次数的PPNN进行研究. 采用10折交叉验证结果的平均值,可以避免参数优化过程中训练集和验证集的选择对结果的影响;为了避免PPNN中速度更新公式中随机参数对识别结果的影响,对训练集和验证集进行10次10折交叉验证,以10次10折交叉验证结果的平均值作为不同超参数下PPNN算法识别能力的评价指标. 根据文献[39 ],概率神经网络中的平滑因子一般取值为0.1. 为了保证平滑因子的搜索空间足够大,算法中粒子空间位置的上限为0.1×1 000=100,下限为0.1/1 000=0.000 1. 对于种群规模,一般取 20~40 个粒子就能解决大多数问题,对于一些特定的或复杂的问题,粒子个数有时可以取到100[40 -41 ] . 为了保证能够选取到最优的种群规模N ,将种群规模设置为10,20,30,···,100. 种群的最大进化次数一般根据具体问题来确定,在本研究中种群进化次数设置为50、100、150、200次. ...