DVA具有良好的抑振性能,在桥梁[6]、大楼[7]及车辆系统[8-10]等领域都有广泛的应用. 隔振[11-12]和动力吸振技术是提高车辆平顺性的重要途径. Hrovat[13]指出被动动力吸振悬架的主要缺点是需要较大的调谐质量,导致DVA的安装位置大多被限制在非簧载质量上,从而对与车辆舒适性紧密相关的低频段振动抑制效果有限;杨晓峰等[14]提出动力吸振被动惯容车辆悬架,改善了车辆低频振动,DVA结构更加紧凑;葛正等[15]提出车辆主动惯容式动力吸振悬架和车身振动加速度补偿控制方法,使惯容式动力吸振悬架性能趋近于理想动力吸振悬架,并拓宽了动力吸振的减振频段;Fu[16]提出比例电磁吸振器,通过电磁参数调节和速度反馈控制,有效减小了设计频段内主系统振动;王维锐等[17]基于车辆悬架动静挠度的功能特性提出DVA的负刚度控制策略,与天棚阻尼控制策略相比具有更好的振动抑制效果;Zhang等[18]在传统被动悬架中引入惯容器、DVA,并采用改进的半主动天棚阻尼控制方法,实现了在更宽频带范围降低车辆振动、提高道路附着力.
在能量回收方面,Elvin等[19]建立单自由度振动系统的机械电磁耦合动力学模型,考虑线圈实际电感、电阻特性获取了最大振动回收功率时的系统参数表达式,并开展了试验验证. Kecik[20]建立摆式磁悬浮结构的机电耦合非线性振动能量回收模型,指出当DVA与主系统共振频率接近时可以增大85%的回收电流、减小10%的主系统振动水平. Zuo等[21]研究发现路面粗糙度、行驶速度和轮胎刚度对悬架油液阻尼器的能量回收潜力有较大影响. Guo等[22]通过齿轮传动将车辆减振器的直线运动转化为电机转子的旋转运动,以实现悬架振动能量回收. 白世鹏等[23]分别对布置在簧上质量和簧下质量的DVA参数进行匹配设计,对比分析2种布置方案对车身振动加速度、悬架动挠度、阻尼器耗散功率等动态特性的影响,该研究仅分析了DVA的振动能量回收潜力.
本研究结合动力吸振和电磁能量回收方法,在车辆簧上质量上引入兼具有减振、能量回收的电磁馈能式动力吸振器(electromagnetic energy regenerative dynamic vibration absorber,EMER-DVA),考虑线圈质量、电感和电阻等物理特性进行EMER-DVA的参数匹配设计,揭示频域、时域中EMER-DVA的振动特性及振动能量回收性能,以在回收部分振动能量的同时提高车辆舒适性.
1. EMER-DVA模型
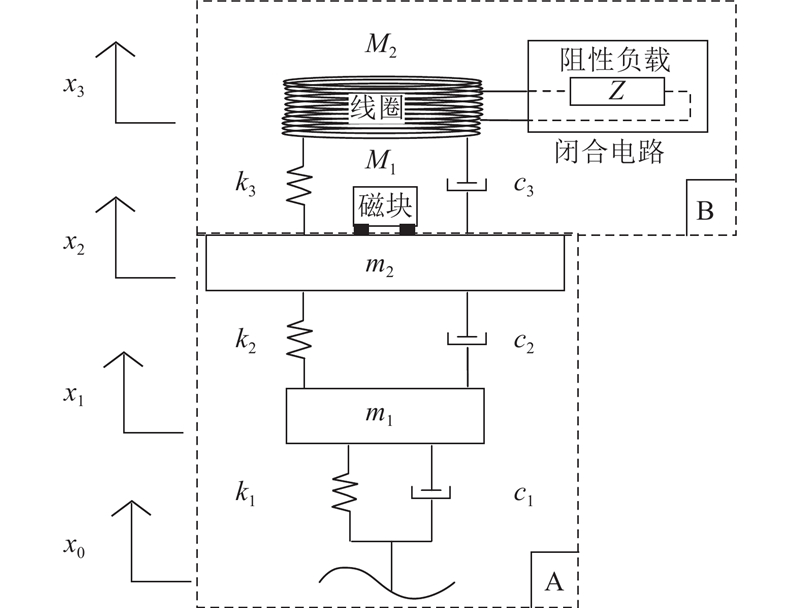
如图1所示,A部分为1/4车辆振动模型. 图中,m1、m2分别为簧下质量与簧上质量,k1、k2分别为轮胎及悬架刚度系数,c1、c2分别为轮胎及悬架阻尼系数,x0 为不平路面位移激励,x1与x2分别为簧下质量与簧上质量位移. B部分为簧上质量所引入的EMER-DVA,由质量为M1的磁块、质量为M2的线圈、刚度系数为k3的弹簧、阻尼系数为c3的阻尼器以及线圈外接闭合电路构成. 其中,磁块与簧上质量固定连接. 若无电磁力,其实质为线圈质量M2、弹簧k3、阻尼c3单元所组成的传统式DVA. 在车辆振动下,磁块与线圈在垂向发生相对运动,由于电磁感应,闭合电路可以产生电能输出,同时产生的电磁力也会对系统振动产生影响.
图 1
图 1 簧上EMER-DVA的1/4车辆动力学模型
Fig.1 Dynamical model of a quarter vehicle with EMER-DVA installed on sprung mass
考虑机械电磁耦合作用,基于牛顿第二定律推导簧上EMER-DVA的1/4车辆振动微分方程矩阵形式:
式中:X为输出位移向量,X = [x1, x2, x3]T;M、K、C、FAP分别为质量、刚度系数、阻尼系数和垂向安培力矩阵.
其中,FA为安培力.
由法拉第电磁感应定律,可以得到安培力矢量:
式中:
感应电动势矢量表达式如下:
式中:
将永磁体近似为一个圈数为Nm、平均半径为Rm的通电螺线管,线圈上的电流可以表示为
式中:Br为剩余磁感应强度;hm为螺线管(永磁体)的高度;μ0为真空中的磁导率,μ0 = 4π×10−7 T·m/A. 根据Biot-Savart定律可以得到任意位置处的磁感应强度:
式中:
图 2
根据电阻定律可以得到感应线圈的电阻为
式中:ρ为电阻率,铜线电阻率为1.75×10−8 Ω·m;l为导线长度,l=2πNRc;A为导线横截面积,A=πr2.
将式(2)、(3)叉乘展开,取垂向安培力分量FA及沿线圈方向的感应电动势分量ε,分别表示为
式中: BR 为垂向相对磁感应强度,因线圈和磁块间的相对位移较小,假设线圈在任何位置受到的磁感应强度 BR为常量.
线圈与外部负载组成闭合回路,根据Kirchoff 电压定律,可以得到
式中:Z 为外部电路电阻.
考虑车辆悬架空间及 DVA 的附加质量匹配以选择相关参数,本研究中感应线圈可取40层,每层150圈,使线圈的平均半径为 0. 16 m,高度为0. 32 m;线圈的电阻及电感根据式(6)、(7)计算而得;线圈与外部电路电阻组成负载型闭合回路,本研究中外部电阻取100 Ω. 磁块的选择应使磁感应强度越大越好,但考虑实际磁块尺寸与磁感应强度间的关系及磁块与线圈的相对位移,本研究选择 N45牌号的磁块,其表面磁感应强度约为4500 Gs,即0. 045 T.
线圈输出功率可以表示为
式中:U为输出电压.
部分模型参数取值如表1所示.
表 1 机械电磁耦合动力学模型参数
Tab.1
| 变量 | 物理含义 | 数值 | 变量 | 物理含义 | 数值 | |
| m1 /kg | 簧下质量 | 40 | Z /Ω | 电路电阻 | 100 | |
| m2 /kg | 簧上质量 | 380 | Li /H | 线圈电感 | 0.017 | |
| k1 /(N·m−1) | 轮胎刚度系数 | 180000 | N /圈 | 线圈圈数 | 6000 | |
| k2 /(N·m−1) | 悬架刚度系数 | 20000 | BR /T | 相对磁感应强度 | 0.02 | |
| c1 / (N·s·m−1) | 轮胎阻尼系数 | 300 | r /m | 线圈导线半径 | 0.001 | |
| c2 /(N·s·m−1) | 悬架阻尼系数 | 1300 | Rc /m | 线圈平均半径 | 0.16 | |
| M1 /kg | 磁块质量 | 1 | h /m | 线圈高度 | 0.32 | |
| Ri /Ω | 线圈内阻 | 5 | c /m | 线圈径向厚度 | 0.02 |
2. EMER-DVA参数匹配
若多自由度动力学系统相邻两阶模态频率之比大于2,则可为每阶模态单独匹配吸振器[25]. 由于本研究1/4车模型的簧下质量和簧上质量固有频率之比大于2,且增大簧下质量不利于车辆平顺性,考虑在簧上质量(主振系统)引入并设计DVA.
2.1. 传统式DVA参数匹配
传统式DVA不考虑电磁力(安培力)作用,其刚度和阻尼系数分别为kd3、cd3. 当线圈材料为铜时,根据表1中线圈参数可以计算出线圈的质量M2约为20 kg,可以得到DVA中调谐质量与簧上质量的质量比 μ =M2 / m1 = 0.05. 将车辆悬架DVA设计转化为优化问题,采用DOE方法获得最优的设计变量kd3和cd3,使频段
式中:
采用全因子DOE方法对上述优化问题进行求解,设计变量DVA刚度kd3分为201个水平,DVA阻尼cd3分为201个水平,对每个因子的每个水平进行配对,最终只需要执行 201×201 次计算就可以得到优化结果.
参数优化结果如下:
将式(1)展开后进行Laplace变换,可以得到:
式中:
式(3)经过Laplace变换可以得到:
令
式中:
式(8)、(9)经Laplace变换后可以得到:
式中: Be=2πRcNBR.
将式(16)代入式(13),可以得到振动传递函数:
式中:
车身振动加速度
给车轮施加不同频率的位移激励x=asin (2πft)(a为幅值,取0. 003 m,f为激振频率),从而获取车辆振动响应相对于激励的频率特性. 车身振动加速度和悬架动挠度相对于谐波输入的幅频特性分别如图3(a)、(b)所示. 可以看出,在车辆簧上质量上加装刚度系数为kd3、阻尼系数为cd3的动力吸振器后,车身加速度和悬架动挠度相对于谐波位移输入的幅频特性曲线在簧上质量固有频率处的峰值分别降低15. 7%和18. 7%.
图 3
图 3 传统式DVA车辆系统振动响应相对于谐波位移输入的幅频特性
Fig.3 Amplitude-frequency characteristics for vibration responses of vehicle with DVA relative to harmonic displacement input
2.2. EMER-DVA参数匹配
在上述DVA模型中考虑振动能量回收装置电磁力的耦合作用,构成了EMER-DVA. 根据式(16),可以得到经过Laplace变换后的安培力为
可以看出安培力的实质是引入了一个随频率变化且和电路参数相关的额外电磁刚度和电磁阻尼.
式中:kem为电磁刚度系数,cem为电磁阻尼系数.
图 4
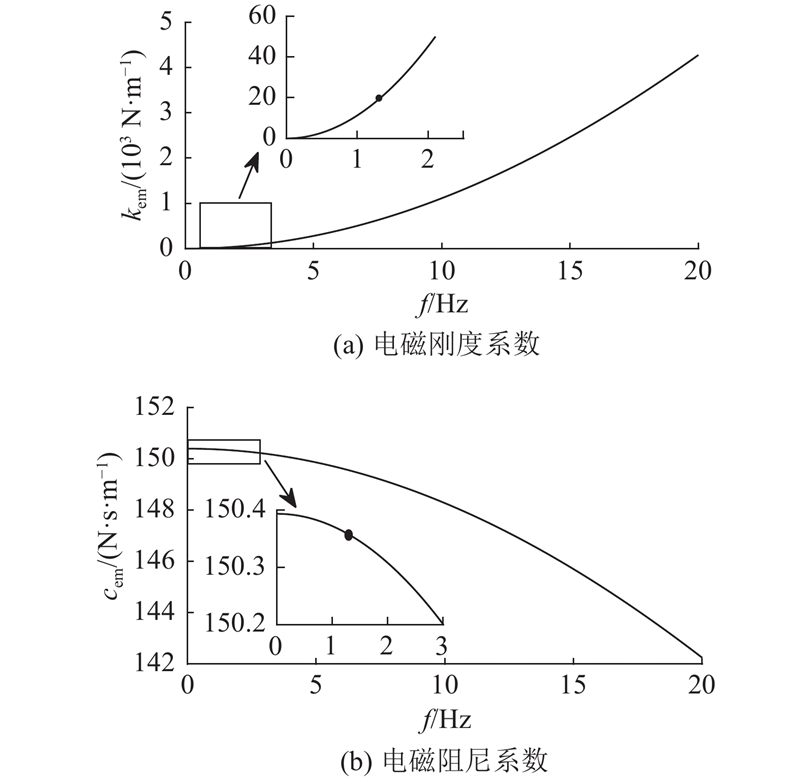
图 4 EMER-DVA电磁系统动态力学特性
Fig.4 Electromagnetic dynamical characteristics of EMER-DVA
在悬架固有频率附近,电磁刚度系数和电磁阻尼系数取整后分别为20 N/m和150 N·s/m,即考虑电磁力后,DVA的刚度和阻尼系数变为740 N/m和190 N·s/m. 因此,为了达到最优的减振效果,原DVA的刚度系数应从720 N/m调整到700 N/m,阻尼系数从40 N·s/m调整到−110 N·s/m,而汽车悬架采用的油气阻尼不会有负阻尼,故阻尼的最小值取0 N·s/m.
根据式(11)可以得到输出功率相对于简谐路面激励输入的传递函数为
表 2 EMER-DVA模型参数
Tab.2
| 变量 | 物理含义 | 数值 |
| M2 /kg | 线圈质量 | 20 |
| k3/(N·m−1) | EMER-DVA刚度系数 | 700 |
| c3/(N·s·m−1) | EMER-DVA阻尼系数 | 0 |
图 5
图 5 EMER-DVA车辆系统振动响应相对于谐波位移输入的幅频特性
Fig.5 Amplitude-frequency characteristics for vibration responses of vehicle with EMER-DVA relative to harmonic displacement input
图 6
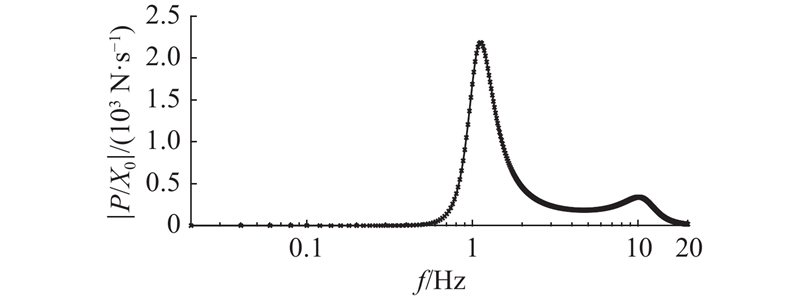
图 6 EMER-DVA 车辆系统输出功率相对于谐波位移输入的幅频特性
Fig.6 Amplitude-frequency characteristics of output power of vehicle with EMER-DVA relative to harmonic displacement input
EMER-DVA的引入会改变1/4车辆的能量分布,为此,基于模型中阻尼的能量耗散,定义总体耗散功率、潜在可回收功率指标来进一步评价能量回收效果.
单个阻尼器
式中:下标i(i=1,2,3)表示第i个阻尼器,
定义总体耗散功率
图 7
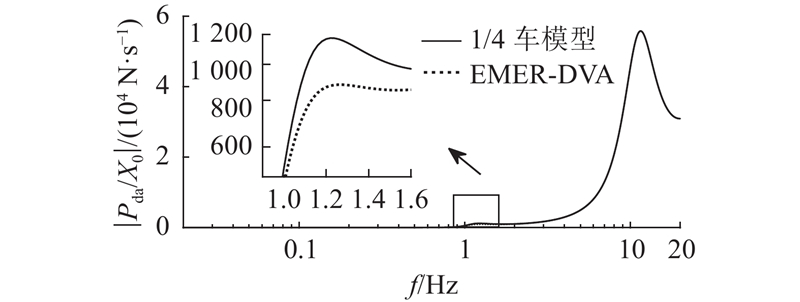
图 7 总体耗散功率相对于谐波位移输入的幅频特性
Fig.7 Amplitude-frequency characteristics of dissipated power relative to harmonic displacement input
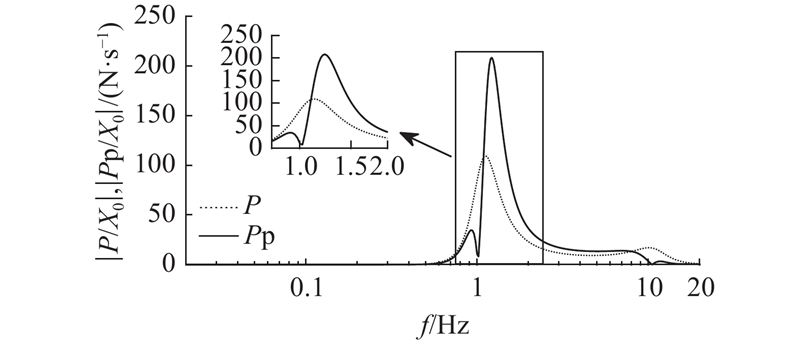
如图8所示为EMER-DVA的输出功率P与潜在可回收功率Pp对比. 可以看出,在簧上质量固有频率附近频段输出功率达到峰值,其幅值占潜在可回收功率的52%.
图 8
图 8 输出功率与潜在可回收功率相对于谐波位移输入的幅频特性对比
Fig.8 Amplitude-frequency characteristics comparison between output power and potential recoverable power relative to harmonic displacement input
总体而言,在簧上引入EMER-DVA或传统式DVA都可以在悬架固有频率附近极大地抑制车辆振动,EMER-DVA的减振效果比传统式DVA略低,但其具有额外的振动能量回收功能.
3. 车辆振动及馈能性能时域分析
传统式DVA仅能实现减振而不具备振动能量回收的功能,因此本研究仅对簧上引入EMER-DVA的车辆模型与无DVA的1/4车模型的车辆振动及馈能时域性能进行对比分析.
3.1. 正弦激励
图 9
图 9 EMER-DVA车辆系统振动时域特性
Fig.9 Vibration responses of EMER-DVA vehicle system in time domain
图 10
为了定量分析车辆性能变化,以系统响应的均方根值(root mean square, RMS)作为评价指标进行对比. RMS表达式如下:
式中:Xi为第i个数值点的数值,M为数值点总数.
车辆振动响应RMS对比结果如表3所示. 可以看出,在正弦激励下,EMER-DVA可以使车身振动加速度和悬架动挠度RMS分别减小13.2%和10.6%,总体耗散功率RMS降低19.0%. 此外,定义EMER-DVA动挠度为 fdd = x3 − x2 ,根据式(24)可以得到回收功率和动挠度RMS分别为0.167 W和5.1 mm,回收功率占潜在可回收功率的44.3%. 以上结果表明,EMER-DVA在抑制车辆振动的同时可以回收一定的功率,且在安装空间方面具有可行性.
表 3 车辆振动响应RMS
Tab.3
| 模型 | RMS( | RMS( | RMS( |
| 1/4车模型 | 0.273 | 4.7 | 1.983 |
| EMER-DVA | 0. 237 | 4.2 | 1.606 |
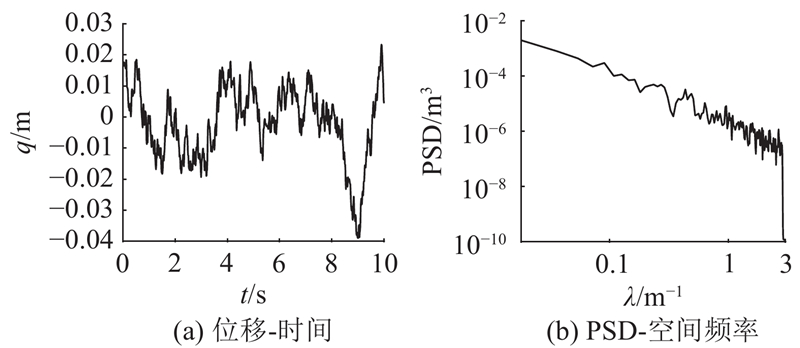
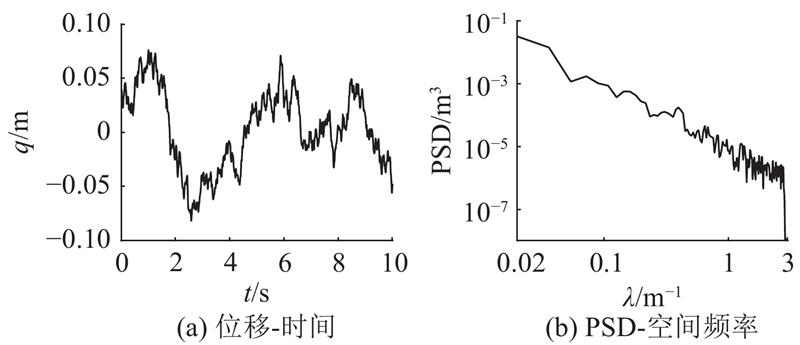
3.2. 随机路面激励
图 11
图 12
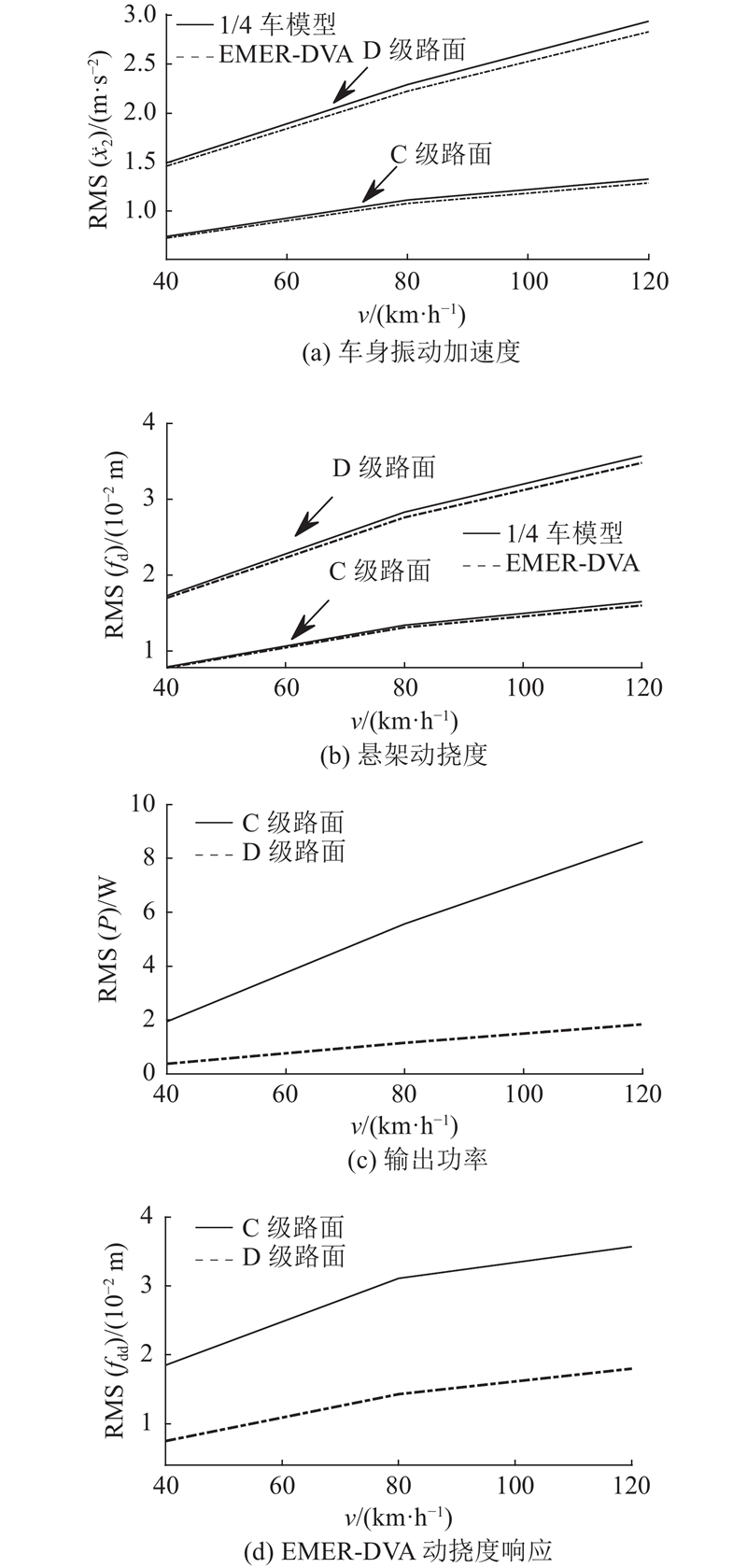
如图13所示为不同路面激励、不同车速工况下车身振动加速度、悬架动挠度、输出功率和EMER-DVA动挠度的RMS. 可以看出,随路面激励由C级变为D级(即路况变差)、车速升高,车身振动加速度、悬架动挠度、输出功率和EMER-DVA动挠度均增大. 引入EMER-DVA后车身振动加速度、悬架动挠度均低于不含DVA的1/4车辆模型的. 在C级路面激励工况下,当车速不超过90 km/h时,回收功率均小于2 W、EMER-DVA动挠度小于15 mm;在D级路面激励工况下,输出功率随车速变化增幅较为明显,当车速为90 km/h时,输出功率可达4 W,当车速不超过90 km/h时,EMER-DVA动挠度小于25 mm.
图 13
图 13 EMER-DVA车辆在不同车速、路况下的动态响应
Fig.13 Dynamic responses of vehicle with EMER-DVA under different velocities and road excitation conditions
如表4所示为引入EMER-DVA后不同车速下车辆动态响应均值结果. 表中,
表 4 EMER-DVA车辆系统动态响应均值
Tab.4
| 模型 | 路面 等级 | (m·s−2) | mm | W | mm |
| 1/4车模型 | C | 0.95 | 11.4 | — | — |
| D | 1.76 | 20.1 | — | — | |
| EMER-DVA | C | 0.92 | 11.1 | 0.98 | 11.8 |
| D | 1.68 | 19.5 | 2.8 | 21.3 |
4. 试验验证
4.1. 试验台架描述
如图14所示为在簧上质量安装EMER-DVA的1/4车振动试验台架,由于试验条件限制,试验台架系统参数与本研究模型参数并不完全一致,但通过将模型参数设置为与试验参数相同,仍可以验证本研究建模方法的正确性. 试验台架由激励部分、车辆系统和测量部分组成. 激励部分包括振动台(VEST-6160ST,Econ)和功率放大器,振动台面与驱动底板连接,以给轮胎提供路面位移激励. 车辆系统中簧上质量与簧下质量沿竖直导轨平滑运动,为了保护EMER-DVA模型中的电磁系统和支撑线圈,将线径为1 mm的铜导线缠绕固定在半径为5 mm的亚克力管上,缠绕4层,每层100圈,磁块由2块牌号为N35、高度半径均为20 mm的钕铁硼永磁体吸附在一起,试验台架中未考虑减振器阻尼. 测量部分由振动加速度传感器(LW272377,PCB)、激光位移传感器(LT-0030-20K,JULIGHT)和示波器(TBS1032B-EDU,Tektronix)组成,分别通过测试系统测量车身振动加速度、激励位移和电磁系统输出电压(可以换算为功率). 由于振动台设备原因不能精确输出正弦激励,通过对驱动底板施加类正弦工况,对比分析模型仿真与台架试验动态响应. EMER-DVA模型振动试验台架的相关参数如表5所示.
图 14
图 14 簧上EMER-DVA的1/4车振动台架试验
Fig.14 Vibration bench test of a quarter car with EMER-DVA installed on sprung mass
表 5 EMER-DVA车辆台架试验系统参数
Tab.5
| 变量/单位 | 物理含义 | 数值 |
| m1 /kg | 簧下质量 | 2.4 |
| m2 /kg | 簧上质量 | 2.5 |
| k1 /(N·m−1) | 轮胎刚度系数 | 1000 |
| k2 /(N·m−1) | 悬架刚度系数 | 400 |
| M1 /kg | 磁块质量 | 0.05 |
| M2 /kg | 线圈质量 | 0.5 |
| k3 /(N·m−1) | EMER-DVA刚度系数 | 80 |
| Ri /Ω | 线圈电阻 | 5 |
| Z /Ω | 电路电阻 | 100 |
| BR /T | 相对磁感应强度 | 0.02 |
4.2. 试验结果分析
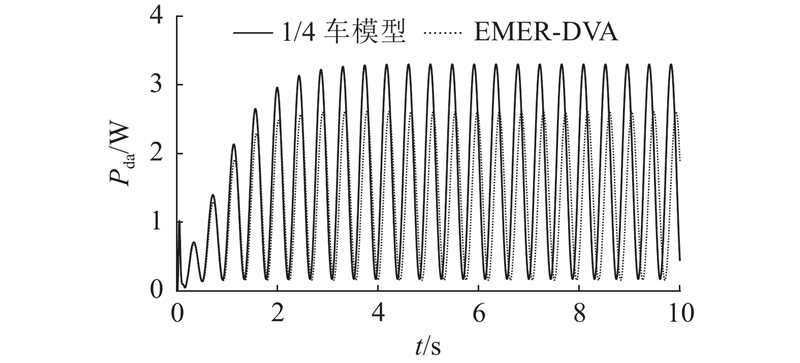
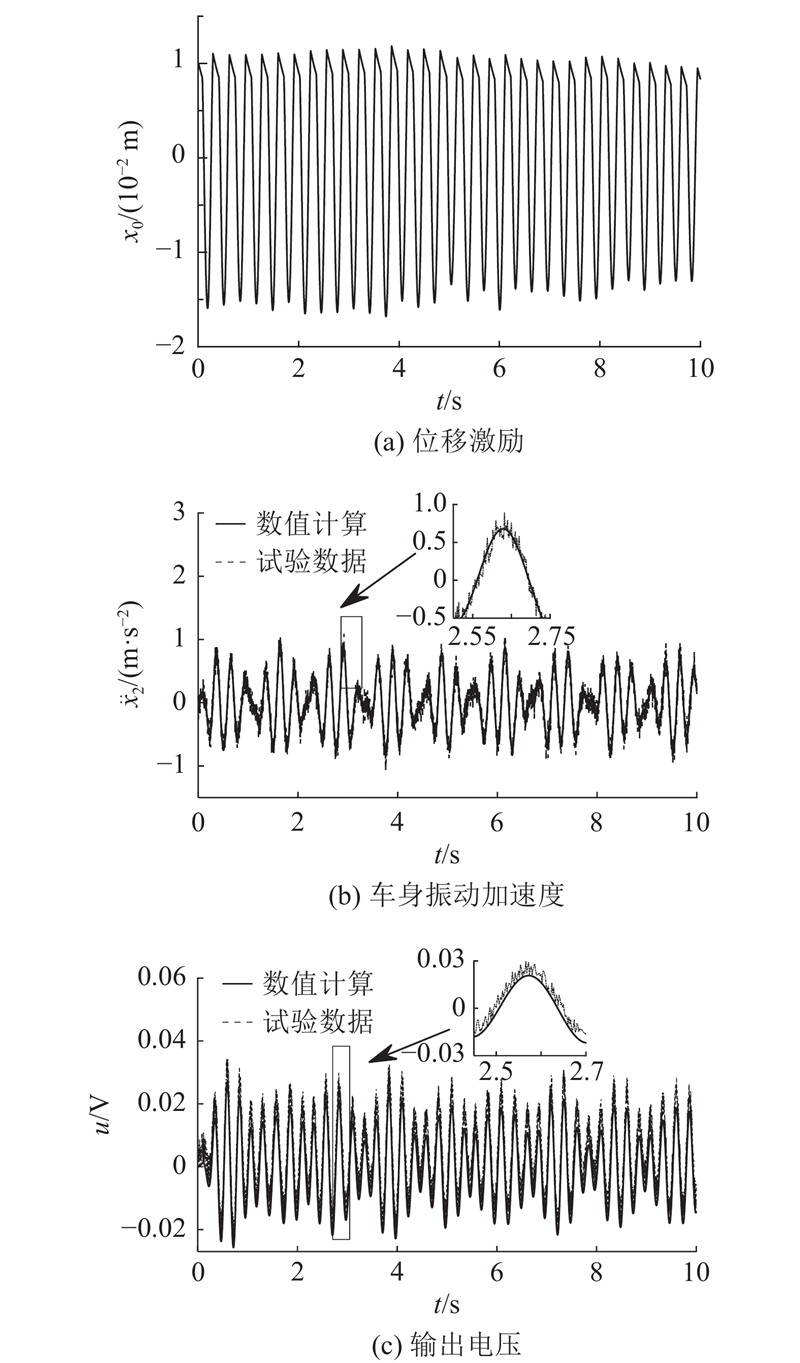
本研究主要关注EMER-DVA对簧上质量的振动抑制特性与其实际可回收功率,因此以车身加速度及输出电压作为分析对象. 施加于轮胎的路面位移输入通过布置在驱动底板的位移传感器测量得到,如图15(a)所示,将该位移激励x0施加于理论模型作为路面激励,可以得到理论模型与台架试验的车身加速度
图 15
图 15 EMER-DVA车辆振动台架试验输入与动态响应
Fig.15 Input and dynamic responses of vehicle with EMER-DVA in bench test
表 6 理论模型与台架试验动态响应RMS
Tab.6
| RMS( | RMS( | |
| 理论模型 | 0.393 | 1.152 |
| 台架试验 | 0.406 | 1.232 |
5. 结 论
(1)EMER-DVA在悬架固有频率处对车身振动加速度、悬架动挠度峰值具有较好的抑制作用,且振动回收功率曲线在该频率处呈现峰值.
(2)随着路况变差和车速增加,在引入EMER-DVA后车辆振动性能可以获得改善,振动回收功率受路况和车速影响较大,更差路况、更高车速下可回收更多的振动能量,且具有较好的空间布置可行性.
(3)振动系统理论模型与台架试验结果误差小于 7%,验证了本研究模型的准确性.
(4)本研究在建模过程中假设线圈在任何位置受到的磁感应强度为常量,未来工作中可以通过有限元方法获取准确的磁感应强度空间分布,可以提高大位移激励下的建模精度.
参考文献
一种半主动动力吸振器参数优化及性能比较
[J].DOI:10.13465/j.cnki.jvs.2019.17.023 [本文引用: 1]
Parametric optimization and performance comparison for 2 semi-active Voigt DVAs
[J].DOI:10.13465/j.cnki.jvs.2019.17.023 [本文引用: 1]
基于遗传算法的悬架动力吸振器优化
[J].DOI:10.3969/j.issn.1009-0134.2014.20.022 [本文引用: 1]
Optimization of suspension dynamic absorbers based on genetic algorithm
[J].DOI:10.3969/j.issn.1009-0134.2014.20.022 [本文引用: 1]
含放大机构的三要素型动力吸振器的H∞优化
[J].
H∞ optimization of 3-factor types dynamic vibration absorber with amplification mechanism
[J].
Fuzzy logic control of vibrations due to interaction one DOF vehicle suspension and flexible structure with tuned mass damper
[J].
Reliable fuzzy H∞ control for active suspension of in-wheel motor driven electric vehicles with dynamic damping
[J].DOI:10.1016/j.ymssp.2016.10.032 [本文引用: 1]
竖弯涡振控制的调谐质量阻尼器TMD参数优化设计
[J].
Parameter optimization of TMD for vortex-induced vibration control
[J].
自适应多重TMD在大跨楼板结构减振中的应用
[J].DOI:10.16450/j.cnki.issn.1004-6801.2020.03.022 [本文引用: 1]
Adaptive-passive multiple tuned mass damper on large-span floor structure
[J].DOI:10.16450/j.cnki.issn.1004-6801.2020.03.022 [本文引用: 1]
动力吸振器在驱动桥减振降噪上的应用
[J].DOI:10.13465/j.cnki.jvs.2018.14.028 [本文引用: 1]
Application of dynamic vibration absorbers in vibration and noise reduction of drive axles
[J].DOI:10.13465/j.cnki.jvs.2018.14.028 [本文引用: 1]
动力吸振器在传动轴扭振控制上的应用
[J].
Application of turned mass damper or torsional vibration of transmission shaft
[J].
动力总成动力吸振器特性研究
[J].DOI:10.3969/j.issn.1000-6494.2020.01.009 [本文引用: 1]
Research on tuned mass damper in power assembly
[J].DOI:10.3969/j.issn.1000-6494.2020.01.009 [本文引用: 1]
Ride comfort improvement with preview control semi-active suspension system based on supervised deep learning
[J].
Research on maglev vibration isolation technology for vehicle road noise control
[J].
Optimal active suspension structures for quarter-car vehicle models
[J].DOI:10.1016/0005-1098(90)90002-Y [本文引用: 1]
基于动力吸振理论的车辆ISD悬架设计与性能分析
[J].DOI:10.19562/j.chinasae.qcgc.2014.10.021 [本文引用: 1]
Design and performances analysis of vehicle ISD suspension based on dynamic vibration absorber theory
[J].DOI:10.19562/j.chinasae.qcgc.2014.10.021 [本文引用: 1]
车辆主动惯容式动力吸振悬架系统研究
[J].DOI:10.13465/j.cnki.jvs.2017.01.025 [本文引用: 1]
Vehicle active ISD-DVA suspension system
[J].DOI:10.13465/j.cnki.jvs.2017.01.025 [本文引用: 1]
车辆半主动悬架负刚度控制策略研究
[J].
Negative stiffness-based control strategy of vehicle semi-active suspension
[J].
An experimentally validated electromagnetic energy harvester
[J].DOI:10.1016/j.jsv.2010.11.024 [本文引用: 1]
Simultaneous vibration mitigation and energy harvesting from a pendulum-type absorber
[J].DOI:10.1016/j.cnsns.2020.105479 [本文引用: 1]
Energy harvesting, ride comfort, and road handling of regenerative vehicle suspensions
[J].
Performance evaluation and parameter sensitivity of energy-harvesting shock absorbers on different vehicles
[J].DOI:10.1080/00423114.2016.1174276 [本文引用: 1]
动力吸振器对车辆垂向振动能量及悬架性能的影响
[J].DOI:10.13465/j.cnki.jvs.2020.22.023 [本文引用: 1]
Impact of dynamic vibration absorbers on vehicle vertical vibration energy and suspension performances
[J].DOI:10.13465/j.cnki.jvs.2020.22.023 [本文引用: 1]
簧下调谐系统回收车辆轮胎的垂向振动能量
[J].
Vehicle tire vertical vibration energy harvesting using unsprung tuned mass damper
[J].
阻尼动力吸振器减振问题的进一步研究
[J].DOI:10.13465/j.cnki.jvs.1994.01.001 [本文引用: 1]
A further investigation of using dynamic vibration absorber to reduce vibration
[J].DOI:10.13465/j.cnki.jvs.1994.01.001 [本文引用: 1]
Study on vibration characteristics of the towbarless aircraft taxiing system
[J].
Design and characterization of an electromagnetic energy harvester for vehicle suspensions.
[J].DOI:10.1088/0964-1726/19/4/045003 [本文引用: 1]