现有的锅炉操作优化研究存在可执行性、工况适应性和计算效率不足的问题,需要进一步探索实时优化[22]场景下的方法. 本文提出适用于多工况在线应用的代理模型模式匹配(pattern matching of agent model, PMAM)建模框架,以提升燃煤锅炉的效率,优化锅炉运行. 主要贡献如下. 1) 提出新的模式匹配方法,解决锅炉操作优化的可执行性问题. 2) 提出基于模式匹配方法的优化操作库构建方法,解决锅炉操作优化的工况适应性问题. 3) 提出基于神经网络算法的在线应用代理模型,解决锅炉操作优化的计算效率问题.
1. 锅炉实时操作优化建模方法
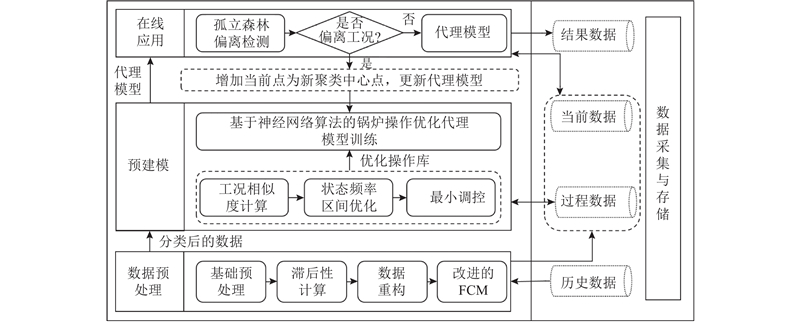
燃煤锅炉转化煤为蒸汽驱动发电,需要控制煤量、风量参数,保证安全并实现需要的蒸汽量. 为了提高锅炉效率,需要根据输入的工况数据进行优化操作建议. 采用反平衡方法[23]计算锅炉效率,输出给煤机、引风机、送风机的变频数据,以达到效率最高的目标. 如图1所示为PMAM锅炉实时操作优化建模方法. 该方法基于改进的模式匹配算法及神经网络算法,分为预建模、在线应用2个部分. 预建模部分基于考虑滞后及时间窗的模式匹配优化模型,引入注意力机制参数、状态参数区间频率法、调控最小3层方案优化机制,得到各个工况的优化操作,构建工况参数与优化操作的最优代理模型. 在线应用部分基于工况参数与优化操作参数的最优代理模型,实现在线优化计算.
图 1
图 1 基于代理模型模式匹配的锅炉实时操作优化计算框架
Fig.1 Boiler real-time operation optimization calculation framework based on pattern matching of agent model
1.1. 数据预处理
1.1.1. 滞后性计算
锅炉操作中的滞后性主要体现在给煤机的频率与锅炉主蒸汽流量的关系. 基于相关性分析,开展滞后性计算.
算法1:滞后性计算
输入:样本个数为
输出:滞后时长
1) 将样本
2) 构造数据集合
3)
4) 删掉带有空值的行,得到修改后的数据集合
5) 计算
6) 取
设
数据归一化方法采用最大最小化方法,具体公式如下:
图 2
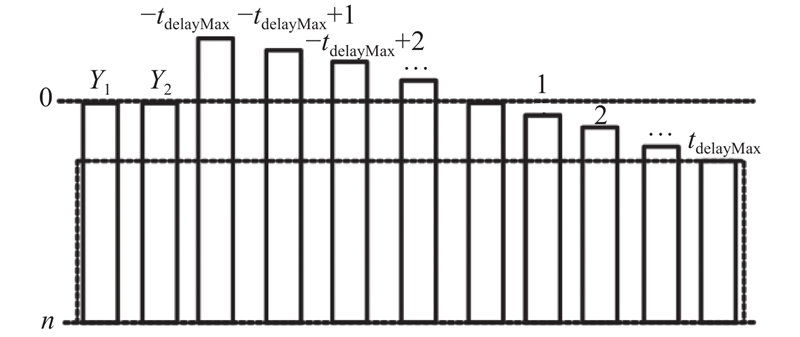
图 2 滞后性计算中的数据重构示意图
Fig.2 Schematic diagram of data reconstruction in hysteresis calculation
1.1.2. 基于主成分分析及k-均值改进的模糊C均值聚类模型
设置数据集
由于不同的参数数据范围不同,对数据集进行最大最小化的归一化处理. 为了提高后续模式匹配优化的计算效率,处理后的数据使用主成分分析模型(principal component analysis, PCA)[24]降低维度. PCA降低数据维度的算法如下.
算法2:PCA降低数据维度
输入:样本个数为
输出:低维样本
1) 样本的每一列去均值化,得到
2) 求协方差矩阵
3) 求协方差矩阵的特征值与特征向量.
4) 将特征值从大到小排序,并依次取出,直到取出的特征值加和大于
5) 计算降维后的数据
6) 返回低维样本
针对PCA降维后的数据,采用k-均值(k-means)改进的模糊C均值聚类模型(fuzzy C-means, FCM)[25]进行工况聚类. 记
式中:
采用k-means方法改进FCM方法中的初始模糊矩阵生成步骤,可以降低聚类结果的随机性,加快算法的收敛. 改进FCM方法的计算步骤如下.
1)初始化聚类参数:
2)利用k-means聚类法生成初始的模糊矩阵
算法3:k-means聚类生成初始的模糊矩阵
输入:样本
输出:模糊矩阵
1) 初始化,令l = 0,随机选择
2) 对样本进行聚类,计算每个样本到类中心的距离. 将每个样本分配到与其最近的中心的所属类,生成聚类结果
3) 计算聚类结果
4) 若符合停止条件(划分结果不再改变或得到迭代次数上限),则终止,输出
5) 根据
6) 返回
3)计算聚类中心:
4)更新模糊矩阵:
5)若
1.2. 考虑时间窗口的模式匹配优化模型
经过模型聚类后,得到分类后的数据集:
为了避免测量误差和异常操作的影响,考虑时间维度的因素,将锅炉操作参数模式匹配优化视为带时间序列属性的问题,选取一段时间窗口的数据进行模式匹配优化计算.
对于类别
1)获取匹配分数下限值
2)根据工况表征参数
3)筛选工况表征参数中变动偏差符合匹配分数上、下限的数据,得到更新后的
式中:
4)计算
5)按相似度得分排序更新
6)对于
统计连续长区间的频率,按高到低排序,即为筛选后的关键状态参数的区间.
根据目标参数的优化方向,取在该长区间的50%数据,得到筛选后的数据,令
7)根据输出的关键状态表征参数
8)计算
1.3. 最优代理模型
利用3层方案模式匹配机制,分别对历史生产数据进行优化,生成优化操作库. 为了解决直接搜索优化操作库数据量过大、搜索效率过低的问题,构建基于神经网络算法的最优代理模型. 该代理模型以工况参数为输入,以优化后的操作、效率和关键参数为输出.
式中:
在线应用时,采用孤立森林[26](isolation forest)法进行偏离检测. 若当前工况非偏离点,则调用式(13)计算优化的操作参数;否则更新预建模的聚类中心与最优代理模型,输出当前的操作参数为优化方案.
2. 案例选取
以浙江省某热电公司为案例进行研究. 该公司的机组规模为4台蒸汽质量流量为220 t/h的高温超高压循环流化床锅炉. 选取1#锅炉数据展开计算实验,并以2#锅炉数据开展验证. 选择的工况参数、目标参数、关键状态参数、操作参数如表1所示.
表 1 锅炉操作优化计算的相关参数表
Tab.1
| 序号 | 参数类型 | 参数 |
| 1 | 工况参数 | 主蒸汽质量流量qmsteam/(t·h−1) |
| 2 | 主蒸汽温度θsteam/℃ | |
| 3 | 主蒸汽压力psteam/MPa | |
| 4 | 应用基水分Cwat/% | |
| 5 | 应用基灰分Cash/% | |
| 6 | 应用基挥发分Cvdaf/% | |
| 7 | 收到基低位发热量Qnet/(kJ·kg−1) | |
| 8 | 给水温度θwater/℃ | |
| 9 | 目标参数 | 锅炉效率Eboiler/% |
| 10 | 关键状态参数 | 炉膛温度θfurnace/℃ |
| 11 | 烟气含氧体积分数φoxygen/% | |
| 12 | 一二次风比例Rair | |
| 13 | 一次风体积流量qVprimaryAir/(m3·h−1) | |
| 14 | 二次风体积流量qVsecondaryAir/(m3·h−1) | |
| 15 | 操作参数 | 1#给煤机频率f1#GMJ/Hz |
| 16 | 2#给煤机频率f2#GMJ/Hz | |
| 17 | 3#给煤机频率f3#GMJ/Hz | |
| 18 | 4#给煤机频率f4#GMJ/Hz | |
| 19 | 1#引风机频率f1#YFJ/Hz | |
| 20 | 2#引风机频率f2#YFJ/Hz | |
| 21 | 一次风机频率f1#SFJ/Hz | |
| 22 | 二次风机频率f2#SFJ/Hz |
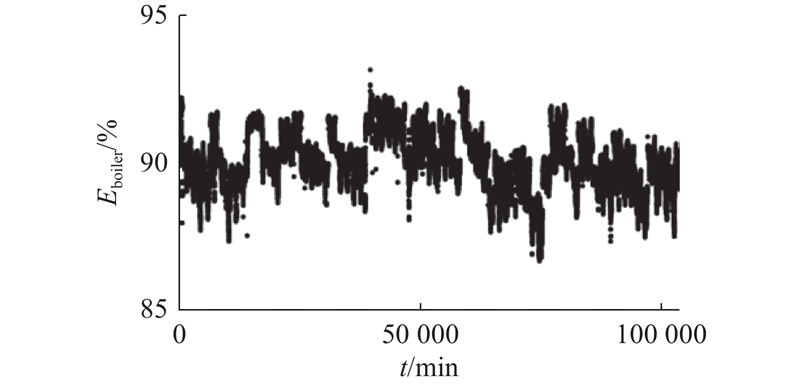
选择历史数据时间段为2022−02−16 22:41—2022−04−29 21:29,时间间隔为1 min,共103 586条数据构成原始数据集. 如图3所示,该锅炉正常运行时的锅炉效率为[86.70%, 93.15%].
图 3
图 3 某热电公司1#锅炉效率的正常运行数据
Fig.3 Normal operation data of 1 # boiler efficiency of thermal power plant
3. 案例结果与讨论
3.1. 滞后性结果
图 4
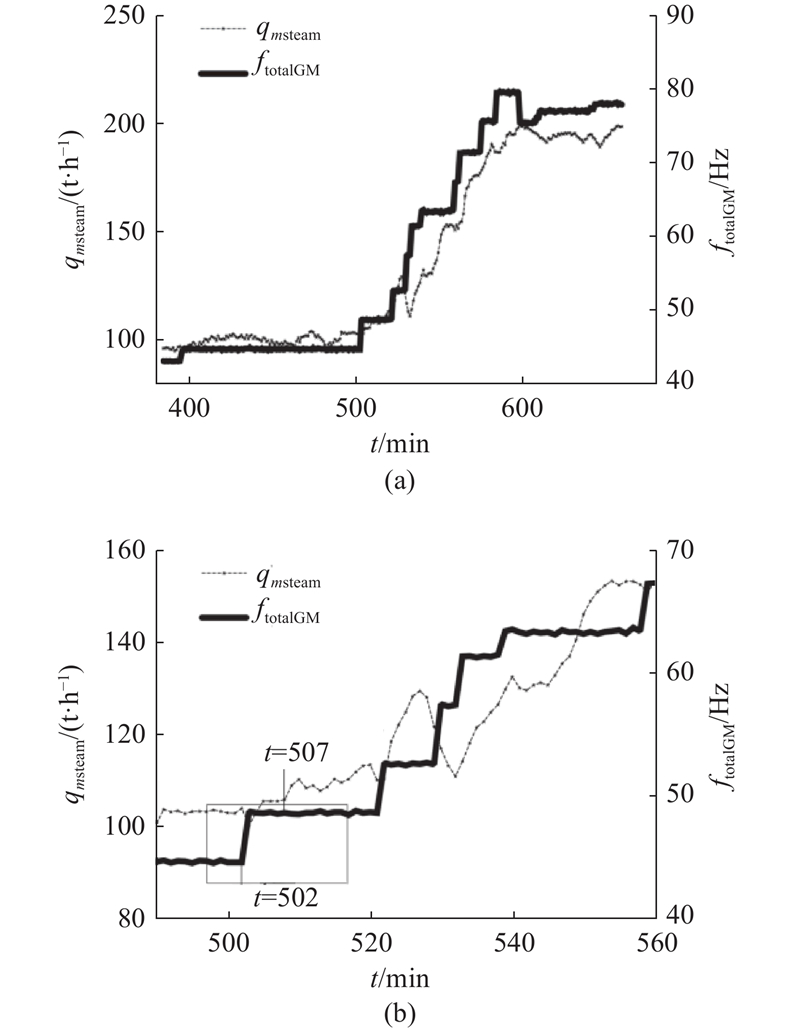
图 4 主蒸汽质量流量与给煤机频率的曲线
Fig.4 Curve between main steam mass flow rate and frequency of coal feeder
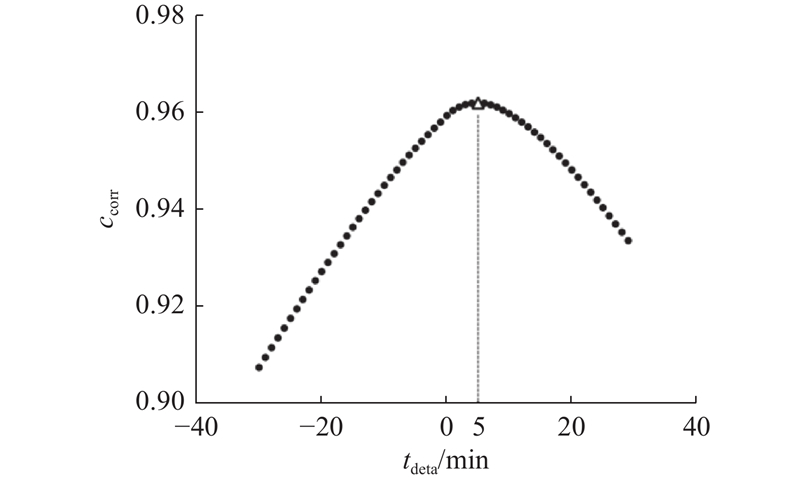
图 5
图 5 主蒸汽质量流量相对给煤机频率的滞后性
Fig.5 Hysteresis of main steam mass flow rate relative to coal feeder frequency
3.2. 工况聚类结果
根据滞后性的计算结果,对原始数据集合进行时间轴对齐,得到的数据长度为102063条.
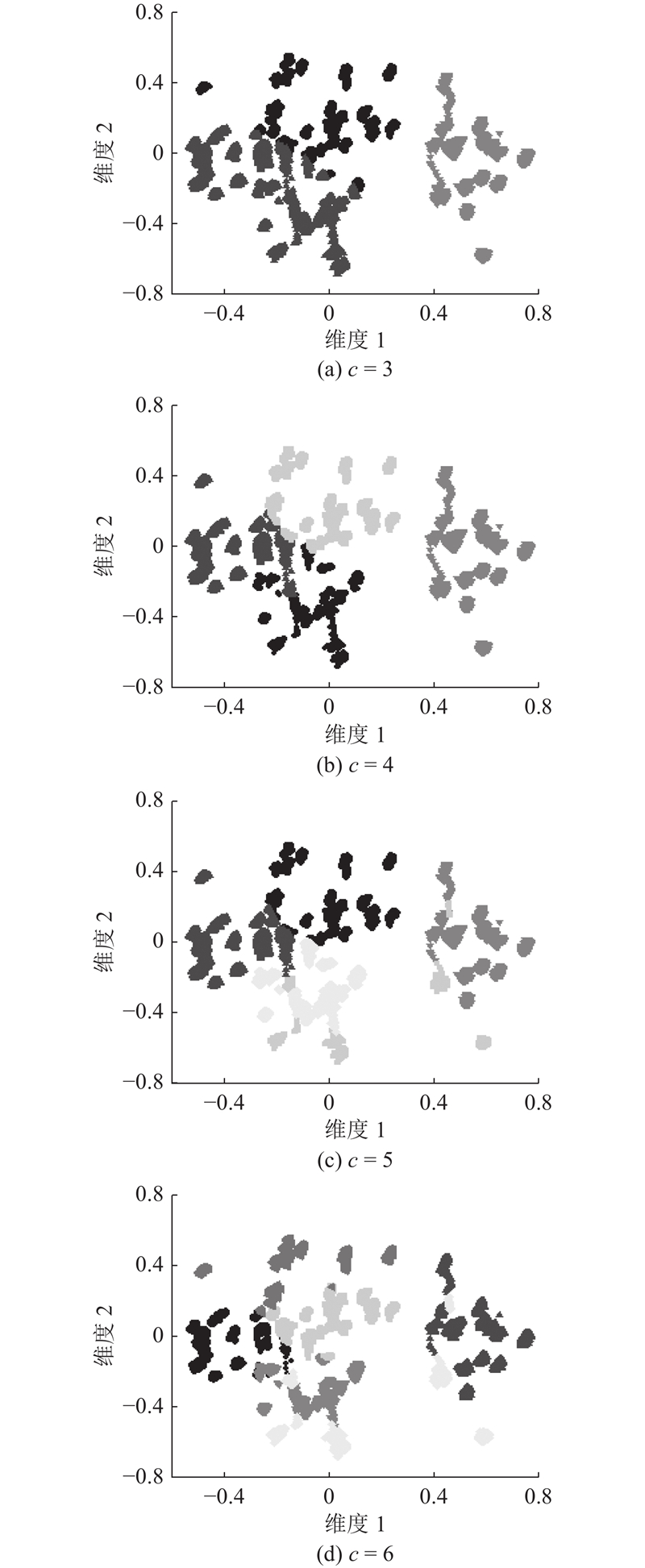
如表2所示为不同的模糊指数对迭代次数与偏差的影响. 当c = 3且
表 2 模糊指数对聚类目标误差及迭代次数的影响
Tab.2
| c | m | | L | lr |
| 3 | 2 | 10 | 8.101 | 22 |
| 3 | 3 | 10 | 8.820 | 22 |
| 3 | 4 | 10 | 9.548 | 38 |
| 3 | 5 | 10 | 9.941 | 85 |
表 3 聚类数对最终误差及迭代次数的影响
Tab.3
| c | m | | L | lr |
| 3 | 2 | 10 | 8.101 | 22 |
| 4 | 2 | 10 | 9.086 | 81 |
| 5 | 2 | 10 | 9.576 | 19 |
| 6 | 2 | 10 | 9.648 | 23 |
图 6
测试不同的更新迭代阈值对迭代次数与偏差的影响,结果如表4所示.
表 4 更新迭代阈值对最终误差及迭代次数的影响
Tab.4
| c | m | | L | lr |
| 3 | 2 | 0.01 | 0.009 | 47 |
| 3 | 2 | 0.1 | 0.081 | 39 |
| 3 | 2 | 1 | 0.927 | 30 |
| 3 | 2 | 10 | 8.101 | 22 |
由表4可知,当固定聚类数为3,模糊指数为2时,更新迭代阈值越小,最终误差越小,而迭代次数在可接受范围内,因此设置更新迭代阈值为0.01.
综上所述,设置聚类数为3,模糊指数为2,更新迭代阈值为0.01,得到3类工况的数据集.
3.3. 预建模结果
设置工况的匹配分数下限值为95,关键参数的优先级按炉膛温度、烟气含氧体积分数、一二次风比例、一次风量、二次风量依次下降.
如表5所示为1#炉多工况模式匹配优化的结果. 表中,
表 5 多工况模式匹配的优化结果-1#炉
Tab.5
| 工况 | qmsteam/(t·h−1) | Sxm/% | Sxo/% | EdeBoiler/% | ftotalGM/Hz | ftotalSF/Hz | ftotalYF/Hz |
| 工况1(原始) | 191.16 | — | — | — | 79.30 | 58.44 | 58.23 |
| 工况1(优化后) | 199.06 | 98.28 | 97.27 | 1.92 | 78.22 | 58.51 | 59.45 |
| 工况1(仅考虑工况相似) | 197.73 | 98.83 | 96.19 | 2.10 | 79.74 | 57.66 | 58.24 |
| 工况1(仅考虑工况相似与操作相似) | 189.96 | 99.84 | 99.89 | 0.06 | 79.19 | 58.42 | 58.24 |
| 工况2(原始) | 170.66 | — | — | — | 71.39 | 56.01 | 52.98 |
| 工况2(优化后) | 162.98 | 98.47 | 95.14 | 0.41 | 67.23 | 54.01 | 51.96 |
| 工况3(原始) | 140.58 | — | — | — | 55.29 | 49.97 | 42.28 |
| 工况3(优化后) | 140.25 | 99.44 | 95.13 | 0.64 | 55.29 | 49.97 | 42.28 |
| 工况4(原始) | 123.29 | — | — | — | 52.55 | 46.14 | 39.46 |
| 工况4(优化后) | 120.31 | 97.00 | 93.76 | 0.22 | 52.15 | 45.73 | 39.68 |
| 工况5(原始) | 103.55 | — | — | — | 47.47 | 45.77 | 39.30 |
| 工况5(优化后) | 111.00 | 98.00 | 95.82 | 0.93 | 46.91 | 44.95 | 38.67 |
| 工况6(原始) | 192.68 | — | — | — | 78.25 | 59.84 | 58.24 |
| 工况6(优化后) | 201.55 | 97.40 | 94.46 | 0.73 | 74.23 | 61.74 | 63.34 |
| 工况7(原始) | 194.62 | — | — | — | 78.06 | 61.89 | 62.31 |
| 工况7(优化后) | 199.60 | 97.99 | 96.92 | 0.60 | 74.13 | 61.76 | 63.33 |
| 工况8(原始) | 195.16 | — | — | — | 83.82 | 61.10 | 61.51 |
| 工况8(优化后) | 201.70 | 97.51 | 92.63 | 0.76 | 74.20 | 61.74 | 63.34 |
| 工况9(原始) | 201.01 | — | — | — | 82.22 | 60.30 | 61.51 |
| 工况9(优化后) | 199.60 | 99.09 | 93.32 | 0.66 | 74.13 | 61.76 | 63.33 |
与传统方法相比,本文方法考虑了关键状态参数的优化调整区域,通过频率区间择优,本文方法的优化结果较原始锅炉效率提升了1.92%. 与仅考虑工况与操作相似的方法相比,锅炉效率提高了1.86%. 此外,各个优化方案的工况相似度均大于设置的95%. 通过对比工况1与工况6~9可知,负荷较高时的锅炉效率通常更高,更具有提升的空间.
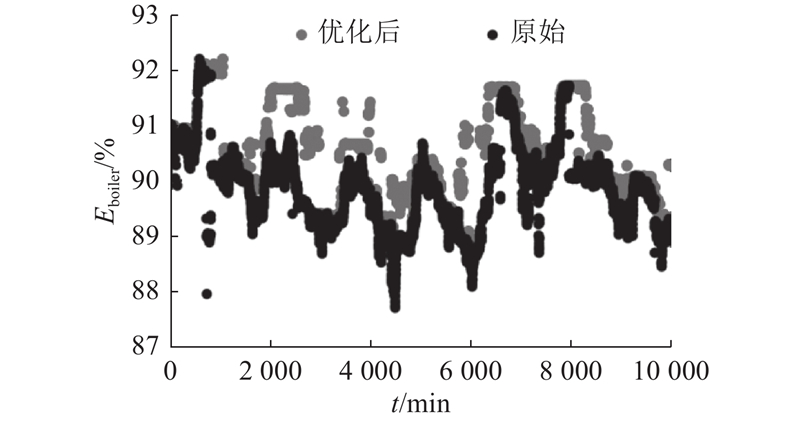
选取1万条历史数据进行模式匹配批量计算,得到的锅炉效率计算结果如图7所示. 利用本文方法,锅炉效率平均提高了0.68%,最多提高了4.54%.
图 7
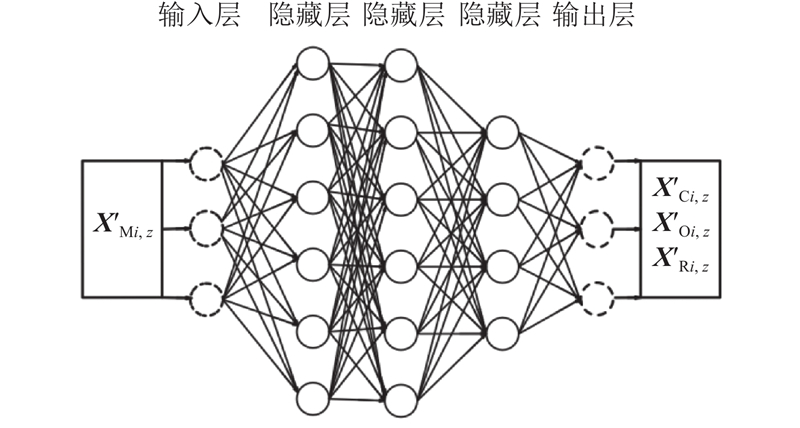
图 8
图 8 PMAM代理模型采用的神经网络结构图
Fig.8 Neural network structure diagram adopted by PMAM agent model
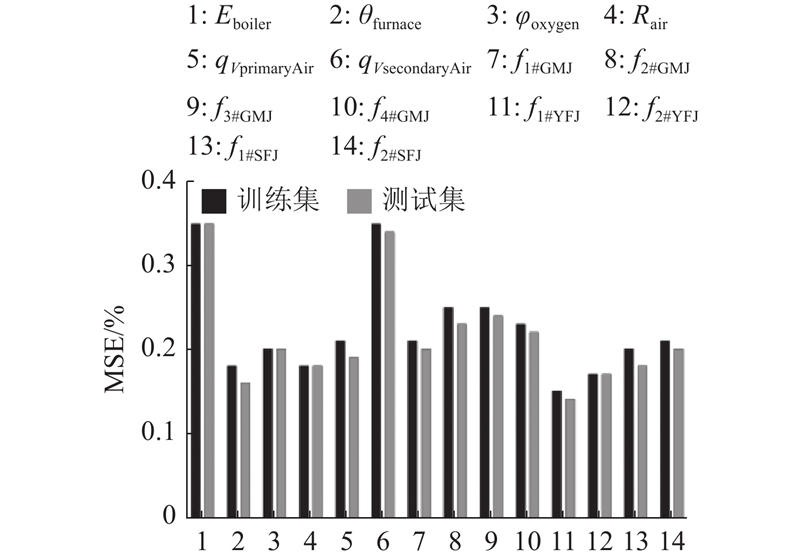
如图9所示为模型的训练结果. 各参数的均方误差(MSE)均不大于0.35%,满足工业预测精度的要求.
图 9
如表6所示为交叉试验结果. 图中,e为误差百分比. 在10次重复试验中,测试集上的误差较稳定,每次预测的最大误差为0.34%~0.38%,说明本文的代理模型具有泛化能力.
表 6 交叉试验-测试集误差百分比
Tab.6
| 序号 | 参数 | e/% | |||||||||
| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 第7次 | 第8次 | 第9次 | 第10次 | ||
| 1 | Eboiler | 0.33 | 0.36 | 0.37 | 0.33 | 0.31 | 0.29 | 0.38 | 0.32 | 0.35 | 0.33 |
| 2 | θfurnace | 0.16 | 0.16 | 0.16 | 0.16 | 0.16 | 0.16 | 0.16 | 0.16 | 0.17 | 0.16 |
| 3 | φoxygen | 0.20 | 0.20 | 0.20 | 0.21 | 0.21 | 0.20 | 0.20 | 0.20 | 0.20 | 0.20 |
| 4 | Rair | 0.18 | 0.18 | 0.18 | 0.19 | 0.17 | 0.18 | 0.19 | 0.17 | 0.17 | 0.16 |
| 5 | qVprimaryAir | 0.18 | 0.19 | 0.19 | 0.19 | 0.19 | 0.19 | 0.18 | 0.19 | 0.18 | 0.18 |
| 6 | qVsecondaryAir | 0.35 | 0.35 | 0.36 | 0.35 | 0.34 | 0.35 | 0.33 | 0.35 | 0.33 | 0.34 |
| 7 | f1#GMJ | 0.19 | 0.19 | 0.19 | 0.19 | 0.19 | 0.20 | 0.20 | 0.19 | 0.20 | 0.19 |
| 8 | f2#GMJ | 0.24 | 0.24 | 0.25 | 0.24 | 0.25 | 0.24 | 0.23 | 0.24 | 0.24 | 0.23 |
| 9 | f3#GMJ | 0.24 | 0.24 | 0.25 | 0.24 | 0.24 | 0.24 | 0.24 | 0.24 | 0.24 | 0.24 |
| 10 | f4#GMJ | 0.20 | 0.21 | 0.21 | 0.22 | 0.20 | 0.20 | 0.20 | 0.22 | 0.21 | 0.21 |
| 11 | f1#YFJ | 0.15 | 0.14 | 0.15 | 0.15 | 0.15 | 0.15 | 0.15 | 0.15 | 0.16 | 0.15 |
| 12 | f2#YFJ | 0.15 | 0.15 | 0.16 | 0.16 | 0.16 | 0.16 | 0.16 | 0.16 | 0.16 | 0.15 |
| 13 | f1#SFJ | 0.18 | 0.18 | 0.19 | 0.19 | 0.18 | 0.19 | 0.18 | 0.18 | 0.18 | 0.18 |
| 14 | f2#SFJ | 0.21 | 0.22 | 0.20 | 0.20 | 0.21 | 0.22 | 0.21 | 0.21 | 0.21 | 0.21 |
3.4. 在线应用结果及对比
采用构建的最优代理模型进行在线计算验证,详见表7. 表中,tc为计算耗时. 代理模型的应用显著降低了计算耗时,在负荷为190 t/h的基础工况下,锅炉效率可以提高1.49%.
表 7 在线应用结果示例
Tab.7
| 数据源 | Eboiler/% | f1#GMJ/Hz | f2#GMJ/Hz | f3#GMJ/Hz | f4#GMJ/Hz | f1#SFJ/Hz | f2#SFJ/Hz | f1#YFJ/Hz | f2#YFJ/Hz | tc/s |
| 原始数据 | 90.22 | 18.54 | 17.08 | 23.05 | 20.63 | 36.05 | 22.39 | 29.09 | 29.14 | — |
| 由模式匹配计算 | 91.95 | 18.46 | 17.88 | 22.17 | 19.71 | 35.51 | 23.00 | 29.72 | 29.73 | 12.00 |
| 由代理模型计算 | 91.56 | 17.90 | 17.20 | 21.99 | 19.23 | 35.63 | 23.00 | 29.38 | 29.05 | 2.00 |
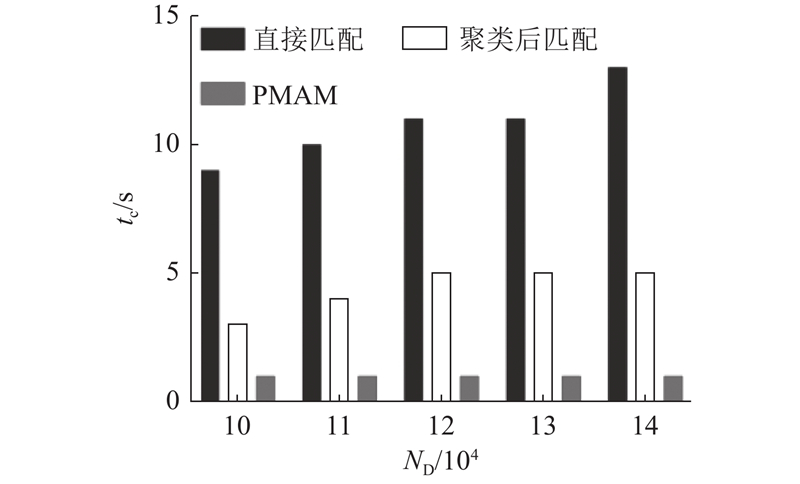
如图10所示,提出的PMAM法的计算耗时稳定在1 s,计算效率优势随着数据量的增大而显著增大. 图中,ND为数据量.
图 10
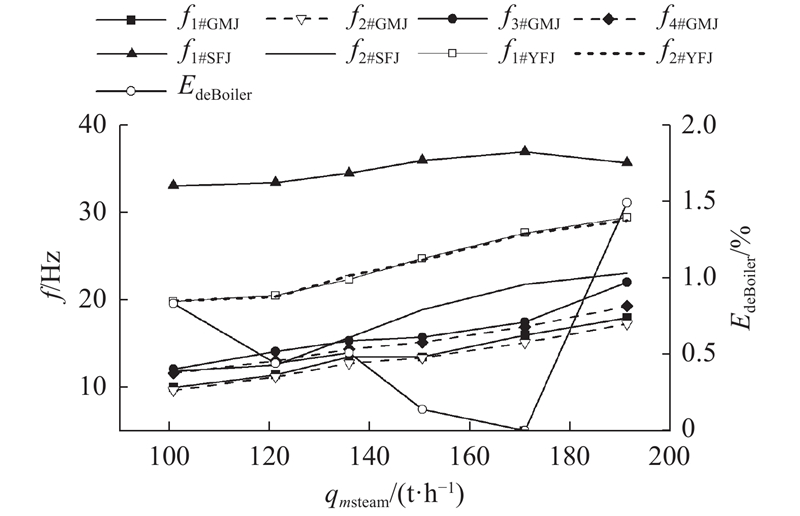
如图11所示为不同负荷的优化结果,效率提升了0~1.49%,平均效率改进了0.57%. 图中,
图 11
图 11 不同负荷下PMAM的在线应用结果
Fig.11 Online application results of PMAM method under different loads
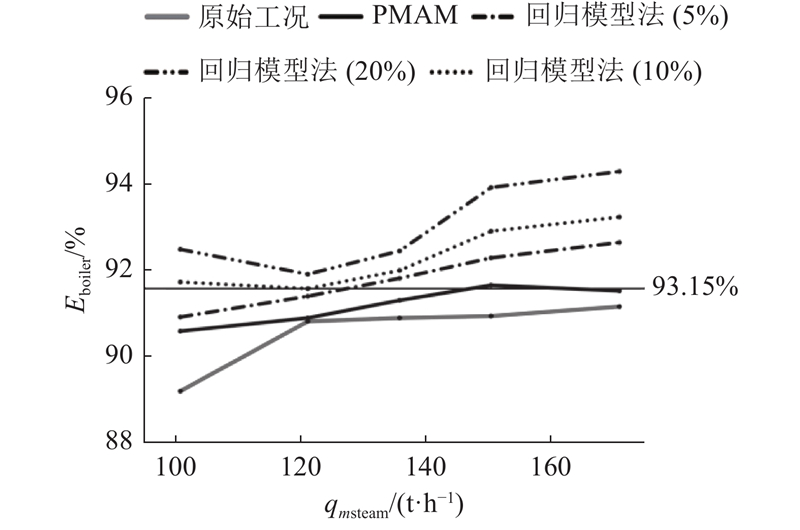
如图12所示为PMAM与回归模型法的优化对比结果. 结果表明,在不同操作参数可调节范围(20%、10%、5%)下,利用传统方法得到的锅炉效率均偏高,且存在失去置信度的风险. 其中,操作参数可调节范围是指操作参数相对于其当前实际值的可接受变化范围.
图 12
以该公司2#锅炉为验证对象,结果如表8所示. 本文的PMAM法能够应用于其余锅炉的操作优化,以提升锅炉效率.
表 8 多工况模式匹配优化结果-2#炉
Tab.8
| 工况 | qmsteam/(t·h−1) | Sxm/% | Sxo/% | EdeBoiler/% | ftotalGM/Hz | ftotalSF/Hz | ftotalYF/Hz |
| 工况1(原始) | 113.57 | — | — | — | 40.69 | 48.87 | 41.42 |
| 工况1(优化后) | 119.95 | 97.57 | 97.57 | 0.65 | 41.42 | 50.29 | 40.61 |
| 工况2(原始) | 133.93 | — | — | — | 46.12 | 52.96 | 45.06 |
| 工况2(优化后) | 131.23 | 98.88 | 98.73 | 1.24 | 46.26 | 51.77 | 44.25 |
| 工况3(原始) | 144.49 | — | — | — | 50.14 | 53.93 | 47.06 |
| 工况3(优化后) | 141.24 | 98.67 | 99.86 | 0.04 | 50.02 | 53.92 | 47.04 |
| 工况4(原始) | 158.02 | — | — | — | 55.72 | 55.68 | 52.96 |
| 工况4(优化后) | 157.98 | 99.68 | 99.80 | 0.05 | 55.72 | 55.68 | 52.96 |
| 工况5(原始) | 181.26 | — | — | — | 62.85 | 61.92 | 62.81 |
| 工况5(优化后) | 189.13 | 97.61 | 99.13 | 0.77 | 64.41 | 62.57 | 62.02 |
| 工况6(原始) | 197.58 | — | — | — | 70.14 | 66.28 | 65.64 |
| 工况6(优化后) | 198.51 | 99.60 | 99.91 | 0.05 | 70.03 | 66.30 | 65.65 |
4. 结 语
本文提出基于代理模型模式匹配的电厂燃煤锅炉实时操作优化框架. 该框架具有以下3个显著特点. 1) 高可执行性的模式匹配方法. 基于相关性分析展开滞后性计算,引入工况注意力机制、状态参数的频率区间优化和调控最小3层优化机制. 2) 优化操作库构建方法. 基于模式匹配方法对历史的生产数据进行寻优处理,将操作经验数字化. 3) 高效在线应用方法. 构建工况和优化操作参数的代理模型,提高在线应用效率. 工程案例表明,该方法避免了优化求解中的泛化误差,较传统方法具有更高的可靠性和实时性. 未来的研究将关注于优化模型的在线更新策略,提高模型的适应性.
参考文献
国内外促进可再生能源消纳的电力现货市场发展综述与思考
[J].
Review and cogitation for worldwide spot market development to promote renewable energy accommodation
[J].
含高比例风光发电的电力系统中抽蓄电站的优化控制策略
[J].
Optimization control strategy of pumped storage station in power system with high proportion wind/photovoltaic power
[J].
面向碳达峰碳中和目标的我国电力系统发展研判
[J].
Analysis and reflection on the development of power system towards the goal of carbon emission peak and carbon neutrality
[J].
双碳目标下的新型电力系统规划新问题及关键技术
[J].
New issues and key technologies of new power system planning under double carbon goals
[J].
热电厂锅炉-汽轮机的优化调度
[J].
Optimal scheduling of boiler-turbine in thermal power plant
[J].
热电厂锅炉-汽轮机的优化调度
[J].
Load assignment optimization in combined heat and power plant
[J].
Constraint-based control of boiler efficiency: a data-mining approach
[J].DOI:10.1109/TII.2006.890530 [本文引用: 1]
基于数据驱动与模式挖掘的循环流化床锅炉运行优化研究
[J].
Operation optimization of CFB boiler based on data-driven and pattern mining
[J].
聚类算法研究
[J].DOI:10.3724/SP.J.1001.2008.00048 [本文引用: 1]
Clustering algorithms research
[J].DOI:10.3724/SP.J.1001.2008.00048 [本文引用: 1]
循环流化床锅炉节能的操作优化
[J].
Operation optimization of circulating fluidized bed boiler for energy saving
[J].
Adaptive nonlinear model predictive control of the combustion efficiency under the NOx emissions and load constraints
[J].
Combustion optimization for coal fired power plant boilers based on improved distributed ELM and distributed PSO
[J].
A novel operation cost optimization system for mix-burning coal slime circulating fluidized bed boiler unit
[J].DOI:10.1016/j.applthermaleng.2018.11.087 [本文引用: 1]
Data-driven framework for boiler performance monitoring
[J].DOI:10.1016/j.apenergy.2016.09.072 [本文引用: 1]
The multi-objective optimization of combustion system operations based on deep data-driven models
[J].
基于梯度信息的实时优化与控制集成策略
[J].
Gradient information-based strategy for real time optimization and control integration
[J].
蒸气动力系统的运行优化研究与应用
[J].
Research and application on the operation optimization of steam power system
[J].
Principal component analysis
[J].DOI:10.1002/wics.101 [本文引用: 1]