近年来时间序列数据的建模引起了学术界极大的关注，因为其在金融营销和生物信息^[1-4]不同领域都有着广泛的应用. 不同的时间序列演变模式反映了不同的用户行为，存在一定的规律性. 若有一种方法能够提取给定流量片段的用户行为，学习每个行为产生的流量片段情况，并捕获用户行为的转换，则可以更好地发挥时间序列的预测效果. 当前大多数的相关研究，如基于深度神经网络的模型（如long short term memory (LSTM)和variational autoencoder (VAE)）^{[3, 5]}，不能区分不同模式. 传统的混合模型（如Gaussian mixed model，GMM和hidden Markov model，HMM）^[6-7]忽略了用户行为随时间产生的变化.

本文提出演变基因（简称基因）的概念，定量描述每种用户行为如何产生相应的时间序列. 将基因 $ {G} $定义为捕获分布模式并学习生成片段的生成模型. 对于给定的时间序列的序列段 $ \{ {{\mathbf{\chi }}_1}{\mathbf{,}}{{\mathbf{\chi }}_2}{\mathbf{,}}\cdots{\mathbf{,}}{{\mathbf{\chi }}_n}\} $，目标是学习和提取每个片段 $ {\mathbf{\chi}} _n $的基因 $ {G} _{\rm{k}} $，在此基础上，预测了未来值 $ {{\mathbf{\chi }}_{n+1}} $以及在 $ n+1 $时间窗口将发生的事件.

本文的目的是基于时间序列的基因去估计未来事件. 传统的工作主要是根据数据值来预测事件，如动态时间扭曲^[8]、复杂性恒定距离^[9]和弹性集合^[8]等. 这些方法聚焦于距离测量方法并找到最近的样本，然而行为的演变在预测任务中更重要.

由此提出新的模型：生成式混合非参数编码器(generative mixture nonparametric encoder，GeNE)，它通过学习生成相应的片段，区分时间序列的分布模式. 本文在1个合成数据集和5个真实数据集上评估所提出的模型. 实验结果表明，在3个不同任务上的测试结果比几种当前最先进的算法更优越(如F1平均提升了10.56%). 通过可视化行为演变，展示了本文方法的解释性. 将本文方法应用到预测国家电网的电表异常波动侦查任务中，帮助减少50%的电气设备维护工作量，每年可节约约3亿美元的费用.

时间序列建模已经应用于许多领域，如异常检测(如异常突变^[2]和逐渐下降^[3-4])、人类行为识别(如昼夜节律和循环变化^[10-11])、生物学应用(如激素循环^[12]). 大多数研究集中在用不同的距离度量来模拟演变数据，如动态时间扭曲^[8,12]、移动分裂合并^[13]、复杂度恒定距离^[9]和弹性集合^[2,8]等.

一些方法侧重于通过距离进行序列聚类^[10,14]，目的是寻找到更好的度量距离的方法来建模，增强聚类性能. 本文的任务与此不同. Baydogan等^[15-16]探索了基于特征的分类器，但它们是以片段重复的频率进行区分，记录重复出现片段的频率，根据生成的直方图建立分类器^[17-18]. 时间序列分类的深度学习算法通常是以循环神经网络（recurrent neural network，RNN）为基础，叠加卷积神经网络（convolutional neural network，CNN）层来提取时间序列特征，最后通过一个输出层进行预测. 有的是生成模型^[19]，有的是判别模型^[20]，有的是利用无标签数据进行半监督学习^[21].

基于模型的算法对每个序列拟合一个生成模型，利用模型参数的相似性来度量序列之间的相似度. 采用的参数化方法包括拟合自回归模型^[22]、隐马尔可夫模型^[7,23]和依赖于人工知识的内核模型^[16]. 近来许多利用神经网络的模型被提出^[24-26]，对于序列数据的深度学习方法大多集中在高级模式表示，主要思想是融合时间或空间多种因素进行建模. Informer是以transformer为基础设计的模型，用以长时间序列预测^[27]. FEDformer 通过傅里叶变换和小波变换在频域使用注意力计算^[28]. Yue等^[29]利用对比学习框架进行时间序列表征学习，假设时间上相似的片段可以视为正样本，远距离的片段可以视为负样本. Shang等^[30]从一组时间序列数据中学习图结构，使用图神经网络（graph neural network, GNN）进行学习. 谱时间图神经网络(StemGNN)在谱域捕获序列间相关性和时间相关性，通过图形傅里叶变换(graph Fourier transform，GFT)和离散傅里叶变换(discrete Fourier transform，DFT)框架进行有效预测^[31].

生成模型最近引起了人们的极大关注，大规模(未标记)数据上的非参数学习能力赋予了它们更多的潜力和活力. Chapfuwa等^[2,18,32-33]都致力于深度生成模型的探索和发展. 由于深度结构能够捕获数据中的复杂结构，这些方法在生成更真实的样本方面比传统生成模型更加优越. 其中有2个重要主题：变分自动编码器(variational autoencoder, VAE)^[5] 和生成对抗网络(generative adversarial network，GAN)^[34]. VAE包含1个变分编码器网络与1个解码器/生成器网络. VAE的缺点是由于噪声和不完美的度量方法（如平方误差），生成的样本往往是模糊的^[35]. GAN是另一种比较流行的生成模型. 它同时训练2个模型：生成样本的生成模型和区分真实样本和合成样本的鉴别模型. GAN模型在训练阶段难以收敛，由GAN生成的样本往往不自然. 利用条件约束，可以显著地提高生成样本的质量^[36-37]. 近年来，许多学者在寻找更好的GAN训练方法^[33]，从理论上更好地理解GAN的训练过程^[32,38].

GAN在各个领域都得到了相当多的关注^[39-40]，包括图像翻译^[41]、图像生成^[42]、目标检测^[43]、视频^[44]和自然语言处理^[45]. 尽管GAN在计算机视觉领域(图像和视频生成)取得了成功，但将GAN应用于时间序列数据预测仍具有挑战性. 最近，GAN已经被应用于时间序列数据的建模，其应用包括时间序列事件的生成^[46]、轨迹预测^[47]、图表示^[48]等.

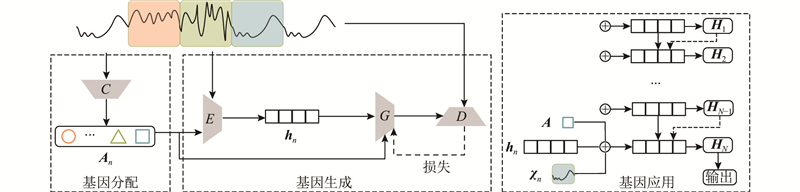
与上述模型不同，本文的模型使用分类器学习片段对应的基因，使用CVAE-GAN结构^[35]估计分布模式. 根据分布的演变情况，预测未来的事件.

本文所考虑的任务是捕捉时间序列背后的行为演变，利用这些演变模式预测未来出现的值和事件.

定义 $ {\boldsymbol{\chi}} \in {\bf{R}}^{N \times T \times S} $是一个时间序列中 $ N $个时间窗口的观测序列. 每个 $ {\boldsymbol{\chi}}_ n = \{ {\boldsymbol{x}}_t\} _{t = 1}^T \in {\bf{R}}^{T \times S} $是长度为 $ T $的时间窗口片段. $ T $具有实际意义，例如一天24 h或一个月30 d. 每个 $ {\boldsymbol{x}}_t \in {\boldsymbol{\chi}}_ n $表示对变量 $ S $的单变量或多变量观测值，记为 $ {\boldsymbol{x}}_t = \{ x_t^{(s)}\} _{s = 1}^S \in {\bf{R}}^S $. $ y = \pi \in \Pi $表示发生在观测序列 $ {\boldsymbol{\chi}} $下的未来事件，其中 $ \Pi \subset {\bf{Z}} $是事件标记的集合， $ \pi $是具体的事件标记. 定义 $ {{\boldsymbol{A}}}_n \in {\bf{R}}^K $为对片段 $ {\boldsymbol{\chi}} _n $的 $ K $个行为的基因识别，其中 $ 0 < {A}_n^{(k)} < 1 $.0且 $\displaystyle \sum\nolimits_{k = 1}^K {{A}_n^{(k)} = 1} $. 本文的目的是预测未来值 $ {{\boldsymbol{\chi }}_{(N+1)}} $和未来事件概率 $ {P} (y|{\boldsymbol{\chi }},{{\boldsymbol{A}}}) $. 本文提出新的生成方法来建模时间序列 $ {\boldsymbol{\chi }} $，该方法侧重于区分分段的分布模式及其在时间序列上的整体行为演变.

本文提出新的模型——生成式混合非参数编码器(generative mixture nonparametric encoder, GeNE)，通过学习相应的基因区分时间序列背后隐藏的不同行为，捕获每个片段 $ {\boldsymbol{\chi}} _n $的分布模式，从而作出预测. 如图1所示，给定基因的数量 $ K $，所提出的模型由3个部分组成：基因识别，目的是识别片段相应的基因；基因生成，旨在生成每个基因的片段；基因应用，旨在将学习到的基因应用于下游任务，如时间序列的预测或分类.

基因识别部分是为了识别每个片段 $ {\boldsymbol{\chi}} _n $相应的基因，这可以通过聚类算法的方式来实现. 为了同时区分片段的分布模式和序列模式，提出适用于序列的分类网络 $ {\text{C}} $(由RNN或LSTM实现)，提高聚类算法的识别能力.

基因生成部分是用来学习生成片段的基因，目的是捕获片段的分布模式. 基因生成是由对抗生成器 $ ({G} |{D} ) $实现的，除了损失函数更简单以外，结构类似于CVAE-GAN^[35]. 该方法捕获了优于其他方法的高级分布模式（详见第2.3节）.

基因应用. 基因可以识别片段所代表的行为. 基因可以在时间序列 $ {\boldsymbol{\chi }} $上按顺序组合，就像生物遗传密码一样. 本文提出递归结构，在时间序列上组合这些基因，并应用于下游任务，得到优越的预测和解释模型，如2.3、2.4节所示.

总的来说，基因识别提供监督信息来指导基因生成，提高了捕获片段分布模式的能力. 基因识别和基因生成与下游任务 $ y $无关，因此可以进行离线训练. 基因应用是基于“端到端”学习，实时调整基因识别和生成.

时间序列数据根据不同的分布模式进行演变，这通常是由不同的行为引起的，因此可以通过捕获分布模式来识别时间序列背后的这些行为. 传统的聚类算法关注不同样本之间的距离. 它们将每个变量作为独立的个体，没有考虑序列的相似性，因此不适合进行基因识别. 本文探索了新的方法，能够克服上述困难.

一般来说，给定基因的数量为 $ K $，通过传统的基于距离的聚类算法 $ f $，如K-means，初始化识别标签 $ A_n^{(0)} $，算法的输入为每个片段变量的均值和方差. 公式为

(1) $\left. \begin{aligned} & {\boldsymbol{u}}_n = \frac{1}{T}\sum\nolimits_{t = 1}^T {{\boldsymbol{\chi }}_n}, \\ & A_n^{(0)} = f\left({\boldsymbol{u}}_n,\;{T}^{-1}\sum\nolimits_{t = 1}^T {({\boldsymbol{\chi }}_n - } {\boldsymbol{u}}_n)^2\right). \end{aligned}\right\} $

若距离的均值和方差接近，则这些片段更可能具有相似的分布^[49]，因此它们应该被识别成同一基因.

可能存在2个片段，具有不同的序列模式，但它们具有相似的分布，如趋势、突变或零数等. 在识别基因的时候，需要区分这些序列模式. 设计适用于序列的分类网络 $ {C} ({\boldsymbol{\chi}} _n;\theta_ {\text{C}}) $，其中 $ \theta $为模型参数，用以捕获片段中的序列模式，提高当前基因识别的质量. 具体来说，网络 $ {C} $接受原始片段 $ {\boldsymbol{\chi}} _n $作为输入，输出 $ K $维向量，通过softmax函数转变成概率. 输出表示每类基因的概率. 在训练阶段，深度神经网络 $ {C} $试图最小化交叉熵损失：

(2) $ {L}_{{C}} = - { E}_{{\boldsymbol{\chi }}\sim {{P}}_{\rm{r}}} [\ln\; {P} (k|{\boldsymbol{\chi}} _n)] . $

式中： $ {{P_{\rm{r}}}} $为片段的真实经验联合分布，可以通过抽样来估计. 将网络 $ C $的基因识别作为新的基因类别，并重复这些步骤，直至错误率 $ {{|A^{\rm{o}} \ominus A^{\rm{n}}|}}\;/\;{{|A^{\rm{o}}|}} $收敛，其中 $ A^{\rm{o}} $和 $ A^{\rm{n}} $分别为每次迭代中旧的和新的基因类别数. 分类网络 $ C $的实现，使用RNN或变体LSTM，RNN和变体LSTM擅长捕获时间序列中的序列模式.

属于同一基因的片段具有相似的分布，因此非参数生成模型是评估它们的一种自然、有效的方法. 如图1所示，将具有基因识别的片段输入到CVAE-GAN结构中，它将片段编码到隐空间中，对利用变分方法生成的假样本进行区分.

更具体地说，对于每个片段 $ {\boldsymbol{\chi}} _n $及其基因识别 $ {\boldsymbol{A}}_n $，每个基因通过编码器网络 $ E({\boldsymbol{\chi}} _n,{\boldsymbol{A}}_n;\theta_ {\text{C}}) $来表示它的分布模式，编码器 $ E $获得从真实片段 $ {\boldsymbol{\chi}} _n $到隐向量 $ {\boldsymbol{h}}_n $的映射. 让变分近似后验是具有对角协方差结构的多元高斯：

(3) $ \ln {{E}}({\boldsymbol{h}}_n|{\boldsymbol{\chi}} _n,{\boldsymbol{A}}_n) = \ln N({\boldsymbol{h}}_n;{\boldsymbol{u}};{\delta ^2}{\boldsymbol{I}},{\boldsymbol{A}}_n). $

基于变分方法，对于每个片段，编码器网络 $ E $输出隐藏向量的平均值 $ {\boldsymbol{u}} $和方差 $ \delta $，可以采样得到隐藏向量 $ {\boldsymbol{h}}_n = {\boldsymbol{u}}+{\boldsymbol{z}}{\rm{e}}^\delta $，其中 $ {\boldsymbol{z}}\sim {N}(0,{\boldsymbol{I}}) $是随机向量. 使用KL损失函数，减小先验分布 $ {P} ({\boldsymbol{h}}_n) $和建议分布之间的差距，例如

(4) $ L_{{\rm{KL}}} = \frac{1}{2}\left[{{\boldsymbol{u}}^{\rm{T}}}{\boldsymbol{u}}+\sum \left({\rm{e}}^\delta - \delta - 1\right)\right] . $

在得到 $ {\boldsymbol{\chi}} _n $到 $ {\boldsymbol{h}}_n $的映射后，每个基因都可以通过生成器网络来映射生成的片段，形式为 $ {{\boldsymbol{\chi }}_n}' = {{G} _k}({{\boldsymbol{h}}_n}, {{\boldsymbol{A}}_n};{\theta _{\text{G}}}) $. 鉴别器网络 $ {D} ({\boldsymbol{\chi}}_ n;{\theta _{{\rm{D}}} }) $用来估计一个片段来自真实样本或生成样本 $ {{\boldsymbol{\chi }}_n}' $的概率，并试图最小化损失函数：

(5) $ \begin{split} L_{\text{D}} = - {{E}_{{\boldsymbol{\chi }\sim} {{P}}_{\rm{r}} }}[\ln D({{\boldsymbol{\chi }}_n})] - {{E}_{{{{\boldsymbol{h}}}\sim }{P}_{\rm{z}}}}[\ln\; (1 - D({{\boldsymbol{\chi }}_n}'))] . \end{split} $

式中： $ P_{\rm{z}} $为简单分布，如均匀分布. $ {G_k} $的训练过程是最大化 $ D $出错的概率，因此 $ {G_k} $试图最小化目标函数：

(6) $ L'_{{G_k}D}= - {E}_{{{\boldsymbol{h}}}\sim{P}_{\rm{z}}}[\ln\; (D({{\boldsymbol{\chi }}_n}'))] . $

在实际中，样本和“假”样本的分布可能不会相互重叠，特别是在训练过程的初期. 鉴别器网络 $D $可以将它们完美地分开，即始终有 $D({{\boldsymbol{\chi }}_n}{\text{)}} \to {\text{1}} $和 $ D({\boldsymbol{\chi}} _n'{\text{)}} \to 0 $. 当更新 $ G$的参数时，梯度 $ \partial L'_{{\text{GD}}}/\partial D({\boldsymbol{\chi}} _n') \to - \infty $，因此 $ G $的训练过程将会不稳定. 近年来，一些研究从理论上说明训练GAN往往涉及到处理 $G $的不稳定梯度的问题^[50].

为了解决该问题，对基因采用均值特征匹配目标. 目标要求生成样本的中心特征与真实样本的中心特征相匹配. 用 $ {F_{\text{D}}}({{\boldsymbol{\chi}} _n}) $表示鉴别器网络中间层的特征. $ {G_k} $试图最小化损失函数：

(7) $ L_{{G_k}D}^{} = ||{{E}_{{\boldsymbol{\chi }}\sim P_{\rm{r}} }}{F_{\text{D}}}({\boldsymbol{\chi}}_n) - {{E}_{{\boldsymbol{h}}\sim{P}_{{\rm{z}}}}}{F_{\text{D}}}({\boldsymbol{\chi }}^{'}_n)||_2^2 . $

为了让实验更简单，选择 $ D $最后一个全连接层的输入作为特征 $ {F_{\rm{D}}} $. $ G $和 $ D $都采用随机梯度下降( stochastic gradient descent，SGD)优化算法进行训练.

基因可以识别不同的分布模式所代表的片段背后的行为，它们可以像生物遗传密码一样在时间序列上按顺序组合. 基因的序列揭示了这个时间序列的行为演变，获得优越的预测和解释模型（详细介绍见第2.4节）. 本文提出递归结构，在时间序列上组合这些基因，并应用于下游任务中，主要是时间序列的预测和分类.

形式上，给定的观测序列 $ {\boldsymbol{\chi }} \in {\bf{R}}^{N \times T \times S} $，通过网络 $ C $得到所有的基因识别 ${\boldsymbol{ A}} $以及基因最有可能的分布模式 $ {\boldsymbol{h}} $. 如图1所示，使用混合的RNN结构来融合这些特征，融合后的隐向量被表示为 $ {\boldsymbol{H}} $.

特征融合. 在接收到由过去片段 $ {\boldsymbol{\chi}} _n $、基因识别 $ {\boldsymbol{A}}_n $、基因分布模式 $ {{\boldsymbol{h}}_n} $及来自过去的记忆 $ {{\boldsymbol{H}}_{n - 1}} $后，更新隐向量 $ {{\boldsymbol{H}}_n} $，公式为

(8) $ {{\boldsymbol{H}}_n} = \tanh\; ({\boldsymbol{W}} \cdot ({{\boldsymbol{\chi }}_n};{\boldsymbol{A}}_n;{{\boldsymbol{h}}_n})+{\boldsymbol{U}} \cdot {{\boldsymbol{H}}_{n - 1}}+{\boldsymbol{b}}) . $

式中： $ {\boldsymbol{W}}、{\boldsymbol{U}} $为可学习的权重矩阵，b为偏差向量，“·”为矩阵乘积符号.

输出. 最后一个应用层将“端到端”机制应用于下游任务(预测未来值 $ {{\boldsymbol{\chi }}_{N+1}} $和事件 $ y $)， $ \varPsi $表示神经网络，它以最后的隐向量 $ {{\boldsymbol{H}}_N} $为输入. 对于数值的预测， $ \varPsi $输出一个向量，利用Relu函数转化为预测值. 在实验中，使用DCNN^[51]作为 $ \varPsi $，利用反向传播均方损失对网络进行训练，损失可以表示为

(9) $ L_{{\rm{app}}} = ||{{\boldsymbol{\chi }}_{N+1}} - \varPsi ({{\boldsymbol{H}}_N})||_2^2 . $

对于事件的预测，可以转化为分类问题. $ \varPsi $输出 $ \Pi $维向量，用softmax函数转换成概率. 在训练阶段，模型试图最小化交叉熵损失函数：

(10) $ L_{{\rm{app}}} = - { E_{{\boldsymbol{H}}\sim {{P}}_{\rm{r}} }}[\ln\; {P} (y = \pi |{{\boldsymbol{H}}_N})]. $

模型学习. GeNE网络的损失函数 $ {L} $为

(11) $ L = L_{{\rm{app}}}+a_1(L_{\text{D}}+L_{{\text{G}}_k{\text{D}}}+L_{{\rm{KL}}})+a_2L_{\text{C}} . $

式中： $ a_1、a_2 > 0 $为调节参数. 在实验中，设 $ a_1 = a_2 = 1 $.

直觉上，分类器 $ C $被训练来拟合当前片段的基因识别. 通过对真/假样本的对抗过程来训练 $ {E}、{G}、{D} $. 更具体地说，在每次迭代中，训练 $ C $输出当前基因识别的类别，然后训练 $ {E}、{G}、{D} $来捕获片段的分布. 分类器 $ C $的识别区分了片段 $ {\boldsymbol{\chi}} _n $，并赋予它们特定的基因索引 $ k $，因此，无监督的对抗训练转变为有监督的对抗训练，提高了基因捕捉分布模式的能力. 比较新、旧基因识别，确定是否结束迭代. 在应用层，隐向量 $ {\boldsymbol{H}} $融合了这些从基因识别和基因生成转化的模式，将隐向量应用到预测任务. 反向传播损失 $ L_{{\rm{app}}} $学习基因应用，使用较低的学习率来调整 $ C $和 $ (E,G,D) $参数.

使用6个数据集开展实验，其中包括1个合成数据集和5个真实数据集. 在真实数据集中，2个来自UCR Suite和Kaggle，其他3个由国家电网和中国电信提供.

1）合成数据集. 生成了5簇 $ {\bf{R}}^{N \times T \times S }$形式的合成样本. 每个样本都是有10个序列窗口的多元序列；每个片段有20个时间点，每个点包含3个变量. 每个簇有10 000个样本，对于第i个簇，样本的每一维都是用均值为 $ u $和标准差为 $ \sigma $: $ {{\boldsymbol{X}}_{\boldsymbol{i}}}\sim N({u_{i1}},\sigma _{i1}^2)+ N({u_{i2}},\sigma _{i2}^2) $的混合高斯分布生成的，其中均值 $ \mu $和标准差 $ \sigma $是随机获得的， $ u \in {\text{[20,\;30]}} $， $ \sigma \in {{[0,\;5]}} $.

2）地震. 该数据集来自于UCR，取自从1967年12月1日到2003年的数据，每个数据点为1个传感器在1 h内的平均读数. 根据最近的读数预测一个重大事件是否可能发生，此处重大事件定义为在里氏尺度上读数超过5的事件. 从86 000 h的读数中，共提取368个正例、93个负例. 设定24 h为1个窗口，将长度为512的序列分割为21个窗口.

3）网络流量时间序列预测（web traffic time series forecasting, WebTraffic）. 该数据集来自于Kaggle，取自2015年7月1日至2016年12月31日，每个数据点表示维基百科文章的每日浏览量. 设置一个分类任务，根据过去一年（12个月）的最近读数，预测下个月（30 d）是否会有快速增长（曲线斜率大于1）. 总共从145 000个每日浏览量中提取了105 000个负例和38 000个正例.

4）信息网络监督(information networks supervision, INS). 该数据集由中国电信提供. 它由约242 000条网络流量序列组成，每条流量记录2017年4月1日至2017年5月10日期间不同服务器每小时的进出流量. 当异常流量通过服务器端口时，被记录为出现异常流量. 目标是利用15 d内的网络流量数据，预测下一天是否会出现异常流量. 共鉴别出2 000条异常流量序列和240 000条正常流量序列.

5）电信月计划(Telecom monthly plan, TMP). 该数据集由中国电信提供. 它包括2017年8月1日至2017年11月30日间120 000个用户的每日移动流量使用量. 对于每一个用户，有12种流量使用记录(如总使用量). 在该数据集中，预测用户是否会切换新的月计划套餐，这与移动流量的速度限制有关. 考虑到只有0.05%的用户采用了新的计划套餐，采用欠采样的方法，获得包含16 000个实例的平衡数据子集，开展交叉验证.

6）电表时钟误差(Watt-hour meter clock error, MCE). 该数据集由国家电网提供. 它由2016年2月至2018年2月期间的大约400万个时钟误差序列组成，每个误差序列描述与标准时间相比的偏离时间以及每周不同电表的通信延迟. 当偏差时间超过120 s时，仪表将被标记为异常. 目标是利用过去12个月的数据，预测下一个月可能出现的异常的电表. 总共鉴别出50万个异常的时钟错误序列和350万个正常时钟序列.

不同来源的时间序列有不同的格式，详细情况如表1所示. 表中，N为样本数，T为时间窗口，P_t为取样时间点，V为变量数.

对于不同的数据集，若有明确的训练/测试分割，比如UCR数据集，则使用该明确的训练/测试集进行实验；否则，以0.8为时间线将训练/测试集拆开，前面的窗口序列用于训练，后面的窗口序列用于测试. 从训练集中抽取10%的样本作为验证，控制训练过程，避免过拟合.

在所有的实验中，将隐向量 $ {\boldsymbol{h}} $和递归向量 $ {\boldsymbol{H}} $的维数分别设为32和128. 在一台单GPU机器上训练，设置2 000为一个批次. 对于UCR的小规模数据集，设置50为一个批次. 基因识别的迭代次数为5，训练周期为30，此时性能最好. 在初始的时候，用0.01和0.001的学习率训练分类器和基因. 对基因应用进行100次迭代的训练，学习率从0.01开始，每20次迭代减少10倍，然后用0.000 1的学习率调整基因识别和基因生成. 数据量越大，批数越多，收敛所需的训练周期越少. MCE数据集仅训练30个周期即可实现收敛，在地震数据集上则训练了100个周期.

模型准确识别基因的性能验证. 在合成数据中，设置有监督（同质性）和无监督（轮廓系数）评价指标. 同质性指标表示它的所有子集是否只包含单个基因的数据点，轮廓系数结合内聚度和分离度2种因素，是评价聚类效果好坏的一种方式. 将GeNE的结果与几种不同的聚类算法得到的结果进行比较，包括K-means聚类、凝聚聚类（Agglomerative，Agglo）、桦树聚类（Birch clustering， Birch）、隐马尔可夫模型(HMM)^[7]和高斯混合模型(GMM)^[6]. 结果如表2所示. 表中，H表示同质性指标，C_o为轮廓系数. K-means的表现相对优于凝聚、桦树聚类，说明距离是表示高维时间序列的重要指标. HMM和GMM的性能表明分布是建模时间序列的关键. GeNE在同质性指标和轮廓系数上都得分最高，表明分类网络 $ {\text{C}} $捕获了片段中的序列模式，更适合于区分基因.

本节关注预测下一个窗口的值. 具体来说，任务是在给定过去观察序列 $ {\boldsymbol{\chi }} \in {\bf{R}}^{N \times T \times S} $的情况下，预测 $ {{\boldsymbol{\chi}} }_{（N+1）} $. 使用平均绝对百分比误差(mean absolute percentage error，MAPE)作为评价指标，这可以避免来自离群值的影响. 将5种基线方法进行比较如下.

1) 整合移动平均自回归模型(autoregressive integrated moving average model, ARIMA)：这是Liu等^[52]提出的用于时间序列预测的算法.

2) 长短期记忆网络(long short-term memory, LSTM)：这是Hochreiter等^[53]提出的常见的神经网络.

3) 时间正则矩阵分解(temporally regularized matrix factorization, TRMF)：这是Yu等^[54]用于时间序列预测的时间正则化矩阵分解.

4) 条件变分编码器(conditional variational autoencoder, CVAE)：该方法使用CVAE作为没有鉴别器的基因 $ G $，采用相同的特征融合方法进行预测.

5) GeNE：本文提出的方法. 使用 $ L_{\rm{value}} $作为 $ {L_{{\rm{app}}}} $，训练GeNE网络.

实验结果如表3所示. 可知，ARIMA和LSTM在5个数据集上的表现都较差. 可能是因为ARIMA和LSTM假设较强，而本身泛化能力较差，因此更应该被应用于特定的任务. TRMF模型善于捕获特定的变化，在所有数据集上都表现良好且稳定. CVAE和GeNE的MAPE都低于ARIMA和LSTM，因此表示学习到的基因的分布模式有助于提高性能. CVAE在一些小规模数据集上的表现不佳，这可能是由于样本不足造成的，但整体性能相对稳定. 不同的是，由于具有行为信息和更好的策略，GeNE模型具有最低的MAPE和相对稳定的性能.

评估提出的模型在预测未来事件的准确性，即转变成给定 $ {\boldsymbol{\chi }} $时 $ y = \pi $的分类问题. 对以下9种基线模型进行比较，这些模型已在各种预测任务中被证明具有竞争力.

1) 高斯距离(Euclidean distance，NN-ED)、动态时间规整(dynamic time warping，NN-DTW)和复杂度不变距离(complexity invariant distance，NN-CID)：给定一个样本，利用这些方法计算它们在训练数据中的最近邻居，使用最近邻居的标签对给定的样本进行分类. 为了量化样本之间的距离，它们考虑了不同的度量标准，分别是欧氏距离、动态时间扭曲^[55]和复杂性不变距离^[56].

2) 快速子序列(fast shapelets, FS)：这是使用子序列作为特征的分类算法^[57].

3) 时间序列森林(time series forest，TSF)：这是树状集成方法，从每个序列的间隔中获得特征^[58].

4) 向量空间模型中的符号聚合近似(symbolic aggregate approximation in vector space model, SAX-VSM)：这是字典方法，它从每个序列的间隔中获得特征^[59].

5) 长短期记忆网络(long short-term memory, LSTM)和多通道深度卷积神经网络(multi-channel deep convolutional neural network, MC-DCNN)：这是Hochreiter等^[53]和Zheng等^[60]分别提出的2种基于深度神经网络的方法.

除上述方法外，考虑将以下生成模型作为基线.

1) CVAE：该方法使用CVAE作为没有鉴别器的基因 $ G $，利用相同的特征融合方法进行预测.

2) GeNE: 本文提出的方法. 使用 $ {L_{{\rm{event}}}} $作为 $ {L_{{\rm{app}}}} $，训练GeNE网络.

比较结果. 如表4、5所示为事件预测的结果. 表中，A为准确度，P为精确度，R为召回率，粗体表示所有方法中能达到的最佳性能. 对于公共数据集，使用准确度作为指标，因为使用的数据有相对平衡的正/负样本比率，Bagnall等^[49]使用准确度作为指标. 对于真实数据集，使用精确度、召回率和F指标(F1、F0.5)作为指标. 通常，使用F0.5作为异常检测的度量，因为在减少工作量方面，精确度比召回率更重要. 所有基于最近邻的量化距离方法的性能相似，但不稳定，这可能归因于数据的特殊性，因为NN-DTW方法在INS和TMP数据集上的表现不佳. 特征提取方法在MCE和TMP数据集上有相对较高的召回率(Recall)，如字典方法SAX-VSM，但精确度不高，因此不太适合不平衡的样本. 神经网络方法(MC-DCNN、LSTM)由于模型的复杂性高，在小规模数据（地震）上表现不佳，它们可能更适合处理大规模数据. 生成模型利用基因的分布模式，对行为演变进行建模，在5个真实世界的数据集上获得了更好的性能. CVAE在所有数据集上的表现都优于临近邻居方法，这得益于对时间序列反映的行为演变进行建模.

将GeNE应用到国家电网温州供电有限公司的电表异常检测任务. 具体来说，GeNE将在每月初检测高风险仪表，通过分析仪表的行为演变来识别导致异常的因素，根据模型的结果建议工程师提前采取相应的应对策略. 结果显示，GeNE能够减少50%的电表维护工作量，每年可以节省约3亿美元的花费.

介绍应用的背景，以一个案例研究来证明GeNE不仅达到了约80%的异常预测精确度，而且精确地捕获了电表的不同演变模式. 为了简便起见，用4种基因类别来展示这个应用.

背景：在电表中，时钟是最基本和最重要的组成部分之一，时钟的精度直接与该表是否能够准确地测量不同时间段的数据相关联. 由于时钟同步信号不准确、设备的晶体振荡器、通信延迟、设备响应延迟等各种因素，电表所记录的时间很可能偏离标准时间. 此外，不同影响因素会导致时钟误差以不同的模式演变. 例如晶体振荡器会导致时钟误差在一个方向上波动，不稳定的通信环境会导致时钟误差摆动. 这些不同的时钟误差演变模式对诊断和维护电表具有重要意义. 利用该方法，不仅可以预测给定电表的误差状态，而且可以揭示时钟误差的不同演变模式. 通过人工发现了以下4种最具代表性的演变模式.

1）单调模式：时钟误差随时间在一个方向上波动（12个月），这可能是由于设备的晶体振荡器引起的.

2）修复模式：时钟误差会在一定的时间内恢复，这可能是由于从上级终端接收到时钟同步信号而造成的.

3）波动模式：时钟误差波动剧烈，这可能是由于通信环境较差造成的.

4）平静模式：时钟误差轻微波动，属于正常电表的理想状态.

上述4种模式已经覆盖了超过93%的样本，因此主要研究这些具有代表性的模式，忽略其他模式（比如时钟误差的突然下降或上升).

如图2(a)~(d)所示为4种遵循不同演变模式的电表时钟误差类型以及GeNE将基因类别分配到每个片段的过程. 图2中，P为每个基因在不同时间被分配到片段的概率. 例如遵循单调模式演变的时钟误差最初保持较小的值，随着时间的推移不断增长(见图2(a)). 相应地，模型捕捉到了这个变化过程，它最开始倾向于给样本赋值“正常行为”，虽然最终确定它具有“异常行为”(即基因3 ). 可以看出，利用该模型学习基因的方式与单调模式是相同的，在其他3种模式下可以观察到类似的结果. 特别的是，该模型将“正常行为”和“异常行为”交替分配给修复模式和波动模式的电表(见图2(b)、(c))，持续将“正常行为”分配给平静模式的电表(见图2(d)).

本文研究捕捉时间序列背后的行为演变，预测未来事件的问题. 基于此目的，定义“基因”，以建模从不同的行为中产生的时间序列. 利用CVAE-GAN结构来学习基因，估计片段的分布模式. 此外，学习分类器，为每个片段选择基因. 本文提出生成混合非参数编码器(GeNE)，将2个任务置于统一的框架中，该框架包括学习不同片段“基因”的分类器以及由对抗生成器学习到的分布模式. 通过递归结构，将这些模式应用到对行为演变的建模中. 为了验证提出模型的有效性，在合成数据集和真实数据集上开展实验. 结果表明，该模型优于几种先进的基线方法. 将该模型应用于国家电网公司的电表维护，证明了该模型的可解释性.