工业过程较复杂，难以建立精确的机理模型、且产生的数据形式多样，如何利用工业过程中积累的海量数据辅助和提升过程数据分析是当前的研究热点. 基于数据驱动的多元统计建模方法在过程监测领域中得到了广泛应用^[1-3]，常用的建模算法有主成分分析^[4-6](principal component analysis，PCA)、独立成分分析^[7-8](independent component analysis，ICA)、偏最小二乘分析^[9-10](partial least squares，PLS)等^[11].

与其他数据驱动的建模方法不同，PLS方法通过迭代提取过程变量和质量变量相关性最大的潜在变量空间，能够有效地监测质量相关故障. Li等^[12]研究发现，PLS引导的斜交分解方式没有按照输入X的方差降序提取潜变量，容易出现误报警的现象. Zhou等^[13]提出全潜结构投影(total PLS, TPLS)的方法. Yin等^[14]提出改进潜结构投影(modified of PLS, MPLS)的方法，采用奇异值(singular value decomposition, SVD)分解代替迭代过程，对输入进行正交分解. Peng等^[15]提出高效潜结构(efficient PLS，EPLS)的方法. Qin等^[16]提出并行潜结构投影(concurrent PLS，CPLS)的方法.

上述方法不能提取过程变量和质量变量之间的动态变化. 近年来，诸多学者提出动态扩展算法. 常用的动态扩展方法^[17]有数据预处理和模型修正方法. 基于数据预处理的方法，Ricker^[18]结合有限脉冲响应(finite impulse response, FIR)矩阵格式，提出FIR-PLS动态模型. Ku等^[19]提出动态主成分分析(dynamic PCA，DPCA)方法等. Kaspar等^[20]构建外静、内动的DPLS模型修正方法. Lakshminarayanan等^[21]提出改进内部模型的算法. 上述模型未克服内、外部模型不一致的缺点，Li等^[22]提出外部模型与输入输出分数之间的内部模型一致的DPLS算法，结合动态潜变量模型(dynamic latent variable，DLV)将其扩展至DTPLS. Dong等^[23]提出内、外模型一致的动态内潜结构投影方法(dynamic inner projection to latent structures，DiPLS)，给出动态内部模型和外部模型的明确解释. Dong等^[24]提出DiPCA算法来捕获动态变化的数据，又提出动态内典型相关分析(Di canonical correlation analysis，DiCCA)算法^[25].

DiPLS模型^[26]仅提取可预测输入数据中与输出相关的动态特征，忽略了不可预测输入数据中与输出有关的变化. Kong等^[27]提出考虑时延的在线监测动态并发PLS(online monitoring dynamic PLS，OMD-PLS)模型，该模型虽然提供了较全面的故障检测方法，但仅考虑了PLS外部模型的动态优化，在实际工业过程中会产生较多的误报情况. 为了保证在缺失部分时段质量数据时，能够较好地提取质量相关的动态信息，给出内外模型的明确描述，本文将时延的质量数据引入DiPLS的目标函数中，提出在线监测动态内潜结构投影(online monitoring-DiPLS，OM-DiPLS)模型. 结合CPLS算法，将OM-DiPLS模型进行扩展，提出在线监测动态内并行潜结构投影模型(OM-Di CPLS)模型. 对自相关的得分采用向量自回归模型分离动态、静态信息，构造合适的统计量进行故障检测，建立完整的故障检测流程. 所提方法提供了较完整的空间划分方式，考虑了时滞的输出变量数据，提高了质量相关故障的检测效果.

Dong等^[23]提出内部、外部关系一致的动态PLS模型，即DiPLS模型，推导该模型的几何性质，给出详细的证明过程. 该模型最大限度地提高了输入得分与输出得分之间的协方差，得到的动态模型使得输出与潜变量动态相关，潜变量是输入变量向低维子空间的投影. 动态潜在变量是在输出数据的监督下提取的，保证了外部模型的导出，提高了模型的可解释性.

设输入矩阵X包含n次采样m个过程变量，输出矩阵Y包含n次采样p个质量变量，如下所示：

(1) $ \boldsymbol{X}=\left[{\boldsymbol{x}}_1, {\boldsymbol{x}}_2, \cdots, {\boldsymbol{x}}_n\right]^{\mathrm{T}} \in {{\bf{R}}}^{n \times m} ，$

(2) $ \boldsymbol{Y}=\left[\begin{array}{lll} {\boldsymbol{y}}_1, & {\boldsymbol{y}}_2, \cdots, & {\boldsymbol{y}}_n \end{array}\right]^{\mathrm{T}} \in {{\bf{R}}}^{n \times p} . $

假定X的潜在变量可以表示为 ${\boldsymbol{t}}{\text{ = }}{\boldsymbol{Xw}}$，Y的潜在变量可以表示为 ${\boldsymbol{ u}}{\text{ = }}{\boldsymbol{Yq }}$，其中 ${\boldsymbol{ w}}$和 ${\boldsymbol{q}}$均为权重向量. 由于PLS提取潜变量的原则是包含最多的变异信息和最大化相关程度，则潜变量的选取问题可以转化为求下式的最优解：

(3) $ \left.\begin{gathered} \begin{array}{*{20}{c}} {\max }&{{{\boldsymbol{w}}^{\rm{T}}}} \end{array} {{\boldsymbol{X}}^{\rm{T}}}{\boldsymbol{Y}}{\boldsymbol{q}} ; \\ \begin{array}{*{20}{c}} {s.t.}&{\left\| {\boldsymbol{w}} \right\|} \end{array} = \left\| {\boldsymbol{q}} \right\| = 1 . \\ \end{gathered}\right\} $

通过结合特征值分解对上述目标函数求解，可以推导得到PLS的外部模型：

(4) $ \left. \begin{gathered} {\boldsymbol{X}}{\text{ = }}{\boldsymbol{T}}{{\boldsymbol{P}}^{\rm{T}}}+{\boldsymbol{E}} , \\ {\boldsymbol{Y}} = {\boldsymbol{U}}{{\boldsymbol{Q}}^{\rm{T}}}+{\boldsymbol{F}} . \\ \end{gathered} \right\} $

式中： ${\boldsymbol{T}}$、 ${\boldsymbol{ U}}$为 ${\boldsymbol{X}}$、 ${\boldsymbol{Y}}$对应的得分矩阵， $ {\boldsymbol{P}} $、 $ {\boldsymbol{Q}} $为 $ {\boldsymbol{X}} $、 $ {\boldsymbol{Y}} $对应的负载矩阵， $ {\boldsymbol{E}} $、 $ {\boldsymbol{F }}$为 $ {\boldsymbol{X}} $、 $ {\boldsymbol{Y }}$对应的残差矩阵. 若 $ {\boldsymbol{B}} $为回归系数矩阵，则表示潜变量之间关系的内部模型可以表示为 $ {\boldsymbol{U}} = {\boldsymbol{TB}} $.

传统的PLS方法不适用于动态数据的建模过程. 将当前时刻的输出潜变量 $ {u_k}{\text{ = }}{\boldsymbol{y}}_k^{\rm{T}}{\boldsymbol{q}} $与输入潜变量 $ {t_k} = {\boldsymbol{x}}_k^{\rm{T}}{\boldsymbol{w}} $之间动态关系的模型构造如下：

(5) $ {u_k}{\text{ = }}{\beta _0}{t_k}+{\beta _1}{t_{k - 1}}+ \cdots +{\beta _s}{t_{k - s}}+{r_k} . $

式中： $ {r_k} $为当前时刻的残差； $ \;{\beta _i} $为输入潜变量 $ t $的权重系数， $ i=0，1，\cdots ，s $，其中 $ s $为动态模型的阶数，由最小化信息准则(Akaike information criterion，AIC)确定. 线性PLS的动态内部模型可以被预测为

(6) $ \begin{split} {{\hat u}_k} =& {\boldsymbol{x}}_k^{\rm{T}}{\boldsymbol{w}}{\beta _0}+{\boldsymbol{x}}_{k - 1}^{\rm{T}}{\boldsymbol{w}}{\beta _1}+ \cdots +{\boldsymbol{x}}_{k - s}^{\rm{T}}{\boldsymbol{w}}{\beta _s} = \\ & \begin{array}{*{20}{c}}[ {{\boldsymbol{x}}_k^{\rm{T}}}&{{\boldsymbol{x}}_{k - 1}^{\rm{T}} \cdots } \end{array}{\boldsymbol{x}}_{k - s}^{\rm{T}}]({\boldsymbol{\beta}} \otimes {\boldsymbol{w}}) . \\ \end{split} $

式中：权重系数矩阵 $\; {\boldsymbol{\beta}} \;=\;[{\beta }_{0}，{\beta }_{1}，\cdots ，{\beta }_{s}{]}^{{\rm{T}}}$， $\; {\boldsymbol{\beta}} \otimes {\boldsymbol{w}}$为克罗内克积. 为了使构造的外部模型与内部模型保持一致，可以寻找 $ {u_k} $与 $ {\hat u_k} $之间相关程度(或协方差)的最大化，DiPLS的目标函数为

(7) $ \frac{1}{n}\sum\limits_{k = s}^n {{{\boldsymbol{q}}^{\rm{T}}}{{\boldsymbol{y}}_k}} [\begin{array}{*{20}{c}} {{\boldsymbol{x}}_k^{\rm{T}}}&{{\boldsymbol{x}}_{k - 1}^{\rm{T}} \cdots } \end{array}{\boldsymbol{x}}_{k - s}^{\rm{T}}]({\boldsymbol{\beta}} \otimes {\boldsymbol{w}}) . $

结合文献[19]的方法，将输入输出矩阵进行扩充，可得

(8) $ {{\boldsymbol{X}}_i} = {\begin{array}{*{20}{c}}[ {{{\boldsymbol{x}}_i}}&{{{\boldsymbol{x}}_{i+1}}} \end{array} \cdots {{\boldsymbol{x}}_{i{\text+}n{ - }s}}]^{\rm{T}}} \in {{\bf{R}}^{(n - s+1) \times m}} ,$

(9) $ {{\boldsymbol{Z}}_s} = \begin{array}{*{20}{c}}[ {{{\boldsymbol{X}}_s}}&{{{\boldsymbol{X}}_{s - 1}} \cdots {{\boldsymbol{X}}_1}} ] \end{array} \in {{\bf{R}}^{(n - s+1) \times sm}} ,$

(10) $ {{\boldsymbol{Y}}_{\rm{g}}} = {\begin{array}{*{20}{c}}[ {{{\boldsymbol{y}}_s}}&{{{\boldsymbol{y}}_{s+1}} \cdots {{\boldsymbol{y}}_{s+n - s}}} ]^{\rm{T}} \end{array}} \in {{\bf{R}}^{(n - s+1) \times p}} .$

结合式(8)~(10)，可以将目标函数重新表述为

(11) $ \left.\begin{gathered} \begin{array}{*{20}{c}} {\max }&{J = {{\boldsymbol{q}}^{\rm{T}}}} \end{array} {\boldsymbol{Y}}_{\rm{g}}^{\rm{T}}{{\boldsymbol{Z}}_{{s}}}\left( {{\boldsymbol{\beta}} \otimes {\boldsymbol{w}}} \right) ; \\ \begin{array}{*{20}{c}} {{\rm{s}}.{\rm{t}}.}&{\left\| {\boldsymbol{w}} \right\| = 1,\;\left\| {\boldsymbol{q}} \right\| = 1,\;\left\| {\boldsymbol{\beta}} \right\| = 1} .\end{array} \\ \end{gathered}\right\} $

为了解决实际工业过程中的质量数据相较于过程数据存在滞后的问题，对DiPLS算法进行改进，提出在线监测DiPLS模型. 该模型通过引入 $ t $个时延的质量数据，提高了对故障的检测能力.

令 ${{\boldsymbol{Y}}_s}{\text{ = [}}{{\boldsymbol{Y}}_t}{\text{,}}{{\boldsymbol{Y}}_{t+1}}{\text{,}} \cdots ,{{\boldsymbol{Y}}_{s - 1}}{]} \in {{\bf{R}}^{(n - s+1) \times (s - t)p}}$，并代替 ${{\boldsymbol{Y}}_{\rm{g}}}$，则新的目标函数为

(12) $ \left.\begin{gathered} \begin{array}{*{20}{c}} {\max }&{J = {{\boldsymbol{q}}^{\rm{T}}}} \end{array} {{\boldsymbol{Y}}_{s}}^{\rm{T}}{{\boldsymbol{Z}}_{s}}\left( {{\boldsymbol{\beta}} \otimes {\boldsymbol{w}}} \right) ; \\ \begin{array}{*{20}{c}} {{\rm{s}}.{\rm{t}}.}&{\left\| {\boldsymbol{w}} \right\| = 1,\;\left\| {\boldsymbol{q }}\right\| = 1,\;\left\| {\boldsymbol{\beta}} \right\| = 1} .\end{array} \\ \end{gathered}\right\} $

采用拉格朗日乘子法，优化该目标函数：

(13) $ \begin{split} J =& {{\boldsymbol{q}}^{\rm{T}}}{{\boldsymbol{Y}}_{s}}^{\rm{T}}{{\boldsymbol{Z}}_{s}}({\boldsymbol{\beta}} \otimes {\boldsymbol{w}})+{\lambda _q}(1 - {{\boldsymbol{q}}^{\rm{T}}}{\boldsymbol{q}})/2+ \\ &{\lambda _\beta }(1 - {{\boldsymbol{\beta}} ^{\rm{T}}}{\boldsymbol{\beta}} )/2+{\lambda _w}(1 - {{\boldsymbol{w}}^{\rm{T}}}{\boldsymbol{w}})/2\;. \\ \end{split} $

分别关于 $ {\boldsymbol{q}} $、 $\; {\boldsymbol{\beta}} $和 $ {\boldsymbol{w}} $求偏导并令等式为零，得到下式：

(14) $ \frac{{\partial J}}{{\partial {\boldsymbol{q}}}} = {{\boldsymbol{Y}}_{s}}^{\rm{T}}{{\boldsymbol{Z}}_{s}}({\boldsymbol{\beta}} \otimes {\boldsymbol{w}}) - {\lambda _q}{\boldsymbol{q}} = {\boldsymbol{0}} , $

(15) $ \frac{{\partial J}}{{\partial {\boldsymbol{w}}}} = {({\boldsymbol{\beta}} \otimes {\boldsymbol{I}})^{\rm{T}}}{{\boldsymbol{Z}}_{s}}^{\rm{T}}{{\boldsymbol{Y}}_{s}}{\boldsymbol{q}} - {\lambda _w}{\boldsymbol{w}} = {\boldsymbol{0}} , $

(16) $ \frac{{\partial J}}{{\partial {\boldsymbol{\beta}} }} = {({\boldsymbol{I}} \otimes {\boldsymbol{w}})^{\rm{T}}}{{\boldsymbol{Z}}_{s}}^{\rm{T}}{{\boldsymbol{Y}}_{s}}{\boldsymbol{q}} - {\lambda _\beta }{\boldsymbol{\beta}} = {\boldsymbol{0}} . $

根据克罗内克积的性质，可得

(17) $ {\boldsymbol{\beta}} \otimes{\boldsymbol{ w}}{\text{ = (}}{\boldsymbol{\beta}} \otimes {\boldsymbol{I}}{\text{)}}{\boldsymbol{w}}{\text{ = }}({\boldsymbol{I}} \otimes {\boldsymbol{w}}){\boldsymbol{\beta}} . $

将式(14)~(16)分别左乘 ${{\boldsymbol{q}}^{\rm{T}}}$、 ${{\boldsymbol{w}}^{\rm{T}}}$和 $\;{{\boldsymbol{\beta}} ^{\rm{T}}}$，结合式(14)~(17)，可得目标函数 $ J $的最大值：

(18) $ {J_{\max }} = {\lambda _q} = {\lambda _w} = {\lambda _\beta }{\text{ = }}{{\boldsymbol{q}}^{\rm{T}}}{{\boldsymbol{Y}}_{s}}^{\rm{T}}{{\boldsymbol{Z}}_{s}}({\boldsymbol{\beta}} \otimes{\boldsymbol{w}}) . $

因此可以得到

(19) $ {\boldsymbol{q}}={{\boldsymbol{Y}}}_{{s}}{}^{{\rm{T}}}{{\boldsymbol{Z}}}_{s}({\boldsymbol{\beta}} \otimes {\boldsymbol{w}});\,\,\,\,{\boldsymbol{q}}={\boldsymbol{q}}/\Vert {\boldsymbol{q}}\Vert . $

(20) $ {\boldsymbol{w}}={({\boldsymbol{\beta}} \otimes {{\boldsymbol{I}}}_{m})}^{{\rm{T}}}{{\boldsymbol{Z}}}_{s}{}^{{\rm{T}}}{{\boldsymbol{Y}}}_{s}{\boldsymbol{q}};\,\,\,\,{\boldsymbol{w}}={\boldsymbol{w}}/\Vert {\boldsymbol{w}}\Vert . $

(21) $ {\boldsymbol{\beta}} ={({{\boldsymbol{I}}}_{q}\otimes {\boldsymbol{w}})}^{{\rm{T}}}{{\boldsymbol{Z}}}_{s}{}^{{\rm{T}}}{{\boldsymbol{Y}}}_{s}{\boldsymbol{q}};\,\,\,\,{\boldsymbol{\beta}} ={\boldsymbol{\beta}} /\Vert {\boldsymbol{\beta}} \Vert . $

从式(19)~(21)可以看出， ${\boldsymbol{q}}$、 ${\boldsymbol{w}}$和 $\; {\boldsymbol{\beta}}$无法直接计算得到. 将 ${\boldsymbol{q}}$、 ${\boldsymbol{w}}$和 $\; {\boldsymbol{\beta}}$初始化为单位向量，循环迭代直到参数收敛，得到的3个值能够使目标函数取得最大值，避免了局部最值的产生. 以上为OM-DiPLS外部模型的建立过程.

从外部模型可以得到输入输出的动态得分，计算公式为 ${{\boldsymbol{t}}_i} = {{\boldsymbol{X}}_i}{\boldsymbol{w }}\in {{\bf{R}}^{n \times 1}}$， ${{\boldsymbol{u}}_s} = {{\boldsymbol{Y}}_s}{\boldsymbol{q}} \in {{\bf{R}}^{(n - s+1) \times 1}}$. 类似于式(6)，为了捕捉 ${{\boldsymbol{t}}_i}$与 ${{\boldsymbol{u}}_s}$之间的动态变化，可以建立动态内部预测模型： $ {\hat u_s}{\text{ = }}{\beta _0}{t_s}+{\beta _1}{t_{s - 1}}+ \cdots +{\beta _s}{t_0} $.

若 ${{\boldsymbol{t}}_i}$是自相关的，则可以通过最小二乘法进行参数估计，得到

(22) $ {\hat u_s} = {{\boldsymbol{T}}_s}{\boldsymbol{b}}{\text{ = }}{{\boldsymbol{T}}_s}{\left( {{{\boldsymbol{T}}_s}^{\rm{T}}{{\boldsymbol{T}}_s}} \right)^{ - 1}}{{\boldsymbol{T}}_s}^{\rm{T}}{u_s} . $

式中： ${{\boldsymbol{T}}_s} = \left[ {{t_s},{t_{s - 1}}, \cdots ,{t_0}} \right]$. 为了方便从输入扩展矩阵 ${{\boldsymbol{Z}}_s}$直接计算输出的得分矩阵 ${{\boldsymbol{\hat U}}_s}$，引入系数矩阵 ${{\boldsymbol{R}}_{\rm{g}}}$：

(23) $ \left.\begin{array}{l}{{\boldsymbol{R}}}_{f}={\boldsymbol{W}}\left({{{\boldsymbol{P}}}_{f}^{{\rm{T}}}{\boldsymbol{W}}}\right)^{-1}\in {{{\bf{R}}}}^{m\times A\times s},\\ {{\boldsymbol{R}}}_{\beta (f)}=\left[{\beta }_{f(1)}{{\boldsymbol{R}}}_{f(1)}\text{，}{\beta }_{f(2)}{{\boldsymbol{R}}}_{f(2)}\text{，}\cdots \text{，}{\beta }_{f(A)}{{\boldsymbol{R}}}_{f(A)}\right],\\ {{\boldsymbol{R}}}_{{\rm{g}}}=\left[{{\boldsymbol{R}}}_{\beta (1)}\text{；}{{\boldsymbol{R}}}_{\beta (2)}\text{；}\cdots \text{；}{{\boldsymbol{R}}}_{\beta (s)}\right]\in {{{\bf{R}}}}^{ms\times A}.\end{array} \right\}$

式中： $ {\boldsymbol{\beta}}_{f(i)} $为 ${\boldsymbol{R}}_{f(i)} $对应的权重， $ f = 1,2, \cdots ,s $. ${{\boldsymbol{\hat U}}_s}$的求解公式为 ${{\boldsymbol{\hat U}}_s}{\text{ = }}{{\boldsymbol{Z}}_s}{{\boldsymbol{R}}_{\rm{g}}}$.

综上所述，构建的OM-DiPLS模型如下：

(24) $ \left. \begin{gathered} {{\boldsymbol{Z}}_s} = {\boldsymbol{T}}{{\boldsymbol{P}}^{\rm{T}}}{\text+}{{{\boldsymbol{\tilde Z}}}_s}{\text{ = }}{{{\boldsymbol{\hat Z}}}_s}{\text+}{{{\boldsymbol{\tilde Z}}}_s} , \\ {{\boldsymbol{Y}}_s} = {{{\boldsymbol{\hat U}}}_s}{{\boldsymbol{Q}}^{\rm{T}}}{\text+}{{{\boldsymbol{\tilde Y}}}_s}{\text{ = }}{{{\boldsymbol{\hat Y}}}_s}{\text+}{{{\boldsymbol{\tilde Y}}}_s} . \\ \end{gathered} \right\} $

式中： $ {\boldsymbol{T}} $、 $ {{\boldsymbol{\hat U}}_s} $为 $ {{\boldsymbol{Z}}_s} $、 $ {{\boldsymbol{Y}}_s} $对应的得分矩阵， $ {\boldsymbol{P}} $、 $ {\boldsymbol{Q}} $为相应的负载矩阵， $ {{\boldsymbol{\tilde Z}}_s} $、 $ {{\boldsymbol{\tilde Y}}_s} $为相应的残差矩阵.

OM-DiPLS模型仅关注从输入数据中预测的与输出数据相关的变化，忽视了不可预测的输出数据存在与过程和质量扰动有关的变化. 将OM-DiPLS模型扩展为在线监测动态内并行潜结构投影(OM-DiCPLS)模型. 该模型从OM-DiPLS算法中提取的与可预测输出 ${{\boldsymbol{\hat Y}}_s}$相关的动态得分，形成联合输入、输出的协变子空间(covariation subspace, CVS)，记为 ${S_{{\rm{CVS}}}}$. 将输出残差 ${{\boldsymbol{\tilde Y}}_s}$用PCA分解为输出主子空间(output principal subspace，OPS，记为 ${S_{{\rm{OPS}}}}$)和输出残差子空间(output residual subspace，ORS，记为 ${S_{{\rm{ORS}}}}$). 将输入残差 ${{\boldsymbol{\tilde Z}}_s}$用PCA分解为输入主子空间(input principal subspace，IPS，记为 ${S_{{\rm{IPS}}}}$)和输入残差子空间(input residual subspace，IRS，记为 ${S_{{\rm{IRS}}}}$). 具体步骤如下.

1）对可预测输出值 $\hat{\boldsymbol{Y}}_{s}$进行SVD分解：

(25) $ {{\boldsymbol{\hat Y}}_{s}}{\text{ = }}{{\boldsymbol{U}}_{\rm{c}}}{{\boldsymbol{D}}_{\rm{c}}}{{\boldsymbol{V}}_{\rm{c}}}^{\rm{T}} \equiv {{\boldsymbol{U}}_{\rm{c}}}{{\boldsymbol{Q}}_{\rm{c}}^{\rm{T}}} .$

式中： $\boldsymbol{Q}_{{\rm{c}}}=\boldsymbol{V}_{{\rm{c}}} \boldsymbol{D}_{{\rm{c}}}^{\rm{T}}$，其中 $\boldsymbol{U}_{{\rm{c}}}$、 ${\boldsymbol{V}}_{{\rm{c}}}$为选取 $l_{{\rm{c}}}=\operatorname{rank}\left({\boldsymbol{Q}}_{{\rm{c}}}\right)$个主元的降维矩阵， ${\boldsymbol{V}}_{{\rm{c}}}$为标准正交矩阵.

在式(25)两边右乘 $\boldsymbol{V}_{{\rm{c}}} \boldsymbol{D}_{{\rm{c}}}^{-1}$，可以得到 $\boldsymbol{U}_{{\rm{c}}}$的表达式：

(26) $ \begin{split} {{\boldsymbol{U}}_{\rm{c}}}& = {{\boldsymbol{\hat Y}}_s}{{\boldsymbol{V}}_{\rm{c}}}{\boldsymbol{D}}_{\rm{c}}^{ - 1}{\text{ = }}{{{\boldsymbol{\hat U}}}_s}{{\boldsymbol{Q}}^{\rm{T}}}{{\boldsymbol{V}}_{\rm{c}}}{\boldsymbol{D}}_{\rm{c}}^{ - 1} = \\ & {{\boldsymbol{Z}}_s}{{\boldsymbol{R}}_{\rm{g}}}{{\boldsymbol{Q}}^{\rm{T}}}{{\boldsymbol{V}}_{\rm{c}}}{\boldsymbol{D}}_{\rm{c}}^{ - 1} \equiv {{\boldsymbol{Z}}_s}{{\boldsymbol{R}}_{{\rm{gc}}}} \in {{\bf{R}}^{(n - s+1) \times p}} . \end{split} $

式中： $\boldsymbol{R}_{{\rm{gc}}}=\boldsymbol{R}_{\rm{g}} \boldsymbol{Q}^{\mathrm{T}} \boldsymbol{V}_{ {c}} \boldsymbol{D}_{\rm{c}}^{-1} \in {\bf{R}}^{m p \times p}$.

2）对输出残差 ${{\boldsymbol{\tilde{ Y }}}}_{s}$进行PCA分解：

(27) $ \tilde{\boldsymbol{Y}}_s=\boldsymbol{Y}_{\boldsymbol{s}}-\boldsymbol{U}_{\rm{c}} \boldsymbol{Q}_{\rm{c}}^{\mathrm{T}}=\boldsymbol{T}_{\boldsymbol{y}} \boldsymbol{P}_{\boldsymbol{y}}^{\mathrm{T}}+\tilde{\boldsymbol{Y}}_{\boldsymbol{y}} \in {\bf{R}}^{(n-s+1) \times(n-1) p} . $

3）对输入残差 ${{\boldsymbol{\tilde Z}}_s}$进行PCA分解：

(28) $ \tilde{\boldsymbol{Z}}_s=\boldsymbol{Z}_s-\boldsymbol{U}_{\rm{c}} \boldsymbol{R}_{\rm{c}}^{\dagger}=\boldsymbol{T}_x \boldsymbol{P}_x^{\mathrm{T}}+\tilde{\boldsymbol{X}}_x \in {\bf{R}}^{(n-s+1) \times m p}. $

式中： $\boldsymbol{R}_{\rm{c}}^{\dagger}=\left(\boldsymbol{R}_{\rm{c}}^{\mathrm{T}} \boldsymbol{R}_{ {c}}\right)^{-1} \boldsymbol{R}_{\rm{c}}^{\mathrm{T}} \in {\bf{R}}^{p \times m p}$.

此时，得到的OM-DiCPLS模型如下：

(29) $ \left.\begin{array}{l} \boldsymbol{Z}_s=\boldsymbol{U}_{\rm{c}} \boldsymbol{R}_{\rm{c}}^{\dagger}+\boldsymbol{T}_x \boldsymbol{P}_x^{\mathrm{T}}+\tilde{\boldsymbol{X}}_x \;,\\ \boldsymbol{Y}_s=\boldsymbol{U}_{\rm{c}} \boldsymbol{Q}_{\rm{c}}^{\mathrm{T}}+\boldsymbol{T}_{\boldsymbol{y}} \boldsymbol{P}_{\boldsymbol{y}}^{\mathrm{T}}+\tilde{\boldsymbol{Y}}_{\boldsymbol{y}} \;.\end{array}\right\} $

式中： $\boldsymbol{U}_{{\rm{c}}}$为从可预测输出得到的动态得分矩阵， $ \boldsymbol{T}_{x} $为从可预测输出无关得到的主要得分矩阵， ${\boldsymbol{T}}_{y}$为从不可预测输出得到的主要得分矩阵， ${\boldsymbol{R}}_{{\rm{c}}}{ }^{\dagger}、 {\boldsymbol{P}}_{x}、 {\boldsymbol{P}}_{y}、 {\boldsymbol{Q}}_{{\rm{c}}}$均为负载矩阵， $\tilde{\boldsymbol{X}}_{x}、 \tilde{\boldsymbol{Y}}_{y}$为残差矩阵.

结合文献[26]的方法，基于OM-DiCPLS算法的回归建模步骤如下.

1) 数据预处理. 将给定的训练集输入输出数据进行归一化处理，结合式(8)~(10)进行数据扩充，得到 $ {{\boldsymbol{Z}}_s} $和 $ {{\boldsymbol{Y}}_s} $.

2) 动态外部模型. 令 $ j = 1 $，初始化 ${{\boldsymbol{w}}_{d(j)}}= [1, 0, \cdots {\text{,0}}{\text{]}}^{\rm{T}}$，计算负载向量并归一化：

${{\boldsymbol{q}}_j} = {{\boldsymbol{Y}}_s}_{(j)}^{\rm{T}}{{\boldsymbol{X}}_s}_{(j)} ({\boldsymbol{\beta}} \otimes {{\boldsymbol{w}}_j})$， ${{\boldsymbol{q}}_j} = { { {{\boldsymbol{q}}_j} } \mathord{\left/ {\vphantom { { {{\boldsymbol{q}}_j} } {\left\| { {{\boldsymbol{q}}_j} } \right\|} } } \right. } {\left\| { {{\boldsymbol{q}}_j} } \right\|} }$；

计算 ${{\boldsymbol{w}}_j}$并归一化，进行收敛性判定：

${{\boldsymbol{w}}_j} = {({{\boldsymbol{\beta}} _j} \otimes {{\boldsymbol{I}}_m})^{\rm{T}}}{{\boldsymbol{X}}_s}_{(j)}{{\boldsymbol{Y}}_{s(j)} }{{\boldsymbol{q}}_j}$， ${{\boldsymbol{w}}_j} = { { {{\boldsymbol{w}}_j} } \mathord{\left/ {\vphantom { { {{\boldsymbol{w}}_j} } {\left\| { {{\boldsymbol{w}}_j} } \right\|} } } \right. } {\left\| { {{\boldsymbol{w}}_j} } \right\|} }$；计算权重向量并归一化：

$\;{{\boldsymbol{\beta}} _j} = {({{\boldsymbol{I}}_q} \otimes {{\boldsymbol{w}}_j})^{\rm{T}}}{{\boldsymbol{X}}_s}_{(j)}{{\boldsymbol{Y}}_{s(j)} }{{\boldsymbol{q}}_j},\;{{\boldsymbol{\beta}} _j} = { { {{\boldsymbol{\beta}} _j} } \mathord{\left/ {\vphantom { { {{\boldsymbol{\beta}} _j} } {\left\| { {{\boldsymbol{\beta}} _j} } \right\|} } } \right. } {\left\| { {{\boldsymbol{\beta}} _j} } \right\|} }$；

计算第 $ j $个潜在分量的得分向量 $ {{\boldsymbol{t}}_j} = {\boldsymbol{X}}_s{{\boldsymbol{w}}_j} $；输出潜变量为 $ {{\boldsymbol{u}}_s}_{(j)} = {{\boldsymbol{Y}}_{s(j)}}{{\boldsymbol{q}}_j} $.

3) 动态内部模型. 用式(22)对得分进行估计： ${\hat u_{s(j)} } = {{\boldsymbol{T}}_s}{\left( { {{\boldsymbol{T}}_s}^{\rm{T}}{{\boldsymbol{T}}_s} } \right)^{ - 1} }{{\boldsymbol{T}}_s}^{\rm{T}}{u_s}_{(j)}$，其中 ${{\boldsymbol{T}}_s}{\text{ = } }\left[ { {t_s},{t_{s - 1} }, \cdots ,{t_0} } \right] .$

4) 矩阵压缩. 输入矩阵： ${{\boldsymbol{X}}}_{(j\text{+}1)}={{\boldsymbol{X}}}_{(j)}-{{\boldsymbol{t}}}_{j}{{\boldsymbol{p}}}_{j}^{{\rm{T}}}， \text{其中}{{\boldsymbol{p}}}_{j}\text{=}{\boldsymbol{X}}{{\boldsymbol{t}}}_{j}/({{\boldsymbol{t}}}_{j}^{{\rm{T}}}{{\boldsymbol{t}}}_{j})$；输出矩阵： ${{\boldsymbol{Y}}_{s(j{\text{+} }1)} } = {{\boldsymbol{Y}}_{s(j)} } - {\hat u_s}{\boldsymbol{q}}_j^{\rm{T}}$，其中 ${ {\boldsymbol{q} }_j} = { { {\boldsymbol{X} }_{s(j)}^{\rm{T}}{ {\boldsymbol{t} }_j} } \mathord{\left/ {\vphantom { {{\boldsymbol{X}}_{s(j)}^T{{\boldsymbol{t}}_j} } {{\boldsymbol{t}}_j^{\rm{T}}{{\boldsymbol{t}}_j} } } } \right. } ({{\boldsymbol{t}}_j^{\rm{T}}{{\boldsymbol{t}}_j} }) }$.

5) 更新X_s. 令滞后样本 $ f = 1 $，则分块数据的得分为 ${{\boldsymbol{t}}_{j(f)}} = {\boldsymbol{X}}_{j(f)}^{\rm{T}}{{\boldsymbol{w}}_j}$，负载为 ${ {\boldsymbol{p} }_{j(f)} } = { { {\boldsymbol{X} }_{j(f)}^{\rm{T} }{ {\boldsymbol{t} }_{j(f)} } } / ({{\boldsymbol{t}}_{j(f)}^{\rm{T}}{{\boldsymbol{t}}_{j(f)} } }) }$；矩阵压缩： ${{\boldsymbol{X}}_{j(f+1)} } = {{\boldsymbol{X}}_{j(f)} } - {{\boldsymbol{t}}_{j(f)} }{\boldsymbol{p}}_{j(f)}^{\rm{T}}$；循环迭代，直到 $f > s$；最终得到： $ {{\boldsymbol{X}}_s}_{(f+1)} = \left[ { {{\boldsymbol{X}}_1}_{(f + 1)},{{\boldsymbol{X}}_2}_{(f + 1)}, \cdots ,{{\boldsymbol{X}}_s}_{(f + 1)} } \right]$；返回步骤2)，循环迭代直到 $ j > A $， $ A $为主元个数；用式(25)将由OM-DiPLS算法得到的可预测输出值进行SVD分解，得到 ${{\boldsymbol{U}}_{\rm{c}}}$、 ${{\boldsymbol{Q}}_{\rm{c}}}$；用式(27)将输出残差 ${\boldsymbol{\tilde{ Y }}}_{s}$进行PCA分解，得到 ${{\boldsymbol{T}}_y}$、 ${{\boldsymbol{\tilde Y}}_y}$；用式(28)将输入残差 ${{\boldsymbol{\tilde Z}}_s}$进行PCA分解，得到 ${{\boldsymbol{T}}_x}$、 ${{\boldsymbol{\tilde X}}_x}$.

Qin等^[28]指出潜在变量在数据中包含了较多的动态特性，须通过建立动态模型，体现内部的自相关特性. 由于工业过程通常在一个固定点下运行，可以假设当前时刻的得分向量 ${\boldsymbol{ t}}_{k} $是准平稳过程，此时可以用平稳的时间序列模型(即向量自回归(vector autoregressive，VAR)模型) 描述 ${\boldsymbol{t}}_{k}$，如下所示：

(30) $ \boldsymbol{t}_k^{\rm{T}}=\sum_{i=1}^s \alpha_i {\boldsymbol{t}}_{(k-i)}+\boldsymbol{v}_k={{\boldsymbol{ \varTheta}}}^{\mathrm{T}} {{\bf\textit{φ}}}_k+\boldsymbol{v}_k. $

式中： $\boldsymbol{\varTheta} = \left[ \begin{array}{lll}\alpha_1, \alpha_2,\cdots , \alpha_s\end{array} \right]^{\mathrm{T}}$， $\bf\textit{φ}_k = \left[ \begin{array}{llll}{\boldsymbol{t}}_{(k-1)}^{\mathrm{T}}, {\boldsymbol{t}}_{(k-2)}^{\mathrm{T}} ,\cdots,{\boldsymbol{t}}_{(k-s)}^{\mathrm{T}}\end{array} \right]^{\mathrm{T}}$. 若 ${\boldsymbol{\nu}}_{k}$可以看作是零均值白噪声序列，则可以采用多元最小二乘(LS)算法估计参数： ${\boldsymbol{\hat \varTheta}}= \left(\displaystyle\sum\nolimits_{i=s+1}^{{s} + N} \bf\textit{φ}_i \bf\textit{φ}_i^{\mathrm{T}}\right)^{-1}\left(\displaystyle\sum\nolimits_{i=s+1}^{{s} + N} \bf\textit{φ}_i {\boldsymbol{t}}_i^{\mathrm{T}}\right)$. 可以看出，动态得分残差 ${\boldsymbol{v}}_{k}$与动态得分向量 ${\boldsymbol{t}}_{k}$是时间无关的，故在进行动态得分统计量监测时，可以通过对 ${\boldsymbol{v}}_{k}$的监测实现对 ${\boldsymbol{t}}_{k}$的监测，即

(31) $ T_{\rm{c}}^2=\boldsymbol{v}_k \boldsymbol{\varLambda}_k^{-1} \boldsymbol{v}_k^{\mathrm{T}} . $

式中： $\boldsymbol{\varLambda}_k=\boldsymbol{v}_k^{\mathrm{T}} \boldsymbol{v}_k /(n-s+1)$. 类似地，对于输入主子空间的动态得分 $ \boldsymbol{{\boldsymbol{T}}}_{x} $和输出主子空间的动态得分 ${\boldsymbol{T}}_{y}$，可以采用上述方法进行统计量监测.

Q统计量作为衡量样本在残差空间中投影变化的指标，可以使用Q统计量对输入输出残差子空间 $ \tilde{\boldsymbol{X}_{x}} $、 $ \tilde{\boldsymbol{Y}}_{\boldsymbol{y}} $进行监测，如下所示：

(32) $ {Q}_x=\left\|{\boldsymbol{\tilde{X}}}_x\right\|^2, \quad {Q}_y=\left\|{\boldsymbol{\tilde{Y}}}_y\right\|^2 . $

当统计指标超过控制限时，表明故障发生，给出相应控制限的计算公式. 对于T²统计量，控制限由主元个数 $ A $、样本数 $ n $及置信度 $ \alpha $确定，且服从 $ F $分布，如下所示：

(33) $ J_{{\rm{t h}}, T^2}=\chi_{A, \alpha}^2=\frac{A\left(n^2-1\right)}{n(n-A)} F_{A, n-A, \alpha}. $

对于Q统计量，控制限由样本均值 $ \;\mu $和样本方差 $ S $确定，且服从 $ \chi^{2} $分布，如下所示：

(34) $ J_{{\rm{t h}}, Q}=g \chi_{h, \alpha}^2 . $

基于OM-DiCPLS模型构建的统计指标及相应的控制限如表1所示.

对于给定的测试集输入 ${{\boldsymbol{X}}_{{\rm{ce}}}}$、输出 ${{\boldsymbol{Y}}_{{\rm{ce}}}}$，须经离线建模、在线监测以及故障检测3个阶段，才能对测试集实现在线故障检测.

1) 离线建模阶段. 采用表1的OM-DiCPLS算法步骤建立完整的模型，得到模型参数. 由训练集经VAR建模，结合式(33)、(34)计算模型的控制限： ${J_{{\rm{th}},T_{\rm{c}}^2}}$、 ${J_{{\rm{th}},T_x^2}}$、 ${J_{{\rm{th}},T_y^2}}$、 ${J_{{\rm{th}},{Q_x}}}$、 ${J_{{\rm{th}},{Q_y}}}$.

2) 在线监测阶段. 将 ${{\boldsymbol{X}}_{{\rm{ce}}}}$、 ${{\boldsymbol{Y}}_{{\rm{ce}}}}$进行归一化预处理，得到标准化的输入输出 ${{\boldsymbol{X}}_{{\rm{new}}}}$、 ${{\boldsymbol{Y}}_{{\rm{new}}}}$，构建新的增广数据矩阵 ${{\boldsymbol{Z}}_{s\_{\rm{new}}}}$、 ${{\boldsymbol{Y}}_{s\_{\rm{new}}}}$. 计算共变子空间的新动态得分矩阵 ${{\boldsymbol{U}}_{{\rm{c}}\_{\rm{new}}}} = {{\boldsymbol{Z}}_{s\_{\rm{new}}}}{{\boldsymbol{R}}_{{\rm{gc}}}}$，由式(31)计算统计量 ${T}_{{\rm{c}}\_{\rm{new}}}^2 = {{\boldsymbol{v}}_{{\rm{c}}\_{\rm{new}}}}{\boldsymbol{\varLambda}} _{\rm{c}}^{ - 1}{{\boldsymbol{v}}^{\rm{T}}_{\rm{c}\_{\rm{new}}}}$. 计算新的输入残差矩阵 ${{\boldsymbol{\tilde X}}_{x\_{\rm{new}}}} = {{\boldsymbol{Z}}_{s\_{\rm{new}}}} - {{\boldsymbol{Z}}_{s\_{\rm{new}}}}{{\boldsymbol{R}}_{\rm{c}}}^\dagger$，计算输入主子空间新的得分矩阵 ${{\boldsymbol{T}}_{x\_{\rm{new}}}} = {{\boldsymbol{Z}}_{s\_{\rm{new}}}}{{\boldsymbol{P}}_x}$，由式(31)计算统计量 ${T}_{x\_{\rm{new}}}^2 = {{\boldsymbol{v}}_{x\_{\rm{new}}}}{\boldsymbol{\varLambda}} _x^{ - 1}{{\boldsymbol{v}}^{\rm{T}}_{x\_{\rm{new}}}}$. 计算新的输出残差矩阵 ${{\boldsymbol{\tilde Y}}_{s\_{\rm{new}}}} = {{\boldsymbol{Y}}_{s\_{\rm{new}}}} - {{\boldsymbol{U}}_{{\rm{c}}\_{\rm{new}}}}{\boldsymbol{Q}}_{\rm{c}}^{\rm{T}}$，计算输入主子空间新的得分矩阵 ${{\boldsymbol{T}}_{y\_{\rm{new}}}} = {{\boldsymbol{Y}}_{s\_{\rm{new}}}}{{\boldsymbol{P}}_y}$，由式(31)计算统计量 ${T}_{y\_{\rm{new}}}^2 = {{\boldsymbol{v}}_{y\_{\rm{new}}}}{\boldsymbol{\varLambda}} _y^{ - 1}{{\boldsymbol{v}}^{\rm{T}}_{y\_{\rm{new}}}}$. 由式(32)计算新的输入残差统计量 ${{Q}_{x\_{\rm{new}}}} = {\left\| {{{{\boldsymbol{\tilde X}}}_{x\_{\rm{new}}}}} \right\|^2}$和新的输出残差统计量 ${{Q}_{y\_{\rm{new}}}} = {\left\| {{{{\boldsymbol{\tilde Y}}}_{y\_{\rm{new}}}}} \right\|^2}$.

3) 故障检测阶段. 将控制限与新的统计量进行比较，判断故障发生的类型.

当 ${J_{{\rm{th}},T_{\rm{c}}^2}} < T_{{\rm{c}}\_{\rm{new}}}^2$时，表明发生了质量相关的故障. 当 ${J_{{\rm{th}},T_x^2}} < T_{x\_{\rm{new}}}^2$时，表明发生了质量无关但过程相关的故障. 当 ${J_{{\rm{th}},T_y^2}} < T_{y\_{\rm{new}}}^2$时，表明发生了质量无关的不可预测故障. 当 ${J_{{\rm{th}},{Q_x}}} < {Q_{x\_{\rm{new}}}}$或 ${J_{{\rm{th}},{Q_y}}} < {Q_{y\_{\rm{new}}}}$时，表明数据采集时存在噪声或其他干扰.

1993年美国化学公司的Downs和Vogel基于真实的化学过程开发了仿真平台，即田纳西-伊斯曼过程(Tennessee-Eastman process，TEP). TEP中基于气液平衡、物料平衡、能量平衡等平衡方程式，建立30个微分方程和148个代数方程. 实际工业过程中方程的数目比仿真平台所有模型方程的总和多. 这是由于实际工业过程各部分间耦合严重，难以建模，只能通过优化部分分母、平方根和对数等参数，使得模型具有更加良好的性能^[29-32]. 为了确保TEP的模型具有真实工业过程的动态行为，Downs和Vogel采用线性特征值分析方法求解系统的最快模态；因此，TEP是包含快速和缓慢变化的动态复杂过程，被广泛应用于动态类算法的试验验证^[33-34].

TE仿真平台可以获得52个变量，其中有41个过程变量和11个操纵变量. 同时，可以模拟21种故障类型，其中有15种已知故障和6种未知故障. 该平台通过人为设置不同的故障，相应生成不同的故障样本，样本集中包含了160个正常样本和800个故障样本. 当平台正常运行时，可以获得正常样本. 正常样本中通常包含了500个样本，对TEP详细的描述可以参见文献[35]. 将已知故障进行分类，分为质量相关故障(1,2,5~8,10,12,13)和质量无关故障(3,4,9,11,14,15). 在质量相关故障的检测实验中，常用实际检测检测到的故障样本数占故障样本数的百分比，即有效故障检测率(fault detection rate, FDR)作为衡量算法有效性的指标. 在质量无关故障的检测实验中，将实际检测到的异常样本占故障样本总数的百分比，即误报率(false alarm rates, FAR)作为衡量算法有效性的标准.

在实验仿真中，选取22个过程变量 XMEAS(1~22)和11个操纵变量XMV(1~11)作为输入变量，选取5个输出变量：XMEAS(37~41). 通过二维交叉验证，求取最优的 $ A = 7,s = 6 $. 为了验证所提算法的故障检测性能，选取的比较对象为OMDC-PLS和DTPLS算法^[18]. OM-DCPLS模型的空间划分方式与OM-DiCPLS一致. DTPLS算法将输入空间分解成4个空间：质量相关的动态空间 $ {S_{\rm{D}}} $、质量无关的动态空间 $ {S_{{\rm{WD}}}} $、质量无关的静态空间 $ {S_{{\rm{WG}}}} $和残差空间 $ {S_{{\rm{DT}}}} $. 各子空间对应的统计量为 $T_{y\_{\rm{new}}}^2$、 $T_{{\rm{d}}\_{\rm{new}}}^2$、 $T_{s\_{\rm{new}}}^2$和 ${Q_{s\_{\rm{new}}}}$. 将输出空间分解为可预测的动态输出空间和残差空间. 通过交叉验证求取DTPLS的最优参数为 ${A_{{\rm{DT}}}} = 5,{s_{{\rm{DT}}}} = 4$，OMDC-PLS的最优参数为 ${A_{{\rm{OMDC}}}} = 6,{s_{{\rm{OMDC}}}} = 4$. 分析2种模型可知，DTPLS模型分解得到的质量相关的动态空间与OM-DiCPLS和OMDC-PLS模型得到的质量相关的可预测空间都可以描述为动态的质量相关空间；DTPLS模型分解得到的质量无关的静态空间与OM-DiCPLS和OMDC-PLS模型得到的输入主子空间都可以描述为静态的质量无关空间，故二者可以作为比较的对象. 相较于DTPLS和OMDC-PLS算法，本文方法提供了更合理的空间划分方式，也更关注输入数据中存在的不可预测的信息，使得残差空间的监控更合理.

DTPLS算法和OM-DiCPLS算法关于质量相关故障的检测实验结果如表2所示，用加粗的字体标记较好的检测结果. 在质量相关的动态子空间，对于阶跃故障(1, 2, 6)，利用3种算法均能够较好地检测到质量相关故障的发生，有效故障检测率大于99%. 对于随机变化的供料浓度故障(8)和缓慢漂移的故障(13)，DTPLS检测效果不如OM-DiCPLS和OMDC-PLS，但3种算法的故障检测率大于92%. 对于反映冷却水温度变化的阶跃故障(5, 7)，相较于其他2种算法，OM-DiCPLS的故障检测效果较差，这可能是因为水温变化受反应器的级联控制影响. 在质量无关的静态子空间中，3种算法对故障(1, 2, 6~8, 13)的监测效果较理想，能够检测到90%的故障. 对于故障(5)和供料温度变化的故障(10)，DTPLS和OM-DiCPLS的故障检测效果较一般，且检测结果较相近，而OMDC-PLS算法的故障检测率分别较其他2种方法提高了将近10%和18%. 对于方差随机增大的故障(12)，OM-DiCPLS和OMDC-PLS的检测效果提高了约8%. 输入残差子空间主要用来监测噪声的干扰情况. 从表2可以看出，OM-DiCPLS算法经过PCA分解后得到的输入残差中包含较少的质量相关信息，更适合Q统计量的监测，故障检测率均有一定幅度的提升. OM-DiCPLS相较于OMDC-PLS，能够更好地提取出数据间的动态相关性，使得输出主子空间和输出残差子空间中仅包含静态的信息，更适合统计量的监测，实现较好的故障检测效果.

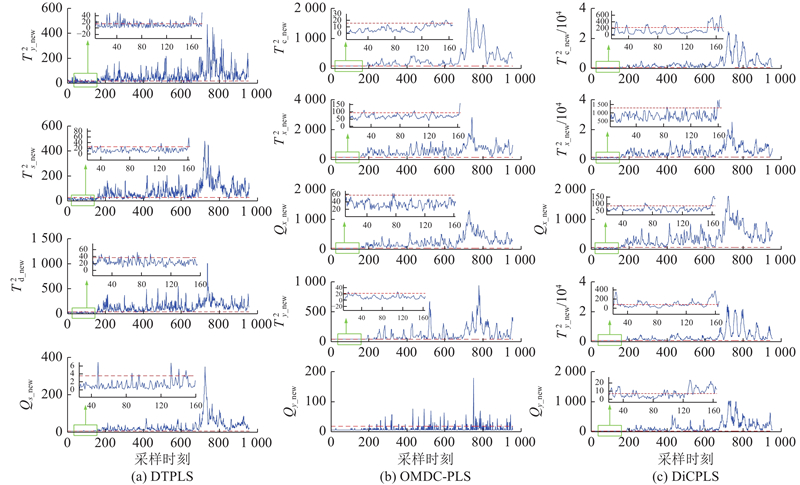
质量相关故障(12)的监测效果如图1所示. 给出测试集正常样本的局部监测结果放大图.从图1可以看出，OM-DiCPLS和OMDC-PLS算法的质量相关动态子空间能够较好地建立正常数据的模型，使得测试集的前160个正常样本能够较好地维持在控制限以下，对测试集的故障样本有更好的监测效果. DTPLS算法存在少量样本超出控制限的现象. 出现这种现象的原因一方面是置信度 $ \alpha $选取为0.99，另一方面可能是DTPLS在建模阶段提取的动态特征不够彻底，构建的模型不够准确. 在质量无关的静态子空间，3种算法对正常样本都有较好的建模效果. 在质量相关的动态子空间中，与DTPLS算法相比，OM-DiCPLS和OMDC-PLS检测到更多的故障样本. 输入主子空间又称为质量无关静态子空间. 对于质量相关故障而言，该空间不应检测到故障的发生. 从图1可知，利用3种方法均能够监测到大量误报警的情况. 这可能是因为数据中包含了大量与质量无关、但与过程相关的信息. 在输入残差子空间和输出残差子空间中，相较于OMDC-PLS方法，较小变化的噪声或其他干扰能够更容易超过OM-DiCPLS的控制限，这说明Q统计量能够实现对残差空间的在线监测.

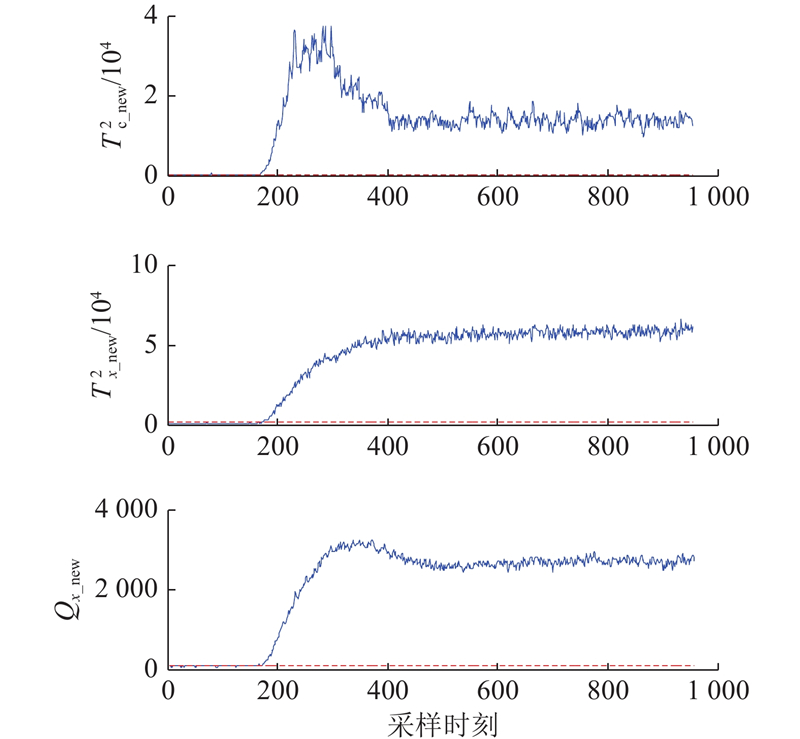
如图2所示为OM-DiCPLS对故障(2)的监测效果图. 可以看出，OM-DiCPLS具有CPLS方法的优势：对于呈现阶跃变化的质量相关故障，在阶跃变化发生后，统计量 $T_{{\rm{c}}\_{\rm{new}}}^2$先上升后下降，而与输入相关的变异性指标 $ T_{x\_{\rm{new}}}^2 $较高. 这说明TEP中的反馈控制器可以减少部分故障的影响，使质量变量趋于正常状态，但是 $T_{{\rm{c}}\_{\rm{new}}}^2$没有完全回归到正常状态.

3种算法关于质量无关故障的检测实验结果如表3所示，用加粗的字体标记检测结果较好的值。在质量相关的动态子空间中，对于质量无关的故障(3, 4, 9, 11, 15)，应对输出无影响，不应检测到故障的发生。在实际在线监测过程中，却能发现少量的故障，此时认为发生了误报警情况。从表3可以看出，本文算法在质量相关的动态子空间中对质量无关故障有更少的误报警情况，误报警率分别降低了6%~17%。这是因为通过对得分进行VAR建模，将动态信息与静态信息分离，通过对静态信息的监测能够更好地反映数据的变化情况。在输入残差子空间中，利用3种方法能够较好地监测到阶跃变化的故障(4)的噪声干扰，故障检测率大于95%。对于反应供料温度变化的微小变化故障(3, 9, 15)，利用OM-DiCPLS能够较好地监测到噪声干扰，故障检测率比DTPLS提高了约92%，比OMDC-PLS提高了约97%。对于反应冷却水内部温度的随机故障(11)，3种算法的监测效果相差不大，但利用OM-DiCPLS能够监测到所有的噪声。将质量无关的不可预测输出值通过PCA分解得到输出主子空间与输出残差空间中不包含质量相关的动态信息，因此故障检测率提高了约40%。通过对得分进行VAR建模，剔除了数据间的自相关变化，能够更加真实地反映数据的变化，因此可以实现较好的故障检测效果。

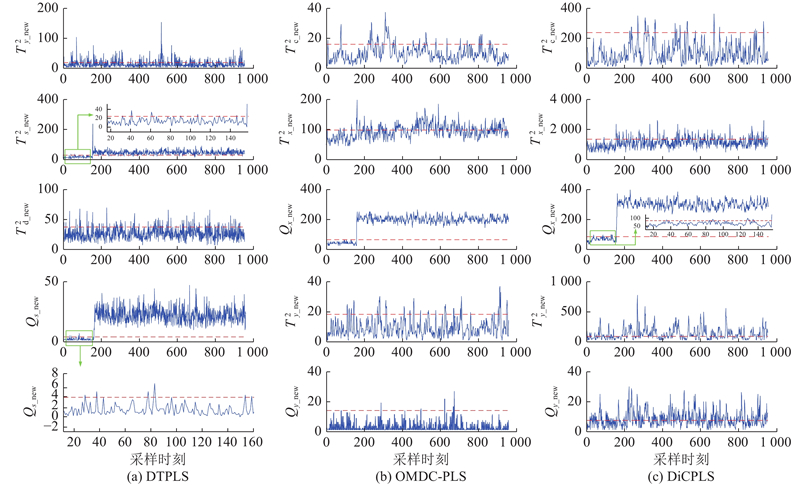
反映冷却水内部温度的阶跃故障(4)的监测效果如图3所示. 从图3可知，在质量相关的动态子空间中，DTPLS算法对所有样本的监测都存在较多误报警的情况，OMDC-PLS在200~350个样本之前发生较多的误报警情况，而OM-DiCPLS算法仅对故障样本存在少量误报警的情况，能够快速地回到控制限以下，故采用VAR监测的OM-DiCPLS算法对质量无关故障的建模效果优于DTPLS和OMDC-PLS. 在前160个正常样本监测阶段，DTPLS存在较多样本超出控制限的现象. OMDC-PLS尽管在第40个正常样本附近出现了越过控制限的情况，但能够立即回到控制限下方. OM-DiCPLS的特征提取能力和建模效果最好，在正常样本时未发生越过控制限的情况. 对于质量无关的故障而言，在质量无关的静态子空间中，故障检测率越高越好. 从图3可知，OM-DiCPLS不能很好地监测到故障的发生. 这可能是数据中包含了较多与质量无关但与过程相关的信息. 在输入残差空间中，3种算法都对噪声较敏感，能够很好地监测到噪声干扰的存在. 在输出主子空间和输出残差子空间中，OMDC-PLS在前160个正常样本监测阶段即未发生故障时，误报警情况更少. OM-DiCPLS虽然在故障发生后具有较好的故障检测效果，但在故障发生前对正常样本有更多的误报警情况. 可能的原因如下：引入的时滞质量数据导致经过动态特征提取后的 ${{\boldsymbol{\tilde Y}}_{s}}$中包含轻微的偏差，使得对不可预测输出值进行PCA分解后，在线监测的统计量对轻微的偏差更敏感.

综上所述，相较于DTPLS和OMDC-PLS，OM-DiCPLS算法更适合构建时滞过程数据与时滞质量数据之间的动态模型，对于质量相关故障能够维持较好的监测效果. 利用VAR模型得到的统计指标能够分离动、静态信息，使得质量无关故障保持较低的误报率. 较完整的空间划分方式使得残差主子空间能够更好地监测微小变化的噪声故障.

本文提出的OM-DiCPLS算法模型关注了不可预测的输入输出数据中存在的扰动信息，考虑了输入输出变量，提供了较完整的空间划分方式，能够更好地适用于存在时滞数据的在线监测. 与DTPLS和OMDC-PLS算法模型相比，OM-DiCPLS算法模型有更好的质量相关故障检测效果. 通过对自相关的得分进行VAR建模后再开展统计指标监测，能够减少质量无关故障的误报警情况.

尽管本文所提的OM-DiCPLS算法成功应用于动态过程的故障检测中，但实际工业过程受周围环境的影响，往往具有时变特性，如何实现模型的自适应更新是亟须解决的问题. 将现有方法进行改进并应用于非高斯、多模态、非平稳等其他复杂工业特性中，是未来研究的方向.