动力电池包是新能源车辆的核心部件,高温或温差过大,会造成动力电池包的容量衰减增加[1]、自放电趋势升高[2-3],严重影响新能源车的续航里程和电池的循环寿命[4-5],甚至造成车辆热失控和灾难性故障[6-7]. 通过热管理技术实现动力电池包高效、低能耗散热,保持各电池单体温度均匀,对提升车辆的续航里程和安全性能至关重要. 其中的液冷技术因导热系数大、冷却效率高、实用性强等优点被广泛应用于动力电池包散热[8]. 液冷技术使用具有内部流道的液冷板与动力电池包接触,通过换热能力较强的冷却介质循环流动,实现对电池包的快速降温[9]. 流道结构多种多样,如蛇形流道[10]、并行流道[11]、米字形流道[12]、双层枝晶流道[13]、仿生蜘蛛网流道[14]等,改变流道结构能够增强液冷板的散热性能. 对已有的流道结构,学者们研究了冷却介质流量、温度、入口尺寸对散热效果的影响. 为了进一步提升液冷板传热性能,改进或优化流道内部结构以改善冷却介质流动状态的相关研究增多. Li等[15]提出在流道中布置圆柱体、矩形体、凸起体、凹窝和V形槽等扰流元结构来增强液冷板传热性能. 以纳米流体混合物为介质,将三角形、矩形和梯形3种不同几何肋扰流元结构引入液冷板流道中的研究结果表明,相比梯形肋,虽然三角肋的传热性能更好,但压降损失较大[16]. Khan等[17]对6种带肋扰流元结构流道(矩形、半圆形、三角形、矩形-三角形、矩形-半圆形和三角形-圆形)的液冷板进行数值分析,结果表明肋条虽然能够降低流道热阻(其中三角形肋条降低的热阻最多),但会引起压降增大(其中矩形肋引起的压降最大). Liu等[18]计算矩形流道内壁面内5种不同形状的沟槽湍流流动特性和换热性能,结果表明圆形沟槽表面在强化传热和降低压降压损失方面具有很大的优势.
以上研究通过在流道内增加不同几何形状的扰流元结构,分析扰流元对流动特性和换热性能的影响,存在不足之处:一方面,如扰流元结构及其在流道布置的特征参数对液冷板传热性能的影响机理尚不清晰;另一方面,扰流元结构均为基本几何形状,未考虑扰流元结构的长度参数对液冷板传热性能的影响. 为了深入研究扰流元对液冷板传热性能影响规律,探寻热阻低、均温性好的最优结构,本研究以某款液冷板为例,构建新型全特征扰流元结构,开展扰流元特征参数和布置参数寻优. 为了实现定量评价,本研究提出温度均匀性系数,搭建液冷板传热实验台进行实验验证.
1. 液冷板传热计算方法
1.1. 几何模型与发热量实验
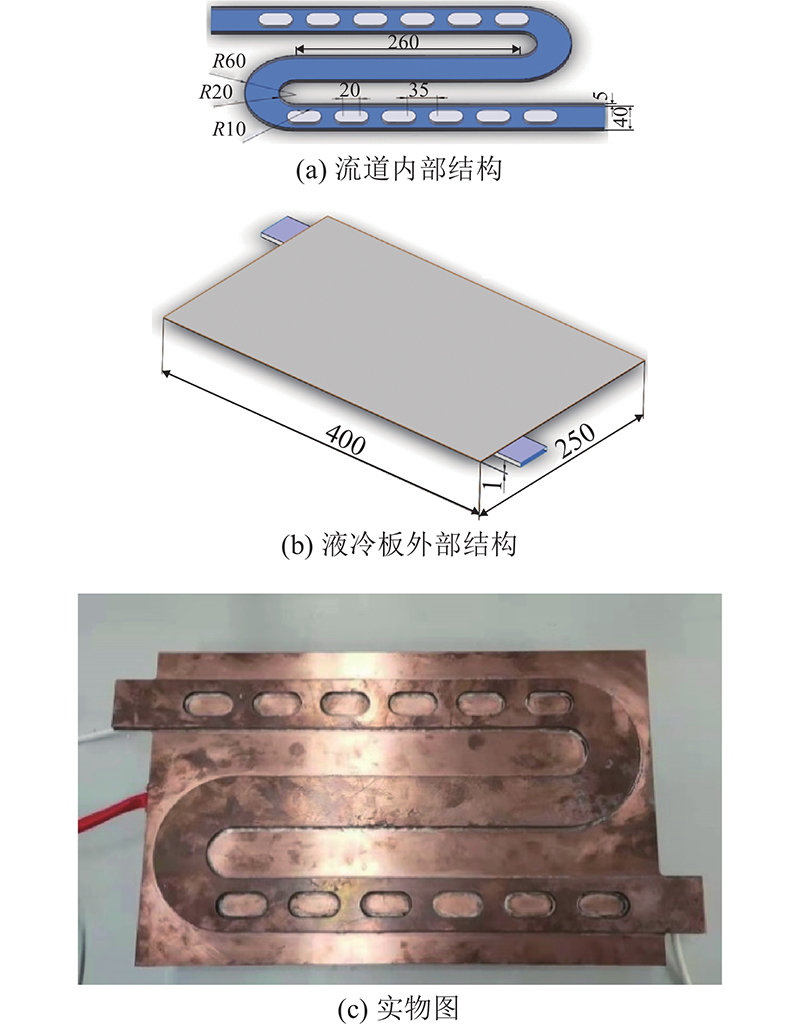
某工程车用动力电池包液冷板为一进一出标准蛇形液冷板,对其进行适度简化,几何模型如图1所示. 为了节约计算资源、更好地表征液冷板的散热特性,排除电池包不均匀发热对液冷板散热均匀性的影响,采用均匀发热的加热膜代替电池包. 单体电芯在恒温箱下的发热量实验如图2所示,电芯采用型号为LF50K-73103的方形锂电池(额定容量为50 Ah、额定电压为3.2 V、电池类型为磷酸铁锂),恒温箱温度设为15 ℃,在电芯外表面布置温度传感器,经过1个充放电循环,记录时间与温度的变化,得到该电芯1充放电倍率C下平均产热为6.42 W,2C下平均产热为20 W,3C下平均产热为28.6 W,这与Xu等[19]测得的结果吻合. 热源采用与7块电芯在3C下近相似的200 W功率加热膜代替发热源,加热膜长为390 mm,宽为240 mm,厚为2 mm,加热膜紧贴在液冷板表面,实验安装如图3所示.
图 1
图 2
图 3
1.2. 控制方程
电池包工作中,产生的热量由热传导的方式传递到液冷板,再由冷却介质将热量带出. 在传热过程中,冷却介质遵循质量守恒方程、动量守恒方程、能量守恒方程,控制方程[11]如下.
1)连续性方程:
2)动量守恒方程:
3)能量守恒方程:
式中:t为液冷板传热时间,θ为冷却介质温度,ρy为冷却液密度, cy为冷却介质比热容,K为冷却介质传热系数,v为冷却液流速,vx、vy、vz为冷却液速度v在x、y、z方向的分量,μ为动力黏度,p为流体微元上的压力,Sx、Sy、Sz为动量方程的广义源项,Sθ为流体内热源及由于黏性作用机械能转换为热能的部分.
液冷板传热过程的能量守恒方程为
式中:ρ1为液冷板的密度,c1为液冷板比热容,λ为液冷板导热系数. 液冷板的流固交界面上存在控制方程:
1.3. 边界条件与网格无关性验证
研究选取水为冷却介质,系统初始温度均设为20 ℃. 仿真边界条件为1)入口和出口:入口流速为0.25 m/s,入口温度为 20 ℃,出口压力相对大气压为0 Pa. 2)交界面:流固边界须满足无滑移边界条件. 3)热源边界:液冷板接触面紧贴200 W功率加热膜,其余各边界为绝热边界条件. 加热膜、液冷板、冷却介质的物性参数如表1所示. 液冷板表面积较大,厚度偏薄,采用薄壁层网格,加密流固耦合边界层. 使用网格分别为9.6×105、17.3×105、32.7×105、41.5×105 的模型进行网格无关性验证,结果表明,当网格从32.7×105增加到41.5×105时,流道压降和液冷板最高温度变化甚微,因此采用32.7×105的网格模型进行计算分析.
表 1 仿真材料的热物性参数
Tab.1
| 材料 | ρ/(kg·m-³) | c/(J·kg−1∙K−1) | K/(W·m−2∙K−1) | v/(m·s−1) |
| 热源 | 1 300 | 1 973 | 150 | — |
| 液冷板 | 2 700 | 900 | 209 | — |
| 冷却介质 | 997 | 4 181 | 0.62 | 0.25 |
1.4. 温度均匀性系数
为了改变液冷板均温性能评价的模糊性,参考文献[20]中速度均匀性系数,提出温度均匀性系数Tc,该系数通过统计液冷板各监测点与平均值的偏差来反映板面的温度分布特性,计算式为
图 4
1.5. 结果分析
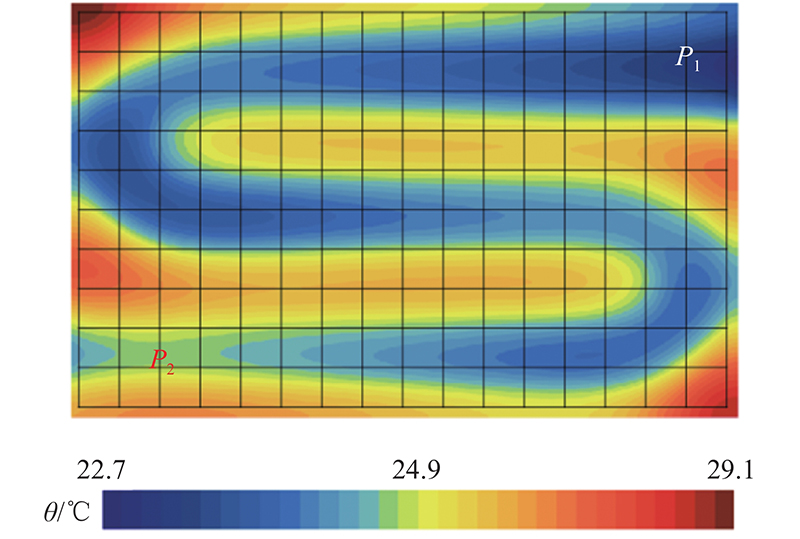
热源表面温度稳定后,液冷板压降为369 Pa,液冷板散热云图如图5所示. 可以看出,热源的最高温度为29.1 ℃,最低温度为22.7 ℃,温差为6.4 ℃;流道入口附近点P1处的温度较低,随着冷却介质的流动,冷却性能变差,流道出口附近点P2处的温度较高,为24.7 ℃. 由于冷却介质黏性力的作用,流道中热边界层难破碎,导致热量逐渐富集,热阻升高,换热性能降低,温度均匀性变差,按式(8)得到温度均匀性系数Tc1=0.339. 若长期使用该液冷板,如此高的温度和温差将影响车辆的续航里程和电池包寿命. 周全等[21]的研究表明,流道流体处于湍流状态时,热边界层被破坏,换热效果显著提升,热阻降低. 对流道流动状态进行优化,能够降低热阻,改善均温性.
图 5
图 5 原始液冷板的散热云图
Fig.5 Heat dissipation cloud diagram of original liquid-cooled plate
2. 全特征扰流元模型与传热规律
2.1. 全特征扰流元模型与计算方法
图 6
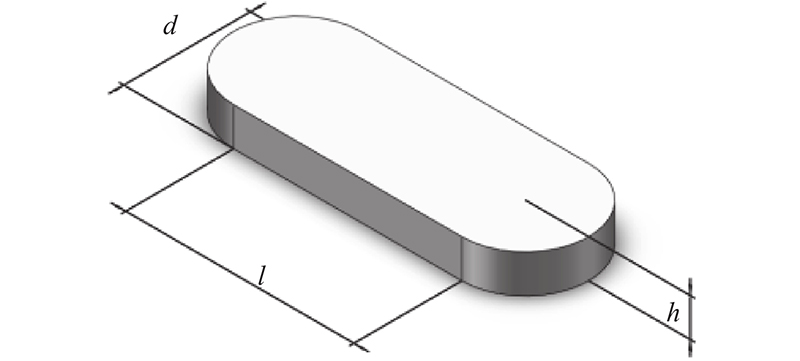
全特征扰流元模型属于对称结构,为使流场均匀,采用流道中心对称布置. 流道深度较小,扰流元高度的变化量有限,对传热效果影响较小,扰流元高度h与流道高度一致,不予研究. 如图7所示,以单体扰流元为研究对象,探究扰流元特征参数对流道传热影响的规律. 此时流道尺寸为90 mm×40 mm×3 mm,冷却介质为纯净水,温度为20 ℃,黏度为0.01011 Pa·s,流速为0.45 m/s. 计算采用四面体网格、Realizable k-ε湍流模型,当控制方程的残差均小于1.0×10−6时,视计算结果为收敛;经网格无关性验证,当采用1.5×105的网格规模进行计算分析时,精度满足计算要求.
图 7
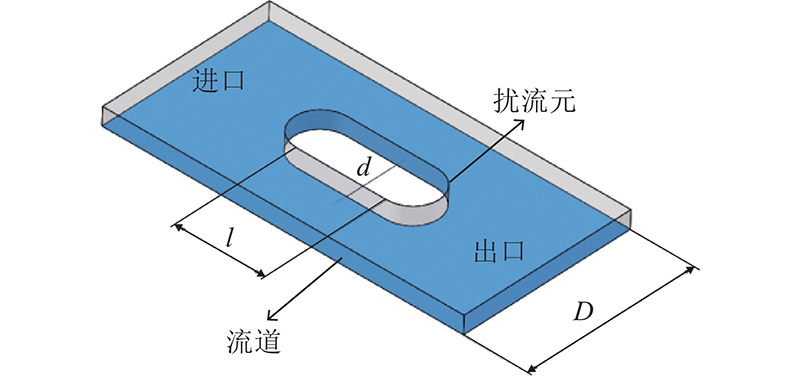
图 7 含扰流元的流道单体几何模型
Fig.7 Geometrical model of single runner with disturbance element
增加扰流元结构后,流道湍流强度将发生变化,进而改变雷诺数Re,对此,通过分析流道中心截面平均雷诺数比较不同扰流元结构强化流道传热的效果.
式中:De为流道当量直径,vc为平均流速. 采用截面平均速度公式计算平均流速:
式中: vn为对应区域流速,
2.2. 几何特征参数对传热效果的影响
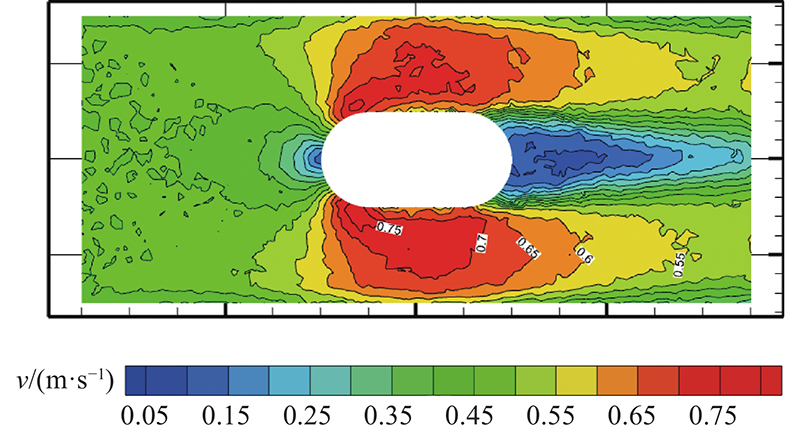
探究扰流元长宽比F对流道传热性能和压降损失的影响规律. 内置宽度d=13 mm的扰流元结构,对流道传热性能与压降损失进行仿真计算分析,长宽比分别取0.2、0.4、0.6、0.8、1.0、1.2、1.4、1.6、1.8、2.0. 扰流元长宽比与湍流强度、流道压降的变化关系如图8所示,其中∆p为流道压降. 可以看出,F-∆p曲线呈单调递增;F-Re曲线呈先增加,后降低的趋势. 当扰流元长宽比从0.2增至1.0时,由于扰流元长度增加,扰流元两侧较高流速区域的面积占比增加,Re递增,湍流强度增加,热边界层破坏,热阻降低,换热效果升高. 在F>1.0后,由于扰流元长度过大,两侧靠近扰流元中心偏后区域出现低速层,低流速区域的占比增加,造成Re降低,这些区域湍流强度降低,热边界层破坏较小,热阻较高,换热效果降低. 因此当F=1.0时,Re最高,湍流强度最强,换热效果最好. F=1.0时冷却介质的速度分布如图9所示. 受扰流元影响,流道当量直径变小,为了保证冷却介质流量进出相等,扰流元两侧流速增加.
图 8
图 8 扰流元的长宽比与湍流强度、流道压降的变化关系
Fig.8 Variation of aspect ratio of disturbance element to turbulence intensity, pressure drop of flow channel
图 9
图 9 当扰流元的长宽比为1时,冷却介质的速度分布云图
Fig.9 Cloud diagram of velocity distribution of cooling medium when aspect ratio of disturbance element is 1
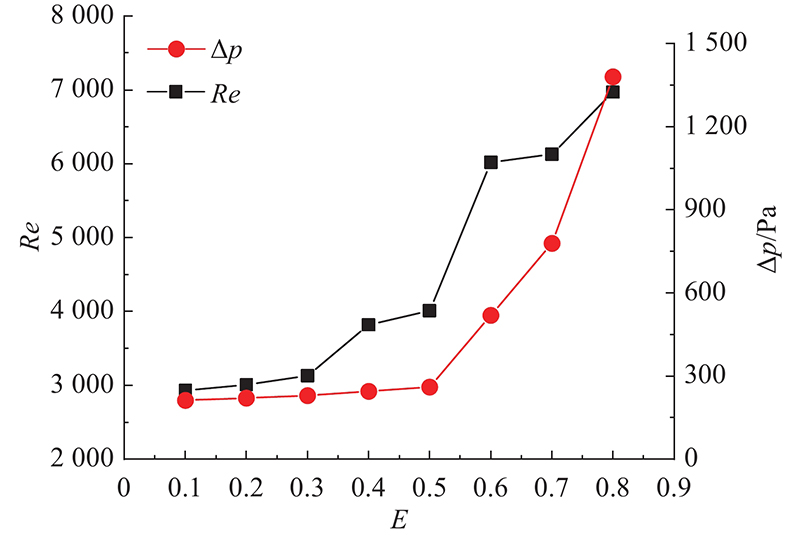
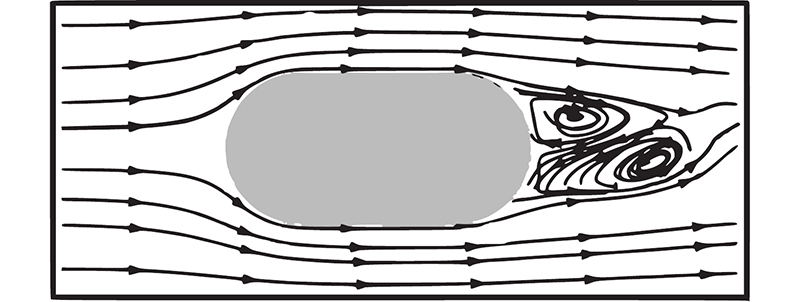
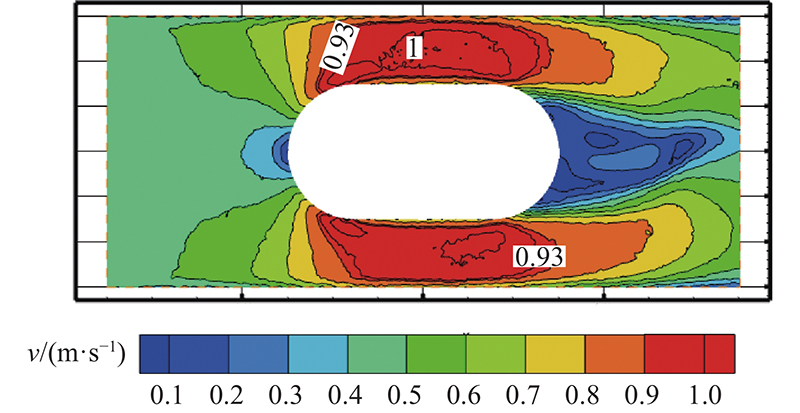
探究扰流元宽度d与流道宽度D的比E对流道传热性能和压降损失的影响规律,采用流道内布置l与d相等的扰流元结构进行仿真,分别取E=0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8. E与湍流强度、流道压降的变化关系如图10所示. 可以看出,E与流道压降和湍流强度成正比. 扰流元宽度增加,流道当量直径变小,迫使两侧冷却介质流速升高,Re增加,湍流强度加强,热边界层破坏,热阻降低,换热效果升高,当E=0.5时,Re=4 032,处于边界湍流状态. 如图11所示,当E>0.5时,扰流元后方出现大幅度的回流现象,造成流道压降呈指数上升,对此综合考虑,当取E=0.5时,效果最佳,速度分布云图如图12所示.
图 10
图 10 扰流元和流道的宽度比与湍流强度、流道压降的变化关系
Fig.10 Variation of width ratio of disturbance element and flow channel to turbulence intensity, pressure drop of flow channel
图 11
图 12
图 12 当扰流元和流道的宽度比为0.5时,冷却介质的速度分布云图
Fig.12 Cloud diagram of velocity distribution of cooling medium when width ratio of disturbance element and flow channel is 0.5
综上所述,扰流元长宽比对流道换热效果呈先上升后降低趋势,扰流元和流道的宽度比对流道换热效果呈递增趋势. 当E>0.5时,流道中会出现大幅度回流,造成流道压降剧增;当E=0.5、F=1.0时,流道综合效果最佳.
2.3. 布置参数对传热效果的影响
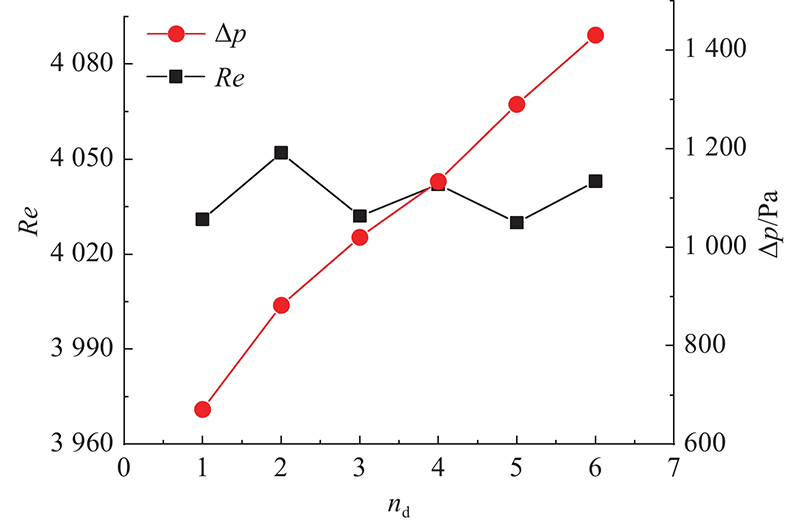
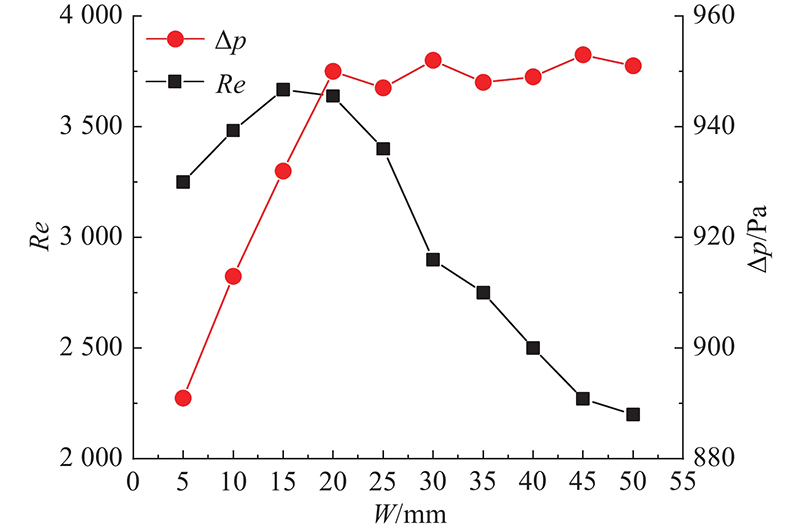
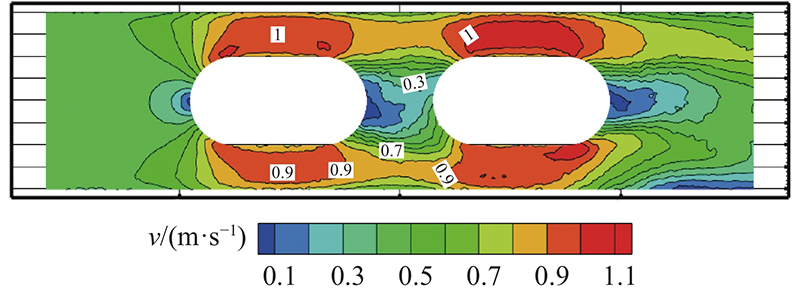
在保证低压损、低热阻的扰流元结构特征参数基础上,分析布置参数. 将流道原有长度90 mm增至400 mm,设置扰流元的数量nd=1~6、扰流元间隔W=15 mm,得出nd与湍流强度、流道压降变化关系如图13所示. 可以看出,Re-nd曲线的变化不大,∆p-nd曲线呈单调递增. 为了降低流道压降,扰流元数量越少越好,因此探究2个扰流元的间隔大小对湍流强度效果影响,在传热效果保证最优前提下,寻找最大间隔. 在流道中布置2个扰流元结构,将原有流道长度90 mm增至160 mm,分别取W=5、10、15、20、25、30、35、40、45、50 mm. 由图14可以看出,∆p-W曲线先递增,在W>20 mm时达到最大值,之后曲线逐渐趋近于平缓.Re-W曲线呈先上升,后降低趋势. 原因是当间隔较小时,2个扰流元间出现低速区域,导致Re较小,湍流强度降低,热边界层破坏较小,换热能力降低,随着间隔增加,低速区域减少,Re升高,湍流强度升高,换热能力增强,当W=15 mm时,Re最高,间隔超过15 mm,中间区域扰流效果降低,
图 13
图 13 扰流元数量与湍流强度、流道压降的变化关系
Fig.13 Variation of number of disturbance element to turbulence intensity, pressure drop of flow channel
图 14
图 14 扰流元间隔与湍流强度、流道压降的变化关系
Fig.14 Variation of interval of disturbance element to turbulence intensity, pressure drop of flow channel
图 15
图 15 当扰流元间隔为15 mm时,冷却介质的速度分布云图
Fig.15 Cloud diagram of velocity distribution of cooling medium when interval of disturbance element is 15 mm
综上所述,扰流元间隔对流道换热效果呈先上升后降低趋势,扰流元间隔为15 mm时,流道综合效果最佳.
3. 最优结构与实验验证
3.1. 最优结构
扰流元结构会使液冷板压降升高,保证冷却介质保持在湍流状态,结合液冷板尺寸,布置扰流元的位置如图16所示,在扰流元的结构中,l=20 mm、d=20 mm. 同原始液冷板仿真方法研究布置全特征扰流元结构液冷板的散热性能,优化后液冷板压降为764 Pa,散热云图如图17所示. 由图可见,热源的最高温度为24.4 ℃,最低温度为21.7 ℃,温差为3 ℃. 流道中的冷却介质处于湍流状态,热边界层被破坏,热阻降低,换热性能升高,温度均匀性变好,由式(8)得到温度均匀性系数Tc2=0.121,加入全特征扰流元结构后,液冷板的温度均匀性明显提高,从优化前的0.339降到优化后的0.121,优化幅度为180.16%,将提升电池包续航里程和减缓寿命衰减.
图 16
图 16 全特征扰流元结构的液冷板
Fig.16 Liquid-cooled plate of fully-featured disturbance element structure
图 17
图 17 优化后的液冷板散热云图
Fig.17 Heat dissipation cloud diagram of optimized liquid-cooled plate
3.2. 实验验证
为了验证仿真结果的准确性,搭建液冷板传热实验平台如图18所示. 平台由加热膜、液冷板、Neolab-L200冷却水循环冷凝器(温度量程为−5~100 ℃,精度为±0.5 ℃;速度量程为0~4.5 m/s,精度为±0.50 m/s)、Fluke TiX660热成像仪(量程为−40~1 200 ℃,精度为±1.5 ℃)、HY-P300压力测量仪(量程为0~5.0×104 Pa,精度为±2.0 Pa)、水管和电源等构成. 实验步骤如下: 1)将液冷板、冷却水循环冷凝器、压力测量仪依次连接成循环通路,并将加热膜紧贴液冷板表面. 2)设置冷却水循环冷凝器流速为0.25 m/s、初始温度为20 ℃,将加热膜与冷却水循环冷凝器打开. 3)待表面温度稳定后,用红外热成像仪进行测量,记录数据,压降数据由2个压力测量仪相减得出.
图 18
图 18 液冷板的传热实验平台
Fig.18 Heat transfer experiment platform of liquid-cooled plate
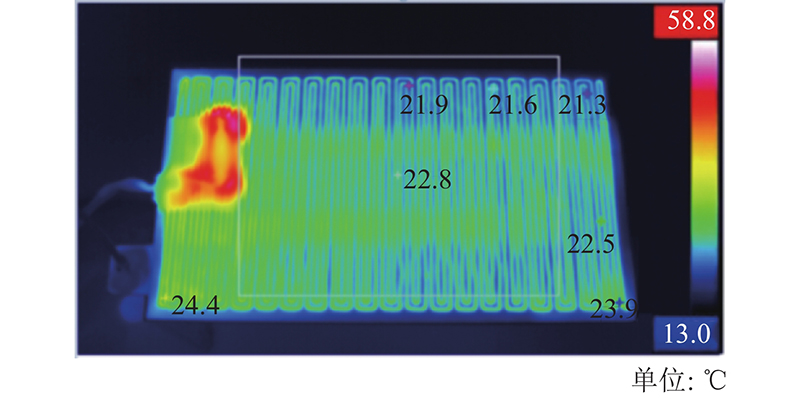
如图19所示为加热膜的热成像图. 图左侧高温区域为加热膜接线处,受线束影响,温度偏高. 排除此区域实验测得结果,加热膜最高温度为24.4 ℃,温差3.1 ℃,压降为813 Pa,与仿真结果的综合误差为3.79%.
图 19
图 19 热成像仪拍摄的加热膜散热云图
Fig.19 Heat dissipation cloud picture of heated film from thermal imager takes
4. 结 语
本研究以某款动力电池包液冷板为对象,构建温度均匀性系数,提出新型全特征扰流元模型,通过对扰流元特征参数和布置参数寻优,改善液冷板传热性能,提出温度均匀性系数来衡量液冷板均温性能,通过实验进行验证,得到如下结论:1)在液冷板流道内布置全特征扰流元结构可以打破热边界层,减小热阻影响,增强传热并提升均温性能. 2)扰流元长宽比与间隔参数对流道换热效果呈先上升后降低的趋势,扰流元和流道的宽度比对流道换热效果呈递增的趋势,当扰流元结构宽度与流道宽度之比小于0.5时,流道中会出现大幅度回流,造成流道压降剧增. 3)当全特征扰流元结构宽度与流道宽度之比为0.5、宽度与长度之比为1、扰流元间隔为15 mm时,液冷板综合效果最佳,可以有效将温度均匀性系数由 0.339降低到0.121,优化幅度为180.16%.本研究未考虑扰流元细微高度的变化对流场的影响.下一步计划针对电池发热的特性与扰流元强化传热规律,建立热场与布置扰流元后流场之间的联系,在液冷板流道中更加有指定性的布置扰流元结构,以实现使电池包温差更低,性能更佳.
参考文献
A critical review of thermal issues in lithium-ion batteries
[J].DOI:10.1149/1.3515880 [本文引用: 1]
Capacity loss induced by lithium deposition at graphite anode for LiFePO4/graphite cell cycling at different temperatures
[J].DOI:10.1016/j.electacta.2013.08.074 [本文引用: 1]
Power fade and capacity fade resulting from cycle-life testing of advanced technology development program lithium-ion batteries
[J].
A review on the key issues for lithium-ion battery management in electric vehicles
[J].DOI:10.1016/j.jpowsour.2012.10.060 [本文引用: 1]
Temperature response of a high power lithium-ion battery subjected to high current discharge
[J].
Abuse behavior of high-power, lithium-ion cells
[J].DOI:10.1016/S0378-7753(02)00488-3 [本文引用: 1]
Nonuniform temperature distribution in Li-ion batteries during discharge: a combined thermal imaging, X-ray micro-tomography and electrochemical impedance approach
[J].DOI:10.1016/j.jpowsour.2013.11.059 [本文引用: 1]
新型动力电池热管理系统设计及性能研究
[J].
Design and performance study of a new type of thermal management system for traction battery
[J].
Multi-objective design optimization of battery thermal management system for electric vehicles
[J].DOI:10.1016/j.applthermaleng.2021.117235 [本文引用: 2]
锂电池并行流道液冷板结构设计和散热性能分析
[J].
Structure design and thermal dissipation performance analysis of liquid cooling plates with parallel flow channels for lithium batteries
[J].
Multi-objective optimization design of thermal management system for lithium-ion battery pack based on non-dominated sorting genetic algorithm II
[J].DOI:10.1016/j.applthermaleng.2019.114394 [本文引用: 1]
Multi-objective optimization design of lithium-ion battery liquid cooling plate with double-layered dendritic channels
[J].DOI:10.1016/j.applthermaleng.2021.117541 [本文引用: 1]
Numerical optimization of the cooling effect of the bionic spider-web channel cold plate on a pouch lithium-ion battery
[J].DOI:10.1016/j.csite.2021.101124 [本文引用: 1]
Flow and heat transfer characteristics and optimization study on the water-cooled microchannel heat sinks with dimple and pin-fin
[J].DOI:10.1016/j.ijheatmasstransfer.2017.11.112 [本文引用: 2]
Forced convection enhancement in channels with transversal ribs and nanofluids
[J].DOI:10.1016/j.applthermaleng.2015.12.140 [本文引用: 1]
Performance analysis of a microchannel heat sink with various rib configurations
[J].
Turbulent flow and heat transfer enhancement in rectangular channels with novel cylindrical grooves
[J].DOI:10.1016/j.ijheatmasstransfer.2014.10.021 [本文引用: 3]
Review on the heat dissiPation performance of battery pack with different structures and operation conditions
[J].DOI:10.1016/j.rser.2013.08.057 [本文引用: 1]
Optimization of catalytic converter gas flow distribution by CFD prediction
[J].