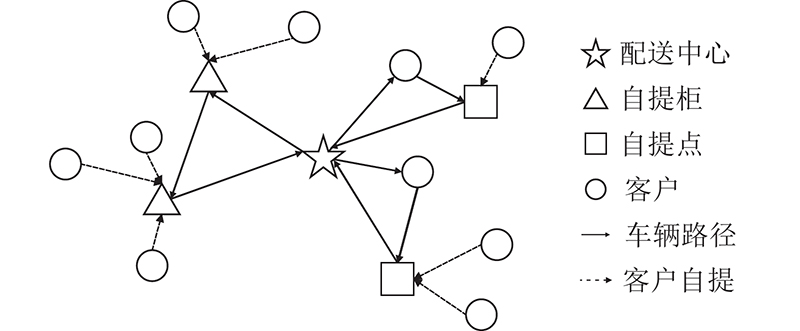
目前常见的末端配送服务模式包括送货上门、自提柜和自提点3种模式[5]. 送货上门是物流企业将货物送达客户指定地点的服务模式;自提柜是设置在公共区域的自助取货柜,存放的货物数量及种类有一定限制,客户可在任意时间取件,但是初始投资成本较高[4];自提点是与物流企业合作的超市、店铺等,投资成本低,客户只能在自提点开放时间段取货[6]. 末端配送服务模式与路径规划的协同优化问题是在考虑多种末端配送服务模式的情况下,以总成本最小化[7]或总运输距离最小化[8-9]等作为优化目标,对客户的末端配送服务模式和配送路线进行综合决策. Du等[10-11]研究末端配送服务模式与同时取送货型路径规划的联合优化问题. Enthoven等[12-13]研究送货上门和自提柜模式下的两阶段车辆路径规划问题. Zhou等[14]进一步研究多个配送中心下的两阶段车辆路径规划问题.周翔等[15-16]考虑自提柜位置对配送路径的影响,研究多种末端配送服务模式共存情景下的自提柜选址和配送路径联合优化问题.常见的末端配送服务模式与路径联合优化问题求解算法有模拟退火算法[11]、大邻域搜索算法[12]、遗传算法[17]和分支定界算法[18].在进行配送路径规划时,鲜有研究同时考虑到送货上门、自提柜和自提点3种末端配送服务模式,从而无法充分发挥配送系统的最大效能. Suwatcharachaitiwong等[19]虽然考虑到3种末端配送服务模式,但是只从物流服务商角度对末端配送服务模式进行选择,忽略客户对于不同模式的偏好,难以高质量提供配送服务.
为了弥补现有研究的不足,本研究同时考虑送货上门、自提柜和自提点3种末端配送服务模式,从平衡物流企业成本与服务质量的新角度出发,研究末端配送服务模式与路径联合优化问题. 以配送成本和客户满意度为双目标,考虑到车辆容量限制、客户收货模式以及收货时间窗等约束建立模型,改进NSGA-Ⅱ算法求解模型实现客户配送模式与配送路径的联合优化,为建立高效、高服务质量的末端配送系统提供决策依据与方法.
1. 问题描述
图 1
图 1 末端配送服务模式与路径联合优化问题示意图
Fig.1 Joint optimization diagram of terminal distribution service mode and routing
表 1 不同末端配送服务模式对比
Tab.1
| 末端配送服务模式 | 送货上门 | 自提柜 | 自提点 |
| 服务形式 | 车辆配送 | 客户自取 | 客户自取 |
| 收货地点 | 客户所在地 | 自提货柜 | 超市、商铺等 |
| 服务成本 | 高 | 中 | 低 |
| 货物类型限制 | 无 | 有 | 无 |
| 取货时间限制 | 客户时间窗 | 无 | 营业时间 |
| 客户满意度 | 高 | 较高 | 低 |
2. 末端配送服务模式与路径联合优化模型构建
2.1. 模型假设
1)各个客户点的位置、需求量、服务时间窗和可接受的末端配送服务模式已知;2)各个自提柜或自提点的位置和所能服务的客户已知,并且容量是能够满足配送需求;3)考虑到3种末端配送服务模式,分别为送货上门、自提柜和自提点;4)单配送中心,车辆只提供配送服务,不提供收揽服务;5)每个客户点仅被服务1次,不存在二次配送的情况;6)配送车辆为同类型车,客户点需求量不可拆分.
2.2. 符号定义
构建末端配送服务模式与路径联合优化模型所用符号如表2所示.
表 2 所提模型定义的符号及含义
Tab.2
| 集合 | 含义 |
| | 配送中心集合, |
| | 客户点集合, |
| | 节点集合, |
| | 末端配送服务模式集合, |
| | 配送车辆集合, |
| 参数 | 含义 |
| | 当客户 |
| | 车辆行驶速度 |
| | 客户 |
| | 客户 |
| | 如果客户 |
| | 时间窗早到惩罚成本 |
| | 时间窗晚到惩罚成本 |
| | 车辆的额定载重量 |
| | 客户点 |
| | 单位里程的车辆行驶成本 |
| | 车辆的固定使用成本,包括折旧和驾驶员工资 |
| | |
| | |
| | 无穷大的数 |
| 决策变量 | 含义 |
| | 当客户 |
| | 当客户 |
| | 车辆到达节点 |
| | 车辆离开节点 |
2.3. 模型构建
建立的末端配送服务模式与路径联合优化模型为
式中:
式中:
式(4)为每位客户有且仅有一辆车采用一种配送模式为其提供服务.
式(5)为末端配送服务模式选择约束.
式(6)为限制每位客户选择的模式,和配送路径决策出的模式为同种模式.
式(7~9)为路径约束.
式(10)限制一条路径由同一辆车行驶.
式(11)为车辆到达客户点的时间约束.
式(12)为车辆到达客户点的配送量约束.
式(13)为车辆的最大载重量约束.
式(14~15)为决策变量的取值约束.
3. 末端配送服务模式与路径联合优化模型求解
图 2
3.1. 编码
末端配送服务模式与路径联合优化问题,需要将客户服务模式、配送车辆指派及配送路径等决策目标融入编码过程,将问题的实际方案表达为染色体基因.本研究采用实数编码,设定每条染色体长度为2×A+B+1(A、B分别为客户点和配送车辆数量),前A位为末端配送服务模式,后续基因为车辆配送路径. 以5个客户点生成的染色体为例(如图3所示),客户1、3采用上门服务,客户2、5采用自提柜服务,客户4采用自提点服务,2辆车的配送路径由0划分.
图 3
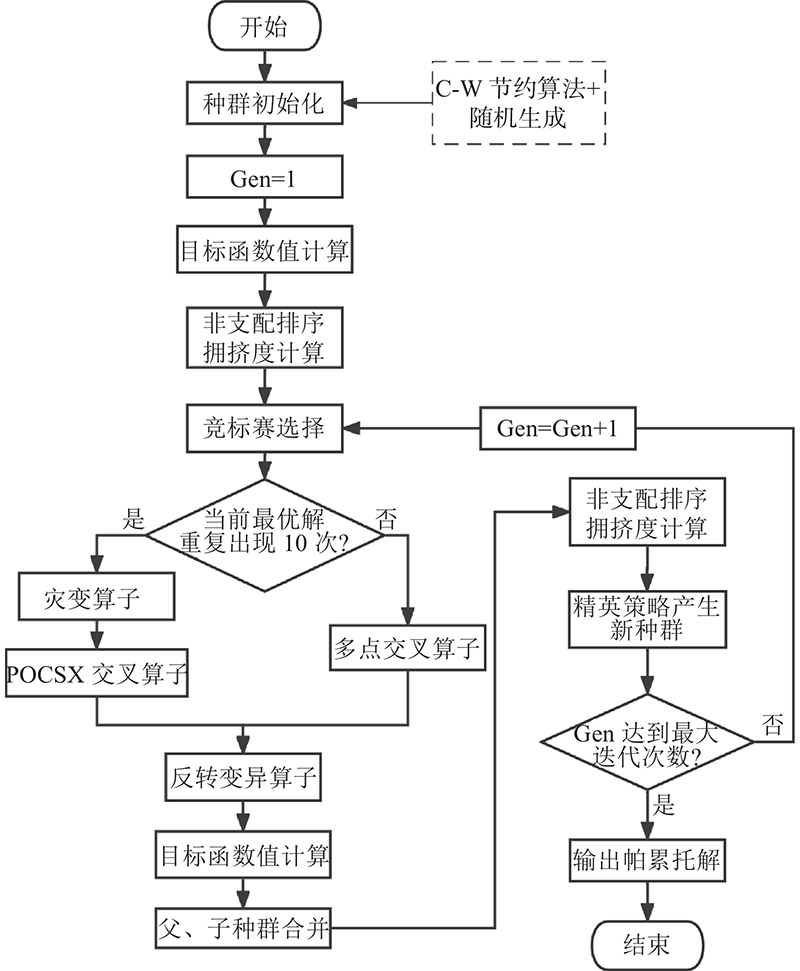
3.2. 初始种群
为了提高初始解的质量,采用节约里程法(clarke-wright,CW)和随机生成相结合的策略生成初始种群. CW算法的原理是在满足车辆容量限制的条件下,尽可能多地将2个配送回路合并,以此减小运输距离. 利用CW算法生成初始解质量较高但易造成种群单一化,因此30%的初始解由CW算法生成,其余70%初始解随机生成. 此方法既加快了收敛,又保证了种群的多样性.
3.3. 快速非支配排序
设共有
图 4
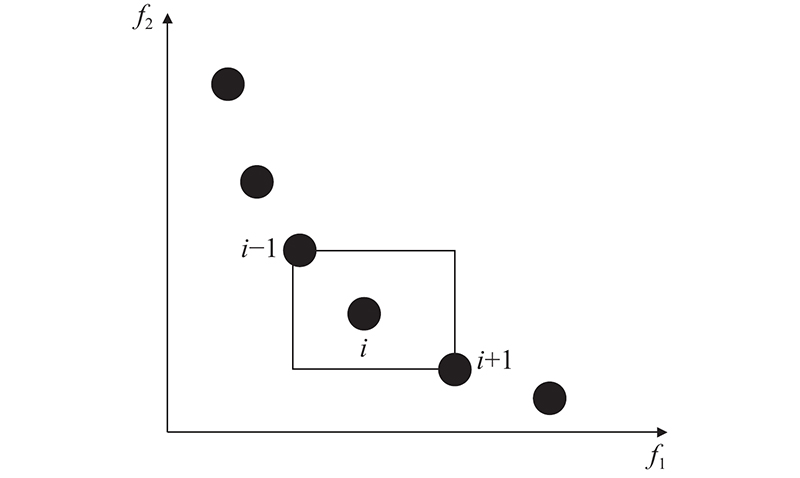
3.4. 拥挤度计算
NSGA-Ⅱ用拥挤度表示种群染色体的空间密度,染色体的拥挤度越大代表种群多样性越好. 以图5所示染色体分布为例,两端的染色体拥挤度设为
图 5
式中:
3.5. 遗传算子
3.5.1. 选择算子
在进行非支配排序和拥挤度计算后,运用竞标赛机制选择父代染色体.随机选出2条不同的染色体,将排序等级较高的作为父代染色体,如果选出的2条染色体排序等级相同,则选择拥挤度较大的成为父代染色体.
3.5.2. 交叉算子
图 6
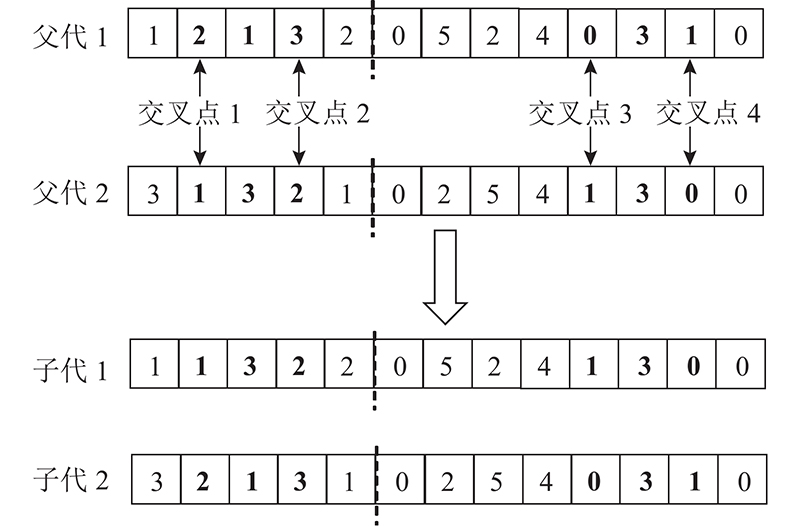
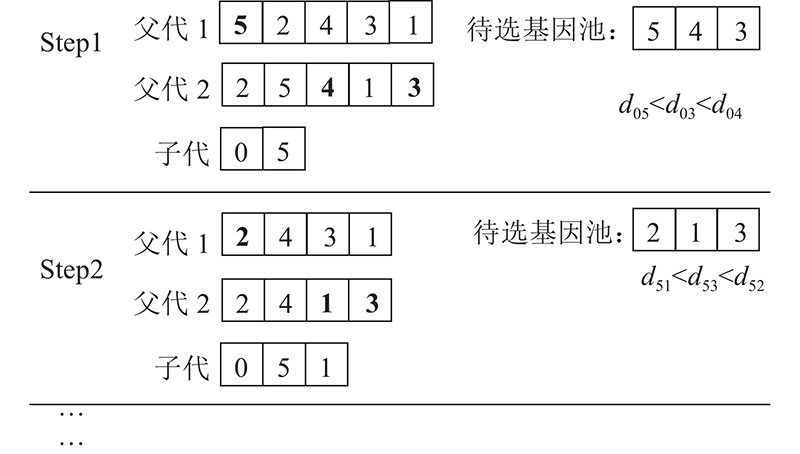
当最优解重复出现10次,表明算法陷入局部最优.为了提高种群进化效率,染色体配送路径段采取POCSX交叉. POCSX交叉是以子代上一个添加的节点和待选基因池中节点的代价(一般以节点间距离表示)确定子代的下一个节点. 待选基因池的生成规则为待选基因池的第1位基因取父代1的第1个基因,剩余基因在父代2中随机选取. 如图7所示,若设待选基因池大小为3,则需从父代选择3个基因节点构成待选基因池[5,4,3]. 在子代首位添加0表示车辆配送的开始,并将待选基因池中距离节点0最小的节点5添进子代,同时将父代中的节点5删除;按照待选基因池生成规则生成新的待选基因池 [2,1,3],并将待选基因池中与节点5距离最短的节点1添加到子代,同时父代删除节点1,重复此过程直至删除父代染色体全部节点生成子代.
图 7
3.5.3. 变异算子
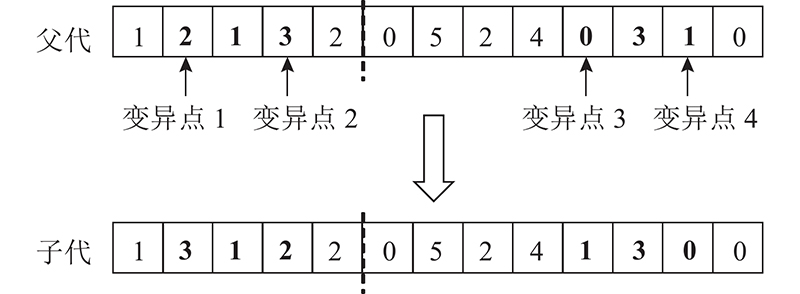
变异是对生物遗传过程中染色体基因突变的模仿. 本研究采取反转突变策略,即在一条染色体的配送服务模式段和配送路径段分别随机选择一对变异点,将变异点间的基因序列颠倒. 如图8所示,将父代变异点1和2之间的染色片段、变异点3和4之间的染色片段都反转得到子代.
图 8
3.5.4. 灾变算子
灾变模仿了自然进化中的重大灾害,是帮助算法跳出局部最优的一种手段. 当最优解连续重复出现10次时,算法进行灾变操作,即只保留当前种群中质量最好的前30%的染色体,其余70%的染色体重新生成.
4. 算例分析
基于Solomon RC102算例,对模型和算法进行验证. 为了使案例符合研究问题,根据自提柜和自提点数量与人口密度显著正相关的特点[24],增加自提柜和自提点位置;按照客户对送货上门、自提柜、自提点的满意度高低[3,25]为客户设置可选末端配送服务模式. 例如,客户对送货上门模式的满意度最高,则将送货上门作为可选模式的客户数量设置成最多. 其余案例参数参照文献[26-27]设置,具体如表3所示. 改进NSGA-Ⅱ利用Matlab编译,在配置为Intel(R)Core(TM)i5-5200U、2.20 GHz、4 GB RAM,Windows10(64位)的电l脑上运行.算法参数如下:种群规模为100,交叉概率为0.75,变异概率为0.10,Pareto解集数量为150.
表 3 算例参数及取值
Tab.3
| 参数 | 取值 | 参数 | 取值 | |
| | 60 | | 1.00 | |
| | 200 | | 3.00 | |
| | 1 | | 2.18 | |
| | 100 | | 1.71 | |
| | 0.7 | | 1.38 |
4.1. 模型验证
为了验证末端配送模式与路径联合优化模型的正确性,调用求解器GUROBI对5个客户点的小规模算例进行求解. 在调用求解器GUROBI对模型进行求解时,采用将配送总成本
表 4 GUROBI对小规模算例的求解结果
Tab.4
| 配送路径 | 约束检验 | ||||||||
| 末端配送服务模式 | 车辆载重 | 时间窗 | |||||||
| 选择模式 | 是否为接受模式 | 累计载重 | 是否超载 | 到达时间/min | 客户收货时间窗 | ||||
| 1 | 1 | 是 | 0 | 否 | 0 | [0,1 236] | |||
| ↓ | |||||||||
| 6 | 2 | 是 | 2 | 否 | 38.42 | [15,67] | |||
| ↓ | |||||||||
| 3 | 2 | 是 | 22 | 否 | 48.42 | [825,870] | |||
| ↓ | |||||||||
| 4 | 3 | 是 | 30 | 否 | 77.39 | [65,146] | |||
| ↓ | |||||||||
| 5 | 3 | 是 | 49 | 否 | 87.39 | [727,782] | |||
| ↓ | |||||||||
| 2 | 1 | 是 | 72 | 否 | 105.88 | [912,967] | |||
| ↓ | |||||||||
| 1 | 1 | 是 | 72 | 否 | 119.30 | [0,1 236] | |||
4.2. 算法性能分析
4.2.1. 算法稳定性
表 5 改进NSGA-Ⅱ算法稳定性分析
Tab.5
| 算例规模 | | | |
| 5 | 328.14 | 331.32 | 0.97 |
| 10 | 427.52 | 433.09 | 1.30 |
| 15 | 691.35 | 702.68 | 1.64 |
| 20 | 864.72 | 875.12 | 1.20 |
| 25 | 1 139.30 | 1 157.45 | 1.59 |
| 30 | 1 401.65 | 1 423.59 | 1.57 |
| 35 | 1 549.90 | 1 566.23 | 1.05 |
| 40 | 1 908.04 | 1 924.35 | 0.85 |
| 60 | 2 768.94 | 2 797.44 | 1.03 |
| 80 | 3 605.01 | 3 652.57 | 1.32 |
| 100 | 4 712.09 | 4 759.59 | 1.01 |
4.2.2. 算法性能优越性
为了验证改进NSGA-Ⅱ的性能,本节将改进NSGA-Ⅱ与GUROBI和传统NSGA-II算法的求解结果进行对比,17个中小案例的求解结果如表6所示. 其中,GUROBI列展示的结果为2 000 s求解时间限制下的结果,“−”表明在限制时间内没有发现可行解.
表 6 三种算法求解末端配送服务模式与路径联合优化模型的性能
Tab.6
| 客户规模 | GUROBI | 传统NSGA-Ⅱ | 改进NSGA-Ⅱ | |||||||
| | | | | | | | | |||
| 注:表中加粗数据为最优配送总成本. | ||||||||||
| 5 | 328.14 | 0.62 | 328.14 | 7.84 | 0.00 | 328.14 | 7.95 | 0.00 | ||
| 8 | 379.81 | 13.61 | 379.81 | 8.24 | 0.00 | 379.81 | 8.10 | 0.00 | ||
| 10 | 427.52 | 1 907 | 427.52 | 7.04 | 0.00 | 427.52 | 11.17 | 0.00 | ||
| 12 | 485.95 | 2 000 | 486.84 | 19.25 | 0.18 | 486.45 | 13.84 | 0.10 | ||
| 15 | 691.84 | 2 000 | 693.03 | 11.78 | 0.17 | 691.35 | 15.45 | −0.07 | ||
| 18 | 778.49 | 2 000 | 853.26 | 23.61 | 9.60 | 777.19 | 17.21 | −0.17 | ||
| 20 | 862.31 | 2 000 | 867.34 | 21.92 | 0.58 | 864.72 | 32.60 | 0.28 | ||
| 22 | 1 041.16 | 2 000 | 1 098.32 | 25.14 | 5.49 | 1 041.16 | 32.00 | 0.00 | ||
| 25 | 1 141.36 | 2 000 | 1 192.04 | 64.77 | 4.44 | 1 139.30 | 75.75 | −0.18 | ||
| 28 | 1 374.71 | 2 000 | 1 398.04 | 31.52 | 1.70 | 1 378.31 | 47.96 | 0.26 | ||
| 30 | 1 400.46 | 2 000 | 1 424.48 | 47.63 | 1.72 | 1 401.65 | 91.76 | 0.09 | ||
| 32 | 1 438.93 | 2 000 | 1 481.33 | 72.40 | 2.95 | 1 432.38 | 97.74 | −0.46 | ||
| 35 | 1 568.04 | 2 000 | 1 658.35 | 81.48 | 5.76 | 1 549.90 | 91.25 | −1.16 | ||
| 40 | − | − | 1 933.94 | 103.15 | − | 1 908.04 | 144.67 | − | ||
| 60 | − | − | 2 857.98 | 114.22 | − | 2 768.94 | 198.44 | − | ||
| 80 | − | − | 3 812.10 | 171.75 | − | 3 605.01 | 252.70 | − | ||
| 100 | − | − | 4 922.93 | 230.35 | − | 4 712.09 | 292.69 | − | ||
通过对比求解器GUROBI和改进NSGA-Ⅱ对相同案例的求解结果可知,当客户规模小于15时,GUROBI和改进NSGA-Ⅱ的求解质量基本相同,平均差异小于0.1%.当客户规模大于15时,75%的案例,改进NSGA-Ⅱ得到的解比GUROBI优. GUROBI的求解时间会随着客户规模的增大急剧增加.当客户规模为10时,GUROBI就需要1 907 s的求解时间. 而改进NSGA-Ⅱ的求解时间增加并不明显,最大求解时间也不超过240 s,只是GUROBI所用求解时间的1/10. 除此之外,改进NSGA-Ⅱ可以一次性求解出Pareto前沿,而GUROBI只能求解出一个解. 对比传统NSGA-Ⅱ和改进NSGA-Ⅱ的结果可知,求解时间平均仅增加23 s,求解质量平均提升了3.37%. 综上可知,所设计的改进NSGA-Ⅱ求解效果优于GUROBI和传统NSGA-Ⅱ.
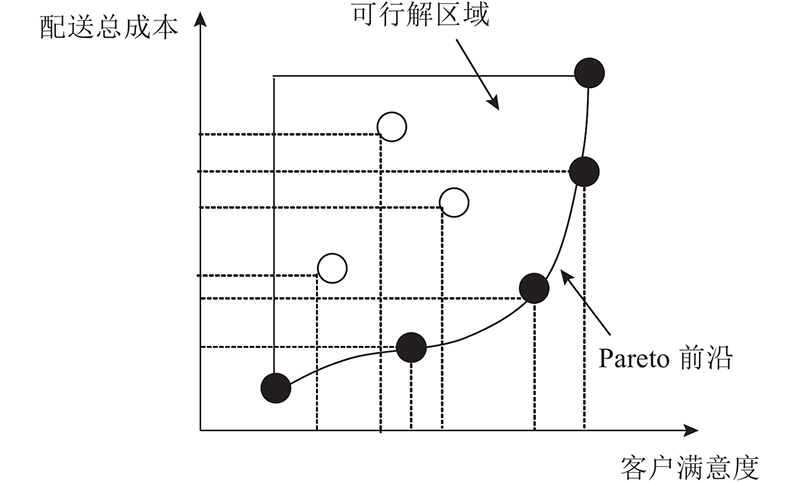
4.2.3. Pareto解集
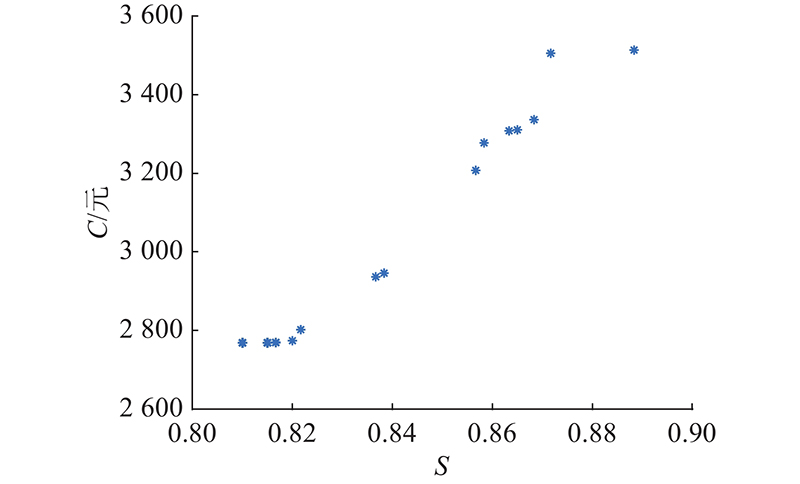
图9展示60个客户算例求解的Pareto前沿,可以看出客户满意度
图 9
4.3. 敏感度分析
4.3.1. 末端配送服务模式分析
为了体现末端配送服务模式与路径联合决策模型的优势,将采用送货上门、自提柜和自提点的单一末端配送服务模式与三种配送模式混合使用下的配送总成本与客户满意度进行对比分析. 客户的可选末端配送服务模式限定为单一模式,即成为相应模式下的只考虑配送成本的路径决策问题. 客户不可接受末端配送服务模式的满意度变为相应末端配送服务模式的0.5倍,5个算例求解20次所得配送成本最低的解如表7所示.
表 7 不同末端配送服务模式的配送总成本与客户满意度
Tab.7
| 算例规模 | 模式 | 目标 | |
| C/元 | S | ||
| 30 | 送货上门 | 1 768.64 | 0.87 |
| 自提柜 | 1 398.08 | 0.65 | |
| 自提点 | 1 205.29 | 0.54 | |
| 混合模式 | 1 401.65 | 0.79 | |
| 40 | 送货上门 | 2 386.60 | 0.90 |
| 自提柜 | 1 890.74 | 0.66 | |
| 自提点 | 1 616.21 | 0.54 | |
| 混合模式 | 1 908.04 | 0.81 | |
| 60 | 送货上门 | 3 570.58 | 0.88 |
| 自提柜 | 2 720.96 | 0.65 | |
| 自提点 | 2 297.28 | 0.54 | |
| 混合模式 | 2 768.94 | 0.80 | |
| 80 | 送货上门 | 4 581.11 | 0.87 |
| 自提柜 | 3 454.38 | 0.65 | |
| 自提点 | 3 004.65 | 0.55 | |
| 混合模式 | 3 605.01 | 0.80 | |
| 100 | 送货上门 | 5 767.31 | 0.86 |
| 自提柜 | 4 352.84 | 0.65 | |
| 自提点 | 3 969.52 | 0.55 | |
| 混合模式 | 4 712.09 | 0.81 | |
从表7可以看出,送货上门服务模式能够得到最高的客户满意度,但其配送成本也最高;自提点服务模式的配送成本最低,客户满意度也最低;自提柜模式的成本和客户满意度均介于送货上门和自提点模式之间. 混合模式与自提柜和自提点模式相比,成本分别增加了3.11%和18.71%,但客户满意度分别提高了22.48%和47.78%,整体提升了19.37%和29.07%;与送货上门相比,客户满意度降低了8.56%,同时配送成本降低了20.57%,整体提升了12.01%. 综合来看,混合利用多种末端配送服务模式能够发挥各模式的优势,达到既控制配送成本又能提升客户满意度的目标.
4.3.2. 自提柜和自提点数量分析
将100个客户算例中的自提柜和自提点数量均增加3个,相同客户满意度下成本最低的配送方案如表8所示. 表中Ct、Cf、Cs和Cw分别为运输成本、车辆固定成本、服务成本、时间窗成本. 增加自提柜和自提点数量后配送总成本降低了115.94元,其中运输成本降低了11.88%. 这说明管理者在投资建设成本允许的情况下,可以通过适当增加自提点和自提柜数量降低配送总成本.
表 8 不同自提柜和自提点数量下成本最低的配送方案
Tab.8
| 配送方案 | 对比值 | ||||
| C/元 | Ct/元 | Cf/元 | Cs/元 | Cw/元 | |
| 7个自提柜+5个自提点 | 4 712.09 | 927.08 | 800.00 | 2 462.59 | 522.42 |
| 10个自提柜+8个自提点 | 4 596.15 | 816.94 | 800.00 | 2 450.18 | 529.03 |
4.3.3. 时间窗宽度分析
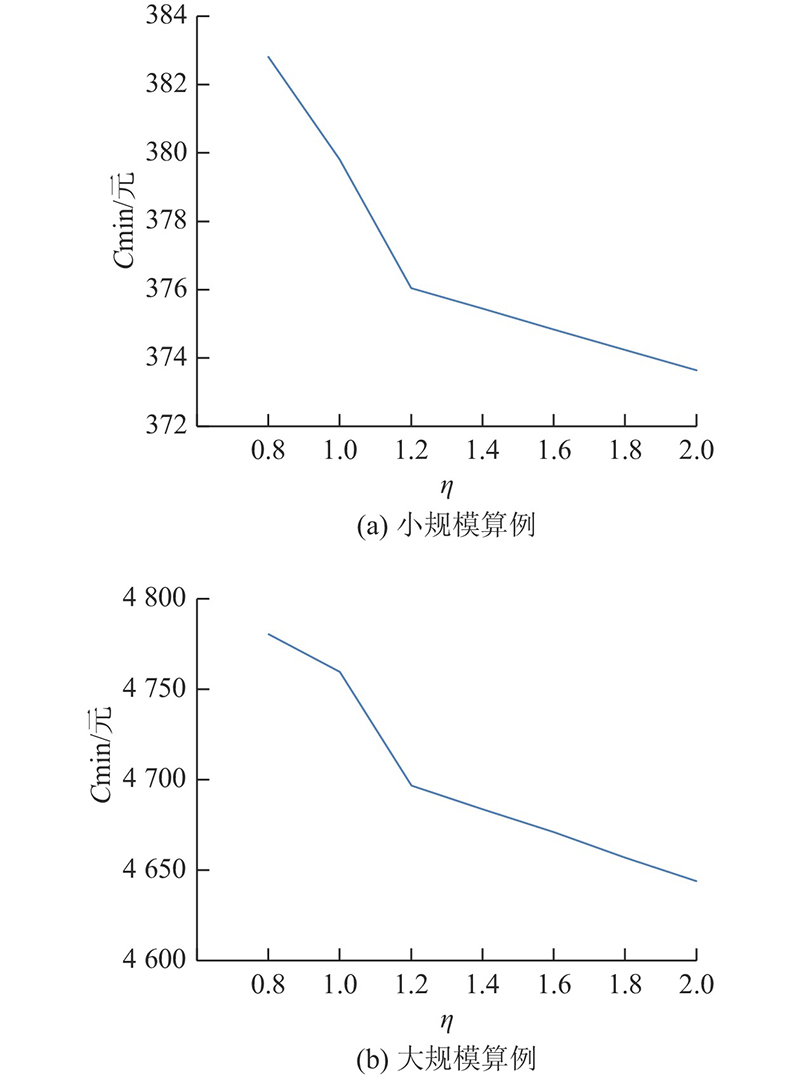
在分析时间窗宽度影响时,保持其它参数不变. 在不同时间窗宽度下,利用求解器GUROBI求解8个客户的小规模算例,利用改进NSGA-Ⅱ求解100个客户的大规模算例,结果如图10所示. 图中
图 10
图 10 不同时间窗宽度倍数下的最低配送成本
Fig.10 Minimum distribution cost with different time window width multiples
表 9 不同时间窗宽度倍数下的配送方案
Tab.9
| 原时间窗宽度 | 对比值 | ||||
| C/元 | Ct/元 | Cf/元 | Cs/元 | Cw/元 | |
| 0.8倍原时间窗宽度 | 4 725.60 | 943.43 | 800.00 | 2 424.22 | 557.95 |
| 2.0倍原时间窗宽度 | 4 592.54 | 945.67 | 800.00 | 2 414.25 | 432.62 |
5. 结 语
本研究提供了末端配送服务模式与路径联合优化方法. 考虑到车辆容量限制、客户对不同配送服务模式的接受度、收货时间窗等约束,以配送成本和客户满意度为目标,建立了一个混合整数规划模型,改进NSGA-Ⅱ算法对模型进行求解. 算例分析证实了模型的准确性以及所设计算法的优越性能.算例参数敏感度分析发现:
1)相较于单一末端配送服务模式,末端配送服务模式与路径联合优化能够同时对配送成本和客户满意度进行改善.
2)管理者可以通过适当增加自提点和自提柜数量,争取与客户达成更宽松的收货时间窗的途径,实现降低配送成本的目标.
参考文献
基于客户点行政地址的自提点选址—路径优化
[J].DOI:10.13196/j.cims.2019.08.021 [本文引用: 1]
Location-routing problem of pickup point based on administrative address of customer points
[J].DOI:10.13196/j.cims.2019.08.021 [本文引用: 1]
需求依赖末端交付与时间窗的城市配送自提柜选址—路径问题
[J].
Reception box locating-vehicle routing problems in urban distribution considering demand depending on last-mile delivery and time slots
[J].
The last-mile vehicle routing problem with delivery options
[J].DOI:10.1007/s00291-021-00633-0 [本文引用: 1]
On the medication distribution system for home health care through convenience stores, lockers, and home delivery
[J].DOI:10.1177/1460458220936395 [本文引用: 1]
基于众包模式的两级开闭混合车辆路径优化
[J].
Vehicle routing optimization of two echelon opening and closing hybrid based on crowdsourcing mode
[J].
NSGA-II algorithm for multi-objective generation expansion planning problem
[J].DOI:10.1016/j.jpgr.2008.09.011 [本文引用: 1]
A stochastic multi-period industrial hazardous waste location-routing problem: integrating NSGA-II and Monte Carlo simulation
[J].DOI:10.1016/j.ejor.2018.07.024 [本文引用: 1]
Integrating first-mile pickup and last-mile delivery on shared vehicle routes for efficient urban e-commerce distribution
[J].DOI:10.1016/j.trb.2019.09.013 [本文引用: 1]
A review of last mile logistics innovations in an externalities cost reduction vision
[J].
Choice of prevailing delivery methods in e-grocery: a stated preference ranking experiment
[J].DOI:10.1108/IJRDM-08-2019-0260 [本文引用: 3]
Analysis of parcel lockers’ efficiency as the last mile delivery solution the results of the research in Poland
[J].DOI:10.1016/j.trpro.2016.02.018 [本文引用: 3]
Acceptability of collection and delivery points from consumers’ perspective: a qualitative case study of Christchurch city
[J].DOI:10.1016/j.cstp.2017.10.009 [本文引用: 1]
Addressing the last mile problem: transport impacts of collection and delivery points
[J].
Flexible parcel delivery to automated parcel lockers: models, solution methods and analysis
[J].DOI:10.1007/s13676-019-00144-7 [本文引用: 1]
The vehicle routing problem with heterogeneous locker boxes
[J].
Capacitated vehicle routing problem with pick-up and alternative delivery (CVRPPAD): model and implementation using hybrid approach
[J].
Simultaneous pickup and delivery traveling salesman problem considering the express lockers using attention route planning network
[J].
The vehicle routing problem with simultaneous pickup and delivery and parcel lockers
[J].DOI:10.3390/math10060920 [本文引用: 2]
The two-echelon vehicle routing problem with covering options: city logistics with cargo bikes and parcel lockers
[J].
A simulated annealing algorithm for solving two-echelon vehicle routing problem with locker facilities
[J].DOI:10.3390/a13090218 [本文引用: 1]
A multi-depot two echelon vehicle routing problem with delivery options arising in the last mile distribution
[J].DOI:10.1016/j.ejor.2017.08.011 [本文引用: 1]
Stochastic partially optimized cyclic shift crossover for multi-objective genetic algorithms for the vehicle routing problem with time-windows
[J].
Final deliveries for online shopping: the deployment of pickup point networks in urban and suburban areas
[J].DOI:10.1016/j.rtbm.2014.03.002 [本文引用: 1]
An investigation of customers’ intention to use self-collection services for last-mile delivery
[J].DOI:10.1016/j.tranpol.2018.03.001 [本文引用: 1]