[1]
VAUGHAN T, HEETDERKS W, TREJO L, et al Brain-computer interface technology: a review of the second international meeting
[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering , 2003 , 11 (2 ): 94 - 109
DOI:10.1109/TNSRE.2003.814799
[本文引用: 1]
[2]
PUTZE F, SCHULTZ T Adaptive cognitive technical systems
[J]. Journal of Neuroscience Methods , 2014 , (234 ): 108 - 115
[本文引用: 1]
[3]
LEE S H, LEE M, LEE S W. EEG representations of spatial and temporal features in imagined speech and overt speech [C]// Asian Conference on Pattern Recognition. Cham: Springer, 2019: 387-400.
[本文引用: 1]
[4]
PIOTR W, DARIUSZ Z, GRZEGORZ M, et al Most popular signal processing methods in motor-imagery BCI: a review and meta-analysis
[J]. Frontiers in Neuroinformatics , 2018 , (12 ): 78
[本文引用: 1]
[5]
AMIRI S, RABBI A, AZINFAR L, et al. A review of P300, SSVEP, and hybrid P300/SSVEP brain-computer interface systems [M]// Brain-computer interface systems: recent progress and future prospects. Fargo: Intech, 2013.
[本文引用: 1]
[6]
ROSENFELD J, HU X, LABKOVSKY E, et al Review of recent studies and issues regarding the P300-based complex trial protocol for detection of concealed information
[J]. International Journal of Psychophysiology , 2013 , 90 (2 ): 118 - 134
DOI:10.1016/j.ijpsycho.2013.08.012
[本文引用: 1]
[7]
于淑月, 李想, 于功敬, 等 脑机接口技术的发展与展望
[J]. 计算机测量与控制 , 2019 , (10 ): 5 - 12
[本文引用: 1]
YU Shu-yue, LI Xiang, YU Gong-jing, et al Development and prospect of brain-computer interface technology
[J]. Computer Measurement and Control , 2019 , (10 ): 5 - 12
[本文引用: 1]
[8]
WESTER M. Unspoken speech-speech recognition based on electroencephalography [D]. Karlsruher: University of Karlsruhe, 2006.
[本文引用: 1]
[9]
TORRES A, REYES A, VILLASENOR L, et al Implementing a fuzzy inference system in a multi-objective EEG channel selection model for imagined speech classification
[J]. Expert Systems with Applications , 2016 , (59 ): 1 - 12
[本文引用: 1]
[10]
QURESHI I, MIN B, PARK H, et al Multiclass classification of word imagination speech with hybrid connectivity features
[J]. IEEE Transactions on Biomedical Engineering , 2017 , 65 (10 ): 2168 - 2177
[本文引用: 1]
[11]
HASHIM N, ALI A, MOHD N. Word-based classification of imagined speech using EEG [C]// International Conference on Computational Science and Technology . Singapore: Springer, 2017: 195-204.
[本文引用: 1]
[12]
LEE S, LEE M, JEONG H, et al. Towards an EEG-based intuitive BCI communication system using imagined speech and visual imagery [C]// 2019 IEEE International Conference on Systems, Man and Cybernetics . Bari: IEEE, 2019.
[本文引用: 1]
[13]
SRIRAAM N, RAGHU S Classification of focal and non focal epileptic seizures using multi-features and SVM classifier
[J]. Journal of Medical Systems , 2017 , 41 (10 ): 160
DOI:10.1007/s10916-017-0800-x
[本文引用: 1]
[14]
MA L, ZHANG T, DONG C A novel ECG data compression method using adaptive Fourier decomposition with security guarantee in e-health applications
[J]. IEEE Journal of Biomedical and Health Informatics , 2015 , 19 (3 ): 986 - 994
DOI:10.1109/JBHI.2014.2357841
[本文引用: 1]
[15]
ZENG W, LI M, YUAN C, et al Identification of epileptic seizures in EEG signals using time-scale decomposition (ITD), discrete wavelet transform (DWT), phase space reconstruction (PSR) and neural networks
[J]. Artificial Intelligence Review , 2020 , 53 (4 ): 3059 - 3088
DOI:10.1007/s10462-019-09755-y
[本文引用: 1]
[16]
HUANG E, SHEN Z, LONG R, et al The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis
[J]. Proceedings Mathematical Physical and Engineering Sciences , 1998 , 454 (1971 ): 903 - 995
DOI:10.1098/rspa.1998.0193
[本文引用: 2]
[17]
GAUR P, KAUSHIK G, PACHORI B, et al. Comparison analysis: single and multichannel EMD-based filtering with application to BCI [C]// Machine Intelligence and Signal Analysis. Singapore: Springer, 2019.
[本文引用: 1]
[18]
SHARMA R, PACHORI B. Automated classification of focal and non-focal EEG signals based on bivariate empirical mode decomposition [M]// Biomedical Signal and Image Processing in Patient Care. Indore: IGI, 2017.
[本文引用: 1]
[19]
GAUR P, PACHORI B, HUI W, et al. An empirical mode decomposition based filtering method for classification of motor-imagery EEG signals for enhancing brain-computer interface [C]// The International Joint Conference on Neural Networks . Killarney: IEEE, 2015.
[本文引用: 1]
[20]
CORETTO P, LEPORE N, BRIEVA J, et al. Open access database of EEG signals recorded during imagined speech [C]// 12th International Symposium on Medical Information Processing and Analysis. Tandil: SPIE, 2017: 1016002.
[本文引用: 5]
[21]
LI G, WANG S, LI M, et al Towards real-life EEG applications: novel superporous hydrogel-based semi-dry EEG electrodes enabling automatically ‘charge–discharge’electrolyte
[J]. Journal of Neural Engineering , 2021 , 18 (4 ): 046016
DOI:10.1088/1741-2552/abeeab
[本文引用: 1]
[22]
CAO Y, OOSTENVELD R, ALDAY M, et al Are alpha and beta oscillations spatially dissociated over the cortex in context-driven spoken-word production?
[J]. Psychophysiology , 2022 , (6 ): e13999
[本文引用: 1]
[23]
ALYASSERI A, KHADER T, Al A, et al. EEG signal denoising using hybridizing method between wavelet transform with genetic algorithm [C]// Proceedings of the 11th National Technical Seminar on Unmanned System Technology . Singapore: Springer, 2021: 449-469.
[本文引用: 1]
[24]
ALBORZ R, ROBERT T, AURELIEN B, et al EEG classification of covert speech using regularized neural networks
[J]. IEEE/ACM Transactions on Audio, Speech and Language Processing , 2017 , 25 (12 ): 2292 - 2300
DOI:10.1109/TASLP.2017.2758164
[本文引用: 1]
[26]
RAJASHEKHAR U, NEELAPPA D, RAJESH L EEG signal classification for brain–computer interface using discrete wavelet transform (DWT)
[J]. International Journal of Intelligent Unmanned Systems , 2021 , 10 (1 ): 181 - 188
[本文引用: 1]
[27]
ALSALEH M. Toward an imagined speech-based brain computer interface using EEG signals [D]. Sheffield: University of Sheffield, 2019.
[本文引用: 1]
[28]
王楚涵. 基于融合特征和集成分类的在线EEG情感识别系统研究[D]. 天津: 天津理工大学, 2021.
[本文引用: 1]
WANG Chu-han. Research on online EEG emotion recognition system based on Fusion feature and ensemble classification [D]. Tianjin: Tianjin University of Technology, 2021.
[本文引用: 1]
[29]
ZHOU J, HUANG S, WANG M, et al Performance evaluation of hybrid GA–SVM and GWO–SVM models to predict earthquake-induced liquefaction potential of soil: a multi-dataset investigation
[J]. Engineering with Computers , 2021 , (2 ): 1 - 19
[本文引用: 1]
[30]
曾靖翔, 张金喜, 曹丹丹, 等 利用kNN方法的沥青路面平整度智能检测
[J]. 华南理工大学学报: 自然科学版 , 2022 , 50 (3 ): 50 - 56
[本文引用: 1]
ZENG Jing-xiang, ZHANG Jin-xi, CAO Dan-dan, et al Intelligent detection of asphalt pavement flatness by kNN method
[J]. Journal of South China University of Technology: Natural Science Edition , 2022 , 50 (3 ): 50 - 56
[本文引用: 1]
[31]
GARCIA S, VILLASENOR L, REYES A, et al. Tensor decomposition for imagined speech discrimination in EEG [C]// Mexican International Conference on Artificial Intelligence . Cham: Springer, 2018: 239-249.
[本文引用: 2]
[32]
COONEY C, FOLLI R, COYLE D. Optimizing layers improves CNN generalization and transfer learning for imagined speech decoding from EEG [C]// IEEE International Conference on Systems, Man and Cybernetics . Bari: IEEE, 2019: 1311-1316.
[本文引用: 2]
[33]
LEE Y, LEE M, LEE W. Classification of imagined speech using siamese neural network [C]// IEEE International Conference on Systems, Man and Cybernetics . Toronto: IEEE, 2020: 2979-2984.
[本文引用: 2]
Brain-computer interface technology: a review of the second international meeting
1
2003
... 脑-机接口是不依赖于正常的由外周神经和肌肉组成的输出通路的通信系统[1 -2 ] ,为瘫痪患者提供了全新的交流方式. 语言想象是最新出现的范式[3 ] ,它表示在不发出声音或清晰地做出面部动作的情况下想象单词发音的心理过程,相比于其他类型的脑电信号,如运动想象[4 ] 、稳态视觉诱发电位(SSVEP)[5 ] 和P300[6 ] ,想象语言最接近自然的沟通通路. ...
Adaptive cognitive technical systems
1
2014
... 脑-机接口是不依赖于正常的由外周神经和肌肉组成的输出通路的通信系统[1 -2 ] ,为瘫痪患者提供了全新的交流方式. 语言想象是最新出现的范式[3 ] ,它表示在不发出声音或清晰地做出面部动作的情况下想象单词发音的心理过程,相比于其他类型的脑电信号,如运动想象[4 ] 、稳态视觉诱发电位(SSVEP)[5 ] 和P300[6 ] ,想象语言最接近自然的沟通通路. ...
1
... 脑-机接口是不依赖于正常的由外周神经和肌肉组成的输出通路的通信系统[1 -2 ] ,为瘫痪患者提供了全新的交流方式. 语言想象是最新出现的范式[3 ] ,它表示在不发出声音或清晰地做出面部动作的情况下想象单词发音的心理过程,相比于其他类型的脑电信号,如运动想象[4 ] 、稳态视觉诱发电位(SSVEP)[5 ] 和P300[6 ] ,想象语言最接近自然的沟通通路. ...
Most popular signal processing methods in motor-imagery BCI: a review and meta-analysis
1
2018
... 脑-机接口是不依赖于正常的由外周神经和肌肉组成的输出通路的通信系统[1 -2 ] ,为瘫痪患者提供了全新的交流方式. 语言想象是最新出现的范式[3 ] ,它表示在不发出声音或清晰地做出面部动作的情况下想象单词发音的心理过程,相比于其他类型的脑电信号,如运动想象[4 ] 、稳态视觉诱发电位(SSVEP)[5 ] 和P300[6 ] ,想象语言最接近自然的沟通通路. ...
1
... 脑-机接口是不依赖于正常的由外周神经和肌肉组成的输出通路的通信系统[1 -2 ] ,为瘫痪患者提供了全新的交流方式. 语言想象是最新出现的范式[3 ] ,它表示在不发出声音或清晰地做出面部动作的情况下想象单词发音的心理过程,相比于其他类型的脑电信号,如运动想象[4 ] 、稳态视觉诱发电位(SSVEP)[5 ] 和P300[6 ] ,想象语言最接近自然的沟通通路. ...
Review of recent studies and issues regarding the P300-based complex trial protocol for detection of concealed information
1
2013
... 脑-机接口是不依赖于正常的由外周神经和肌肉组成的输出通路的通信系统[1 -2 ] ,为瘫痪患者提供了全新的交流方式. 语言想象是最新出现的范式[3 ] ,它表示在不发出声音或清晰地做出面部动作的情况下想象单词发音的心理过程,相比于其他类型的脑电信号,如运动想象[4 ] 、稳态视觉诱发电位(SSVEP)[5 ] 和P300[6 ] ,想象语言最接近自然的沟通通路. ...
脑机接口技术的发展与展望
1
2019
... 基于语言想象的脑-机接口(BCI)系统可以根据大脑活动信号采集技术的不同分为2类,分别是侵入式 BCI系统和非侵入式BCI系统[7 ] . 侵入式BCI系统采用的信号采集技术为皮层脑电图,非侵入式BCI系统采用的信号采集技术有脑电图(EEG)、功能性近红外光谱技术、功能性磁共振成像、脑磁图等. 其中EEG设备具有便携、性价比高的优点,在脑-机接口研究中得到广泛的应用. ...
脑机接口技术的发展与展望
1
2019
... 基于语言想象的脑-机接口(BCI)系统可以根据大脑活动信号采集技术的不同分为2类,分别是侵入式 BCI系统和非侵入式BCI系统[7 ] . 侵入式BCI系统采用的信号采集技术为皮层脑电图,非侵入式BCI系统采用的信号采集技术有脑电图(EEG)、功能性近红外光谱技术、功能性磁共振成像、脑磁图等. 其中EEG设备具有便携、性价比高的优点,在脑-机接口研究中得到广泛的应用. ...
1
... Wester[8 ] 开展基于脑电信号的语言想象研究,运用隐马尔可夫模型对脑电信号进行分类. Torres等[9 ] 提出基于模糊推理系统的通道选择方法,使用7个通道时的分类平均精度为68.18%,使用所有通道时的分类平均精度为70%. Qureshi等[10 ] 使用极限学习机对脑电信号进行分类,五分类平均准确率最高为40.30%. Hashim等[11 ] 利用14通道的EEG装置进行实验,运用梅尔倒频谱参数和KNN算法对EEG信号进行分类,二分类平均准确率为58%. Lee等[12 ] 利用64通道EEG设备进行实验,采用随机森林算法进行13个类别的分类,分类平均准确率为20.7%. ...
Implementing a fuzzy inference system in a multi-objective EEG channel selection model for imagined speech classification
1
2016
... Wester[8 ] 开展基于脑电信号的语言想象研究,运用隐马尔可夫模型对脑电信号进行分类. Torres等[9 ] 提出基于模糊推理系统的通道选择方法,使用7个通道时的分类平均精度为68.18%,使用所有通道时的分类平均精度为70%. Qureshi等[10 ] 使用极限学习机对脑电信号进行分类,五分类平均准确率最高为40.30%. Hashim等[11 ] 利用14通道的EEG装置进行实验,运用梅尔倒频谱参数和KNN算法对EEG信号进行分类,二分类平均准确率为58%. Lee等[12 ] 利用64通道EEG设备进行实验,采用随机森林算法进行13个类别的分类,分类平均准确率为20.7%. ...
Multiclass classification of word imagination speech with hybrid connectivity features
1
2017
... Wester[8 ] 开展基于脑电信号的语言想象研究,运用隐马尔可夫模型对脑电信号进行分类. Torres等[9 ] 提出基于模糊推理系统的通道选择方法,使用7个通道时的分类平均精度为68.18%,使用所有通道时的分类平均精度为70%. Qureshi等[10 ] 使用极限学习机对脑电信号进行分类,五分类平均准确率最高为40.30%. Hashim等[11 ] 利用14通道的EEG装置进行实验,运用梅尔倒频谱参数和KNN算法对EEG信号进行分类,二分类平均准确率为58%. Lee等[12 ] 利用64通道EEG设备进行实验,采用随机森林算法进行13个类别的分类,分类平均准确率为20.7%. ...
1
... Wester[8 ] 开展基于脑电信号的语言想象研究,运用隐马尔可夫模型对脑电信号进行分类. Torres等[9 ] 提出基于模糊推理系统的通道选择方法,使用7个通道时的分类平均精度为68.18%,使用所有通道时的分类平均精度为70%. Qureshi等[10 ] 使用极限学习机对脑电信号进行分类,五分类平均准确率最高为40.30%. Hashim等[11 ] 利用14通道的EEG装置进行实验,运用梅尔倒频谱参数和KNN算法对EEG信号进行分类,二分类平均准确率为58%. Lee等[12 ] 利用64通道EEG设备进行实验,采用随机森林算法进行13个类别的分类,分类平均准确率为20.7%. ...
1
... Wester[8 ] 开展基于脑电信号的语言想象研究,运用隐马尔可夫模型对脑电信号进行分类. Torres等[9 ] 提出基于模糊推理系统的通道选择方法,使用7个通道时的分类平均精度为68.18%,使用所有通道时的分类平均精度为70%. Qureshi等[10 ] 使用极限学习机对脑电信号进行分类,五分类平均准确率最高为40.30%. Hashim等[11 ] 利用14通道的EEG装置进行实验,运用梅尔倒频谱参数和KNN算法对EEG信号进行分类,二分类平均准确率为58%. Lee等[12 ] 利用64通道EEG设备进行实验,采用随机森林算法进行13个类别的分类,分类平均准确率为20.7%. ...
Classification of focal and non focal epileptic seizures using multi-features and SVM classifier
1
2017
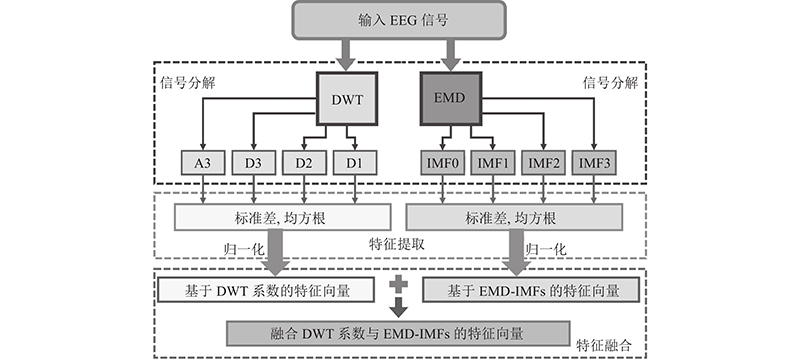
... BCI系统由信号预处理、特征提取和特征分类组成,其中特征提取和特征分类是2个关键步骤. 近年来,诸多学者对EEG信号分解与特征提取方法进行研究,如特征值分解[13 ] 、傅里叶分解方法[14 ] 、离散小波变换(discrete wavelet transform,DWT)[15 ] 和经验模态分解(empirical mode decomposition,EMD)[16 ] 算法. 其中,EMD和DWT被广泛应用于非线性和非平稳信号的分解和特征提取,在脑电信号[17 ] 分析中具有广阔的应用前景,如癫痫脑电信号检测[18 ] 和运动想象BCI分类问题[19 ] ,但其在语言想象BCI中的应用很少. DWT能够在频域和时域对脑电信号进行局部定位,EMD对于去除肌电伪迹的适用性更好. 目前针对语言想象BCI的大多数研究分别采用DWT或EMD进行分析,但2种分解具有一定的互补性,融合2种方法可以得到更好的性能. 为了提高语言想象脑电信号分类的准确率,本文提出融合DWT与EMD的语言想象脑电信号特征提取与分类方法,对该方法的分类性能进行评估与分析. ...
A novel ECG data compression method using adaptive Fourier decomposition with security guarantee in e-health applications
1
2015
... BCI系统由信号预处理、特征提取和特征分类组成,其中特征提取和特征分类是2个关键步骤. 近年来,诸多学者对EEG信号分解与特征提取方法进行研究,如特征值分解[13 ] 、傅里叶分解方法[14 ] 、离散小波变换(discrete wavelet transform,DWT)[15 ] 和经验模态分解(empirical mode decomposition,EMD)[16 ] 算法. 其中,EMD和DWT被广泛应用于非线性和非平稳信号的分解和特征提取,在脑电信号[17 ] 分析中具有广阔的应用前景,如癫痫脑电信号检测[18 ] 和运动想象BCI分类问题[19 ] ,但其在语言想象BCI中的应用很少. DWT能够在频域和时域对脑电信号进行局部定位,EMD对于去除肌电伪迹的适用性更好. 目前针对语言想象BCI的大多数研究分别采用DWT或EMD进行分析,但2种分解具有一定的互补性,融合2种方法可以得到更好的性能. 为了提高语言想象脑电信号分类的准确率,本文提出融合DWT与EMD的语言想象脑电信号特征提取与分类方法,对该方法的分类性能进行评估与分析. ...
Identification of epileptic seizures in EEG signals using time-scale decomposition (ITD), discrete wavelet transform (DWT), phase space reconstruction (PSR) and neural networks
1
2020
... BCI系统由信号预处理、特征提取和特征分类组成,其中特征提取和特征分类是2个关键步骤. 近年来,诸多学者对EEG信号分解与特征提取方法进行研究,如特征值分解[13 ] 、傅里叶分解方法[14 ] 、离散小波变换(discrete wavelet transform,DWT)[15 ] 和经验模态分解(empirical mode decomposition,EMD)[16 ] 算法. 其中,EMD和DWT被广泛应用于非线性和非平稳信号的分解和特征提取,在脑电信号[17 ] 分析中具有广阔的应用前景,如癫痫脑电信号检测[18 ] 和运动想象BCI分类问题[19 ] ,但其在语言想象BCI中的应用很少. DWT能够在频域和时域对脑电信号进行局部定位,EMD对于去除肌电伪迹的适用性更好. 目前针对语言想象BCI的大多数研究分别采用DWT或EMD进行分析,但2种分解具有一定的互补性,融合2种方法可以得到更好的性能. 为了提高语言想象脑电信号分类的准确率,本文提出融合DWT与EMD的语言想象脑电信号特征提取与分类方法,对该方法的分类性能进行评估与分析. ...
The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis
2
1998
... BCI系统由信号预处理、特征提取和特征分类组成,其中特征提取和特征分类是2个关键步骤. 近年来,诸多学者对EEG信号分解与特征提取方法进行研究,如特征值分解[13 ] 、傅里叶分解方法[14 ] 、离散小波变换(discrete wavelet transform,DWT)[15 ] 和经验模态分解(empirical mode decomposition,EMD)[16 ] 算法. 其中,EMD和DWT被广泛应用于非线性和非平稳信号的分解和特征提取,在脑电信号[17 ] 分析中具有广阔的应用前景,如癫痫脑电信号检测[18 ] 和运动想象BCI分类问题[19 ] ,但其在语言想象BCI中的应用很少. DWT能够在频域和时域对脑电信号进行局部定位,EMD对于去除肌电伪迹的适用性更好. 目前针对语言想象BCI的大多数研究分别采用DWT或EMD进行分析,但2种分解具有一定的互补性,融合2种方法可以得到更好的性能. 为了提高语言想象脑电信号分类的准确率,本文提出融合DWT与EMD的语言想象脑电信号特征提取与分类方法,对该方法的分类性能进行评估与分析. ...
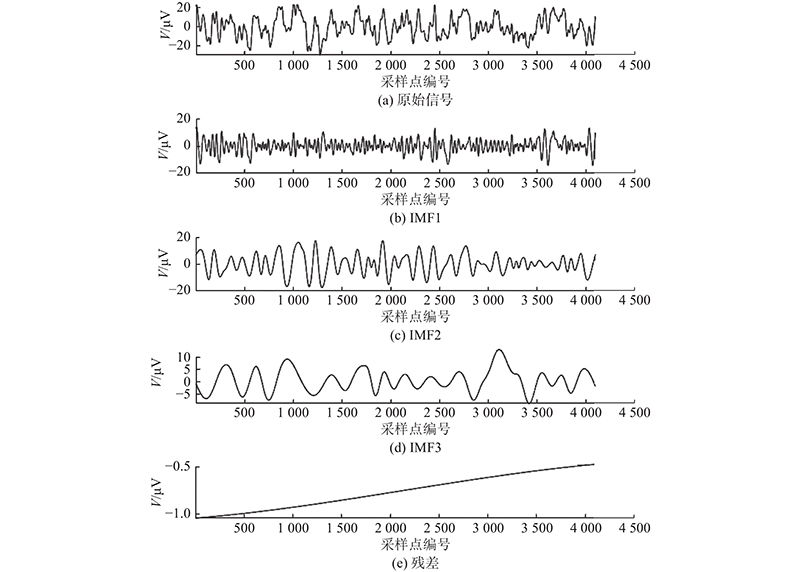
... 经验模态分解(EMD)是Hilbert-Huang变换的重要组成部分,它是处理非平稳信号的有效方法[16 ] . EMD是自适应信号分解框架,用于将非平稳数据分解为1组本征模态函数(intrinsic mode function, IMF)和1个残差分量. IMF需要满足以下2个条件. ...
1
... BCI系统由信号预处理、特征提取和特征分类组成,其中特征提取和特征分类是2个关键步骤. 近年来,诸多学者对EEG信号分解与特征提取方法进行研究,如特征值分解[13 ] 、傅里叶分解方法[14 ] 、离散小波变换(discrete wavelet transform,DWT)[15 ] 和经验模态分解(empirical mode decomposition,EMD)[16 ] 算法. 其中,EMD和DWT被广泛应用于非线性和非平稳信号的分解和特征提取,在脑电信号[17 ] 分析中具有广阔的应用前景,如癫痫脑电信号检测[18 ] 和运动想象BCI分类问题[19 ] ,但其在语言想象BCI中的应用很少. DWT能够在频域和时域对脑电信号进行局部定位,EMD对于去除肌电伪迹的适用性更好. 目前针对语言想象BCI的大多数研究分别采用DWT或EMD进行分析,但2种分解具有一定的互补性,融合2种方法可以得到更好的性能. 为了提高语言想象脑电信号分类的准确率,本文提出融合DWT与EMD的语言想象脑电信号特征提取与分类方法,对该方法的分类性能进行评估与分析. ...
1
... BCI系统由信号预处理、特征提取和特征分类组成,其中特征提取和特征分类是2个关键步骤. 近年来,诸多学者对EEG信号分解与特征提取方法进行研究,如特征值分解[13 ] 、傅里叶分解方法[14 ] 、离散小波变换(discrete wavelet transform,DWT)[15 ] 和经验模态分解(empirical mode decomposition,EMD)[16 ] 算法. 其中,EMD和DWT被广泛应用于非线性和非平稳信号的分解和特征提取,在脑电信号[17 ] 分析中具有广阔的应用前景,如癫痫脑电信号检测[18 ] 和运动想象BCI分类问题[19 ] ,但其在语言想象BCI中的应用很少. DWT能够在频域和时域对脑电信号进行局部定位,EMD对于去除肌电伪迹的适用性更好. 目前针对语言想象BCI的大多数研究分别采用DWT或EMD进行分析,但2种分解具有一定的互补性,融合2种方法可以得到更好的性能. 为了提高语言想象脑电信号分类的准确率,本文提出融合DWT与EMD的语言想象脑电信号特征提取与分类方法,对该方法的分类性能进行评估与分析. ...
1
... BCI系统由信号预处理、特征提取和特征分类组成,其中特征提取和特征分类是2个关键步骤. 近年来,诸多学者对EEG信号分解与特征提取方法进行研究,如特征值分解[13 ] 、傅里叶分解方法[14 ] 、离散小波变换(discrete wavelet transform,DWT)[15 ] 和经验模态分解(empirical mode decomposition,EMD)[16 ] 算法. 其中,EMD和DWT被广泛应用于非线性和非平稳信号的分解和特征提取,在脑电信号[17 ] 分析中具有广阔的应用前景,如癫痫脑电信号检测[18 ] 和运动想象BCI分类问题[19 ] ,但其在语言想象BCI中的应用很少. DWT能够在频域和时域对脑电信号进行局部定位,EMD对于去除肌电伪迹的适用性更好. 目前针对语言想象BCI的大多数研究分别采用DWT或EMD进行分析,但2种分解具有一定的互补性,融合2种方法可以得到更好的性能. 为了提高语言想象脑电信号分类的准确率,本文提出融合DWT与EMD的语言想象脑电信号特征提取与分类方法,对该方法的分类性能进行评估与分析. ...
5
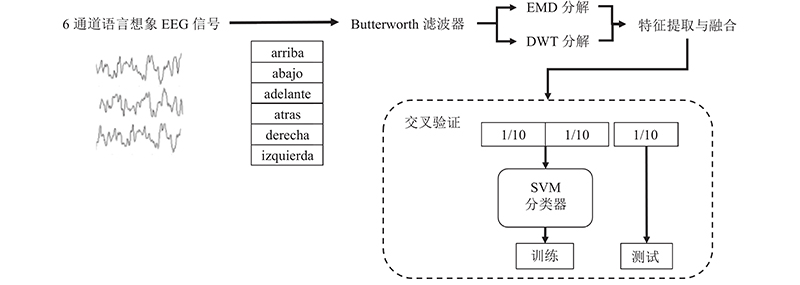
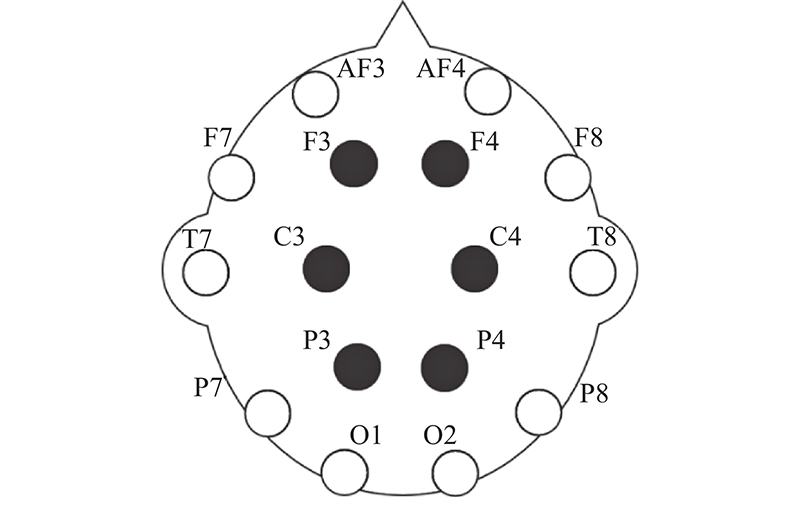
... 使用的数据集由Coretto等[20 ] 在恩特雷里奥斯国立大学记录. 研究对象包括15名阿根廷志愿者. 当受试者进行西班牙语单词和元音的想象语言任务时,开展脑电信号的采集. 针对想象单词时产生的脑电信号数据集进行研究. 在该数据集中,参与者想象6个西班牙语单词,包括“arriba”、“abajo”、“derecha”、“izquierda”、“adelante”和“atras”(对应上、下、左、右、后、前6个中文单词). 想象单词任务的实验方案要求参与者在4 s的试验期间想象出其中一个单词3次. 在试验之前,用视觉和听觉的方式呈现刺激,向每个受试者展示每个单词2 s. 根据10-20国际标准,采集电极被置于F3、F4、C3、C4、P3和P4位置,如图2 所示. 脑电信号采用Grass脑电采集设备进行采集,采样频率为1024 Hz. ...
... 脑电信号通常含有工频噪声和伪影信息,在特征提取和分类前需要进行滤波处理. 当受试者想象说话时,大脑语言区域的α β [22 ] . 在对想象语音脑电信号进行处理时,需要对脑电信号进行带通滤波处理,得到α β [20 ] . 采用0~40 Hz的巴特沃斯带通滤波器对脑电信号进行滤波,去除噪声和伪影. ...
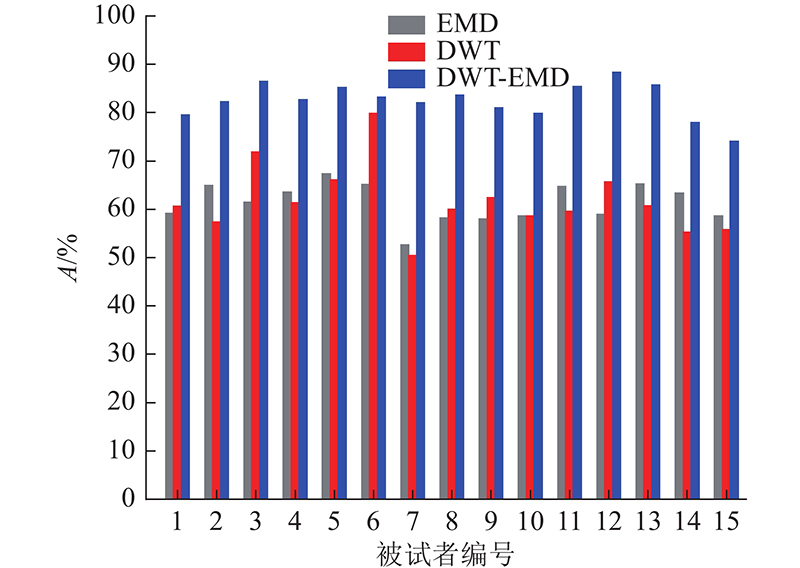
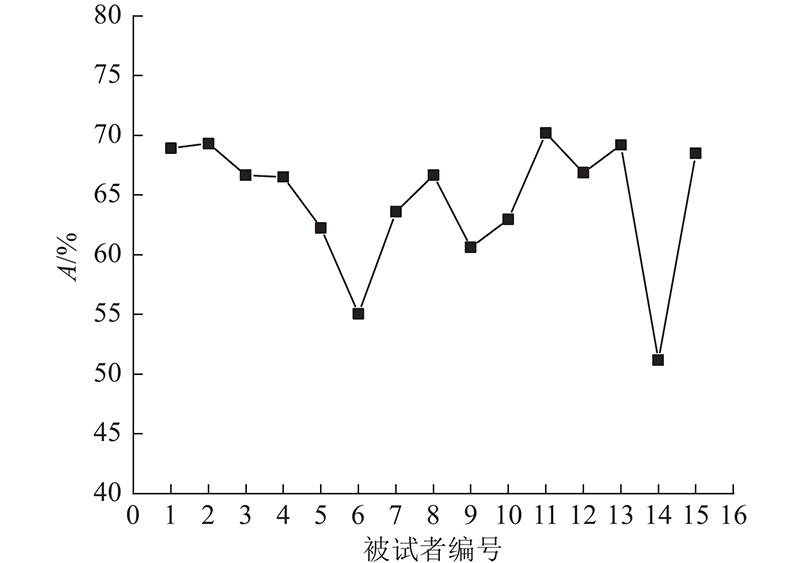
... 针对Coretto等[20 ] 记录的语言想象脑电信号数据集,分别利用DWT和EMD提取EEG信号特征,将各特征进行融合得到DWT-EMD融合特征. 分别利用基于RBF的支持向量机和KNN分类器对EEG信号进行分类,采用10折交叉验证的方法,对每个受试者各自的脑电信号进行分类性能评估. 实验结果表明,采用RBF支持向量机对DWT提取的特征进行分类的最高准确率为79.78%,平均准确率为61.69%. 对EMD提取的特征进行分类的最高准确率为67.30%,平均准确率为61.34%. 分别使用DWT和EMD提取的特征获得的分类平均准确率相近,但针对不同受试者的语言想象EEG信号,使用DWT方法得到的分类准确率在不同个体之间差异较大,所有受试者中分类的最高准确率与最低准确率之差达到29.34%,使用EMD方法得到的分类最高准确率与最低准确率之差仅为14.66%. 融合DWT与EMD特征后得到的分类最高准确率达到88.34%,平均分类准确率达到82.46%,相较于前2种方法,分类准确率得到显著提升,受试者的最高准确率与最低准确率之差仅为14.31%. 采用KNN对融合DWT与EMD的特征进行分类的最高准确率为70.20%,平均准确率为64.57%,相较于SVM分类器,准确率偏低. 可知,基于RBF核函数的SVM分类器在语言想象脑电信号分类方面具有较好的性能. 上述结果表明,提出的融合EMD与DWT的方法具有更高的准确性和稳定性. 基于SVM和KNN方法得到的不同个体EEG信号的分类准确率A 如图7 、8 所示. ...
... 表1 给出在相同数据集条件下提出的方法与其他文献方法的分类平均准确率 $\bar A $ . 可以看出,对于相同的数据集,本文运用的3种方法均取得较高的平均准确率,其中融合DWT与EMD的方法3的平均准确率最高. 与文献[20 ]相比,虽然采取DWT进行信号分解,但本文方法1的准确率得到显著提升,原因主要有以下两点. 1)特征的选取,本文选取均方根和标准差作为分类的特征,能够较好地表现不同语言想象脑电信号的差异. 2)分类器的选择,本文采用基于RBF核函数的SVM进行分类,更适用于语言想象EEG信号的分类. Garcia等[31 ] 采用张量分解的方法进行脑电信号分类,分类准确率为59.7%,与方法1和方法2持平,低于本文方法3,张量分解的计算成本较大,耗时较长,难以在BCI系统上直接实现. Cooney等[32 -33 ] 采用的方法都是神经网络,但分类结果都不理想,表明神经网络方法不适合处理语言想象EEG信号的分类问题. ...
... Comparison of accuracy of imaged speech EEG signal classification
Tab.1 研究方法 方法 $\bar A $ 文献[20 ]方法 DWT+随机森林 19.60 文献[31 ]方法 张量分解法 59.70 文献[32 ]方法 卷积神经网络 35.68 文献[33 ]方法 Siamese神经网络 31.40 本文方法1 DWT+SVM 61.69 本文方法2 EMD+SVM 61.34 本文方法3 DWT-EMD+SVM 82.46 本文方法4 DWT-EMD+KNN 64.57
在开源的语言想象数据集上,融合离散小波变换和经验模态分解算法,提取语言想象脑电信号特征,运用基于RBF核函数的SVM分类器进行分类,取得了优异的分类结果. 实验结果表明,基于RBF核函数的支持向量机与其他分类方法相比,在语言想象脑电信号分类上具有更好的分类效果. 分别测试单独使用DWT或EMD提取信号特征的方法,由于均方根和标准差更好地表现了信号的差异以及支持向量机较好的分类效果,这2种方法相较于其他研究均取得了较高的准确率. 考虑到仅使用DWT或EMD提取的脑电信号特征具有局限性与片面性,融合DWT与EMD提取的特征,将融合后的特征输入到SVM中进行分类. 结果表明,利用该方法得到的准确率取得了显著的提升. ...
Towards real-life EEG applications: novel superporous hydrogel-based semi-dry EEG electrodes enabling automatically ‘charge–discharge’electrolyte
1
2021
... 脑电信号是非常微弱的生物电信号,易受眨眼、吞咽、肢体动作等肌肉活动以及电源和声音的干扰[21 ] . 在特征提取和分类之前,需要对脑电信号进行预处理,以提高信号质量和分类精度. ...
Are alpha and beta oscillations spatially dissociated over the cortex in context-driven spoken-word production?
1
2022
... 脑电信号通常含有工频噪声和伪影信息,在特征提取和分类前需要进行滤波处理. 当受试者想象说话时,大脑语言区域的α β [22 ] . 在对想象语音脑电信号进行处理时,需要对脑电信号进行带通滤波处理,得到α β [20 ] . 采用0~40 Hz的巴特沃斯带通滤波器对脑电信号进行滤波,去除噪声和伪影. ...
1
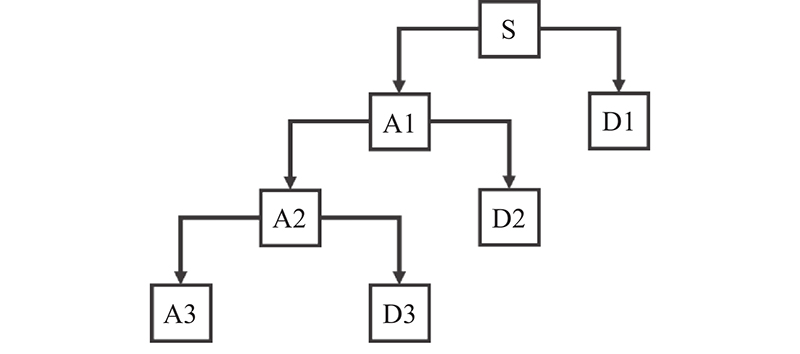
... 小波理论是时频域信号分析理论,基本思想是用一组函数来表示或近似一个信号,这类函数由一个基本小波(也称为母小波)进行不同尺度的平移和缩放得到. 小波变换具有多分辨率分析和自适应信号处理的特点,适合于处理非平稳信号[23 ] . 在实际应用中,为了便于计算,减少计算量,通常对信号进行离散处理,称为离散小波变换(DWT). DWT特征已被证明对语言想象脑电图信号具有区分性[24 ] ,由于DWT能够在频域和时域对信息进行局部定位,被频繁应用于脑电分析中[25 -26 ] . DWT原理如图3 所示,其中S表示原始输入信号,A和D信号由2个互补滤波器产生. 信号A表示信号的低频分量,是原始信号的近似量. 信号D表示信号的高频分量,是原始信号的细节量. ...
EEG classification of covert speech using regularized neural networks
1
2017
... 小波理论是时频域信号分析理论,基本思想是用一组函数来表示或近似一个信号,这类函数由一个基本小波(也称为母小波)进行不同尺度的平移和缩放得到. 小波变换具有多分辨率分析和自适应信号处理的特点,适合于处理非平稳信号[23 ] . 在实际应用中,为了便于计算,减少计算量,通常对信号进行离散处理,称为离散小波变换(DWT). DWT特征已被证明对语言想象脑电图信号具有区分性[24 ] ,由于DWT能够在频域和时域对信息进行局部定位,被频繁应用于脑电分析中[25 -26 ] . DWT原理如图3 所示,其中S表示原始输入信号,A和D信号由2个互补滤波器产生. 信号A表示信号的低频分量,是原始信号的近似量. 信号D表示信号的高频分量,是原始信号的细节量. ...
基于DD-DWT和Log-Logistic参数回归的癫痫脑电自动识别方法
1
2017
... 小波理论是时频域信号分析理论,基本思想是用一组函数来表示或近似一个信号,这类函数由一个基本小波(也称为母小波)进行不同尺度的平移和缩放得到. 小波变换具有多分辨率分析和自适应信号处理的特点,适合于处理非平稳信号[23 ] . 在实际应用中,为了便于计算,减少计算量,通常对信号进行离散处理,称为离散小波变换(DWT). DWT特征已被证明对语言想象脑电图信号具有区分性[24 ] ,由于DWT能够在频域和时域对信息进行局部定位,被频繁应用于脑电分析中[25 -26 ] . DWT原理如图3 所示,其中S表示原始输入信号,A和D信号由2个互补滤波器产生. 信号A表示信号的低频分量,是原始信号的近似量. 信号D表示信号的高频分量,是原始信号的细节量. ...
基于DD-DWT和Log-Logistic参数回归的癫痫脑电自动识别方法
1
2017
... 小波理论是时频域信号分析理论,基本思想是用一组函数来表示或近似一个信号,这类函数由一个基本小波(也称为母小波)进行不同尺度的平移和缩放得到. 小波变换具有多分辨率分析和自适应信号处理的特点,适合于处理非平稳信号[23 ] . 在实际应用中,为了便于计算,减少计算量,通常对信号进行离散处理,称为离散小波变换(DWT). DWT特征已被证明对语言想象脑电图信号具有区分性[24 ] ,由于DWT能够在频域和时域对信息进行局部定位,被频繁应用于脑电分析中[25 -26 ] . DWT原理如图3 所示,其中S表示原始输入信号,A和D信号由2个互补滤波器产生. 信号A表示信号的低频分量,是原始信号的近似量. 信号D表示信号的高频分量,是原始信号的细节量. ...
EEG signal classification for brain–computer interface using discrete wavelet transform (DWT)
1
2021
... 小波理论是时频域信号分析理论,基本思想是用一组函数来表示或近似一个信号,这类函数由一个基本小波(也称为母小波)进行不同尺度的平移和缩放得到. 小波变换具有多分辨率分析和自适应信号处理的特点,适合于处理非平稳信号[23 ] . 在实际应用中,为了便于计算,减少计算量,通常对信号进行离散处理,称为离散小波变换(DWT). DWT特征已被证明对语言想象脑电图信号具有区分性[24 ] ,由于DWT能够在频域和时域对信息进行局部定位,被频繁应用于脑电分析中[25 -26 ] . DWT原理如图3 所示,其中S表示原始输入信号,A和D信号由2个互补滤波器产生. 信号A表示信号的低频分量,是原始信号的近似量. 信号D表示信号的高频分量,是原始信号的细节量. ...
1
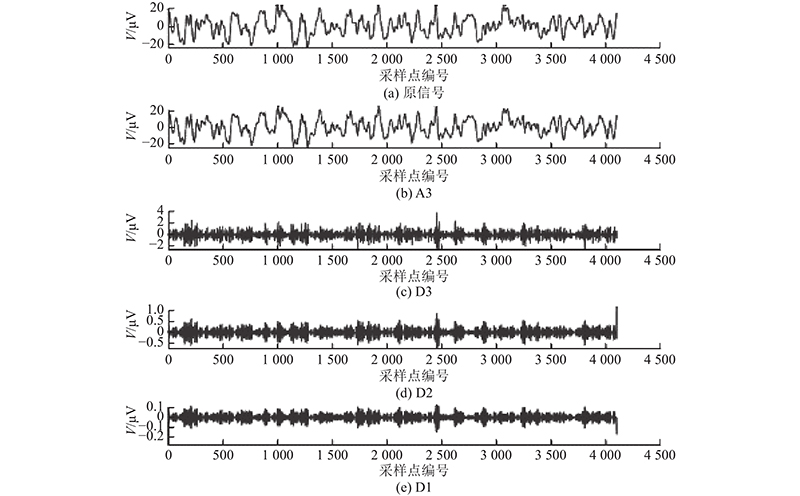
... 在小波变换中,母小波的合理选择对于实际应用非常重要. Daubechies(dbN , N 为小波阶数)极值相位小波是指特定的小波族,函数dbN 中的N 与小波函数的消失矩相同. 一般情况下,消失矩越大,对应的滤波器越平坦,但计算量越大,信号处理的实时性降低. 在大多数脑电图研究中,使用Daubechies2(db2)或Daubechies4(db4)作为母小波,提高信号处理的实时性[27 ] . 采用db2作为母小波对EEG信号进行3次小波分解,通过第1次小波分解得到低频信号A1和高频信号D1,再依次分解得到A2、A3、D2、D3信号,如图4 所示. 图4 中,V 为信号电压幅值,信号为被试1在想象单词“arriba”时记录的一段F3通道的脑电信号,分别计算A3、D1、D2和D3信号的标准差(standard deviation, SD)和均方根(root mean square, RMS)作为脑电信号的特征. 由于采集了6个通道(F3、F4、C3、C4、P3和P4)的脑电信号,每个通道有8个特征,利用DWT提取的特征总数为48. ...
1
... 仅通过DWT或EMD提取的特征均是计算不同分解后通道的标准差和均方根,但是侧重点不同. 为了提高特征的鲁棒性,提出将2类特征向量(基于DWT系数的统计特征向量和基于EMD的IMF统计特征向量)进行融合,将融合后的特征向量作为脑电信号的特征. 常用的特征融合方法包括串联特征融合算法、主成分分析算法和基于深度学习理论的算法. 其中串联特征融合算法的计算速度快,运算时间短,更适合于脑-机接口的实时应用场景[28 ] ,故采用串联特征融合算法对DWT与EMD提取的特征进行融合. ...
1
... 仅通过DWT或EMD提取的特征均是计算不同分解后通道的标准差和均方根,但是侧重点不同. 为了提高特征的鲁棒性,提出将2类特征向量(基于DWT系数的统计特征向量和基于EMD的IMF统计特征向量)进行融合,将融合后的特征向量作为脑电信号的特征. 常用的特征融合方法包括串联特征融合算法、主成分分析算法和基于深度学习理论的算法. 其中串联特征融合算法的计算速度快,运算时间短,更适合于脑-机接口的实时应用场景[28 ] ,故采用串联特征融合算法对DWT与EMD提取的特征进行融合. ...
Performance evaluation of hybrid GA–SVM and GWO–SVM models to predict earthquake-induced liquefaction potential of soil: a multi-dataset investigation
1
2021
... 支持向量机(SVM)是经典的机器学习分类技术, 目标是根据输入的数据样本找到最优的分类超平面. SVM基于统计学习理论和结构风险最小化准则,前者降低了对样本量的需求,后者提高了分类的泛化能力,因此支持向量机在小样本训练集上通常能够得到比其他算法更好的结果,在若干领域得到了广泛应用[29 ] . ...
利用kNN方法的沥青路面平整度智能检测
1
2022
... KNN是分类算法中被广泛应用的一种,是利用K 个最邻近的数据样本反映数据集分类特性的方法[30 ] . KNN的核心思想如下:若一个样本在特征空间中的K 个最相似的样本中的大部分属于某一个类别,则该样本被分类到该类别. ...
利用kNN方法的沥青路面平整度智能检测
1
2022
... KNN是分类算法中被广泛应用的一种,是利用K 个最邻近的数据样本反映数据集分类特性的方法[30 ] . KNN的核心思想如下:若一个样本在特征空间中的K 个最相似的样本中的大部分属于某一个类别,则该样本被分类到该类别. ...
2
... 表1 给出在相同数据集条件下提出的方法与其他文献方法的分类平均准确率 $\bar A $ . 可以看出,对于相同的数据集,本文运用的3种方法均取得较高的平均准确率,其中融合DWT与EMD的方法3的平均准确率最高. 与文献[20 ]相比,虽然采取DWT进行信号分解,但本文方法1的准确率得到显著提升,原因主要有以下两点. 1)特征的选取,本文选取均方根和标准差作为分类的特征,能够较好地表现不同语言想象脑电信号的差异. 2)分类器的选择,本文采用基于RBF核函数的SVM进行分类,更适用于语言想象EEG信号的分类. Garcia等[31 ] 采用张量分解的方法进行脑电信号分类,分类准确率为59.7%,与方法1和方法2持平,低于本文方法3,张量分解的计算成本较大,耗时较长,难以在BCI系统上直接实现. Cooney等[32 -33 ] 采用的方法都是神经网络,但分类结果都不理想,表明神经网络方法不适合处理语言想象EEG信号的分类问题. ...
... Comparison of accuracy of imaged speech EEG signal classification
Tab.1 研究方法 方法 $\bar A $ 文献[20 ]方法 DWT+随机森林 19.60 文献[31 ]方法 张量分解法 59.70 文献[32 ]方法 卷积神经网络 35.68 文献[33 ]方法 Siamese神经网络 31.40 本文方法1 DWT+SVM 61.69 本文方法2 EMD+SVM 61.34 本文方法3 DWT-EMD+SVM 82.46 本文方法4 DWT-EMD+KNN 64.57
在开源的语言想象数据集上,融合离散小波变换和经验模态分解算法,提取语言想象脑电信号特征,运用基于RBF核函数的SVM分类器进行分类,取得了优异的分类结果. 实验结果表明,基于RBF核函数的支持向量机与其他分类方法相比,在语言想象脑电信号分类上具有更好的分类效果. 分别测试单独使用DWT或EMD提取信号特征的方法,由于均方根和标准差更好地表现了信号的差异以及支持向量机较好的分类效果,这2种方法相较于其他研究均取得了较高的准确率. 考虑到仅使用DWT或EMD提取的脑电信号特征具有局限性与片面性,融合DWT与EMD提取的特征,将融合后的特征输入到SVM中进行分类. 结果表明,利用该方法得到的准确率取得了显著的提升. ...
2
... 表1 给出在相同数据集条件下提出的方法与其他文献方法的分类平均准确率 $\bar A $ . 可以看出,对于相同的数据集,本文运用的3种方法均取得较高的平均准确率,其中融合DWT与EMD的方法3的平均准确率最高. 与文献[20 ]相比,虽然采取DWT进行信号分解,但本文方法1的准确率得到显著提升,原因主要有以下两点. 1)特征的选取,本文选取均方根和标准差作为分类的特征,能够较好地表现不同语言想象脑电信号的差异. 2)分类器的选择,本文采用基于RBF核函数的SVM进行分类,更适用于语言想象EEG信号的分类. Garcia等[31 ] 采用张量分解的方法进行脑电信号分类,分类准确率为59.7%,与方法1和方法2持平,低于本文方法3,张量分解的计算成本较大,耗时较长,难以在BCI系统上直接实现. Cooney等[32 -33 ] 采用的方法都是神经网络,但分类结果都不理想,表明神经网络方法不适合处理语言想象EEG信号的分类问题. ...
... Comparison of accuracy of imaged speech EEG signal classification
Tab.1 研究方法 方法 $\bar A $ 文献[20 ]方法 DWT+随机森林 19.60 文献[31 ]方法 张量分解法 59.70 文献[32 ]方法 卷积神经网络 35.68 文献[33 ]方法 Siamese神经网络 31.40 本文方法1 DWT+SVM 61.69 本文方法2 EMD+SVM 61.34 本文方法3 DWT-EMD+SVM 82.46 本文方法4 DWT-EMD+KNN 64.57
在开源的语言想象数据集上,融合离散小波变换和经验模态分解算法,提取语言想象脑电信号特征,运用基于RBF核函数的SVM分类器进行分类,取得了优异的分类结果. 实验结果表明,基于RBF核函数的支持向量机与其他分类方法相比,在语言想象脑电信号分类上具有更好的分类效果. 分别测试单独使用DWT或EMD提取信号特征的方法,由于均方根和标准差更好地表现了信号的差异以及支持向量机较好的分类效果,这2种方法相较于其他研究均取得了较高的准确率. 考虑到仅使用DWT或EMD提取的脑电信号特征具有局限性与片面性,融合DWT与EMD提取的特征,将融合后的特征输入到SVM中进行分类. 结果表明,利用该方法得到的准确率取得了显著的提升. ...
2
... 表1 给出在相同数据集条件下提出的方法与其他文献方法的分类平均准确率 $\bar A $ . 可以看出,对于相同的数据集,本文运用的3种方法均取得较高的平均准确率,其中融合DWT与EMD的方法3的平均准确率最高. 与文献[20 ]相比,虽然采取DWT进行信号分解,但本文方法1的准确率得到显著提升,原因主要有以下两点. 1)特征的选取,本文选取均方根和标准差作为分类的特征,能够较好地表现不同语言想象脑电信号的差异. 2)分类器的选择,本文采用基于RBF核函数的SVM进行分类,更适用于语言想象EEG信号的分类. Garcia等[31 ] 采用张量分解的方法进行脑电信号分类,分类准确率为59.7%,与方法1和方法2持平,低于本文方法3,张量分解的计算成本较大,耗时较长,难以在BCI系统上直接实现. Cooney等[32 -33 ] 采用的方法都是神经网络,但分类结果都不理想,表明神经网络方法不适合处理语言想象EEG信号的分类问题. ...
... Comparison of accuracy of imaged speech EEG signal classification
Tab.1 研究方法 方法 $\bar A $ 文献[20 ]方法 DWT+随机森林 19.60 文献[31 ]方法 张量分解法 59.70 文献[32 ]方法 卷积神经网络 35.68 文献[33 ]方法 Siamese神经网络 31.40 本文方法1 DWT+SVM 61.69 本文方法2 EMD+SVM 61.34 本文方法3 DWT-EMD+SVM 82.46 本文方法4 DWT-EMD+KNN 64.57
在开源的语言想象数据集上,融合离散小波变换和经验模态分解算法,提取语言想象脑电信号特征,运用基于RBF核函数的SVM分类器进行分类,取得了优异的分类结果. 实验结果表明,基于RBF核函数的支持向量机与其他分类方法相比,在语言想象脑电信号分类上具有更好的分类效果. 分别测试单独使用DWT或EMD提取信号特征的方法,由于均方根和标准差更好地表现了信号的差异以及支持向量机较好的分类效果,这2种方法相较于其他研究均取得了较高的准确率. 考虑到仅使用DWT或EMD提取的脑电信号特征具有局限性与片面性,融合DWT与EMD提取的特征,将融合后的特征输入到SVM中进行分类. 结果表明,利用该方法得到的准确率取得了显著的提升. ...