$\left. \begin{array}{l} {\rm{minimize}}: \;\;\; {C_{\rm{d}}};\\ {\rm{s.t.}} \quad\quad\quad\quad{C_{\rm{l}}} \geqslant{C_{{\rm{l,}}}}_{{\rm{ini}}},\\ \;\;\quad\quad\quad\quad\quad {d_{{\rm{s1}}}} \geqslant {d_{{\rm{s1,ini}}}},\\ \;\;\quad \quad\quad\quad\quad {d_{{\rm{s2}}}} \geqslant {d_{{\rm{s2,ini}}}},\\ \;\;\quad\quad\quad\quad\quad S \geqslant {S_{{\rm{ini}}}}. \end{array} \right\} $
[1]
张宇飞, 陈海昕, 符松, 等 一种实用的运输类飞机机翼/发动机短舱一体化优化设计方法
[J]. 航空学报 , 2012 , 33 (11 ): 1993 - 2001
[本文引用: 1]
ZHANG Yu-fei, CHEN Hai-xin, FU Song, et al A practical optimization design method for transport aircraft wing/nacelle integration
[J]. Acta Aeronautica et Astronautica Sinica , 2012 , 33 (11 ): 1993 - 2001
[本文引用: 1]
[2]
白俊强, 徐家宽, 黄江涛, 等 多区域自由变形技术在短舱安装位置减阻设计中的应用研究
[J]. 空气动力学学报 , 2014 , 32 (5 ): 682 - 687
BAI Jun-qiang, XU Jia-kuan, HUANG Jiang-tao, et al Drag reduction design of install position of nacelle based on multi-zone FFD technology
[J]. Acta Aerodynamica Sinica , 2014 , 32 (5 ): 682 - 687
[3]
邱亚松, 白俊强, 黄琳, 等 翼吊发动机短舱对三维增升装置的影响及改善措施研究
[J]. 空气动力学学报 , 2012 , 30 (1 ): 7 - 13
[本文引用: 1]
QIU Ya-song S, BAI Jun-qiang, HUANG Lin, et al Study about influence of wing-mounted engine nacelle on high-lift system and improvement measures
[J]. Acta Aerodynamica Sinica , 2012 , 30 (1 ): 7 - 13
[本文引用: 1]
[4]
TEJERO F, ROBINSON M, MACMANUS D G, et al Multi-objective optimisation of short nacelles for high bypass ratio engines
[J]. Aerospace Science and Technology , 2019 , 91 : 410 - 421
DOI:10.1016/j.ast.2019.02.014
[本文引用: 1]
[5]
TEJERO F, GOULOS I, MACMANUS D G, et al. Effects of aircraft integration on compact nacelle aerodynamics [C]// AIAA Scitech 2020 Forum . Orlando: AIAA, 2020: 2020-2225 .
[本文引用: 1]
[6]
张冬云, 张美红, 王美黎, 等 翼吊布局民机短舱位置气动影响
[J]. 空气动力学学报 , 2017 , 35 (6 ): 781 - 786
[本文引用: 1]
ZHANG Dong-yin, ZHANG Mei-hong, WANG Mei-li, et al Aero-dynamic influence of nacelle position of a wing-mounted civil aircraft
[J]. Acta Aerodynamica Sinica , 2017 , 35 (6 ): 781 - 786
[本文引用: 1]
[7]
KOC S, KIM H J, NAKAHASHI K. Aerodynamic design of wing-body-nacelle-pylon configuration [C]// 17th AIAA Computational Fluid Dynamics Conference . Toronto: AIAA, 2005: 2005-4856.
[本文引用: 1]
[8]
SAITOH T, KIM H J, TAKENAKA K, et al. Multi-Point design of wing-body-nacelle-pylon configuration [C]// 24th Applied Aerodynamics Conference . San Francisco: AIAA, 2006: 3461.
[本文引用: 1]
[9]
EPSTEIN B, PEIGIN S Automatic optimization of wing–body–under-the-wing-mounted-nacelle configurations
[J]. Journal of Aircraft , 2016 , 53 (3 ): 691 - 700
DOI:10.2514/1.C033641
[本文引用: 1]
[10]
BONS N P, MADER C A, MARTINS J R R A, et al. High-fidelity aerodynamic shape optimization of a full configuration regional jet [C]// AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference . Kissimmee: AIAA, 2018: 106.
[本文引用: 1]
[11]
LI J, GAO Z H, HUANG J T, et al Aerodynamic design optimization of nacelle/pylon position on an aircraft
[J]. Chinese Journal of Aeronautics , 2013 , 26 (4 ): 850 - 857
DOI:10.1016/j.cja.2013.04.052
[本文引用: 1]
[12]
LEI R W, BAI J Q, XU D Y Aerodynamic optimization of civil aircraft with wing-mounted engine jet based on adjoint method
[J]. Aerospace Science and Technology , 2019 , 93 : 105285
DOI:10.1016/j.ast.2019.07.018
[本文引用: 2]
[13]
王景. 基于Stackelberg博弈与连续伴随方法的气动外形优化设计 [D]. 杭州: 浙江大学, 2018.
[本文引用: 1]
WANG Jing. Aerodynamic shape optimization by Stackelberg game coupled with the continuous adjoint method [D]. Hangzhou: Zhejiang University, 2018.
[本文引用: 1]
[14]
张玄武, 郑耀, 杨波威, 等 基于级联前向网络的翼型优化设计
[J]. 浙江大学学报: 工学版 , 2017 , 51 (7 ): 1405 - 1411
[本文引用: 1]
ZHANG Xuan-wu, ZHENG Yao, YANG Bo-wei, et al Aerodynamic optimization design of airfoil configurations based on cascade feedforward neural network
[J]. Journal of Zhejiang University: Engineering Science , 2017 , 51 (7 ): 1405 - 1411
[本文引用: 1]
[15]
HOOKER J R, WICK A, ZEUNE C, et al. Over wing nacelle installations for improved energy efficiency [C]// 31st AIAA Applied Aerodynamics Conference . San Diego: AIAA, 2013: 2013-2920.
[本文引用: 1]
[16]
REDEKER G. A selection of experimental test cases for the validation of cfd codes [R]. [S.l.]: AGARD, 1994.
[本文引用: 2]
[17]
STRAATHOF M H, VAN TOOREN M J L Extension to the class-shape-transformation method based on B-splines
[J]. AIAA Journal , 2011 , 49 (4 ): 780 - 790
DOI:10.2514/1.J050706
[本文引用: 1]
[18]
ZHU F, QIN N Intuitive class/shape function parameterization for airfoils
[J]. AIAA Journal , 2014 , 52 (1 ): 17 - 25
DOI:10.2514/1.J052610
[本文引用: 1]
[19]
SPALART P R, ALLMARAS S R. A one-equation turbulence model for aerodynamic flows [C]// 30th Aerospace Sciences Meeting and Exhibit . [S.l.]: AIAA, 1992: 1992-0439.
[本文引用: 1]
[20]
HIROSE N, ASAI K, IKAWA K, et al Euler flow analysis of turbine powered simulator and fanjet engine
[J]. Journal of Propulsion and Power , 1991 , 7 (6 ): 1015 - 1022
DOI:10.2514/3.23421
[本文引用: 1]
[21]
LI J, LI F W, QIN E Numerical simulation of transonic flow over wing-mounted twin-engine transport aircraft
[J]. Journal of Aircraft , 2000 , 37 (3 ): 469 - 478
DOI:10.2514/2.2621
[本文引用: 1]
[22]
刘凯礼, 姬昌睿, 谭兆光, 等 大涵道比涡扇发动机TPS短舱低速气动特性分析
[J]. 推进技术 , 2015 , 36 (2 ): 186 - 193
DOI:10.13675/j.cnki.tjjs.2015.02.004
[本文引用: 1]
LIU Kai-li, JI Chang-rui, TAN Zhao-guang, et al Numerical study on low speed aerodynamic performance of large bypass ratio engine TPS nacelle
[J]. Journal of Propulsion Technology , 2015 , 36 (2 ): 186 - 193
DOI:10.13675/j.cnki.tjjs.2015.02.004
[本文引用: 1]
[23]
TAN Z G, CHEN Y C, SI J T Study of power influences to the wing-mounted civil aircraft aerodynamic characteristics
[J]. Journal of Aircraft , 2014 , 51 (2 ): 629 - 636
DOI:10.2514/1.C032356
[本文引用: 3]
一种实用的运输类飞机机翼/发动机短舱一体化优化设计方法
1
2012
... 翼吊式布局是现代大型民用飞机常见的发动机布局方式,该布局将发动机短舱吊挂在机翼下方,具有发动机进气效率高、降低翼根弯矩和减轻客舱噪声等优点. 对于翼吊式布局飞机而言,在飞行过程中,机翼和短舱之间会产生强烈的气动干扰,可能严重破坏全机的气动性能[1 -3 ] . 为了提高发动机的推进效率和降低发动机的燃油消耗率,民用航空发动机呈现出涵道比越来越大和风扇压力比越来越小的发展趋势[4 ] . 预计未来涡扇发动机的涵道比将为14~23 [5 ] . 大的涵道比会带来更大的发动机重量和尺寸,而发动机直径和进气面积的增大会导致机翼和短舱之间的气动干扰更加强烈[6 ] . 因此,亟须对机翼/短舱进行一体化气动优化设计,来减弱部件间的流动干扰,提升飞机的整体气动性能. ...
一种实用的运输类飞机机翼/发动机短舱一体化优化设计方法
1
2012
... 翼吊式布局是现代大型民用飞机常见的发动机布局方式,该布局将发动机短舱吊挂在机翼下方,具有发动机进气效率高、降低翼根弯矩和减轻客舱噪声等优点. 对于翼吊式布局飞机而言,在飞行过程中,机翼和短舱之间会产生强烈的气动干扰,可能严重破坏全机的气动性能[1 -3 ] . 为了提高发动机的推进效率和降低发动机的燃油消耗率,民用航空发动机呈现出涵道比越来越大和风扇压力比越来越小的发展趋势[4 ] . 预计未来涡扇发动机的涵道比将为14~23 [5 ] . 大的涵道比会带来更大的发动机重量和尺寸,而发动机直径和进气面积的增大会导致机翼和短舱之间的气动干扰更加强烈[6 ] . 因此,亟须对机翼/短舱进行一体化气动优化设计,来减弱部件间的流动干扰,提升飞机的整体气动性能. ...
多区域自由变形技术在短舱安装位置减阻设计中的应用研究
0
2014
多区域自由变形技术在短舱安装位置减阻设计中的应用研究
0
2014
翼吊发动机短舱对三维增升装置的影响及改善措施研究
1
2012
... 翼吊式布局是现代大型民用飞机常见的发动机布局方式,该布局将发动机短舱吊挂在机翼下方,具有发动机进气效率高、降低翼根弯矩和减轻客舱噪声等优点. 对于翼吊式布局飞机而言,在飞行过程中,机翼和短舱之间会产生强烈的气动干扰,可能严重破坏全机的气动性能[1 -3 ] . 为了提高发动机的推进效率和降低发动机的燃油消耗率,民用航空发动机呈现出涵道比越来越大和风扇压力比越来越小的发展趋势[4 ] . 预计未来涡扇发动机的涵道比将为14~23 [5 ] . 大的涵道比会带来更大的发动机重量和尺寸,而发动机直径和进气面积的增大会导致机翼和短舱之间的气动干扰更加强烈[6 ] . 因此,亟须对机翼/短舱进行一体化气动优化设计,来减弱部件间的流动干扰,提升飞机的整体气动性能. ...
翼吊发动机短舱对三维增升装置的影响及改善措施研究
1
2012
... 翼吊式布局是现代大型民用飞机常见的发动机布局方式,该布局将发动机短舱吊挂在机翼下方,具有发动机进气效率高、降低翼根弯矩和减轻客舱噪声等优点. 对于翼吊式布局飞机而言,在飞行过程中,机翼和短舱之间会产生强烈的气动干扰,可能严重破坏全机的气动性能[1 -3 ] . 为了提高发动机的推进效率和降低发动机的燃油消耗率,民用航空发动机呈现出涵道比越来越大和风扇压力比越来越小的发展趋势[4 ] . 预计未来涡扇发动机的涵道比将为14~23 [5 ] . 大的涵道比会带来更大的发动机重量和尺寸,而发动机直径和进气面积的增大会导致机翼和短舱之间的气动干扰更加强烈[6 ] . 因此,亟须对机翼/短舱进行一体化气动优化设计,来减弱部件间的流动干扰,提升飞机的整体气动性能. ...
Multi-objective optimisation of short nacelles for high bypass ratio engines
1
2019
... 翼吊式布局是现代大型民用飞机常见的发动机布局方式,该布局将发动机短舱吊挂在机翼下方,具有发动机进气效率高、降低翼根弯矩和减轻客舱噪声等优点. 对于翼吊式布局飞机而言,在飞行过程中,机翼和短舱之间会产生强烈的气动干扰,可能严重破坏全机的气动性能[1 -3 ] . 为了提高发动机的推进效率和降低发动机的燃油消耗率,民用航空发动机呈现出涵道比越来越大和风扇压力比越来越小的发展趋势[4 ] . 预计未来涡扇发动机的涵道比将为14~23 [5 ] . 大的涵道比会带来更大的发动机重量和尺寸,而发动机直径和进气面积的增大会导致机翼和短舱之间的气动干扰更加强烈[6 ] . 因此,亟须对机翼/短舱进行一体化气动优化设计,来减弱部件间的流动干扰,提升飞机的整体气动性能. ...
1
... 翼吊式布局是现代大型民用飞机常见的发动机布局方式,该布局将发动机短舱吊挂在机翼下方,具有发动机进气效率高、降低翼根弯矩和减轻客舱噪声等优点. 对于翼吊式布局飞机而言,在飞行过程中,机翼和短舱之间会产生强烈的气动干扰,可能严重破坏全机的气动性能[1 -3 ] . 为了提高发动机的推进效率和降低发动机的燃油消耗率,民用航空发动机呈现出涵道比越来越大和风扇压力比越来越小的发展趋势[4 ] . 预计未来涡扇发动机的涵道比将为14~23 [5 ] . 大的涵道比会带来更大的发动机重量和尺寸,而发动机直径和进气面积的增大会导致机翼和短舱之间的气动干扰更加强烈[6 ] . 因此,亟须对机翼/短舱进行一体化气动优化设计,来减弱部件间的流动干扰,提升飞机的整体气动性能. ...
翼吊布局民机短舱位置气动影响
1
2017
... 翼吊式布局是现代大型民用飞机常见的发动机布局方式,该布局将发动机短舱吊挂在机翼下方,具有发动机进气效率高、降低翼根弯矩和减轻客舱噪声等优点. 对于翼吊式布局飞机而言,在飞行过程中,机翼和短舱之间会产生强烈的气动干扰,可能严重破坏全机的气动性能[1 -3 ] . 为了提高发动机的推进效率和降低发动机的燃油消耗率,民用航空发动机呈现出涵道比越来越大和风扇压力比越来越小的发展趋势[4 ] . 预计未来涡扇发动机的涵道比将为14~23 [5 ] . 大的涵道比会带来更大的发动机重量和尺寸,而发动机直径和进气面积的增大会导致机翼和短舱之间的气动干扰更加强烈[6 ] . 因此,亟须对机翼/短舱进行一体化气动优化设计,来减弱部件间的流动干扰,提升飞机的整体气动性能. ...
翼吊布局民机短舱位置气动影响
1
2017
... 翼吊式布局是现代大型民用飞机常见的发动机布局方式,该布局将发动机短舱吊挂在机翼下方,具有发动机进气效率高、降低翼根弯矩和减轻客舱噪声等优点. 对于翼吊式布局飞机而言,在飞行过程中,机翼和短舱之间会产生强烈的气动干扰,可能严重破坏全机的气动性能[1 -3 ] . 为了提高发动机的推进效率和降低发动机的燃油消耗率,民用航空发动机呈现出涵道比越来越大和风扇压力比越来越小的发展趋势[4 ] . 预计未来涡扇发动机的涵道比将为14~23 [5 ] . 大的涵道比会带来更大的发动机重量和尺寸,而发动机直径和进气面积的增大会导致机翼和短舱之间的气动干扰更加强烈[6 ] . 因此,亟须对机翼/短舱进行一体化气动优化设计,来减弱部件间的流动干扰,提升飞机的整体气动性能. ...
1
... 针对机翼/短舱的一体化气动优化设计已经开展了大量研究工作. Koc等[7 ] 使用序列二次规划算法对DLR-F6翼-身-短舱-挂架结构进行优化设计,在减小阻力的同时极大地消除了挂架表面的强激波. Saitoh等[8 ] 在此基础上进行低升力条件和跨声速巡航条件下的多点设计,优化设计后的构型在2种工况下都具有较好的气动性能. Epstein等[9 ] 使用遗传算法与降阶模型相结合的方法实现翼吊式飞机的机翼结构的多点优化设计,并取得显著的减阻效果. Bons等[10 ] 采用基于高精度气动建模的梯度优化方法对喷气式客机的完整配置进行优化设计,优化设计后构型的气动性能比初始提升了2%. Li等[11 ] 使用基于Kringing代理模型和粒子群优化算法的优化框架,对DLR-F6翼-身-短舱-挂架几何中短舱的安装位置进行优化.结果表明,优化后飞机各部件间的流动干扰显著减弱.Lei等[12 ] 使用基于伴随法的梯度优化算法,对某典型长程双通道运输机构型进行一体化气动优化,得到翼-身-短舱-挂架一体化的全耦合设计. ...
1
... 针对机翼/短舱的一体化气动优化设计已经开展了大量研究工作. Koc等[7 ] 使用序列二次规划算法对DLR-F6翼-身-短舱-挂架结构进行优化设计,在减小阻力的同时极大地消除了挂架表面的强激波. Saitoh等[8 ] 在此基础上进行低升力条件和跨声速巡航条件下的多点设计,优化设计后的构型在2种工况下都具有较好的气动性能. Epstein等[9 ] 使用遗传算法与降阶模型相结合的方法实现翼吊式飞机的机翼结构的多点优化设计,并取得显著的减阻效果. Bons等[10 ] 采用基于高精度气动建模的梯度优化方法对喷气式客机的完整配置进行优化设计,优化设计后构型的气动性能比初始提升了2%. Li等[11 ] 使用基于Kringing代理模型和粒子群优化算法的优化框架,对DLR-F6翼-身-短舱-挂架几何中短舱的安装位置进行优化.结果表明,优化后飞机各部件间的流动干扰显著减弱.Lei等[12 ] 使用基于伴随法的梯度优化算法,对某典型长程双通道运输机构型进行一体化气动优化,得到翼-身-短舱-挂架一体化的全耦合设计. ...
Automatic optimization of wing–body–under-the-wing-mounted-nacelle configurations
1
2016
... 针对机翼/短舱的一体化气动优化设计已经开展了大量研究工作. Koc等[7 ] 使用序列二次规划算法对DLR-F6翼-身-短舱-挂架结构进行优化设计,在减小阻力的同时极大地消除了挂架表面的强激波. Saitoh等[8 ] 在此基础上进行低升力条件和跨声速巡航条件下的多点设计,优化设计后的构型在2种工况下都具有较好的气动性能. Epstein等[9 ] 使用遗传算法与降阶模型相结合的方法实现翼吊式飞机的机翼结构的多点优化设计,并取得显著的减阻效果. Bons等[10 ] 采用基于高精度气动建模的梯度优化方法对喷气式客机的完整配置进行优化设计,优化设计后构型的气动性能比初始提升了2%. Li等[11 ] 使用基于Kringing代理模型和粒子群优化算法的优化框架,对DLR-F6翼-身-短舱-挂架几何中短舱的安装位置进行优化.结果表明,优化后飞机各部件间的流动干扰显著减弱.Lei等[12 ] 使用基于伴随法的梯度优化算法,对某典型长程双通道运输机构型进行一体化气动优化,得到翼-身-短舱-挂架一体化的全耦合设计. ...
1
... 针对机翼/短舱的一体化气动优化设计已经开展了大量研究工作. Koc等[7 ] 使用序列二次规划算法对DLR-F6翼-身-短舱-挂架结构进行优化设计,在减小阻力的同时极大地消除了挂架表面的强激波. Saitoh等[8 ] 在此基础上进行低升力条件和跨声速巡航条件下的多点设计,优化设计后的构型在2种工况下都具有较好的气动性能. Epstein等[9 ] 使用遗传算法与降阶模型相结合的方法实现翼吊式飞机的机翼结构的多点优化设计,并取得显著的减阻效果. Bons等[10 ] 采用基于高精度气动建模的梯度优化方法对喷气式客机的完整配置进行优化设计,优化设计后构型的气动性能比初始提升了2%. Li等[11 ] 使用基于Kringing代理模型和粒子群优化算法的优化框架,对DLR-F6翼-身-短舱-挂架几何中短舱的安装位置进行优化.结果表明,优化后飞机各部件间的流动干扰显著减弱.Lei等[12 ] 使用基于伴随法的梯度优化算法,对某典型长程双通道运输机构型进行一体化气动优化,得到翼-身-短舱-挂架一体化的全耦合设计. ...
Aerodynamic design optimization of nacelle/pylon position on an aircraft
1
2013
... 针对机翼/短舱的一体化气动优化设计已经开展了大量研究工作. Koc等[7 ] 使用序列二次规划算法对DLR-F6翼-身-短舱-挂架结构进行优化设计,在减小阻力的同时极大地消除了挂架表面的强激波. Saitoh等[8 ] 在此基础上进行低升力条件和跨声速巡航条件下的多点设计,优化设计后的构型在2种工况下都具有较好的气动性能. Epstein等[9 ] 使用遗传算法与降阶模型相结合的方法实现翼吊式飞机的机翼结构的多点优化设计,并取得显著的减阻效果. Bons等[10 ] 采用基于高精度气动建模的梯度优化方法对喷气式客机的完整配置进行优化设计,优化设计后构型的气动性能比初始提升了2%. Li等[11 ] 使用基于Kringing代理模型和粒子群优化算法的优化框架,对DLR-F6翼-身-短舱-挂架几何中短舱的安装位置进行优化.结果表明,优化后飞机各部件间的流动干扰显著减弱.Lei等[12 ] 使用基于伴随法的梯度优化算法,对某典型长程双通道运输机构型进行一体化气动优化,得到翼-身-短舱-挂架一体化的全耦合设计. ...
Aerodynamic optimization of civil aircraft with wing-mounted engine jet based on adjoint method
2
2019
... 针对机翼/短舱的一体化气动优化设计已经开展了大量研究工作. Koc等[7 ] 使用序列二次规划算法对DLR-F6翼-身-短舱-挂架结构进行优化设计,在减小阻力的同时极大地消除了挂架表面的强激波. Saitoh等[8 ] 在此基础上进行低升力条件和跨声速巡航条件下的多点设计,优化设计后的构型在2种工况下都具有较好的气动性能. Epstein等[9 ] 使用遗传算法与降阶模型相结合的方法实现翼吊式飞机的机翼结构的多点优化设计,并取得显著的减阻效果. Bons等[10 ] 采用基于高精度气动建模的梯度优化方法对喷气式客机的完整配置进行优化设计,优化设计后构型的气动性能比初始提升了2%. Li等[11 ] 使用基于Kringing代理模型和粒子群优化算法的优化框架,对DLR-F6翼-身-短舱-挂架几何中短舱的安装位置进行优化.结果表明,优化后飞机各部件间的流动干扰显著减弱.Lei等[12 ] 使用基于伴随法的梯度优化算法,对某典型长程双通道运输机构型进行一体化气动优化,得到翼-身-短舱-挂架一体化的全耦合设计. ...
... 综上所述,机翼/短舱气动优化设计的研究缺少同时考虑机翼形状、短舱形状和短舱安装位置的机翼/短舱一体化气动优化设计,并且考虑短舱真实进气和排气效应的研究较少. 实际上短舱射流和飞机外流的相互干扰不可忽略,飞机的气动性能在很大程度上会受到短舱射流的影响[12 ] .优化方法一直是气动优化设计工作的重点,优化方法能否高效并充分地搜索整个设计空间是气动优化设计工作面临的巨大挑战之一[13 ] . 对于机翼/短舱一体化设计的三维气动优化问题,设计变量个数众多,设计空间维度巨大,本质上是求解高维非线性优化问题,因此往往需要大规模地调用高精度计算流体力学(CFD)数值模拟分析,这对优化方法的高效性和全局性都提出了较高的要求[14 ] . ...
1
... 综上所述,机翼/短舱气动优化设计的研究缺少同时考虑机翼形状、短舱形状和短舱安装位置的机翼/短舱一体化气动优化设计,并且考虑短舱真实进气和排气效应的研究较少. 实际上短舱射流和飞机外流的相互干扰不可忽略,飞机的气动性能在很大程度上会受到短舱射流的影响[12 ] .优化方法一直是气动优化设计工作的重点,优化方法能否高效并充分地搜索整个设计空间是气动优化设计工作面临的巨大挑战之一[13 ] . 对于机翼/短舱一体化设计的三维气动优化问题,设计变量个数众多,设计空间维度巨大,本质上是求解高维非线性优化问题,因此往往需要大规模地调用高精度计算流体力学(CFD)数值模拟分析,这对优化方法的高效性和全局性都提出了较高的要求[14 ] . ...
1
... 综上所述,机翼/短舱气动优化设计的研究缺少同时考虑机翼形状、短舱形状和短舱安装位置的机翼/短舱一体化气动优化设计,并且考虑短舱真实进气和排气效应的研究较少. 实际上短舱射流和飞机外流的相互干扰不可忽略,飞机的气动性能在很大程度上会受到短舱射流的影响[12 ] .优化方法一直是气动优化设计工作的重点,优化方法能否高效并充分地搜索整个设计空间是气动优化设计工作面临的巨大挑战之一[13 ] . 对于机翼/短舱一体化设计的三维气动优化问题,设计变量个数众多,设计空间维度巨大,本质上是求解高维非线性优化问题,因此往往需要大规模地调用高精度计算流体力学(CFD)数值模拟分析,这对优化方法的高效性和全局性都提出了较高的要求[14 ] . ...
基于级联前向网络的翼型优化设计
1
2017
... 综上所述,机翼/短舱气动优化设计的研究缺少同时考虑机翼形状、短舱形状和短舱安装位置的机翼/短舱一体化气动优化设计,并且考虑短舱真实进气和排气效应的研究较少. 实际上短舱射流和飞机外流的相互干扰不可忽略,飞机的气动性能在很大程度上会受到短舱射流的影响[12 ] .优化方法一直是气动优化设计工作的重点,优化方法能否高效并充分地搜索整个设计空间是气动优化设计工作面临的巨大挑战之一[13 ] . 对于机翼/短舱一体化设计的三维气动优化问题,设计变量个数众多,设计空间维度巨大,本质上是求解高维非线性优化问题,因此往往需要大规模地调用高精度计算流体力学(CFD)数值模拟分析,这对优化方法的高效性和全局性都提出了较高的要求[14 ] . ...
基于级联前向网络的翼型优化设计
1
2017
... 综上所述,机翼/短舱气动优化设计的研究缺少同时考虑机翼形状、短舱形状和短舱安装位置的机翼/短舱一体化气动优化设计,并且考虑短舱真实进气和排气效应的研究较少. 实际上短舱射流和飞机外流的相互干扰不可忽略,飞机的气动性能在很大程度上会受到短舱射流的影响[12 ] .优化方法一直是气动优化设计工作的重点,优化方法能否高效并充分地搜索整个设计空间是气动优化设计工作面临的巨大挑战之一[13 ] . 对于机翼/短舱一体化设计的三维气动优化问题,设计变量个数众多,设计空间维度巨大,本质上是求解高维非线性优化问题,因此往往需要大规模地调用高精度计算流体力学(CFD)数值模拟分析,这对优化方法的高效性和全局性都提出了较高的要求[14 ] . ...
1
... 在不考虑发动机进排气效应的机翼/短舱一体化优化研究中,初始几何较常使用带通流短舱的DLR-F6翼-身-挂架-短舱标模. 国际上暂不存在带有动力短舱的全机标模,因此本研究选择将DLR-F4翼身组合体、BPR9动力短舱模型和斜挂架进行组合作为翼-身-短舱-挂架的初始几何. DLR-F4翼身组合体来自第一届AIAA计算流体力学阻力预测研讨会(DPW-Ⅰ). BPR9动力短舱模型是涵道比为9并带有一定前倾角的非对称发动机短舱模型[15 ] . 斜挂架使用NACA0012翼型放样生成. 如表1 所示为初始几何构型的参数[16 ] . ...
2
... 在不考虑发动机进排气效应的机翼/短舱一体化优化研究中,初始几何较常使用带通流短舱的DLR-F6翼-身-挂架-短舱标模. 国际上暂不存在带有动力短舱的全机标模,因此本研究选择将DLR-F4翼身组合体、BPR9动力短舱模型和斜挂架进行组合作为翼-身-短舱-挂架的初始几何. DLR-F4翼身组合体来自第一届AIAA计算流体力学阻力预测研讨会(DPW-Ⅰ). BPR9动力短舱模型是涵道比为9并带有一定前倾角的非对称发动机短舱模型[15 ] . 斜挂架使用NACA0012翼型放样生成. 如表1 所示为初始几何构型的参数[16 ] . ...
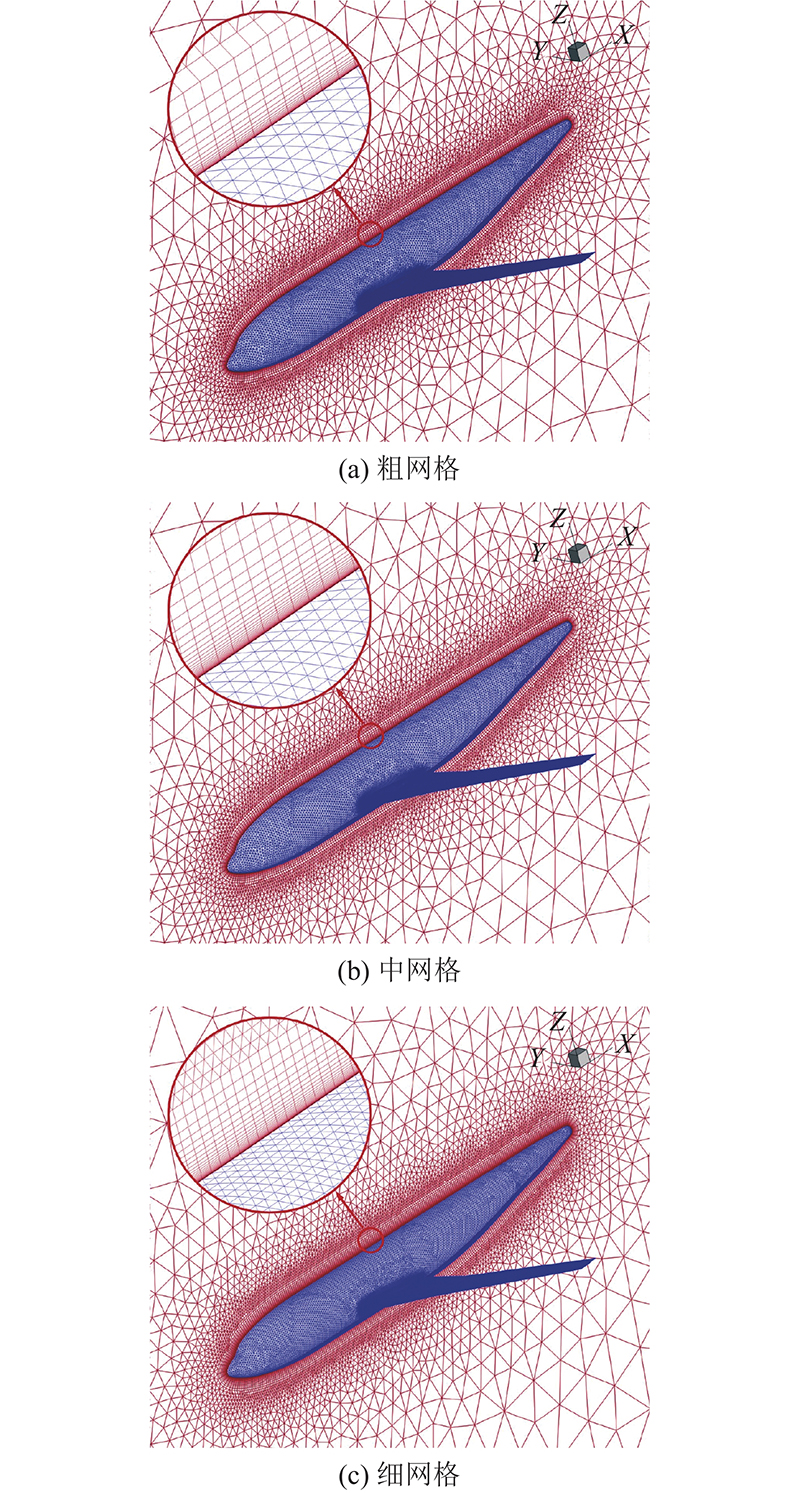
... 使用可压缩求解器SU2在Ma =0.75、Re =3.0×106 的工况下对DLR-F4翼身组合体几何模型进行了数值模拟. DLR-F4模型采用T-Rex非结构网格划分,共生成3种质量不同的网格,网格单元数分别为1.91×106 、4.13×106 和6.30×106 ,分别对应粗网格、中网格和细网格. 不同网格体现在壁面层网格厚度以及表面网格尺度的不同,壁面层第1层网格厚度分别为1×10−4 、5×10−5 和3×10−5 m,中网格和细网格均有无量纲壁面距离y + <1,如图6 所示. 如图7 所示为DLR-F4几何模型的机翼压力系数分布C p . 将3种质量网格的计算结果与文献[16 ]的实验数据进行对比,其中实验工况与数值模拟工况一致. 结果表明,数值模拟结果和实验结果符合良好,且中网格和细网格的计算结果基本一致,网格无关性得到验证. ...
Extension to the class-shape-transformation method based on B-splines
1
2011
... 三维机翼形状包括平面形状和截面形状. 当控制截面确定下来时,可以通过平面形状参数对控制截面进行插值来得到三维机翼形状. 本研究使用类别形状函数变换(class and shape transformation,CST)方法对二维翼型截面进行参数化,再通过平面形状参数创建三维机翼形状. CST方法适用于很多复杂构型的参数化,它由类函数 $ C_{{N_2}}^{{N_1}}\left( \psi \right) $ $ S\left( \psi \right) $ [17 ] , ...
Intuitive class/shape function parameterization for airfoils
1
2014
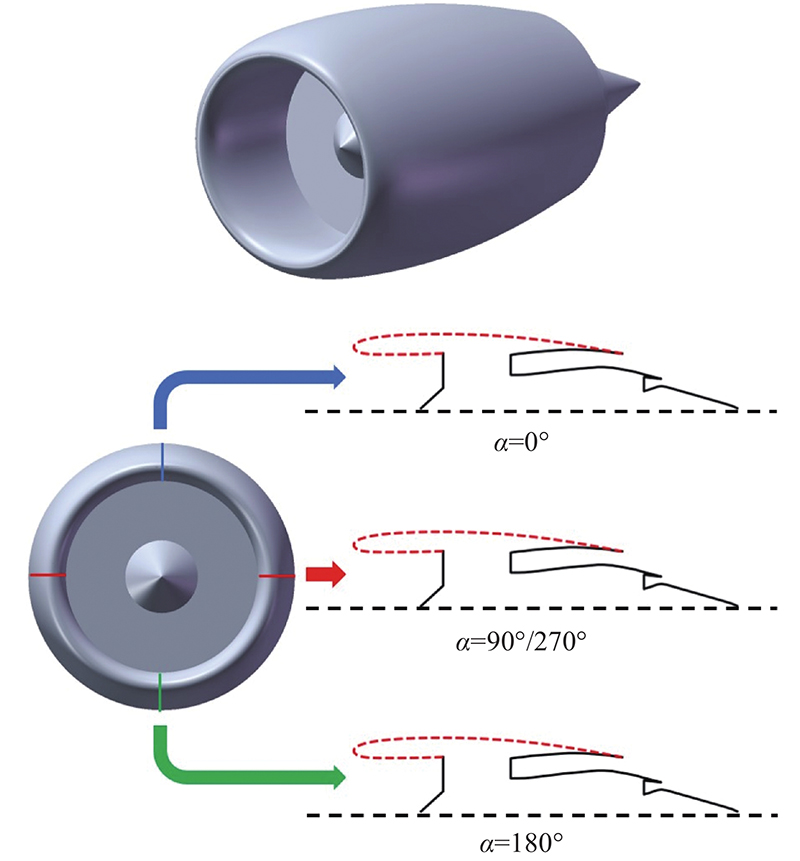
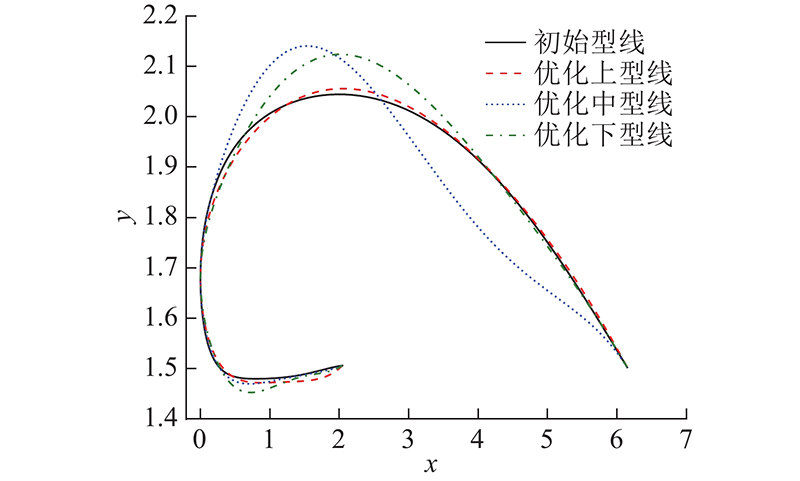
... 对于短舱的外形优化设计,本研究关注它的部分直观参数,如前缘曲率半径、风扇罩最大半径,因此使用直观类别形状函数变换(intuitive CST,iCST)参数化方法对BPR9发动机短舱型线进行参数化. iCST方法是在CST方法的基础上,建立直观参数到权重系数的变换矩阵,将CST方法中的权重系数转化成直观参数,再对直观参数进行设计[18 ] . 由于短舱和发动机存在的几何约束和硬性要求,对于单个短舱型线,本研究关注的几何参数有前缘曲率半径 $ {r_{{\text{if}}}} $ $ {r_{{\text{max}}}} $ $ {f_{{\text{max}}}} $ $ {\;\beta _{{\text{nac}}}} $ $ {r_{{\text{hi}}}} $ $ {f_{\text{i}}} $ $ {\;\beta _{{\text{int}}}} $ 图3 所示. 其中l nac 为风扇罩的最大长度,l int 为进气道的最大长度.通过对7个直观几何参数的设计和iCST参数化方法,能够生成对应的短舱风扇罩型线和进气道型线,再与整流锥、排气系统型线相结合,即可生成完整的短舱型线,再将短舱型线沿着风扇的轴向进行旋转,能够生成轴对称短舱几何. 如图4 所示,考虑5°前倾角的非轴对称短舱的设计,由3条短舱型线组成,共有21个直观几何设计参数. 图中, $ \alpha $
1
... 对于跨声速流动而言,通常使用可压缩的Navier-Stokes方程来求解流体动力学问题. 本研究使用雷诺平均Navier-Stokes(RANS)法和涡黏滞模型来模拟高雷诺数影响下的湍流流动,并使用Spalart-Allmaras(SA)湍流模型来评估雷诺应力模型中湍流黏度的变化[19 ] . ...
Euler flow analysis of turbine powered simulator and fanjet engine
1
1991
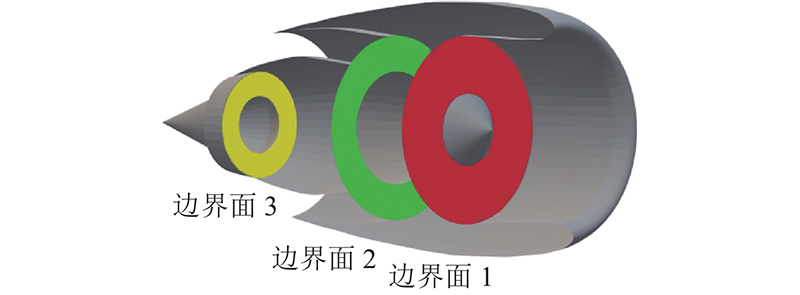
... 当发动机处于工作状态时,由于发动机内部的燃烧和工作过程非常复杂,很难直接精确计算发动机的内部工况来模拟实际的进气和排气效应. 发动机的实际物理边界条件同样难以精准确定,例如,扇叶在风扇边界处不断旋转,其真实边界条件为三维时变流场,必须作为扇叶流动问题来求解[20 ] . 为了降低计算成本,选择对发动机短舱的边界条件进行简化. 如图5 为短舱边界示意图,边界面1是风扇进口面,来流在该进口面经过风扇压缩作用进入发动机;边界面2为风扇出口面,即外涵道排气面,这一部分排出的气体是仅经过风扇加压的低能量气体;边界面3为核心机出口面,即内涵道排气面,这一部分排出的气体是经过燃烧做功的高能量燃气. ...
Numerical simulation of transonic flow over wing-mounted twin-engine transport aircraft
1
2000
... 在边界条件的设置上,将机身、机翼和除3个进出口面外的所有短舱表面均设置成无滑移壁面边界,风扇进口面设置成流场的出口边界条件,风扇出口面和核心机出口面均设置成流场的入口边界条件,将计算域的外边界设置成远场边界条件. 对于某个特定几何的短舱,知道以下工况参数:涵道比 $ \lambda $ 21 ]. 为了简化优化问题,暂不考虑工况参数的变化,将发动机短舱的各工况参数设定为恒定值. 动力短舱阻力的计算式[22 ] 为 ...
大涵道比涡扇发动机TPS短舱低速气动特性分析
1
2015
... 在边界条件的设置上,将机身、机翼和除3个进出口面外的所有短舱表面均设置成无滑移壁面边界,风扇进口面设置成流场的出口边界条件,风扇出口面和核心机出口面均设置成流场的入口边界条件,将计算域的外边界设置成远场边界条件. 对于某个特定几何的短舱,知道以下工况参数:涵道比 $ \lambda $ 21 ]. 为了简化优化问题,暂不考虑工况参数的变化,将发动机短舱的各工况参数设定为恒定值. 动力短舱阻力的计算式[22 ] 为 ...
大涵道比涡扇发动机TPS短舱低速气动特性分析
1
2015
... 在边界条件的设置上,将机身、机翼和除3个进出口面外的所有短舱表面均设置成无滑移壁面边界,风扇进口面设置成流场的出口边界条件,风扇出口面和核心机出口面均设置成流场的入口边界条件,将计算域的外边界设置成远场边界条件. 对于某个特定几何的短舱,知道以下工况参数:涵道比 $ \lambda $ 21 ]. 为了简化优化问题,暂不考虑工况参数的变化,将发动机短舱的各工况参数设定为恒定值. 动力短舱阻力的计算式[22 ] 为 ...
Study of power influences to the wing-mounted civil aircraft aerodynamic characteristics
3
2014
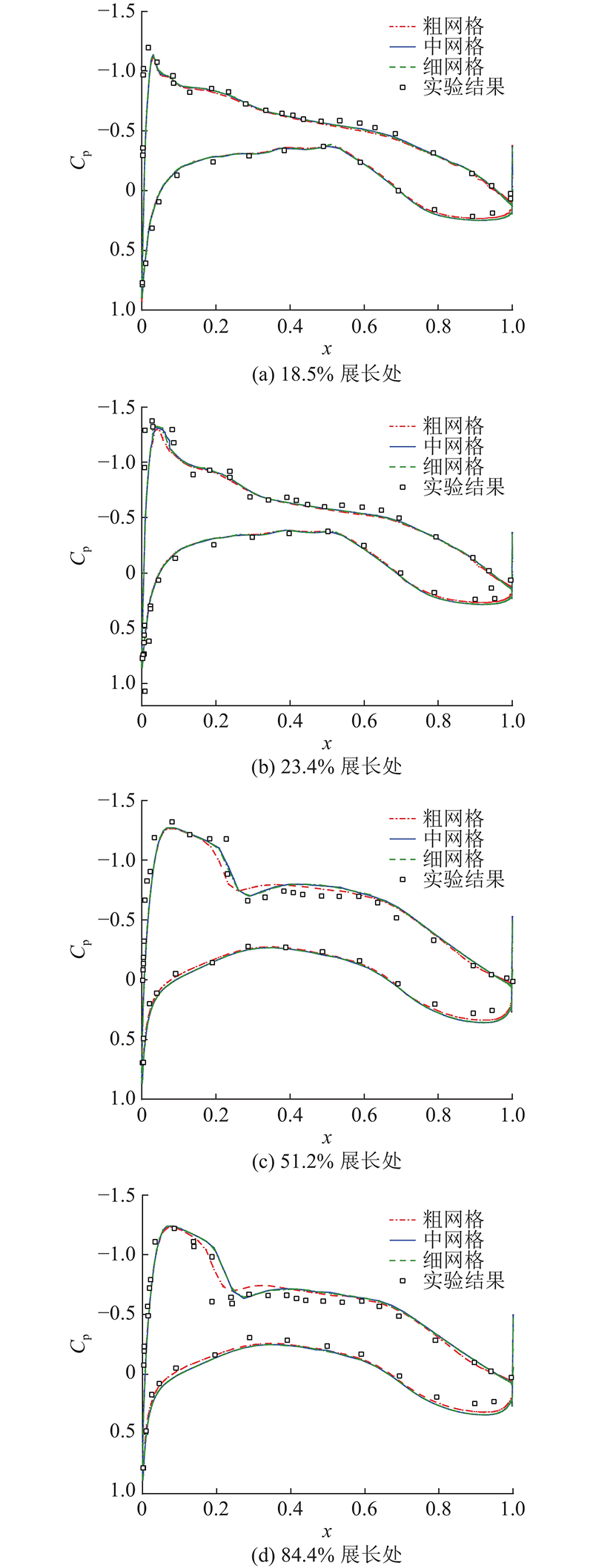
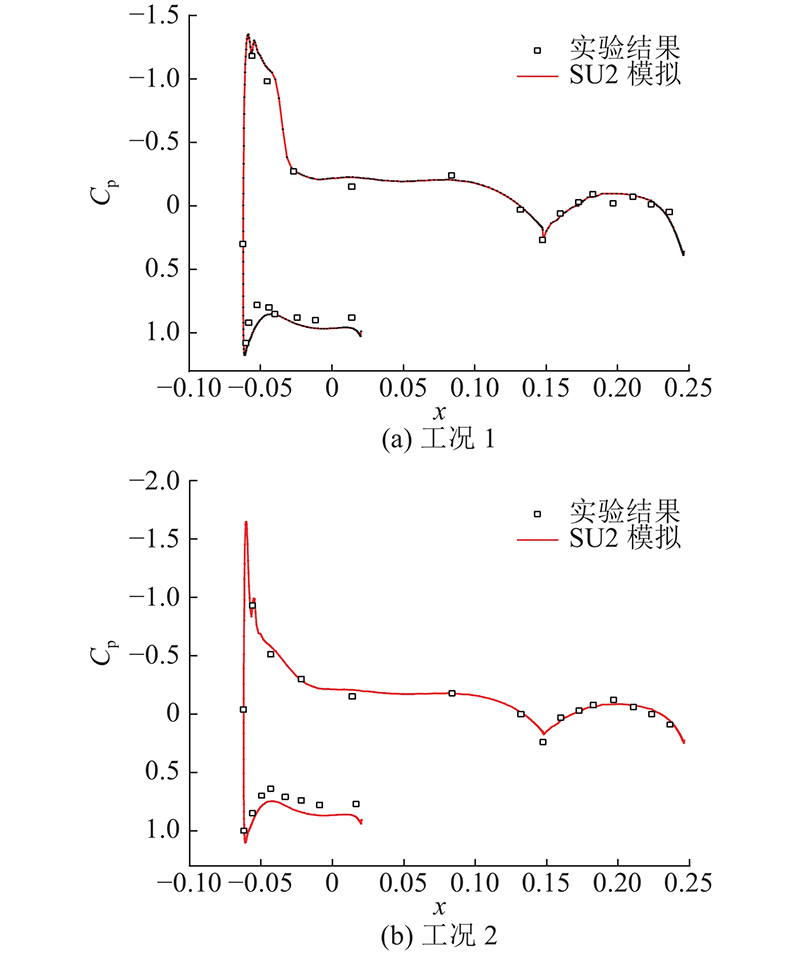
... 为了验证短舱边界条件简化处理的正确性,在2种工况下对隔离发动机短舱模型NAL-AERO-02-01进行数值模拟,模型采用T-Rex非结构网格划分,壁面层第1层网格厚度设为2.5×10−6 m,以确保y + <1,黏性层网格增长率设为1.2,总网格数为3.48×106 . NAL-AERO-02-01是日本航天技术研究所的隔离涡扇发动机模型[23 ] . 模型具体参数及工况见文献[23 ]. 如图8 所示为NAL-AERO-02-01几何模型在短舱风扇罩、进气道和核心机整流罩处的压力系数分布,计算结果与文献[23 ]的实验数据符合良好,短舱边界条件处理的合理性得到验证. ...
... . 模型具体参数及工况见文献[23 ]. 如图8 所示为NAL-AERO-02-01几何模型在短舱风扇罩、进气道和核心机整流罩处的压力系数分布,计算结果与文献[23 ]的实验数据符合良好,短舱边界条件处理的合理性得到验证. ...
... 所示为NAL-AERO-02-01几何模型在短舱风扇罩、进气道和核心机整流罩处的压力系数分布,计算结果与文献[23 ]的实验数据符合良好,短舱边界条件处理的合理性得到验证. ...