浙江大学学报(工学版)

浙江大学学报(工学版), 2023, 57(1): 10-20 doi: 10.3785/j.issn.1008-973X.2023.01.002

机械与能源工程

基于LSTM与牛顿迭代的两轴系统轮廓误差控制

黄华,, 赵秋舸, 何再兴, 李嘉然

1. 兰州理工大学 机电工程学院，甘肃 兰州 730050

2. 浙江大学 机械工程学院，浙江 杭州 310027

Contour error control of two-axis system based on LSTM and Newton iteration

HUANG Hua,, ZHAO Qiu-ge, HE Zai-xing, LI Jia-ran

1. School of Mechanical and Electronical Engineering, Lanzhou University of Technology, Lanzhou 730050, China

2. School of Mechanical Engineering, Zhejiang University, Hangzhou 310027, China

收稿日期: 2022-08-9  

基金资助: 国家自然科学基金资助项目(51965037，51565030)

Received: 2022-08-9  

Fund supported: 国家自然科学基金资助项目(51965037，51565030)

作者简介 About authors

黄华（1978—），男，副教授，博导，从事数控技术的研究.orcid.org/0000-0002-4945-5888.E-mail：hh318872@126.com , E-mail：hh318872@126.com

摘要

针对轮廓误差影响运动系统精度的问题，提出结合长短期记忆神经网络(LSTM)和牛顿迭代法对轮廓误差进行预测、通过转换任务坐标系对轮廓误差进行补偿的方法. 在运动平台上提取特征轮廓与数据，将牛顿迭代法应用于对轮廓误差的计算，通过计算出的轮廓误差对优化后的LSTM神经网络进行训练，建立更准确的轮廓误差预测模型. 通过转换任务坐标系，将预测的轮廓误差作为前馈补偿到参考轮廓中，提高轮廓控制性能. 通过试验对比PID、迭代法和神经网络法，利用随机NRBUS轨迹验证泛化性，表明提出的方法能够有效地预测并控制轮廓误差，在精密运动控制领域有良好的应用前景.

关键词： 两轴运动控制 ; 轮廓误差 ; 长短期记忆神经网络 ; 前馈补偿

Abstract

An approach of contour error prediction based on long short-term memory neural network (LSTM) and Newton iteration and the contour error compensation by transforming the task coordinate system was proposed in order to address the problem that the accuracy of two-axis motion was affected by contour error. The feature contour and data were extracted from the control system of the two-axis motion platform, and the contour error was obtained by Newton’s method, which was employed as the training data of LSTM neural network. Then a more accurate prediction model of contour error was obtained. The predicted contour error was compensated to the reference contour through feedforward control by transforming the task coordinate system so as to improve the contour control performance. The random NRBUS curve was used to verify its generalization by comparing PID, ILC and neural network. The experimental results show that the proposed approach can effectively predict and control the contour error, and has good potential application value in the precision motion control.

Keywords： two-axis motion control ; contour error ; long short-term memory neural network ; feedforward compensation

PDF (2998KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

黄华, 赵秋舸, 何再兴, 李嘉然. 基于LSTM与牛顿迭代的两轴系统轮廓误差控制. 浙江大学学报(工学版)[J], 2023, 57(1): 10-20 doi:10.3785/j.issn.1008-973X.2023.01.002

HUANG Hua, ZHAO Qiu-ge, HE Zai-xing, LI Jia-ran. Contour error control of two-axis system based on LSTM and Newton iteration. Journal of Zhejiang University(Engineering Science)[J], 2023, 57(1): 10-20 doi:10.3785/j.issn.1008-973X.2023.01.002

现代制造技术的发展对精密运动系统的要求日益提高，而轮廓误差控制作为加工质量的关键指标，是多轴精密运动控制的核心技术之一，需要通过复杂的计算得出[1]. 轮廓误差与不同轴之间的动力学关系不匹配密切相关，需要通过轮廓误差补偿来补偿这种不匹配. 在进行轮廓控制时，需要考虑轮廓误差估计和轮廓误差补偿2个方面.

在轮廓误差估计方面，主要有几何法和解析法2种. 几何法简单便捷，但当运动系统执行高速大曲率运动时会出现严重的轮廓误差估计偏差[2]. 解析法作为几何法的深入扩展，能够更准确地计算轮廓误差[3]. 轮廓误差的定义为实际位置到参考轮廓的最短距离，本质为极值的求解，因此可以通过极值搜索的方法来求解轮廓误差. Wang等[4]利用牛顿迭代实现了精确求解轮廓误差，在高速大曲率处不失真，但在参考轮廓不同的情况下需要重新迭代，实际应用有一定的困难.

在轮廓误差控制方面，根据控制方式的不同，可以分为反馈控制和前馈控制2类. 反馈控制利用轮廓误差的实时估计结果进行轮廓控制. 反馈控制中应用最广泛的是Koren[5]提出的交叉耦合控制(cross couple control，CCC)，胡楚雄等[6-7]结合CCC与各种先进控制方法，取得了一定的效果，但在执行高速大曲率轮廓时，存在较大的偏差，而且增益参数难以确定，控制算法复杂，设计难度较大[2]. 前馈控制不依赖误差的实时估计，可以通过预补偿来抑制轮廓误差. Zhang等[8]通过求解伺服系统的逆向模型对轮廓误差进行建模，通过修正插补轨迹减小轮廓误差. 利用神经网络良好的逼近能力，能够构造复杂的非线性模型和预测非线性系统的输出，因此神经网络与前馈控制相结合并广泛应用于对机械手的控制，在多轴轮廓运动中的研究较少. Chen等[9]提出结合迭代学习和神经网络的方法，利用参考轮廓和相应的轨迹输入训练神经网络，预测并补偿跟踪误差. Huo等[10]利用非线性自回归网络(nonlinear auto regressive model with exogenous inputs，NARX)预测下一时刻的输出位置，实时估计轮廓误差进行补偿. Hu等[11]利用GRU神经网络对多轴运动系统的轮廓误差进行预测，将预测的轮廓误差作为预补偿，实现了对轮廓误差的控制. 轮廓误差与运动参数并非简单的映射关系，各种扰动对轮廓误差的影响不仅与当前时刻的运动状态有关，还与过去和未来时刻的运动状态相关. 考虑LSTM神经网络作为特殊的递归神经网络(recursive neural network，RNN)，在序列对序列响应的模型拟合方面具有优异的性能，近年来在语音识别和语言处理相关领域得到了广泛的应用. 通过向标准RNN中添加长期记忆序列来容纳长期和短期记忆，解决了RNN存在长期依赖性、经常出现梯度消失和梯度爆炸等问题.

综上所述，利用神经网络对多轴运动的轮廓误差预测有着良好的优势，但由于训练特征选取单一，训练数据缺乏有效性，映射关系简单，导致神经网络对轮廓误差预测不精确，影响轮廓误差的控制效果. 为了提高多轴运动系统对非线性轮廓的轮廓精度，本文提出结合LSTM神经网络与牛顿迭代法预测轮廓误差、通过转换任务坐标系补偿轮廓误差的方法.

1. 两轴进给系统的动态特性建模

从机构刚度、运行可靠性和经济性等方面考虑，滚珠丝杠有着较大的优势. 选择滚珠丝杠机构作为试验平台.

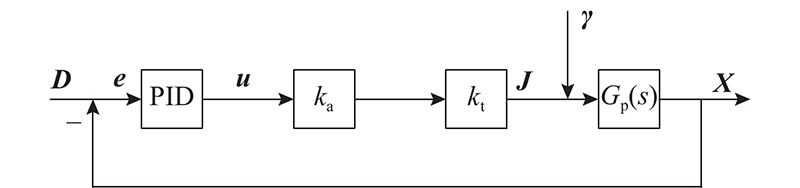
为了便于控制轮廓误差，将滚珠丝杠进给系统中的丝杠与螺母之间的动力学关系用弹性阻尼环节代替. 在两轴进给系统中，联轴器具有较大的刚度，但产生的偏移量不可忽略，通过进给系统的闭环控制可以有效地解决该问题. 在建立单轴进给系统动力学模型时，将电机转子、滚珠丝杠、支撑轴承和联轴器认为是刚性连接，将单轴进给系统中的摩擦视为外接干扰γ，得到单轴系统动力学简化模型，如图1所示. 图中，k为推力系数，m为惯性系数，b为黏滞摩擦系数. 单轴动力学方程表示为

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   单轴伺服系统动力学模型

Fig.1   Dynamic model of uniaxial servo system


$ m{{\ddot {\boldsymbol{x}}}}+b{{\dot {\boldsymbol{x}}}} = k{\boldsymbol{u}}+{\boldsymbol{\gamma}} . $
(1)

式中：x、u分别为实际位置和控制器输出. 将式(1)进行拉普拉斯变换，得到被控对象的线性模型:

$ {G_{{\rm{p}}}}(s) = \frac{k}{{m{s^2}+bs}} . $
(2)

单轴伺服驱动进给系统采用全闭环控制，其中伺服控制环由内往外分别为电流环、速度环、位置环. 由于直接选用工业级伺服电机与驱动器，控制系统采用相对封闭的技术封装，保证系统的稳定性及可靠性，难以对内部封装的控制算法及控制器结构进行调整. 选用伺服驱动器所采用的PID控制作为基础的闭环反馈控制方法，采用光栅尺作为位置反馈输入，电机、伺服驱动器和光栅尺形成闭环，如图2所示.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   进给伺服系统的控制模型

Fig.2   Control model of feed servo system


跟踪误差e为期望位置D与实际位置X之间的偏差. PID控制器的传递函数为

$ {G_{{\rm{c}}}}(s) = {k_{{\rm{p}}}}+{k_{{\rm{i}}}}/s+{k_{{\rm{d}}}}s . $
(3)

式中：kp为比例增益系数，ki为积分增益系数，kd为微分增益系数. 控制器产生的控制信号由驱动器进行线性放大后作为电机的输入，放大倍数为ka、kt. 滚珠丝杠伺服进给系统的线性定常系统的传递函数为

$ G(s) = \frac{{({k_{{\rm{p}}}}s+{k_{{\rm{i}}}}+{k_{{\rm{d}}}}{s^2}) {k_{{\rm{a}}}}{k_{{\rm{t}}}}}}{{m{s^3}+(b+{k_{{\rm{a}}}}{k_{{\rm{t}}}}{k_{{\rm{d}}}}){s^2}+{k_{{\rm{a}}}}{k_{{\rm{t}}}}{k_{{\rm{p}}}}s+{k_{{\rm{a}}}}{k_{{\rm{t}}}}{k_{{\rm{i}}}}}} . $
(4)

利用无偏差最小二乘法进行系统辨识，对电机转动惯量、黏滞阻尼、弹簧刚度系数、弹簧阻尼系数和Stribeck摩擦模型中的库仑摩擦力进行辨识，得到两轴运动平台各轴线性系统的辨识结果如下:

$ X轴: {G_{{{x}}}} = \frac{{95.34{s^{2}}+7\;177s+143}}{{{s^{3}}+149{s^{2}}+7\;179s+132.3}} , $
(5)

$ Y轴: {G_{{{y}}}} = \frac{{ - 975.6{s^{2}}+243\;200s+709.5}}{{{s^{3}}+942.7{s^{2}}+243\;200s+584.6}} . $
(6)

试验平台如图3所示. 采用Beckhoff工控机作为控制器，通过与之配套的TwinCAT3软件实时控制伺服系统，伺服系统选用OMRON工业伺服驱动器和电机，采用外部光栅作为位置反馈.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   两轴运动系统

Fig.3   Two-axis motion system


2. 基于牛顿迭代学习的轮廓误差估计

轮廓误差与可以直接测量得出的跟踪误差不同，需要通过复杂的计算求解，计算的准确性对轮廓误差控制至关重要. 轮廓误差的计算本质为极值的求解问题，将求解非线性方程极值的牛顿迭代法应用于轮廓误差的计算. 与现在广泛使用的几何法相比，可以在提高轮廓误差的计算准确度的同时，克服几何法在大曲率点处轮廓误差计算失真的问题.

迭代学习控制(ILC)，即系统通过多次执行同一任务并从多次迭代的误差(试验、迭代、补偿)中学习，以提高运动控制性能，因此每次迭代的初始条件必须相同. 在二维轮廓控制中，将已知参考轮廓按时间参数化，将t时刻的期望位置与实际位置分别表示为 $ {\boldsymbol{D}}({{t}}) $与 $ {\boldsymbol{X}}{{(}}{{t}}) $，表达形式如下：

$ {\boldsymbol{D}}({{t}}) = {[{{{d}}_1}({{t}}),{{{d}}_2}({{t}})]^{{\rm{T}}}} , $
(7)

$ {\boldsymbol{X}}({{t}}) = {[{{{x}}_1},{{{x}}_2}]^{{\rm{T}}}} . $
(8)

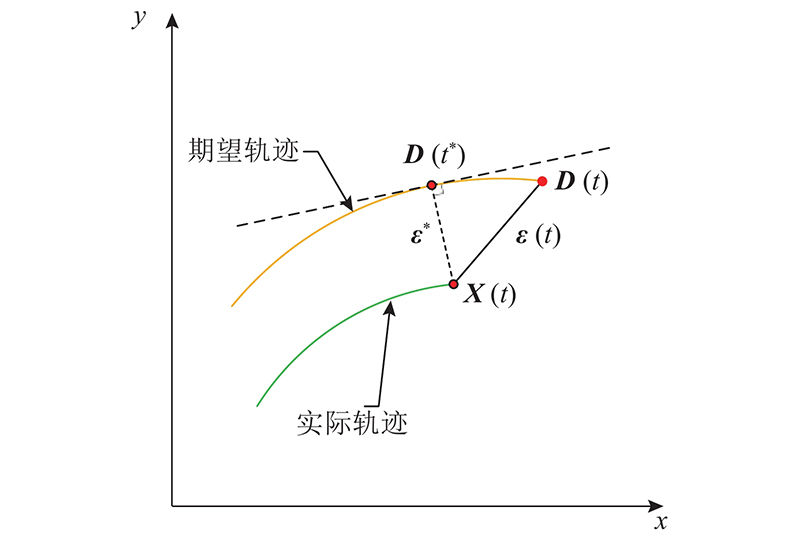
两轴平台轮廓误差示意图，如图4所示. 将 ${\boldsymbol{\varepsilon }}({{\hat {{t}}}})$定义为t时刻期望位置与实际位置之间的距离，即

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   两轴平台轮廓误差的示意图

Fig.4   Schematic diagram of contour error of two axis platform


$ {\boldsymbol{\varepsilon }}({{\hat {{t}}}}) = {\boldsymbol{D}}({{t}}{)} - {\boldsymbol{X}}({{t}}) . $
(9)

假设 $ {\boldsymbol{\varepsilon }}({{\hat {{t}}}}) $的最小值在 $ {{{t}}^*} $处，最小距离为 ${{\boldsymbol{\varepsilon}}^{\rm{*}}}$，

$ {{\boldsymbol{\varepsilon }}^*} = {\boldsymbol{D}}({{{t}}^*}) - {\boldsymbol{X}}({{t}}) . $
(10)

式中： ${\boldsymbol{D}}({{{t}}^*})$为轮廓误差点. 为了方便计算，定义代价函数为

$ {{E}}({\hat {{t}}}) = \frac{1}{2}{{\left\| {{\boldsymbol{\varepsilon}}({\hat {{t}}})} \right\|}^2} . $
(11)

式中： $ \left\| {{\boldsymbol{\varepsilon }}({{\hat {{t}}}})} \right\| $为 $ {\boldsymbol{\varepsilon }}({{\hat {{t}}}}) $的欧几里得范数，

$ {\left\| {{\boldsymbol{\varepsilon }}({{\hat {{t}}}})} \right\|^2}{{ = }}\sum\limits_{i = 1}^n {{{\varepsilon }}_i^2} . $
(12)

代价函数的最小值与 $ {{\boldsymbol{\varepsilon }}^*} $和 $ {{{t}}^{\rm{*}}} $有关，采用牛顿迭代法计算代价函数的最小值，得到轮廓误差. 假设代价函数E存在非零的二次导数，导数为零处即为最小值，利用泰勒展开得到E的二次导数，即在 $ {{E}}({{\hat {{t}}}}) $处导数的切线方程为

$ {{\dot {{E}}}}({{t}}) = {{\dot {{E}}}}({{\hat {{t}}}})+{{\ddot {{E}}}}({{\hat {{t}}}}) ({{t}} - {{\hat {{t}}}}) . $
(13)

式中： $ {{\dot {{E}}}} $和 $ {{\ddot {{E}}}} $分别为 $ {{E}} $的一阶导数和二阶导数. 当 $ {{\dot {{E}}}} = 0 $时轮廓误差为极值，设 $ {{\dot {{E}}}} = 0 $，得到牛顿算法的递推公式:

$ {{{t}}_{{{{{i}}+}}1}} = {{{t}}_{{i}}} - \frac{{{{\dot {{E}}}}({{{t}}_{{i}}})}}{{{{\ddot {{E}}}}({{{t}}_{{i}}})}} . $
(14)

式中： ${{i}}$为迭代次数. 为了验证牛顿算法的收敛性，假设

$ {{s}}({{{t}}_{{i}}}) = {{{t}}_{{i}}} - \frac{{{{\dot {{E}}}}({{{t}}_{{i}}})}}{{{{\ddot {{E}}}}({{{t}}_{{i}}})}} . $
(15)

得到

$ \begin{split} {{\dot {{s}}}}({{{t}}_{{i}}}) =& 1 - \frac{{{{\ddot {{E}}}}({{{t}}_{{i}}}) {{\ddot {{E}}}}({{{t}}_{{i}}}) - {{\dot {{E}}}}({{{t}}_{{i}}}) {{\dddot {{E}}}}({{{t}}_{{i}}})}}{{{{[{{\ddot {{E}}}}({{{t}}_{{i}}})]}^2}}} = \\ & \frac{{{{\dot {{E}}}}({{{t}}_{{i}}}) {{\dddot {{E}}}}({{{t}}_{{i}}})}}{{{{[{{\ddot {{E}}}}({{{t}}_{{i}}})]}^2}}} . \\ \end{split} $
(16)

将 ${{s}}({{{t}}_{{i}}})$泰勒展开，得到

$ {{s}}({{{t}}_{{i}}}) = {{s}}({{{t}}^*})+{{\dot {{s}}}}({{{t}}^*}) ({{{t}}_{{i}}} - {{{t}}^*})+\frac{1}{2}{{\ddot {{s}}}}({{{t}}^*}) {{{t}}^*} {({{{t}}_{{i}}} - {{{t}}^*})^2}+{{\sigma}} . $
(17)

式中： $ {{\sigma}} $为高阶无穷小. $ {{\dot {{E}}}}({{{t}}^*}) = 0 $， $ {{s}}({{{t}}^*}) = 0 $， $ {{\dot{{s}}}}({{{t}}^*}) = 0 $，可得

$ \frac{{{{{t}}_{{{i}}+1}} - {{{t}}^*}}}{{{{({{{t}}_{{i}}} - {{{t}}^*})}^2}}} = \frac{1}{2}{{\ddot {{s}}}}({{{t}}^*})+\frac{{{\sigma }}}{{{{({{{t}}_{{i}}} - {{{t}}^*})}^2}}} = 0 = {{c}} . $
(18)

式中： ${{\sigma}}/{({{{t}}_{{i}}} - {{{t}}^*})^2}$可以省略， $0.5{{\ddot {{s}}}}({{{t}}^*})$为有界常数. 由收敛定理验证可得， ${{s}}({{{t}}_{{i}}})$即牛顿算法二阶收敛. 根据式(9)，可得

$ {{\dot {\boldsymbol{\varepsilon}} }}({{\hat {{t}}}}) = {{\dot {\boldsymbol{D}}}}({{\hat {{t}}}}) , $
(19)

$ {{\dot {{E}}}}({{\hat {{t}}}}) = {\boldsymbol{\varepsilon }}({{\hat {{t}}}}) \cdot {{\dot {\boldsymbol{\varepsilon}} }}({{\hat {{t}}}}) = {\boldsymbol{\varepsilon }}({{\hat {{t}}}}) \cdot {{\dot {\boldsymbol{D}}}}({{t}}) , $
(20)

$ {{\ddot {{E}}}}({{\hat {{t}}}}) = {\boldsymbol{\varepsilon }}({{\hat {{t}}}}) \cdot {{\ddot {\boldsymbol{D}}}}({{\hat {{t}}}})+{\left\| {{{\dot {\boldsymbol{D}}}}({{\hat {{t}}}})} \right\|^2} . $
(21)

假设 $ {\boldsymbol{\varepsilon }} $足够小且加速度不大，则可将 ${\boldsymbol{\varepsilon }}({{\hat {{t}}}}) \cdot{{\ddot {\boldsymbol{D}}}}({{\hat {{t}}}})$忽略不计，得到

$ {{\ddot {{E}}}}({{\hat {{t}}}}) \approx {\left\| {{{\dot {\boldsymbol{D}}}}({{\hat {{t}}}})} \right\|^2} , $
(22)

$ {{{t}}_{{{i}}+1}} = {{{t}}_{{i}}} - \frac{{{{\dot {{E}}}}({{{t}}_{{i}}})}}{{{{\ddot {{E}}}}({{{t}}_{{i}}})}} = {{{t}}_{{i}}} - \frac{{\left( {{{{\boldsymbol{D}}}}({{{t}}_{{i}}}) - {{{\boldsymbol{X}}}}({{{t}}_{{i}}})} \right) \cdot {{\dot {{{\boldsymbol{D}}}}}}({{{t}}_{{i}}})}}{{{{\left\| {{{\dot {{{\boldsymbol{D}}}}}}({{{t}}_{{i}}})} \right\|}^2}}} . $
(23)

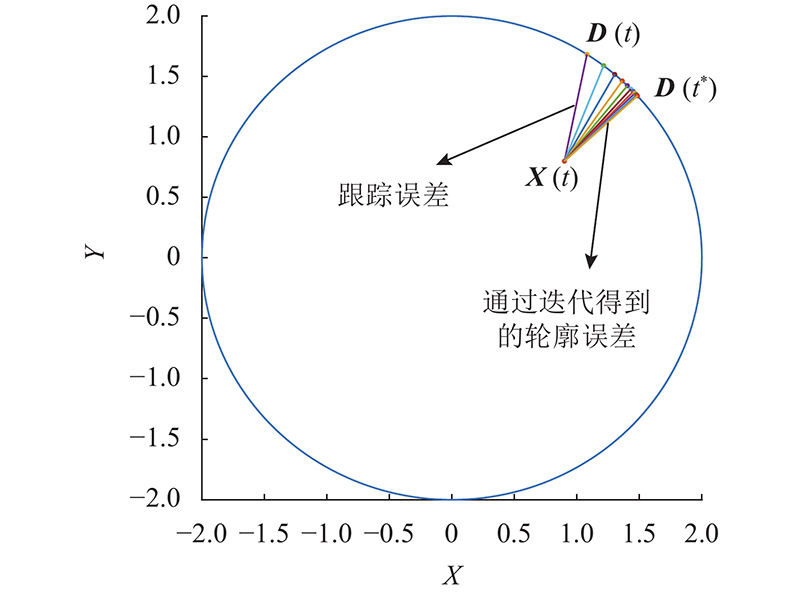
从式(23)可知，通过期望速度、期望位置和实际位置，利用牛顿算法可以计算轮廓误差. 通过不断迭代，可得准确的轮廓误差. 利用牛顿迭代法求解圆的轮廓误差的仿真试验如图5所示. 利用式(23)开展仿真试验，参考位置与实际位置间轮廓误差的理论值为0.795 8，跟踪误差为0.918 7，迭代次数为10. 从图5可以看出，在从跟踪误差 ${\boldsymbol{D}}({{t}}) - {\boldsymbol{X}}({{t}})$向轮廓误差 ${\boldsymbol{D}}({{t}^*})-{\boldsymbol{X}}({{{t}}})$迭代的过程中，迭代4次后逐渐趋于稳定. 表1中，i为迭代次数. 从表1可知，前4次迭代后轮廓误差计算值变化较大，迭代到第7次以后轮廓误差计算值变化微小. 综上分析可知，当利用牛顿迭代法计算轮廓误差时，迭代4~7次后可以得到相对准确的轮廓误差.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   轮廓误差估计的仿真试验

Fig.5   Simulation test of contour error estimation


表 1   轮廓误差计算的仿真结果

Tab.1  Simulation results of contour error calculation

${{i} }$ $\|{\boldsymbol{\varepsilon } }({ {\hat {{t} } } })\|$ ${{i} }$ $\| {\boldsymbol{\varepsilon } }({ {\hat {{t} } } })\|$
1 0.918 7 6 0.796 4
2 0.861 3 7 0.795 9
3 0.820 9 8 0.795 4
4 0.798 8 9 0.795 4
5 0.797 1 10 0.795 4

新窗口打开| 下载CSV


将牛顿迭代法与传统轮廓误差计算方法(几何法)进行对比，验证牛顿迭代法对轮廓误差计算的准确性.

3. 基于LSTM神经网络的轮廓误差离线预测

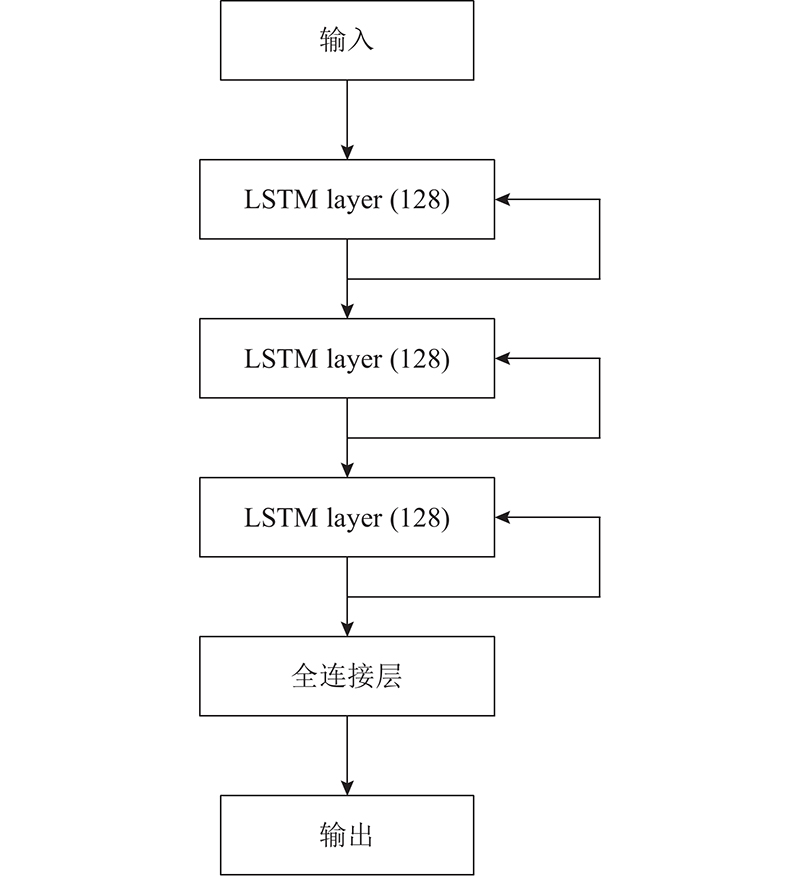
利用牛顿迭代法计算重复轮廓的轮廓误差有着显著的优势，在经过多次迭代后可以计算得出相对准确的轮廓误差. 若改变参考轮廓或初始条件，则需要重新迭代，这在实际应用中会相当耗时. 神经网络对非线性系统的拟合有着很好的优势，与迭代法相比，利用神经网络对轮廓误差进行预测，将极大地缩短时间，具有良好的泛化性. 目前利用神经网络对轮廓误差进行预测时，由于训练特征选取的单一性，训练数据缺乏有效性，映射关系简单，对轮廓误差预测不精确. 结合优化后的LSTM神经网络与牛顿迭代，利用LSTM神经网络对轮廓误差动态模型进行建模. 采用牛顿迭代法计算出的轮廓误差作为神经网络的训练输出数据，对优化后的LSTM神经网络进行训练. 训练好的LSTM神经网络在不需要通过实际的运动信息和离线迭代的情况下，仅通过输入已知数据就可以预测出轮廓误差且和牛顿迭代法达到相当的精度. 该方法弥补了牛顿迭代法单一耗时的缺点，具有很好的泛化性. LSTM神经网络框图如图6所示.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6   LSTM神经网络框架

Fig.6   LSTM neural network framework


3.1. 基于LSTM神经网络的轮廓误差预测模型

将数据集分为训练集与验证集，合理的选择对神经网络训练起着至关重要的作用. 训练集用于训练神经网络，验证集是在一定的训练频率下对神经网络进行损失验证. 有效的训练数据能够涵盖绝大部分的特征空间. 本文所考虑的特征包括速度、加速度、位置，要求训练轨迹既能够涵盖速度规划的最大速度−100~100 mm/s，也包含丰富的尖角、反向越冲、动态响应等特征. NURBS曲线作为工业制造中广泛应用的插补轨迹，利用程序实现随机NURBS曲线生成. 因插补点的随机性，包含丰富的轨迹特征，特征在各个轴之间分布均匀，所以利用随机NURBS曲线作为数据集是较好的选择.

使用随机点生成随机NURBS二维路径，该路径由自变量 $ {{t}} $和因变量 $ {{y}} $组成，路径描述如下：

$ \left. \begin{array}{l} \begin{split}& {{t}} = \{0,1,2, \cdots ,14\}, \\& {{y}} \sim {\rm{N}}(\mu ,{\sigma ^2}) . \end{split} \end{array} \right\} $
(24)

设 $ \;\mu = 50 $， $ \sigma = 10 $，在随机点序列 $f( t, y)$上进行5次Hermite样条插值以保证加速度连续，以1 kHz频率采样以获得参考轮廓. 参考轮廓被输入到倍福控制器，获得两轴的理论速度、理论加速度和理论位置. 将得到的数据集中的前75%作为训练集，后25%为验证集，如图6所示. LSTM神经网络在t时刻的前向传播公式为

$ \left. \begin{array}{l} {{\boldsymbol{f}}^{\langle t\rangle }} = {\boldsymbol{\sigma }}({{{\boldsymbol{\tilde f}}}^{\langle t\rangle }}) = {\boldsymbol{\sigma }}({{\boldsymbol{W}}^{xf}}{{\boldsymbol{X}}^{\langle t\rangle }} + {{\boldsymbol{W}}^{hf}}{{\boldsymbol{H}}^{\langle t\rangle }} + {{\boldsymbol{b}}_f}),\\ {{\boldsymbol{i}}^{\langle t\rangle }} = {\boldsymbol{\sigma }}({{{\boldsymbol{\tilde i}}}^{\langle t\rangle }}) = {\boldsymbol{\sigma }}({{\boldsymbol{W}}^{xi}}{{\boldsymbol{X}}^{\langle t\rangle }} + {{\boldsymbol{W}}^{hi}}{{\boldsymbol{H}}^{\langle t\rangle }} + {{\boldsymbol{b}}_i}),\\ {{\boldsymbol{g}}^{\langle t\rangle }} = \tanh \; ({{{\boldsymbol{\tilde g}}}^{\langle t\rangle }}) = \tanh \; ({{\boldsymbol{W}}^{xg}}{{\boldsymbol{X}}^{\langle t\rangle }} + {{\boldsymbol{W}}^{hg}}{{\boldsymbol{H}}^{\langle t\rangle }} + {{\boldsymbol{b}}_g}),\\ {{\boldsymbol{o}}^{\langle t\rangle }} = {\boldsymbol{\sigma }}({{{\boldsymbol{\tilde o}}}^{\langle t\rangle }}) = {\boldsymbol{\sigma }}({{\boldsymbol{W}}^{xo}}{{\boldsymbol{X}}^{\langle t\rangle }} + {{\boldsymbol{W}}^{ho}}{{\boldsymbol{H}}^{\langle t\rangle }} + {{\boldsymbol{b}}_o}),\\ {{\boldsymbol{C}}^{\langle t\rangle }} = {{\boldsymbol{C}}^{\langle t - 1\rangle }} \odot {{\boldsymbol{f}}^{\langle t\rangle }}_t + {{\boldsymbol{g}}^{\langle t\rangle }} \odot {{\boldsymbol{i}}^{\langle t\rangle }},\\ {{\boldsymbol{m}}^{\langle t\rangle }} = \tanh \; ({{\boldsymbol{C}}^{\langle t\rangle }}),\\ {{\boldsymbol{h}}^{\langle t\rangle }} = {{\boldsymbol{o}}^{\langle t\rangle }} \odot {{\boldsymbol{m}}^{\langle t\rangle }},\\ {{\boldsymbol{Y}}^{\langle t\rangle }} = {{\boldsymbol{W}}^{yh}}{{\boldsymbol{h}}^{\langle t\rangle }} + {{\boldsymbol{b}}_y}. \end{array} \right\} $
(25)

式中： $ {{\boldsymbol{c}}_i} $为记忆细胞， $ {{\boldsymbol{h}}_i} $为状态， $ {\boldsymbol{\sigma}} $为门单元， $ {{\boldsymbol{f}}^{\langle t\rangle }} $为遗忘门， $ {{\boldsymbol{i}}^{\langle t\rangle }} $为更新门， $ {{\boldsymbol{o}}^{\langle t\rangle }} $为输出门， $ {\boldsymbol{W}} $为权重， $ {\boldsymbol{b}} $为偏差. 为了找到使损失函数最优化的 $ {{\boldsymbol{W}}^f} $、 $ {{\boldsymbol{W}}^i} $、 $ {{\boldsymbol{W}}^g} $、 $ {{\boldsymbol{W}}^o} $，定义损失函数为

$ {{{E}}^{\langle t\rangle }} = \frac{1}{2}{\left\| {{{\boldsymbol{Y}}^{\langle t\rangle }} - {{\boldsymbol{Y}}_{\rm{d}}}^{\langle t\rangle }} \right\|^2} . $
(26)

式中： ${{\boldsymbol{Y}}_{\rm{d}}}^{\langle t\rangle }$为 $ t $时刻的期望输出. 连续时间 $ T $内的总损耗函数为 ${{E}} = \displaystyle \sum\nolimits_t^T {{{{E}}^{\langle t\rangle }}}$， $ t $时刻输入门的梯度为

$ \frac{{\partial {{E}}}}{{\partial {{{{W}}_{jk}^i}}}}{{ = }}\frac{{\partial {{E}}}}{{\partial {{C}}_j^{\langle t\rangle }}}\frac{{\partial {{C}}_j^{\langle t\rangle }}}{{\partial {{i}}_j^{\langle t\rangle }}}\frac{{\partial {{i}}_j^{\langle t\rangle }}}{{\partial {{a}}_j^i}}\frac{{\partial a_j^i}}{{\partial {{{{W}}_{jk}^i}}}} \;. $
(27)

式中： ${{{W}}_{jk}^i }$为 ${{{{{\boldsymbol{W}}}}^i}}$第 $ k $行 $ j $列的元素. $ t $时刻输出门的梯度为

$ \frac{{\partial {{E}}}}{{\partial {{{{W}}_{jk}^o}}}}{{ = }}\frac{{\partial {{E}}}}{{\partial {{o}}_j^{\langle t\rangle }}}\frac{{\partial {{o}}_j^{\langle t\rangle }}}{{\partial {{a}}_j^o}}\frac{{\partial {{a}}_j^o}}{{\partial {{{{W}}_{jk}^o}}}} \;. $
(28)

式中： ${{{W}}_{jk}^o}$为 ${{{{\boldsymbol{W}}}}_{}^o}$第 $ k $行 $ j $列的元素. $ t $时刻记忆细胞的梯度为

$ \frac{{\partial {{E}}}}{{\partial {{{{W}}_{jk}^g}}}}{{ = }}\frac{{\partial {{E}}}}{{\partial {{C}}_j^{\langle t\rangle }}}\frac{{\partial {{C}}_j^{\langle t\rangle }}}{{\partial {{\tilde {{C}}}}_j^{\langle t\rangle }}}\frac{{\partial {{\tilde {{C}}}}_j^{\langle t\rangle }}}{{\partial {{a}}_j^g}}\frac{{\partial {{a}}_j^g}}{{\partial {{{{W}}_{jk}^g}}}} \;. $
(29)

式中： $ {{{W}}_{jk}^g} $为 ${{{{\boldsymbol{W}}}}_{}^g}$第 $ k $行 $ j $列的元素. $ t $时刻遗忘门的梯度为

$ \frac{{\partial {{E}}}}{{\partial {{{{W}}_{jk}^f}}}}{\rm{ = }}\frac{{\partial {{E}}}}{{\partial {{C}}_j^{\langle t\rangle }}}\frac{{\partial {{C}}_j^{\langle t\rangle }}}{{\partial {{f}}_j^{\langle t\rangle }}}\frac{{\partial {{f}}_j^{\langle t\rangle }}}{{\partial {{a}}_j^f}}\frac{{\partial {{a}}_j^f}}{{\partial {{{{W}}_{jk}^g}}}} \;. $
(30)

式中： $ {{{W}}_{jk}^f} $为 ${{{{\boldsymbol{W}}}}_{}^f}$第 $ k $行 $ j $列的元素，在连续时间 $ T $中有

$ \dfrac{\partial {E}}{\partial {\boldsymbol{W}}^{o}}={\displaystyle \sum _{t=1}^{T}\dfrac{\partial {E}}{{(\partial {\boldsymbol{W}}^{o})}^{\langle t\rangle }}}, \;\;\; \dfrac{\partial {E}}{\partial {\boldsymbol{W}}^{i}} ={\displaystyle \sum _{t=1}^{T}{\dfrac{\partial {E}}{{(\partial {\boldsymbol{W}}^{i})}^{\langle t\rangle }}}},$
(31)

$ \dfrac{\partial {E}}{\partial {\boldsymbol{W}}^{g}}={\displaystyle \sum _{t=1}^{T}\dfrac{\partial {E}}{{(\partial {\boldsymbol{W}}^{g})}^{\langle t\rangle }}}, \;\;\; \dfrac{\partial {E}}{\partial {\boldsymbol{W}}^{f}} ={{\displaystyle \sum _{t=1}^{T}\dfrac{\partial {E}}{{(\partial {\boldsymbol{W}}^{f})}^{\langle t\rangle }}}}. $
(32)

定义 $ \alpha $为正学习率，权重 $ {{\boldsymbol{W}}^f} $、 $ {{\boldsymbol{W}}^i} $、 $ {{\boldsymbol{W}}^g} $、 $ {{\boldsymbol{W}}^o} $的更新公式分别为

$ {{\boldsymbol{W}}^f} = {{\boldsymbol{W}}^f} - \alpha \frac{{\partial {{E}}}}{{\partial {{\boldsymbol{W}}^f}}} , $
(33)

$ {{\boldsymbol{W}}^i} = {{\boldsymbol{W}}^i} - \alpha \frac{{\partial {{E}}}}{{\partial {{\boldsymbol{W}}^i}}} , $
(34)

$ {{\boldsymbol{W}}^g} = {{\boldsymbol{W}}^g} - \alpha \frac{{\partial {{E}}}}{{\partial {{\boldsymbol{W}}^g}}} , $
(35)

$ {{\boldsymbol{W}}^o} = {{\boldsymbol{W}}^o} - \alpha \frac{{\partial {{E}}}}{{\partial {{\boldsymbol{W}}^o}}} . $
(36)

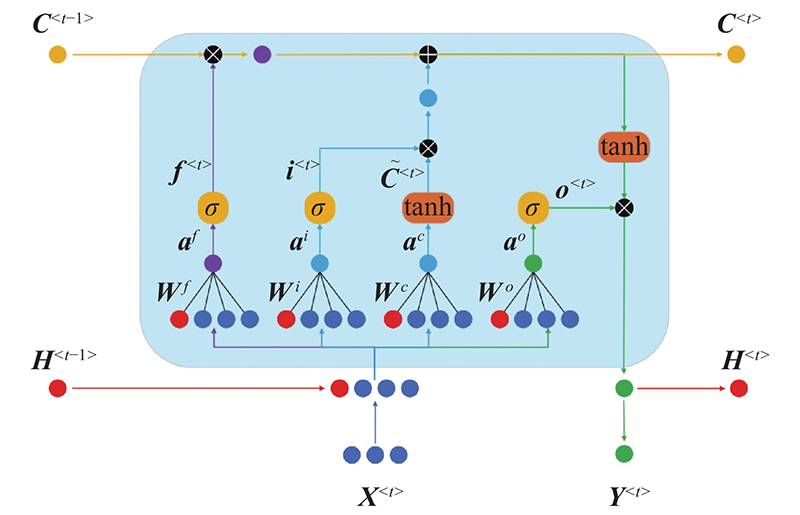
LSTM结构如图7所示，其中包含3个隐藏层，每层128个神经元. 解算器为Adam，预设最大训练次数为1 000，每次迭代最小批次大小为10，梯度阈值为1， $ \alpha $的初始值为0.005，根据分段常数衰减进行更新. 下降周期为150，下降因子为0.2，验证频率为每6个轮次一次. 训练截止条件为允许验证损失大于或等于先前的最小损失的次数为6. 输入有6类，分别为理论位置、理论速度、理论加速度、实际位置和实际加速度，通过控制器获得. 输出为轮廓误差，是利用牛顿迭代法计算得出的轮廓误差.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7   LSTM神经网络训练的流程图

Fig.7   Flow chart of LSTM neural network training


3.2. 基于LSTM神经网络的轮廓误差预测模型

利用LSTM神经网络对轮廓误差预测模型进行建模时，输入特征的选择至关重要. 考虑到对轮廓误差的预测，不仅与当前时刻的运动状态有关，也与过去及未来时刻的运动状态相关. 提出将过去、当前、未来时段的理论位置、理论速度、理论加速度作为输入特征，对LSTM神经网络进行训练，参考目前已有的研究，将提出方法C与目前已有的2种输入特征A和B进行对比.

1)当前时刻的轴理论速度、前K个时刻的轴理论速度[9].

2)当前时刻的轴理论位置、速度、理论加速度[11].

3)当前时刻的轴规划位置、速度、加速度；前K个时刻的轴规划位置、速度、加速度；后K个时刻的轴规划位置、速度、加速度.

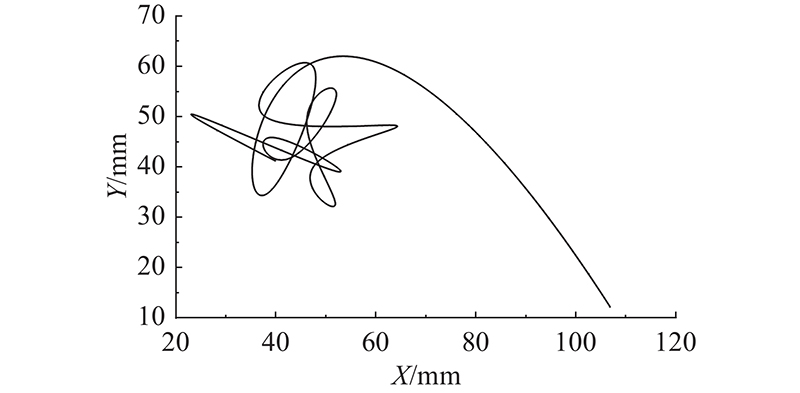
测试轨迹采用随机NURBS轨迹，如图8所示.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8   随机NURBS A

Fig.8   Random NURBS A


对比A、B、C 3种不同特征训练下的LSTM神经网络对轮廓误差的预测准确度，如图9所示，定义评价指标预测偏差 $ {\rm{\varepsilon }}' $. 当仅使用速度特征且不包含未来信息时，预测结果中存在较多偏差较大的区域，如图9(a)所示. $ {\rm{\varepsilon }}' $的最大值为49.4 μm，均方根值为25 μm，如表2所示. 采用B方式的训练方法，同时考虑当前时刻的位置、速度和加速度信息时，预测偏差较A方式有所减小，如图9(b)所示. $ {\rm{\varepsilon }}' $的最大值 $ {\rm{\varepsilon }}{'_{\max }} $为24.9 μm，均方根值 ${\rm{\varepsilon }}{'_{{{\rm{rms}}}}}$为12.6 μm，如表2所示. 采用提出C方式的训练方法，同时考虑过去、当前和未来时， $ {\rm{\varepsilon }}' $较B方式减小，如图9(c)所示. $ {\rm{\varepsilon }}' $的最大值为10.4 μm，均方根值为5 μm，如表2所示. 综上所述，在C方式训练下的 $ {\rm{\varepsilon }}' $较A方式平均减小了80%，较B方式下降了60.1%. 运用提出的训练方法优化的LSTM神经网络，与目前已有的训练方法相比，可以更有效地预测轮廓误差.

图 9

新窗口打开| 下载原图ZIP| 生成PPT

图 9   不同训练特征下的LSTM神经网络轮廓误差预测偏差

Fig.9   Contour error prediction deviation of LSTM neural network under different training characteristics


表 2   不同训练特征下LSTM神经网络轮廓误差预测效果的对比

Tab.2  Comparison of contour error prediction effect of LSTM neural network under different training characteristics

特征 ${{\varepsilon } }{'_{\max } }$/μm ${{\varepsilon } }{'_{ {{\rm{rms}}} } }$/μm
A 49.4 25.0
B 24.9 12.6
C 10.4 5.0

新窗口打开| 下载CSV


4. 基于转换任务坐标系的轮廓误差补偿

在得到轮廓误差后，通过额外的控制对轮廓误差进行补偿，提高轨迹的运动精度. 由于工业伺服电机与驱动器中的采用封装式的控制算法，对控制系统进行改变难度较大. 选择将轮廓误差直接补偿到参考轨迹作为前馈，实现轮廓误差离线控制. 提出的轮廓误差控制方法是简单、有效的前馈补偿方法，易于实现，对闭环控制器的稳定性影响不大，可以与现有的其他控制器结合，通过前馈补偿提高控制性能.

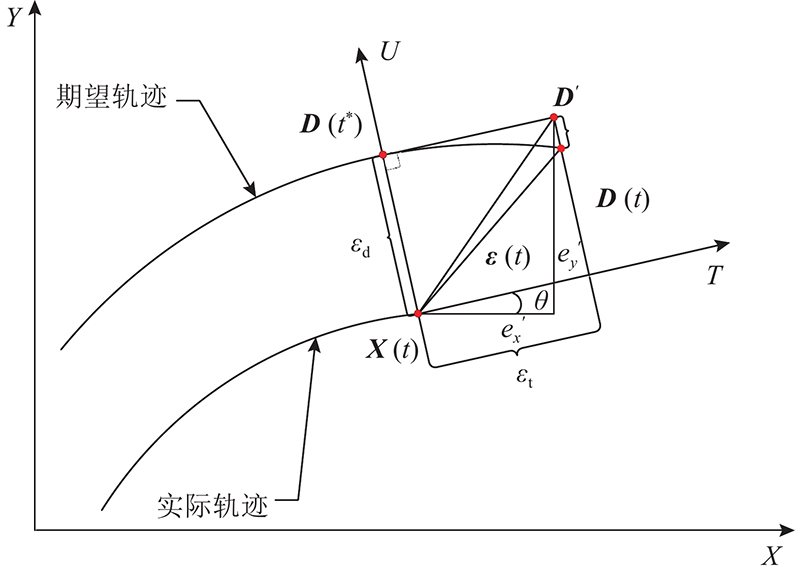
为了实现轮廓误差分量和与之正交的切向误差分量的解耦，建立转换任务坐标系，如图10所示.

图 10

新窗口打开| 下载原图ZIP| 生成PPT

图 10   转换任务坐标系的示意图

Fig.10   Schematic diagram of converting task coordinate system


轮廓误差和切向误差经过合理的权值调整后，补偿到参考轮廓，提高轮廓误差控制性能. 对两轴系统建立任务坐标系，以实际位置 $ {\boldsymbol{X}}({{t}}) $点为原点，以原点到轮廓误差点之间的向量为 $ U$轴，过原点选取与 $ U $正交的向量为 $ T $轴，以此作为两轴系统的转换任务坐标系.

将 $ {\boldsymbol{X}}({{t}}){\boldsymbol{D}}' $定义为等效轨迹跟踪误差，将其表示为 ${\boldsymbol{e}}' = {[{{{e}}_{{{x}}}}',{{{e}}_{{{y}}}}']^{{\rm{T}}}}$，根据几何关系可以得到 ${\boldsymbol{e}}' = {\boldsymbol{e}}+{\boldsymbol{\varDelta }}$. 通过如下坐标变换的方式获得切向误差 ${{{\varepsilon }}_{{\rm{t}}}}$和轮廓误差 ${{{\varepsilon }}_{{\rm{d}}}}$:

$ \left[ \begin{gathered} {{{\varepsilon }}_{{\rm{t}}}} \\ {{{\varepsilon }}_{{\rm{d}}}} \\ \end{gathered} \right] = \underbrace {\left[ {\begin{array}{*{20}{l}} {\cos {{\theta}}}&{\sin {{\theta}}} \\ { - \sin {{\theta}}}&{\cos {{\theta}}} \end{array}} \right]}_{\boldsymbol{A}}\left[ {\begin{array}{*{20}{c}} {{{{e}}_{{{x}}}}'} \\ {{{{e}}_{{{y}}}}'} \end{array}} \right] = {\boldsymbol{A}}({\boldsymbol{e}}+{\boldsymbol{\varDelta }}) . $
(37)

式中： ${{\theta}}$为 $ X $轴和 $ T $轴之间的夹角， $ {\boldsymbol{A}} $为转换任务坐标系下的转换矩阵. 令 $ {\boldsymbol{\psi }} = {[{{{\varepsilon }}_{{\rm{t}}}},{{{\varepsilon }}_{{\rm{d}}}}]^{{\rm{T}}}} $， $ {\boldsymbol{E}}' = {[{{{e}}_{{{x}}}}',{{{e}}_{{{y}}}}']^{{\rm{T}}}} $，式(37)可以表示为 $ {\boldsymbol{\psi }} = {\boldsymbol{AE}}' $. 将 $ X $、 $ Y $轴的参考轮廓表示为 $ {\boldsymbol{D}} = {[{{{D}}_{{{x}}}},{{{D}}_{{{y}}}}]^{{\rm{T}}}} $，与之对应的实际轨迹为 $ {\boldsymbol{S}} = [{{{X}}_{{{}}}},{{{Y}}_{{{}}}}] $，全闭环模型 $ {\boldsymbol{G}} = {{\rm{diag}}}\;[{{{G}}_{{{x}}}},{{{G}}_{{{y}}}}] $，得到切向误差和轮廓误差为

$ {{\boldsymbol{\psi }}_0} = {\boldsymbol{AE}}' = {\boldsymbol{A}} ({\boldsymbol{I}} - {\boldsymbol{G}}){\boldsymbol{D}}+{\boldsymbol{A}}{{\boldsymbol{\varDelta }}_0} . $
(38)

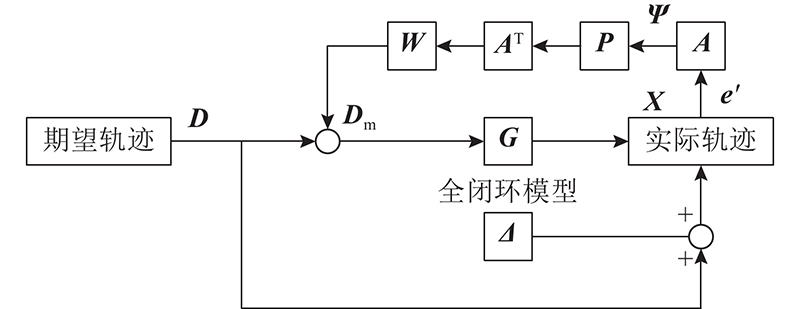
轮廓误差的控制系统如图11所示. 图中，Dm为补偿后的参考轨迹， ${{\boldsymbol{D}}_{\rm{m}}} = [{{{D}}_{{\rm{m}}{x}}},{{{D}}_{{\rm{m}}{y}}}]$；W为在笛卡尔坐标系下各轴的权值向量， ${\boldsymbol{W}} = {{\rm{diag}}}\;[{{{W}}_{{{x}}}},{{{W}}_{{{y}}}}]$；P为轮廓误差和切向误差的权值向量， ${\boldsymbol{P}} = {{\rm{diag}}}\;[{{{P}}_{{{{\rm{t}}}}}},{{{P}}_{{{{\rm{d}}}}}}]$.

图 11

新窗口打开| 下载原图ZIP| 生成PPT

图 11   轮廓误差控制框图

Fig.11   Contour error control block diagram


修正后的参考轨迹为

$ {{\boldsymbol{D}}_{\rm{m}}} = {\boldsymbol{D}}+{\boldsymbol{W}}{{\boldsymbol{A}}^{{\rm{T}}}}{\boldsymbol{P}}{{\boldsymbol{\psi }}_{\rm{m}}} . $
(39)

实际位置为

$ {\boldsymbol{S}} = {\boldsymbol{G}}{{\boldsymbol{D}}_{\rm{m}}} = {\boldsymbol{G}} ({\boldsymbol{D}}+{\boldsymbol{W}}{{\boldsymbol{A}}^{{\rm{T}}}}{\boldsymbol{P}}{{\boldsymbol{\psi }}_{\rm{m}}}) , $
(40)

$ {{\boldsymbol{\psi }}_{\rm{m}}} = {({\boldsymbol{I}}+{\boldsymbol{AGW}}{{\boldsymbol{A}}^{{\rm{T}}}}{\boldsymbol{P}})^{ - 1}} \cdot \{ {\boldsymbol{A}}[({\boldsymbol{I}} - {\boldsymbol{G}}){\boldsymbol{D}}+{{\boldsymbol{\varDelta }}_{\rm{m}}}]\} . $
(41)

由图10的几何关系，可得

$ {\boldsymbol{A}}{{\boldsymbol{\varDelta }}_0} = {[{{{a}}_{0}}{\varepsilon _{{{\rm{d}}0}}},\;\;0]^{{\rm{T}}}}, $
(42)

$ {\boldsymbol{A}}{{\boldsymbol{\varDelta }}_{\rm{m}}} = {[{{{a}}_{\rm{m}}}{{{\varepsilon }}_{{{\rm{d}}}{\rm{m}}}},\;\;0]^{{\rm{T}}}} . $
(43)

式中： $ {{{a}}_0} $、 $ {{{a}}_{\rm{m}}} $为常数. $ {{\boldsymbol{\psi }}_{\rm{m}}} $与 $ {{\boldsymbol{\psi }}_0} $之间的关系为

$ \begin{array}{c}\left[ \begin{array}{l}{{\varepsilon}}_{\rm{t}m}\\ {{\varepsilon}}_{\rm{d}m}\end{array} \right] = \left[ \begin{array}{cc} \dfrac{1}{1+{{G}}_{{x}}{{W}}_{{x}}{{P}}_{{{\rm{t}}}}{\mathrm{cos}}^{2}{\theta}} & 0\\ 0& \dfrac{1}{1+{{G}}_{{y}}{{W}}_{{y}}{{P}}_{\rm{d}}{\mathrm{cos}}^{2}{\theta}}\end{array} \right] \times \\ \left[\begin{array}{l}{\boldsymbol{\varepsilon}}_{\rm{t0}}\\ {\boldsymbol{\varepsilon}}_{\rm{d0}}\end{array}\right]+ {\left[\begin{array}{c}0\\ \dfrac{{{a}}_{{\rm{m}}}{{\varepsilon}}_{\rm{d}m}-{{a}}_{0}{{\varepsilon}}_{\rm{d0}}}{1+{G}_{{y}}{W}_{{y}}{P}_{\rm{d}}{\mathrm{cos}}^{2}{\theta}}\end{array}\right]}_{·}\end{array} $
(44)

补偿后的轮廓误差 $ {{{\varepsilon }}_{{{\rm{dm}}}}} $与没有补偿时的轮廓误差 $ {{{\varepsilon }}_{{{\rm{d}}}0}} $之间的关系为

$ {{{\varepsilon }}_{{{\rm{d}}}{\rm{m}}}} = \frac{{1 - {{{a}}_0}}}{{1+{{{G}}_{{{y}}}}{{{W}}_{{{y}}}}{{{P}}_{{\rm{d}}}}{{\cos }^2}{{\theta }} - {{{a}}_{\rm{m}}}}}{{{\varepsilon }}_{{{\rm{d}}}0}} . $
(45)

在满足

$ 0 \leqslant \left\| {\frac{{1 - {{{a}}_0}}}{{1+{{{G}}_{{{y}}}}{{{W}}_{{{y}}}}{{{P}}_{{\rm{d}}}}{{\cos }^2}{{\theta }} - {{{a}}_{\rm{m}}}}}} \right\| \leqslant 1.0 $
(46)

的情况下，可以保证轮廓误差补偿的收敛性. 在通常情况下， $\left| {{{{a}}_0}} \right|、\left| {{{{a}}_{\rm{m}}}} \right| \ll 1$， ${{{G}}_{{{y}}}}{{{W}}_{{{y}}}}{{{P}}_{{\rm{d}}}}{\cos ^2}{{\theta }} > 0$，因此满足条件.

5. 系统试验分析

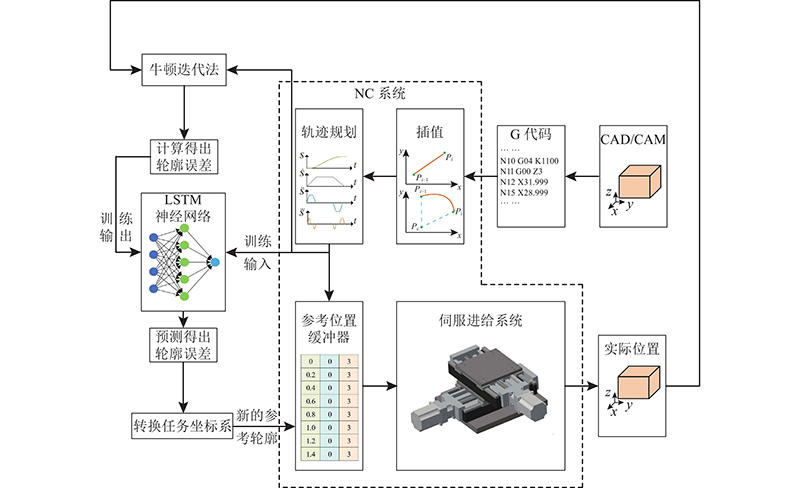
本文的整体方法框图如图12所示. 可以看出，提出的轮廓误差控制是通过修改参考轨迹来实现的. 控制系统包括2部分：控制器和伺服. 在这2个部分之间有一个缓冲器，用于存储参考位置点. 本文主要通过更新缓冲区来实现. 利用牛顿迭代法计算轮廓误差，获得训练数据. 对LSTM神经网络模型进行训练，并利用训练好的LSTM神经网络模型预测给定的任意轮廓的轮廓误差. 将轮廓误差输入到转换任务坐标系中，通过合理的权值调整计算得到各轴合适的补偿量，补偿到原始的参考轮廓，获得新的参考位置. 将新的参考轮廓写入参考位置缓冲区，减小轮廓误差.

图 12

新窗口打开| 下载原图ZIP| 生成PPT

图 12   轮廓误差总体控制框图

Fig.12   Block diagram of overall control strategy


5.1. 基于牛顿迭代的轮廓误差估计准确性验证

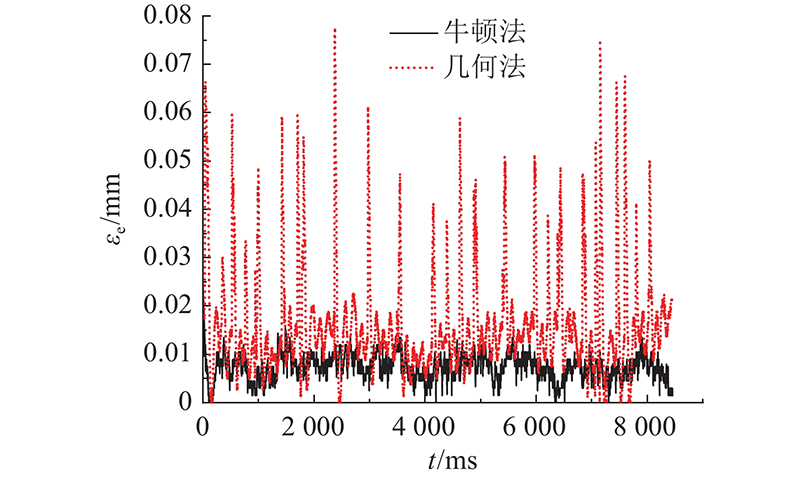
将利用牛顿迭代法计算得到的轮廓误差作为LSTM神经网络的训练输出，计算得到的轮廓误差的准确性直接影响LSTM神经网络对轮廓误差预测的准确性. 在进给伺服平台上，通过试验将牛顿迭代法、几何法与真实的轮廓误差进行对比，验证牛顿迭代法轮廓误差估计的准确性.

由于圆的特殊性，可以根据实际位置点、圆心位置及圆弧半径，确定准确的真实轮廓误差，如下所示:

$ {{{\varepsilon }}_{\rm{da}}} = \sqrt {{{D}}_{{{x}}}^{2}+{{D}}_{{{y}}}^{2}} - r . $
(47)

利用圆轮廓验证轮廓误差估计的准确性，选取参考轮廓为

$ \boldsymbol{D}({t})={\left[\begin{array}{l}r\, \mathrm{cos}\;(2\text{π} {t})\\ r\, \mathrm{sin}\;(2\text{π} {t})\end{array}\right]} . $
(48)

式中： $ r = 30 $ mm. 计算出的轮廓误差与实际轮廓误差的偏差为 $ {{{\varepsilon }}_{{\rm{e}}}} = \left| {{{\boldsymbol{\varepsilon }}_{{{\rm{da}}}}} - {{\boldsymbol{\varepsilon }}_{{\rm{d}}}}} \right| $. 在进给伺服平台上执行跟踪任务，通过倍福控制器采集得到实际轨迹的数据. 分别利用几何近似法、牛顿迭代法计算轮廓误差，与真实轮廓误进行对比，计算得到偏差，如图13所示. 通过计算得出几何近似法的估计偏差最大值为77.5 μm，均方根值为19.6 μm. 利用牛顿迭代法的估计偏差最大值为24 μm，均方根值为7.8 μm，证明了牛顿迭代法对轮廓误差估计的准确性，验证了对LSTM神经网络模型训练输出数据的可靠性.

图 13

新窗口打开| 下载原图ZIP| 生成PPT

图 13   轮廓误差估计偏差的对比

Fig.13   Comparison of contour error estimation deviation


5.2. 轮廓误差控制效果的验证

将LSTM神经网络预测的轮廓误差，通过转换任务坐标系进行合理的调整后补偿到参考轮廓，将补偿后的轮廓输入到进给系统，实现轮廓误差控制. 为了验证本文方法的准确性和泛化性，使用新的随机NURBS轨迹进行验证，如图14所示. 将提出的方法(C6)与PID控制(C1)和交叉耦合控制(C2)[12]、基于NARX[13]神经网络的轮廓误差控制(C3)和基于GRU[11]神经网络轮廓误差控制(C4)及牛顿迭代控制(C5)开展比较.

图 14

新窗口打开| 下载原图ZIP| 生成PPT

图 14   随机NURBS B

Fig.14   Random NURBS B


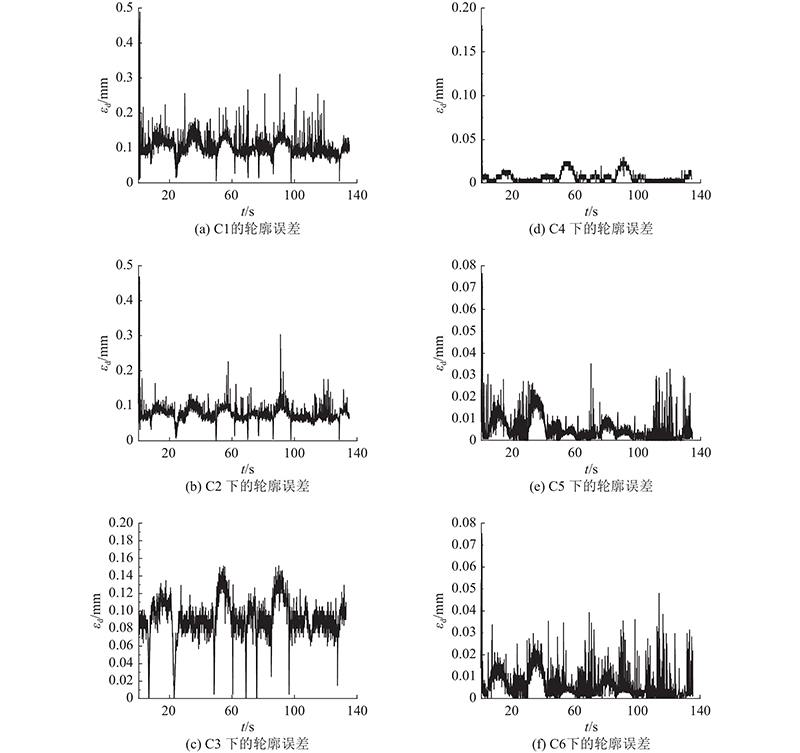
C1: 伺服控制器本身即PID控制，无额外的轮廓控制. C2: 交叉耦合控制. C3: 基于NARX神经网络的轮廓误差控制. C4: 基于GRU神经网络的轮廓误差控制. C5: 基于牛顿迭代的轮廓误差补偿控制. C6: 基于LSTM神经网络和转换任务坐标系的轮廓误差补偿控制.

试验结果如图15所示. 本文方法C6相对于传统的PID控制和交叉耦合控制，极大地减小了轮廓误差的峰值与均值，如图15(a)、(b)、(f)所示. 本文方法C6对轮廓误差的控制优于近些年应用在运动控制领域的NARX与GRU神经网络，如图15(c)、(d)、(f)所示. 本文方法C6对轮廓误差的控制可以完全取代牛顿迭代法，如图15(e)、(f)所示，不需要耗时的迭代过程，弥补了迭代法的单一性缺点.

图 15

新窗口打开| 下载原图ZIP| 生成PPT

图 15   轮廓误差的对比

Fig.15   Comparison of contour error


轮廓误差控制的性能指标如表3所示. 可以看出，二维随机NURBS轨迹在原始控制即C1控制下，最大轮廓误差为489 μm，轮廓误差均方根值为109.1 μm，利用本文方法C6补偿后，轮廓误差最大值降低到75.4 μm，相比于C1降低了84.6%，轮廓误差均方根值降低到8.2 μm，相比于C1降低了92.5%. 本文方法C6相比于应用广泛的C2，轮廓误差最大值降低了89.1%，轮廓误差均方根值降低了83.9%. 本文方法C6相比于C3，轮廓误差最大值降低了49.7%，轮廓误差均方根值降低了90.2%. 综合分析图15(d)和表3可知，C4对轮廓误差有着良好的控制，但在电机启动瞬间对轮廓误差的控制效果较差，本文方法相较于C4，轮廓误差最大值降低了61.3%，轮廓误差均方根值降低了20.2%. 综合分析图15(e)、(f)和表3可知，本文方法与基于牛顿迭代的轮廓误差控制在峰值与均方根值上极接近，证明了本文方法对于轮廓误差控制尤其在大曲率处的有效性与泛化性.

表 3   轮廓误差控制的对比

Tab.3  Comparison of contour error control

方法 ${\left| { { {\boldsymbol{\varepsilon } }_{\rm{d}}} } \right|_{ \rm{rms} } }$/μm ${\left| { { {\boldsymbol{\varepsilon } }_{\rm{d}}} } \right|_{ {\max} } }$/μm
C1 109.1 489
C2 83.5 468
C3 93.7 150
C4 11.4 195
C5 8.2 76.6
C6 9.1 75.4

新窗口打开| 下载CSV


6. 结　语

本文针对两轴精密运动控制系统，提出基于LSTM神经网络、结合牛顿迭代学习的轮廓误差预测方法. 该方法在弥补牛顿迭代法单一耗时缺点的同时，拥有与牛顿迭代法相当的精度，优化后的LSTM神经网络对轮廓误差的预测优于同类型的其他神网络，可以有效地应用于轮廓误差预测. 利用转换任务坐标系对预测轮廓误差进行补偿，克服了传统的控制方法需要改变原有各轴的独立控制系统的问题，精确解耦了轮廓误差，确定了相应的权值调整方案,实现了轮廓误差在大曲率处的有效控制. 该方法可以扩展到多轴系统，有效应用于多轴系统的轮廓误差控制，具有良好的泛化性.

参考文献

CHEN Z, LI C, YAO B, et al

Integrated coordinated/synchronized contouring control of a dual-linear-motor-driven gantry

[J]. IEEE Transactions on Industrial Electronics, 2020, 67 (5): 3944- 3954

DOI:10.1109/TIE.2019.2921287      [本文引用: 1]

LI J, QI C, LI Y, et al

Prediction and compensation of contour error of CNC systems based on LSTM neural network

[J]. IEEE/ASME Transactions on Mechatronics, 2021, 3 (99): 1- 8

[本文引用: 2]

LIAO J, HUANG F, CHEN Z, et al

Optimization-based motion planning of mobile manipulator with high degree of kinematic redundancy

[J]. International Journal of Intelligent Robotics and Applications, 2019, 3 (2): 115- 130

DOI:10.1007/s41315-019-00090-7      [本文引用: 1]

WANG Z, HU C, ZHU Y, et al

Newton-ILC contouring error estimation and coordinated motion control for precision multi-axis systems with comparative experiments

[J]. IEEE Transactions on Industrial Electronics, 2017, 65 (2): 1470- 1480

[本文引用: 1]

KOREN Y

Cross-coupled biaxial computer control for manufacturing systems

[J]. Journal of Dynamic Systems Measurement and Control, 1980, 102 (4): 265- 272

DOI:10.1115/1.3149612      [本文引用: 1]

胡楚雄, 王庆丰, 姚斌

基于全局任务坐标系的精密轮廓运动控制研究

[J]. 机械工程学报, 2012, 48 (20): 79- 88

[本文引用: 1]

HU Chu-xiong, WANG Qing-feng, YAO Bin

Research on precision contour motion control based on global task coordinate system

[J]. Journal of Mechanical Engineering, 2012, 48 (20): 79- 88

[本文引用: 1]

CHEN Z, YAO B, WANG Q

Adaptive robust precision motion control of linear motors with integrated compensation of nonlinearities and bearing flexible modes

[J]. IEEE Transactions on Industrial Informatics, 2012, 9 (2): 965- 973

[本文引用: 1]

ZHANG D, CHEN Y, CHEN Y

Iterative precompensation scheme of tracking error for contouring error reduction

[J]. The International Journal of Advanced Manufacturing Technology, 2016, 87 (9): 3279- 3288

[本文引用: 1]

CHEN S, WEN J. Adaptive neural trajectory tracking control for flexible-joint robots with online learning [C]// IEEE International Conference on Robotics and Automation. Paris: IEEE, 2020: 2358-2364.

[本文引用: 2]

HUO F, POO A N

Nonlinear autoregressive network with exogenous inputs based contour error reduction in CNC machines

[J]. International Journal of Machine Tools and Manufacture, 2013, 67 (1): 45- 52

[本文引用: 1]

HU C, OU T, CHANG H, et al

Deep GRU neural-network prediction and feedforward compensation for precision multi-axis motion control systems

[J]. IEEE/ASME Transactions on Mechatronics, 2020, 1 (99): 1377- 1388

[本文引用: 3]

FU S, LU H, XU Y, et al. Research on contour error control based on cross-coupled structure [C]//IEEE International Conference on Information and Automation. Wuyishan: IEEE, 2018: 150-154.

[本文引用: 1]

ERWINSKI K, PAPROCKI M, WAWRZAK A, et al. Neural network contour error predictor in CNC control systems [C]// 21st International Conference on Methods and Models in Automation and Robotics. Miedzyzdroje: IEEE, 2016.

[本文引用: 1]

/

〈 〉