针对星敏感器的姿态确定问题,国内外学者基于不同的理论方法给出了相应的解决方案。Markley等[3]开发的奇异值分解(singular value decomposition, SVD)方法稳健且准确. 虽然SVD具有鲁棒的数值矩阵运算能力,但矩阵分解的时间消耗较大. Yang等[4]提出针对Wahba问题的解析方法,通过求解四次方程的根得到最大特征值. 该算法计算速度快,但可能会由于特征多项式没有实根导致无法得到正确的旋转四元数. Shuster等[5]提出的QUEST算法通过Cayley-Hamilton定理给出对应矩阵的闭型特征多项式. 数据矩阵的最大特征值非常接近1,因此基于牛顿算法,以1为初始值迭代,得到最大特征值. Mortari[6]提出采用ESOQ和ESOQ2方法计算最优旋转四元数. 其中ESOQ推导
随着我国航空航天事业以及军事装备的飞速发展,空间载体的自主导航问题成为研究热点. 相较于太阳敏感器、地平仪、磁力计等姿态测量设备,星敏感器测量精度高,抗干扰能力及自主导航能力强. 本研究就星敏感器设备的姿态解算问题给出既考虑解算精度、又保证实时性的方法. 将从四元数的角度出发,联立所有星光矢量的信息;考虑不同信息间的权重分布,将三轴旋转角的求解问题转换成求解构造出的数据矩阵的特征值特征向量问题;给出解决迭代过程中出现的不确定性和四元数向量奇异性的具体方案.
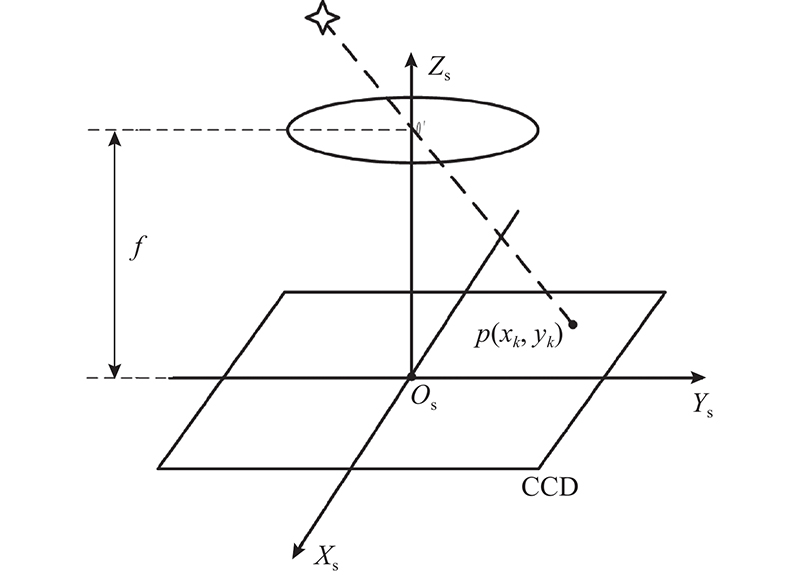
1. 星敏感器测量模型
图 1
式中:
式中:
可以得到
令
考虑星敏感器散粒噪声、读出噪声的影响,将式(5)简写为
式中:
2. 三轴旋转角求解算法推导
式中:
Wahba问题构造的目标优化函数为
式中:
化简
式中:
展开式(12),得到
同理,得到
将
得到
解耦
同理,可知
得到
矩阵
将式(23)左侧展开, 得到
式中:
对
对
得到
因为星敏感器在测量星光矢量时的系统偏差与随机噪声不可避免,所以星光矢量
可以看出,
证明 数据矩阵
令
则
若存在特征值
计算得到
将
令
则
得到
式(39)与式(35)矛盾,因此
证明结果表明,可以基于牛顿-辛普森梯度迭代法,以迭代初始值为1求解
在星敏感器输出星光矢量的天球系坐标和星敏系坐标后,可以并行计算得到
经过6次迭代,使所得特征值达到符合要求的精度. 求出特征值
令
实施初等行变换,将
只有
其中
由于特征向量
在式(45)中,若令
即
求出的2个最优旋转四元数互为负向量. 用旋转四元数的轴角表示角度,得到
即旋转四元数
3. 仿真验证及分析
利用数值仿真对比验证三轴旋转角求解算法和传统的三轴旋转角求解算法的姿态解算精度. 仿真步骤如下.
1)随机生成单位正交矩阵. 2)随机生成三维矢量
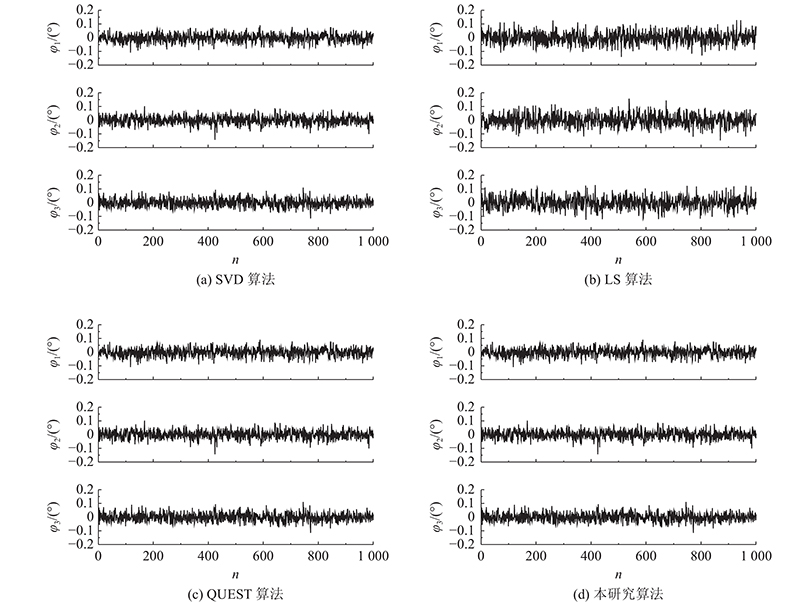
如图2所示为噪声标准差
图 2
图 2 1.0×10−3噪声标准差下不同算法的三轴姿态角误差曲线
Fig.2 Three-axis attitude angle error curve of different algorithms under 1.0×10−3 standard deviation of noise
表 1 不同噪声标准差下不同算法的姿态角误差标准差
Tab.1
| 算法 | σA/(°) | |||
| σs=1.0×10−2 | σs=1.0×10−3 | σs=1.0×10−4 | σs=1.0×10−5 | |
| SVD | 2.071×10−1 | 2.751×10−2 | 3.084×10−3 | 4.055×10−4 |
| LS | 3.679×10−1 | 3.794×10−2 | 4.286×10−3 | 4.622×10−4 |
| QUEST | 2.071×10−1 | 2.751×10−2 | 3.084×10−3 | 4.055×10−4 |
| 本研究 | 2.071×10−1 | 2.751×10−2 | 3.084×10−3 | 4.055×10−4 |
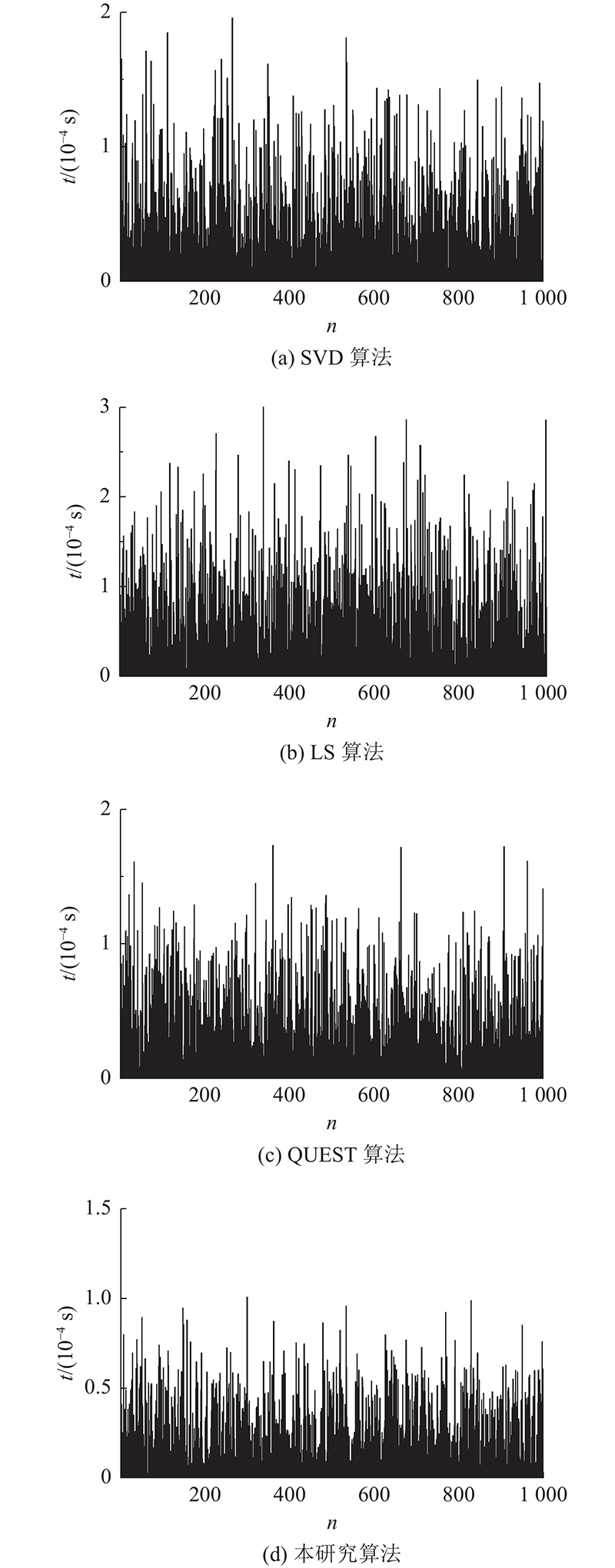
不同的噪声强度对上述4种算法的处理速度影响不大,因此以σs=
图 3
图 3 1.0×10−3噪声标准差下不同算法的时间消耗曲线
Fig.3 Time consumption curve of different algorithms under 1.0×10−3 standard deviation of noise
表 2 不同噪声标准差下不同算法的耗时表
Tab.2
| 算法 | t/s | |||
| σs=1×10−2 | σs=1×10−3 | σs=1×10−4 | σs=1×10−5 | |
| SVD | 6.021×10−5 | 5.971×10−5 | 6.153×10−5 | 6.568×10−5 |
| LS | 9.354×10−5 | 9.219×10−5 | 9.612×10−5 | 9.674×10−5 |
| QUEST | 5.721×10−5 | 5.671×10−5 | 5.953×10−5 | 5.368×10−5 |
| 本研究 | 3.284×10−5 | 3.322×10−5 | 3.268×10−5 | 3.109×10−5 |
星敏感器是嵌入式设备,其运行环境也是嵌入式环境. 为了检验本研究算法在工程实践的应用价值,在嵌入式平台上对本研究算法与对比算法进行测试. 嵌入式设备型号为DSP6748,星敏感器的视场为
仿真与试验验证可知,在旋转角精度方面,本研究算法和SVD算法、QUEST算法的精度相当,LS算法稍差. 实际上,前3种算法满足Wahba问题的极限精度,由于算法运用的数学手段不同,导致三者在算法形式上有所差异,但结果一致,都是对三轴旋转角的最优估计. 在耗时方面,本研究算法的计算效率最高,QUEST算法和SVD算法的计算效率居中,LS算法的计算效率最低,结果体现出本研究算法在算法性能上的进步. 试验结果表明,与3种传统算法相比,保持相同最高估计精度的情况下,本研究算法在计算效率上有一定的提高.
4. 结 语
本研究算法基于单个星光矢量在天球坐标系与星敏坐标系中的三维坐标推导得到四元数变换形式,充分利用伪逆矩阵的性质对二次四元数矩阵方程进行降次,并将最优旋转四元数的求解转变为求解矩阵的最大特征值及其对应的特征向量问题. 本研究从理论上证明了特征值的取值范围,解决了三轴旋转角求解过程中迭代问题的前提条件;详细分析了四元数矢量方向问题,排除了方向奇异性带来的三轴旋转角求解问题. 对本研究算法与传统算法的性能仿真与试验对比分析结果表明,本研究算法和SVD算法、QUEST算法的三轴旋转角求解精度最高,本研究算法的计算效率较高、综合性能较好.
参考文献
A novel backtracking scheme for attitude determination-based initial alignment
[J].DOI:10.1109/TASE.2014.2346581 [本文引用: 1]
Inertial aided cycle slip detection and identification for integrated PPP GPS and INS
[J].DOI:10.3390/s121114344 [本文引用: 1]
How to estimate attitude from vector observations
[J].
An analytic solution to Wahba’s problem
[J].DOI:10.1016/j.ast.2013.07.002 [本文引用: 1]
Three-axis attitude determination from vector observations
[J].
ESOQ: a closed-form solution to the Wahba problem
[J].
A least squares estimate of spacecraft attitude
[J].
On-orbit geometric calibration of ZY-3 three-linear array imagery with multistrip data sets
[J].DOI:10.1109/TGRS.2013.2237781 [本文引用: 1]
Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients
[J].
Fast linear quaternion attitude estimator using vector observations
[J].
A position loci-based in-motion initial alignment method for low-cost attitude and heading reference system
[J].
A robust quaternion Kalman filter method for MIMU/GPS in-motion alignment
[J].
Bias compensation in rational functions for Ikonos satellite imagery
[J].DOI:10.14358/PERS.69.1.53 [本文引用: 1]
Low-cost, high-performance monocular vision system for air bearing table attitude determination
[J].DOI:10.2514/1.A32465
Real-time magnetometer disturbance estimation via online nonlinear programming
[J].
Generalized linear quaternion complementary filter for attitude estimation from multisensor observations: an optimization approach
[J].DOI:10.1109/TASE.2018.2888908 [本文引用: 1]
In-orbit geometric calibration and validation of ZY-3 linear array sensors
[J].DOI:10.1111/phor.12052 [本文引用: 1]
Kalman filtering for spacecraft attitude estimation
[J].DOI:10.2514/3.56190
Gradient descent optimization-based self-alignment method for stationary SINS
[J].
Precise 3-D GNSS attitude determination based on Riemannian manifold optimization algorithms
[J].DOI:10.1109/TSP.2019.2959226 [本文引用: 1]
Fast star-pattern recognition using planar triangles
[J].
Star trackers for attitude determination
[J].
Attitude determination studies for the earth observation system AM1 (EOS-AM1) mission
[J].DOI:10.2514/3.21789
Robust attitude estimation using IMU-only measurements
[J].