熔融沉积成型(fused deposition modeling, FDM),是增材制造(additive manufacturing, AM)工艺[1-3]. 这项3D打印技术由Scott Crump[4]研制成功. 目前,该工艺在工业制造[5]、建筑[6]、航空航天[7]、医疗[8]、食品[9]等领域都有广泛的应用. 3D打印技术在加工制造过程中很耗时间,在打印过程中容易出现各种质量问题,如零件脱离平台或翘曲[10]、打印喷头发生堵塞[11]、零件的尺寸精度不准确[12-13]或者结构太弱[14]等质量问题. 为了得到高质量的打印零件,需要在零件打印过程中监控关键的工艺参数和典型的故障模式. 一种具有传感、信息处理和反馈调整能力的闭环监控控制系统[15]对提高机器的可靠性和打印零件的质量是至关重要的.
以上研究是针对增材制造过程中挤出机喷嘴堵塞、零件翘曲变形、丝材断裂等缺陷进行研究,很少对打印过程中的拉丝缺陷进行监测研究. 拉丝,又称为渗漏、挂须或起毛,是3D打印最常见的问题之一.拉丝会在模型表面留下许多塑料细丝,是因为打印机喷头移动至新的位置时喷嘴里的塑料渗漏出来导致的. 它是FDM打印过程中的主要缺陷之一,严重影响零件最后成型的质量. 潘俊锋等[16]对FDM打印工艺参数进行研究,通过模型试验分析,确定了影响模型拉丝缺陷的切片参数有打印温度、回抽距离和回抽速度.王微等[17]研究打印温度、分层厚度和打印速度对打印件质量的影响,通过三因素三水平正交试验,确定了各因素对打印件的影响水平不同且具有方向性. 上述对影响熔融沉积3D打印零件质量因素的研究,没有具体地区分各因素影响的主次顺序. 上述研究都是在工件打印完成后再进行分析的,无法实现在打印过程中及时发现因打印参数的异常引起的异常打印工况问题.
针对FDM打印过程中出现拉丝缺陷异常打印的工况,本文提出基于振动信号的3D打印拉丝缺陷诊断方法. 通过单因素试验确定拉丝缺陷与所研究因素之间的关系,通过正交实验进行具体的分析验证. 试验结果表明,基于振动信号时域特征参数对打印过程中的拉丝缺陷具有较好的识别效果.
1. 试验方法
1.1. 试验材料与设备
试验中打印耗材选用聚乳酸(PLA),熔点为155~185 ℃,熔融指数为8~10 g/10 min,直径为1.75 mm. 3D打印机选用DOBOT越疆MOOZ1桌面级3D打印机. 该3D打印机整体设计采用模块化,便于组装. 整体由XYZ导轨轴组成,采用丝杆机构,相对于同步带而言,丝杆机构传动更加准确且刚性更强,不会出现丢转的现象.选用双Z轴设计,减少因喷头系统运动到一端时产生的形变误差[18],增大了整个打印机的稳定性. 送丝电机及运动控制电机均选用工业级步进电机,控制精度可以达到0.005 mm.
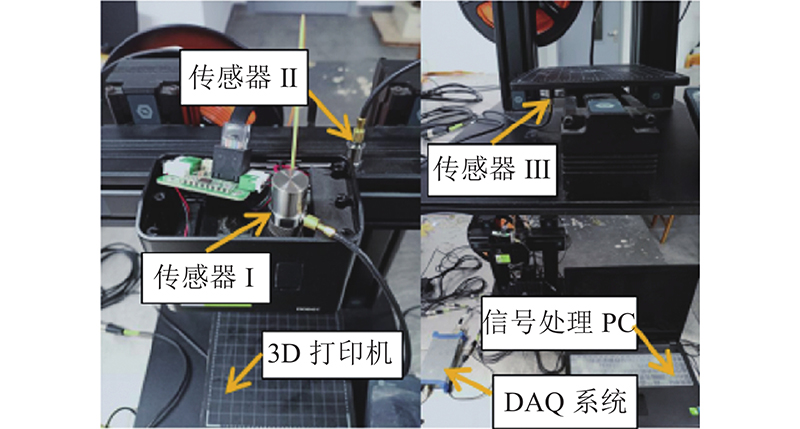
振动监测平台如图1所示,由FDM型3D打印机、打印工作台、数据采集系统、加速度振动传感器和笔记本电脑组成. 3个传感器使用东华测试的通用压电式加速度传感器,其中传感器Ⅰ型号为1A111E,工作频率为0.5~7 000 Hz,传感器Ⅱ和Ⅲ型号为1A102E,工作频率为1~10 000 Hz. 传感器Ⅰ采集送丝电机的振动信号,传感器Ⅱ采集X导轨轴振动信号,传感器Ⅲ采集成型底板的振动信号. 采用IEPE型信号传输,该种传感器低阻抗输出,抗干扰能力强,可以进行长电缆输出而不会引起机械振动声压增加. 数据采集系统采用东华测试的DH5981动态信号采集仪.
图 1
使用如图1所示的3D打印振动监测平台进行试验,采用直径为1.75 mm的PLA材料作为打印耗材. 试验时,在切片软件中设置打印层厚为0.2 mm,填充密度设为15%,打印速度取50 mm/s,打印平台温度为60 ℃,信号采样频率为1 000 Hz. 通过改变回抽速率、回抽距离、喷头温度、空驶速率,开展单因素试验与正交试验.
1.2. 振动信号的时域分析方法
时域分析主要是指对各种信号进行处理,计算各种时域参数指标,识别不同故障类型. 时域信号的特征值分为有量纲和无量纲2种. 有量纲的特征参数虽然对信号间的差异比较敏感,但是外界环境对振动信号的干扰极大,如负载或转速发生变化时,它们随之产生变化能. 在对信号进行特征分析时,经常使用峭度、峰值因子、脉冲因子、裕度因子等无量纲特征参数. 通过对加速度振动传感器采集的信号进行时域分析,提取峭度、峰值因子、脉冲因子作为单因素试验与正交试验的评价指标,对试验数据进行分析处理.
峭度反映了时域信号波形的平陡程度. 当曲线波形较“陡”时,峭度大于3. 当曲线波形较平缓时,峭度小于3. 当曲线为正态分布时,峭度等于3. 信号峭度可以反映信号的某些特征,特别是对冲击性的反应,计算公式如下:
式中:
峰值因子是指曲线波形信号在一段时间内的信号幅度峰值与信号幅度有效值(RMS)的比值,反映了该信号的波峰明显程度,波峰越明显,峰值因子越大. 峰值因子的计算公式如下:
式中:
脉冲因子是指曲线波形信号在一段时间内的信号幅度峰值与整流平均值(绝对值的平均值)的比值.峰值因子和脉冲因子都与信号幅度峰值有关,它们之间的区别在于分母,对于同一组数据,有效值大于整流平均值,所以峰值因子小于脉冲因子. 脉冲因子的计算公式如下:
1.3. 单因素试验设计
采用零件打印方法,对喷头温度T、回抽速率VW、回抽距离LW和空驶速率VL进行单因素试验设计. 将峭度、峰值因子、脉冲因子作为指标,对试验数据进行分析处理,利用传感器将回抽速率、喷头温度、回抽距离和空驶速率各取30组,通过计算得到它们对应特征量的平均值和误差范围. 如表1所示为单因素试验水平表. 保持回抽速率为50 mm/s,喷头温度为190 ℃,空驶速率为50 mm/s,在回抽距离为1、3、6、9、12 mm的条件下,考察零件的拉丝情况. 保持回抽距离为6 mm,喷头温度为190 ℃,空驶速率为50 mm/s,在回抽速率为10、30、50、60、80 mm的条件下考察零件的拉丝情况. 保持空驶速率为50 mm/s,回抽速率为50 mm,回抽距离为6 mm,在喷头温度为190、195、200、205、210 ℃的条件下考察零件的拉丝情况. 保持回抽速率为50 mm/s,喷头温度为190 ℃,回抽距离为6 mm,在空驶速率为10、30、50、60、80 mm的条件下考察零件的拉丝情况.
表 1 单因素试验水平表
Tab.1
| 水平 | VW/(mm·s−1) | t/℃ | LW/mm | VL/(mm·s−1) |
| 1 | 10 | 190 | 1 | 10 |
| 2 | 30 | 195 | 3 | 30 |
| 3 | 50 | 200 | 6 | 50 |
| 4 | 60 | 205 | 9 | 60 |
| 5 | 80 | 210 | 12 | 80 |
1.4. 正交试验方案设计
当需要对多因素多水平进行试验研究时,通常选用正交试验方法. 该方法不需要做全部试验,只需要选择正交表中的元素进行试验,极大地节约了试验时间和试验次数,提高了试验效率[21].
在单因素试验的基础上,以回抽速率、空驶速率、喷头温度和回抽距离4个因素,每个因素选择3个水平进行正交试验,查表选择L9(34)正交试验设计. 其中L表征正交试验表,下标“9”表征要做9组试验;上标“4”表征有4种试验因素;底数3表征每个因素安排3个水平. 以峭度、峰值因子、脉冲因子特征参数为评价指标,确定最佳的打印参数组合,正交试验表如表2所示.
表 2 正交设计试验表
Tab.2
| 试验编号 | t/℃ | VW/(mm·s−1) | LW/mm | VL/(mm·s−1) |
| S1 | 190 | 10 | 1 | 10 |
| S2 | 190 | 50 | 6 | 50 |
| S3 | 190 | 80 | 12 | 80 |
| S4 | 200 | 10 | 6 | 80 |
| S5 | 200 | 50 | 12 | 10 |
| S6 | 200 | 80 | 1 | 50 |
| S7 | 210 | 10 | 12 | 50 |
| S8 | 210 | 50 | 1 | 80 |
| S9 | 210 | 80 | 6 | 10 |
2. 试验结果与分析
2.1. 单因素试验结果与分析
2.1.1. 打印实物图
初始参数如下:回抽速率为50 mm/s,喷头温度为190 ℃,空驶速率为50 mm/s,回抽距离为6 mm. 在保持其他初始参数不变的情况下,如图2(a)~(c)所示分别为当喷头温度为190、200、210 ℃时的拉丝现象. 可以看出,当喷头温度为190 ℃时只有轻微拉丝的现象,210 ℃时拉丝现象有些明显. 如图2(d)~(f)所示分别为当回抽速率为30、50、80 mm/s时的拉丝现象. 可以看出,当回抽速率为80 mm/s时的打印效果较好,当回抽速率为20和50 mm/s时都有拉丝产生. 如图2(g)~(i)所示分别为当回抽距离为3、8、12 mm时的拉丝现象. 可以看出,当回抽距离为3 mm时拉丝较明显,随着回抽距离的增大,拉丝情况越来越不明显. 如图2(j)~(l)所示分别为当空驶速率为20、50、80 mm/s时的拉丝现象. 可以看出,在3种不同空驶速率的情况下都有拉丝产生.
图 2
2.1.2. 振动信号时域图分析
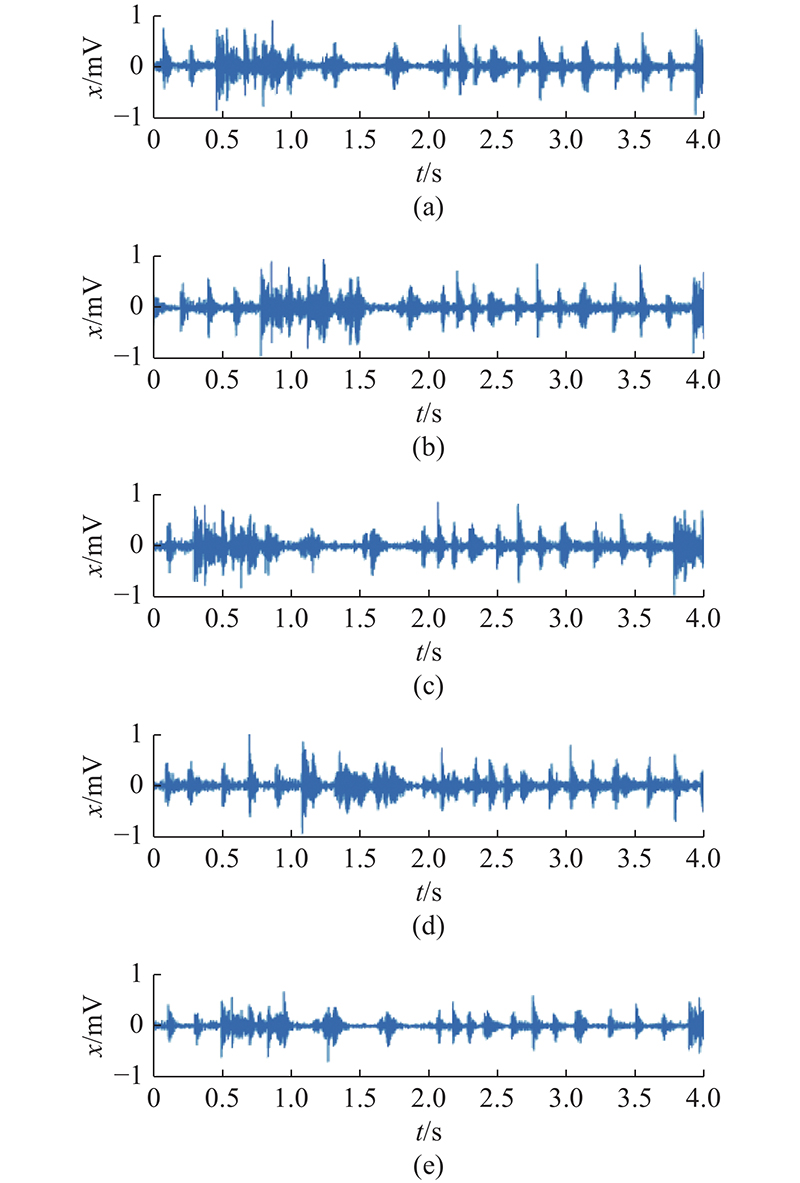
在单因素试验过程中,3个传感器对试验过程中的振动信号进行采集. 通过分析采集的振动信号可知,传感器Ⅲ采集的不同振动信号在时域图分析上具有明显的特征差异,因此以传感器Ⅲ采集的单因素试验振动信号时域图分析为例进行说明. 如图3所示,从单因素试验组中选出5组试验进行分析,得到它们的振动信号时域图. 如图3(a)所示为当喷头温度为190 ℃,回抽速率为50 mm/s,回抽距离为6 mm,空驶速率为50 mm/s时的振动信号时域图. 如图3(b)所示为在回抽距离为1 mm,其他因素水平不变的条件下的振动信号时域图. 如图3(c)所示为当回抽速率为80 mm,其他因素水平不变时的振动信号时域图. 如图3(d)所示为当空驶速率为80 mm,其他因素水平不变时的振动信号时域图. 如图3(e)所示为当喷头温度为210 ℃,其他因素水平不变时的振动信号时域图. 从图3可以看出,相同因素下不同水平时域特征具有明显的不同,但是从时域图上只能看出特征趋势,无法得到具体的时域特征值进行特征分析.
图 3
图 3 传感器Ⅲ不同因素和水平振动信号的时域图
Fig.3 Time domain diagram of sensor Ⅲ different factors and horizontal vibration signals
对同因素不同水平的时域图直接进行分析,可以得出不同水平之间存在差异,不同的打印参数影响零件的拉丝缺陷. 基于时域图分析无法确定同因素不同水平对零件拉丝缺陷的影响,需要在时域范围内提取出相关的峭度、峰值因子和脉冲因子进行进一步的分析.
2.1.3. 不同因素水平与峭度指标的关系
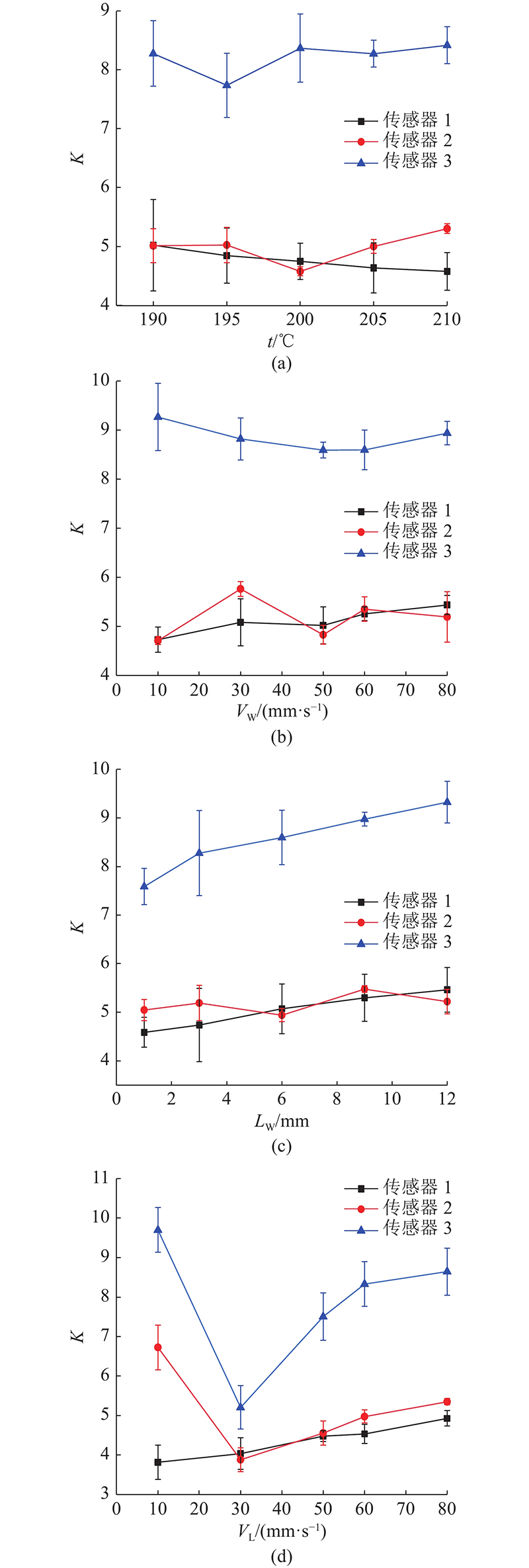
如图4所示为在峭度评价指标下,3个传感器采集计算的4种因素在不同大小的情况下振动信号峭度的误差棒图. 从图4(a)、(b)可知,对于喷头温度和回抽速率,由传感器Ⅰ信号的峭度可知,峭度关于喷头温度呈单调递减关系,峭度关于回抽速率呈单调递增关系. 由传感器Ⅱ和Ⅲ信号的峭度可知,2个传感器所采集到的振动信号不能完全识别不同喷头温度和回抽速率对峭度指标的影响. 从图4(c)可知,对于因素回抽距离,由传感器Ⅰ和Ⅲ信号的峭度可知,峭度关于回抽距离呈单调递增关系. 由传感器Ⅱ信号的峭度可知,传感器所采集到的振动信号不能完全识别不同回抽距离对峭度指标的影响. 从图4(d)可知,对于因素空驶速率,由传感器Ⅰ信号的峭度可知,峭度关于空驶速率呈单调递增关系. 由传感器Ⅱ和Ⅲ信号的峭度可知,在空驶速率达到30 mm/s前,峭度关于空驶速率呈单调递减关系,之后呈单调递增关系. 原因可能是当空驶速率为10 mm/s时,其他因素对峭度的作用开始凸显,产生这种现象. 根据以上4种因素在不同大小的情况下与峭度之间的关系,结合图2的零件拉丝现象可知,峭度越高,零件拉丝现象越不明显. 仅凭峭度这个单一特征值无法完全说明这4个因素与零件拉丝之间的关系,为了识别不同喷头温度、回抽速率、回抽距离对峭度指标的影响,借助极差分析和方差分析,在分析过程中引入峭度,可以发现喷头温度、回抽速率、回抽距离与峭度之间的规律.
图 4
图 4 不同因素水平与峭度指标的关系
Fig.4 Relationship between different factor levels and kurtosis indexes
2.1.4. 不同因素水平与峰值因子指标的关系
如图5所示为在峰值因子评价指标下,3个传感器采集计算得到的不同因素、不同水平下振动信号峰值因子的误差棒图. 从图5(a)~(d)可知,对于喷头温度、回抽速率、回抽距离、空驶速率,由传感器Ⅰ信号的峰值因子可知,峰值因子关于喷头温度呈单调递减关系. 峰值因子关于回抽速率、回抽距离、空驶速率呈单调递增关系. 由传感器Ⅲ信号的峰值因子可知,在空驶速率达到30 mm/s前,峰值因子关于空驶速率呈单调递减关系,之后呈单调递增关系. 原因可能是当空驶速率为10 mm/s时,其他因素对峰值因子的作用开始凸显,从而产生这种现象.由传感器Ⅱ和Ⅲ信号的峰值因子可知,2个传感器所采集到的振动信号无法完全识别不同喷头温度、回抽速率和回抽距离对峰值因子指标的影响.由以上这4个因素在不同情况下与峰值因子之间的关系,结合图2的零件拉丝现象可知,峰值因子越高,零件拉丝现象越不明显.
图 5
图 5 不同因素水平与峰值因子指标的关系
Fig.5 Relationship between different factor levels and peak factor indexes
2.1.5. 不同因素水平和脉冲因子指标的关系
图 6
图 6 不同因素水平与脉冲因子指标的关系
Fig.6 Relationship between different factor levels and impulse factor index
2.2. 正交试验结果与分析
2.2.1. 打印实物图
如图7所示为9组正交试验实物图. 可以看出,正交试验组S1、S8、S9拉丝比较严重,试验组S2和S6拉丝轻微,试验组S3、S5、S7几乎不拉丝. 从S1、S2和S3的试验结果对比可以看出,随着回抽速率、回抽距离和空驶速率的提高,打印零件拉丝缺陷越来越不明显. 从S3、S6和S9的试验结果对比可以看出,喷头温度、回抽距离和空驶速率对打印零件拉丝缺陷均有影响,但喷头温度与空驶速率的影响较明显. 从S2、S5和S9的试验结果对比可以看出,喷头温度、回抽速率和空驶速率对打印零件拉丝缺陷均有影响,但喷头温度和空驶速率的影响较明显. 从S2、S6和S7的试验结果对比可以看出,喷头温度、回抽距离和回抽速率对打印零件拉丝缺陷均有影响,但喷头温度与回抽距离的影响较明显.
图 7
图 7 9组正交试验的打印实物图
Fig.7 Printed physical pictures of 9 groups of orthogonal tests
从正交试验打印实物图可以看出,4个因素对打印零件拉丝缺陷均有影响,不同因素对拉丝缺陷有不同程度的影响. 仅从实物图分析,无法区别不同因素对拉丝缺陷具体的影响,需要借助统计学分析原理开展进一步的分析.
2.2.2. 极差分析
开展9组正交试验,对3个传感器所采集的振动信号进行分析处理. 在时域分析中提取出每组振动信号中相关的峭度、峰值因子和脉冲因子作为评价指标,具体的数值结果如表3所示.
表 3 3个传感器振动信号的特征指标
Tab.3
| 试验编号 | 传感器Ⅰ | 传感器Ⅱ | 传感器Ⅲ | ||||||||
| K | C | I | K | C | I | K | C | I | |||
| S1 | 6.38 | 5.54 | 5.89 | 5.17 | 3.82 | 5.18 | 4.83 | 5.48 | 6.70 | ||
| S2 | 4.88 | 4.64 | 5.73 | 4.94 | 4.32 | 5.05 | 5.71 | 4.37 | 5.71 | ||
| S3 | 6.58 | 5.47 | 7.98 | 6.62 | 4.95 | 6.33 | 6.64 | 5.77 | 7.58 | ||
| S5 | 7.24 | 7.98 | 8.26 | 7.01 | 6.07 | 6.96 | 6.86 | 6.03 | 6.45 | ||
| S6 | 4.48 | 4.40 | 5.13 | 3.90 | 3.92 | 5.27 | 3.87 | 3.79 | 4.54 | ||
| S7 | 6.05 | 5.20 | 6.58 | 5.30 | 5.32 | 6.12 | 5.07 | 5.32 | 7.02 | ||
| S8 | 4.35 | 4.81 | 5.36 | 4.56 | 3.62 | 5.34 | 4.39 | 4.83 | 5.54 | ||
| S9 | 3.65 | 4.32 | 5.02 | 3.73 | 3.29 | 5.08 | 4.14 | 3.83 | 4.96 | ||
选择极差分析法对正交试验结果进行分析,如表4所示. 表中,K1、K2、K3为特征值,
表 4 传感器Ⅰ下的指标极差分析
Tab.4
| 指标 | 因素 | K1 | K2 | K3 | | | | R | 水平主次 | 因素主次 |
| 峭度 | A | 17.85 | 17.40 | 14.04 | 5.95 | 5.80 | 4.68 | 1.27 | 1 2 3 | C > A > B > D |
| B | 18.09 | 16.47 | 14.70 | 6.03 | 5.49 | 4.90 | 1.13 | 1 2 3 | ||
| C | 15.21 | 14.19 | 19.86 | 5.07 | 4.73 | 6.62 | 1.89 | 3 1 2 | ||
| D | 17.28 | 15.42 | 16.59 | 5.76 | 5.14 | 5.53 | 0.62 | 1 3 2 | ||
| 峰值因子 | A | 15.66 | 18.75 | 14.34 | 5.22 | 6.25 | 4.78 | 1.47 | 2 1 3 | A > C > D > B |
| B | 17.10 | 17.43 | 14.19 | 5.70 | 5.81 | 4.73 | 1.08 | 2 1 3 | ||
| C | 14.76 | 15.33 | 18.66 | 4.92 | 5.11 | 6.22 | 1.30 | 3 2 1 | ||
| D | 17.85 | 14.25 | 16.65 | 5.95 | 4.75 | 5.55 | 1.20 | 1 3 2 | ||
| 脉冲因子 | A | 19.59 | 19.44 | 16.95 | 6.53 | 6.48 | 5.65 | 0.88 | 1 2 3 | C > A > D > B |
| B | 18.54 | 19.35 | 18.12 | 6.18 | 6.45 | 6.04 | 0.41 | 2 1 3 | ||
| C | 16.38 | 16.80 | 22.83 | 5.46 | 5.60 | 7.61 | 2.15 | 3 2 1 | ||
| D | 19.17 | 17.43 | 19.41 | 6.39 | 5.81 | 6.47 | 0.66 | 3 1 2 |
在对正交试验结果进行评价分析时,选择多种评价指标进行衡量,虽然会使结果更具有可信度,但是某些指标之间的矛盾性可能会使分析结果出现错误. 为了兼顾每个评价指标,找到各个指标下都尽可能好的因素和水平,选择综合平衡法[22]对试验结果进行评价分析. 在各个评价指标中,选取传感器Ⅰ下的峭度、峰值因子和脉冲因子作为主要评价指标. 原因是传感器Ⅰ监测的是送丝电机的振动信号,各个因素水平的改变都会在电机上间接体现出来,监测电机的振动信号能够准确地找到不同因素、不同水平的差异.
极差R与因素的主次有关,R大的因素为主要因素,R小的因素为次要因素. 试验结果如下. 在传感器Ⅰ下的3项试验指标中,最主要因素出现的次数为:1次A、0次B和D、2次C;最次要因素出现的次数为:0次A和C、2次B、1次D. 根据传感器Ⅰ下的指标极差分析可以确定:C为最主要因素,A为较主要因素,D为较次要因素,B为最次要因素. 在传感器Ⅱ下的3项试验指标中,最主要因素出现的次数为:0次A、B和D,3次C;最次要因素出现的次数为:0次A和C,1次B,2次D. 根据传感器Ⅱ下的指标极差分析可以确定:C为最主要因素,A为较主要因素,B为较次要因素,D为最次要因素. 在传感器Ⅲ下的3项试验指标中,最主要因素出现的次数为:0次A、B和D,1次C;最次要因素出现的次数为:1次A,1次B,0次C,1次D. 根据传感器Ⅲ下的指标极差分析可以确定:C为主要因素,A、B和D为次要因素.
根据试验结果可知,在9项试验指标中,最主要因素出现的次数为:1次A,0次B和D,7次C;最次要因素出现的次数为:1次A,4次B,0次C,4次D. 在3项主要的试验指标中,最主要因素出现的次数为:1次A,0次B和D,2次C;最次要因素出现的次数为:0次A和C,1次B,2次D. 综上所述,可以确定回抽距离C为最主要因素,喷头温度A为较主要因素,回抽速率B为较次要因素,空驶速率D为次要因素.
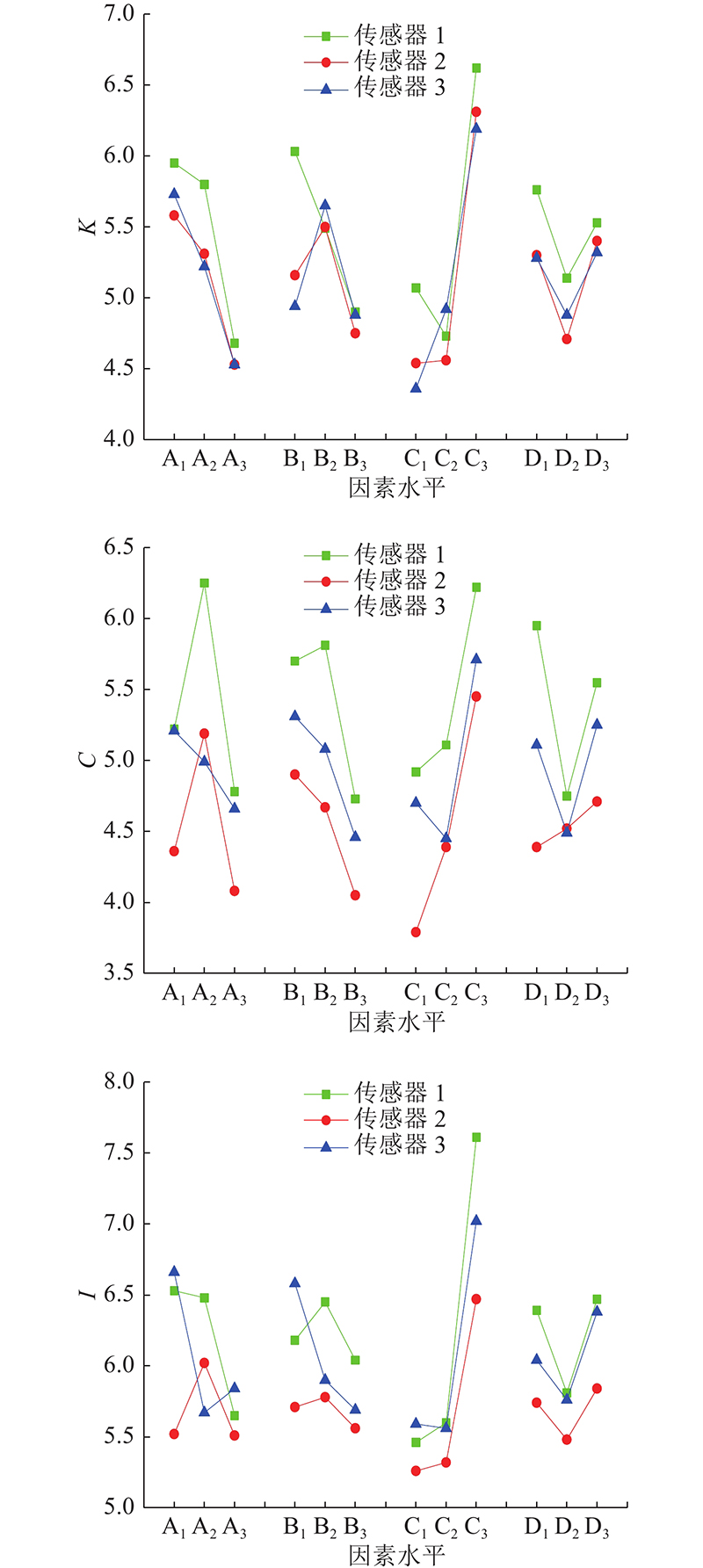
从实验结果和图8可知,对于喷头温度因素A,最优水平出现的次数为:5次A1,3次A2,1次A3;最次水平出现的次数为:1次A1,1次A2,7次A3. 在3个主要指标中,A1出现2次,A2出现1次,A3出现0次;最次水平出现的次数为:0次A1和A2,3次A3. 综合分析可以确定最优水平为A1. 同理可知,对于回抽速率因素B,最优水平为B2;对于回抽距离因素C,最优水平为C3;对于空驶速率因素D,最优水平为D3.
图 8
图 8 各传感器指标与因素的水平趋势图
Fig.8 Horizontal trend diagram of various sensor indicators and factors
综上所述,在极差分析方法下,根据结果可以确定最优组合为A1B2C3D3. 考虑到打印效率与机械的寿命问题,将空驶速率从D3调到D2,故该研究推荐的最优组合为A1B2C3D2,即喷头温度为190 ℃,回抽速率为50 mm/s,回抽距离为12 mm,空驶速率为50 mm/s.
2.2.3. 方差分析
极差分析没有考虑试验数据波动是由试验误差引起的还是由试验条件改变引起的,仅通过极差分析法对正交试验进行分析. 引入方差分析法,能够更好地对结论进行佐证. 上述正交试验设计是四因素三水平,没有误差项,因此每组试验重复3次.
通过查询F分布表可知,F0.05 (2,18) = 3.55,F0.01(2,18) = 6.01. 表5中,df为自由度,SS为平方和,MS为均方和. 根据表5可知,满足F > F0.01(2,18)的情况只有A出现了1次,C出现了2次;满足F > F0.05(2,18)的情况,A出现了3次,B出现了1次,C出现了3次,D出现了1次. 从总体评估可以确定C为极显著因素,A为显著因素,B和D为不显著因素. 从因素的主次顺序来看,最主要因素出现的次数为:1次A,0次B和D,2次C;最次要因素出现的次数为:0次A和C,1次B,2次D. 通过因素的主次顺序可以确定:C为极显著因素,A为显著因素,B为较显著因素,D为不显著因素. 综合2种评估方法可知,C为极显著因素,A为显著因素,B为较显著因素,D为不显著因素,所得的结论与极差分析一致.
表 5 峭度指标方差分析
Tab.5
| 指标 | 方差来源 | df | SS | MS | F |
| 传感器Ⅰ峭度 | A | 2 | 8.53 | 4.27 | 5.47 |
| B | 2 | 5.00 | 2.50 | 3.21 | |
| C | 2 | 17.34 | 8.67 | 11.13 | |
| D | 2 | 1.85 | 0.93 | 1.19 | |
| 传感器Ⅱ峭度 | A | 2 | 9.94 | 4.97 | 7.42 |
| B | 2 | 5.88 | 2.94 | 4.39 | |
| C | 2 | 7.49 | 3.75 | 5.59 | |
| D | 2 | 5.01 | 2.51 | 3.74 | |
| 传感器Ⅲ峭度 | A | 2 | 5.56 | 2.78 | 4.09 |
| B | 2 | 1.03 | 0.52 | 0.76 | |
| C | 2 | 26.59 | 13.29 | 19.59 | |
| D | 2 | 2.05 | 1.02 | 1.51 |
根据峰值因子方差的结果可知,满足F > F0.01(2,18)的情况只有C出现了2次;满足F > F0.05(2,18)的情况,只有A出现了2次,C出现了3次. 从总体评估可以确定:C为极显著因素,A为显著因素,B和D为不显著因素. 从因素的主次顺序来看,最主要因素出现的次数为:0次A、B和D,3次C;最次要因素出现的次数为:0次A和C,1次B,2次D. 通过因素的主次顺序可以确定:C为极显著因素,A为显著因素,B为较显著因素,D为不显著因素. 综合2种评估方法可知,C为极显著因素,A为显著因素,B为较显著因素,D为不显著因素,所得的结论与极差分析一致.
根据脉冲因子方差的结果可知,满足F > F0.01(2,18)的情况,只有C出现了3次;满足F > F0.05(2,18)的情况,A出现了2次,B出现了1次,C出现了3次,D出现了0次. 从总体评估可以确定:C为极显著因素,A为显著因素,B为较显著因素,D为不显著因素. 从因素的主次顺序来看,最主要因素出现的次数为:0次A、B和D,3次C;最次要因素出现的次数为:1次A,0次B和C,1次D. 通过因素的主次顺序可以确定:C为极显著因素,B为显著因素,A和D为较显著因素. 综合2种评估方法可知,C为极显著因素,A为显著因素,B为较显著因素,D为不显著因素,所得的结论与极差分析一致.
综上所述,满足F > F0.01(2,18)的情况,只有A出现了1次,C出现了7次;满足F > F0.05(2,18)的情况,A出现了7次,B出现了2次,C出现了9次,D出现了1次. 从总体评估可以确定:C为极显著因素,A为显著因素,B为较显著因素,D为不显著因素. 对于3组主要的试验指标,最主要因素出现的次数为:0次A、B和D,3次C;最次要因素出现的次数为:0次A、B和C,3次D. 通过3组主要试验指标可以确定:C为极显著因素,A为显著因素,B为较显著因素,D为不显著因素. 从上述多角度方差分析可知,所得的结论与极差分析一致.
3. 结 论
(1)基于加速度振动传感器在线监测方法,可以对打印零件拉丝缺陷进行识别. 通过对采集的振动信号在时域中进行分析,提取出峭度、峰值因子和脉冲因子这些特征参数,利用不同因素、不同水平下得到的信号特征参数,可以确定打印零件的拉丝缺陷情况.
(2)通过单因素试验与正交试验,分析喷头温度、回抽速率、回抽距离、空驶速率这4个因素对零件打印拉丝缺陷的影响,用特征参数对试验结果进行分析.极差分析与方差分析均表明,回抽距离为极显著因素,喷头温度为显著因素,回抽速率为较显著因素,空驶速率为不显著因素.
(3)综合考虑3D打印过程中零件的质量与机器的使用寿命,避免PLA材料在打印过程中出现拉丝缺陷的4个因素的最优组合为:喷头温度为190 ℃,回抽速率为50 mm/s,回抽距离为12 mm,空驶速率为50 mm/s.该参数可以为其他FDM型3D打印提供参考.
(4) 从单因素试验分析结果可以看出,本试验选择的振动传感器监测点有待进一步的优化,应使每个监测点尽可能地监测到每个因素水平改变时振动信号的变化.
参考文献
Overview on additive manufacturing technologies
[J].DOI:10.1109/JPROC.2017.2676643 [本文引用: 1]
Metal additive manufacturing: technology, metallurgy and modeling
[J].
增材制造技术: 现状与未来
[J].
Additive manufacturing technology: status quo and future
[J].
激光增材制造技术及现状研究
[J].
Research on laser additive manufacturing technology and present situation
[J].
3D printing technology and its application in industrial manufacturing
[J].DOI:10.1088/1757-899X/782/2/022065 [本文引用: 1]
3D打印混凝土层条间界面抗拉性能与本构模型
[J].
Tensile performance and constitutive model of interface between 3D printed concrete layers
[J].
航空航天高性能金属材料构件激光增材制造
[J].
Laser additive manufacturing of high-performance metal material components in aerospace
[J].
3D printing for developing patient specific cosmetic prosthetics at the point of care
[J].
Recent advances and future perspective in additive manufacturing of foods based on 3D printing
[J].DOI:10.1016/j.cofs.2020.01.009 [本文引用: 1]
Factors effecting real-time optical monitoring of fused filament 3D printing
[J].DOI:10.1007/s40964-017-0027-x [本文引用: 1]
A dynamic model for current-based nozzle condition monitoring in fused deposition modeling
[J].
Dimensional accuracy evaluation of temporary dental restorations with different 3D printing systems
[J].DOI:10.3390/ma14061487 [本文引用: 1]
Improving geometric accuracy of 3D printed parts using 3D metrology feedback and mesh morphing
[J].DOI:10.3390/jmmp4040112 [本文引用: 1]
Effects of part build orientations on fatigue behaviour of FDM-processed PLA material
[J].DOI:10.1007/s40964-015-0002-3 [本文引用: 1]
In situ monitoring of FDM machine condition via acoustic emission
[J].
熔融层积成型(FDM)3D打印中切片参数对拉丝现象的工艺影响研究
[J].DOI:10.3969/j.issn.1009-9492.2019.06.005 [本文引用: 1]
Effect of slice parameters on wiredrawing phenomenon in FDM 3D printing
[J].DOI:10.3969/j.issn.1009-9492.2019.06.005 [本文引用: 1]
FDM 3D打印参数对打印件精度的影响研究
[J].
Study on the influence of FDM 3D printing parameters on the precision of printing parts
[J].
FDM型增材制造中送丝机构动态监测与识别
[J].
Dynamic monitoring and identification of wire feeding mechanism in FDM type additive manufacturing
[J].
基于振动信号指标能量的变压器机械故障检测
[J].DOI:10.19753/j.issn1001-1390.2020.06.020 [本文引用: 1]
Transformer mechanical fault detection based on vibration signal index energy
[J].DOI:10.19753/j.issn1001-1390.2020.06.020 [本文引用: 1]
基于正交试验的并联机构刚度回归模型求解分析
[J].DOI:10.11936/bjutxb2013121798 [本文引用: 1]
Solving and analysis of stiffness regression model of parallel mechanism based on orthogonal test
[J].DOI:10.11936/bjutxb2013121798 [本文引用: 1]
基于正交试验设计的层状盐岩地下储库群多因素优化研究
[J].DOI:10.16285/j.rsm.2014.06.015 [本文引用: 1]
Multi-factor optimization of layered salt rock underground storage group based on orthogonal experimental design
[J].DOI:10.16285/j.rsm.2014.06.015 [本文引用: 1]