[1]
RAISSI M, PERDIKARIS P, KARNIADAKIS G E Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations
[J]. Journal of Computational Physics , 2019 , 378 : 686 - 707
DOI:10.1016/j.jcp.2018.10.045
[本文引用: 1]
[2]
BAYDIN A G, PEARLMUTTER B A, RADUL A A, et al Automatic differentiation in machine learning: a survey
[J]. Journal of Machine Learning Research , 2018 , 18 : 1 - 43
[本文引用: 1]
[3]
RAISSI M, YAZDANI A, KARNIADAKIS G E Hidden fluid mechanics: Learning velocity and pressure fields from flow visualizations
[J]. Science , 2020 , 367 (6481 ): 1026 - 1030
DOI:10.1126/science.aaw4741
[本文引用: 1]
[4]
JIN X W, CAI S Z, LI H, et al NSFnets (Navier-Stokes flow nets): physics-informed neural networks for the incompressible Navier-Stokes equations
[J]. Journal of Computational Physics , 2021 , 426 : 109951
DOI:10.1016/j.jcp.2020.109951
[本文引用: 1]
[5]
MAO Z P, JAGTAP A D, KARNIADAKIS G E Physics-informed neural networks for high-speed flows
[J]. Computer Methods in Applied Mechanics and Engineering , 2020 , 360 : 112789
DOI:10.1016/j.cma.2019.112789
[本文引用: 1]
[6]
KUMAR A, RIDHA S, NARAHARI M, et al Physics-guided deep neural network to characterize non-Newtonian fluid flow for optimal use of energy resources
[J]. Expert Systems with Applications , 2021 , 183 : 115409
DOI:10.1016/j.eswa.2021.115409
[本文引用: 1]
[7]
赵暾, 周宇, 程艳青, 等 基于内嵌物理机理神经网络的热传导方程的正问题及逆问题求解
[J]. 空气动力学学报 , 2021 , 39 (5 ): 19 - 26
DOI:10.7638/kqdlxxb-2020.0176
[本文引用: 1]
ZHAO Tun, ZHOU Yu, CHENG Yan-qing, et al Solving forward and inverse problems of partial differential equations of heat conduction using physics-informed neural networks
[J]. Acta Aerodynamica Sinica , 2021 , 39 (5 ): 19 - 26
DOI:10.7638/kqdlxxb-2020.0176
[本文引用: 1]
[8]
ZOBEIRY N, HUMFELD K D A physics-informed machine learning approach for solving heat transfer equation in advanced manufacturing and engineering applications
[J]. Engineering Applications of Artificial Intelligence , 2021 , 101 : 104232
DOI:10.1016/j.engappai.2021.104232
[9]
陆至彬, 瞿景辉, 刘桦, 等 基于物理信息神经网络的传热过程物理场代理模型的构建
[J]. 化工学报 , 2021 , 72 (3 ): 1496 - 1503
DOI:10.11949/0438-1157.20201879
[本文引用: 2]
LU Zhi-bin, QU Jing-hui, LIU Hua, et al Surrogate modeling for physical fields of heat transfer processes based on physics-informed neural network
[J]. Journal of Chemical Industry and Engineering (China) , 2021 , 72 (3 ): 1496 - 1503
DOI:10.11949/0438-1157.20201879
[本文引用: 2]
[10]
PENG G, ALBER M, TEPOLE A B, et al Multiscale modeling meets machine learning: what can we learn?
[J]. Archives of Computational Methods in Engineering , 2021 , 28 (3 ): 1017 - 1037
DOI:10.1007/s11831-020-09405-5
[本文引用: 1]
[11]
HUANG Y, ZHANG Z, ZHANG X A direct-forcing immersed boundary method for incompressible flows based on physics-informed neural network
[J]. Fluids , 2022 , 7 (2 ): 56
DOI:10.3390/fluids7020056
[本文引用: 1]
[12]
FUKS O, TCHELEPI H A Limitations of physics informed machine learning for nonlinear two-phase transport in porous media
[J]. Journal of Machine Learning for Modeling and Computing , 2020 , 1 (1 ): 19 - 37
DOI:10.1615/JMachLearnModelComput.2020033905
[本文引用: 1]
[13]
JI W, QIU W, SHI Z, et al Stiff-pinn: physics-informed neural network for stiff chemical kinetics
[J]. The Journal of Physical Chemistry A , 2021 , 125 (36 ): 8098 - 8106
DOI:10.1021/acs.jpca.1c05102
[本文引用: 2]
[14]
KNIO O M, NAJM H N, WYCKOFF P S A semi-implicit numerical scheme for reacting flow II. Stiff, operator-split formulation
[J]. Journal of Computational Physics , 1999 , 154 (2 ): 428 - 467
DOI:10.1006/jcph.1999.6322
[本文引用: 1]
[15]
LANSER D, VERWER J G Analysis of operator splitting for advection-diffusion-reaction problems from air pollution modelling
[J]. Journal of Computational and Applied Mathematics , 1999 , 111 (1/2 ): 201 - 216
DOI:10.1016/S0377-0427(99)00143-0
[16]
ORAN E S, BORIS J P, BORIS J P. Numerical simulation of reactive flow [M]. Cambridge: Cambridge University Press, 2001.
[本文引用: 1]
[17]
SPORTISSE B An analysis of operator splitting techniques in the stiff case
[J]. Journal of Computational Physics , 2000 , 161 (1 ): 140 - 168
DOI:10.1006/jcph.2000.6495
[本文引用: 1]
[18]
GICQUEL L, STAFFELBACH G, POINSOT T Large eddy simulations of gaseous flames in gas turbine combustion chambers
[J]. Progress in Energy and Combustion Science , 2012 , 38 (6 ): 782 - 817
DOI:10.1016/j.pecs.2012.04.004
[本文引用: 1]
[19]
夏一帆. 面向航空发动机燃烧室点火问题的数值计算方法研究[D]. 杭州: 浙江大学, 2019.
[本文引用: 1]
XIA Yi-fan. A study of numerical methods for the ignition process in aeroengine combustors [D]. Hangzhou: Zhejiang University, 2019.
[本文引用: 1]
[20]
ECHEKKI T, MASTORAKOS E. Turbulent combustion modeling: Advances, new trends and perspectives [M]. Berlin: Springer, 2010.
[本文引用: 1]
[21]
LU L, MENG X H, MAO Z P, et al DeepXDE: A deep learning library for solving differential equations
[J]. SIAM Review , 2021 , 63 (1 ): 208 - 228
DOI:10.1137/19M1274067
[本文引用: 4]
[22]
NABIAN M A, GLADSTONE R J, MEIDANI H Efficient training of physics-informed neural networks via importance sampling
[J]. Computer-Aided Civil and Infrastructure Engineering , 2021 , 36 (8 ): 962 - 977
DOI:10.1111/mice.12685
[本文引用: 1]
[23]
武育宏. 基于物理机制的深度神经网络在数值求解非线性Degasperis-Procesi方程中的应用[D]. 上海: 上海师范大学, 2020.
[本文引用: 1]
WU Yu-hong. Application of physics-informed neural network in numerical solving of nonlinear Degasperis-Procesi equation [D]. Shanghai: Shanghai Normal University, 2020.
[本文引用: 1]
[24]
WANNER G, HAIRER E. Solving ordinary differential equations II [M]. Berlin: Springer, 1996.
[本文引用: 2]
[25]
ABADI M, BARHAM P, CHEN J, et al. TensorFlow: a system for large-scale machine learning [C]// 12th USENIX Symposium on Operating Systems Design and Implementation . Savannah: USENIX Association, 2016: 265-283.
[本文引用: 1]
[26]
WELLER H G, TABOR G, JASAK H, et al A tensorial approach to computational continuum mechanics using object-oriented techniques
[J]. Computers in Physics , 1998 , 12 (6 ): 620 - 631
DOI:10.1063/1.168744
[本文引用: 1]
[28]
GLOROT X, BENGIO Y. Understanding the difficulty of training deep feedforward neural networks [C]// Proceedings of the 13th International Conference on Artificial Intelligence and Statistics . Sardinia: [s. n.], 2010: 249-256.
[本文引用: 1]
[29]
KINGMA D P, BA J. Adam: A method for stochastic optimization [EB/OL]. [2022-03-01]. https://arxiv.org/abs/1412.6980.
[本文引用: 1]
[30]
LAGARIS I E, LIKAS A, FOTIADIS D I Artificial neural networks for solving ordinary and partial differential equations
[J]. IEEE Transactions on Neural Networks , 1998 , 9 (5 ): 987 - 1000
DOI:10.1109/72.712178
[本文引用: 1]
[31]
VAN OIJEN J A, LAMMERS F A, DE GOEY L Modeling of complex premixed burner systems by using flamelet-generated manifolds
[J]. Combustion and Flame , 2001 , 127 (3 ): 2124 - 2134
DOI:10.1016/S0010-2180(01)00316-9
[本文引用: 1]
[32]
PIERCE C D, MOIN P Progress-variable approach for large-eddy simulation of non-premixed turbulent combustion
[J]. Journal of Fluid Mechanics , 2004 , 504 : 73 - 97
DOI:10.1017/S0022112004008213
[本文引用: 1]
[33]
BILGER R W, STARNER S H, KEE R J On reduced mechanisms for methane air combustion in nonpremixed flames
[J]. Combustion and Flame , 1990 , 80 (2 ): 135 - 149
DOI:10.1016/0010-2180(90)90122-8
[本文引用: 1]
[34]
NAKAMURA M, AKAMATSU F, KUROSE R, et al Combustion mechanism of liquid fuel spray in a gaseous flame
[J]. Physics of Fluids , 2005 , 17 (12 ): 123301
DOI:10.1063/1.2140294
[本文引用: 1]
[35]
POINSOT T, VEYNANTE D. Theoretical and numerical combustion [M]. Philadelphia: R. T. Edwards Inc. , 2005.
[本文引用: 3]
Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations
1
2019
... 近年来,机器学习(machine learning,ML)方法在计算机视觉、自然语言处理和智能机器人等多项任务中取得了成功的应用,近期在科学计算领域中掀起了机器学习的热潮. 湍流、多相流和燃烧数值模拟技术以计算流体力学(computational fluid dynamics,CFD)为核心,本质上是各种偏微分方程和常微分方程的求解,求解微分方程组是代价高昂的计算密集型任务. 研究者们试图利用机器学习技术求解传统数值模拟中的复杂微分方程,以加速数值模拟过程,在保持一定精度的前提下,提高数值模拟的效率. Raissi等[1 ] 利用自动微分的最新进展[2 ] ,提出物理信息神经网络(physics-informed neural networks,PINNs),并成功用于解决涉及非线性偏微分方程的正向问题和反向问题. PINNs模型有别于那些被视为“黑盒”工具的传统机器学习算法,除了可以利用物理系统产生的数据样本,还能够充分利用物理系统的内在规律,将物理信息融入到机器学习模型中,可以在小数据集样本上取得较好的训练效果[3 ] . ...
Automatic differentiation in machine learning: a survey
1
2018
... 近年来,机器学习(machine learning,ML)方法在计算机视觉、自然语言处理和智能机器人等多项任务中取得了成功的应用,近期在科学计算领域中掀起了机器学习的热潮. 湍流、多相流和燃烧数值模拟技术以计算流体力学(computational fluid dynamics,CFD)为核心,本质上是各种偏微分方程和常微分方程的求解,求解微分方程组是代价高昂的计算密集型任务. 研究者们试图利用机器学习技术求解传统数值模拟中的复杂微分方程,以加速数值模拟过程,在保持一定精度的前提下,提高数值模拟的效率. Raissi等[1 ] 利用自动微分的最新进展[2 ] ,提出物理信息神经网络(physics-informed neural networks,PINNs),并成功用于解决涉及非线性偏微分方程的正向问题和反向问题. PINNs模型有别于那些被视为“黑盒”工具的传统机器学习算法,除了可以利用物理系统产生的数据样本,还能够充分利用物理系统的内在规律,将物理信息融入到机器学习模型中,可以在小数据集样本上取得较好的训练效果[3 ] . ...
Hidden fluid mechanics: Learning velocity and pressure fields from flow visualizations
1
2020
... 近年来,机器学习(machine learning,ML)方法在计算机视觉、自然语言处理和智能机器人等多项任务中取得了成功的应用,近期在科学计算领域中掀起了机器学习的热潮. 湍流、多相流和燃烧数值模拟技术以计算流体力学(computational fluid dynamics,CFD)为核心,本质上是各种偏微分方程和常微分方程的求解,求解微分方程组是代价高昂的计算密集型任务. 研究者们试图利用机器学习技术求解传统数值模拟中的复杂微分方程,以加速数值模拟过程,在保持一定精度的前提下,提高数值模拟的效率. Raissi等[1 ] 利用自动微分的最新进展[2 ] ,提出物理信息神经网络(physics-informed neural networks,PINNs),并成功用于解决涉及非线性偏微分方程的正向问题和反向问题. PINNs模型有别于那些被视为“黑盒”工具的传统机器学习算法,除了可以利用物理系统产生的数据样本,还能够充分利用物理系统的内在规律,将物理信息融入到机器学习模型中,可以在小数据集样本上取得较好的训练效果[3 ] . ...
NSFnets (Navier-Stokes flow nets): physics-informed neural networks for the incompressible Navier-Stokes equations
1
2021
... 目前,已有相关研究者基于PINNs求解其遇到的多种微分方程,涵盖的领域包括不可压流动[4 ] 、高速流动[5 ] 、非牛顿流体[6 ] 、传热学[7 -9 ] 、生命科学[10 ] 等,在多相流领域中出现了初步研究[11 -12 ] . 应用于燃烧化学领域内微分方程求解的研究[13 ] 较少,这主要是在燃烧数值模拟中所遇到的化学反应常微分方程组(system of ordinary differential equations,SODEs)具有很强的刚性,即便采用算子分裂方法(operator splitting)[14 -16 ] 将输运方程中的化学反应项与其他输运项解耦[17 ] ,在一定程度上降低了计算量,也需要耗费大量的计算资源. 实际的湍流燃烧系统包含很宽的化学反应时间尺度[18 ] ,一步反应不能描述不同的化学时间尺度,对流动耦合作用的描述存在不足. 许多燃烧过程,比如点火、熄火、污染物生成(NOx [19 ] ,这些过程无法通过简单的一步反应或者两步反应来精确描述[20 ] . 采用包含更多组分、更多步基元反应的机理,这进一步增大了刚性常微分方程组的复杂性,而这些复杂性给湍流燃烧的PINNs建模带来很大挑战. ...
Physics-informed neural networks for high-speed flows
1
2020
... 目前,已有相关研究者基于PINNs求解其遇到的多种微分方程,涵盖的领域包括不可压流动[4 ] 、高速流动[5 ] 、非牛顿流体[6 ] 、传热学[7 -9 ] 、生命科学[10 ] 等,在多相流领域中出现了初步研究[11 -12 ] . 应用于燃烧化学领域内微分方程求解的研究[13 ] 较少,这主要是在燃烧数值模拟中所遇到的化学反应常微分方程组(system of ordinary differential equations,SODEs)具有很强的刚性,即便采用算子分裂方法(operator splitting)[14 -16 ] 将输运方程中的化学反应项与其他输运项解耦[17 ] ,在一定程度上降低了计算量,也需要耗费大量的计算资源. 实际的湍流燃烧系统包含很宽的化学反应时间尺度[18 ] ,一步反应不能描述不同的化学时间尺度,对流动耦合作用的描述存在不足. 许多燃烧过程,比如点火、熄火、污染物生成(NOx [19 ] ,这些过程无法通过简单的一步反应或者两步反应来精确描述[20 ] . 采用包含更多组分、更多步基元反应的机理,这进一步增大了刚性常微分方程组的复杂性,而这些复杂性给湍流燃烧的PINNs建模带来很大挑战. ...
Physics-guided deep neural network to characterize non-Newtonian fluid flow for optimal use of energy resources
1
2021
... 目前,已有相关研究者基于PINNs求解其遇到的多种微分方程,涵盖的领域包括不可压流动[4 ] 、高速流动[5 ] 、非牛顿流体[6 ] 、传热学[7 -9 ] 、生命科学[10 ] 等,在多相流领域中出现了初步研究[11 -12 ] . 应用于燃烧化学领域内微分方程求解的研究[13 ] 较少,这主要是在燃烧数值模拟中所遇到的化学反应常微分方程组(system of ordinary differential equations,SODEs)具有很强的刚性,即便采用算子分裂方法(operator splitting)[14 -16 ] 将输运方程中的化学反应项与其他输运项解耦[17 ] ,在一定程度上降低了计算量,也需要耗费大量的计算资源. 实际的湍流燃烧系统包含很宽的化学反应时间尺度[18 ] ,一步反应不能描述不同的化学时间尺度,对流动耦合作用的描述存在不足. 许多燃烧过程,比如点火、熄火、污染物生成(NOx [19 ] ,这些过程无法通过简单的一步反应或者两步反应来精确描述[20 ] . 采用包含更多组分、更多步基元反应的机理,这进一步增大了刚性常微分方程组的复杂性,而这些复杂性给湍流燃烧的PINNs建模带来很大挑战. ...
基于内嵌物理机理神经网络的热传导方程的正问题及逆问题求解
1
2021
... 目前,已有相关研究者基于PINNs求解其遇到的多种微分方程,涵盖的领域包括不可压流动[4 ] 、高速流动[5 ] 、非牛顿流体[6 ] 、传热学[7 -9 ] 、生命科学[10 ] 等,在多相流领域中出现了初步研究[11 -12 ] . 应用于燃烧化学领域内微分方程求解的研究[13 ] 较少,这主要是在燃烧数值模拟中所遇到的化学反应常微分方程组(system of ordinary differential equations,SODEs)具有很强的刚性,即便采用算子分裂方法(operator splitting)[14 -16 ] 将输运方程中的化学反应项与其他输运项解耦[17 ] ,在一定程度上降低了计算量,也需要耗费大量的计算资源. 实际的湍流燃烧系统包含很宽的化学反应时间尺度[18 ] ,一步反应不能描述不同的化学时间尺度,对流动耦合作用的描述存在不足. 许多燃烧过程,比如点火、熄火、污染物生成(NOx [19 ] ,这些过程无法通过简单的一步反应或者两步反应来精确描述[20 ] . 采用包含更多组分、更多步基元反应的机理,这进一步增大了刚性常微分方程组的复杂性,而这些复杂性给湍流燃烧的PINNs建模带来很大挑战. ...
基于内嵌物理机理神经网络的热传导方程的正问题及逆问题求解
1
2021
... 目前,已有相关研究者基于PINNs求解其遇到的多种微分方程,涵盖的领域包括不可压流动[4 ] 、高速流动[5 ] 、非牛顿流体[6 ] 、传热学[7 -9 ] 、生命科学[10 ] 等,在多相流领域中出现了初步研究[11 -12 ] . 应用于燃烧化学领域内微分方程求解的研究[13 ] 较少,这主要是在燃烧数值模拟中所遇到的化学反应常微分方程组(system of ordinary differential equations,SODEs)具有很强的刚性,即便采用算子分裂方法(operator splitting)[14 -16 ] 将输运方程中的化学反应项与其他输运项解耦[17 ] ,在一定程度上降低了计算量,也需要耗费大量的计算资源. 实际的湍流燃烧系统包含很宽的化学反应时间尺度[18 ] ,一步反应不能描述不同的化学时间尺度,对流动耦合作用的描述存在不足. 许多燃烧过程,比如点火、熄火、污染物生成(NOx [19 ] ,这些过程无法通过简单的一步反应或者两步反应来精确描述[20 ] . 采用包含更多组分、更多步基元反应的机理,这进一步增大了刚性常微分方程组的复杂性,而这些复杂性给湍流燃烧的PINNs建模带来很大挑战. ...
A physics-informed machine learning approach for solving heat transfer equation in advanced manufacturing and engineering applications
0
2021
基于物理信息神经网络的传热过程物理场代理模型的构建
2
2021
... 目前,已有相关研究者基于PINNs求解其遇到的多种微分方程,涵盖的领域包括不可压流动[4 ] 、高速流动[5 ] 、非牛顿流体[6 ] 、传热学[7 -9 ] 、生命科学[10 ] 等,在多相流领域中出现了初步研究[11 -12 ] . 应用于燃烧化学领域内微分方程求解的研究[13 ] 较少,这主要是在燃烧数值模拟中所遇到的化学反应常微分方程组(system of ordinary differential equations,SODEs)具有很强的刚性,即便采用算子分裂方法(operator splitting)[14 -16 ] 将输运方程中的化学反应项与其他输运项解耦[17 ] ,在一定程度上降低了计算量,也需要耗费大量的计算资源. 实际的湍流燃烧系统包含很宽的化学反应时间尺度[18 ] ,一步反应不能描述不同的化学时间尺度,对流动耦合作用的描述存在不足. 许多燃烧过程,比如点火、熄火、污染物生成(NOx [19 ] ,这些过程无法通过简单的一步反应或者两步反应来精确描述[20 ] . 采用包含更多组分、更多步基元反应的机理,这进一步增大了刚性常微分方程组的复杂性,而这些复杂性给湍流燃烧的PINNs建模带来很大挑战. ...
... 实质上,在默认情况下,DeepXDE通过损失函数的方式来使计算结果满足给定的初始和边界条件,这是一种软约束[21 ] . 对于本文案例,可以采用更直接的硬边界方式[30 ] ,使得网络结构输出满足给定的初始条件. 陆至彬等[9 ] 针对传热问题求解,评估了软边界和硬边界2种方法所构建PINNs模型的性能. 结果表明,硬边界PINNs模型的预测能力较优. 为了降低SODEs的刚度,Ji等[13 ] 采用准稳态假设(quasi steady state assumptions,QSSA)的方法对方程进行变换,提出Stiff-PINN模型,取得了较好的预测结果. 本文案例无需QSSA,采用硬边界约束的方式. 下面证明硬边界PINNs的优势. 对于ROBER问题,本文提供的输出转换如下: ...
基于物理信息神经网络的传热过程物理场代理模型的构建
2
2021
... 目前,已有相关研究者基于PINNs求解其遇到的多种微分方程,涵盖的领域包括不可压流动[4 ] 、高速流动[5 ] 、非牛顿流体[6 ] 、传热学[7 -9 ] 、生命科学[10 ] 等,在多相流领域中出现了初步研究[11 -12 ] . 应用于燃烧化学领域内微分方程求解的研究[13 ] 较少,这主要是在燃烧数值模拟中所遇到的化学反应常微分方程组(system of ordinary differential equations,SODEs)具有很强的刚性,即便采用算子分裂方法(operator splitting)[14 -16 ] 将输运方程中的化学反应项与其他输运项解耦[17 ] ,在一定程度上降低了计算量,也需要耗费大量的计算资源. 实际的湍流燃烧系统包含很宽的化学反应时间尺度[18 ] ,一步反应不能描述不同的化学时间尺度,对流动耦合作用的描述存在不足. 许多燃烧过程,比如点火、熄火、污染物生成(NOx [19 ] ,这些过程无法通过简单的一步反应或者两步反应来精确描述[20 ] . 采用包含更多组分、更多步基元反应的机理,这进一步增大了刚性常微分方程组的复杂性,而这些复杂性给湍流燃烧的PINNs建模带来很大挑战. ...
... 实质上,在默认情况下,DeepXDE通过损失函数的方式来使计算结果满足给定的初始和边界条件,这是一种软约束[21 ] . 对于本文案例,可以采用更直接的硬边界方式[30 ] ,使得网络结构输出满足给定的初始条件. 陆至彬等[9 ] 针对传热问题求解,评估了软边界和硬边界2种方法所构建PINNs模型的性能. 结果表明,硬边界PINNs模型的预测能力较优. 为了降低SODEs的刚度,Ji等[13 ] 采用准稳态假设(quasi steady state assumptions,QSSA)的方法对方程进行变换,提出Stiff-PINN模型,取得了较好的预测结果. 本文案例无需QSSA,采用硬边界约束的方式. 下面证明硬边界PINNs的优势. 对于ROBER问题,本文提供的输出转换如下: ...
Multiscale modeling meets machine learning: what can we learn?
1
2021
... 目前,已有相关研究者基于PINNs求解其遇到的多种微分方程,涵盖的领域包括不可压流动[4 ] 、高速流动[5 ] 、非牛顿流体[6 ] 、传热学[7 -9 ] 、生命科学[10 ] 等,在多相流领域中出现了初步研究[11 -12 ] . 应用于燃烧化学领域内微分方程求解的研究[13 ] 较少,这主要是在燃烧数值模拟中所遇到的化学反应常微分方程组(system of ordinary differential equations,SODEs)具有很强的刚性,即便采用算子分裂方法(operator splitting)[14 -16 ] 将输运方程中的化学反应项与其他输运项解耦[17 ] ,在一定程度上降低了计算量,也需要耗费大量的计算资源. 实际的湍流燃烧系统包含很宽的化学反应时间尺度[18 ] ,一步反应不能描述不同的化学时间尺度,对流动耦合作用的描述存在不足. 许多燃烧过程,比如点火、熄火、污染物生成(NOx [19 ] ,这些过程无法通过简单的一步反应或者两步反应来精确描述[20 ] . 采用包含更多组分、更多步基元反应的机理,这进一步增大了刚性常微分方程组的复杂性,而这些复杂性给湍流燃烧的PINNs建模带来很大挑战. ...
A direct-forcing immersed boundary method for incompressible flows based on physics-informed neural network
1
2022
... 目前,已有相关研究者基于PINNs求解其遇到的多种微分方程,涵盖的领域包括不可压流动[4 ] 、高速流动[5 ] 、非牛顿流体[6 ] 、传热学[7 -9 ] 、生命科学[10 ] 等,在多相流领域中出现了初步研究[11 -12 ] . 应用于燃烧化学领域内微分方程求解的研究[13 ] 较少,这主要是在燃烧数值模拟中所遇到的化学反应常微分方程组(system of ordinary differential equations,SODEs)具有很强的刚性,即便采用算子分裂方法(operator splitting)[14 -16 ] 将输运方程中的化学反应项与其他输运项解耦[17 ] ,在一定程度上降低了计算量,也需要耗费大量的计算资源. 实际的湍流燃烧系统包含很宽的化学反应时间尺度[18 ] ,一步反应不能描述不同的化学时间尺度,对流动耦合作用的描述存在不足. 许多燃烧过程,比如点火、熄火、污染物生成(NOx [19 ] ,这些过程无法通过简单的一步反应或者两步反应来精确描述[20 ] . 采用包含更多组分、更多步基元反应的机理,这进一步增大了刚性常微分方程组的复杂性,而这些复杂性给湍流燃烧的PINNs建模带来很大挑战. ...
Limitations of physics informed machine learning for nonlinear two-phase transport in porous media
1
2020
... 目前,已有相关研究者基于PINNs求解其遇到的多种微分方程,涵盖的领域包括不可压流动[4 ] 、高速流动[5 ] 、非牛顿流体[6 ] 、传热学[7 -9 ] 、生命科学[10 ] 等,在多相流领域中出现了初步研究[11 -12 ] . 应用于燃烧化学领域内微分方程求解的研究[13 ] 较少,这主要是在燃烧数值模拟中所遇到的化学反应常微分方程组(system of ordinary differential equations,SODEs)具有很强的刚性,即便采用算子分裂方法(operator splitting)[14 -16 ] 将输运方程中的化学反应项与其他输运项解耦[17 ] ,在一定程度上降低了计算量,也需要耗费大量的计算资源. 实际的湍流燃烧系统包含很宽的化学反应时间尺度[18 ] ,一步反应不能描述不同的化学时间尺度,对流动耦合作用的描述存在不足. 许多燃烧过程,比如点火、熄火、污染物生成(NOx [19 ] ,这些过程无法通过简单的一步反应或者两步反应来精确描述[20 ] . 采用包含更多组分、更多步基元反应的机理,这进一步增大了刚性常微分方程组的复杂性,而这些复杂性给湍流燃烧的PINNs建模带来很大挑战. ...
Stiff-pinn: physics-informed neural network for stiff chemical kinetics
2
2021
... 目前,已有相关研究者基于PINNs求解其遇到的多种微分方程,涵盖的领域包括不可压流动[4 ] 、高速流动[5 ] 、非牛顿流体[6 ] 、传热学[7 -9 ] 、生命科学[10 ] 等,在多相流领域中出现了初步研究[11 -12 ] . 应用于燃烧化学领域内微分方程求解的研究[13 ] 较少,这主要是在燃烧数值模拟中所遇到的化学反应常微分方程组(system of ordinary differential equations,SODEs)具有很强的刚性,即便采用算子分裂方法(operator splitting)[14 -16 ] 将输运方程中的化学反应项与其他输运项解耦[17 ] ,在一定程度上降低了计算量,也需要耗费大量的计算资源. 实际的湍流燃烧系统包含很宽的化学反应时间尺度[18 ] ,一步反应不能描述不同的化学时间尺度,对流动耦合作用的描述存在不足. 许多燃烧过程,比如点火、熄火、污染物生成(NOx [19 ] ,这些过程无法通过简单的一步反应或者两步反应来精确描述[20 ] . 采用包含更多组分、更多步基元反应的机理,这进一步增大了刚性常微分方程组的复杂性,而这些复杂性给湍流燃烧的PINNs建模带来很大挑战. ...
... 实质上,在默认情况下,DeepXDE通过损失函数的方式来使计算结果满足给定的初始和边界条件,这是一种软约束[21 ] . 对于本文案例,可以采用更直接的硬边界方式[30 ] ,使得网络结构输出满足给定的初始条件. 陆至彬等[9 ] 针对传热问题求解,评估了软边界和硬边界2种方法所构建PINNs模型的性能. 结果表明,硬边界PINNs模型的预测能力较优. 为了降低SODEs的刚度,Ji等[13 ] 采用准稳态假设(quasi steady state assumptions,QSSA)的方法对方程进行变换,提出Stiff-PINN模型,取得了较好的预测结果. 本文案例无需QSSA,采用硬边界约束的方式. 下面证明硬边界PINNs的优势. 对于ROBER问题,本文提供的输出转换如下: ...
A semi-implicit numerical scheme for reacting flow II. Stiff, operator-split formulation
1
1999
... 目前,已有相关研究者基于PINNs求解其遇到的多种微分方程,涵盖的领域包括不可压流动[4 ] 、高速流动[5 ] 、非牛顿流体[6 ] 、传热学[7 -9 ] 、生命科学[10 ] 等,在多相流领域中出现了初步研究[11 -12 ] . 应用于燃烧化学领域内微分方程求解的研究[13 ] 较少,这主要是在燃烧数值模拟中所遇到的化学反应常微分方程组(system of ordinary differential equations,SODEs)具有很强的刚性,即便采用算子分裂方法(operator splitting)[14 -16 ] 将输运方程中的化学反应项与其他输运项解耦[17 ] ,在一定程度上降低了计算量,也需要耗费大量的计算资源. 实际的湍流燃烧系统包含很宽的化学反应时间尺度[18 ] ,一步反应不能描述不同的化学时间尺度,对流动耦合作用的描述存在不足. 许多燃烧过程,比如点火、熄火、污染物生成(NOx [19 ] ,这些过程无法通过简单的一步反应或者两步反应来精确描述[20 ] . 采用包含更多组分、更多步基元反应的机理,这进一步增大了刚性常微分方程组的复杂性,而这些复杂性给湍流燃烧的PINNs建模带来很大挑战. ...
Analysis of operator splitting for advection-diffusion-reaction problems from air pollution modelling
0
1999
1
... 目前,已有相关研究者基于PINNs求解其遇到的多种微分方程,涵盖的领域包括不可压流动[4 ] 、高速流动[5 ] 、非牛顿流体[6 ] 、传热学[7 -9 ] 、生命科学[10 ] 等,在多相流领域中出现了初步研究[11 -12 ] . 应用于燃烧化学领域内微分方程求解的研究[13 ] 较少,这主要是在燃烧数值模拟中所遇到的化学反应常微分方程组(system of ordinary differential equations,SODEs)具有很强的刚性,即便采用算子分裂方法(operator splitting)[14 -16 ] 将输运方程中的化学反应项与其他输运项解耦[17 ] ,在一定程度上降低了计算量,也需要耗费大量的计算资源. 实际的湍流燃烧系统包含很宽的化学反应时间尺度[18 ] ,一步反应不能描述不同的化学时间尺度,对流动耦合作用的描述存在不足. 许多燃烧过程,比如点火、熄火、污染物生成(NOx [19 ] ,这些过程无法通过简单的一步反应或者两步反应来精确描述[20 ] . 采用包含更多组分、更多步基元反应的机理,这进一步增大了刚性常微分方程组的复杂性,而这些复杂性给湍流燃烧的PINNs建模带来很大挑战. ...
An analysis of operator splitting techniques in the stiff case
1
2000
... 目前,已有相关研究者基于PINNs求解其遇到的多种微分方程,涵盖的领域包括不可压流动[4 ] 、高速流动[5 ] 、非牛顿流体[6 ] 、传热学[7 -9 ] 、生命科学[10 ] 等,在多相流领域中出现了初步研究[11 -12 ] . 应用于燃烧化学领域内微分方程求解的研究[13 ] 较少,这主要是在燃烧数值模拟中所遇到的化学反应常微分方程组(system of ordinary differential equations,SODEs)具有很强的刚性,即便采用算子分裂方法(operator splitting)[14 -16 ] 将输运方程中的化学反应项与其他输运项解耦[17 ] ,在一定程度上降低了计算量,也需要耗费大量的计算资源. 实际的湍流燃烧系统包含很宽的化学反应时间尺度[18 ] ,一步反应不能描述不同的化学时间尺度,对流动耦合作用的描述存在不足. 许多燃烧过程,比如点火、熄火、污染物生成(NOx [19 ] ,这些过程无法通过简单的一步反应或者两步反应来精确描述[20 ] . 采用包含更多组分、更多步基元反应的机理,这进一步增大了刚性常微分方程组的复杂性,而这些复杂性给湍流燃烧的PINNs建模带来很大挑战. ...
Large eddy simulations of gaseous flames in gas turbine combustion chambers
1
2012
... 目前,已有相关研究者基于PINNs求解其遇到的多种微分方程,涵盖的领域包括不可压流动[4 ] 、高速流动[5 ] 、非牛顿流体[6 ] 、传热学[7 -9 ] 、生命科学[10 ] 等,在多相流领域中出现了初步研究[11 -12 ] . 应用于燃烧化学领域内微分方程求解的研究[13 ] 较少,这主要是在燃烧数值模拟中所遇到的化学反应常微分方程组(system of ordinary differential equations,SODEs)具有很强的刚性,即便采用算子分裂方法(operator splitting)[14 -16 ] 将输运方程中的化学反应项与其他输运项解耦[17 ] ,在一定程度上降低了计算量,也需要耗费大量的计算资源. 实际的湍流燃烧系统包含很宽的化学反应时间尺度[18 ] ,一步反应不能描述不同的化学时间尺度,对流动耦合作用的描述存在不足. 许多燃烧过程,比如点火、熄火、污染物生成(NOx [19 ] ,这些过程无法通过简单的一步反应或者两步反应来精确描述[20 ] . 采用包含更多组分、更多步基元反应的机理,这进一步增大了刚性常微分方程组的复杂性,而这些复杂性给湍流燃烧的PINNs建模带来很大挑战. ...
1
... 目前,已有相关研究者基于PINNs求解其遇到的多种微分方程,涵盖的领域包括不可压流动[4 ] 、高速流动[5 ] 、非牛顿流体[6 ] 、传热学[7 -9 ] 、生命科学[10 ] 等,在多相流领域中出现了初步研究[11 -12 ] . 应用于燃烧化学领域内微分方程求解的研究[13 ] 较少,这主要是在燃烧数值模拟中所遇到的化学反应常微分方程组(system of ordinary differential equations,SODEs)具有很强的刚性,即便采用算子分裂方法(operator splitting)[14 -16 ] 将输运方程中的化学反应项与其他输运项解耦[17 ] ,在一定程度上降低了计算量,也需要耗费大量的计算资源. 实际的湍流燃烧系统包含很宽的化学反应时间尺度[18 ] ,一步反应不能描述不同的化学时间尺度,对流动耦合作用的描述存在不足. 许多燃烧过程,比如点火、熄火、污染物生成(NOx [19 ] ,这些过程无法通过简单的一步反应或者两步反应来精确描述[20 ] . 采用包含更多组分、更多步基元反应的机理,这进一步增大了刚性常微分方程组的复杂性,而这些复杂性给湍流燃烧的PINNs建模带来很大挑战. ...
1
... 目前,已有相关研究者基于PINNs求解其遇到的多种微分方程,涵盖的领域包括不可压流动[4 ] 、高速流动[5 ] 、非牛顿流体[6 ] 、传热学[7 -9 ] 、生命科学[10 ] 等,在多相流领域中出现了初步研究[11 -12 ] . 应用于燃烧化学领域内微分方程求解的研究[13 ] 较少,这主要是在燃烧数值模拟中所遇到的化学反应常微分方程组(system of ordinary differential equations,SODEs)具有很强的刚性,即便采用算子分裂方法(operator splitting)[14 -16 ] 将输运方程中的化学反应项与其他输运项解耦[17 ] ,在一定程度上降低了计算量,也需要耗费大量的计算资源. 实际的湍流燃烧系统包含很宽的化学反应时间尺度[18 ] ,一步反应不能描述不同的化学时间尺度,对流动耦合作用的描述存在不足. 许多燃烧过程,比如点火、熄火、污染物生成(NOx [19 ] ,这些过程无法通过简单的一步反应或者两步反应来精确描述[20 ] . 采用包含更多组分、更多步基元反应的机理,这进一步增大了刚性常微分方程组的复杂性,而这些复杂性给湍流燃烧的PINNs建模带来很大挑战. ...
1
... 目前,已有相关研究者基于PINNs求解其遇到的多种微分方程,涵盖的领域包括不可压流动[4 ] 、高速流动[5 ] 、非牛顿流体[6 ] 、传热学[7 -9 ] 、生命科学[10 ] 等,在多相流领域中出现了初步研究[11 -12 ] . 应用于燃烧化学领域内微分方程求解的研究[13 ] 较少,这主要是在燃烧数值模拟中所遇到的化学反应常微分方程组(system of ordinary differential equations,SODEs)具有很强的刚性,即便采用算子分裂方法(operator splitting)[14 -16 ] 将输运方程中的化学反应项与其他输运项解耦[17 ] ,在一定程度上降低了计算量,也需要耗费大量的计算资源. 实际的湍流燃烧系统包含很宽的化学反应时间尺度[18 ] ,一步反应不能描述不同的化学时间尺度,对流动耦合作用的描述存在不足. 许多燃烧过程,比如点火、熄火、污染物生成(NOx [19 ] ,这些过程无法通过简单的一步反应或者两步反应来精确描述[20 ] . 采用包含更多组分、更多步基元反应的机理,这进一步增大了刚性常微分方程组的复杂性,而这些复杂性给湍流燃烧的PINNs建模带来很大挑战. ...
DeepXDE: A deep learning library for solving differential equations
4
2021
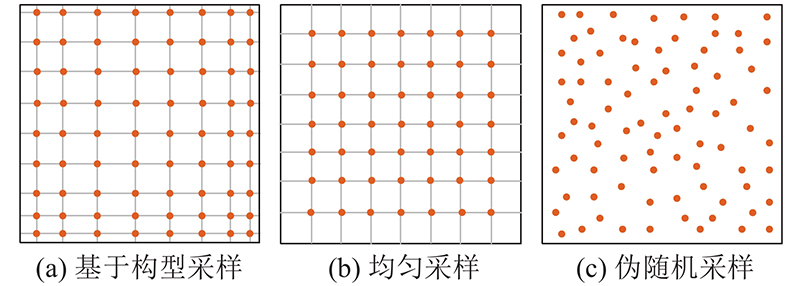
... 与传统的偏微分方程数值解法相比,PINNs是无网格方法,需要计算域内及边界上的残差点(residual points)进行梯度计算、评估损失及更新训练参数. 残差点的选取至关重要,一组理想的残差点可以改善PINNs训练的收敛行为,提高计算效率. 残差点的选取较灵活,一般采用类网格点均匀采样或伪随机采样以及其他方法[21 -22 ] . 针对燃烧化学领域内的复杂微分方程,残差点的选取对结果的影响需要更具体的分析. ...
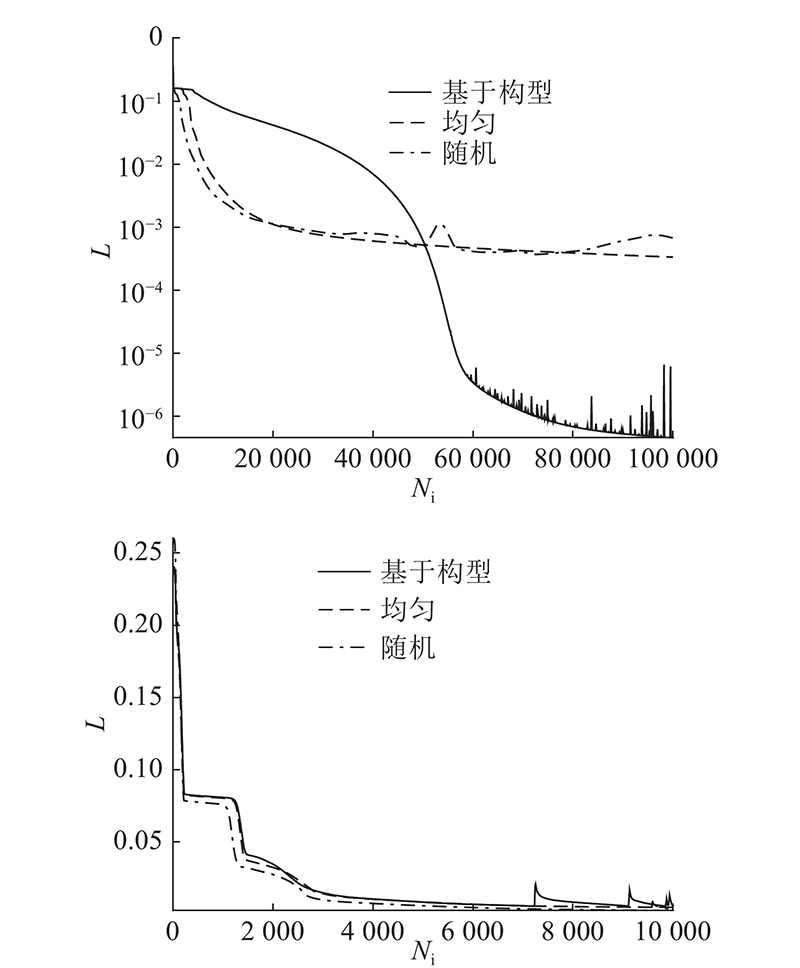
... 使用的PINNs代码基于开源代码库DeepXDE[21 ] ,选用的后端是基于TensorFlow 2.5.0框架[25 ] ,本文算例均是在NVIDIA GeForce GTX 1660 Ti GPU上进行训练,使用Windows操作系统. 数值求解器基于开源CFD代码OpenFOAM[26 ] 中的刚性ODE求解器seulex[24 , 27 ] ,求出数值解作为参考值,以验证PINNs解. 对于2个算例,均在计算域[0, T e ]上按照对数分布进行采样. 对于计算域终点T e = 1 s的算例,采集了1 000个数据点;对于T e = 103 s的算例,采集了3 000个数据点,以评估残差. 考虑到组分演化曲线在线性坐标轴中会出现突变,按照线性分布采样将难以捕捉到组分演化过程,所以按照对数分布取样. 网络输入为时间t ,预测输出是3种组分对应的y 1 、y 2 和y 3 . 网络结构和超参数配置基于DeepXDE[21 ] 代码库中经过验证的案例,隐藏层激活函数为tanh函数,损失函数为均方误差(见式(4)),函数网络权重使用Xavier[28 ] 初始化,通过Adam优化器[29 ] 进行优化,学习率为10−5 . 考虑本文算例的复杂性,对隐藏层数目和神经元节点数以网格搜索方式进行超参数优化,搜索的隐藏层数目为3、4和5,搜索的每层神经元节点数N l 为50、100、150和200,结果如表1 所示. 表中,L 为训练损失. ...
... [21 ]代码库中经过验证的案例,隐藏层激活函数为tanh函数,损失函数为均方误差(见式(4)),函数网络权重使用Xavier[28 ] 初始化,通过Adam优化器[29 ] 进行优化,学习率为10−5 . 考虑本文算例的复杂性,对隐藏层数目和神经元节点数以网格搜索方式进行超参数优化,搜索的隐藏层数目为3、4和5,搜索的每层神经元节点数N l 为50、100、150和200,结果如表1 所示. 表中,L 为训练损失. ...
... 实质上,在默认情况下,DeepXDE通过损失函数的方式来使计算结果满足给定的初始和边界条件,这是一种软约束[21 ] . 对于本文案例,可以采用更直接的硬边界方式[30 ] ,使得网络结构输出满足给定的初始条件. 陆至彬等[9 ] 针对传热问题求解,评估了软边界和硬边界2种方法所构建PINNs模型的性能. 结果表明,硬边界PINNs模型的预测能力较优. 为了降低SODEs的刚度,Ji等[13 ] 采用准稳态假设(quasi steady state assumptions,QSSA)的方法对方程进行变换,提出Stiff-PINN模型,取得了较好的预测结果. 本文案例无需QSSA,采用硬边界约束的方式. 下面证明硬边界PINNs的优势. 对于ROBER问题,本文提供的输出转换如下: ...
Efficient training of physics-informed neural networks via importance sampling
1
2021
... 与传统的偏微分方程数值解法相比,PINNs是无网格方法,需要计算域内及边界上的残差点(residual points)进行梯度计算、评估损失及更新训练参数. 残差点的选取至关重要,一组理想的残差点可以改善PINNs训练的收敛行为,提高计算效率. 残差点的选取较灵活,一般采用类网格点均匀采样或伪随机采样以及其他方法[21 -22 ] . 针对燃烧化学领域内的复杂微分方程,残差点的选取对结果的影响需要更具体的分析. ...
1
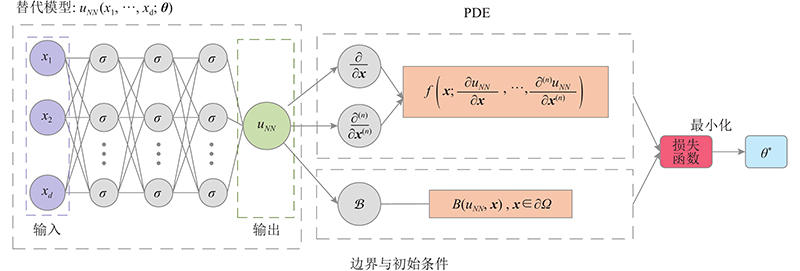
... 本文的求解算法均不依赖已有参考解作为训练数据,属于对微分方程的正向求解. 下面以求解非线性偏微分方程(partial differential equations,PDE)的正向问题为例,简要阐释PINNs的基本网络结构及训练方式. 求解PDE的PINNs网络结构如图1 所示,考虑解为u (x [23 ] : ...
1
... 本文的求解算法均不依赖已有参考解作为训练数据,属于对微分方程的正向求解. 下面以求解非线性偏微分方程(partial differential equations,PDE)的正向问题为例,简要阐释PINNs的基本网络结构及训练方式. 求解PDE的PINNs网络结构如图1 所示,考虑解为u (x [23 ] : ...
2
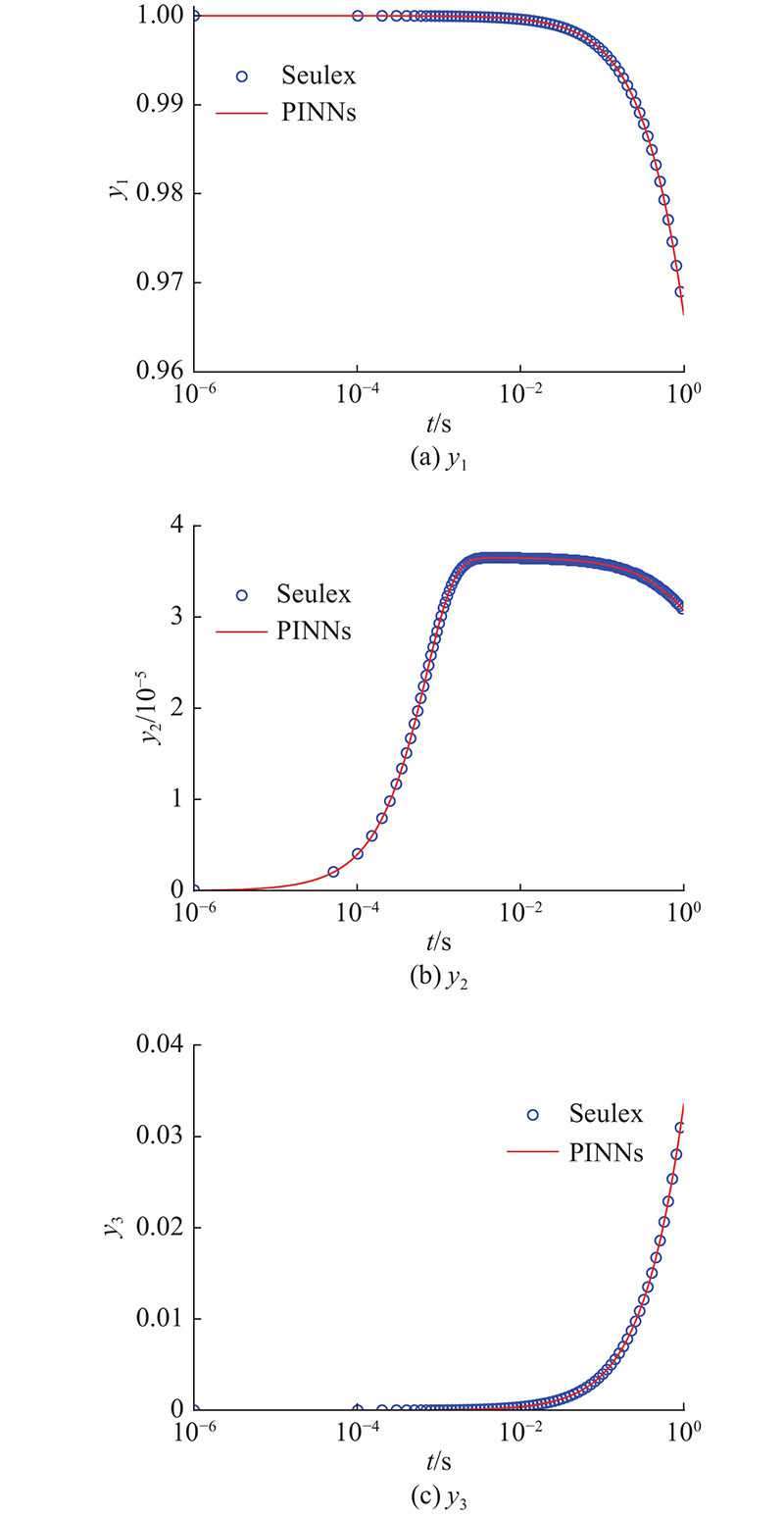
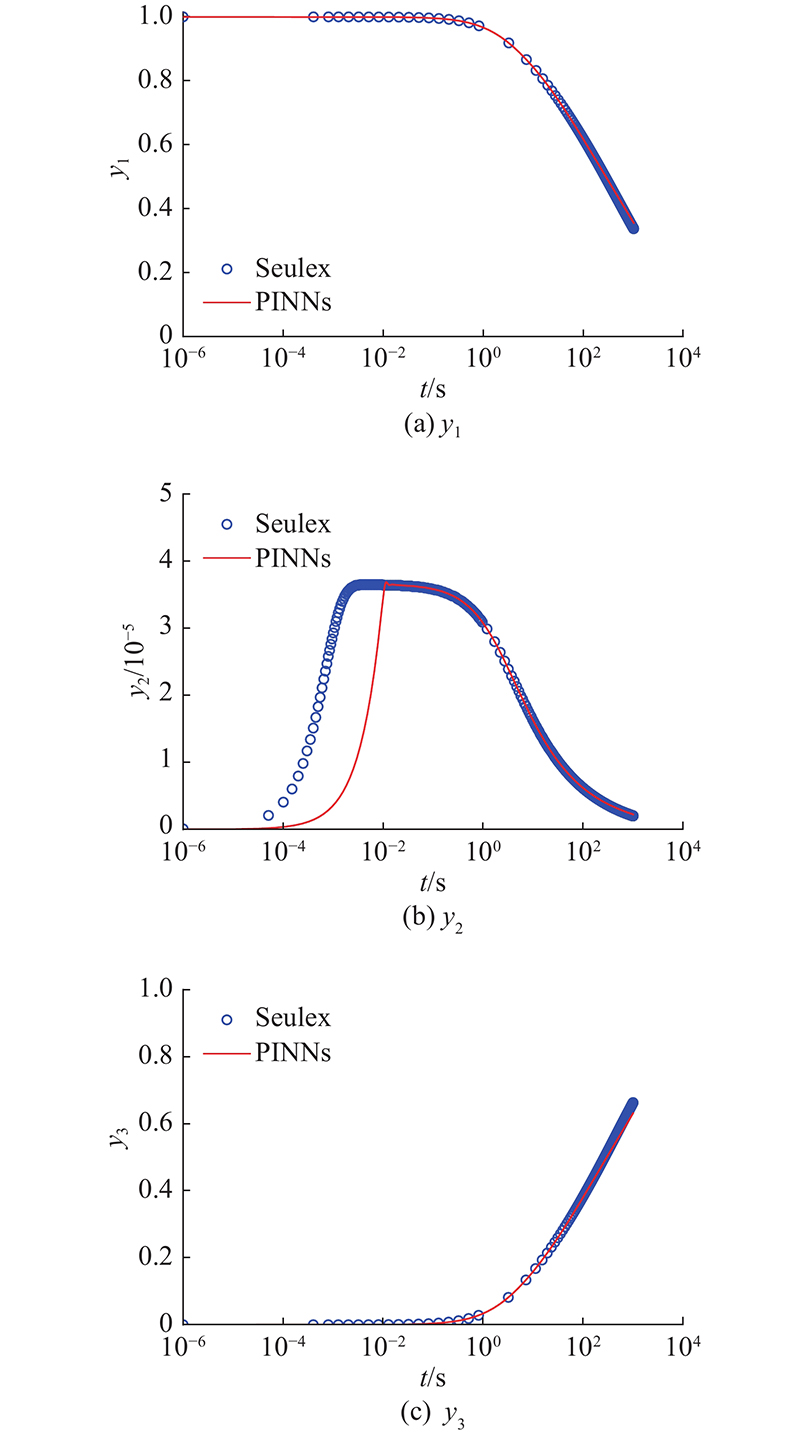
... 在化学动力学中,组分演化过程可以描述为以组分的净反应速率为源项的常微分方程系统(SODEs). 若组分的特征时间尺度跨越很大的范围,则整个SODEs积分求解需要大量的迭代计算. 以经典的刚性常微分方程组ROBER问题[24 ] 为例,评估PINNs在解决刚性动力学问题时的性能. ROBER问题由3种组分和3步反应组成,由于反应速率常数有着较大的差异,方程组具有很强的刚性. ROBER问题的反应网络如下: ...
... 使用的PINNs代码基于开源代码库DeepXDE[21 ] ,选用的后端是基于TensorFlow 2.5.0框架[25 ] ,本文算例均是在NVIDIA GeForce GTX 1660 Ti GPU上进行训练,使用Windows操作系统. 数值求解器基于开源CFD代码OpenFOAM[26 ] 中的刚性ODE求解器seulex[24 , 27 ] ,求出数值解作为参考值,以验证PINNs解. 对于2个算例,均在计算域[0, T e ]上按照对数分布进行采样. 对于计算域终点T e = 1 s的算例,采集了1 000个数据点;对于T e = 103 s的算例,采集了3 000个数据点,以评估残差. 考虑到组分演化曲线在线性坐标轴中会出现突变,按照线性分布采样将难以捕捉到组分演化过程,所以按照对数分布取样. 网络输入为时间t ,预测输出是3种组分对应的y 1 、y 2 和y 3 . 网络结构和超参数配置基于DeepXDE[21 ] 代码库中经过验证的案例,隐藏层激活函数为tanh函数,损失函数为均方误差(见式(4)),函数网络权重使用Xavier[28 ] 初始化,通过Adam优化器[29 ] 进行优化,学习率为10−5 . 考虑本文算例的复杂性,对隐藏层数目和神经元节点数以网格搜索方式进行超参数优化,搜索的隐藏层数目为3、4和5,搜索的每层神经元节点数N l 为50、100、150和200,结果如表1 所示. 表中,L 为训练损失. ...
1
... 使用的PINNs代码基于开源代码库DeepXDE[21 ] ,选用的后端是基于TensorFlow 2.5.0框架[25 ] ,本文算例均是在NVIDIA GeForce GTX 1660 Ti GPU上进行训练,使用Windows操作系统. 数值求解器基于开源CFD代码OpenFOAM[26 ] 中的刚性ODE求解器seulex[24 , 27 ] ,求出数值解作为参考值,以验证PINNs解. 对于2个算例,均在计算域[0, T e ]上按照对数分布进行采样. 对于计算域终点T e = 1 s的算例,采集了1 000个数据点;对于T e = 103 s的算例,采集了3 000个数据点,以评估残差. 考虑到组分演化曲线在线性坐标轴中会出现突变,按照线性分布采样将难以捕捉到组分演化过程,所以按照对数分布取样. 网络输入为时间t ,预测输出是3种组分对应的y 1 、y 2 和y 3 . 网络结构和超参数配置基于DeepXDE[21 ] 代码库中经过验证的案例,隐藏层激活函数为tanh函数,损失函数为均方误差(见式(4)),函数网络权重使用Xavier[28 ] 初始化,通过Adam优化器[29 ] 进行优化,学习率为10−5 . 考虑本文算例的复杂性,对隐藏层数目和神经元节点数以网格搜索方式进行超参数优化,搜索的隐藏层数目为3、4和5,搜索的每层神经元节点数N l 为50、100、150和200,结果如表1 所示. 表中,L 为训练损失. ...
A tensorial approach to computational continuum mechanics using object-oriented techniques
1
1998
... 使用的PINNs代码基于开源代码库DeepXDE[21 ] ,选用的后端是基于TensorFlow 2.5.0框架[25 ] ,本文算例均是在NVIDIA GeForce GTX 1660 Ti GPU上进行训练,使用Windows操作系统. 数值求解器基于开源CFD代码OpenFOAM[26 ] 中的刚性ODE求解器seulex[24 , 27 ] ,求出数值解作为参考值,以验证PINNs解. 对于2个算例,均在计算域[0, T e ]上按照对数分布进行采样. 对于计算域终点T e = 1 s的算例,采集了1 000个数据点;对于T e = 103 s的算例,采集了3 000个数据点,以评估残差. 考虑到组分演化曲线在线性坐标轴中会出现突变,按照线性分布采样将难以捕捉到组分演化过程,所以按照对数分布取样. 网络输入为时间t ,预测输出是3种组分对应的y 1 、y 2 和y 3 . 网络结构和超参数配置基于DeepXDE[21 ] 代码库中经过验证的案例,隐藏层激活函数为tanh函数,损失函数为均方误差(见式(4)),函数网络权重使用Xavier[28 ] 初始化,通过Adam优化器[29 ] 进行优化,学习率为10−5 . 考虑本文算例的复杂性,对隐藏层数目和神经元节点数以网格搜索方式进行超参数优化,搜索的隐藏层数目为3、4和5,搜索的每层神经元节点数N l 为50、100、150和200,结果如表1 所示. 表中,L 为训练损失. ...
On the merits of extrapolation-based stiff ODE solvers for combustion CFD
1
2016
... 使用的PINNs代码基于开源代码库DeepXDE[21 ] ,选用的后端是基于TensorFlow 2.5.0框架[25 ] ,本文算例均是在NVIDIA GeForce GTX 1660 Ti GPU上进行训练,使用Windows操作系统. 数值求解器基于开源CFD代码OpenFOAM[26 ] 中的刚性ODE求解器seulex[24 , 27 ] ,求出数值解作为参考值,以验证PINNs解. 对于2个算例,均在计算域[0, T e ]上按照对数分布进行采样. 对于计算域终点T e = 1 s的算例,采集了1 000个数据点;对于T e = 103 s的算例,采集了3 000个数据点,以评估残差. 考虑到组分演化曲线在线性坐标轴中会出现突变,按照线性分布采样将难以捕捉到组分演化过程,所以按照对数分布取样. 网络输入为时间t ,预测输出是3种组分对应的y 1 、y 2 和y 3 . 网络结构和超参数配置基于DeepXDE[21 ] 代码库中经过验证的案例,隐藏层激活函数为tanh函数,损失函数为均方误差(见式(4)),函数网络权重使用Xavier[28 ] 初始化,通过Adam优化器[29 ] 进行优化,学习率为10−5 . 考虑本文算例的复杂性,对隐藏层数目和神经元节点数以网格搜索方式进行超参数优化,搜索的隐藏层数目为3、4和5,搜索的每层神经元节点数N l 为50、100、150和200,结果如表1 所示. 表中,L 为训练损失. ...
1
... 使用的PINNs代码基于开源代码库DeepXDE[21 ] ,选用的后端是基于TensorFlow 2.5.0框架[25 ] ,本文算例均是在NVIDIA GeForce GTX 1660 Ti GPU上进行训练,使用Windows操作系统. 数值求解器基于开源CFD代码OpenFOAM[26 ] 中的刚性ODE求解器seulex[24 , 27 ] ,求出数值解作为参考值,以验证PINNs解. 对于2个算例,均在计算域[0, T e ]上按照对数分布进行采样. 对于计算域终点T e = 1 s的算例,采集了1 000个数据点;对于T e = 103 s的算例,采集了3 000个数据点,以评估残差. 考虑到组分演化曲线在线性坐标轴中会出现突变,按照线性分布采样将难以捕捉到组分演化过程,所以按照对数分布取样. 网络输入为时间t ,预测输出是3种组分对应的y 1 、y 2 和y 3 . 网络结构和超参数配置基于DeepXDE[21 ] 代码库中经过验证的案例,隐藏层激活函数为tanh函数,损失函数为均方误差(见式(4)),函数网络权重使用Xavier[28 ] 初始化,通过Adam优化器[29 ] 进行优化,学习率为10−5 . 考虑本文算例的复杂性,对隐藏层数目和神经元节点数以网格搜索方式进行超参数优化,搜索的隐藏层数目为3、4和5,搜索的每层神经元节点数N l 为50、100、150和200,结果如表1 所示. 表中,L 为训练损失. ...
1
... 使用的PINNs代码基于开源代码库DeepXDE[21 ] ,选用的后端是基于TensorFlow 2.5.0框架[25 ] ,本文算例均是在NVIDIA GeForce GTX 1660 Ti GPU上进行训练,使用Windows操作系统. 数值求解器基于开源CFD代码OpenFOAM[26 ] 中的刚性ODE求解器seulex[24 , 27 ] ,求出数值解作为参考值,以验证PINNs解. 对于2个算例,均在计算域[0, T e ]上按照对数分布进行采样. 对于计算域终点T e = 1 s的算例,采集了1 000个数据点;对于T e = 103 s的算例,采集了3 000个数据点,以评估残差. 考虑到组分演化曲线在线性坐标轴中会出现突变,按照线性分布采样将难以捕捉到组分演化过程,所以按照对数分布取样. 网络输入为时间t ,预测输出是3种组分对应的y 1 、y 2 和y 3 . 网络结构和超参数配置基于DeepXDE[21 ] 代码库中经过验证的案例,隐藏层激活函数为tanh函数,损失函数为均方误差(见式(4)),函数网络权重使用Xavier[28 ] 初始化,通过Adam优化器[29 ] 进行优化,学习率为10−5 . 考虑本文算例的复杂性,对隐藏层数目和神经元节点数以网格搜索方式进行超参数优化,搜索的隐藏层数目为3、4和5,搜索的每层神经元节点数N l 为50、100、150和200,结果如表1 所示. 表中,L 为训练损失. ...
Artificial neural networks for solving ordinary and partial differential equations
1
1998
... 实质上,在默认情况下,DeepXDE通过损失函数的方式来使计算结果满足给定的初始和边界条件,这是一种软约束[21 ] . 对于本文案例,可以采用更直接的硬边界方式[30 ] ,使得网络结构输出满足给定的初始条件. 陆至彬等[9 ] 针对传热问题求解,评估了软边界和硬边界2种方法所构建PINNs模型的性能. 结果表明,硬边界PINNs模型的预测能力较优. 为了降低SODEs的刚度,Ji等[13 ] 采用准稳态假设(quasi steady state assumptions,QSSA)的方法对方程进行变换,提出Stiff-PINN模型,取得了较好的预测结果. 本文案例无需QSSA,采用硬边界约束的方式. 下面证明硬边界PINNs的优势. 对于ROBER问题,本文提供的输出转换如下: ...
Modeling of complex premixed burner systems by using flamelet-generated manifolds
1
2001
... 在湍流燃烧的数值模拟中,小火焰类燃烧模型[31 -32 ] 能够以合理的计算成本考虑详细的化学机理,受到广泛的应用. 燃烧数值模拟中一个重要参数是混合分数Z ,在一般的两股流动组成的系统中,混合分数定义为来自燃料流的质量流量与总质量流之比. 基于系统中的元素质量守恒,可以得到更具普遍意义的基于元素的混合分数[33 ] . 基于Lewis数为1的假设[34 ] ,可以将含有源项的主动标量组分质量分数w i Z 的输运方程: ...
Progress-variable approach for large-eddy simulation of non-premixed turbulent combustion
1
2004
... 在湍流燃烧的数值模拟中,小火焰类燃烧模型[31 -32 ] 能够以合理的计算成本考虑详细的化学机理,受到广泛的应用. 燃烧数值模拟中一个重要参数是混合分数Z ,在一般的两股流动组成的系统中,混合分数定义为来自燃料流的质量流量与总质量流之比. 基于系统中的元素质量守恒,可以得到更具普遍意义的基于元素的混合分数[33 ] . 基于Lewis数为1的假设[34 ] ,可以将含有源项的主动标量组分质量分数w i Z 的输运方程: ...
On reduced mechanisms for methane air combustion in nonpremixed flames
1
1990
... 在湍流燃烧的数值模拟中,小火焰类燃烧模型[31 -32 ] 能够以合理的计算成本考虑详细的化学机理,受到广泛的应用. 燃烧数值模拟中一个重要参数是混合分数Z ,在一般的两股流动组成的系统中,混合分数定义为来自燃料流的质量流量与总质量流之比. 基于系统中的元素质量守恒,可以得到更具普遍意义的基于元素的混合分数[33 ] . 基于Lewis数为1的假设[34 ] ,可以将含有源项的主动标量组分质量分数w i Z 的输运方程: ...
Combustion mechanism of liquid fuel spray in a gaseous flame
1
2005
... 在湍流燃烧的数值模拟中,小火焰类燃烧模型[31 -32 ] 能够以合理的计算成本考虑详细的化学机理,受到广泛的应用. 燃烧数值模拟中一个重要参数是混合分数Z ,在一般的两股流动组成的系统中,混合分数定义为来自燃料流的质量流量与总质量流之比. 基于系统中的元素质量守恒,可以得到更具普遍意义的基于元素的混合分数[33 ] . 基于Lewis数为1的假设[34 ] ,可以将含有源项的主动标量组分质量分数w i Z 的输运方程: ...
3
... 基于混合分数,可以将扩散火焰的计算解耦为混合问题和火焰构型问题[35 ] . 其中,混合问题主要用于获得混合分数场Z (x ,t ),火焰构型问题是建立热化学标量(例如温度和组分质量分数)与Z 之间的联系. 对于后者,经典的火焰结构是Burke-Schumann火焰构型[35 ] ,它假设燃烧化学反应是一步、无限快且不可逆的,此时热化学标量仅依赖于Z . Burke-Schumann火焰构型的关系式如下. ...
... [35 ],它假设燃烧化学反应是一步、无限快且不可逆的,此时热化学标量仅依赖于Z . Burke-Schumann火焰构型的关系式如下. ...
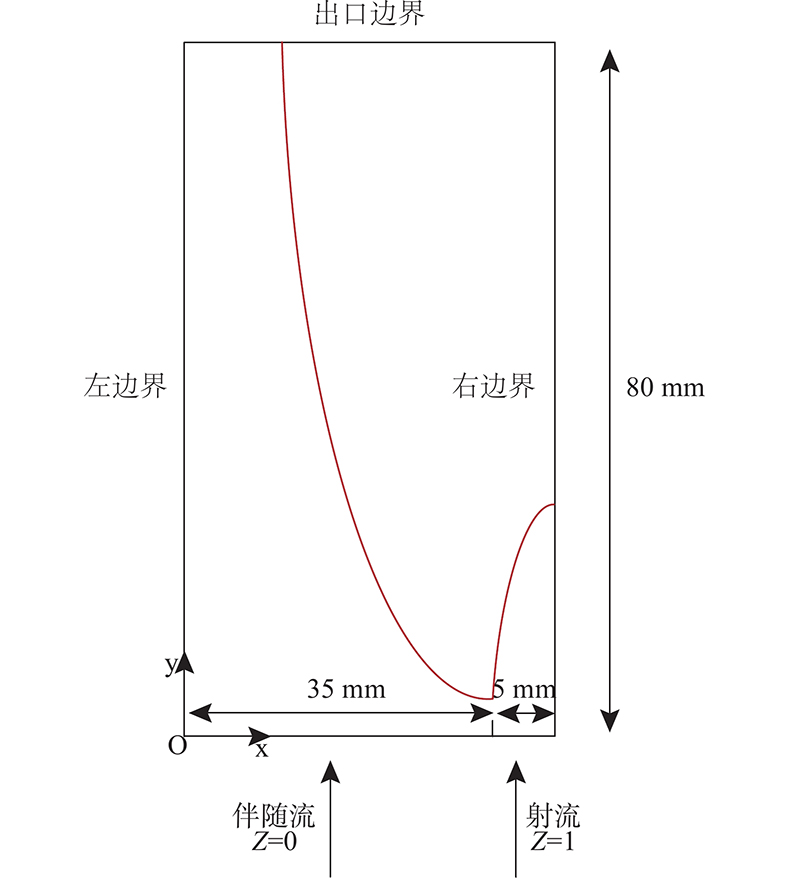
... 将燃料射流(Z = 1、密度为 $\;\rho_{\rm{F}}^{0}$ $u_{{\rm{F}}}^{0}$ D F = 1.5×10−3 m2 /s)注入到氧化剂伴随流(Z = 0、密度为 $\;\rho_{{\rm{O}}}^{0}$ $u_{{\rm{O}}}^{0}$ Z 输运方程式中只保留对流项和扩散项[35 ] ,如下所示: ...