柔顺性控制的主要方法为阻抗控制. 1985年, Hogan[5]提出将机器人与环境的力看作整体,根据二者的动态关系,通过改变反馈的位置误差、速度误差或刚度完成力控制任务. 阻抗控制通过设置参考位置来间接实现力控制,控制精度依赖于对接触环境模型的认知程度. 为了实现机器人对目标力的有效控制,张光辉等[6]采用末端六维力传感器将末端力的控制转换到机器人关节空间,以基于位置控制的阻抗策略方式实现重力环境下的柔顺控制,使机械臂的大范围柔顺控制具有适应性. Duan等[7]针对机器人末端力控制跟踪问题,提出自适应变阻抗的控制策略. 该策略根据接触力变换自适应调整阻抗参数,实时补偿动态环境未知性,力跟踪控制效果较好. Izadbakhsh等[8]利用具有未知系数的线性微分方程设计通用逼近器,并提出计算量更小,更适用于机械臂的鲁棒阻抗控制方法. Li等[9]针对串联弹性执行器驱动的机器人设计的迭代学习阻抗控制器,将控制目标指定为所需的阻抗模型,期望的阻抗模型以迭代的方式实现. 这样既保证了机器人的重复性,又保证了瞬态性能. Abu-dakka等[10]提出集成力感测和可变阻抗的控制方法. 该方法从示教中估计完整的刚度矩阵,再结合感知力拟合概率模型,使机器人能够对新的任务条件做出调整. Zhao等[11]提出的模型加速强化学习方法,利用最大熵强化学习框架学习装配策略,利用阻抗控制器执行装配策略. 该方法的装配技能学习能力强,适于实际装配环境. Ye等[12]针对导纳控制,将重力摩擦力关节弹性纳入机器人的动力学模型,使该模型比传统模型更具有现实意义. 董悫等[13]针对微重力环境下机器人装配任务,提出适应于多销孔对接阶段的弹簧虚拟项阻抗控制,解决了姿态误差调节错误的问题. 潘立等[14]针对六自由度装配机器人提出的动态柔顺控制方法,实现了在未接触时滑膜控制和接触时阻抗控制的切换,使装配过程具有高速、高精的跟踪能力和良好的柔顺性能.
上述控制策略的性能对接触环境模型认知程度的依赖性大. 在实际装配任务中,由于精确的接触环境参数获取困难,会导致控制策略产生较大的接触力误差[15],当装配精度要求较高时,阻抗控制难以适用. 本研究1)将自抗扰控制(active disturbance rejection control,ADRC)应用于阻抗控制,通过扰动观测器观测环境信息并补偿,提高控制系统对环境参数的适应性. 2)提出改进型自抗扰阻抗控制策略,引入阻抗模型,增大扰动观测器的响应速度,提高力跟踪效果的精度. 3)基于六自由度装配平台进行轴孔装配实验,对比阻抗控制、自抗扰阻抗控制和改进型自抗扰控制的效果,验证自抗扰阻抗控制方法的有效性.
1. 轴孔接触状态
机器人在执行柔顺装配任务时,会根据不共线轴孔的接触关系将接触状态分为接近、一点接触、两点接触3个阶段,且各接触状态下的接触力与轴孔相对位姿有关.
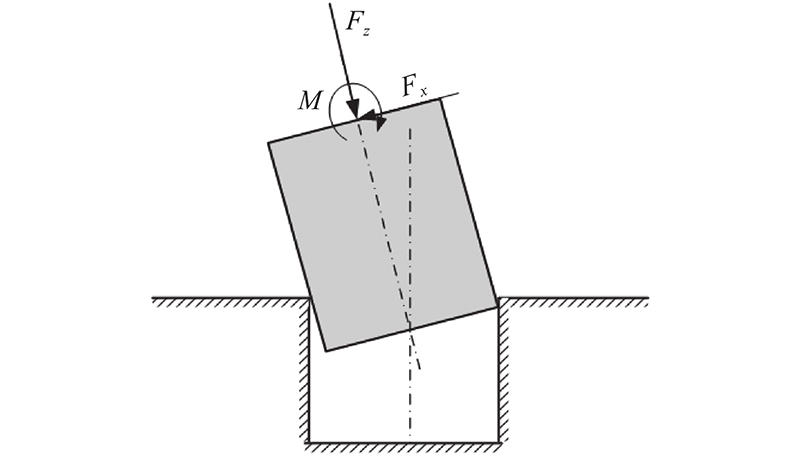
两点接触是轴孔装配的关键阶段. 如图1所示,当轴孔处于两点接触阶段时,轴会在内壁两点作用力的合力下产生较大的Z方向上的接触力FZ、接触力矩M,阻止轴入孔的运动. 调整轴的位姿,可以减小X方向上的接触力FX、M,直到M、FX=0,FZ趋于设定值,此时轴与孔的轴线平行,轴完全入孔. 柔顺控制算法根据传感器测得的力/力矩信息得到轴各方向的位姿调整量,使得FX、FZ和M达到设定值.
图 1
2. 改进型自抗扰阻抗控制策略
2.1. 阻抗控制
轴孔接触时,采用具有质量−弹簧−阻尼系统的二阶线性微分方程来表述期望的阻抗关系. 合理设置阻抗参数矩阵,使轴孔在各个方向解耦,以机器人操作空间某一维阻抗关系为例,关系表达式为
式中:
式中:
式(3)表明,稳态力误差与接触面位置和工件刚度均有关. 在实际轴孔装配过程中,接触面位置和工件刚度无法精确获得,系统的稳态力误差始终存在. 对于精密轴孔装配作业,过大的装配力误差会使轴孔调整不到位,导致装配任务失败.
2.2. 改进型自抗扰阻抗控制
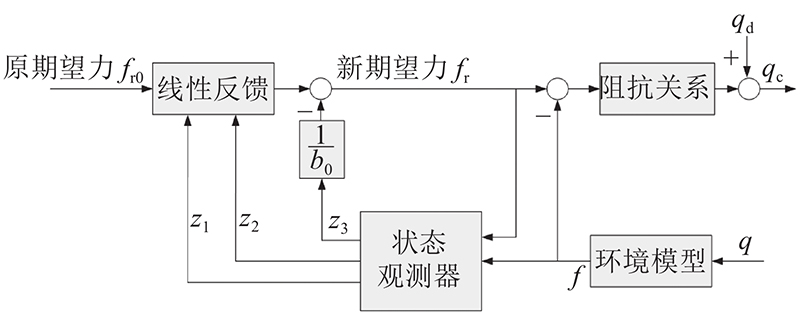
阻抗控制存在稳态力误差,ADRC能够实现不依赖系统模型的无静差控制[16-17],因此在阻抗控制的基础上设计自抗扰控制来消除力误差. 如图2所示,在原期望力的基础上,通过自抗扰控制器算出新期望力;再根据式(1)的阻抗关系决定末端位置值,发送给位置执行器. 图中,z1、z2、z3均为状态观测量,
图 2
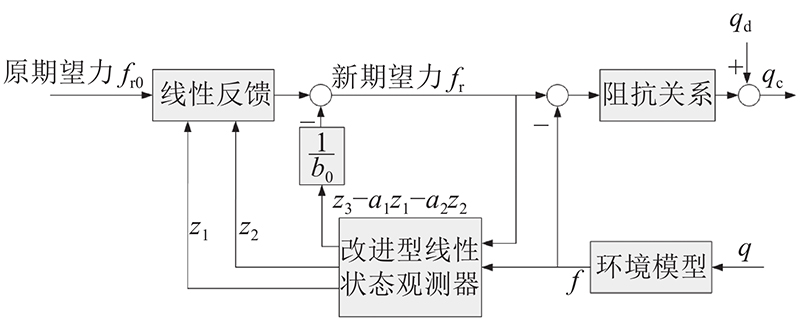
图 3
图 3 改进型自抗扰阻抗控制策略
Fig.3 Improved active disturbance rejection impedance control strategy
令
式中:
改进型的ADRC引入已知模型
式中:e为输出误差,
式中:A、B、C均为状态观测器的增益矩阵,Z为状态变量观测值矩阵,L为观测器误差反馈增益矩阵,
按带宽参数化的方法整定,把观测器特征方程的全部极点放置在
得到
按带宽法求观测器增益为
状态反馈控制器的形式为
式中:
3. 仿真与分析
为了验证上述改进型扩张状态观测器的有效性,对观测器的扰动跟踪能力进行仿真分析.
基于式(5),消去
消去
再消去
令观测误差
式中:
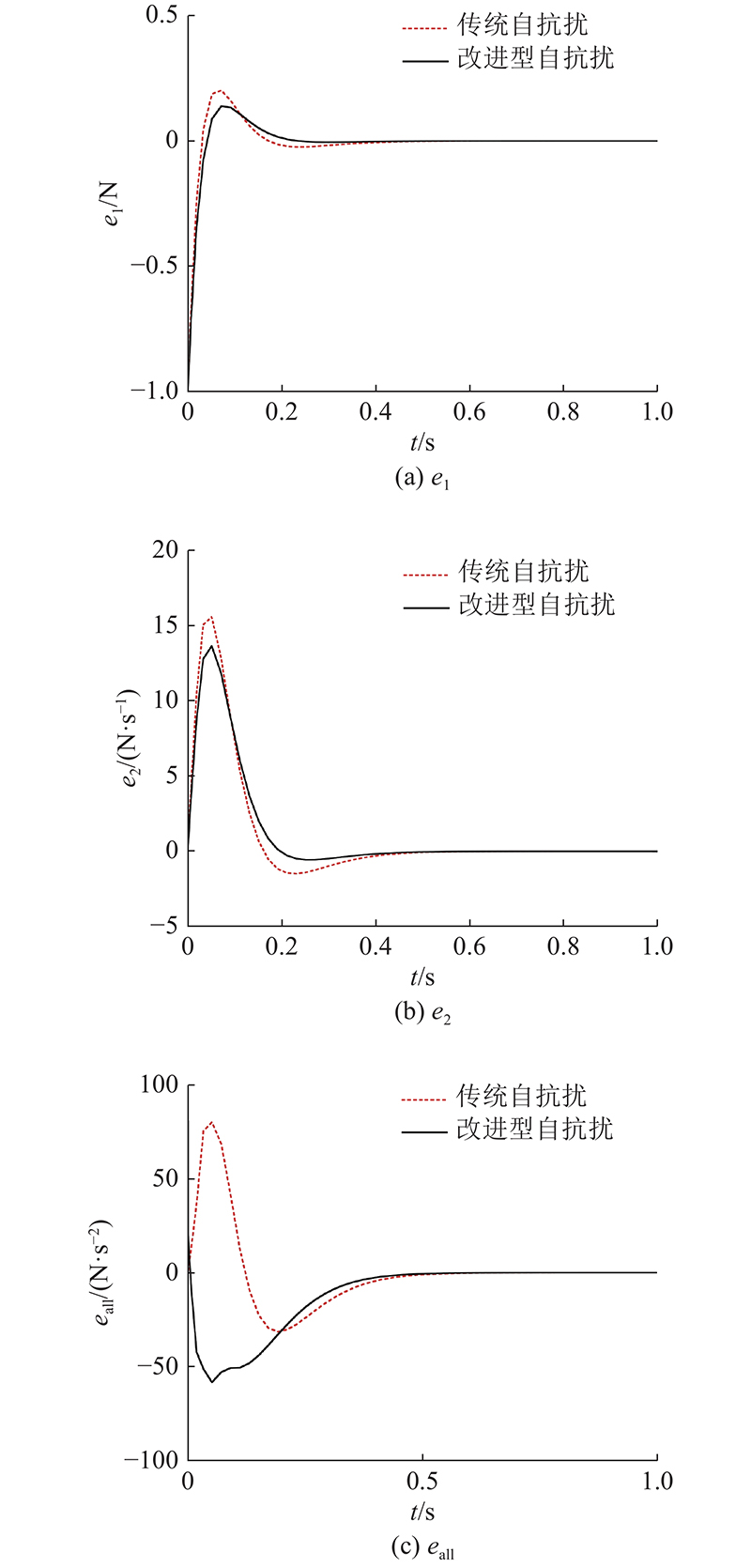
图 4
图 4 2种自抗扰控制下扩张状态观测器的状态观测误差
Fig.4 State observation error of extended state observer under two kinds of active disturbance rejection control
4. 轴孔装配实验
4.1. 实验系统
图 5
图 6
在此平台上分别采用阻抗控制、自抗扰阻抗控制与改进型自抗扰阻抗控制进行实验. 装配性能的优良程度由装配过程力与力矩误差衡量,选取合理的数据以求取装配接触力控制的平均误差,末端接触力和力矩的平均误差定义为
式中:N为数据采样点的个数,
4.2. 轴孔装配实验
实验时,给工件轴与工件孔设置初始位姿偏差,对X、Y、Z、A(绕X轴的旋转轴)、B(绕Y轴的旋转轴)5个方向上分别进行接触力的控制,阻抗控制、自抗扰阻抗控制和改进型自抗扰控制算法各个轴的
表 1 轴孔装配过程中3种算法在各方向的阻抗参数
Tab.1
| 方向 | md | bd | kd |
| X、Y | 5 | 100 | 0.1 |
| Z | 30 | 200 | 0.2 |
| A、B | 10 | 300 | 0.1 |
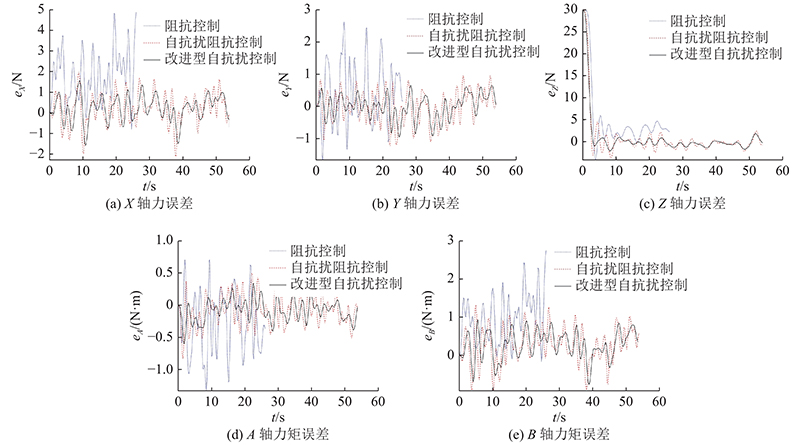
图 7
图 7 装配过程中3种算法在各方向的力误差
Fig.7 Force error of three algorithms in all directions during assembly
装配过程接触力和力矩的平均误差如表2所示,eAEF,X、eAEF,Y、eAEF,Z、eAEF,A、eAEF,B分别为X、Y、Z、A、B轴上的力或力矩平均误差. 相较于自抗扰阻抗控制,施加改进型自抗扰使X轴力误差降低12.6%, Y轴力误差降低26.9%,A轴力矩降低28.2%,B轴力矩降低12.0%. 可见,装配过程中的力波动幅度明显减小,力跟踪精度有较大提升. 证明与自抗扰阻抗控制相比,改进型自抗扰阻抗控制的环境适应性更好,力跟踪效果更优.
表 2 装配过程中不同算法的接触力和力矩平均误差
Tab.2
| 算法 | eAEF,X/N | eAEF,Y/N | eAEF,Z/N | eAEF,A/(N·m) | eAEF,B/(N·m) |
| 阻抗 | 1.707 | 0.742 | 2.620 | 0.399 | 0.910 |
| 自抗扰阻抗 | 0.644 | 0.431 | 0.954 | 0.220 | 0.459 |
| 改进型自抗扰 | 0.563 | 0.315 | 0.649 | 0.158 | 0.404 |
5. 结 语
针对工业六自由度机器人的轴孔装配任务,提出改进型自抗扰阻抗控制策略. 该策略以基于位置型阻抗控制方法设计自抗扰控制算法,实现机器人的装配过程控制. 设计改进型扩张状态观测器,使整个控制系统的性能提高. 针对小间隙轴孔装配任务设计轴孔装配实验,实验结果表明:自抗扰阻抗控制能够实现间隙为0.04 mm 轴孔的自动化装配,并在整个装配过程中保持较高的力跟踪精度,弥补阻抗控制的不足;改进型自抗扰阻抗控制能进一步提高力跟踪精度. 实验结果证明,所提控制策略的可行性和高效性. 在后续的研究中,将考虑不同尺寸轴孔的装配任务要求,制定合理的装配策略,优化阻抗参数和自抗扰参数,实现不同轴孔的柔顺装配.
参考文献
工业机器人的研发及应用综述
[J].DOI:10.16183/j.cnki.jsjtu.2016.S.025 [本文引用: 1]
A review of the research and development of industrial robots
[J].DOI:10.16183/j.cnki.jsjtu.2016.S.025 [本文引用: 1]
Peg-on-hole: mathematical investigation of motion of a peg and of forces of its interaction with a vertically fixed hole during their alignment with a three-point contact
[J].
基于力/位混合控制的工业机器人精密轴孔装配
[J].
Industrial robot high precision peg-in-hole assembly based on hybrid force/position control
[J].
Compliant peg-in-hole assembly using partial spiral force trajectory with tilted peg posture
[J].DOI:10.1109/LRA.2020.3000428 [本文引用: 1]
末端 F/T传感器的重力环境下大范围柔顺控制方法
[J].
A wide range compliance control method in gravity environment based on end force/ torque sensor
[J].
Adaptive variable impedance control for dynamic contact force tracking in uncertain environment
[J].DOI:10.1016/j.robot.2018.01.009 [本文引用: 1]
Robust impedance control of robot manipulators using differential equations as universal approximator
[J].DOI:10.1080/00207179.2017.1336669 [本文引用: 1]
Iterative learning impedance control for rehabilitation robots driven by series elastic actuators
[J].DOI:10.1016/j.automatica.2017.12.031 [本文引用: 1]
Force-based variable impedance learning for robotic manipulation
[J].DOI:10.1016/j.robot.2018.07.008 [本文引用: 1]
Model accelerated reinforcement learning for high precision robotic assembly
[J].DOI:10.1007/s41315-020-00138-z [本文引用: 1]
基于动力学前馈的空间机器人多销孔装配力柔顺控制
[J].DOI:10.3901/JME.2019.04.207 [本文引用: 1]
Force compliance control of multi-peg-in-hole assembling by space robot based on dynamic feedforward
[J].DOI:10.3901/JME.2019.04.207 [本文引用: 1]
六自由度装配机器人的动态柔顺性控制
[J].
Dynamic compliant control of six DOF assembly robot
[J].
Adaptive impedance control for an upper limb robotic exoskeleton using biological signals
[J].
自抗扰控制思想探究
[J].DOI:10.7641/CTA.2013.31087 [本文引用: 1]
On the foundation of active disturbance rejection control
[J].DOI:10.7641/CTA.2013.31087 [本文引用: 1]
Active vibration control of flexible manipulator using auto disturbance rejection and input shaping
[J].