齿轮齿条机构因其结构简单紧凑、传动精度高、支撑刚度高、运动换向能力强被广泛应用于各类军事和民用装备中. 充分了解齿轮副动态特性,对减少传动过程中的振动和噪声、延长轮齿系统的寿命至关重要,因此齿轮齿条传动过程中的非线性动态特性一直是国内外的研究热点[1]. Kahraman等[2]利用单自由度集中参数模型描述轮齿间的时变动态特性,并试验验证了其模型的准确性[3]. 为了更准确地表征复杂的齿轮特性,多自由度的集中参数模型被研究和应用于不同工况的齿轮系统中[4-5]. 集中参数模型虽然可以提供极高的计算效率,但是该模型基于确定的定义参数来获得系统的动态响应,使得计算精度在很大程度上受参数选择的影响. 时变啮合刚度作为关键参数是影响模型预测准确性的重要因素,准确、高效、方便地确定不同结构与工况的轮齿啮合刚度也是获得齿轮系统动态特性的关键[6].
在实际工作环境中,啮合齿副间存在润滑作用,润滑状况和齿轮系统动力传动间存在强耦合关系[7]. 为了研究齿轮的润滑机理及其对齿轮动态性能的影响,许多学者开展了基于润滑摩擦原理的建模理论研究. 黄立等[8]将渐开线斜齿圆柱齿轮啮合等效为长椭圆接触,建立了齿轮弹流润滑计算的数学模型;针对平稳运行和启动工况,研究了油膜受瞬态挤压效应的影响. De la Cruz等[9]提出新颖的多啮合传动摩擦动力学模型,用以研究减速器的噪声和振动响应. 该模型建立时考虑了瞬态条件下的热弹性流体动力润滑、轮系动力学和粗糙体的界面作用等因素的耦合作用. 菅光霄等[10]基于六自由度集中参数齿轮摩擦动力模型,探究齿轮啮合过程中接触冲击现象对齿轮弹流润滑特性的影响. 该研究表明,接触冲击振动使油膜厚度和油膜压力产生较大的突变. Tao等[11]建立三维线接触混合弹流动力润滑模型,表征在接触面积和形貌影响下大模数齿轮齿条的润滑行为,并基于此模型对齿面的形态进行优化设计,以期在稀油供应条件下获得更好的传动性能. 上述模型大多是在固定负载和转速情况下考虑啮合刚度变化引起的啮合齿接触负载变化,这种先验地分配啮合齿负载的方法存在武断性[7]. 同时,大多数齿轮齿条机构须频繁地启停转向,这会引起齿轮齿条啮合处速度和负载大范围变化,对轮齿间油脂润滑性能有极大的影响[12].
本研究基于渐开线标准直齿轮传动的啮合原理,结合齿轮齿条增程机构的传动特性,考虑齿轮啮合时的结构时变啮合刚度和瞬态热弹流润滑刚度的耦合效应影响,建立脂润滑齿轮齿条增速机构的动力学模型. 根据测定剪切稳定状态下的润滑脂流变参数和热力学参数,研究传动过程中啮合处脂润滑热成膜与摩擦特性以及脂润滑对齿轮齿条传动性能的影响.
1. 脂润滑齿轮齿条动力学模型
1.1. 物理模型与运动方程
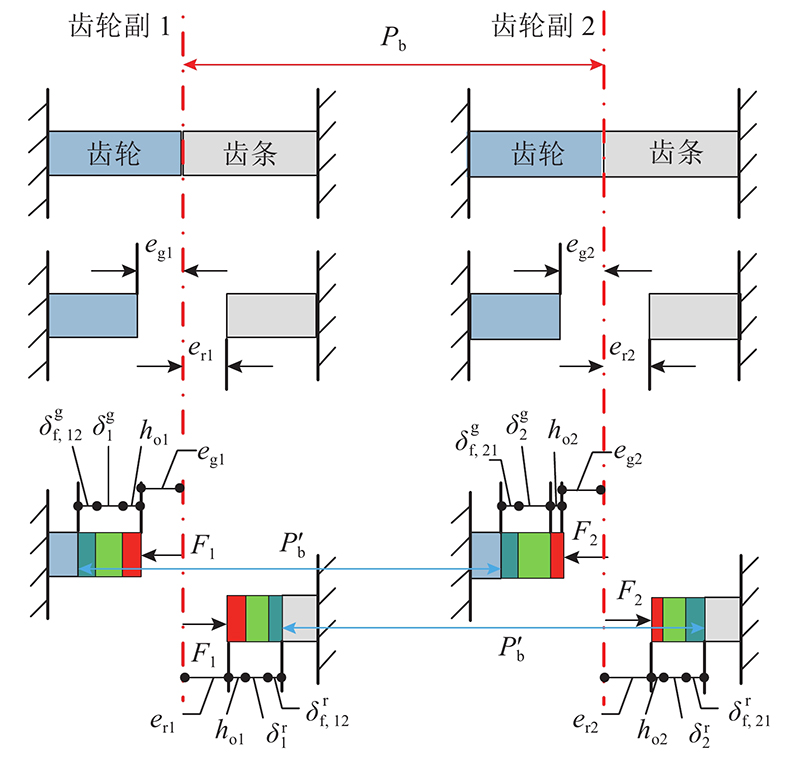
如图1所示为齿轮齿条增程机构示意图. 图中,
图 1
图 1 齿轮齿条增程机构示意图
Fig.1 Configuration of pinion and rack stroke-increment mechanism
式中:
1.2. 脂膜润滑下的耦合啮合刚度
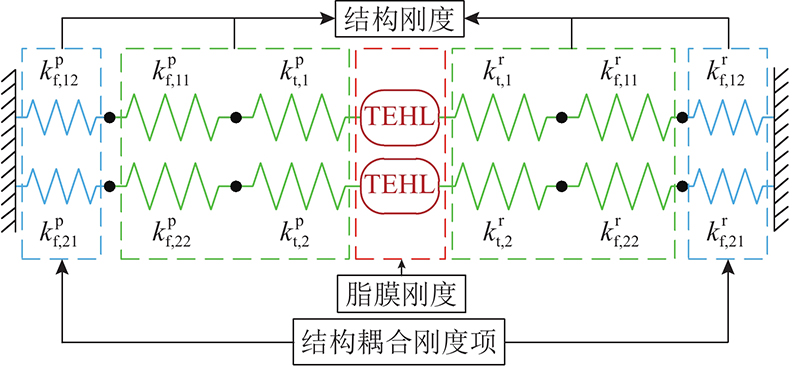
大多数已有研究基于预设的载荷分配因子在确定负载的情况下进行齿轮的弹流润滑分析,忽略了非稳态运动下脂膜刚度对总时变啮合刚度的影响. 本研究考虑齿轮啮合时的结构时变啮合刚度和热弹流润滑(thermal elastohydrodynamic lubrication,TEHL)的耦合效应,提出结构−脂膜耦合啮合刚度模型.
1.2.1. 考虑邻近齿的耦合柔性和线外啮合的渐开线直齿轮啮合刚度
利用势能理论建立啮合结构刚度模型,由于重合度大于1,将多齿同时啮合时引起的邻近齿耦合柔性引入啮合刚度模型中,表达式为
式中:
图 2
表 1 结构耦合刚度的常系数项
Tab.1
| 参数 | 数值 | 参数 | 数值 | 参数 | 数值 | ||
| | 3.922 6 | | 0.409 5 | | −0.285 7 | ||
| | 1.625 4 | | 0.330 8 | | 0.104 0 | ||
| | 2.697 9 | | 0.236 8 | | 0.577 7 | ||
| | 0.434 7 | | 0.085 1 | | 0.104 0 | ||
| | −0.511 4 | | −0.080 4 | | 0.577 7 | ||
| | 0.339 7 | | 1.685 9 | | 1.440 4 | ||
| | 0.330 8 | | −1.248 0 | | 0.095 2 | ||
| | 0.330 8 | | −0.071 4 | | −0.096 7 | ||
| | 0.330 8 | | 0.322 6 | | −0.118 2 | ||
| | 0.236 8 | | 2.007 9 | | 0.285 7 | ||
| | −0.085 1 | | 0.357 1 | | −0.104 0 | ||
| | 0.080 4 | | 2.007 9 | | 0.577 7 | ||
| | 1.685 9 | | 1.440 4 | | −0.104 0 | ||
| | −0.511 4 | | −0.095 2 | | 0.577 7 | ||
| | −0.399 7 | | 0.096 7 | — | — | ||
| | 0.330 8 | | −0.118 2 | — | — |
1.2.2. 结构−脂膜耦合啮合刚度
图 3
图 3 考虑耦合现象的变形协调条件
Fig.3 Deformation compatibility condition considering coupling phenomenon
2)离去过程:
式中:
1.3. 脂润滑控制方程
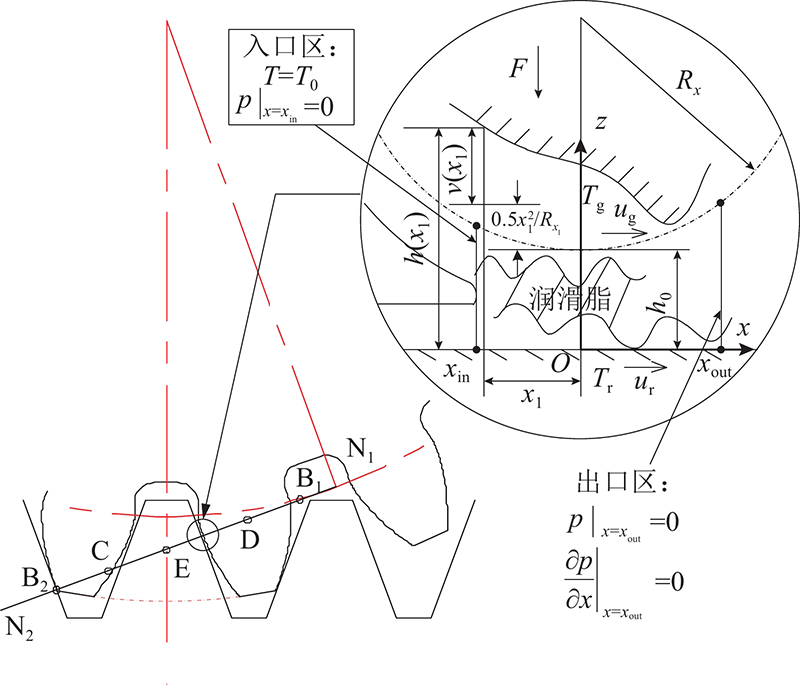
根据渐开线直齿轮的啮合特点,将接触齿间的流体润滑视为线接触进行建模,如图4所示,本研究考虑在剪切稳定后的润滑情况,因此忽略两侧的微量端泄效应. 结合润滑脂Power-law流变模型,推导瞬态啮合齿对的线接触Relynolds方程为
图 4
图 4 啮合点脂润滑热弹流膜示意图
Fig.4 Schematic diagram of grease lubrication thermal elastohydrodynamic film at meshing point
式中:
2)下侧齿:
式中:
式中:
不计热辐射和体积力的影响,忽略
式中:
能量方程的边界条件,即上下界面温度的计算式[12]为
式中:
1.4. 摩擦模型
式中:
式中:
2. 仿真与求解
表 2 齿轮齿条结构参数
Tab.2
| 参数 | 数值 | 参数 | 数值 | |
| 齿轮质量 | 4.91 | 齿宽 | 20 | |
| 齿轮转动惯量 | 4.2×10−4 | 弹性模量 | 207 | |
| 上侧齿条质量 | 12.91 | 泊松比 | 0.3 | |
| 模数 | 3 | 齿侧间隙 | 0.10 | |
| 齿轮齿数 | 20 | — | — |
表 3
润滑脂的流变参数(
Tab.3
| 名称 | c/ (J·kg·K−1) | k/ (W·m−1·K−1) | ρ/ (kg·m−3) | ρT/ (m·k−1) | φ0/ (Pa·sn) | n |
| 齿轮 | 470 | 46 | 7850 | — | — | — |
| 齿条 | 470 | 46 | 7850 | — | — | — |
| 润滑脂 | 1646 | 0.14 | 880 | 0.00065 | 8.634 | 0.754 |
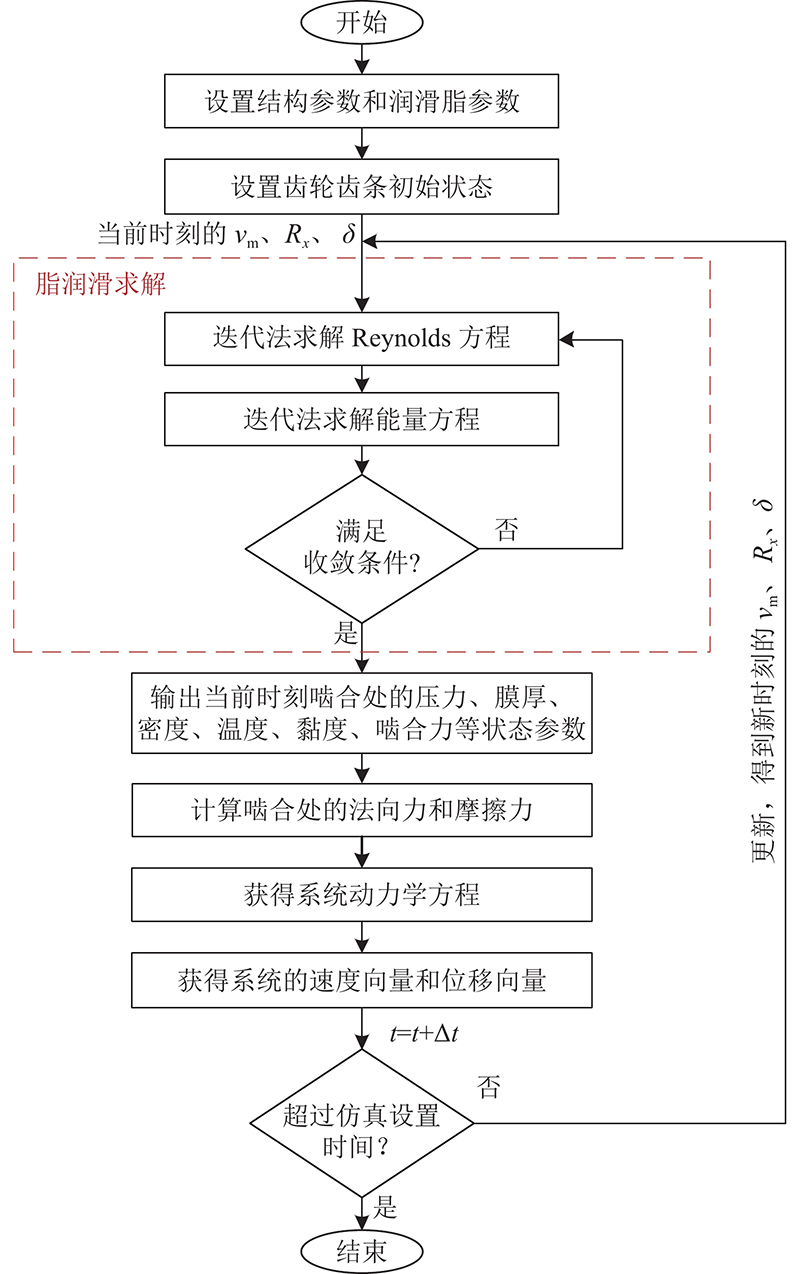
如图5所示为脂润滑齿轮齿条动力学模型求解的流程,其步骤如下.1)设置基本参数(包括齿轮结构参数与润滑脂参数)以及齿轮齿条初始状态. 2)将根据当前时刻的齿轮齿条状态得到的脂卷吸速度
图 5
图 5 脂润滑齿轮齿条动力学模型求解流程图
Fig.5 Flowchart of solving dynamic model of pinion and rack with grease lubrication
在脂润滑求解过程中,压力的求解采用5层多重网格法,最密层的节点数为961. 在每层压力修正过程中,Gauss-Seidel、Jacobi双极子迭代法被分别应用在低压和高压区域的压力迭代中,表面弹性变形的计算采用DC-FFT方法. 温度场仅在最密层进行求解,温度场
3. 脂润滑齿轮齿条动态特性分析
齿轮齿条增程机构的前向(图1中X轴的正方向为前向)输送过程为主工况,与反向收回过程相比,前向输送的运行条件更为苛刻,因此将向前输送过程中的动态特性作为主要研究对象. 在该工况下,执行装置提供的力规律为
在整个工作周期内,齿轮与齿条的运动状态不仅受到外负载的影响,还与啮合点处的结构刚度和脂膜刚度有关,齿轮与齿条的瞬时运动状态影响润滑脂的成膜特性,这种齿轮齿条动力特性与热弹流体动压润滑特性的耦合作用,使啮合处的受力情况更为复杂. 上、下齿条的运动状态不同,导致同时刻上、下齿条啮合处的成膜特性不同,但在每个齿的啮合周期内的成膜规律是相同的,且上齿条作为输出端,其动态特性更为研究者所关注,因此仅提取并分析上齿条与齿轮的啮合动态特性.
3.1. 机构动作特性
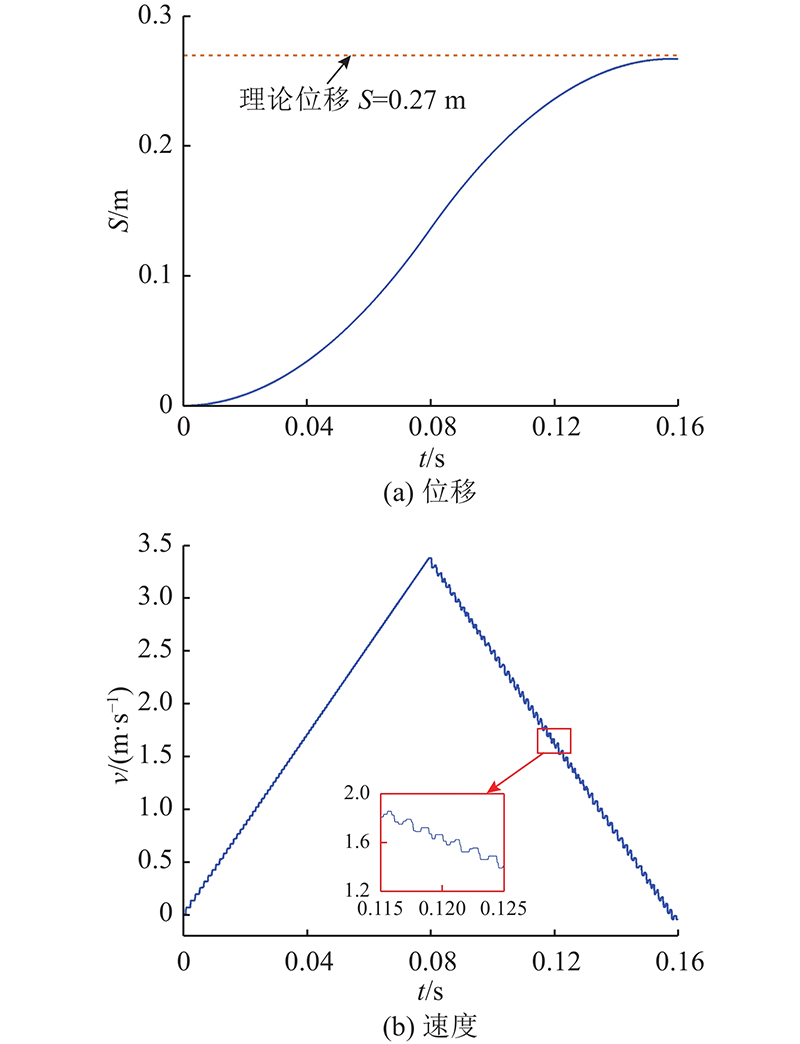
如图6所示为上齿条的位移S、速度v随时间变化的关系曲线. 可以看出,上齿条实际位移与理论位移存在偏差,说明在传动过程中有能量被耗散. 速度曲线整体上满足先均匀加速后均匀减速的规律,但是在较小的时间域里存在明显波动. 波动的存在表明,传动系统是高频的强非线性系统. 传动过程中啮合状态的转换、总啮合刚度随运动状态的变化都是导致速度波动的原因. 由图还可以发现,减速段的速度波动明显强于加速段. 说明在减速阶段,啮合刚度的变化更强烈,还可能存在更频繁的冲击效应.
图 6
3.2. 总啮合刚度与脂膜特性
选取2个啮合齿对,分别为第2、8啮合齿,讨论它们在各自啮合周期内的动态传动误差、动态啮合力、总啮合刚度与脂膜特性的变化. 第2啮合齿是初始加速阶段对应的啮合齿,第8啮合齿是传动从加速阶段切换到减速阶段过程对应的啮合齿.
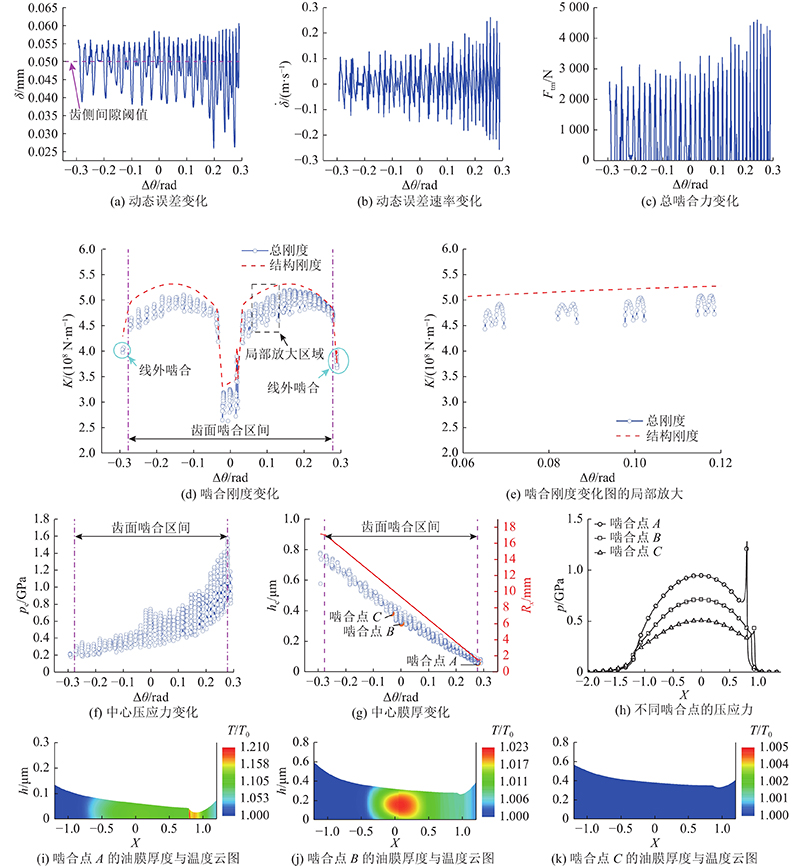
如图7所示为第2啮合齿在啮合周期内的状态特性. 由图7(a)~(c)可知,啮合周期内仅包含2种啮合状态:齿面啮合、齿轮脱啮。随着啮合齿从啮入运行到啮出(接触点到节点的转角偏差
图 7
图 7 齿轮与上齿条在第2齿啮合周期内的啮合状态特性
Fig.7 Meshing state characteristics during second tooth meshing cycle of gear and upper rack
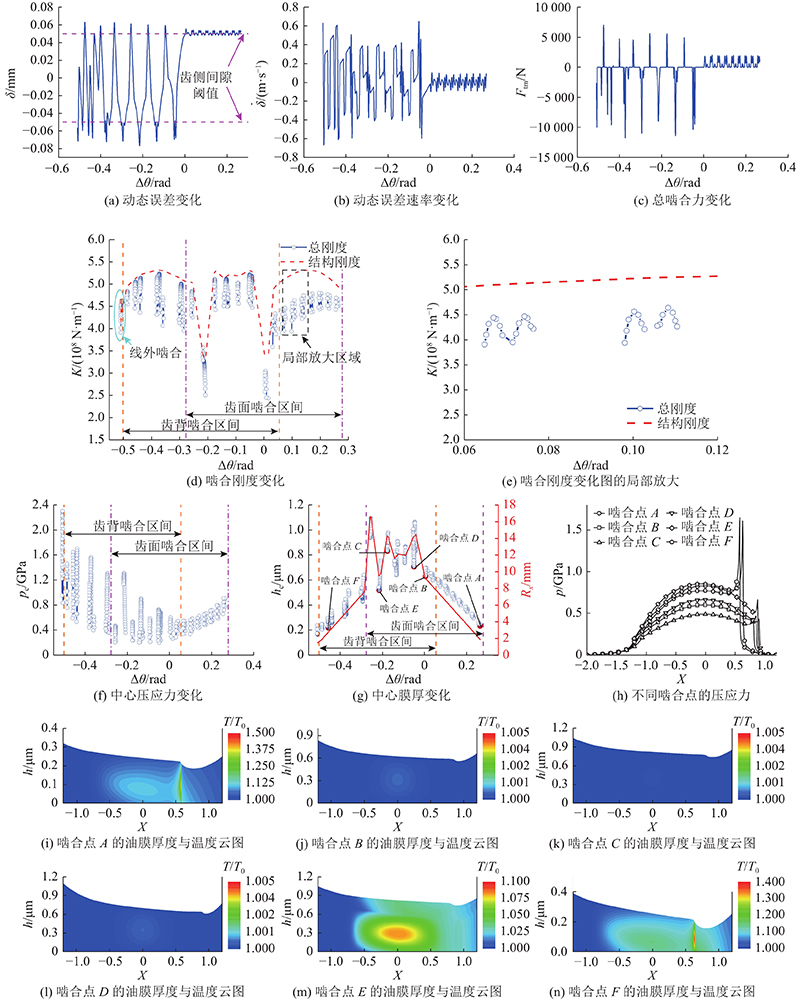
系统继续运行,进入第8齿啮合期,此周期内的状态特性如图8所示. 第8齿啮合的前半段时期处于上齿条加速阶段,后半段转入减速阶段,因此啮合齿对的状态特性比第2齿啮合时期的更为复杂. 由图8(a)~(c)可知,啮合周期内3种啮合状态均出现,齿背啮合的存在使得第8齿的啮合周期明显增加. 在该齿啮合周期初期,动态误差速率和总啮合力的波动幅值较为稳定且处于较低水平,其中动态误差速率的波动幅值为0.2 m/s,总啮合力振荡幅值为2 000 N. 当系统突然转入减速阶段出现齿背啮合状态时,会引起动态误差速率和总啮合力大幅振荡. 如图8(d)所示,不同于第2齿啮合时的双齿−单齿−双齿的3段刚度,此时的结构刚度变为双齿−单齿−双齿−单齿−双齿的5段刚度,且在−0.28<
图 8
图 8 齿轮与上齿条在第8齿啮合周期内的啮合状态特性
Fig.8 Meshing state characteristics during eighth tooth meshing cycle of gear and upper rack
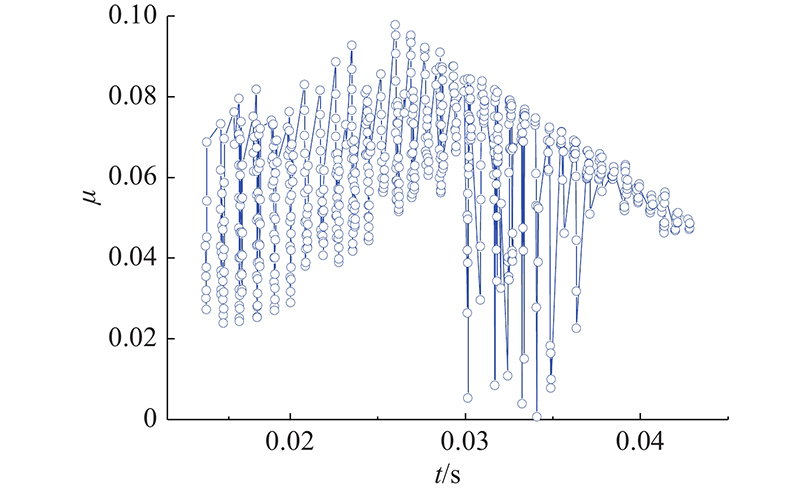
3.3. 动态过程中摩擦系数
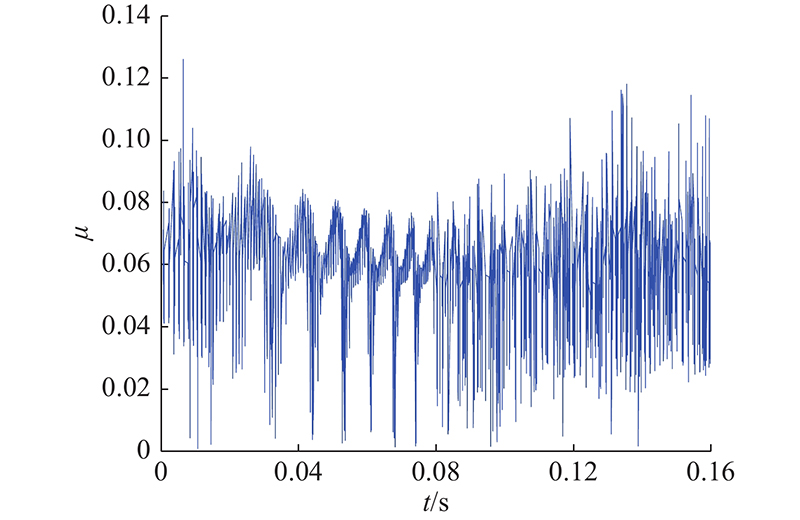
啮合齿对间脂膜特性的动态变化,使摩擦力呈现复杂的波动特性,啮合齿间的摩擦作用进一步影响系统的整体特性,导致出现如图6(a)所示的上齿条未达到理论位置的情况. 通过摩擦系数表征系统运行过程中摩擦特性的变化,定义摩擦系数为
图 9
图 10
图 10 第2齿啮合过程中摩擦系数的变化
Fig.10 Variation of friction coefficient during second tooth meshing process
4. 对比分析
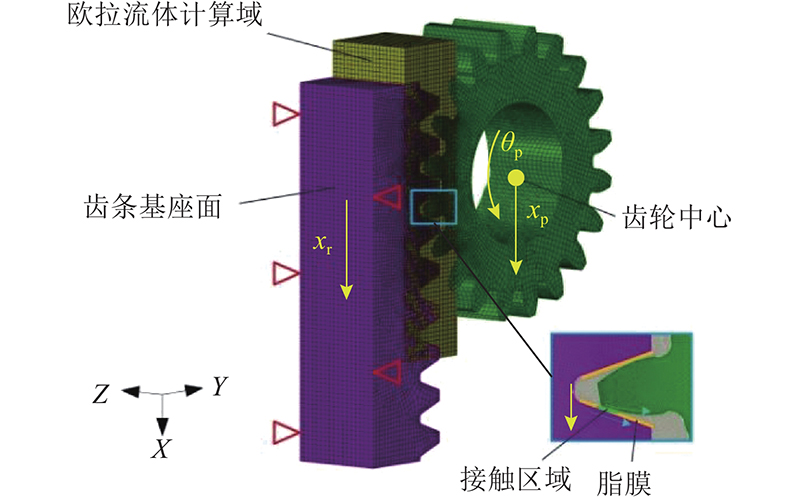
选取总刚度模型为验证目标,将本研究所提出方法与有限元模型(finite element modelling,FEM)的计算结果进行对比. 齿轮齿条的有限元模型的基本参数与表2、3相同. 如图11所示,在有限元模型的齿条基座面上施加Z方向的强制平动位移边界条件,并约束其他方向上的自由度. 齿轮中心处施加Z方向的强制平动位移和X轴方向的强制角位移,并约束其他方向上的自由度. 在齿轮的间隙部位,使用欧拉格式的有限元背景网格离散润滑脂可能的运动区域. 对于润滑脂的初始几何形态,同样使用欧拉网格再次离散,并赋予初始体积分数为1. 对背景网格进行布尔运算,取其余区域的体积分数为0. 在接触区域对网格进行加密处理,并采用增广拉格朗日方法防止结构体互穿.
图 11
图 11 齿轮齿条啮合有限元模型
Fig.11 Finite element model of engagement of tooth and pinion engagement
如图12所示为第2齿的啮合刚度对比. 可以看出,本研究所提结构−脂膜耦合啮合刚度模型与FEM的计算结果基本相同. 在单齿啮合到双齿啮合的过渡阶段,线外啮合的现象在2种模型的计算结果中都得到体现,该阶段2种计算结果的误差均较大,但是均未超过3.5%,其他啮合阶段的计算结果误差均未超过2%. 在FEM计算中得到与上文分析一致的规律,即考虑脂膜影响后的齿轮齿条啮合刚度低于仅考虑结构影响的,且啮合刚度随着啮合处作用力的下降而显著下降. 因此,本研究所提方法在计算脂润滑条件下的齿轮齿条啮合刚度时,不仅具有较高的计算精度和效率,而且能够有效地反映齿轮齿条啮合过程中的动态特性变化.
图 12
5. 结 论
(2)齿轮齿条传动系统在运行过程中存在3种工作状态:齿面啮合、齿背啮合、齿轮脱啮. 系统在前期加速运动时仅出现齿面啮合和脱啮的状态,此阶段系统呈现规律性运行:随着轮齿啮合位置沿啮合线正方向移动,中心脂膜厚度增加,中心压应力下降. 系统在后期减速运动时,由于齿面啮合与齿背啮合的交替出现,当量曲率半径将出现较大的阶跃变化,使得单齿啮合周期内总啮合刚度、中心膜厚、中心压应力和摩擦系数均出现较大幅度的阶跃,系统运行无规律可循.
(3)无论是齿背啮合状态还是齿面啮合状态,最小油膜厚度、最大温升以及最大压应力即系统最恶劣润滑状态,均出现在齿轮轮齿面上靠近基圆的位置及与其啮合的齿条齿顶附近. 当每对啮合齿啮合到靠近节点位置时,脂膜温升和摩擦系数明显下降.
(4)本研究建立的在脂润滑情况下齿轮齿条动力学模型较为真实地体现了实际传动过程中的动态特性,并很好地反映了各阶段的润滑情况。期望本研究所得结论能够为后续齿轮磨损性能的研究奠定基础.
参考文献
计及摩擦的多状态啮合渐开线直齿轮系统动力学建模分析
[J].DOI:10.3969/j.issn.1000-2758.2020.02.022 [本文引用: 2]
Dynamic modeling and analysis of involute spur gear transmission system considering friction and multi–state meshing conditions
[J].DOI:10.3969/j.issn.1000-2758.2020.02.022 [本文引用: 2]
Non-linear dynamics of a spur gear pair
[J].DOI:10.1016/0022-460X(90)90582-K [本文引用: 1]
Experiments on nonlinear dynamic behavior of an oscillator with clearance and periodically time-varying parameters
[J].DOI:10.1115/1.2787276 [本文引用: 1]
Mathematical modelling and computer simulations as an aid to gearbox diagnostics
[J].DOI:10.1006/mssp.2001.1411 [本文引用: 1]
Modeling and dynamics analyzing of a torsional-bending-pendular face-gear drive system considering multi-state engagements
[J].DOI:10.1016/j.mechmachtheory.2020.103790 [本文引用: 1]
A new mesh stiffness model for modified spur gears with coupling tooth and body flexibility effects
[J].
Behavior of lubricant fluid film in gears under dynamic conditions
[J].DOI:10.1016/j.triboint.2013.01.017 [本文引用: 3]
斜齿轮非稳态等温弹流润滑数值分析
[J].DOI:10.3969/j.issn.0254-0150.2009.07.006 [本文引用: 1]
Numerical analysis of transient elastohydrodynamic lubrication of helical gears
[J].DOI:10.3969/j.issn.0254-0150.2009.07.006 [本文引用: 1]
Transient mixed thermo-elastohydrodynamic lubrication in multi-speed transmissions
[J].DOI:10.1016/j.triboint.2011.12.006 [本文引用: 1]
振动与接触冲击耦合作用下的齿轮弹流润滑研究
[J].DOI:10.13465/j.cnki.jvs.2020.21.030 [本文引用: 1]
Elasto-hydrodynamic lubrication of gears under coupling of vibration and contact impact
[J].DOI:10.13465/j.cnki.jvs.2020.21.030 [本文引用: 1]
Lean lubrication of ultra large modulus open gear and rack pair: a case study of the gear-rack drive mechanism of the Chinese "Three Gorge Dam" ship lift
[J].DOI:10.1016/j.jclepro.2020.124450 [本文引用: 3]
Analytical formulas for gear body-induced tooth deflections of spur gears considering structure coupling effect
[J].DOI:10.1016/j.ijmecsci.2018.08.022 [本文引用: 1]
Analytical modeling of spur gear corner contact effects
[J].DOI:10.1016/j.mechmachtheory.2015.10.001 [本文引用: 2]
Gear transmission error outside the normal path of contact due to corner and top contact
[J].
Numerical analysis of grease thermal elastohydrodynamic lubrication problems using the Herschel-Bulkley model
[J].DOI:10.1016/S0301-679X(96)00069-2 [本文引用: 1]
圆锥滚子轴承滚子/滚道副的脂润滑热成膜性能
[J].
Thermal film-forming ability of grease lubrication at roller-raceway pair in tapered roller bearings
[J].
Elastohydrodynamic lubrication with Herschel-Bulkley model greases
[J].
Effects of surface texturing on ring/liner friction under starved lubrication
[J].DOI:10.1016/j.triboint.2015.10.024 [本文引用: 3]
An improved mesh stiffness model for double-helical gear pair with spalling defects considering time-varying friction coefficient under mixed EHL
[J].DOI:10.1016/j.engfailanal.2020.105174 [本文引用: 1]
The Contact of Two Nominally Flat Rough Surfaces
[J].DOI:10.1243/PIME_PROC_1970_185_069_02 [本文引用: 1]