随着我国城市化高速发展,机动车数量快速增长,城市道路拥堵问题日益严重. 智能交通系统(intelligence traffic system,ITS)是目前缓解交通拥堵,提高交通效率的重要途径.
车辆路径规划是ITS中一项重要的研究内容. 目前对于路径规划的研究,大致可以分为反应型和预测型2种[1]. 反应型路径规划指利用道路交通设施采集的实时动态信息,基于当前交通状况为出行者计算最短路径.预测型路径规划指利用已有的交通信息预测未来的交通状态,根据未来的交通状态为出行者计算最短路径,期望在拥堵发生前采取措施. 相比反应型的路径规划,Liang等[2]指出基于拥堵预测的主动道路诱导是提高诱导有效性的关键. Yuan等[3]利用线圈检测器收集的交通流数据进行短时交通流预测,提出基于堆叠网络模型的上下层交替规划算法. 曹政才等[4]利用路段历史流量数据预测该路段的交通流量,并把预测的交通代价融入改进A*算法的路径搜索过程. Zhu等[5]利用车辆的历史GPS数据集进行交通流预测,提出基于神经网络的加权最短路径A-Dijkstra算法. Liebig等[6]通过实时交通信息预测未来交通状况,设计了具有态势感知的出行规划系统;郭畅[7]将基于实时信息估计的行驶时间结果作为性能指标,提出车辆在动态时隙内的最优路径方法模型;杜茂等[8]指出考虑到达时间的路径搜索应在三维时空领域展开,并设计了基于交通时空特征的车辆全局路径规划算法. Lecluyse等[9]提出利用交通的拥挤程度预测行程时间的变化范围,通过建立交通流的时空特性网络来求解动态路径选择问题.李妍峰等[10]考虑常发性拥堵和偶发性拥堵的区别,提出了基于交通流预测的动态路径选择更新方法.
上述研究使用的数据大多来源于线圈、超声波、微波等采集的历史数据,不仅采集成本大、数据容易缺失[11],而且历史数据并不能较好地反映短时交通流高度不确定性的特点.在此背景下,针对“未来时刻的交通流能否由‘不确定’变为‘确定’?”这一关键科学问题,本研究团队提出了“出行计划”的思想[12-15]−利用出行者的“出行计划”数据,即未发生但即将发生的路径请求数据,计算车辆未来经过的地点和相应到达这些地点的时刻,该计算结果蕴含着重要的时间-位置信息元素(即未来某个时刻这辆车会走到哪里),这是将未来交通状态由“混沌”变为“清晰”的关键.利用该计算结果,可以获知路网的未来交通状况,改变交通流的混沌状态,引导车辆顺利抵达目的地,最终建立一个基于出行计划数据的未来路况计算及诱导系统[16]. 使用出行计划信息,可以让数据的资源属性充分释放出来,把“交通流预测”提升到“交通流计算”的新高度,引领交通拥堵研究深入到新开拓的交通流计算领域.
本研究的研究重点是该系统中的一个核心部分−基于出行计划数据的路径规划方法(path planning method based on travel plan data,RPTP),用来确定车辆在道路网络中从出发地到目的地的最优路径. 本研究以预测型路径规划为导向,创新性地提出利用出行计划数据计算未来多时段路网交通密度,并在路径规划时考虑未来路网交通密度的影响,以期提高车辆的通行效率,解决多个车辆在同一时间段内对某一最优路段的共同选择造成的交通拥塞滞后性问题.
1. 出行计划思想
1.1. 出行计划定义
本研究提出的“出行计划数据”指的是用户在驾车出发前使用导航软件形成的信息,一条原始的出行计划数据包括:用户ID、出发时间、出发地、目的地. 该信息在一定程度上代表了用户对路网未来的交通需求,理论上聚合所有车辆发布的出行计划数据便可以计算出路网在未来时刻的交通状况. 基于未来出行透明化引导出行者趋利避害,规避拥堵的设想,兼顾未来自动驾驶发展的需要, 此项研究将使用导航变得简单方便,“用户ID、出发时间、出发地”自动采集,目的地只要说出要去的地点即可. 以此,可以提高导航的使用率.
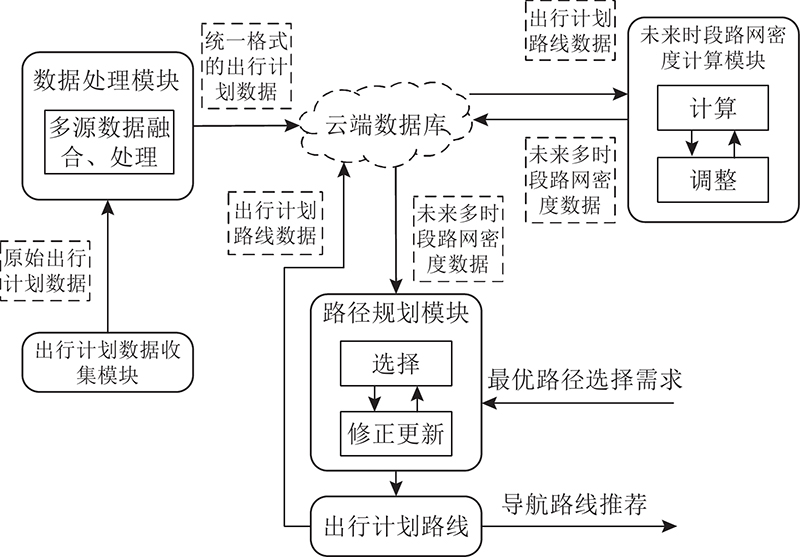
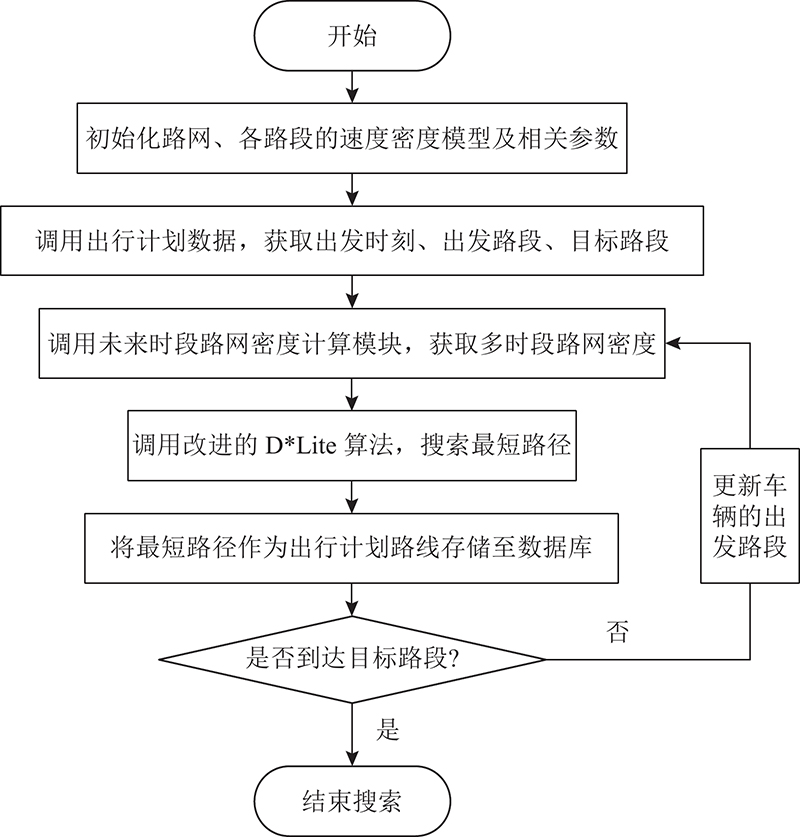
传统意义上人们出行,实际上也是在出发前制定了出行计划,只是该计划并未发布和被收集. 因此,本团队提出了基于出行计划数据的未来路况计算及诱导系统,该系统能够收集用户在出发前发布的出行计划数据,并以此为依据计算路网未来的交通状况,向用户推荐出行路线. 基于出行计划数据的路径规划整体框架如图1所示.
图 1
上述框架主要分为4个模块. 1)出行计划数据收集模块,主要用于收集用户的原始出行计划数据. 2)数据处理模块,主要用于融合不同来源的出行计划数据,并将其转换成统一格式. 3)未来时段路网密度计算模块,主要利用已收集的出行计划路线数据,以选定出行计划要经过的各个路段为参照,关联在时间和空间上并行的其他所有出行计划,对未来多个时段的路网密度进行计算,并将计算结果存储至云端数据库. 4)路径规划模块,通过调用云端数据库中未来各时段的路网密度计算结果,根据车辆实时位置不断进行最优路径搜索,并将搜索结果作为出行计划路线存储至云端数据库,同时把出行路线推荐给用户. 云端数据库则存储并实时更新用户的出行计划数据、出行计划路线数据以及路网密度数据.
当某一用户发布其出行计划后,系统收集该出行计划并将其转换成统一格式,存储至云端数据库;接着,路径规划模块调用未来时段路网密度计算结果,为该用户搜索最优路径,搜索结果一方面推荐给用户,另一方面作为出行计划路线存储至云端数据库;未来时段路网密度计算模块则不断对未来时段路网密度进行计算,并将计算结果存储至云端数据库. 另外,考虑到实时交通状况的影响,上述过程还引入了“修正更新”机制−每完成一次路径搜索,对车辆的实时位置进行更新,将更新后的车辆位置作为起点,再次进行路径搜索.
1.2. 出行计划可行性分析
在技术方面,目前人们在出行时越来越依赖导航软件,且少数几个导航软件覆盖了大多数用户,因此通过融合各导航软件中发布的出行计划数据,可以在一定程度上反映对路网未来的总体需求. 另外,5G、车联网、大数据、云平台等技术的不断发展,为计算海量的出行计划数据提供了良好的基础.
2. 城市路网模型
2.1. 时变路网模型
时变路网模型是一个复杂结构,很难用一个具体的函数精确表征整个城市路网的交通状况.为了便于问题分析,本研究采用一种简洁但足以研究路径规划过程的路网模型,对时间进行离散化处理,将时间划分为一系列连续的时段,这样可以把某一路段在某一时段内的交通状况视作近似不变,并由相应的预测模型确定,时变路网的数学表达式如下:
式中:
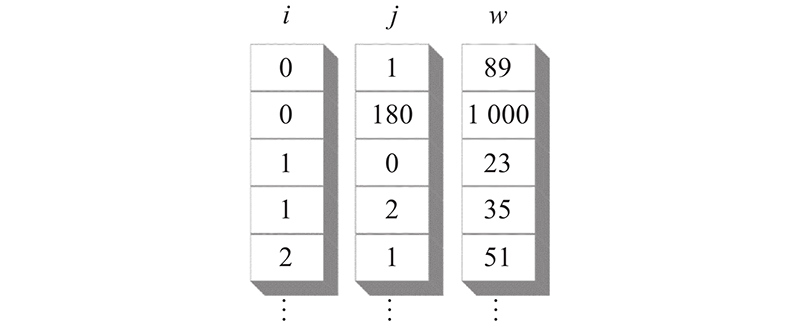
关于路网数据的存储目前已经有邻接表、邻接矩阵、十字链表等多种建模存储方法. 考虑城市路网作为大型稀疏网络的特性,为了减少数据冗余,便于路径搜索算法对其进行操作,本研究使用一种数组实现的邻接表存储路网信息. 该数据存储结构较为简单,且易于查找某节点的邻接对象,实现快速访问路网数据,其存储结构如图2所示.
图 2
这里用
2.2. 基于出行计划的路网系统模型
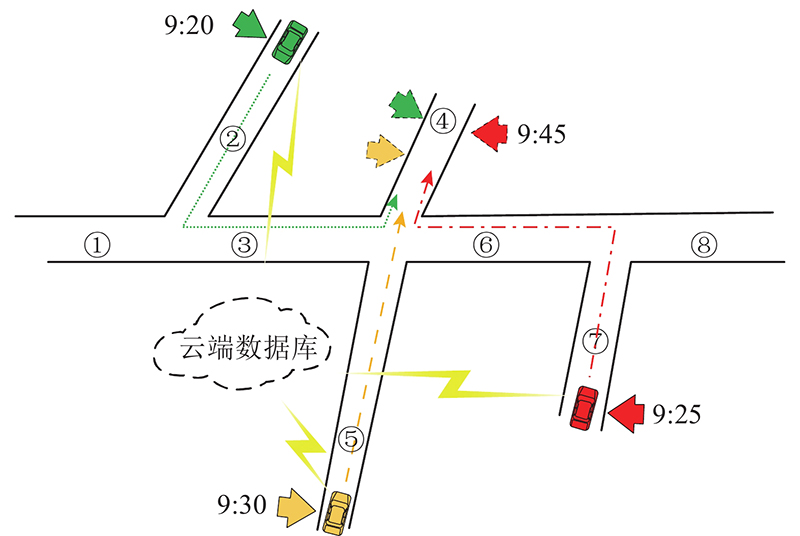
在上述路网基本模型的基础上,本研究考虑车辆出行计划的发布,建立了基于出行计划数据的路网系统模型,如图3所示.
图 3
首先根据路网特点,将道路划分为长度适中的多个路段,如图3中的路网,本研究将其划分为8条路段.假设路网内有红、黄、绿3辆车,每辆车出发前都通过车载导航或导航软件发布了出行计划,该信息被收集至云端数据库.绿车首先发布了出行计划,系统为其推荐的出行计划路线如绿色点线所示,假设根据计算结果,该车辆将在9:45到达路段4. 红车在5 min后发布了出行计划,推荐的路径如红色虚点线所示,同样计算得到其将在9:45到达路段4.系统不断收集出行计划路线数据,则最后发布出行计划的黄车会得知:如果按照图中所示路线行驶,当它到达路段4时,将会有其他2辆车同时到达该路段,这为黄色车辆的出行路线提供了规划依据.另外,由于引入了修正更新机制,数据库在车辆行驶过程中会不断收集、更新出行数据,使得出行者能够持续获得路网的未来交通状况,从而做出合理决策.另外,为了便于分析且不失一般性,本研究暂不考虑红绿灯、车辆种类、非机动车、行人等因素的影响.
3. 基于出行计划路线数据的路网密度估计算法
在本研究提出的路径规划框架中,某用户的路径规划结果不仅会作为导航路线向用户推荐,还会被存储至云端数据库作为其他用户的路径规划依据. 为了聚合已收集到的出行计划路线,以计算未来多个时段的路网密度,本研究针对出行计划路线数据做出如下基本假设:1)假设所有出行计划路线可以实时获取;2)假设用户严格按照导航规定的计划路线行驶;3)假设车辆在进入研究路段前按照与路段密度对应的平均速度行驶,且在1个时段内,路段的平均速度不变.
根据以上假设,将1条出行计划路线投射到空间和时间2个维度:在空间上,将出行计划路线途径的路段按顺序排列,在时间上,将出行计划路线跨越的时段按顺序排列,从而可以得到车辆出行计划路线的时空关系,如图4所示. 图中,横轴代表连续的时段,每个时段长度为
图 4
1)根据路段的速度-密度模型计算路段的平均速度,作为车辆的行驶速度,这里用广义的速度-密度模型代表两者之间的拟合关系. 由于在真实路网中,路段的速度-密度拟合关系受道路属性、驾驶条件、交通流状态等因素影响,不同模型的适用条件与稳定性不同. 因此,在实际应用时应根据不同路段的适用性,选择拟合度高的速度-密度模型.
式中:
2)计算车辆行驶的距离确定未来不同时刻车辆位置. 由于本研究假设车辆在进入某一路段时按照与路段密度对应的平均速度行驶,且1个时段内路段的平均速度视为不变,则车辆的行驶速度只和车辆所处的路段及时段有关. 若车辆在1个时段内没有跨越路段,则车辆速度一直不变;若车辆在1个时段内跨越
式中:
3)计算各路段在未来各时段的密度. 这里的密度不是传统的某一时刻路段上车辆数与路段长度的比值,而是一种引申意义的平均密度,指的是某一时段内途经该路段的车辆数与路段长度的比值. 根据步骤2)计算的车辆未来时刻位置,获取车辆离开每个路段的时刻. 以此为依据,判断车辆在第
式中:
根据上述分析,未来时段路网密度的计算方法用伪代码的形式表示,如下所示.
算法
//调用车辆的出行计划路线集合VRoutes
Input: VRS
//初始化路网邻接表U
Initialization: U
//输出未来n个时段的路网邻接表
Output: U1~Un
Begin
//遍历每一条出行计划路线VRoute
For(VRoute: VRoutes){
//遍历某一VRoute经历的时段VRout.period
For(VRout.period: VRout.periods ){
//计算车辆在该时段内行驶的距离
If(VRout.period == U.period){
//判断车辆在该时段内是否跨越路段
//VRoute.seg.length为路段长度
//U.seg.speed为路段平均速度
//period .length为时段长度
If(VRoute.seg.length/U.seg.speed> period .length){
//车辆没有跨越路段,则速度不变
//VRoute.seg.id为车辆经过的路段id
Return VRoute.seg.id;
//VRoute.dis为车辆的行驶距离
VRoute.dis = U.seg.speed*period.length}else{
//车辆跨越路段,每个路段对应不同速度
//VRoute.timecost为车辆的行驶时间
//VRoute.seg.timecost为车辆在某一路段的行驶时间
While(VRoute.timecost<period.length){
Return VRoute.seg.id;
VRoute.timecost += VRoute.seg.timecost;}
VRoute.dis=ΣVRoute.seg.timecost*U.seg.speed;
//车辆在该时段经过的路段,其密度增加
If(VRoute.seg.id == U.seg.id){
//U.seg.density为路段密度
U.seg.density += 1/U.seg.length;}}}
//计算车辆的累计行驶距离
//VRoute.totaldis为车辆的累计行驶距离
VRoute.totaldis += VRoute.dis;}
//更新路网邻接表
Return U1~Un;}
上述伪代码的核心是通过计算车辆的累计行程,判断车辆在每个时段经过的路段,若车辆在该时段经过该路段,则该路段的车辆数累计增加. 通过不断遍历某一车辆经过的时段,以及每一车辆的出行计划路线,获得车辆在未来到达某一路段时,与该车辆同时段达到该路段的伴随车辆数. 将计算出的伴随车辆数与路段长度相比,最终得到路网在未来多个时段的密度状况.
4. 考虑未来多时段路网密度的路径规划方法
4.1. 道路权值确定
通过上节提出的路网密度估计算法,可以得到未来多个时段的路网密度. 根据交通流的相关理论,连续交通流可以用流量、速度、密度3个参数表示. 交通流密度直接反映了车辆对道路空间的占有率,当密度较小时交通较顺畅,当密度较大时交通偏拥堵. 另外,本研究假设车辆在进入路段前按照与路段密度对应的平均速度行驶,因此速度和密度间具有相关关系. 综上,将密度作为影响路网权值的因素之一,另外又考虑到道路长度因素,最终权值设置为
式中:
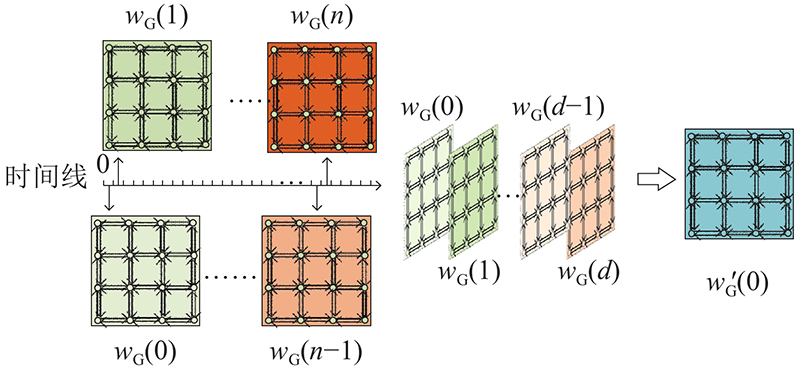
为了考虑未来多个时段路网密度对当前时刻路径规划的影响,使得搜索结果在尽可能多的时段形成的时域中保持最优. 本研究采用一种空间堆叠的方法,以车辆所处时刻为起点,向外发散逐一采样未来不同时段的路网权值,使不同时间维度的路网状态在同一空间中重合. 如图5所示,假设车辆当前处在0时刻,系统通过路网密度估计算法得到未来
图 5
4.2. D*Lite算法改进
基于出行计划的未来路况计算及诱导系统中的交通信息是时刻变化的,在这种情况下为用户推荐导航路线,必须控制系统响应时间. 本研究采用一种高效动态路径规划算法——D*Lite算法,该算法引入了一个关键概念
式中:
D*Lite算法利用启发式函数指导搜索朝着路径最短的方向前进,在传统的D*Lite算法中,启发值用节点间的坐标差表示. 改进的D*Lite算法基于传统的D*Lite算法,将整合后的未来多个时段的路网权值作为启发值. 假设在进行路径搜索时考虑路网未来
式中:
4.3. 算法的实施过程
在对D*Lite算法改进后,提出基于出行计划数据的路径规划算法流程,如图6所示.
图 6
图 6 基于出行计划数据的路径规划算法流程
Fig.6 Path planning algorithm flow based on travel plan data
上述路径规划算法具体实施步骤如下. 1)初始化路网模型,根据路网情况拟合各路段的速度-密度关系式,确定时段数量
5. 仿真实验分析
5.1. 仿真实验说明
本研究选用SUMO(simulation of urban mobility)作为仿真实验平台. SUMO是一个开源、多模态的交通仿真模拟软件,具有较高的执行速度、可自定义路网内的交通需求并利用TraCI接口对车辆进行实时控制,适合进行路径规划仿真实验.
为了模拟基于出行计划的路径规划整体过程,验证RPTP在降低车辆出行时间和减少路网拥堵方面的优越性,将RPTP和静态路径规划(static path planning,SPP)、滚动路径规划(rolling path planning,RPP)进行对比实验,实验共进行3次. 实验1通过单车辆规划过程详细说明RPTP方法的应用步骤和效果;实验2验证RPTP方法在单车辆规避拥堵方面的优越性;实验3验证RPTP方法在提高整体车辆通行效率和减少路网拥堵方面的优越性.
5.2. 实验1
这部分实验采用SUMO中生成的简单路网,以某一车辆的路径规划为例对RPTP方法进行说明和验证,并进行如下设置:1)设置实验车辆,该车辆在0时刻出发;2)假设在0时刻,实验路网内无任何车辆;3)假设进入实验路网的车辆都发布了出行计划,并按照推荐的路线行驶.
5.2.1. 实验路网
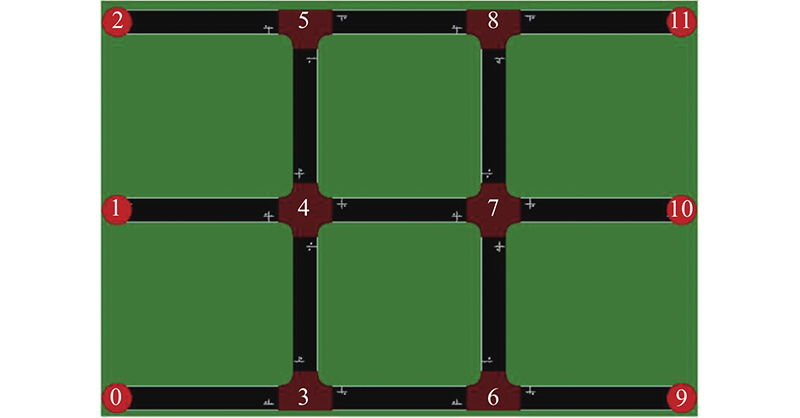
利用SUMO的路网生成工具导出可用于仿真的net. xml文件,得到的实验路网如图7所示. 该实验路网共12个节点、26条边,各路段的长度、车道数之类的物理参数基本一致.实验车辆以交叉口0为起点,交叉口11为终点.
图 7
5.2.2. 速度-密度模型参数标定
为了获取实验路网交通流速度和密度之间的关系模型,本研究通过SUMO自带的randomTrips.py文件随机生成交通流,并以100 s为间隔输出交通流速度及密度数据,如图8所示. 运用统计分析的方法对模型参数标定,拟合出实验路网宏观交通流参数之间的函数关系式.
图 8
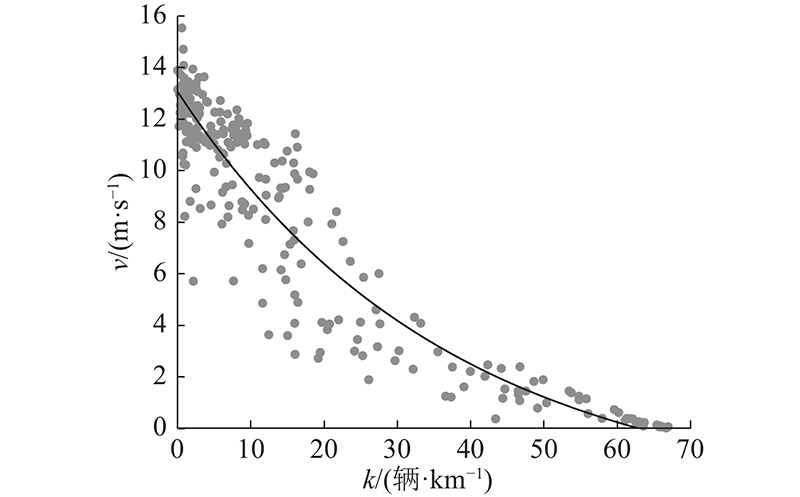
根据以上采集到的速度和密度数据,以密度为横坐标,速度为纵坐标,作速度-密度散点图如图9所示. 可以看出,密度和速度之间的关系有如下特点:速度随着密度的增加而减小,即密度越大,速度越小. 其呈现出的曲线特性与Underwood指数模型基本一致,利用数学拟合工具得到具体关系式如下:
图 9
5.2.3. 出行计划数据获取
由于目前用户的出行计划数据难以从现实中获得,在此利用仿真软件SUMO获取具有替代性的相关数据. 通过SUMO中的trips. xml文件在路网内定义交通需求,该文件包含车辆的出发时间、出发路段、目的路段、途径的路段等信息,可视为系统收集的出行计划路线数据. 本研究在实验车辆发布出行计划前,设置了180条trip数据,可以视作系统已经收集到180条出行计划路线,如图10所示.
图 10
根据设置的出行计划路线数据,利用TraCI接口中的slowDown(self, vehID, speed, duration)函数,使车辆在进入某一路段前按照与路段密度对应的平均速度行驶,以获取车辆离开每一路段的时刻,如图11所示.
图 11
根据上述获取的出行计划路线数据,设置时段长度为100 s. 按照第3节提出的路网密度估计算法,统计每个路段在每个时段经过的车辆数,对所得数据进行统计分析,得到实验路网未来2个时段的路段密度数据,如表1所示,以此作为RPTP进行路径规划的数据来源.
表 1 不同时段各路段的车辆密度
Tab.1
| | | | | ||
| 0~100 s | 100~200 s | 0~100 s | 100~200 s | ||
| (0, 3) | 32. 87 | 14. 12 | (3, 0) | 7. 65 | 14. 72 |
| (1, 4) | 3. 70 | 24. 56 | (4, 1) | 8. 15 | 11. 46 |
| (2, 5) | 0. 98 | 6. 89 | (5, 2) | 1. 38 | 2. 11 |
| (3, 4) | 11. 22 | 29. 09 | (4, 3) | 8. 15 | 8. 13 |
| (3, 6) | 21. 67 | 12. 40 | (6, 3) | 1. 38 | 6. 06 |
| (4, 5) | 19. 49 | 17. 31 | (5, 4) | 1. 50 | 4. 26 |
| (4, 7) | 9. 76 | 40. 02 | (7, 4) | 9. 59 | 1. 18 |
| (5, 8) | 18. 38 | 25. 23 | (8, 5) | 16. 23 | 8. 57 |
| (6, 7) | 39. 61 | 3. 95 | (7, 6) | 9. 82 | 3. 90 |
| (6, 9) | 4. 29 | 19. 93 | (9, 6) | 3. 23 | 23. 09 |
| (7, 8) | 4. 81 | 13. 86 | (8, 7) | 7. 11 | 30. 60 |
| (7, 10) | 7. 23 | 4. 98 | (10, 7) | 10. 61 | 12. 37 |
| (8, 11) | 5. 90 | 7. 09 | (11, 8) | 2. 62 | 2. 71 |
5.2.4. 最优路径获取
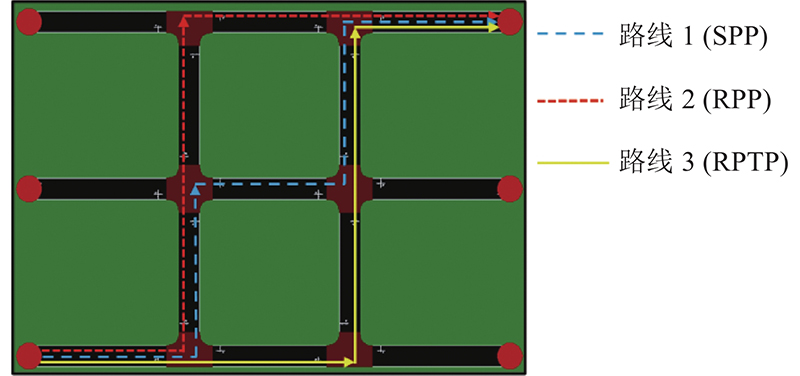
为了验证RPTP在时变权值路网中求解最优路径的优越性,分别采用SPP、RPP和RPTP方法进行路径搜索. SPP只考虑车辆进入路网时刻的路网交通状况,由于在0时刻路网内并无车辆,在进行最优路径搜索时只考虑路段长度. RPP根据每个更新周期的路网实际权值不断更新导航路线,所以在100 s后利用SUMO输出该时刻的路网权值,以此为依据为车辆重新规划路径. RPTP在车辆进入路网的时刻就考虑其未来多个时段的权值,作为当前路径规划的影响因素. 由于实验路网中路段长度几乎一致,因此取权值因子
图 12
5.2.5. 仿真结果分析
根据以上路径规划结果,利用SUMO中的TraCI接口分别赋予实验车辆3条出行路线,并使实验车辆以及设置的180辆车陆续进入实验路网,按照规定的路线行驶. 在仿真结束后获取实验车辆按照3种不同路线行驶全程花费的时间T,如表2所示.
表 2 各出行路径的累计行程时间
Tab.2
| 路径规划方法 | 出行路径 | |
| SPP | 路线1 | 203 |
| RPP | 路线2 | 189 |
| RPTP | 路线3 | 157 |
5.3. 实验2
在实验1的基础上,为了进一步说明 RPTP 方法的有效性,采用不规则路网,对不同拥堵状况下SPP、RPP和RPTP生成的路径进行多次对比分析.
5.3.1. 实验设置
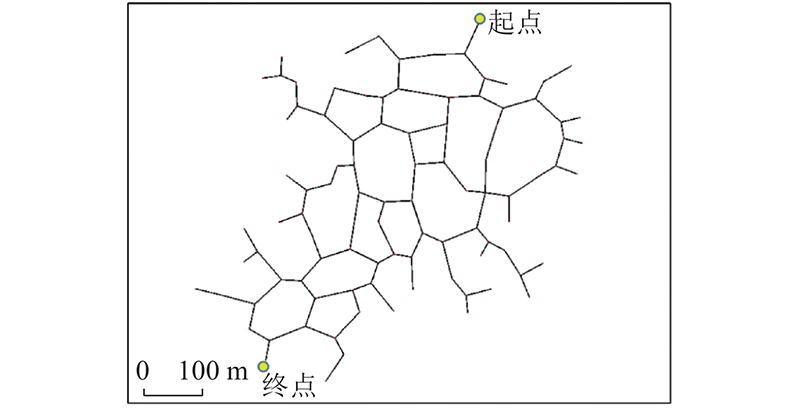
利用SUMO中的随机路网生成器,得到不规则的实验路网.该路网共包含97个节点,218条边,实验车辆起点和终点的设置如图13所示.
图 13
通过编写SUMO的trips.xml文件,设置出行计划的生成频率(从10 s生成1条出行计划到1 s生成1条出行计划),以模拟路网的不同拥堵程度. 在不同拥堵程度的路网中,获取SPP、RPP、RPTP在同一起点和终点之间规划的路径,并比较车辆按照各路径行驶所花费的累计行程时间.
5.3.2. 仿真结果分析
在相同环境下,不同路径规划方法得到的最优路径的累计行程时间如图14所示. 图中,f为出行计划生成频率. 可以看出,当出行计划生成频率较低,即路网的拥堵程度较低时,3种路径规划方法得到的最优路径差别不大. 随着出行计划生成频率的增加,3种方法得到的路径,其累计行程时间都在增加,这和现实情况相符.当出行计划生成频率大于0.7次/s后,采用RPTP方法的车辆,其出行时间明显低于其他方法,说明RPTP确实能够帮助车辆规避拥堵路段.
图 14
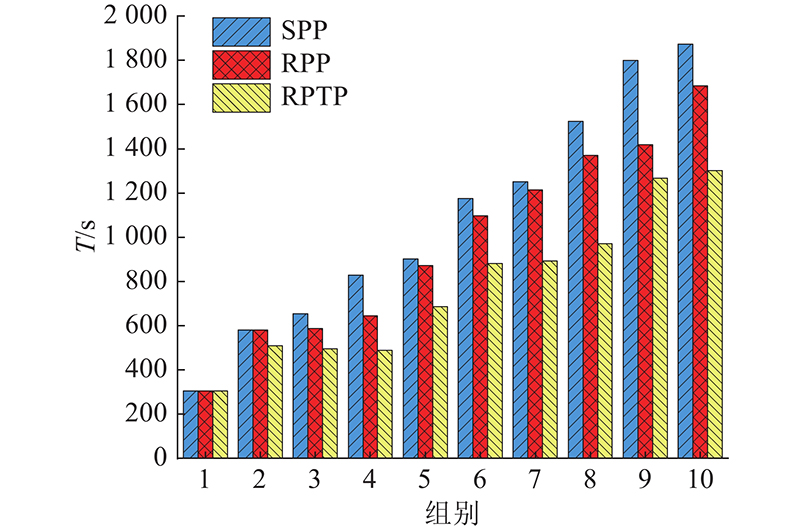
图 15
图 15 不同起终点下各路径规划方法的行程时间
Fig.15 Travel time of each path planning method under different starting and ending points
本研究选取了10组不同的起终点(编号1~10),将其按照SPP方法花费的时间大致排序. 可以看到,在多组起终点中,相比其他2种方法,RPTP方法总能找到花费时间更少的路线,并且随着出行时长的增加,RPTP在降低出行时间方面的优势愈发明显.
5.4. 实验3
在实验1、2的基础上,为了进一步说明RPTP方法的优越性,采用如图13所示的路网,从车辆和路段2个方面,分别对比SPP、RPP和RPTP方法下多车辆路径规划的表现.
5.4.1. 实验设置
为了对比3种规划方法在多车辆路径规划中的表现,共进行3次仿真测试,每次在路网边沿若干节点设置相同的多组车流(车辆的出发地、目的地、出发时间和车辆数量都相同),每次进入路网的车辆分别采用SPP、RPP及RPTP方法规划行驶路径.分别记录测试过程中的数据,包括各车辆的速度随其行驶距离的变化情况,以及各路段的密度和流量情况.
5.4.2. 仿真结果分析
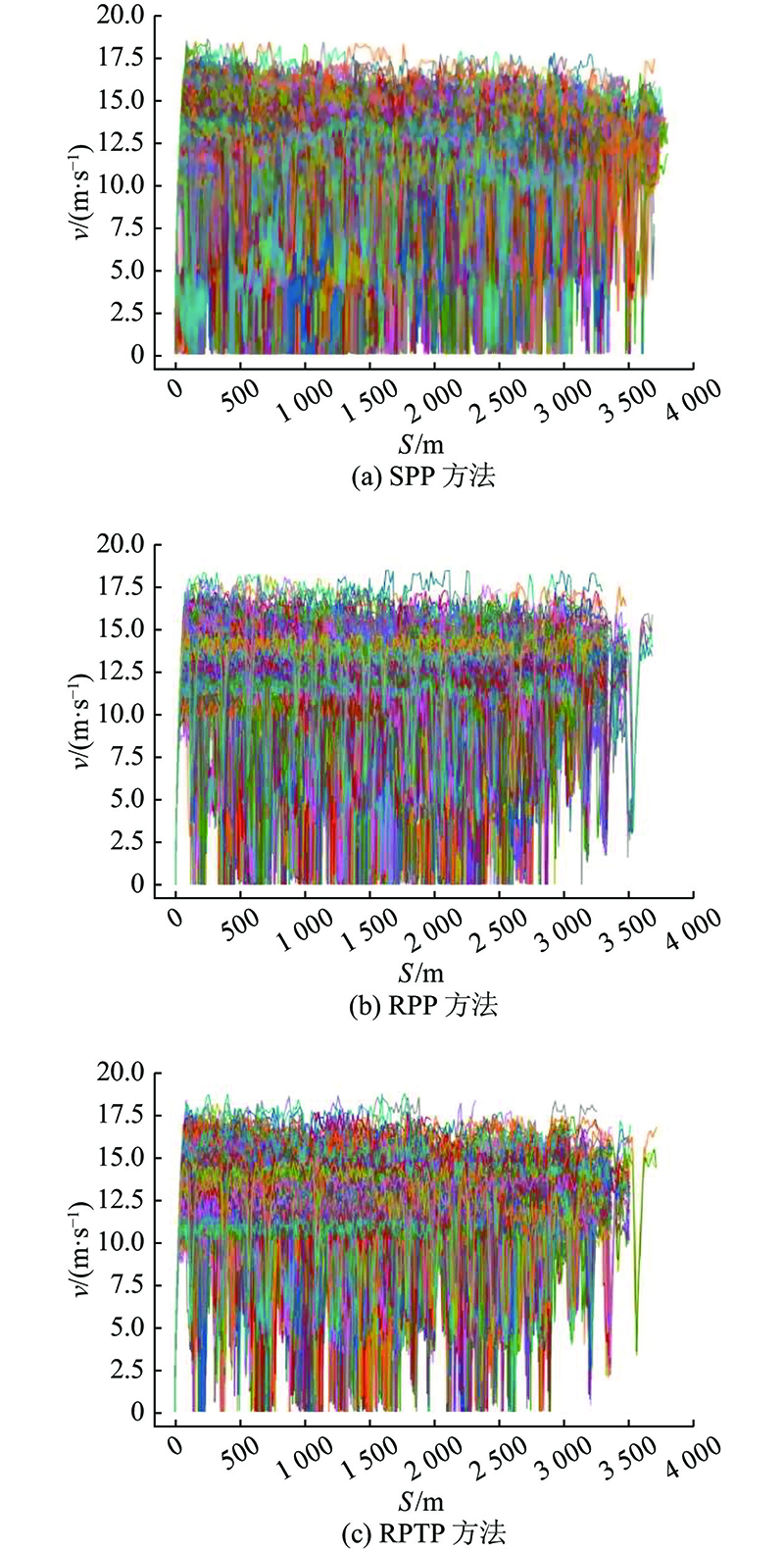
利用SUMO的plot_trajectories.py工具输出不同路径规划方法下各车辆的距离-速度关系,如图16所示. 图中,S为车辆累积行驶的距离,每条线代表一辆车的速度随其行驶距离的变化情况. 可以看出,相比其他2种路径规划方法,采用RPTP方法的车辆在行驶过程中,车速低于5 m/s的情况明显减少. 因此总体来看,RPTP方法在一定程度上提高了整体车辆的通行效率.
图 16
图 16 不同方法下各车辆的距离-速度情况
Fig.16 Vehicles’ distance-speed relationship under different methods
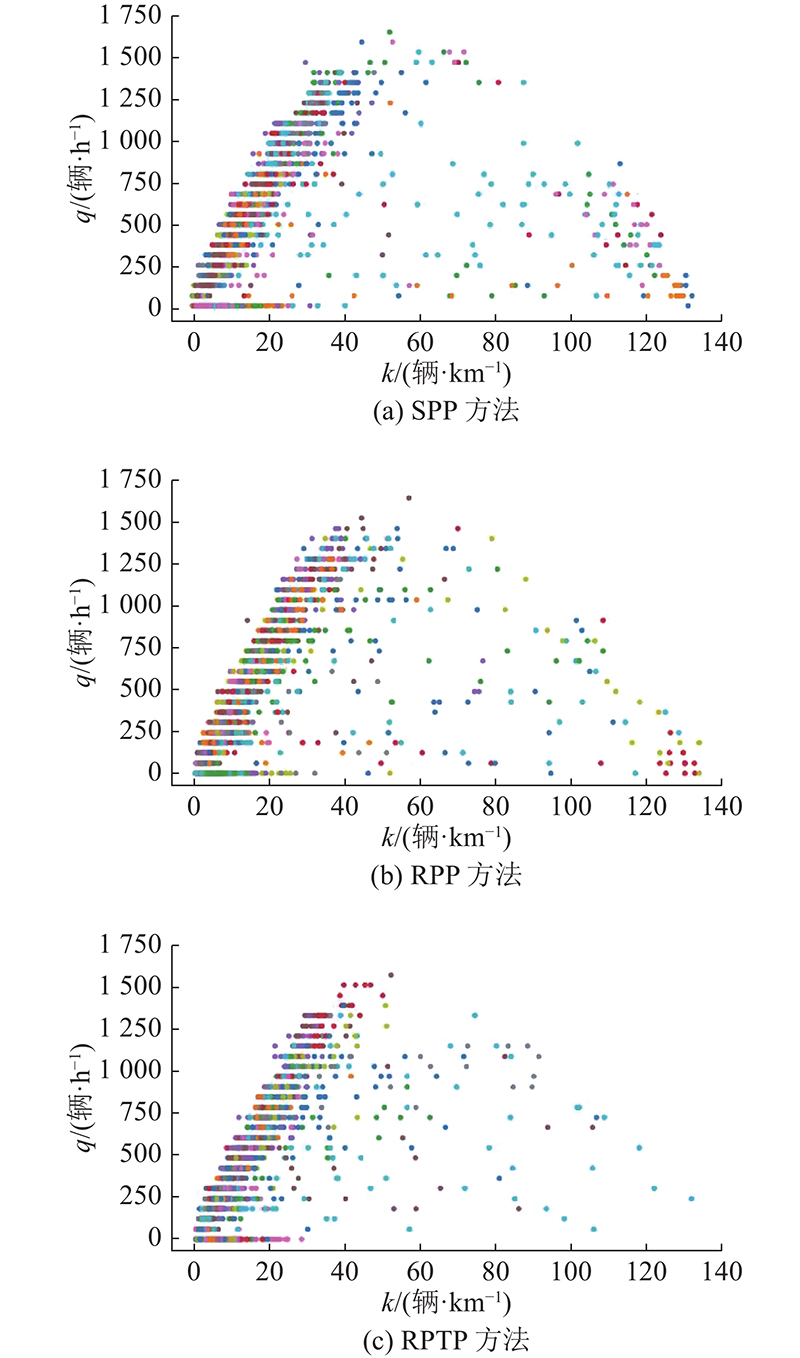
同时,利用SUMO的plotXMLAttributes.py工具,按照1 min间隔输出3次仿真实验中各路段的流量-密度情况,如图17所示. 图中,q为车流量,同样颜色的圆点代表同一路段. 可以发现,三者基本符合交通流的密度-流量抛物线模型,但在采用RPTP方法时,落在“不拥挤区”的路段所占比例更高,且落在密度极高区域的路段明显少于SPP和RPP方法的. 因此,从整体路网角度来看,PRTP方法确实能在一定程度上均衡进入路网的车流,缓解道路交通拥堵.
图 17
图 17 不同方法下各路段的密度-流量情况
Fig.17 Density-flow relationship of sections using RPTP method
6. 结 语
在出行计划的思想下,本研究设计了最优路径规划的整体框架,构建了基于出行计划数据的未来路网密度估计算法,并采用空间堆叠的方式计算路网的权值,改进了D*Lite算法的启发函数,建立了一种基于出行计划数据的路径规划算法. 在以路段为基本元素的路网模型上,采用交通仿真的方式对RPTP进行仿真验证. 实验结果表明,相比SPP和RPP方法,RPTP确实能够提前发现优势路段,为车辆提供时间更短的出行路线,减少滞后、潜在拥堵的生成.
出行计划作为一种新思想,相关研究成果较少,本研究主要是对其进行探索性分析,研究还存在许多不足和未实现的想法:1)对于时段长度
参考文献
基于短时交通流预测的广域动态交通路径诱导方法
[J].DOI:10.16097/j.cnki.1009-6744.2020.01.018 [本文引用: 1]
Wide-area dynamic traffic route guidance method based on short-term traffic flow prediction
[J].DOI:10.16097/j.cnki.1009-6744.2020.01.018 [本文引用: 1]
Real-time urban traffic amount prediction models for dynamic route guidance systems
[J].
Overall traffic mode prediction by VOMM approach and AR mining algorithm with large-scale data
[J].DOI:10.1109/TITS.2018.2852285 [本文引用: 1]
面向城市交通网络的一种新型动态路径寻优方法
[J].
A novel dynamic path optimization method for urban traffic networks
[J].
Research on path planning model based on short-term traffic flow prediction in intelligent transportation system
[J].DOI:10.3390/s18124275 [本文引用: 1]
Dynamic route planning with real-time traffic predictions
[J].DOI:10.1016/j.is.2016.01.007 [本文引用: 1]
基于交通时空特征的车辆全局路径规划算法
[J].DOI:10.3969/j.issn.1674-8484.2021.01.005 [本文引用: 1]
Vehicle global path planning algorithm based on spatiotemporal characteristics of traffic
[J].DOI:10.3969/j.issn.1674-8484.2021.01.005 [本文引用: 1]
A network-consistent time-dependent travel time layer for routing optimization problems
[J].DOI:10.1016/j.ejor.2012.11.043 [本文引用: 1]
基于实时交通信息的城市动态网络车辆路径优化问题
[J].DOI:10.3969/j.issn.1000-6788.2013.07.022 [本文引用: 1]
Vehicle routing problem in dynamic urban network with real-time traffic information
[J].DOI:10.3969/j.issn.1000-6788.2013.07.022 [本文引用: 1]
短时交通流预测模型综述
[J].DOI:10.3969/j.issn.1672-6073.2019.04.009 [本文引用: 1]
Review of short-term traffic flow forecasting models
[J].DOI:10.3969/j.issn.1672-6073.2019.04.009 [本文引用: 1]
An improved algorithm for clustering uncertain traffic data streams based on Hadoop platform
[J].
A multi-path routing protocol based on link lifetime and energy consumption prediction for mobile edge computing
[J].
New quantum-genetic based OLSR protocol (QG-OLSR) for mobile ad hoc network
[J].
An energy-balanced routing method based on forward-aware factor for wireless sensor networks
[J].
Novel optimized link state routing protocol based on quantum genetic strategy for mobile learning
[J].
Novel unequal clustering routing protocol considering energy balancing based on network partition and distance for mobile education
[J].