与此类研究相关的机器人本体和对应的神经控制框架越来越受到研究者的关注. Amrollah等 [ 3] 将Rowat等 [ 4] 的CPG网络生成的节律信号,用于控制下层网络实现关节的运动. Schilling等 [ 5] 利用层次化递归神经网络,即由多种抽象层构成的内部神经网络来调整腿足机器人的整机稳定性和行走行为自适应性. Farina等 [ 6- 7] 应用离线模式识别、比例调控和骨骼−肌肉构建,把众多的运动神经元放电应用于多自由度的调控指令,以解码运动神经元行为的形式驱动机器人. Wang等 [ 8] 应用3个局部CPG神经网络模型模拟生物神经及肌肉运动,构建仿生控制系统,实现对被控对象的驱动. 在利用感觉反馈信息对环境刺激做出反应的步行机器人研究方面,Manoonpong等 [ 9- 11] 提出允许机器人根据环境变化自动调整运动的神经控制算法,使机器人可以在不同路面进行多变的柔顺行走. Dürr等 [ 12] 构建的包含运动−感知协调和学习行为的腿足机器人,体现了更为接近生物的仿生水平. Wang等 [ 13] 整合学习和感知功能设计的神经控制模块,可以让机器人在不同倾斜度的斜坡上产生相应的节律信号. Wang等 [ 14] 构造了2级CPG控制机制,在控制机制中引入各种反馈信息来解决不可预测环境下的跳跃运动控制问题. Owaki等 [ 15- 16] 提出感知反应与预期匹配方法,设计了用于肢体协调的局部感觉反馈机制,重现了多种昆虫的典型步态. Santos等 [ 17] 提出基于自适应振荡器和姿态控制的仿生控制系统来稳定机器人的运动,增强了机器人运动的鲁棒性. Suzuki等 [ 18] 设计的感知反馈可以让步态很快稳定,并研发了腿足机器人交叉耦合控制系统. 上述文献中提出的控制系统为研究感知模型、执行模块,实现预期的环境交互提供了理论依据.
1. 运动协调神经控制系统
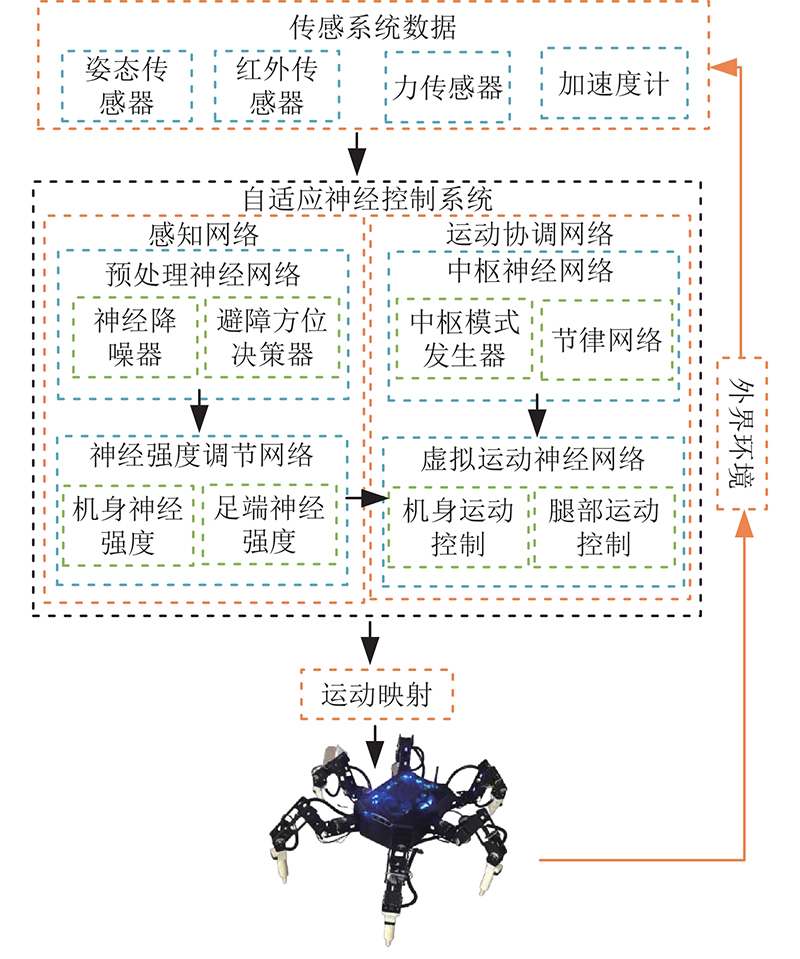
本研究提出的自适应神经控制系统如 图1所示.运动协调神经控制系统主要包含中枢神经网络和虚拟运动神经网络,是控制系统中的规划层.腿足机器人的步态生成和步态模式的切换主要依赖可靠节律信号,该信号由中枢神经网络产生. 虚拟运动网络主要产生机身轨迹和足端轨迹,使机器人在复杂环境中,不仅可以实现多种稳定行为,还能够躲避和跨越各种障碍物,避免倾覆.
图 1
1.1. 中枢神经网络
腿部轨迹和节律信号耦合时,调整节律信号将破坏机器人的稳定性.解耦腿部轨迹和节律信号可以使得机器人的控制系统复杂度降低、加强反应速度和稳定性. 本研究采用σ-Hopf振荡器作为中枢模式发生器 [ 19] ,其公式为
等同于
式中: x、 y为状态变量;( a, b)为极限环的中心; μ为振荡器的幅值; λ为调节速度的可变强度; α为分岔参数; y 0为调节开始处的信号点; φ、 ρ分别为周期参数、占空比, φ、 ρ不相关;
式中: u( t)=−sign ( y) u, u为外部输入; g( t)为耦合输入,若振荡器只有1个,则 g( t)= 0. 机器人多关节的协调通常由振荡器网络信号的相位差完成. 由于全耦合双向环结构具有比单向环结构更好的过渡性能,本研究将构造全耦合的双向环结构. 对于本研究的σ-Hopf振荡器,式(3)可以改为
式中:正标量 k ij ( t)为耦合增益,可以根据不同形式的运动进行实时变化; η为下降因子,与时间相关; κ为初始系数; R (Δ Φ)为第 i、 j个振荡器间的相位差Δ Φ ij 的二维旋转变换,Δ Φ ij 引导 υ i 、 υ j 同步; t 0为参数更改开始的时间. 当信号变得稳定时,较短的时间会导致较大的收敛强度. 收敛过程主要由 k( t)的状态决定 [ 23] .
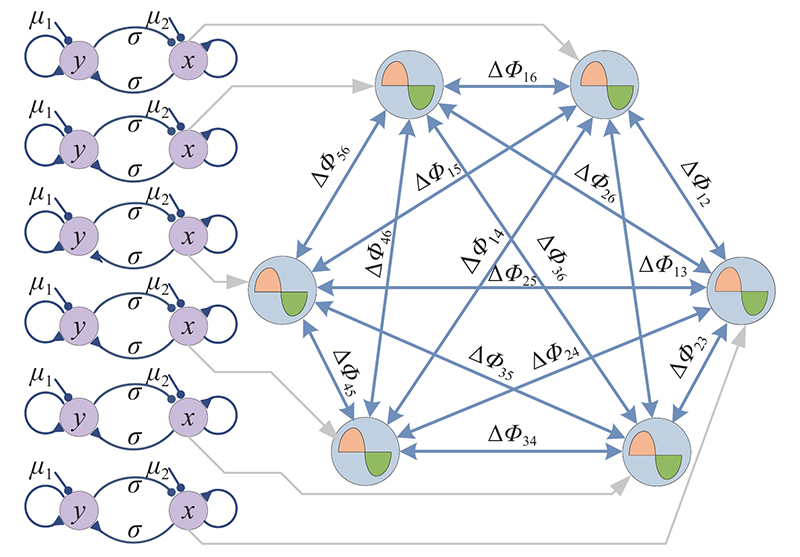
中枢神经网络如 图2所示. 图中
图 2
中枢神经网络包括6个σ-Hopf模块和1个网络同步模块. 网络同步模块通过波形调节因子、频率因子调节整个振荡器网络的协同节律和波形变化. 该网络过渡过程稳定、快速,波形精确,控制步态的波形切换时间为0. 3 s,可以避免当步态行为切换时,机器人因腿部不协调发生触碰或倾覆,具体调节过程可以参考文献[ 19].
1.2. 虚拟运动神经网络
行为规划是机器人运动控制的重要环节.贝塞尔曲线具有很强的可调整性、较少的控制参数,拟合出的曲线比一般的插值曲线光滑,因此被大量应用于机器人轨迹规划 [ 24] .虚拟运动神经元基于贝塞尔曲线的数学原理提出,具有贝塞尔曲线的数学特性,能够根据轨迹变化的需求扩展神经网络层数.
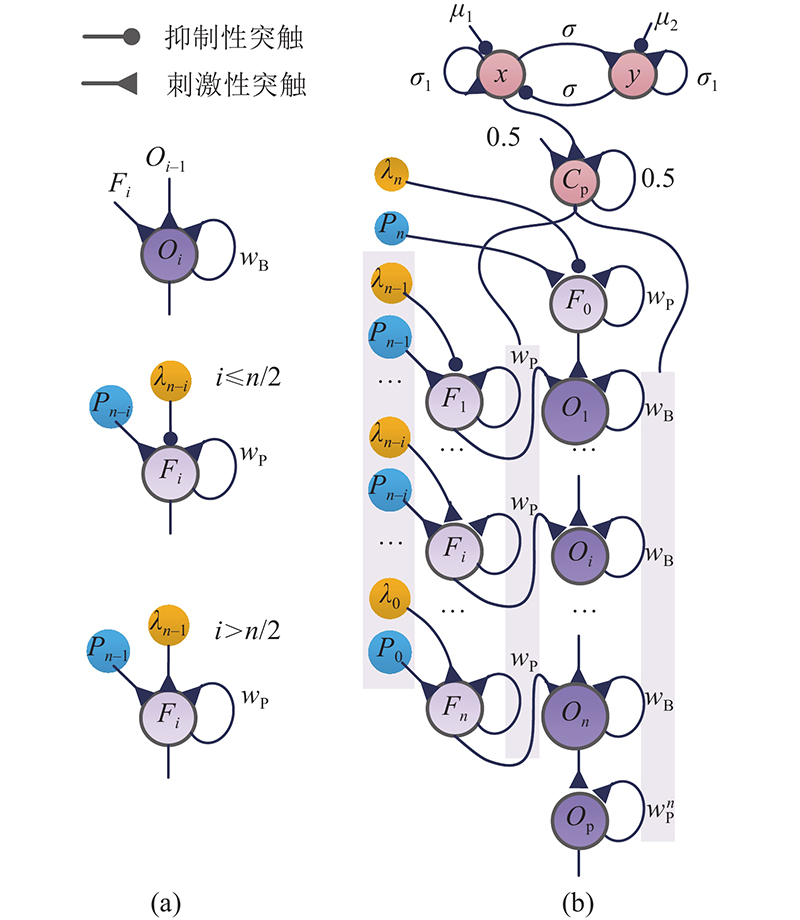
将中枢神经网络的输出进行尺度变换后,得到处理后的节律信号,该信号作为激励信号控制运动神经元,驱动机器人腿部完成运动行为.虚拟运动神经网络如 图3所示. 图中, C p为经过尺度变换后的CPG节律信号;
图 3
式中:
神经网络第1层输出为
第 i层输出为
第 i层的输出进行处理后为
式中:
1.3. 机身运动控制神经网络
如 图4所示为机身虚拟运动神经网络, 神经元、局部激活因子的左上角标的 X、 Y、 Z分别表示该神经元、局部激活因子与机器人的横向、前进方向、高度方向轨迹的控制相关,左上角标B表示与机身轨迹相关. 通过对目标导向点 B P i ( XB P i , YB P i , ZB P i )的调节,该网络可以对机身轨迹进行全局调节. 本研究中,采用3阶( n=3)虚拟机身神经元运动模块. 如果行为复杂,可以采用更高阶次. 根据3阶虚拟运动神经网络模型,目标导向点通过行为约束条件求得
图 4
为了使问题简化,取 λ i =0,从式(10)、(11)也可以看出,目标导向点能够决定并调节行为轨迹和状态. 机身轨迹规划基于全向运动学,将机器人机身轨迹分解为沿机身前进方向以 R 1为半径的旋转运动和沿机身侧方向以 R 2为半径的旋转运动 [ 20] ,机器人在转向运动的起始、终止位置的机身轴向和侧向延长线相交处的夹角即为步态转角
机器人的机身行为轨迹可以写成
式中: X C、 Y C均为机器人机身轨迹的坐标.
1.4. 腿部运动控制神经网络
图 5
在足端支撑相轨迹规划中,处于支撑态的足端相对于大地坐标系是静止的,而相对于机身质心坐标系是移动的.本研究的大地坐标系建立于转弯轨迹圆心处,并以大地坐标系为参考坐标.在旋转运动中, B I、 B E分别为机身质心坐标的起始和末位置,
平移矩阵为
在坐标系 B δ 下的足端位置为
将式(12)、(13)带入式(14)得支撑相足端轨迹为
式中:
2. 感知神经系统
若机器人简单地依照预期设计的运动执行任务,将难以应对外部环境中的突变及不稳定因素. 因此机器人需要模仿动物的应激行为,通过自适应调节机器人运动来减小这些干扰的影响.
2.1. 感知神经网络及信号处理
人工视觉系统模型的搭建可以让机器人在无人干预的复杂外部环境中产生自主应激行为. 基于文献[ 25]中的神经信号处理网络,搭建用于处理红外信号的新信号预处理神经网络,该网络包含方位神经决策模与块神经降噪模块.
在离散时间步长 t d内,激活函数、传递函数分别为
式中: n为人工神经元数目, O j 为神经元 O i 的输入, w ij 为神经元 j到 i的连接突触强度或权重, b i 为神经元内部的固定偏置, a i 为神经元 i的激活函数. tanh函数输出范围为(−1.0, 1.0),平均值为0,在训练时特征值不断扩大,训练效果比sigmoid函数好,因此本研究的传递函数选择tanh函数. 结合式(18)、(19)得到单个人工神经元模型输出为
机器人在移动过程中产生的震动会导致红外传感器接收到的环境数据含有噪声. 实际上,所采集的红外信号的噪声主要为高频噪声,因而需要基于人工神经模型搭建低通滤波模块. 人工神经模型经过训练和学习优化,可得到如 图6(a)所示的神经降噪模块. 机器人左前腿FL上的红外传感器IS1和加速度计AS1,右前腿FR上的红外传感器IS2加速度计AS2的检测信号可以作为该模块的输入. 当红外信号为输入状态时,将经滤波处理后得到不含高频噪声的2个红外信号IFS1、IFS2同时作为方位神经决策模块输入神经元( D 1、 D 2)的输入. 神经降噪模块共由3个神经元组成: H 1为输入层; H 2为单层隐含层; H 3为输出层. 输入信号的幅值先由隐含层权重 H w 21和刺激性自连接权重 H w 22降低,再经刺激性自连接权重 H w 32使得高频噪声的幅值小于低频噪声的幅值,随后信号在隐含层权重 H w 33的作用下被放大.
图 6
递归人工神经元在特定的输入和自连接权重参数域下具有滞回效应 [ 25] . 当机器人检测到障碍物并开始转弯后,传感器可能感应不到障碍物,此时滞回效应可以保留障碍物信息,使机器人继续转弯,且转弯角度与滞回环的宽度相关. 在动态环境中,可以针对动态物体引入刺激信号用以调整自连接权重,进而改变滞回环宽度,使机器人灵活调整转弯角度. 避障方位神经决策模块如 图6(b)所示,IFS1、IFS2为经过降噪后的方位探测信号; D 1、 D 2为输入层; D 3、 D 4组成单层的隐含层; D 5为输出层. 避障方位神经决策模块的主要特点是滞回效应和每个时刻只能有1个正输出(+1). IFS1、IFS2信号分别输入对应的神经元 D 1和 D 2,经决策模块得到避障方位 D 5的输出:DB=−1(表示障碍物在右前方,机器人需向左进行避障)或DB=+1(表示障碍物在左前方,机器人需向右进行避障). D 5的输出用于机身位轨迹调节 B 1的输入.
2.2. 机身运动神经强度调节器
机身运动神经强度调节器主要通过改变机身运动神经控制网络中的目标导向点来控制机身轨迹. 本研究将机身运动神经强度调节应用于障碍物的躲避应激行为中. 实际上,机器人探测到障碍物距离变化时,机器人轨迹须纳入障碍物距离和躲避导向点的函数关系数据. 为此设计机身运动神经强度调节模块,如 图7所示.
图 7
神经元 B 5的输出、 D 5输出和 θ 0的乘积、 D 5输出和 XB P 3的乘积类似, B 11的输出与 B 5和 B 6的乘积类似,即机身运动神经强度调节网络类似于1个双重乘法器,由2个输入神经元、4个隐含层神经元和1个输出神经元组成. 用于生成默认机身避障轨迹的是初始避障导向点 B 5(初始目标导向点与障碍物方位乘积). B s(机身避障调节因子)为 B 6的输入,若 B s=0.5,则 B 11的输出减小, B 5的振动幅值变小,使得目标导向点 XB P 3'的值减小,避障半径变小. 当 B s=−1时,避障方向发生切换,即 B 11的输出与 B 5的相位差为180°. 实际上机身避障调节因子可以由障碍物的距离信息经尺度变换后得到,通过该因子的变化来实时调控避障轨迹.
2.3. 腿部运动神经强度调节器
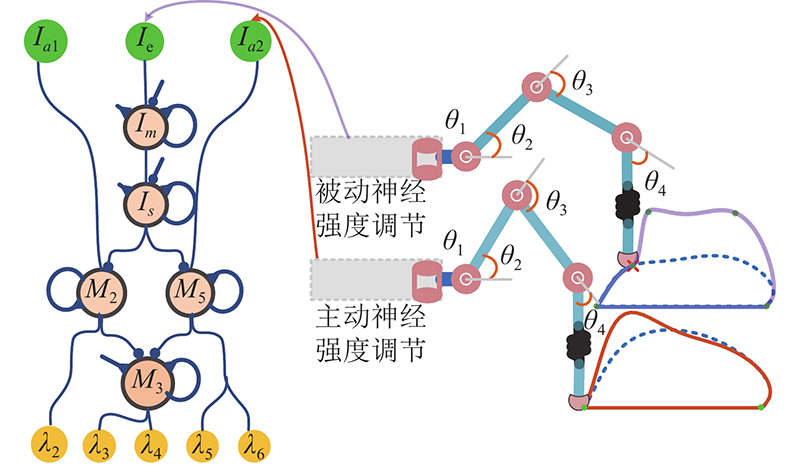
机器人足端触地时,若触碰到障碍物或轨迹存在偏差,机器人的稳定性会受到影响. 机器人通常检测不到较小的障碍物,增加抬腿高度的跨越会造成机器人的额外能耗和不及时的应激反应. 本研究的肌肉激活因子用感官信息触发,以调节足端运动轨迹进行足端应激避障行为,如 图8所示. 图中, θ 1、 θ 2、 θ 3、 θ 4分别为髋关节、髌骨−股骨关节、跖骨−胫骨关节、睑骨−跖骨关节对应的转角.
图 8
在腿部主动运动神经强度调节中, I e为被动调节触发信号, I a1 、 I a2 为障碍信息的输入信号. 机器人准确地获取障碍物的方位信息,再相应调节局部肌肉激活因子,便可得到足端避障轨迹. 设定 T λ i = XS λ i = YS λ i =0;
式中:输入信号 I a1 、 I a2 ∈[0,1.0],局部肌肉调节因子的调节权重
当机器人足端触碰到较小障碍物时,机器人需要做出反应以避免失衡,被动调节应用于此类情况. 足端与障碍物的碰撞将导致位于腿部的加速度计信号发送突变,经判断模块(AS1 || AS2 > Th,Th为预先设定的阈值)后,信号 I e由0变为1, 应激调节机制被触发,局部肌肉调节因子 ZS λ 2、 ZS λ 5变化使机器人跨越障碍物. 这种应激反应的响应时间非常短,太快的响应会引起关节速度突变,因此须权衡时间和速度的影响. 应激调节情况下局部肌肉调节因子为
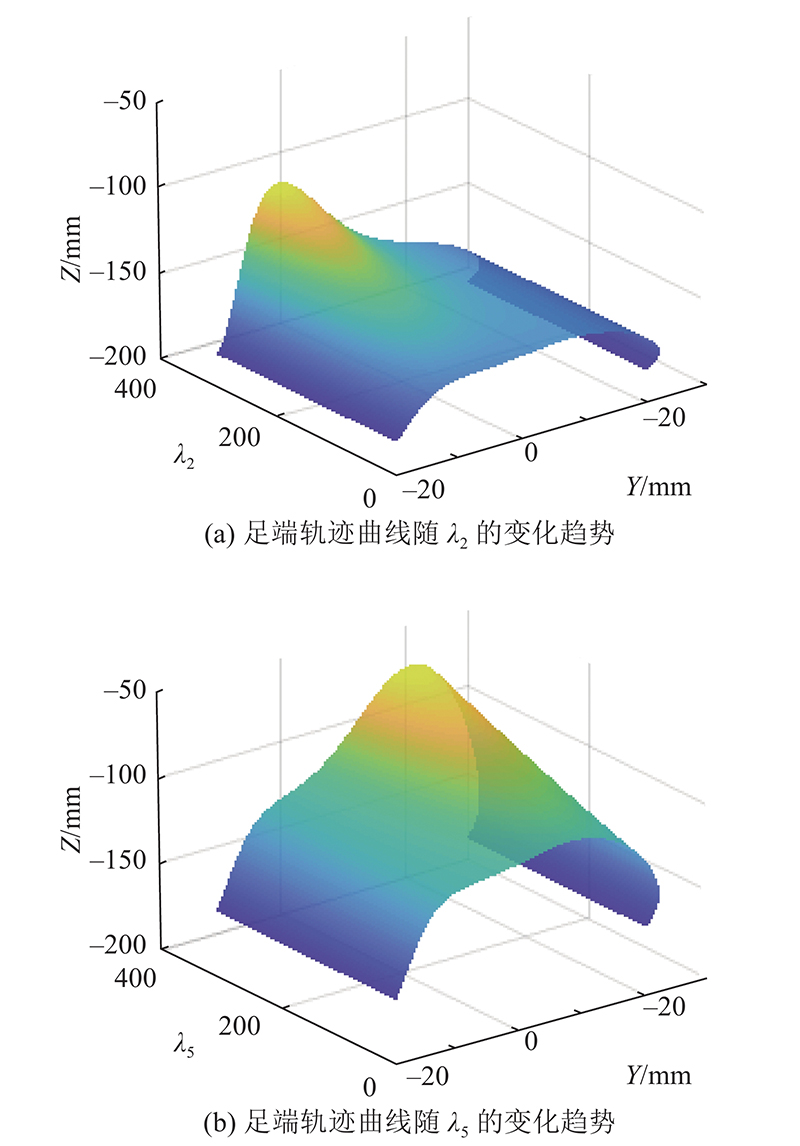
图 9
图 9 肌肉调节因子对足端轨迹的影响
Fig.9 Effect of muscle regulatory factors on foot trajectory
3. 实 验
本研究所用腿足机器人由24个Dynamics-MX 64数字舵机构成,主控制器为NI控制板Sbrio,通过RS-485给舵机发送指令,同时安装有红外传感器、力传感器、姿态传感器. 红外传感器安装于机器人各腿的小腿位置;姿态传感器安装于机器人的质心位置;力传感器安装于机器人各腿足端位置,用于测量足端与地面的接触力.
3.1. 足端变轨迹实验
六足机器人足端轨迹与运动过程如 图10所示.实验由3组局部激活调节和1组虚拟肌肉的全局激活调节组成.
图 10
全局激活实验为第I组,足端轨迹的高度变化可以由调节虚拟神经元模块中的全局因子 H来完成. 当 t∈[1.0, 3.0]s, H=40 mm;当 t∈[3.5, 6.0]s, H=55 mm;当 t∈[6.5, 9.0]s, H=70 mm.局部激活实验为第II~IV组,足端轨迹的局部调整由肌肉激活因子 S λ i ,的改变实现. 只考虑在摆动态时与足端高度方向有关的局部因子 ZS λ i . 在第II组中,当 t∈[1.0, 3.0]s,局部因子 ZS λ 2=0(第III组 ZS λ 5=0,第IV组 ZS λ 7=0);当 t∈[3.5,6.0]s, ZS λ 2=125(第III组 ZS λ 5=125,第IV组 ZS λ 7=125);当 t∈[6.5, 9.0]s, ZS λ 7=250(第III组 ZS λ 5=0,第IV组 ZS λ 7=250). t∈[3.0, 3.5]s与 t∈[6.0, 6.5]s为不同参数值的过渡过程. T λ i =0, ZS λ i 的其余部分等于0.
调整虚拟运动神经网络的全局因子和局部因子对机器人的运动轨迹有不同程度的影响. 全局因子调整会改变运动神经元输出 O p. 类似的,局部因子也部分参与运动神经元输出 O p的改变. 在一定程度上,作为中间神经元输出, O p直接显示了足端轨迹.
局部和全局的肌肉激活过程如式(8). H的变化影响目标导向点 S P 1~ S P 7,导致摆动阶段输入神经元 F 1~ F 7强度的变化,这影响了运动神经元 O p的整体激活. 相比之下,尽管使用不同的 ZS λ 2、 ZS λ 5、 ZS λ 7,目标导向点 S P 1~ S P 7仍保持不变. 只有在摆动态时, F 6、 F 3、 F 1的激活强度会受到局部因子的影响;在支撑态时, F i 的激活强度没有变化.
3.2. 灵巧运动实验
灵巧运动实验由前进、原地转弯、侧移和右前转弯运动等多种组合运动形式组成. 如 图11所示为灵巧运动实验过程,F1处于 t∈[0, 75]s的向前运动,F2处于 t∈[75, 175]s的右前转弯运动,转角为(7/18)π,F3处于 t∈[175, 275]s的平移运动,F4处于 t∈[275, 375]s的原地转弯运动,转角为(−1/3)π. 在稳定状态下,机器人俯仰角
图 11
3.3. 机身应激避障实验
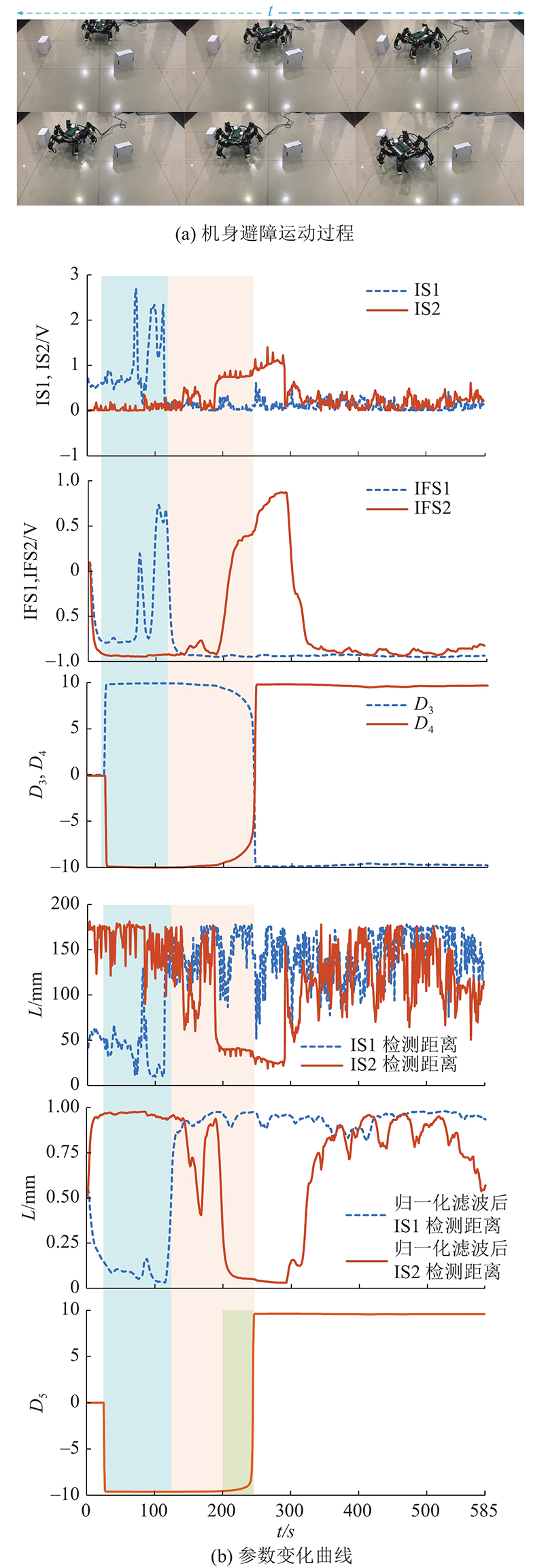
机身应激避障实验如 图12所示. 图中, L为传感器检测到的障碍物距离. 设初始参数 B s=0.5, B P 3=[20, 40, 0]. 当 t∈[0, 25]s时,机器人进行初始默认运动,即前进运动;当 t∈[25, 112]s时,左前方的障碍物被IS2持续检测到,机器人开始向左前方避障;当 t∈[112, 245]s时,IS2丢失障碍物信息,而滞回效应一直在保持障碍物信息,使机器人保持左前转弯;当 t∈[195, 289]s时,右前方障碍物被IS1持续检测到;当 t=245s时,机器人开始向右前方避障;当 t∈[289, 585]s时,IS1基本检测不到障碍物信息,而滞回效应使机器人仍然保持向右前方的避障运动. 经运动神经强度调节模块优化得后到机身避障目标导向点 XB P 3使得机器人成功避障.
图 12
图 12 机器人机身的应激避障实验
Fig.12 Obstacle avoidance experiment of stimulus reaction for robot body
3.4. 腿部应激行为实验
为了验证机器人腿部运动神经强度的可调性和虚拟运动神经网络的局部可调性,进行机器人腿部应激行为实验. 实验分为2组:1)障碍物的方位和大小信息已知,机器人进行主动越障实验;2)障碍物的方位和大小信息未知,机器人利用腿部的加速度计检测足端触碰情况,调节运动神经强度进行被动越障. 2组实验中,机身前进方向的摆动态目标导向点设置为 YS P 0=−20.0, YS P 1=−13.3, YS P 2=−13.3, YS P 3=0, YS P 4=3.3, YS P 5=6.7, YS P 6=20.0, YS P 7=26.7, YS P 8=20.0;机身高度方向的摆动态目标导向点设置为 ZS P 0=−160.00, ZS P 1=−135.00, ZS P 2=−110.00, ZS P 3=−116.25, ZS P 4=−122.50, ZS P 5=−110.00, ZS P 6=−135.00, ZS P 7=−147.50, ZS P 8=−160.00.
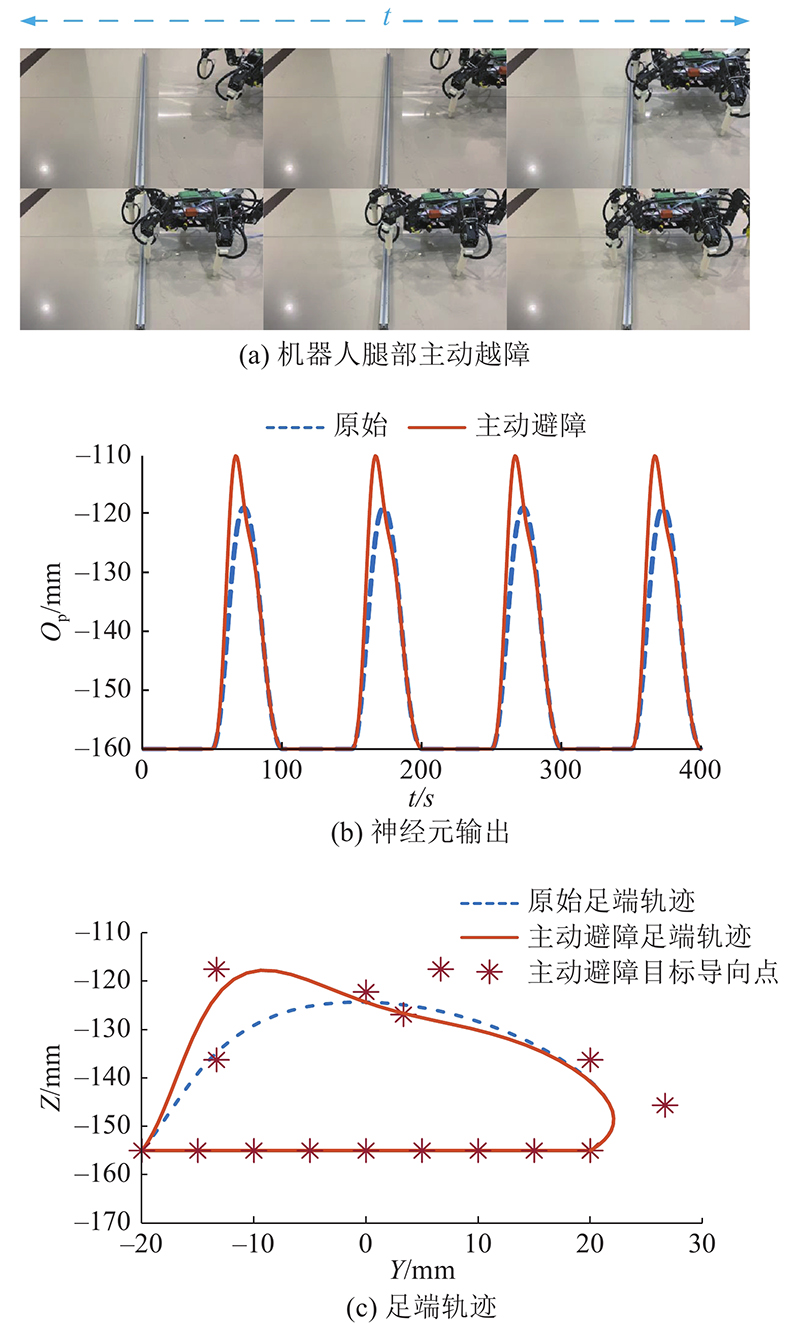
如 图13所示为机器人腿部主动越障过程、神经元输出和足端轨迹曲线. 在主动神经强度调节中,设置参数 I a1 =1, I a2 、 I e=0, ZS λ 2=100, ZS λ 3、 ZS λ 4=300, ZS λ 1、 ZS λ 5、 ZS λ 6、 ZS λ 7、 ZS λ 8 = 0;因为仅局部肌肉调节因子 ZS λ 2、 ZS λ 3和 ZS λ 4的值改变,余下的目标导向点 T P i 、 S P i 及局部肌肉调节因子的值保持不变,所以仅输入神经元 ZS F 4、 ZS F 5及 ZS F 6的值改变,致使摆动态的神经激活强度受局部因素的影响,中间神经元的输出 O p发生局部变化.处于支撑态的机械腿激活强度不会变化.
局部肌肉调节因子的变化对虚拟运动神经网络输出的轨迹影响较大. ZS λ 2、 ZS λ 3和 ZS λ 4的变化致使足端轨迹局部改变,证明局部因素可以部分改变神经元 O p的输出. 作为中间神经元的输出, O p在一定程度上直接反映足端轨迹. 肌肉活动全局和局部因素均由输入神经元处理.
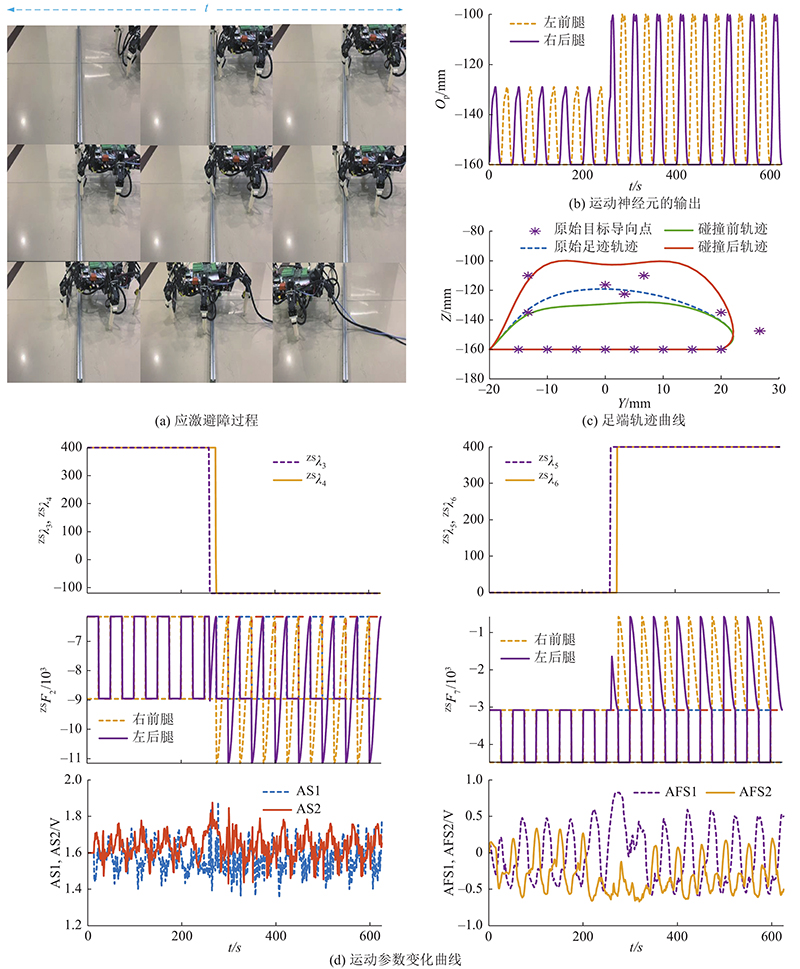
如 图14所示为机器人右前腿和左前腿被动越碍时的运动过程及参数曲线.在运动神经强度调节器中,参数设置为 ZS λ 3、 ZS λ 4=400, ZS λ 1、 ZS λ 2、 ZS λ 5 、 ZS λ 6、 ZS λ 7 、 ZS λ 8 =0.当 t∈[0, 261] s,足端未触碰障碍物, I e=0.当 t=261s时,右前腿足端触碰到障碍物, I e=1;当 t∈[261, 265] s时,被动神经强度调节模块完成足端运动参数的调节过程,局部肌肉调节因子 ZS λ 2、 ZS λ 3 、 ZS λ 4、 ZS λ 5、 ZS λ 6的值迅速发生变化.经过数个时间步长, ZS λ 3、 ZS λ 4=−120, ZS λ 1= 0, ZS λ 2= 100, ZS λ 5、 ZS λ 6 =400, ZS λ 7、 ZS λ 8 =0. 输入神经元 ZS F 2~ ZS F 6的值都会变化,摆动态的激活强度受局部因素的影响,使中间神经元输出 O p发生局部变化,机器人足端轨迹发生改变,快速抬高腿部跨越障碍物,实现应激避障行为.
图 13
图 14
图 14 机器人腿部的应激避障实验
Fig.14 Obstacle avoidance experiment of reaction for robot leg
4. 结 语
提出基于虚拟运动神经网络的腿足式机器人神经行为控制架构,通过调节机器人的虚拟运动神经网络模拟不同的肌肉强度,产生不同环境的响应行为,实现机器人对外部环境变化的适应性行为能力. 通过调节机身轨迹和足端轨迹,虚拟肌肉参数信息,机器人能够自主识别障碍物方位信息,并自主躲避环境中未知信息的障碍物. 所提架构不仅能够完成机器人各部分运动行为的实时调节,实现灵活的运行行为,而且兼具可扩展性和学习能力. 下一步将结合视觉信息和学习算法,通过构建实时环境参数信息,研究机器人整机平衡控制,实现机器人在非结构地形上全自主运动,并进一步提升机器人对复杂多变的自然环境的适应性.
参考文献
Insect walking and robotics
[J].DOI:10.1146/annurev.ento.49.061802.123257 [本文引用: 1]
On the role of sensory feedbacks in Rowat–Selverston CPG to improve robot legged locomotion
[J].
Modeling the gastric mill central pattern generator of the lobster with a relaxation-oscillator network
[J].DOI:10.1152/jn.1993.70.3.1030 [本文引用: 1]
In vivo neuromechanics: decoding causal motor neuron behavior with resulting musculoskeletal function
[J].DOI:10.1038/s41598-017-13766-6 [本文引用: 1]
Man/machine interface based on the discharge timings of spinal motor neurons after targeted muscle sreinnervation
[J].DOI:10.1038/s41551-016-0025 [本文引用: 1]
Neural control and adaptive neural forward models for insect-like, energy-efficient, and adaptable locomotion of walking machines
[J].
Self-organized adaptation of a simple neural circuit enables complex robot behaviour
[J].
Adaptive and energy efficient walking in a hexapod robot under neuromechanical control and sensorimotor learning
[J].
Integrative biomimetics of autonomous hexapedal locomotion
[J].
Matsuoka’s CPG with desired rhythmic signals for adaptive walking of humanoid robots
[J].
CPG control for biped hopping robot in unpredictable environment
[J].DOI:10.1016/S1672-6529(11)60094-2 [本文引用: 1]
A minimal model describing hexapedal interlimb coordination: the tegotae-based approach
[J].DOI:10.3389/fnbot.2017.00029 [本文引用: 1]
A quadruped robot exhibiting spontaneous gait transitions from walking to trotting to galloping
[J].DOI:10.1038/s41598-017-00348-9 [本文引用: 1]
Biped locomotion control through a biomimetic CPG-based controller
[J].DOI:10.1007/s10846-016-0407-3 [本文引用: 1]
Sprawling quadruped robot driven by decentralized control with cross-coupled sensory feedback between legs and trunk
[J].
A backward control based on σ-Hopf oscillator with decoupled parameters for smooth locomotion of bio-inspired legged robot
[J].DOI:10.1016/j.robot.2018.05.009 [本文引用: 1]
Synchronization of non-linear oscillators for neurobiologically inspired control on a bionic parallel waist of legged robot
[J].DOI:10.3389/fnbot.2019.00059 [本文引用: 1]
High speed trot-running: implementation of a hierarchical controller using proprioceptive impedance control on the mit cheetah
[J].DOI:10.1177/0278364914532150 [本文引用: 1]
Sensor-driven neural control for omnidirectional locomotion and versatile reactive behaviors of walking machines
[J].DOI:10.1016/j.robot.2007.07.004 [本文引用: 2]