随着5G时代的到来，电子设备小型化成为了必然趋势. 电子设备中的电源模块通常分为低压差稳压器（low dropout regulator, LDO）与开关模式电压转换器2种，其中开关电源内部含有具备储能功能的电感器与电容器元件. 提高开关电源的工作频率是降低无源元件取值的主要方法，但更快的开关速度往往意味着更大的开关损耗和更加复杂的驱动器结构. 根据能量传输方式可以将开关电源拓扑分为开关电感式^[1]、开关电容式^[2]、谐振式^[3]. 前两者的功率开关采用硬开关工作，且需要较大的无源元件值来控制输出纹波. 而谐振式转换器的功率开关在理想情况下可以在任意频率下工作. 在以零电压开启（zero voltage switching, ZVS）为代表的软开关状态下，其谐振元件也可以在较高开关频率下设计为较小的数值，有利于同时实现高集成度与高效率. 单开关谐振转换器（single switch resonant converter, SSRC）以简单的驱动方式和较少的无源元件数量成为功率电子领域的研究热点^[4-8]. 不过，目前文献所报道的大部分单片集成式转换器输出功率均低于10 W ^[9-12]，且多为用于外部芯片供电的低压芯片.

本研究首次尝试实现单片集成的谐振式DC-DC转换器，使用硅基半导体工艺结合耐受高工作电压的氮化镓功率管设计了高开关频率的驱动电路与功率转换电路，研究其输出功率和转换效率的影响因素. 该设计可以应用在48 V/12 V混合电源新能源汽车发光二极管（light emitting diodes, LEDs）系统的供电设备中.

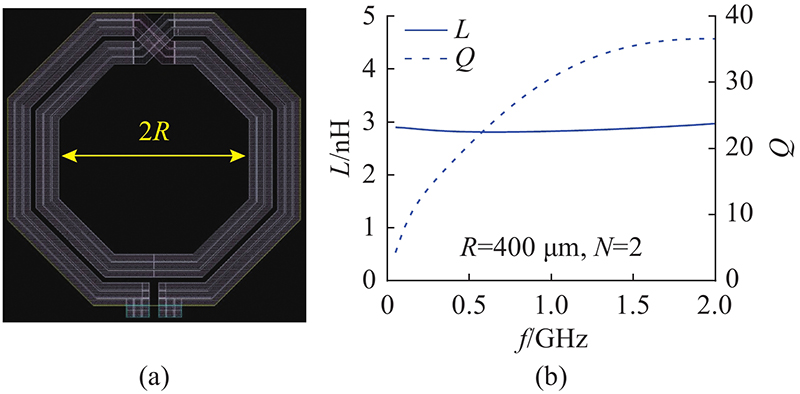
硅基绝缘体上硅（silicon on insulator, SOI）工艺如今被广泛应用在射频集成电路与电源管理芯片设计中，具有与硅基体互补金属氧化物半导体（complementary metal oxide semiconductor, CMOS）工艺的良好兼容性，被称为 “21世纪的硅基集成技术”. 硅基SOI工艺平台已经被证明可以实现高性能的高频电感器^[13-14]. SOI PMOS（positive channel metal oxide semiconductor）与NMOS（negative channel metal oxide semiconductor）件之间无需若干隔离层分隔从而减小了寄生电容，硅片通过智能切割（smart-cut）技术薄技术制备可以得到具有较小栅极寄生电容的薄顶层硅片，因此SOI器件拥有更高的开关速率，适合于高频谐振转换器驱动电路的设计. SSRC电路功率转换的功能是通过谐振电感与谐振电容的能量存放实现的. 电感器作为磁性储能元件，通常占据着大部分低频功率电子电路的体积，而在特高频转换器中，小尺寸低功耗的电感器对转换器的性能影响明显. 电感器的关键指标包括等效直流电阻R_ac、电感L、在给定工作频率下的品质因数Q（Q = ωL/R_ac，ω为工作角频率）以及自谐振频率SRF等. 对于谐振式开关电路，传输基波（开关频率）能量是首要要求，因此电感器须在工作频率处具备准确的电感、较高的品质因数（即较低的直流电阻），同时在满足上述要求条件下最好具有较大的版图线宽以防止电感中的电流纹波损坏元件. 在本研究的设计中，根据130 nm SOI工艺库中的功率电感器选择电路工作频率. 硅基SOI工艺中共提供3种厚金属电感器，分别为平面螺旋电感、半周平面螺旋电感和对称式平面螺旋电感，其中对称式平面螺旋电感器具有可选择的2圈绕线或3圈绕线结构从而可以得到更宽的电感范围. 为了简化命名，分别将绕线2圈和3圈的电感器表示为“PSI2”和“PSI3”. 如图1(a)所示为PSI2电感版图结构，如图1(b)所示为PSI2电感在螺旋电感最内圈的半径R=400 μm时的电感与品质因数在0~2.0 GHz频段内随频率f变化的情况. 图中，N为螺旋电感金属圈数. 可以看出，当PSI2电感器在500 MHz以上频率工作时，品质因数高于20，电感波动较小，表示电感器具有相对小的交流焦耳功耗，2圈的走线使得总的金属宽度不低于120 μm，从而保证该电感器可以通过较大的交流电流.

如图2（a）、（b）所示分别为PSI3电感器的版图示意图和内半径为400 μm时电感与品质因数在0~2 GHz频段内随频率的变化情况. 可以看出，PSI3电感器的品质因数在工作频率为0.5~2.0 GHz时也可以达到20以上，但电感却存在约3 nH的变动，这可能是因为3圈厚金属的走线使得电感器具有较大的寄生电容从而降低了电感器的自谐振频率. 由电感-电容谐振网络的频率特性可知，电感器在自谐振频率附近工作时具有较大的电压放大能力，但同时其特征阻抗随频率变化更加剧烈，将这种电感器应用在谐振式变换器中会导致谐波电流的幅度被明显放大从而导致转换器的损耗增加.

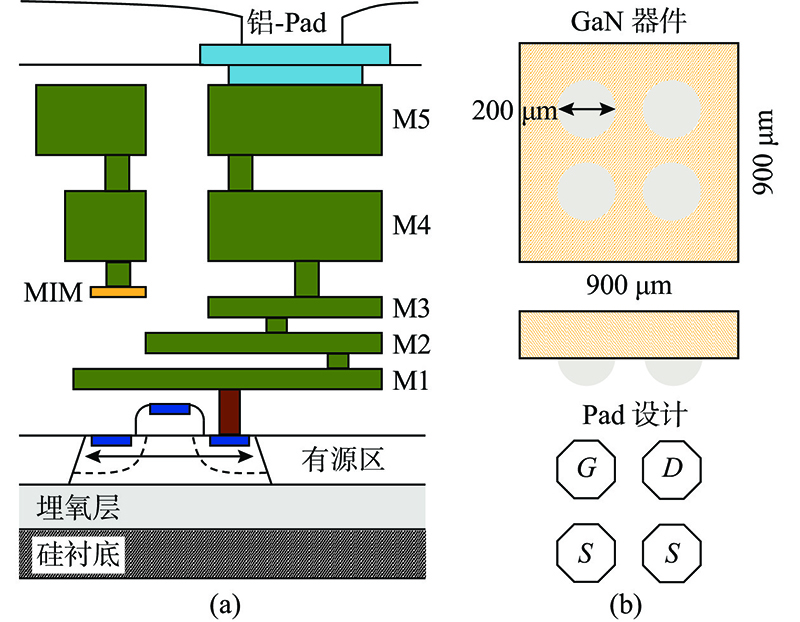
采用宜普电源转换公司制造的EPC2036器件作为功率开关与二极管. 该器件在源极与漏极之间并联一个额外的续流二极管用以在器件关断时通过反向电流，将源极与栅极端子短接即可让器件始终保持关断而同时使并接的二极管保持导通. 连接硅基芯片与分立器件的方式有2种，分别为平面键合与三维堆叠. 前者的工艺流程类似于芯片的键合过程，即用金线将芯片上的I/O Pad与印刷电路板上对应的焊盘连通，这种方法具有较大的设计自由度和容错率，因为片外连接的器件类型与尺寸完全可以按照键合所用电路板/衬底材料的焊盘位置修改. 但拉金丝键合的方式所使用的细度为几十微米的金线具有较大的寄生电感，其数量级在nH量级，相当于在转换器回路之间多引入了较大的电感器，这样会使得谐振电感的电感不准确进而导致转换器性能的恶化. 为了解决寄生效应的问题，很多高频转换器采用集成无源器件（integrated passive device，IPD）工艺平台实现^[15]，功率器件倒装在表面，通过IPD平台的高阻硅衬底上喷镀的低耗金属线连接，有效解决了寄生效应的问题. 但是，IPD平台较昂贵，且无法与主流硅基CMOS工艺兼容，驱动芯片也须通过倒装连接的方式接入，增加了系统的工艺复杂度. 三维堆叠技术最初应用于微波射频电路，其思路是把射频芯片与数字控制芯片通过垂直方向上的触点连接在一起，触点材料为导电率高的金属材质且为直径仅几十微米的球状材料，大大降低了寄生引起的信号衰减. 2017年三维堆叠技术首次被应用在一款40 MHz开关频率的片上降压转换器设计中^[16]，耗尽型GaN芯片与硅基驱动 / 控制芯片通过直径50 μm的锡球封装在一起，通过评估，每个锡球仅具有15 pF的寄生电感，几乎不会产生电压波形抖动与功率衰减，该设计实现了最高550 mW/mm²的片上功率密度. 2019年该技术又一次被成功应用于一款3.3 V转70.0 V的高转换比升压转换器中，实现了291 mW/mm²的片上功率密度^[17].

本研究使用的硅基130 nm SOI工艺包含5层金属层，其中2层厚金属M4、M5用来制作PSI2和PSI3电感器，其他金属层用于驱动电路与I/O信号的走线. 如图3所示为SOI工艺的结构，包含金属层、有源区、MIM电容介质层和铝Pad层，顶层金属M5层用来连接铝Pad层，通过开窗标识层留出芯片顶层连接GaN器件的位置. GaN功率器件引脚的尺寸如图3(b)所示，其包含4个半球形锡质引脚，对应的Pad形状可以设计为外接的八边形.

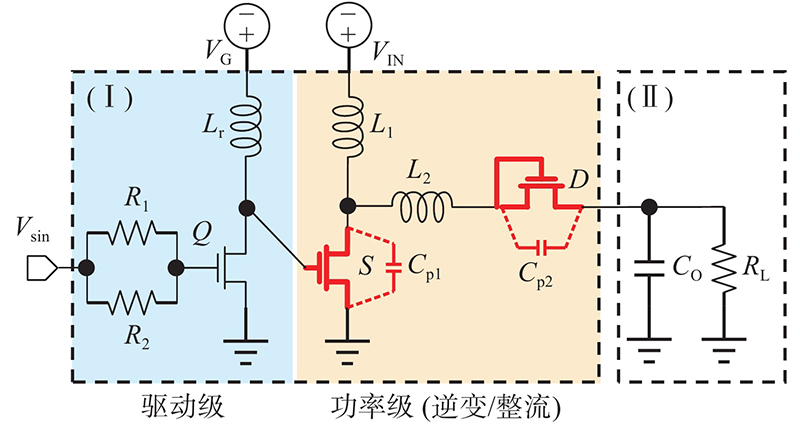
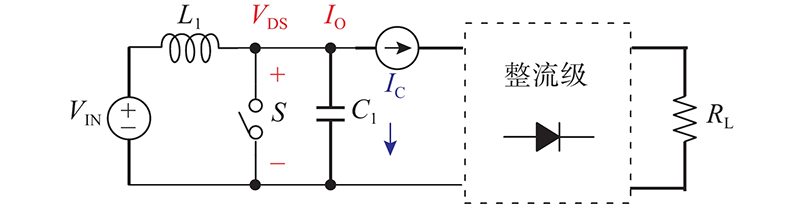
本研究所设计的转换器采用的电路是并联式Class-E拓扑，功率管栅极驱动器采用谐振式驱动器，电路原理图如图4所示. 图中，Ⅰ区域为片上实现电路，Ⅱ区域为片外测试电路，V_sin为外部正弦输入信号，V_G、V_IN分别为驱动级部分和功率级部分的电源电压，L₁、L₂为谐振电感器，C_p1、C_p2为谐振电容器，C_O为输出滤波电容，R_L为负载电阻.

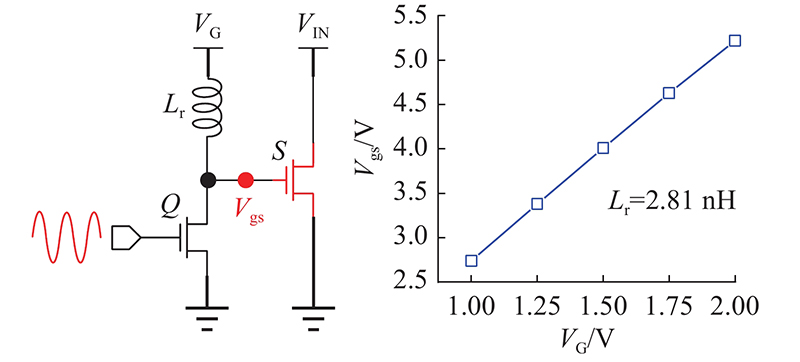
原理图中驱动级电路仅包含驱动NMOS的 Q管、谐振储能电感器L_r、驱动管栅极限流电阻R₁、R₂. 功率管S与二极管D采用GaN器件EPC2036^[18]. 该驱动器利用驱动管Q关断期间谐振电感L_r与功率管S输入寄生电容的谐振使S开启. 谐振电压可以达到V_G的2.2倍，具体放大倍数由L_r与功率管输入寄生电容的谐振频率决定，L_r的取值随开关频率的增加而减小. PSI2电感最小为2.81 nH，氮化镓器件的输入寄生电容约为75 pF，这样计算得到两者的谐振频率为346 MHz（0.692倍开关频率）. 如图5所示为不同电源电压V_G情况下最高驱动电压幅值的仿真结果. 可以看出，当V_G = 1.5 V时，功率管栅-源电压摆幅即可达到4.0 V，为了避免实际转换器中振铃与毛刺导致的电压过冲损坏功率器件，选择V_G = 1.5 V作为驱动器电源电压. 500 MHz的方波信号含有GHz级的高次谐波，很难通过数字系统准确生成，因此，采用正弦波作为Q管的驱动信号，正弦波的直流偏置电压略高于Q管的开启阈值电压以保证驱动管的开关占空比接近0.5.

为了提高片上转换器系统的集成度，整个芯片的面积不可过大，应尽量减少无源元件的数量. 根据图4中的拓扑，转换器功率级电路包括L₁-C₁和L₂-C₂2个谐振网络共4个谐振元件. 谐振电感作为功率传输通路的必要元件不可忽略，本研究尝试将2个谐振电容C₁和C₂在500 MHz的开关频率用功率器件S和D的寄生电容C_p1和C_p2替代，这样可以省略较大面积的片上电容占据的芯片面积，最大化地发挥功率器件的效用从而提升整个GaN转换器系统的功率密度. 因此，功率级电路设计的初始条件如下：

(1) $ C_{1}=C_{2}=C_{\mathrm{p} 1}=C_{\mathrm{p} 2}. $

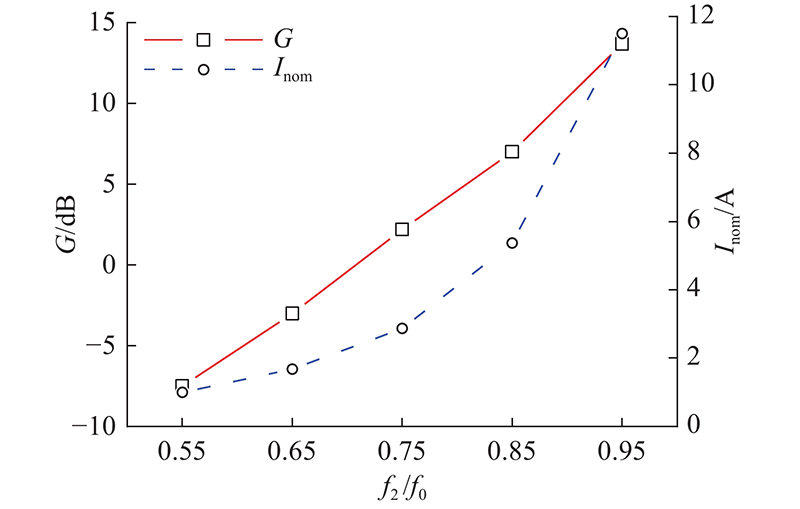
C_p1、C_p2可以通过器件的数据表查阅得到，此处电容为75 pF. 根据目标电压增益，在已知谐振电容C₂数值的情况下首先对L₂-C₂-R_L谐振网络的电压增益进行扫描. 获得较大电压增益的代价是谐振电感中较大的电流幅度，这样会增加电感器的交流焦耳功耗，因此在设计谐振电感L₂数值的同时也要兼顾电流纹波的大小，最后在2个指标之间进行折中设计. 如图6所示为R_L=50 Ω时谐振网络的电压增益G与归一化谐振电流I_nom的值. 图中，f₂为L₂-C₂的谐振频率，f₀为开关频率. 可以看出，f₂越接近f₀，网络的电压增益越大，同时L₂中的谐振电流幅度也越大，这是因为当输入信号的频率（f₀）与网络谐振频率接近时谐振网络对其呈现的阻抗较小. 为了保证较大的电压增益同时避免谐振电流幅值超过10 A，本研究取f₂ = 0.88 f₀，此时可以计算得到谐振电感为1.73 nH. 查阅工艺手册可知可以用2个并联的内半径为475 μm的PSI2电感器实现该谐振电感，这样的设计可以将电感器中的谐振电流幅值均分到2个独立的电感器中，保证转换器正常工作的能力.

分析L₁-C₁谐振网络的设计方法，首先根据电瞬态电路分析推导功率管漏-源电压V_DS的表达式，本研究仅考虑基波电流的传输，分析所用电路模型如图7所示. 图中，I_C为通过电容C₁的电流.

根据正弦电流假设，逆变级电路输出电流I_O可以表达为

(2) $ I_{{\rm{O}}}=I_{\mathrm{AC}} \sin \ \left(\omega_{0} t+\varphi\right) . $

式中：ω₀为开关频率的角频率，I_AC为谐振电流的幅值，φ为初始相位. 根据基尔霍夫定律，当功率开关S断开时，V_DS表达式为

(3) $ L_{1} C_{1} \frac{{\rm{d}} V_{\mathrm{DS}}^{2}}{{\rm{d}} t^{2}}+V_{\mathrm{DS}}=V_{\mathrm{IN}}=\omega_{0} L_{\mathrm{1}} I_{{\rm{O}}} . $

式（3）为一阶非齐次线性方程，其通解可以写为

(4) $ \begin{split} V_{\mathrm{DS}}=\;&C_{\mathrm{A}} \cos \ \frac{t}{\sqrt{L_{1} C_{1}}}+C_{\mathrm{B}} \sin \ \frac{t}{\sqrt{L_{1} C_{1}}}+ \\ \;&\frac{L_{1} \omega_{0} I_{\mathrm{AC}}}{L_{1} C_{1} \omega_{\mathrm{0}}^{2}-1} \cos \ \left(\omega_{0} t+\varphi\right)+V_{\mathrm{IN}} . \end{split} $

代入如下边界条件来确定2个常系数C_A、C_B：

(5) $ \left.V_{\mathrm{DS}}\right|_{t=0}=0 \text{，} $

(6) ${\overline V _{{\rm{DS}}}} = {V_{{\rm{IN}}}}.$

式中： $ {\overline V _{{\rm{DS}}}} $为功率开关漏-源电压在关断期间的平均值. 结合这2个约束条件可以解得C_A、C_B：

(7) $ \left.\begin{array}{l} C_{\mathrm{A}}=-\lambda \cos \ \varphi-V_{\mathrm{IN}}， \\ \mathcal{C}_{\mathrm{B}}=\dfrac{-C_{\mathrm{A}} \sin \ \left(\lambda_{1} \pi\right)+2 \lambda_{1} \sin \ \varphi+\lambda_{1} V_{\mathrm{IN}} \pi}{1-\cos \ \left(\lambda_{1} \pi\right)}. \end{array}\right\} $

系数 $ \lambda_{1} $、 $ \lambda $表达式为

(8) $ \begin{array}{l} \lambda_{1}=\omega_{1} / \omega_{0},\ \ Z_{1}=\sqrt{L_{1} / C_{1}},\ \ \lambda=\dfrac{\lambda_{1} I_{{\rm{A C}}} Z_{1}}{\lambda_{1}{ }^{2}-1}. \end{array} $

式中：ω₁、Z₁分别为谐振元件L₁、C₁的谐振角频率和特征阻抗. 从而式（4）中仅剩下I_AC与φ为未知量，初始相位的数值与图7中的整流级网络输入阻抗有关，即并联L₂-C₂-R_L谐振网络的输入阻抗. 根据推导，整流级网络的输入阻抗Z₂可以表达为

(9) $ Z_{2}=\frac{R_{\mathrm{L}}}{1+R_{\mathrm{L}}{ }^{2} \omega_{0}{ }^{2} C_{2}^{2}}+{\rm{j}}\left(\omega_{0} L_{2}-\frac{R_{\mathrm{L}}{ }^{2} \omega_{0} C_{2}}{1+R_{\mathrm{L}}{ }^{2} \omega_{0}{ }^{2} C_{2}^{2}}\right). $

因此对于频率为f₀的正弦电压输入信号，可以将谐振电流的初始相位表示为

(10) $ \varphi=-\arctan \;\; \left( \frac{\omega_{0} L_{2}\left(1+R_{\mathrm{L}}^{2} \omega_{0}^{2} C_{2}^{2}\right)-R_{\mathrm{L}}^{2} \omega_{0} C_{2}}{R_{\mathrm{L}}}\right). $

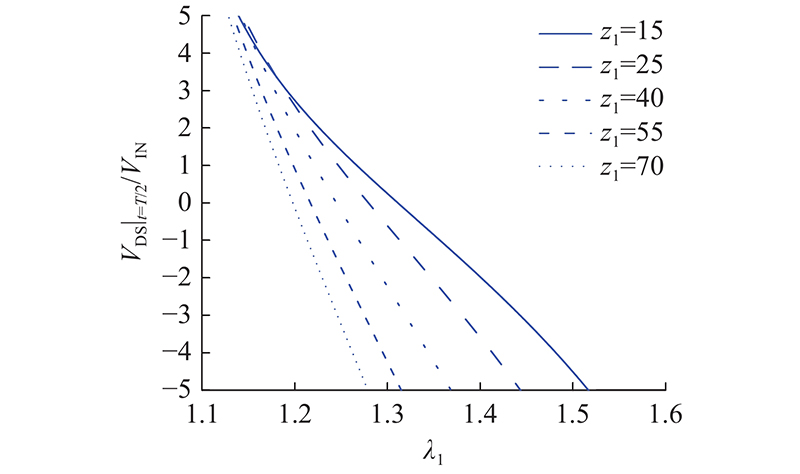
谐振电流中包含基波与同相位的高次谐波电流分量，另外整流级输入电压的基频分量也难以直接计算，因此无法通过基频处的输入阻抗准确确定I_AC. 为了保证ZVS的工作性能，V_DS的波形在开关从关断切换到开启的瞬间或之前的时刻须降到0 V，即V_DS|_t=T/2 = 0. 将R_L= R₀代入式（10）可以确定 $ \varphi$，取I_AC= 1 A，代入式（4）同时扫描式（8）中的自变量即可获得V_DS在开关切换时刻的情况. 如图8、9所示分别为参数 $ \lambda_{1} $在0~1.0和1.0~2.0取值时V_DS|_t=T/2与V_IN的比值，即式（4）的解析解. 图中每条数据图线取得零点时对应的横坐标所代表的谐振网络L₁-C₁参数即可以使得功率管漏-源电压在开关切换为开启的瞬间恰好降到0 V，而 $ \lambda_{1} $取值超过这个零点时对应的数值就会使得V_DS波形提前降到0 V.

这种情况在提高了转换器保持软开关的鲁棒性的同时会增加功率管漏极的电压应力，因为图7中的谐振电容C₁两端电压的平均值等于输入电压V_IN. 由图8、9可以看出，随着Z₁的增加，V_DS波形取得零点对应的 $ \lambda_{1} $会减小，这意味着须取更大的谐振电感L_r. 综上，为了保证转换器在轻载工况下工作时依然可以保持ZVS状态，选择 $ \lambda_{1} $= 0.44和Z₁ = 40作为设计参数. 如表1所示为驱动级、功率级片上电路元件的取值和选型.

在高功率密度转换器设计中，支路电流密度是制约芯片设计的重要因素，为了保证转换器正常工作且具有较长的使用寿命，回路中的电流必须低于按照手册计算出的最高耐流值. 如表2所示为本研究所用130 nm SOI工艺中主要金属层与I/O Pad铝金属在不同温度下的最高电流线密度，其中M1~M5分别表示第1~5层金属. 表中，T_m为金属层温度，A_max为最大电流密度.

通过合理的版图设计，将各个电感器、Pad、驱动电路交叉摆放可以占用更小的芯片面积，这样也会缩短片上走线的长度从而减少额外的寄生. 如图10（a）所示为如图4所示原理图的驱动级电路与功率级电路的位置和器件摆放方式，如图10（b）所示为填充Dummy金属且通过设计规则检查（DRC）与版图-原理图一致性检查（LVS）后的转换器版图. 整个芯片面积为9 mm²（3 mm×3 mm），各个电感器之间开口角度为90º，在最大程度上避免了电感电流间的互感. 顶层金属走线以及Pad的最小金属层宽度为120 μm，在85 ℃条件下可以承受至少6 A的电流，保证了转换器安全工作.

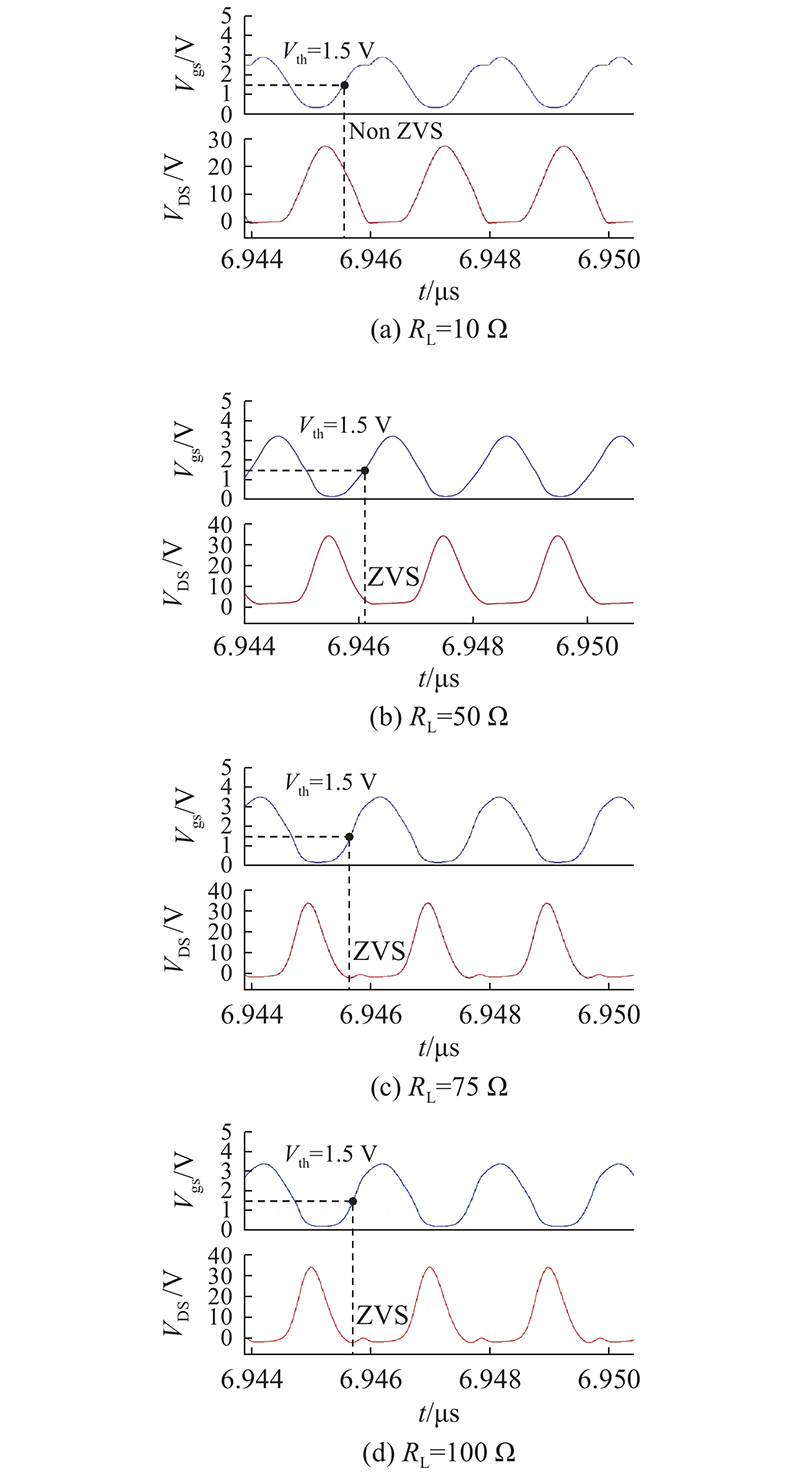
给出所设计的全谐振式并联Class-E升压转换器的仿真结果与分析，并与文献中的同类设计进行对比. 仿真原理图在Cadence Virtuoso软件里搭建，结合GaN器件EPC2036的spectre模型进行时域仿真，观察转换器的瞬态响应与软开关情况. 如图11所示为输入电压为12 V时，负载电阻R_L = 10、 50、75、100 Ω时的驱动器输出电压V_gs波形和功率管漏-源电压V_DS波形. 图中，V_th为EPC2036器件的栅极开启阈值电压，对于以二维电子气为沟道导通机制的功率器件来说，当V_gs > V_th时器件即可实现双向导通. 显然，当R_L等于设计值R₀ = 50 Ω时，转换器可以恰好工作在ZVS状态，而当R_L > 50 Ω时，软开关特性依旧可以保持，且具有一定的时间裕度.

由图11可以看出，当R_L = 10 Ω时驱动电压V_gs的波形存在一段平缓的阶段，这是接在功率器件漏极与栅极之间的米勒电容（C_gd）所导致的. 在功率晶体管开通的过程中，漏-源电压持续下降，在V_gs超过阈值电压V_th后的一段时间内，功率管工作状态进入饱和区，可以等效为一个电流源负载的共源放大器，其电压增益为A_u，米勒电容在功率管漏极与栅极之间起到了负反馈的作用，由于米勒效应该电容被放大了（1+A_u）倍，造成V_gs电压上升缓慢. 当负载电阻较大时，V_DS波形下降到0 V的时刻在功率开关开启之前，因此当功率管开通时V_DS已经降到V_th以下，功率管工作在线性区失去放大功能，从而避免了米勒效应.

如图12所示为输入电压为12 V时各个负载条件下的输出电压以及输出纹波. 可以看出，当负载大于等于R₀时，输出电压可以达到输入电压的2~3倍. 电压输出纹波是在片外输出电容为20 nF时测量的，纹波最大仅有290 mV，容易通过增加输出电容进一步降低. 输出纹波的幅度反映了谐振网络L₂-C₂-R_L的电流放大倍数，与如图6所示的趋势一致.

如图13所示为输入电压恒定时转换器的输出电压V_OUT、转换效率η与负载电阻的关系，负载电阻越大则输出电压越高，这也是谐振网络L₂-C₂-R_L的电压增益变化所导致的. 同时转换器重载下的效率可以达到89%，而在轻载情况下转换器虽然能保持ZVS工作但转换效率却不断降低，这是因为谐振回路中较大的交流电流纹波导致了较大的谐振电感器中的焦耳损耗和二极管的导通损耗.

若仅考虑开关频率的基波分量对损耗的贡献，二极管导通损耗P_D和电感器焦耳损耗P_L可以分别表示为

(11) $ {P_{\rm{D}}} = {I_{{{\rm{D}}_ - } + }}{V_{\rm{F}}}, $

(12) $ P_{\mathrm{L}}=I_{\mathrm{rms}}^{2} R_{{\rm{d c}}}+({I_{\mathrm{rms}}}/{\sqrt{2}})^{2} R_{ \mathrm{ac}} . $

式中：I_{D_+}为通过二极管的正向电流平均值；V_F为二极管的正向导通压降，可以通过查阅器件手册得到，本研究所用EPC2036器件的V_F = 2.2 V；R_ac与R_dc表示谐振电感器的交流等效电阻和金属线寄生电阻；I_rms表示支路电流有效值.

(13) $ \left.\begin{array}{l} R_{{\rm{a c}}}=\omega L / Q, \\ R_{{\rm{d c}}}=\pi r_{{\rm{top}}}[2 N R+(N-1) W]. \end{array}\right\} $

式中：N为螺旋电感圈数（PSI2：N = 2，PSI3：N = 3），W为螺旋电感走线宽度，r_top为顶层金属的电阻率.

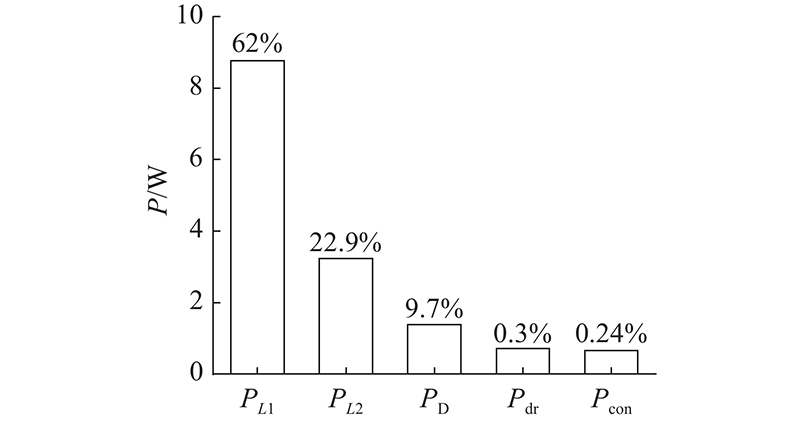
如图14所示为V_IN = 12 V、R_L = 50 Ω时的功耗构成情况. 图中，P_L1为L₁电感的功耗，P_L2为L₂电感的功耗，P_D为二极管导通损耗，P_dr为驱动损耗，P_con为功率管与二极管的导通电阻损耗. 可以看出，谐振电感L₁、L₂分别占了总功耗的62.0%、22.9%，谐振式驱动器的损耗仅为0.72 W. 这也表明本设计中的损耗主要来源于电感器的走线电阻，对于片上集成式全谐振转换器来说，低耗谐振电感器或谐振腔的研发具有很重要的意义，须同时满足储能需求与较高的集成度. 如表3所示，对比本设计与最近文献中报道的片上DC-DC转换器的性能. 表中，f为频率，V_OUT/V_IN为转换比，P_den为功率密度，A为面积. 与开关电感式转换器相比，本设计所用并联Class-E转换器中的元件均为谐振元件，且功率器件的寄生电容能够得到最大程度的利用，在相近输出功率水平的情况下本设计具有更高的转换效率. 与开关电容式转换器相比，本设计无需堆叠密度很高的片上电容器，可以实现更高的输出功率和工作电压，同时本设计仅含有单个功率开关，驱动器设计简单且更容易实现软开关工作.

为了提高电源管理模块的集成度和功率密度，减小无源元件的体积，促进车载照明系统之类的功率电子进一步小型化，首次基于硅基130 nm SOI工艺平台与氮化镓高电子迁移率功率管设计实现了一款500 MHz开关频率、12 V输入电压、输出功率高于10 W的片上单开关谐振式升压DC-DC转换器. 转换器中的谐振电感器使用硅基SOI工艺中顶层厚金属电感器实现，谐振电容器使用功率开关管与二极管的寄生电容实现，最大化利用了器件的寄生效应与芯片面积. 具体给出了谐振驱动电路、功率级转换电路中各个元件的设计依据，通过合理的版图布局将整个转换器电路在9 mm²的芯片上实现，氮化镓功率管与二极管采用垂直方向低寄生倒装的方式与片上电路连接，提高了系统集成度. 仿真结果显示，该片上转换器可以在较宽负载范围内实现软开关ZVS工作，具有良好的负载响应功能，满载时片上功率密度可以达到1.48 W/mm²，转换效率为60%. 与片上开关电感式转换器相比，本设计中的转换器因工作在软开关状态而具有较高的效率，与片上开关电容式转化器相比，本设计不受片上电容器密度限制，可以实现较大的输出功率. 在未来的工作中须进一步减小片上元件的损耗，比如优化电感器的结构使其走线长度更短、使用可集成式的低导通压降功率肖特基二极管，提高整个转换器的效率.