“2030碳达峰”和“2060碳中和”势在必行，已经成为中国节能减排事业的工作重点^[1]. 作为耗能大户，建筑运行约消耗了全国能源消费总量的22%^[2]，其中中央空调系统的能耗约占建筑总能耗的50%^[3]. 因此，中央空调系统运行节能对实现“碳达峰”和“碳中和”至关重要. 准确的建筑负荷预测对中央空调系统运行节能必不可少，被广泛应用于优化控制和故障诊断.

随着楼宇自控系统的普及，大量建筑运行数据被保留下来，促进了基于数据驱动的建筑负荷预测技术的发展^[4]. 与基于物理建模的方法相比，基于数据驱动的技术拥有精度高和建模便捷的优势，具有极大的应用前景^[5]. 目前大多数基于数据驱动的建筑负荷预测研究聚焦于点预测（给出负荷预测值）. 例如，孙超等^[6]使用改进的反向传播（back propagation，BP）神经网络对建筑用电负荷进行预测. Fan等^[7]比较了多种数据驱动算法（多元线性回归、随机森林、极端梯度提升、深度神经网络、支持向量回归等）在建筑冷负荷预测中的性能，结果发现极端梯度提升算法的性能最佳. 实际中，由于数据噪声、极端工况、模型本身的局限性等原因，点预测的结果往往存在不确定性，从而降低了基于点预测的优化控制^[8]和故障诊断^[9]的可靠性.

针对上述问题，研究人员提出使用预测区间估计方法来描述点预测的不确定性. 预测区间被定义为某一范围，实际负荷将以一定概率落在该范围内. 预测区间越窄，表明负荷点预测结果越可靠. 目前的建筑负荷预测区间估计方法大致可以分为3类：残差分布假设法、回归建模法和残差聚类法. 残差分布假设法通过对模型残差的统计分布进行假设来估计模型预测值的残差范围. 标准正态分布^[10-12]和零均值拉普拉斯分布^[13]是该领域最常用的2种分布假设. 由于负荷特征和模型类型各异，较难对残差分布进行准确假设，因此该方法的可靠性较差. 而回归建模法和残差聚类法不需要对模型残差的统计分布进行任何假设，具有更高的可靠性. 回归建模法通过构建模型输入和预测区间上下限之间的函数关系，从而估计模型的预测区间. Quan等^[14-15]使用神经网络来学习模型输入和预测区间上下限之间的函数关系，并用于估计电力负荷预测区间. Xu等^[16]使用分位数回归技术估计递归神经网络的预测区间，并将其应用于住宅建筑电耗预测区间的估计. 残差聚类法使用聚类技术对模型残差进行分组，并根据不同分组内的残差分位数估计模型的预测区间. Zhang等^[9]通过聚类得到某办公建筑冷负荷预测模型在不同输入组合下的残差分布，然后根据不同残差分布下的分位数估计模型的预测区间. 和回归建模法相比，残差聚类法编程难度更低，计算效率更高. 此外，回归建模会引入新的模型不确定性，因此残差聚类法的可靠性也更高. 但是，目前的研究在残差聚类时假设不同输入对模型预测残差的影响程度相同，这一假设在实际中并不合理. 例如，Zhang等^[4]发现历史负荷对建筑负荷预测结果的影响显著大于室外气象参数的. 即使历史负荷和室外气象参数变化程度相同，模型残差的变化程度也是不同的. 传统的残差聚类法将这类残差划分到一组，从而导致残差聚类不合理. 因此，在残差聚类时须考虑模型输入对预测结果的贡献程度，从而获得更合理的残差分组，提高区间估计的可靠性和准确性.

综上所述，本研究提出基于加权残差聚类的建筑负荷预测区间估计方法，并在深圳某建筑1 a的运行数据集上进行验证. 相较于前人的方法，本研究使用了Shapley additive explanations （SHAP）量化模型输入的贡献程度，并基于得到的贡献程度对模型输入进行加权聚类，旨在得到更可靠的残差聚类和区间估计结果. 该方法不对残差的统计分布进行任何假设，理论上适用于所有数据驱动的建筑负荷预测模型.

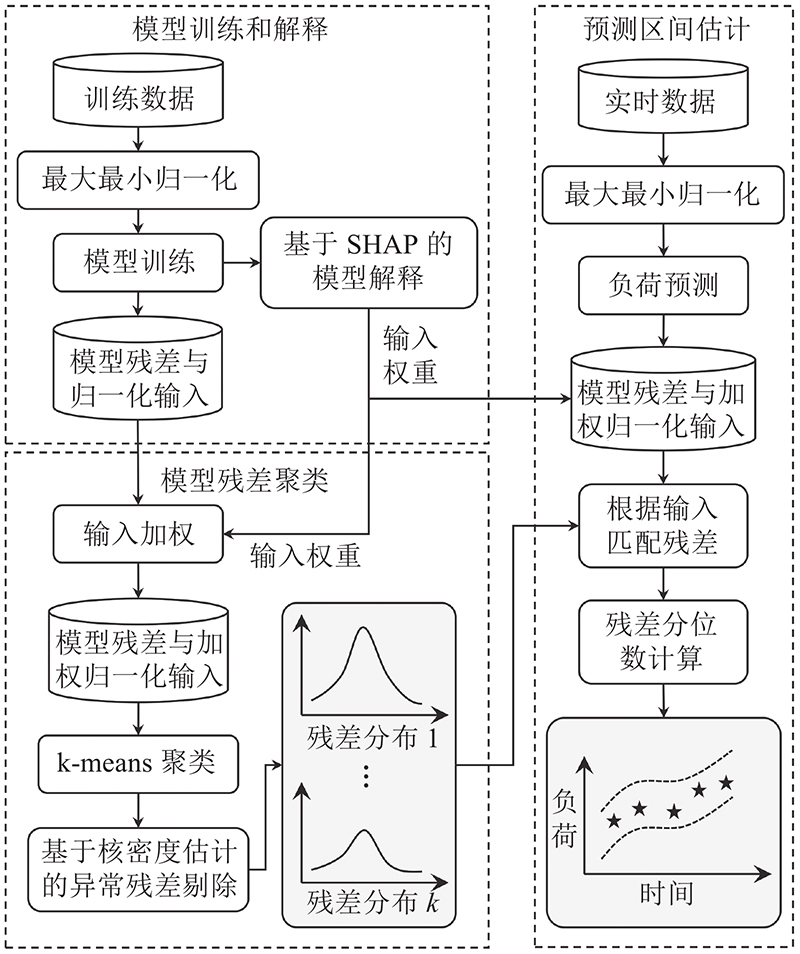
如图1所示，本研究提出的基于加权残差聚类的预测区间估计方法主要包括3个步骤：模型训练和解释、模型残差聚类和预测区间估计. 模型训练和解释旨在利用训练数据训练一个建筑负荷预测模型，然后使用SHAP方法对模型输入的重要程度进行解释，最后根据得到的模型输入重要程度对训练集中的模型输入进行加权. 模型残差聚类旨在使用k-means算法对加权后的模型输入进行聚类，并借助基于核密度估计的方法剔除异常残差，从而得到不同输入组合下的残差分布. 预测区间估计旨在使用训练得到的模型对建筑负荷进行实时预测，然后根据加权后的模型输入找到最匹配的残差分布，并通过计算残差分位数得到模型预测结果的预测区间.

建筑负荷预测模型输入变量的取值范围差别很大，加大了模型训练的难度和时间^[17]. 因此，在模型训练前须对模型输入和输出进行最大最小归一化，将所有变量缩放至[0,1.0].

常用的建筑负荷预测黑箱算法有人工神经网络、支持向量回归、随机森林、极端梯度提升（extreme gradient boosting, XGBoost）等. 其中，XGBoost是一种基于boosting的集成学习算法. 其核心思想为递进地训练多个树模型，每个树模型拟合前一个树模型的预测误差，最终将各个树模型的输出线性相加得到最终的预测值. 目前，XGBoost已经被证明是以上几种算法中精度最高的^[18]. 因此，本研究采用该算法对建筑负荷进行预测.

研究表明不同输入对模型预测结果影响各异^[19]，可以用敏感性分析^[4]、SHAP^[20]和local interpretable model-agnostic explanations（LIME）^[21]等方法进行解释. 敏感性分析只能对模型全局预测性能进行解释，由于忽略了模型局部预测性能，其准确性比SHAP和LIME更低. 此外，根据Främling等^[22]的研究，对于回归任务，SHAP比LIME的准确性更高，后者在某些输入的解释上出现了显著错误. 因此，本研究采用SHAP对模型进行解释. 该方法不仅适用于XGBoost，也可以解释其他数据驱动模型输入对输出的重要程度，因此本研究提出的方法具有通用性.

Shapley一词最早源自博弈论，通常被用作评估每个玩家在博弈游戏中对该游戏的贡献程度. SHAP的原理和Shapley类似，旨在评估每个模型输入对模型输出的贡献程度. 该方法使用了加性特征归因思想，即假设模型输出都是输入的线性相加^[23]. 原始模型的解释模型如下：

(1) $ g\left( {x'} \right) = {\phi _0} + \sum\nolimits_{i = 1}^M {{\phi _i}{x}_{i}{{'}}} . $

式中：g(∙)为解释模型； ${x}_{i}{{'}}\in {\left\{\mathrm{0,1}\right\}}$为简化输入，0表示该输入缺失，1表示该输入存在；M为简化输入的数量； ${\phi }_{i}\in {\bf{R}}$为第i个变量的Shapley值.

(2) $ {\phi _i} = \sum\limits_{S \subseteq N\backslash \left\{ i \right\}} {\frac{{\left| S \right|!\left( {M - \left| S \right| - 1} \right)!}}{{M!}}\left[ {{f_x}\left( {S \cup \left\{ i \right\}} \right) - {f_x}\left( S \right)} \right]} . $

式中：N为所有简化输入的集合，S为N的子集，f_x(S)为模型输入为S时原始模型的输出.

SHAP值能够反映单次预测中每个输入对输出的贡献，其绝对值越大，表示贡献越大. 计算某变量在所有样本上SHAP值的绝对值，取其平均值，便得到了该变量的全局SHAP 值.

模型残差为实际负荷与模型预测负荷之差：

(3) $ e = y - \hat y . $

式中：e为模型残差，y为实际负荷， $ \hat{y} $为模型预测负荷.

模型预测负荷取决于模型输入. 由此可知，模型残差与模型输入之间存在强相关性，不同模型输入下的模型残差分布会存在显著差异^[9]. 因此，为了得到更可靠的残差分布，在进行输入聚类前须根据其SHAP值进行加权，在加权后，贡献大的输入在聚类时将产生更大的作用. 表达式如下：

(4) $ {\tilde x_i} = \frac{{\bar {{\phi _i}} }}{{\displaystyle\sum\nolimits_{i = 1}^p {\bar {{\phi _i}} } }}{x_i} . $

式中： ${\tilde x_i}$为第i个加权归一化输入； $ {x}_{i} $为第i个归一化输入； $ \bar{{\phi }_{i}} $为第i个变量的全局Shapley值，i = 1, 2 $, \cdots , $ p.

在对输入进行加权后，使用k-means算法对输入进行聚类. k-means算法是目前最经典的聚类算法之一，具有收敛快和易于编程的优点. 该算法会首先随机选择k个样本点作为初始聚类中心，然后计算每个样本点到各聚类中心的欧氏距离并将该样本点划分到距离最近的聚类中心，当所有样本点都被划分完毕后，重新计算每个类中样本点的平均值作为新的聚类中心，重复以上步骤直到聚类中心不再改变.

由于数据噪声、数据异常和未知工况等原因，可能会出现部分残差偏大，从而导致预测区间过大. 因此，须对异常残差进行识别和剔除. 本研究使用基于核密度估计的异常残差剔除方法^[24]：

(5) $ P\left( e \right) = \frac{1}{{nb}}\sum\nolimits_{i = 1}^n {K\left( {\frac{{e - {e_i}}}{b}} \right)} . $

式中：P(·)为某残差簇内残差的概率密度分布函数，n为某残差簇内的残差总个数，e_i为某残差簇内第i个残差，b为带宽，K(∙)为核函数.

核密度估计是一种非参数的变量概率密度分布函数估计算法. 通常，如果某个残差出现的概率很低，可以认为是异常残差，须进行剔除. 残差概率密度的阈值通常为概率密度函数最大值P_max乘上一个缩放因子. 若某残差出现的概率低于该阈值，则将被识别为异常残差并剔除.

预测区间估计旨在估计一个区间范围，使得实际负荷落在该范围内的概率等于某一个给定的名义置信水平（prediction interval nominal confidence，PINC）.

本研究采用以下步骤估计某次预测的预测区间：1）对本次预测的输入进行最大最小归一化及加权；2）计算加权归一化输入与残差簇中心之间的欧氏距离，得到与该输入距离最近的残差簇；3）计算预测区间的上下限^[9]. 上下限表达式如下：

(6) $ U=\left\{\begin{array}{l}\;{\hat y}+{Q}_{100\times \left(1-\alpha \right)\text{%}},\;\;\;\;\;\;\;\;\;\;\;\gamma < 0.5 \left(1-\alpha \right);\hfill \\ {\hat y}+{Q}_{100\text{%}},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{1}-\gamma < 0.5 \left(1-\alpha \right);\hfill \\ {\hat y}+{Q}_{100\times \left(\gamma +0.5\left(1-\alpha \right)\right)\text{%}},\;\;\gamma \geqslant 0.5 \left(1-\alpha \right),\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{1}-\gamma \geqslant 0.5\times \left(1-\alpha \right). \end{array}\right. $

(7) $ L=\left\{\begin{array}{l}{\hat y}+{Q}_{0\text{%}},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\gamma < 0.5 \left(1-\alpha \right);\hfill \\ {\hat y}+{Q}_{100\times \alpha \text{%}},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{1}-\gamma < 0.5 \left(1-\alpha \right);\hfill \\ {\hat y}+{Q}_{100\times \left(\gamma -0.5 \times\left(1-\alpha \right)\right)\text{%}},\;\;\gamma \geqslant 0.5 \left(1-\alpha \right),\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\text{1}-\gamma \geqslant 0.5 \left(1-\alpha \right).\hfill \end{array} \right. $

式中：U和L分别为预测区间的上下界， $\hat y$为模型预测负荷，Q为距离最近的残差簇内的残差百分位数，γ为该残差簇中小于0的残差的占比，100×(1−α)%为名义置信水平.

平均绝对误差（mean absolute error，MAE）、均方根误差（root mean squared error，RMSE）、决定系数（coefficient of determination，R²）和均方根误差的变异系数（coefficient of variation of root mean squared error，CV-RMSE）是4个常见的黑箱模型精度评价指标. MAE、RMSE和CV-RMSE越小，模型预测值与实际值越接近. R²越接近1，模型预测值与实际值越接近. 表达式分别如下：

(8) $ {\text{MAE}} = \frac{1}{m}\sum\nolimits_{i = 1}^m {\left| {{y_i} - {{\hat y}_i}} \right|} \text{，} $

(9) $ {\rm{RMSE}} = {\left[ {\dfrac{1}{m}\sum\nolimits_{i = 1}^m {{{\left( {{y_i} - {{\hat y}_i}} \right)}^2}} } \right]^{{1 / 2}}} \text{，} $

(10) $ {{{R}}^2} = 1 - \frac{{\displaystyle\sum\nolimits_{i = 1}^m {{{\left( {{y_i} - {{{\hat y}}_i}} \right)}^2}} }}{{\displaystyle\sum\nolimits_{i = 1}^m {{{\left( {{y_i} - \bar y} \right)}^2}} }} \text{，} $

(11) $ {\rm{CV}} {\text{-}} {\rm{RMSE}} = \left.{{{{{\left[ {\dfrac{1}{m}\displaystyle{\sum\nolimits_{i = 1}^m} {{{\left( {{y_i} - {{\hat y}_i}} \right)}^2}} } \right]}^{{1 / 2}}}}}}\right/{{\bar y}} . $

式中： ${{\hat y}}_{i}$为预测值， $ {y}_{i} $为实际值， $ \bar{y} $为实际值取平均，m为样本个数.

预测区间覆盖概率（prediction interval coverage probability，PICP）和平均覆盖误差（average coverage error，ACE）是最常见的预测区间性能评价指标^[9]. PICP指实际值落在预测区间内的真实概率，值越大，实测值落在预测区间的概率越大. ACE指PICP与PINC之差，值越接近0，实际值落在预测区间内的概率越接近理想值.

(12) $ {\text{PICP}} = \frac{1}{q}\sum\nolimits_{i = 1}^q {{c_i}} \text{，} $

(13) $ {\text{ACE}} = {\text{PICP}} - {\text{PINC}}. $

式中：q为实际值的个数；c_i表示第i个实际值是否落在预测区间内，0表示否，1表示是.

采用深圳某办公建筑1 a的冷负荷数据集（采样间隔10 min）对提出的方法进行验证. 该数据集包含6个变量（月份M、时刻H、周几W、室外温度T_out、室外湿度RH_out和建筑冷负荷CL）从2016年1月1日—2016年12月31日共310 766个测量值. 按85∶15的比例将数据集随机划分为训练集和测试集，并采用最大最小归一化对训练集和测试集的数据进行归一化. 训练集用于模型训练和残差聚类，测试集用于性能验证.

月份、时刻和周几分别反映了建筑冷负荷的季节性规律、日内规律和周内规律，室外温度和室外湿度是冷负荷的重要影响因素，历史冷负荷反映了建筑热惯性. 以上变量是当前建筑冷负荷预测中最常用的输入变量^[25]. 因此，本研究采用月份、时刻、周几、室外温度、室外湿度、前1 h冷负荷（CL₁）和前2 h冷负荷（CL₂）作为模型输入.

为了得到最优的模型结构，首先须优化XGBoost算法的超参数. 本研究中涉及的超参数包括树的最大深度d_max、学习率l、树的特征采集比例p₁、训练样本占比p₂和树的个数N_tree. 采用交叉验证和网格搜索在训练集上对以上超参数进行寻优，寻优范围和结果如表1所示.

基于上述最优超参数，在训练集上训练XGBoost模型，其精度如表2所示. 结果显示该模型具有较高的精度，其在训练集和测试集上的R²均大于0.75，且CV-RMSE小于30.00%，满足工程使用需求^[26].

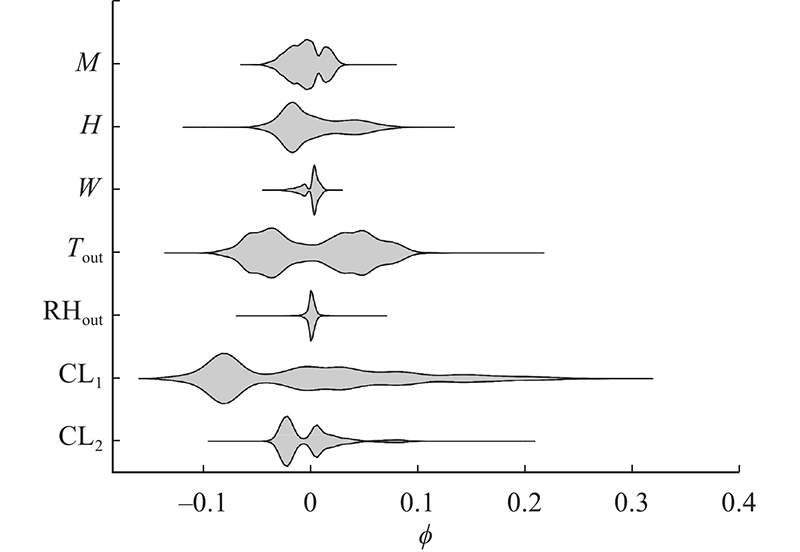
利用SHAP方法对XGBoost模型输入的重要程度进行量化. 如图2所示为模型输入在所有样本上的SHAP值的分布，如表3所示为所有样本点下的归一化全局SHAP值 $ \bar{\phi } $和XGBoost模型本身的特征重要性I. 结果显示归一化全局SHAP值比XGBoost特征重要性更可靠. 根据全局SHAP值，前1 h冷负荷和室外温度是最重要的输入，时刻和前2 h冷负荷也较为重要，而月份、周几和室外湿度最不重要. 这符合工程经验：历史负荷的影响会随时间的增长而减弱，因此前1 h冷负荷比前2 h冷负荷更重要；室外温度是墙体与室外空气换热的主要因素，而室外相对湿度对冷负荷的影响较小；时刻反映了建筑内人员的变化规律，而人体散热是建筑冷负荷的重要组成部分；月份和周几的影响分别可以通过室外温度和历史负荷反映，因此这2个变量的影响较小. 而根据XGBoost特征重要性，重要输入仅为前1 h和前2 h冷负荷，其他重要变量例如时刻和室外温度的重要程度很低，这是不合理的.

基于表3中各输入的全局SHAP值对归一化后的输入进行加权，然后采用k-means算法对训练集上的残差进行聚类. 为了得到最优的k值，对不同k值下的预测区间估计效果进行比选. 如表4所示为k值分别为2~10，名义置信水平分别为10%~90%（间隔10%）时ACE绝对值的平均值与传统方法^[9]（不进行输入加权）的ACE绝对值的平均值的对比. 表中， $\left| { \overline{ {\rm{ACE} } } } \right| $为ACE绝对值的平均值. 可以看出，当k=3时本研究方法的区间估计效果最佳，此时ACE绝对值的平均值最小，为1.87%；传统方法得到的ACE绝对值的平均值的最优值为2.27%. 表明本研究提出的基于输入加权聚类的方法可以提高预测区间估计的精度.

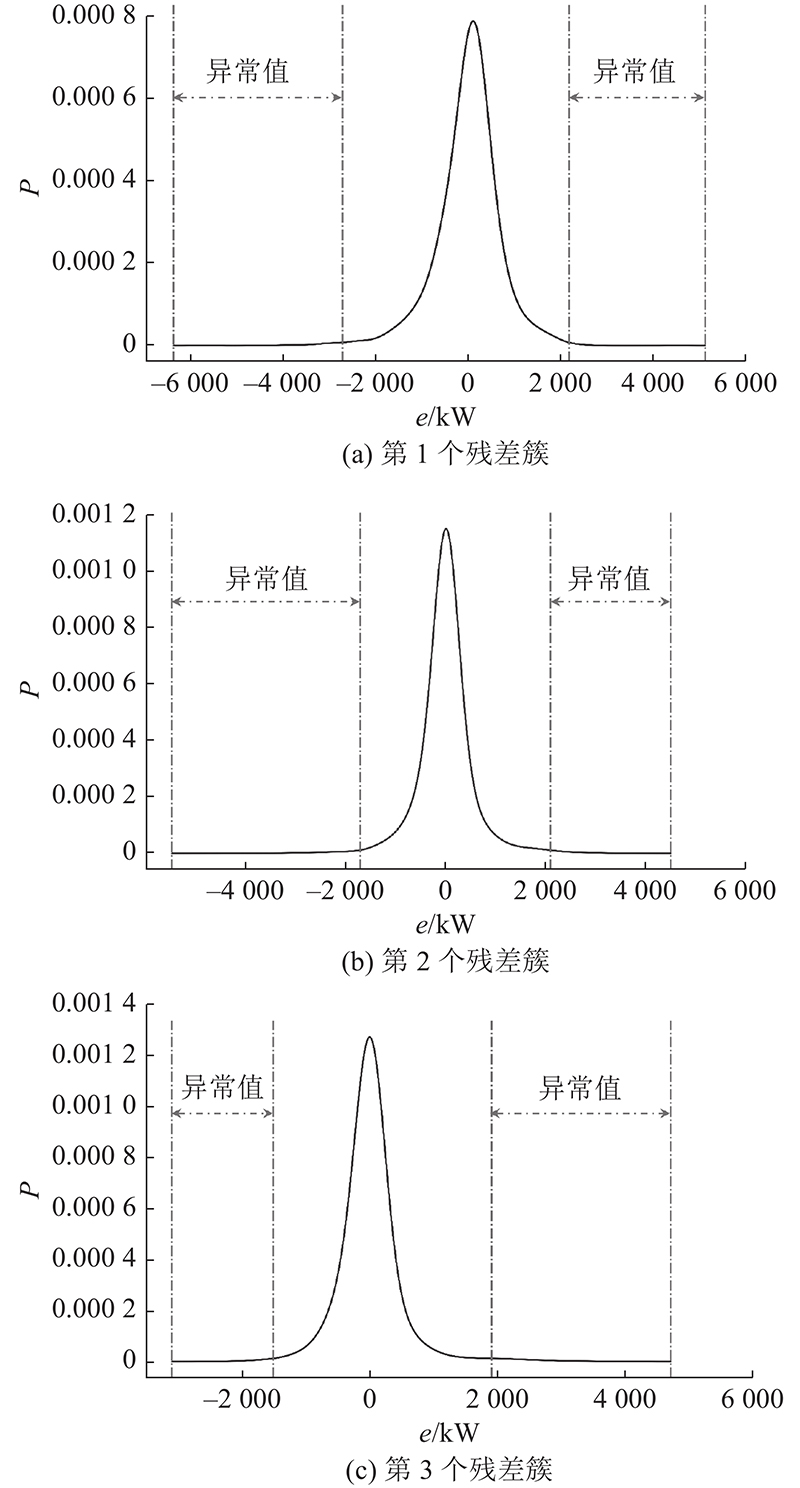
当k=3时，各个残差簇的残差分布如图3所示，其中核密度估计的带宽为200，异常值阈值的缩放因子为0.01. 图中e为预测残差，P为概率密度. 可以看出，不同残差簇中的残差分布各不相同，第1、2、3个残差簇的残差分布范围分别为−2 724.13~2 178.70、−1 710.28~2 095.28、−1515.51~1 904.56 kW.

当k=3时，不同PINC下测试集上的PICP和ACE如表5所示. 可以看出，本研究中提出的预测区间估计方法得到的PICP与PINC十分接近，表明本研究提出的方法十分可靠.

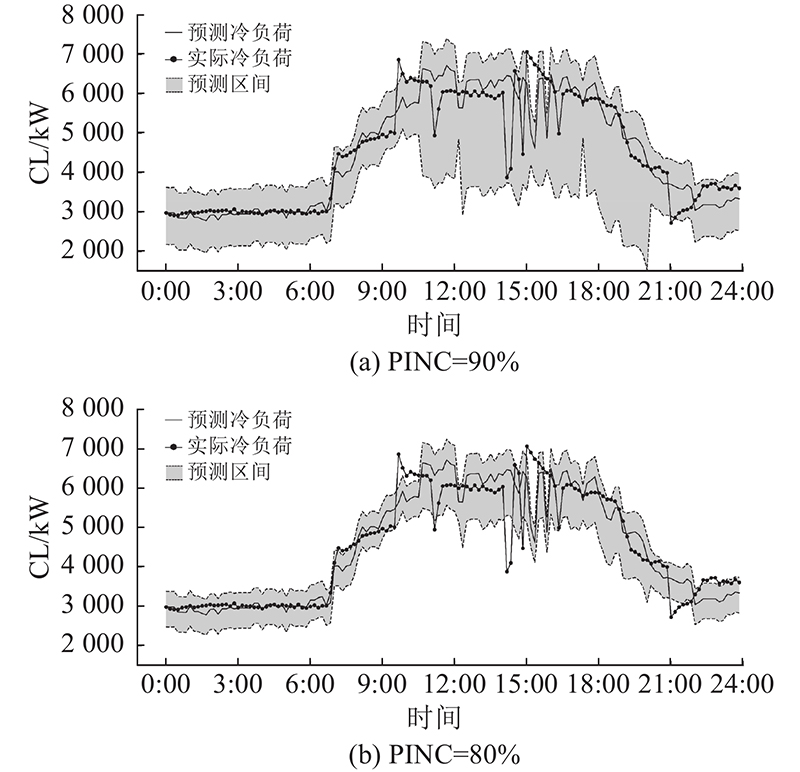
当PINC=80%、90%时，某典型日的预测区间曲线如图4所示. 可以看出，该预测模型在负荷较低时的不确定性较小（预测区间较小），在负荷较高时的不确定性较大（预测区间较大）. 表明本研究提出的方法可以自适应地学习到不同输入下负荷预测模型的不确定性大小.

（1）与传统不对输入进行加权的方法相比，本研究方法可以显著提升预测区间估计的精度. 不对输入进行加权，则ACE绝对值的平均值的最优值为2.27%. 而进行加权后，ACE绝对值的平均值的最优值为1.87%.

（2）在不同输入情况下，模型预测残差的分布存在显著差异. 该方法共得到了3个残差簇，残差簇内的残差分布范围分别为−2 724.13~2 178.70、−1 710.28~2 095.28、−1 515.51~1 904.56 kW，三者存在显著差异.

（3）该方法能够根据模型工况的变化，自适应地估计建筑负荷预测模型的预测不确定性大小. 结果表明，当负荷较低时XGBoost模型的不确定性较小（预测区间较小），当负荷较高时XGBoost模型的不确定性较大（预测区间较大）.

（4）该方法不基于任何残差分布假设，可以用于估计任何数据驱动的建筑负荷预测模型的不确定性. 虽然本研究仅采用了目前最为主流的XGBoost算法对该方法进行了验证，但是理论上如果将XGBoost算法换成其他数据驱动算法，该方法依然适用.

后续工作将围绕更精细化的残差聚类展开，例如可以借鉴分层聚类的思想，先根据时间变量对残差进行分组，然后再根据剩余变量依次对残差进行聚类. 此外，还将进一步论证该预测区间估计方法在本领域其他预测任务上的性能（例如风力发电量和能源价格），并探究该方法在建筑能源系统优化运行和故障诊断中的应用.