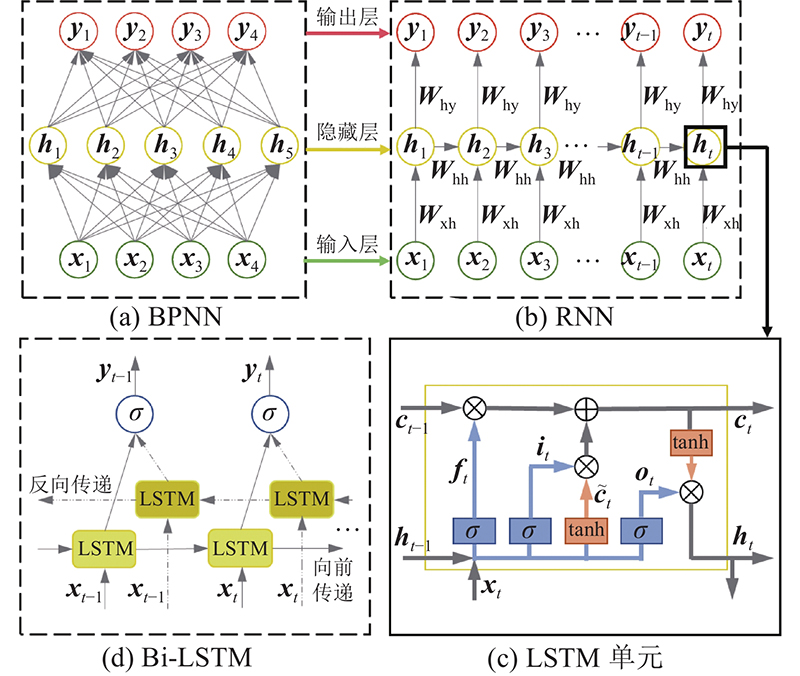
误差反向传播神经网络(back propagation neural network, BPNN)同层间无连接,输入值被相互独立处理,不易学习存在复杂相互关联性的序列问题[6]. 循环神经网络(RNN)具有循环结构的隐藏层,可以将沉降信息按顺序逐次送入网络学习并更新记忆,使得模型更好地理解路堤填筑过程与地基沉降量间复杂的非线性映射关系[10-11]. 长短期记忆网络(long short-term memory,LSTM)通过改进RNN的记忆单元有效避免了梯度消失和爆炸[11],双向长短期记忆网络(bi-directional LSTM, Bi-LSTM)作为LSTM的改进结构,具有较强的处理序列信息的能力,已被广泛应用于滑坡时序位移预测[12]、盾构机稳定掘进参数预测[13]、盾构引发地表最大沉降预测[14]、土体和结构面之间的剪切行为演化[11]等问题.
本文基于Bi-LSTM整合了施工期观测信息进行建模预测. 利用Akima法对“填土高度-时间-地基沉降”进行等时距处理,提取相关的数据特征作为影响因素,组集为符合循环神经网络输入格式的序列样本. 将组集的训练样本送入网络学习,形成地基沉降预测模型. 采用滚动迭代方法进行地基沉降后延更新. 为了体现Bi-LSTM模型的优越性,采用循环网络的LSTM和非循环网络的BPNN,分别与Bi-LSTM模型进行对比.
1. 模型理论
图 1
式中:xt和yt为时间步t的输入与输出;ht和ht−1为时间步t与t−1的隐藏状态;Wxh为输入和隐藏向量间的权重矩阵;Whh为不同时间步隐藏向量间的权重矩阵;Why为隐藏和输出向量间的权重矩阵;bh和by为Whh与Why对应的偏置向量;
式中:ct为存储单元在t时刻的信息;bi、bf、bc和bo为对应的偏置项;σ为Sigmoid激活函数;Wx、Wh、Wc分别为输入与隐藏节点、存储与隐藏节点、存储与输出节点之间的权重矩阵.
式中:
如图1所示为单隐藏层的网络结构. 隐藏层相当于输入信息的特征提取器,对于复杂问题可以堆叠隐藏层以加深网络结构,有利于抽象出更高级的特征,学习到更复杂的非线性关系.
2. 非等时距序列沉降预测方法
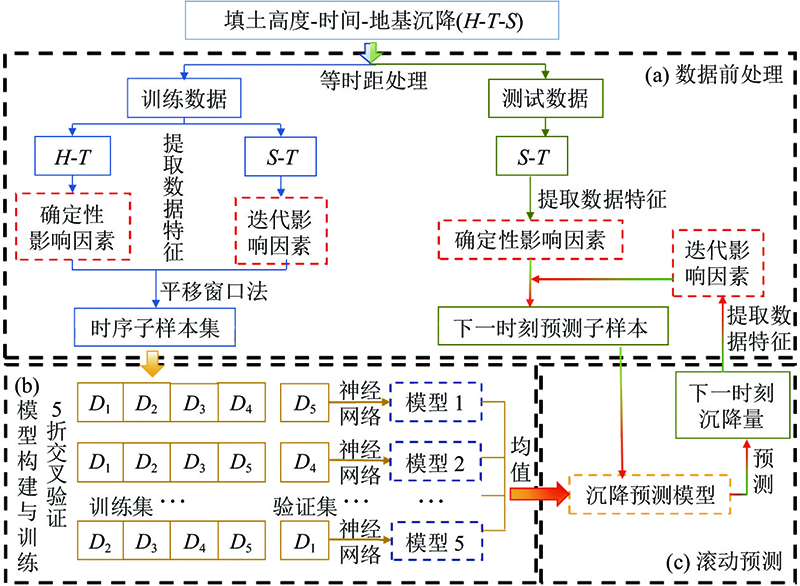
基于非等时距路基沉降观测序列的工后沉降预测方法如图2所示,包括数据前处理、模型构建与训练、滚动预测3部分.
图 2
2.1. 数据前处理
图 3
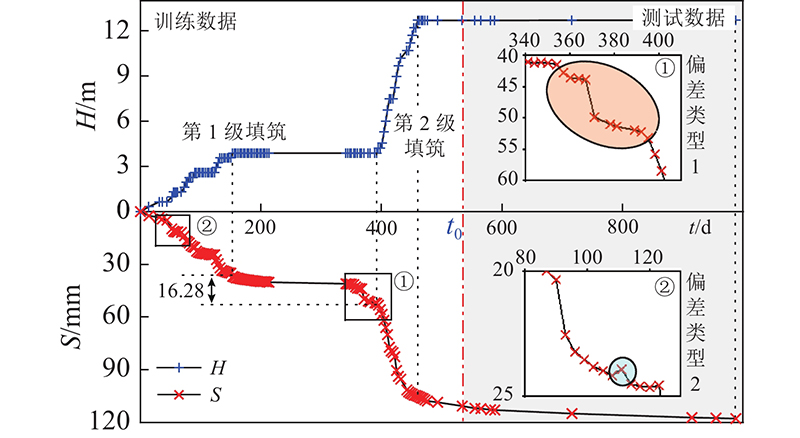
图 3 “填土高度-时间-地基沉降”曲线
Fig.3 Relationship between fill height, time and ground settlement
2) 特征提取. 如图3所示,将等时距后的H-T-S数据分为2个阶段:路堤填筑开始至工后一段时间的数据用于模型训练;除训练数据外的其余工后数据用于预测. 在不显著降低神经网络学习效果的条件下,训练数据应尽可能少,实现地基工后沉降的早期预测.
路堤通常依照设计填筑,预测任意时刻的沉降均可以从H-T曲线上提取对应时刻的数据特征作为确定性影响因素参与预测,如填土高Ht和填土速率vt. 沉降的发展不可以人为设计,如图3所示,对于测试数据部分,预测t+3时刻的沉降时仅能够从T-S曲线上提取到t时刻及以前信息作为影响因素,但t时刻的沉降量须提取t−3时刻及以前信息才能预测,依次反复迭代到沉降信息已知的t0时刻才可以逐步求解t+3时刻的沉降量. 取前3 d沉降速率
3) 样本组集. 用每一时刻的确定性和迭代影响因素向量Gt表征对应时刻的沉降量St,采用平移窗口法将数据组合为一系列长度相等的时序样本dt,如下所示.
式中:
2.2. 模型构建与训练
图 4
建立LSTM和BPNN模型,与Bi-LSTM模型进行对比. LSTM模型与Bi-LSTM模型的结构相似,仅将隐藏层Bi-LSTM单元用LSTM结构进行替换. BPNN模型的输入层节点彼此无关联,须将各时刻时序样本dt拆分为独立变量,在去除重复数据后分别赋给输入层各节点.
2) 模型训练. 为了避免神经网络对训练数据产生过拟合而丧失泛化性能,须将数据划分为训练集和验证集2部分. 将验证集样本的误差近似为泛化误差来调整网络超参数,以期望得到泛化性能良好的模型[18]. 如图2(b)所示,采用五折交叉验证的方法划分总训练样本,以充分利用已知数据并提升模型的学习效果. 具体步骤如下:将总训练样本D划分为大小相似的5个互斥子集,即D = D1∪D2···∪D5,D1∩D2=
2.3. 滚动预测
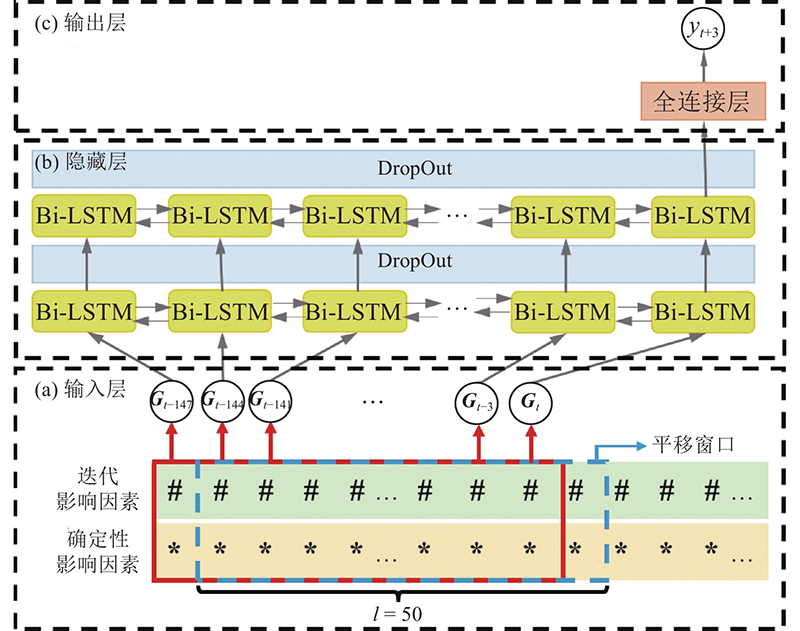
路基下一时刻沉降的发展趋势往往与紧邻时刻的沉降密切相关,但随着时间的发展,相关性会逐步降低,很难通过已知时刻的样本对工后较远时刻的沉降进行精准预测. 为了避免该问题,采用单步沉降预测方法,模型每次只须根据前l个时间步预测相关性最高的下一时刻沉降,如图4所示.
为了实现地基沉降的持续性长期预测,须结合滚动迭代手段来实现,如图2所示,具体的操作步骤如下. 1)向训练好的模型输入测试集的第1组时序样本,即t0+3时刻的
3. 案例分析
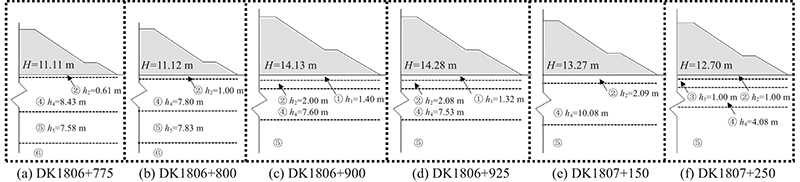
某重载铁路路基DK1806+729~DK1807+325段的地层组成如下:①为Q4dl+pl淤泥质粉质黏土,②为Q4el+dl粉质黏土,③为细角砾土,④~⑥分别为全风化、强风化、弱风化软质千枚岩. 地基土层①和②的粉质黏土压缩系数a1-2为0.1~0.4 MPa−1,为中低压缩性土. 6个观测断面的路堤高度均大于8 m,在路肩以下8 m处设置宽为3 m的平台,平台以下的边坡坡率为1꞉1.75,以上的边坡坡率为1꞉1.5,如图5所示. 图中,h1~h5为从上至下每层地基土的厚度. 采用量程为200 mm的JMDL-4720A型单点沉降计,开展地基面沉降变形测试. 选取水泥搅拌桩加固某高速铁路深厚软土地基沉降观测数据[19],监测断面(K0+180)周围1 m左右的地基表层黏土下分布着15 m厚的淤泥质粉质黏土. 路堤高5.75 m,路肩和边坡下桩间距分别为1.2和1.4 m,桩排距为1.2 m,桩长为12.5~16.5 m,桩径为0.5 m. 路堤中心线地基面处设置多块沉降板,监测路基沉降.
图 5
沉降监测频次在填筑施工期间一般为1次/d,沉降量突变时为2~3次/d,2次填筑间隔较长时为1次/3 d. 路基填筑完成后前3个月为1次/周,4~6个月为1次/2周,6个月后为1次/月. 测试区段的路堤填筑过程与地基沉降发展趋势类似,以DK1807+250断面为主进行分析.
3.1. 数据生成
图 6
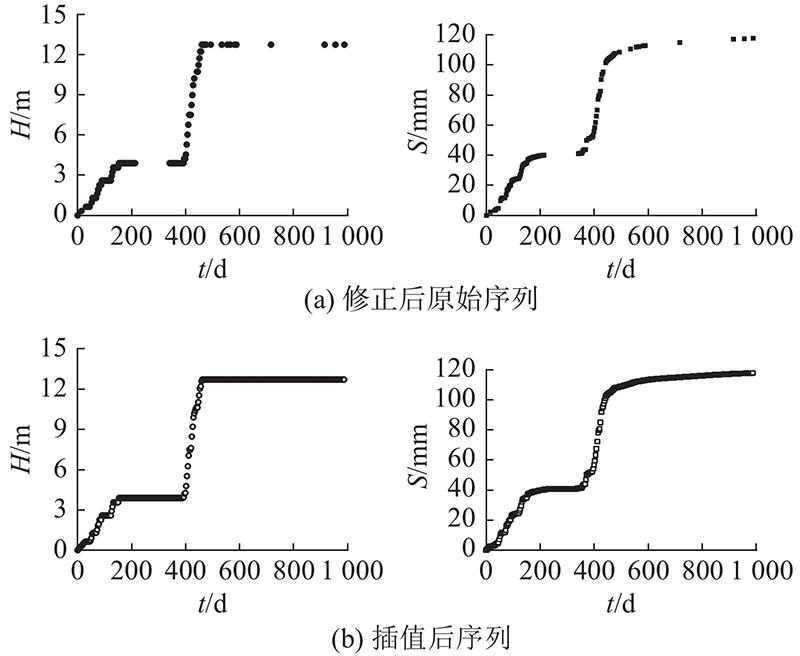
图 6 观测数据的修正与等时距转化
Fig.6 Observational data correction and transformation for equally spaced observations
2) 等时距与标准化. 采用Akima插值法将修正后的非等时距序列观测数据处理为间隔为3 d的等时距序列,DK1807+250断面地基沉降共监测了992 d,将监测数据插值处理为331组数据点. 如图6所示,等时距序列数据与观测数据非常接近. 采用min-max标准化方法对等时距序列数据按式(14)进行处理,使得标准化后的数据
式中:
3) 影响因素变量与数据集生成. 采用灰色关联度(GRG),评价确定性和迭代影响因素变量与地基沉降量间的相关程度. GRG为0~1.0,其大于0.6时两者密切相关;当GRG为0.50~0.60时,两者相关;若GRG小于0.5,则两者不相关[12]. 如表1所示为各影响因素变量与地基沉降量的灰色关联度系数分布,St−3、 St−6、St−9与地基沉降量间的相关性非常高,GRG均大于0.98. vt的GRG大于0.87,与地基沉降量密切相关. 路堤填高Ht与
表 1 各断面的灰色关联度系数分布
Tab.1
| 断面 | | vt | Ht | St−3 | St−6 | St−9 |
| DK1806+925 | 0.59 | 0.96 | 0.58 | 0.99 | 0.99 | 0.98 |
| DK1806+900 | 0.60 | 0.91 | 0.60 | 0.99 | 0.99 | 0.98 |
| DK1806+800 | 0.85 | 0.95 | 0.85 | 0.99 | 0.99 | 0.98 |
| DK1806+775 | 0.76 | 0.87 | 0.77 | 1.00 | 0.99 | 0.99 |
| DK1807+250 | 0.57 | 0.95 | 0.58 | 0.99 | 0.98 | 0.98 |
| DK1807+150 | 0.55 | 0.95 | 0.55 | 0.99 | 0.98 | 0.98 |
输入数据的序列长度l会影响模型的学习及预测能力. 序列长度过短,会导致序列样本内所含信息不完整,网络难以提取到有效特征. 序列过长会使信息特征复杂而难以识别有效特征,从而耗费更多的资源. 路基沉降观测数据具有“分级填筑-填筑间隔”的周期性特征,序列长度的确定应保证多数序列样本所含的信息完整. 如图6所示,DK1807+250断面路堤第1级填筑用时约为150 d,填筑间隔约为200 d,共350 d. 第2级填筑用时约为60 d,取工后3个月为填筑间隔,共150 d. 考虑两级路堤填筑间隔沉降发展缓慢,各影响因素变化不明显,可以取较短周期组集样本,缩短模型训练时间. 按150 d为依据,选取序列长度l为50.
DK1807+250断面的H-T-S数据经插值处理为331组数据,可以组集序列长度为50的时序样本dt共281个. 为了研究初始样本集大小对模型预测性能的影响,按时间顺序分别取前180, 175, 170, ···, 135, 130共11种初始样本量进行分析. 前 130组时序样本恰好对应路堤从开始填筑到工后3个月的数据,每间隔5组样本对应的时间跨度为半个月.
3.2. 模型训练与评估
1) 模型训练. 将初始样本分层抽样为5个不同的独立样本集,采用5折交叉验证手段分别训练5个独立模型,取均值作为输出结果. 神经网络每次训练须随机给各节点赋初始权值,Dropout层在每次迭代过程中会随机舍弃一定比例的神经元,导致网络每次的结果略有差异,因此重复上述交叉验证步骤20次,用平均值来评价模型性能[20]. 采用均方根误差(RMSE)和平均绝对百分误差(MAPE)作为模型性能的评价指标,如下所示:
式中:
实验基于Python语言环境下的TensorFlow -GPU 2.3.0版本深度学习框架,硬件环境如下:CPU为AMD Ryzen™ 7-4800H,内存为16 GB,NVIDIA GeForce RTX 2060显卡.
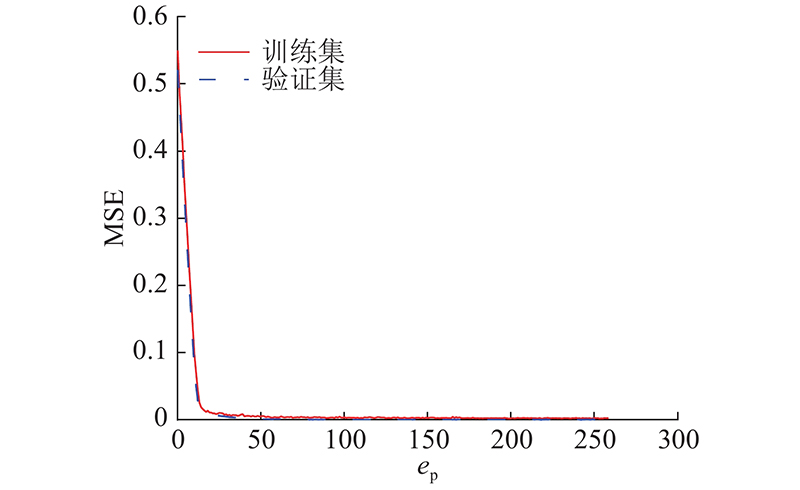
2) 沉降预测模型评估. 以初始样本量为180的样本集为例,展示训练过程. 如图7所示为Bi-LSTM模型在5折交叉验证中不同训练集和验证集上的损失收敛过程. 图中,MSE为均方误差,ep为迭代次数. BPNN、LSTM和Bi-LSTM模型平均须迭代1 200、340和260次. Bi-LSTM对数据进行双向时序特征提取,仅需很少的迭代次数就能达到收敛标准. LSTM的迭代次数稍多,说明单向的特征提取没有充分利用输入信息. BPNN无法对输入信息按时序处理,面对庞大的散乱信息需要成倍的迭代次数才能达到收敛标准.
图 7
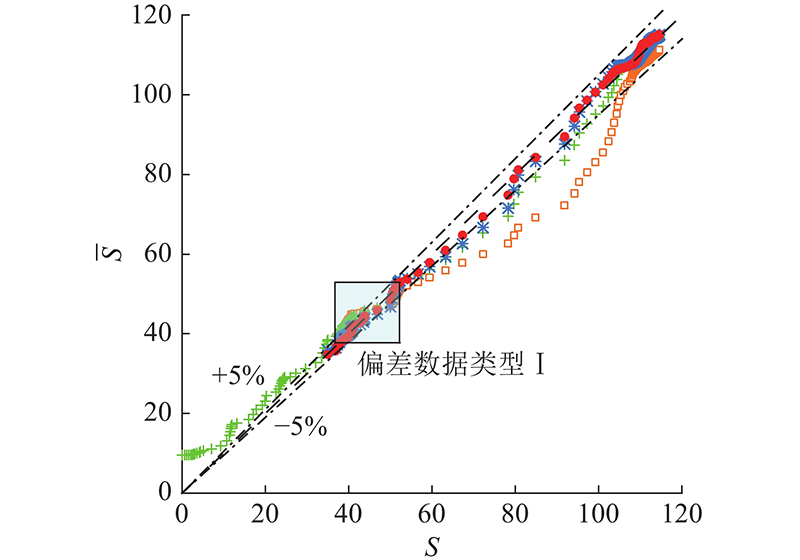
如图8所示为3种模型分别训练20次,在训练集上的平均预测结果. BPNN模型的大部分预测值超出了±5%的误差限,且RMSE为30.04 mm、MAPE为6.29%,误差较大,说明BPNN网络在面对长序列信息时很难提取到相对正确的特征. 减少BPNN模型的输入信息,只保留Ht、St−3、St−6、St−9、St−12、St−15共6个影响因素作为输入. 如图8所示,修正BPNN模型的平均RMSE为7.08 mm,MAPE为4.03%,大幅降低了训练样本的预测误差,表达了地基沉降量与6维影响因素间的非线性回归关系. LSTM模型的RMSE为1.59 mm,MAPE为1.25%,相对误差大部分小于5%,较修正后的BPNN模型误差更小. Bi-LSTM模型的RMSE和MAPE仅为1.03 mm和 1.15%,预测精度最高.
图 8
图 8 地基沉降观测值与预测值的对比
Fig.8 Comparision between observed and predicted values of foundation settlement
如图8所示,在偏差数据类型Ⅰ部分,各模型的预测精度均小于5%,说明所选取的迭代影响因素能够反映施工和环境因素对沉降的影响.
3.3. 预测分析
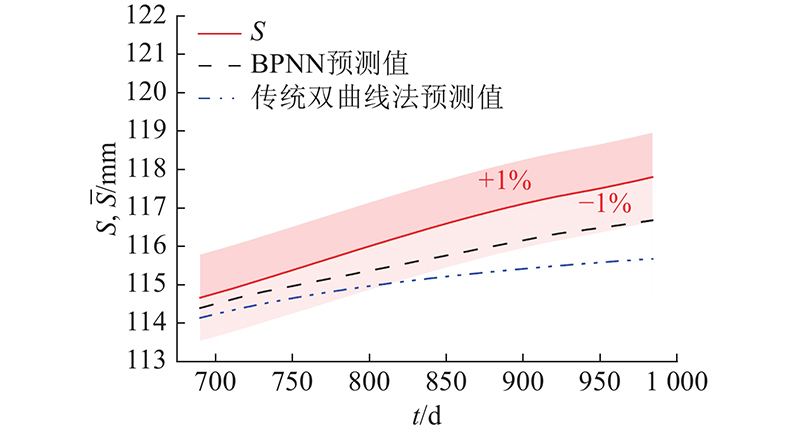
1) 工后沉降预测精度分析. 如图9所示,传统双曲线法无法考虑施工期信息,基于工后240 d内的沉降数据预测发现,825 d后相对误差均超出1%, RMSE为1.91 mm,MAPE为1.10%. 修正BPNN模型可以考虑施工期信息,采用工后240 d以前的沉降观测数据共180组样本进行训练,获得的预测值相对误差<1%,RMSE仅为0. 60 mm,MAPE仅为0.62%,预测效果优于双曲线法. 修正BPNN模型的精度随着滚动迭代而不断降低,主要是因为误差累积导致的.
图 9
图 9 修正BP神经网络模型与双曲线模型的预测结果
Fig.9 Predicted values derived from modified BP neural network model and hyperbolic function model
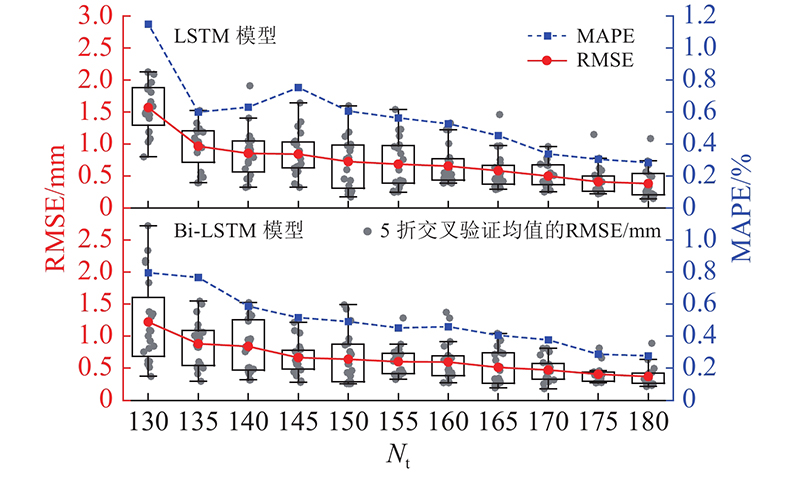
如图10所示,每个点均为对应训练样本集下5个独立交叉验证模型的均值. 图中,Nt为训练集样本组数. 其中,LSTM模型在180组训练样本下,经20次重复训练后平均预测值的RMSE为0.39 mm,MAPE为0.29%,较修正BPNN模型的预测精度有所提高. Bi-LSTM模型平均预测结果的RMSE仅为0.37 mm,MAPE为0.28%,预测精度进一步提升.
图 10
图 10 不同训练集样本下Bi-LSTM模型预测结果
Fig.10 Bi-LSTM based prediction with different training samples
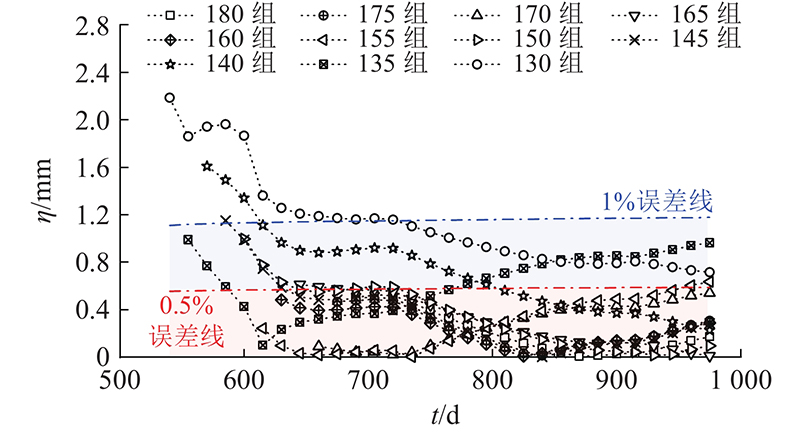
如图11所示为不同训练集样本量下Bi-LSTM模型的绝对误差η. 模型预测误差在450~600 d(路堤填筑完成初期)较大,考虑模型为时序模型,在路堤填筑完成时地基沉降模式发生突变, Bi-LSTM模型受先前信息的影响无法快速转变,随着预测的后延逐步接近观测值. 当样本量大于155组时,相对误差<0.5%,130组时相对误差未超过1%. 对于一般工程和传统预测方法而言,1%的相对误差通常可接受,因此推荐使用工后3个月数据 (130组样本)作为训练样本.
图 11
图 11 不同训练集样本下Bi-LSTM模型的预测绝对误差
Fig.11 Absolute errors of Bi-LSTM model with different training samples
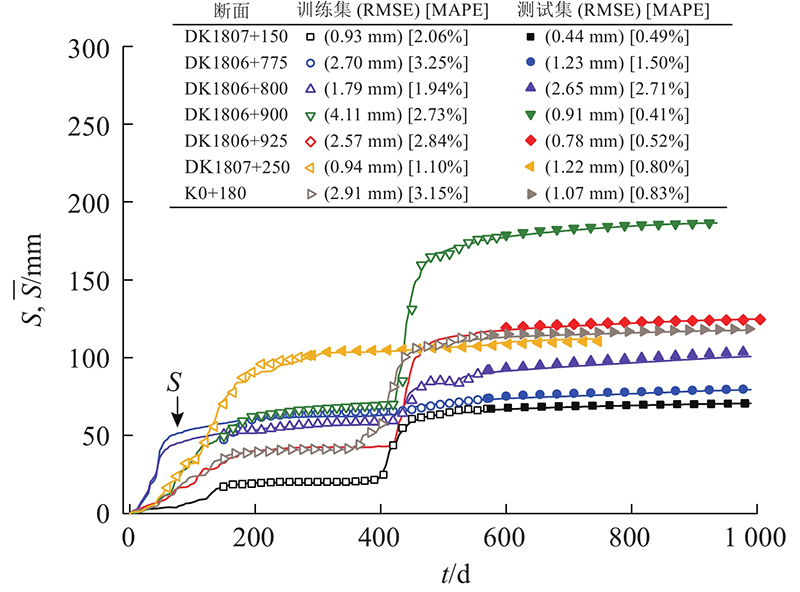
3) 模型适应性评估. 将Bi-LSTM模型应用于其余6个监测断面,训练样本均采用路堤开始填筑至工后3个月数据,预测结果如图12所示. 监测断面测试集的RMSE和MAPE分别为0.44~2.65 mm、0.41%~2.71%,平均值仅为1.19 mm和1.04%,预测精度较高. 其中,DK1806+800断面第2级路堤填筑完成一段时间内(500~600 d)沉降监测信息出现较多的第Ⅱ类数据偏差,Akima法在该部分插值误差较大,导致模型缺失地基沉降模式转变的精确关键信息. 综上所述,Bi-LSTM模型仅利用填筑期及工后3个月信息,可以对工后沉降进行具有较高精度与稳定性的预测.
图 12
图 12 其他断面地基沉降Bi-LSTM模型的预测结果
Fig.12 Bi-LSTM based predictions for foundation settlements in remaining test sections
4. 结 论
(1) 路堤填筑施工具有“分级填筑-填筑间隔”周期性特征,工后沉降可以视为较长的填筑间隔. 采用平移窗口法,将施工填筑数据组集为训练样本;在较短的工后观测时长下可以获得更多的样本,开展神经网络模型训练,有效提升了路基沉降早期预测的可靠性.
(2) 从“填土高度-时间-地基沉降”观测信息中提取全面反映填筑与沉降信息的6维影响因素,采用Bi-LSTM模型按时序进行双向学习. 与样本数据无关联性的BPNN和仅具有单向学习的LSTM模型相比,在更少的迭代次数下Bi-LSTM具有更高精度、更好稳定性的路基沉降量预测效果.
(3) 利用6个中等压缩性土地基和1个水泥搅拌桩加固深厚软土地基的沉降观测数据. 基于Bi-LSTM模型开展路基工后沉降滚动预测,以填筑期及工后3个月的早期信息为训练数据,沉降预测值的RMSE和MAPE分别为1.19 mm、1.04%,多数断面的RMSE和MAPE小于1 mm和1%,具有较高的精度,可以在类似工程中推广应用.
(4) 在突发灾害、极端温度或冻融循环作用下,路基易发生危害较大的不均匀沉降. 本文未考虑该类条件对路基沉降的影响,主要针对地基承载力足够时路基变形收敛的工况,后续工作可以增加温度、降雨、动荷载等因素参与建模和预测.
参考文献
Hyperbolic method for settlements in clays with vertical drains
[J].
Observational procedure of settlement prediction
[J].
高速铁路桥梁桩基工后沉降组合预测研究
[J].DOI:10.3969/j.issn.1000-7598.2011.11.023 [本文引用: 1]
Study of post-construction settlement combination forecast method of high-speed railway bridge pile foundation
[J].DOI:10.3969/j.issn.1000-7598.2011.11.023 [本文引用: 1]
The combination of forecasts
[J].DOI:10.1057/jors.1969.103 [本文引用: 1]
考虑数据异常及新旧程度影响有界性的地基沉降预测方法
[J].
A prediction method of foundation settlement considering anomaly and newness-oldness degree influence boundedness of measured data
[J].
Hybrid meta-heuristic and machine learning algorithms for tunneling-induced settlement prediction: a comparative study
[J].
Application of the Richards model for settlement prediction based on a bidirectional difference-weighted least-squares method
[J].
Study on settlement prediction model of deep foundation pit in sand and pebble strata based on grey theory and BP neural network
[J].DOI:10.1007/s12517-020-06232-7
Field performance of a genetic algorithm in the settlement prediction of a thick soft clay deposit in the southern part of the Korean peninsula
[J].
基于神经网络和双曲线混合模型的高速公路沉降预测
[J].
Highway subsidence prediction based on neural network and hyperbolic hybrid model
[J].
BiLSTM-based soil–structure interface modeling
[J].
Time series analysis and long short-term memory neural network to predict landslide displacement
[J].
基于BLSTM-AM模型的TBM稳定段掘进参数预测
[J].
Predicting boring parameters of TBM stable stage based on BLSTM networks combined with attention mechanism
[J].
基于循环神经网络的盾构隧道引发地面最大沉降预测
[J].
Prediction of maximum ground settlement induced by shield tunneling based on recurrent neural network
[J].
Long short-term memory
[J].DOI:10.1162/neco.1997.9.8.1735 [本文引用: 1]
Forecast of short-term daily reference evapotranspiration under limited meteorological variables using a hybrid bi-directional long short-term memory model (Bi-LSTM)
[J].DOI:10.1016/j.agwat.2020.106386 [本文引用: 1]
A new method of interpolation and smooth curve fitting based on local procedures
[J].DOI:10.1145/321607.321609 [本文引用: 1]
Metamodel-based reliability analysis in spatially variable soils using convolutional neural networks
[J].DOI:10.1061/(ASCE)GT.1943-5606.0002486 [本文引用: 3]
Machine learning–based uncertainty modelling of mechanical properties of soft clays relating to time-dependent behavior and its application
[J].