土石坝是被广泛应用的挡水构筑物. 极端天气导致洪水灾害频发，大量土石坝由于漫顶而发生坝体溃决，对人类的生命和财产安全造成巨大影响. 2020年5月19日，美国密歇根州伊登维尔大坝决堤，下游米德兰县发生严重洪灾，约10000人被疏散^[1-2]. 研究土石坝溃决过程对减轻下游淹没区的损失意义重大.

对土石坝溃决过程的研究主要有2种方法：模型试验、数值模拟. 相较于模型试验，数值模拟具有成本低、结果快速获取和能够进行各种工况计算等优点，已被广泛地应用于土石坝的溃决分析. 根据土石坝溃决模型的特点可将数值模拟方法分为3大类^[3-4]：参数模型、简化物理模型和精细物理模型. 参数模型是统计模型，即通过统计分析已有的溃坝历史资料，建立最终溃口宽度、溃口峰值体积流量(注：下文表述流量均为体积流量)以及溃决时间与土石坝特征参数(坝体高程、库容、水位等)的回归方程. 梅世昂等^[5]建立包含全球共154个溃坝案例的数据库，通过选取相关参数进行回归分析，最终创建可以模拟土石坝溃决峰值流量和最大溃口宽度的数学模型. 这类模型没有考虑水流冲蚀坝体的物理机制，同时由于溃坝实测数据的短缺和难以获得，导致模型对参数极其敏感，在某些特定条件下甚至产生不符合实际的计算结果^[6]. 简化物理模型也称为分析模型，其通过假定溃口的形状(梯形、矩形、三角形)，基于冲蚀公式和边坡失稳分析模拟溃口的发展过程，采用堰流或孔流公式计算溃口流量^[7]. Zhong等^[8]比较3种简化物理模型NWS BREACH、HR BREACH及DL BREACH的模拟能力，得出DL BREACH总体模拟效果最好，同时认为简化物理模型比参数模型的模拟效果更好且可以提供更多详细结果. 尽管简化物理模型被广泛使用，但其没有充分考虑土石坝溃决的物理机制^[9-10]，为此有学者提出精细物理模型，这类模型以一维模型和二维模型为主. 傅旭东等^[11]在Wang等^[12]的研究基础上，通过减少模型参数建立可以模拟泥沙冲淤过程的一维模型；Liu等^[13]考虑泥沙输移过程建立水深平均二维模型. 现有的精细物理模型大多通过求解浅水方程、泥沙输移方程和底床变形方程来详细模拟溃口发展与坝体溃决过程^[14]. 精细物理模型一方面对泥沙输移方程的求解较为复杂且相对耗时，另一方面输沙率是泥沙输移方程的关键参数，现有的输沙率计算公式在恒定均匀流、输沙强度不大、河床变形缓慢条件下得到广泛的验证，但将其直接用于土石坝溃决模拟还存在一定的误差.

本研究基于线性冲蚀公式，建立二维非黏性土石坝溃决模型并对坝顶高程、最终溃口宽度和峰值流量等参数的预测结果进行验证.

水动力模型的控制方程是具有守恒形式的二维浅水方程：

(1) $ \frac{\partial {\boldsymbol{q}}}{\partial t}+\frac{\partial {{\boldsymbol{f}}}}{\partial x}+\frac{\partial {{\boldsymbol{g}}}}{\partial y}={\boldsymbol{S}}_{0}+{\boldsymbol{S}}_{\mathrm{f}}. $

(2) $\begin{split} &\boldsymbol{q}={\left[\eta ,uh,vh\right]}^{{\rm{T}}} \text{，} \boldsymbol{f}={\left[uh,{u}^{2}h+0.5g{h}^{2},{uvh}\right]}^{{\rm{T}}},\\ &\boldsymbol{g}= {\left[vh,uvh,{v}^{2}h+0.5g{h}^{2}\right]}^{{\rm{T}}} ,\\ &{\boldsymbol{S}}_{0}={\left[0,-gh\frac{\partial \text{z}_{\mathrm{b}}}{\partial x},-gh\frac{\partial \text{z}_{\mathrm{b}}}{\partial y}\right]}^{\mathit{{\rm{T}}}},\;\\ &{\boldsymbol{S}}_{\mathrm{f}}={\left[0,-gh\frac{{n}_{{\rm{f}}}^{2}u\sqrt{{u}^{2}+{v}^{2}}}{{h}^{4/3}},\;-gh\frac{{n}_{{\rm{f}}}^{2}v\sqrt{{u}^{2}+{v}^{2}}}{{h}^{4/3}}\right]}^{{\rm{T}}} . \end{split} $

式中：t为时间，x、y分别为水平的横向和纵向坐标，q为守恒变量，f、g分别为x、y方向的通量；S₀为底床坡度源项，S_f为底床摩阻源项，η为水位，u、v分别为x、y方向的水深平均流速，h为水深，g为重力加速度，z_b为底床高程；n_f为曼宁系数.

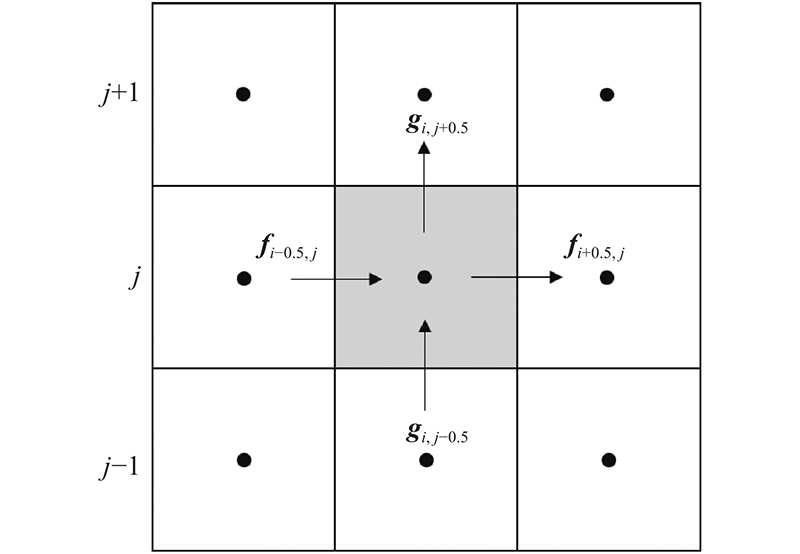
如图1所示，采用基于结构网格的有限体积法对控制方程进行离散：

(3) $\begin{split} &{{\boldsymbol{q}}}_{i,j}^{k+1}={{\boldsymbol{q}}}_{i,j}^{k}-\frac{\Delta t}{\Delta x}\left({{\boldsymbol{f}}}_{i+0.5,j}-{{\boldsymbol{f}}}_{i-0.5,j}\right)-\\ &\;\;\;\;\;\;\;\;\;\; \frac{\Delta t}{\Delta y}\left({{\boldsymbol{g}}}_{i,j+0.5}-{{\boldsymbol{g}}}_{i,j-0.5}\right)+\Delta t\left({{\boldsymbol{S}}}_{0}+{{\boldsymbol{S}}}_{f}\right) . \end{split}$

式中：i，j为单元的序号，k为时间步，Δx、Δy分别为网格x、y方向的尺寸，Δt为时间步长，f_{i+0.5, j}、f_i−0.5,j、g_{i, j+0.5}、g_{i, j−0.5}为单元界面的通量. 浅水方程的离散求解采用显式算法，为了保证计算的稳定性，Δt需要满足柯朗-弗里德里希斯-列维条件（Courant–Friedrichs–Lewy condition，CFL）. 界面通量采用中心迎风格式求解，该格式无须求解黎曼问题，具有计算速度快、精度高的优点. 底床坡度源项的离散采用中心差分格式，底床摩阻源项采用半隐格式进行离散，水动力模块求解的更多细节参见文献[15]、[16].

基于水流切应力的线性冲蚀率公式模拟坝体非黏性泥沙的侵蚀过程：

(4) $ \frac{{\partial {z}}_{\mathrm{b}}}{\partial t}=-\frac{E}{1-p}\text{；} $

(5) $ E = \left\{ {\begin{array}{*{20}{l}} {{k_{\rm{d}}}\left( {\tau - {\tau _{\rm{c}}}} \right),\;\tau > {\tau _{\rm{c}}}\;;}\\ {0{\rm{, }}\;\; \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\tau\leqslant{\tau _{\rm{c}}}.} \end{array}} \right. $

式中：p为材料的孔隙度；E为侵蚀速率，即单位时间单位面积的泥沙侵蚀量；k_d为坝体泥沙的冲蚀系数；τ_c为坝体泥沙起动切应力；τ为水流对底床的切应力，计算式为

(6) $ \tau =\gamma \frac{{n}_{{\rm{f}}}^{2}\left({u}^{2}+{v}^{2}\right)}{{h}^{1/3}}. $

式中：γ为水的重度. 对时间采用向前积分，式 (4) 对应的离散形式为

(7) $ {z_{\mathrm{b}}}_{i,j}^{k+1}={{z}_{\mathrm{b}}}_{i,j}^{k}-\frac{E\left({\tau }_{i,j}\right)}{1-p}\mathrm{\Delta }t. $

由式（7）可知，当水流切应力大于临界切应力时，地形高程会发生改变. 为了提高计算效率，本模型仅对坝体区域进行侵蚀计算. 同时，由式（4）可知，本模型只考虑坝体泥沙的冲刷过程，没有考虑泥沙在下游的沉积过程，即假设坝体泥沙直接被水流冲走未在下游沉积.

边坡坍塌的模拟方法主要有2类^[3]，1）分别给定水面上、下单元的临界坡度，其值一般取为泥沙的休止角的正切值；2）基于土体稳定性分析方法进行失稳判断. 本模型采用方法1）：根据单元的干湿情况，将单元的休止角φ_c分别设置成干休止角φ_c,dry和湿休止角φ_c,wet. 当底床坡度角φ大于休止角φ_c时，边坡发生坍塌，形成新的底床坡度角φ_dep,该角度一般设定为单元休止角φ_c. 如图2所示为边坡坍塌过程示意图，考虑计算单元i以及四周相邻的8个计算单元，当单元i与任一相邻计算单元间的坡度角φ_k大于休止角φ_c时，发生坍塌形成新的坡度角，整个边坡坍塌过程可以表示为

(8) $ \frac{\left({z}_{\mathrm{b}i}+\Delta {z}_{\mathrm{b}i}\right)-({z}_{\mathrm{b}j}+\Delta {z}_{\mathrm{b}j})}{\Delta {l}_{ij}}=\pm \mathrm{t}\mathrm{a}\mathrm{n}\varphi _{\mathrm{c}}. $

式中：z_bi、z_bj分别为边坡坍塌发生前单元i、相邻单元j的底床高程，∆z_bi、∆z_bj分别为单元i、j处因边坡坍塌产生的底床高程改变量，∆l_ij为计算单元i、j间的水平投影距离. 等式右侧的正号表示边坡下降方向为单元j到单元i，负号则相反.

为了保证边坡坍塌过程中泥沙量守恒，单元高程变化引起的泥沙体积改变量应等于0：

(9) $ {\Delta {z}}_{\mathrm{b}i}\Delta {A}_{i}+\sum\nolimits_{j=1}^{{J}_{{\rm{up}}}}\Delta {z}_{bj}\Delta {A}_{j}=0. $

式中：∆A_i、∆A_ji分别为单元i、j的面积. 将式(8)进行移项，并带入式(9),可以得到

(10) $ \Delta {z}_{\mathrm{b}i}=\frac{\displaystyle\sum\nolimits_{j=1}^{{J}_{{\rm{up}}}}\Delta {A}_{j}({z}_{\mathrm{b}j}-{z}_{\mathrm{b}}\pm \Delta {l}_{ij}{\rm{tan}}{\varphi}_{\mathrm{c}})}{\Delta {A}_{i}+\displaystyle\sum \nolimits_{j=1}^{J{\rm{up}}}\Delta {A}_{j}}. $

局部改变单元的高程可能会导致附近其他单元坡度失稳，因此上述边坡坍塌算法须在整个计算网格中迭代多次，直到任意2个相邻计算单元间的坡度角均不超过休止角为止.

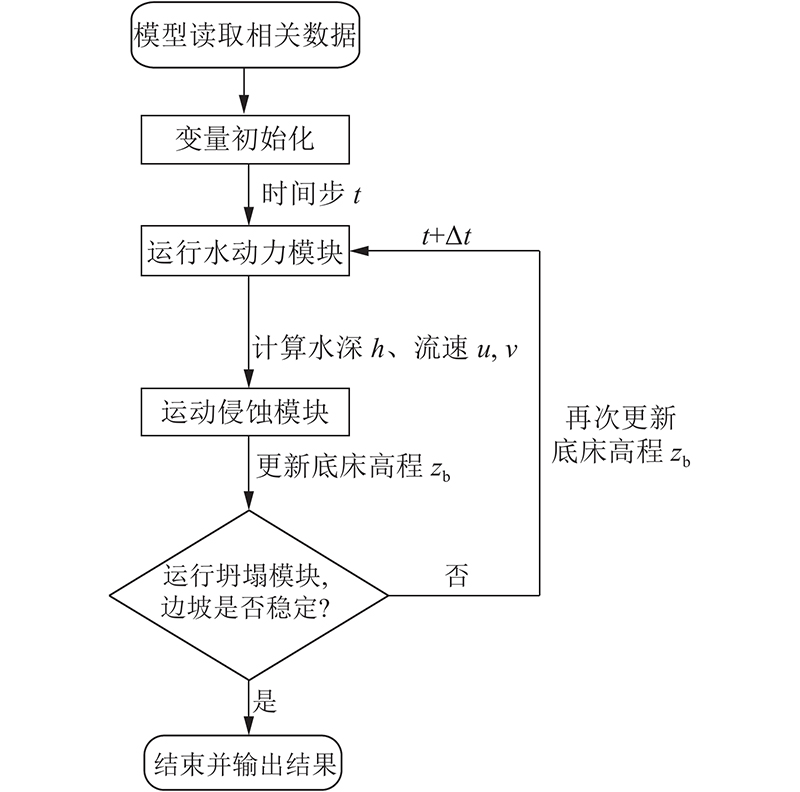
模型的求解过程如图3所示，主要步骤为1）读取相关数据，包括地形数据、边界条件以及模型相关参数；2）利用水动力模块计算得到每个单元的水深h、流速u、v；3）由式（6）计算水流对底床的切应力τ，由式（5）计算侵蚀速率E，由式（4）更新每个计算单元的高程z_b；4）判断是否需要激活边坡坍塌模块，如果需要，则利用边坡坍塌模块进一步更新单元底床高程z_b；5）回到步骤3）开始新时间步的计算，直到整个模拟结束，输出相应计算结果.

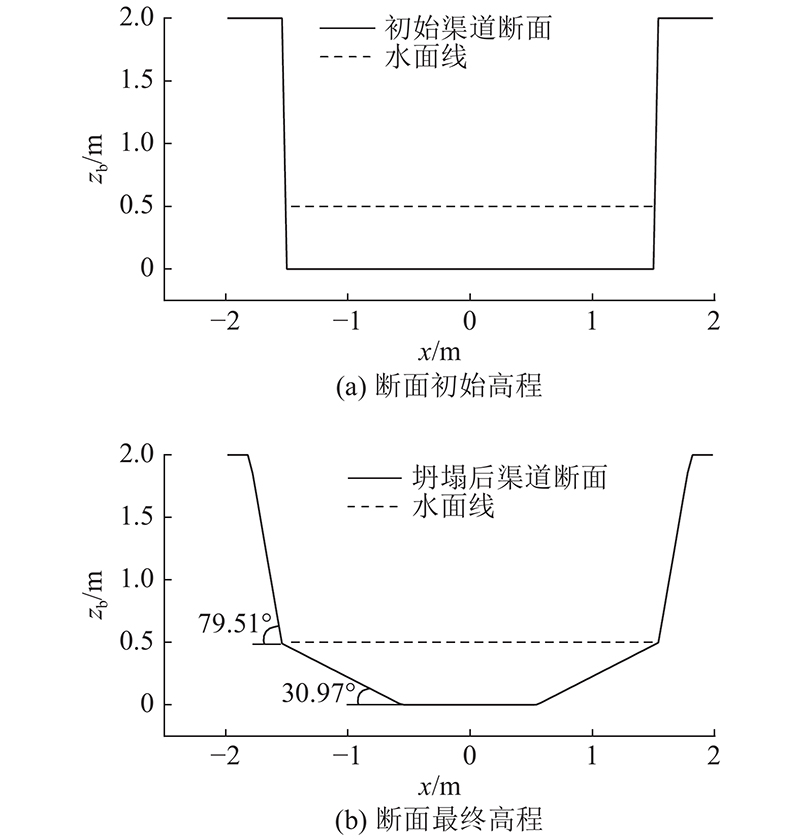
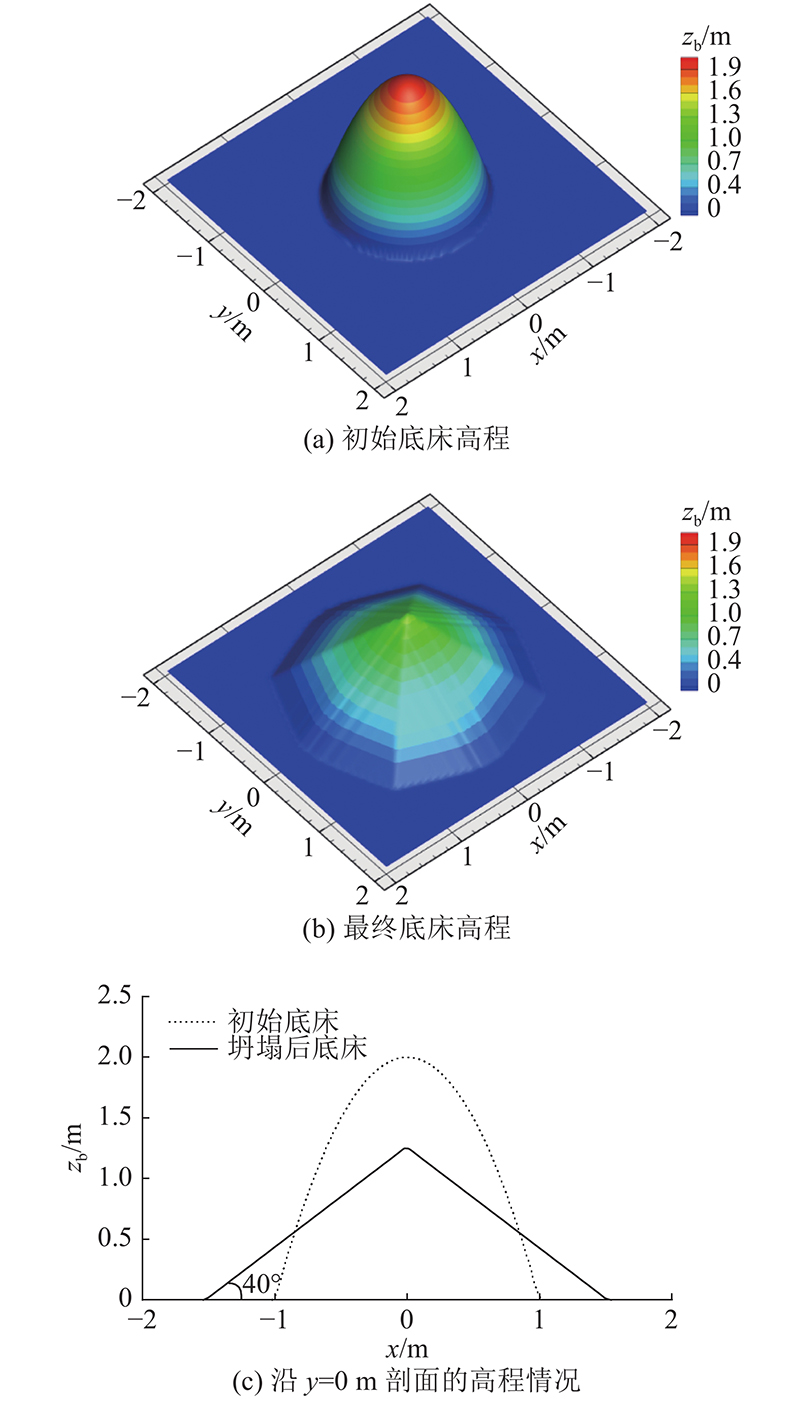
用2个算例验证所采用的边坡坍塌模型的准确性和有效性. 如图4所示为棱柱形渠道断面边坡坍塌计算，图4 (a)为渠道的初始断面高程，渠道内的水深为0.5 m，设定φ_c,dry=80°、φ_c,wet=31°. 图4 (b)为边坡坍塌模型计算后的断面高程情况. 可知，经边坡坍塌模型计算后水上、水下坡度角分别为79.51°和30.97°，与给定的休止角基本一致，表明本模型能够用于一维边坡坍塌计算. 为了进一步验证坍塌模型对于二维边坡坍塌计算的有效性，设计如图5所示的半椭球形隆起的边坡坍塌算例. 假设在2 m×2 m的平面上有一半椭球形隆起，图5 (a)为初始地形高程，设φ_c,dry=40°. 图5 (b)为边坡坍塌模型计算后的地形高程，图5 (c)为初始时刻和计算后y = 0 m剖面的高程情况，可知，计算得到的最终高程坡度与所设定的休止角几乎一致，表明本模型同样能够用于二维边坡的坍塌计算.

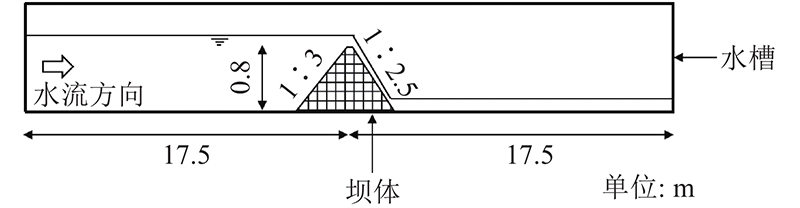
选用Tingsanchali等^[17]开展的一维土石坝漫顶溃决实验验证模型的准确性. 如图6所示，实验在35 m长、1 m宽的矩形水槽内进行. 在距离上游17.5 m处布置0.8 m高的土石坝，坝顶宽度为0.3 m，坝体上下游坡度比分别为1.0∶3.0、1.0∶2.5，同时在坝顶设置挡水板，坝体为非黏性泥沙，泥沙粒径d₅₀ = 0.86 mm、d₃₀ = 0.52 mm、d₉₀ = 3.80 mm、d_m = 1.13 mm，泥沙密度ρ_s = 2 650 kg/m³. 在水槽上游端设置恒定进水为水库蓄水，流量为1.23 L/s，当水库水位高于坝顶高程为3 cm时，撤掉挡水板，水流开始漫过坝顶流向下游，坝体发生溃决.

计算区域采用矩形网格进行离散，网格尺寸为∆x = ∆y = 0.05 m. 总的模拟时间为120 s，时间步长由CFL条件控制. 其他参数设置如下：底床泥沙孔隙度p = 0.4，Wu^[10]指出休止角可根据泥沙类型估算，一般沙子的休止角为32°~38°. 考虑到泥沙中水的质量分数、泥沙密实程度、化学组分等影响，实际休止角可能会与上述建议值相差3°~6°. 根据Wu^[10]的建议，并结合学者在已有精细物理模型中的取值^[18-20]，取泥沙的湿休止角φ_c,wet = 30°，干休止角φ_c,dry = 50°. 曼宁系数n_f= 0.018 m^−1/3·s. 根据Hanson等^[21]的研究，当筑坝材料为低黏性泥沙时，冲蚀系数k_d取值范围为100~800 cm³∙N⁻¹∙s⁻¹, 起动切应力τ_c取值范围为1.0×10⁻³~1.0×10⁻¹ Pa. 对于τ_c，分别选择1.0×10⁻³、1.0×10⁻²、1.0×10⁻¹ Pa进行初步计算，发现τ_c的改变对于模拟结果几乎没有影响，因此设τ_c=1.0×10⁻² Pa，k_d分别为300、400、500 cm³∙N⁻¹∙s⁻¹.

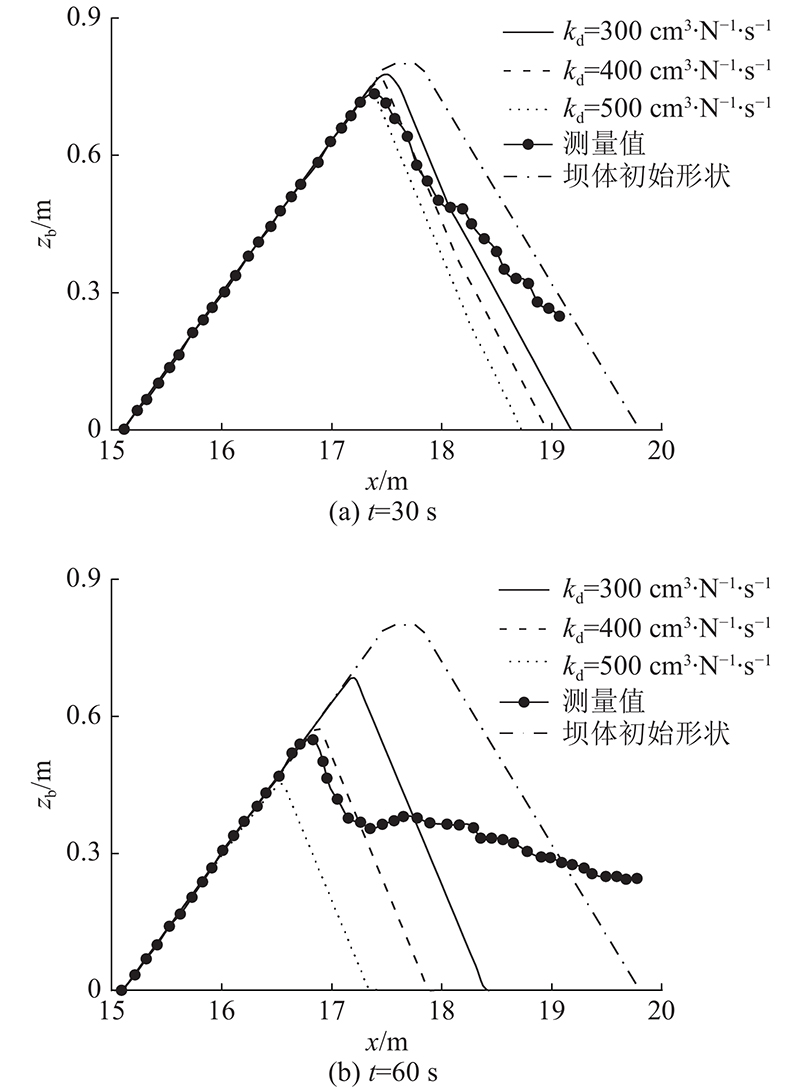
如图7所示分别为t = 30、60 s时，不同冲蚀系数时坝体纵断面高程计算值和测量值的对比结果. 可知，当k_d = 400 cm³∙N⁻¹∙s⁻¹时，模拟结果与测量结果吻合最好，且k_d越大，坝体侵蚀速度越快. 此外，当t = 60 s时，计算得到的坝体下游坡度大于测量值. 主要原因是本模型的泥沙侵蚀模块仅考虑泥沙的侵蚀机制，没有考虑泥沙沉降机制. 在计算模型中，假定坝体泥沙直接被水流冲走未在下游沉积. 由实验数据可知，水流侵蚀坝体产生的泥沙会随着流速减小以及泥沙颗粒自身重力作用逐渐在下游沉降，使得坝体下游坡面的坡度变缓，因此，模型计算得到下游坝体形状与实测值有一定的偏差. 尽管本模型忽略沉降机制，但其仍然能够较为准确地预测坝顶高程的变化过程.

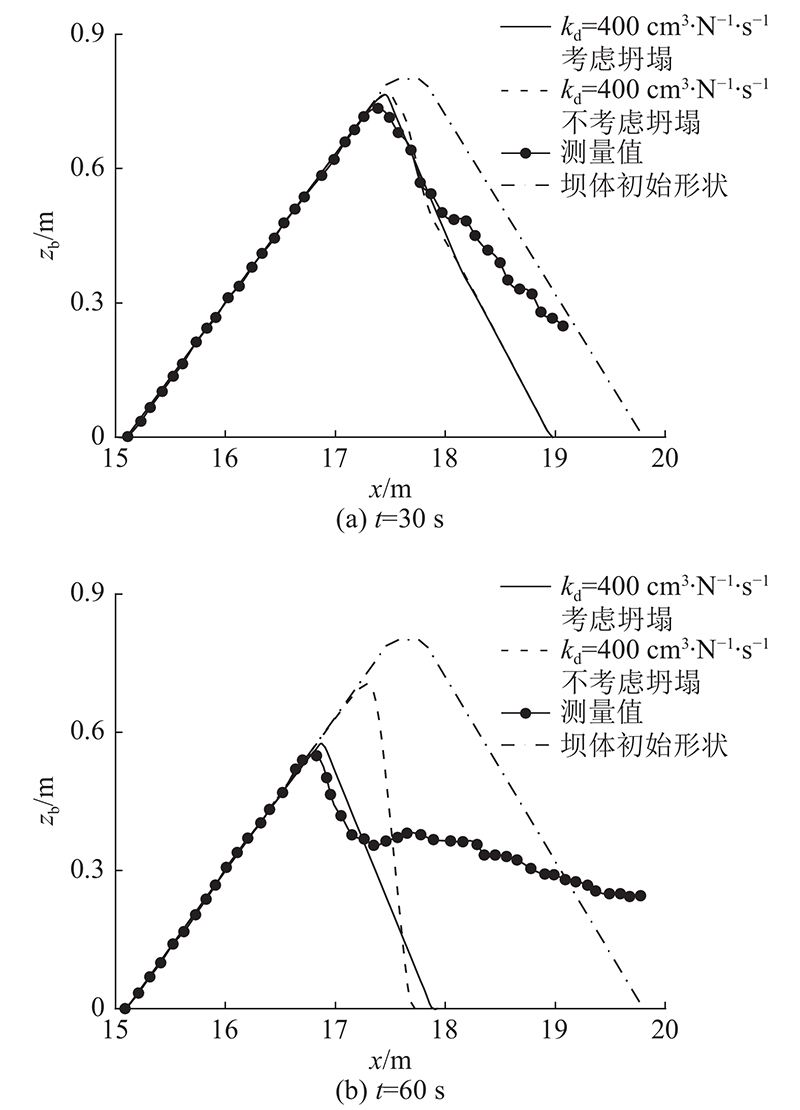
如图8所示为k_d = 400 cm³∙N⁻¹∙s⁻¹时模型分别考虑和不考虑边坡坍塌模块计算得到的坝体纵断面高程. 当t = 30 s时，考虑和不考虑边坡坍塌模块的计算结果基本一致. 当t = 60 s时，不考虑边坡坍塌模块计算所得的坝顶高程远大于测量值，同时坝体下游的坡度非常陡. 因此，该结果一方面表明对于坝体溃决的模拟需要考虑边坡坍塌过程，另一方面也进一步证明本研究所用的边坡坍塌模块算法的有效性.

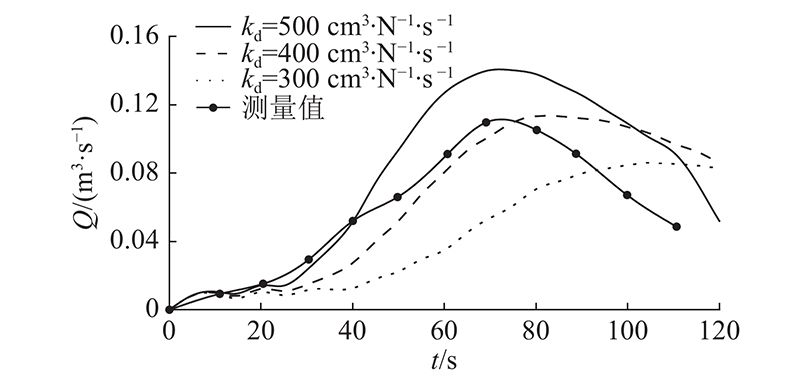
如图9所示为不同冲蚀系数时流量过程线计算值和测量值的对比. 可知，随着冲蚀系数增大，峰值流量计算值也会增大. 当k_d = 400 cm³∙N⁻¹∙s⁻¹时，计算得到的峰值流量以及峰值流量之前的流量过程线与测量值吻合较好，但峰值流量后的流量过程线大于测量结果，存在一定的误差，原因可能是后期计算得到的坝体下游地形高程与实测结果相差较大，影响流量计算结果的准确性.

为了进一步评估模型其他参数对模型计算结果的影响，对n_f、τ_c、φ_c,dry、φ_c,wet进行敏感性分析，结果如表1所示. 表中，Q_max为峰值流量，δ_m为计算值与测量值的相对误差，δ_r为与参照的相对误差，z_bf为最终坝顶高程. 参照组采用参数设置为n_f = 0.018 m^−1/3·s, τ_c = 10⁻² Pa, k_d = 400 cm³·N⁻¹·s⁻¹,φ_c,wet = 30°, φ_c,dry = 50°. 可知，参照组计算得到的峰值流量和60 s时坝顶高程与测量值误差均不超过7%；n_f增大将导致峰值流量增大及60 s时坝体高程降低，φ_c,wet增大则会减小峰值流量并增大60 s坝顶高程. τ_c对于计算结果没有影响，主要原因是水流对底床产生的剪切力 $\tau \gg1$Pa，在本算例中，坝体所有的单元都是湿单元，因此改变φ_c,dry对侵蚀同样没有影响.

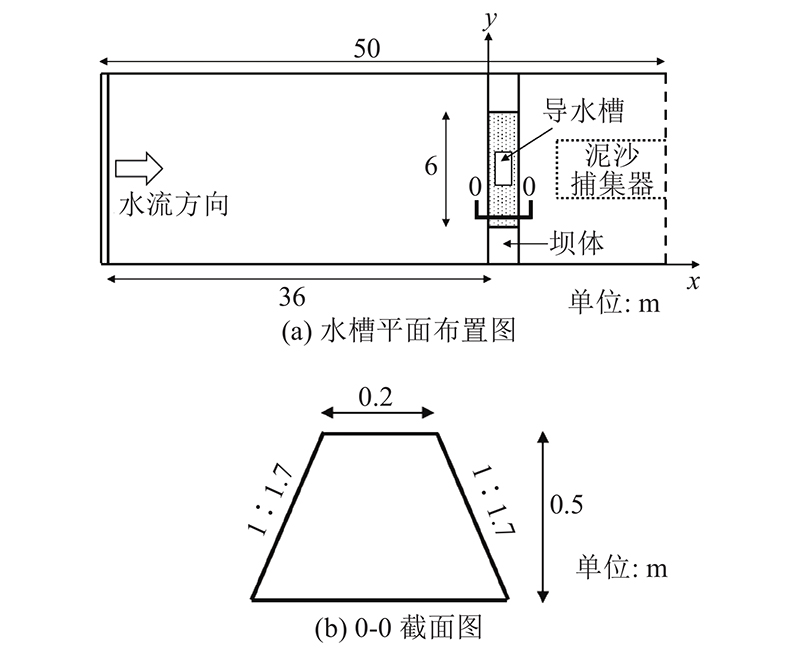
为了进一步验证模型对于坝体溃口横向扩展模拟的准确性，对Morris等^[22]在HR Wallingford实验室开展的2号溃坝实验进行模拟计算. 实验在50 m长， 10 m宽的水槽中进行，实验布置如图10所示. 在距离上游进水口36 m处布置土石坝，坝体高程0.5 m，坝顶宽度为0.2 m，上下游坡度均为1.0∶1.7. 坝体材料为非黏性沙，实验中分别使用宽级配沙与窄级配沙，2种沙的平均粒径相同，均为0.25 mm. 在坝顶中间设有导流槽，该槽的深度为0.02 m，宽度为0.152 m. 通过水泵向上游水库以恒定流注水，入库流量为0.07 m³/s，当水库内水位高于导流槽高程时，水流漫过导流槽，溃坝过程开始. 采用1 000×200个矩形网格划分计算区域，单元尺寸为∆x = ∆y = 0.05 m，其他参数设置如下：坝体非黏性沙的孔隙度p = 0.4，φ_c,wet = 31°，φ_c,dry = 50°. 根据Wu等^[23]的建议，曼宁系数设置用0.018 m^−1/3·s. 此外，基于Hanson等^[21]给定的低黏性泥沙冲蚀系数取值范围，将k_d、τ_c分别设置为200 cm³∙N⁻¹∙s⁻¹、10⁻² Pa.

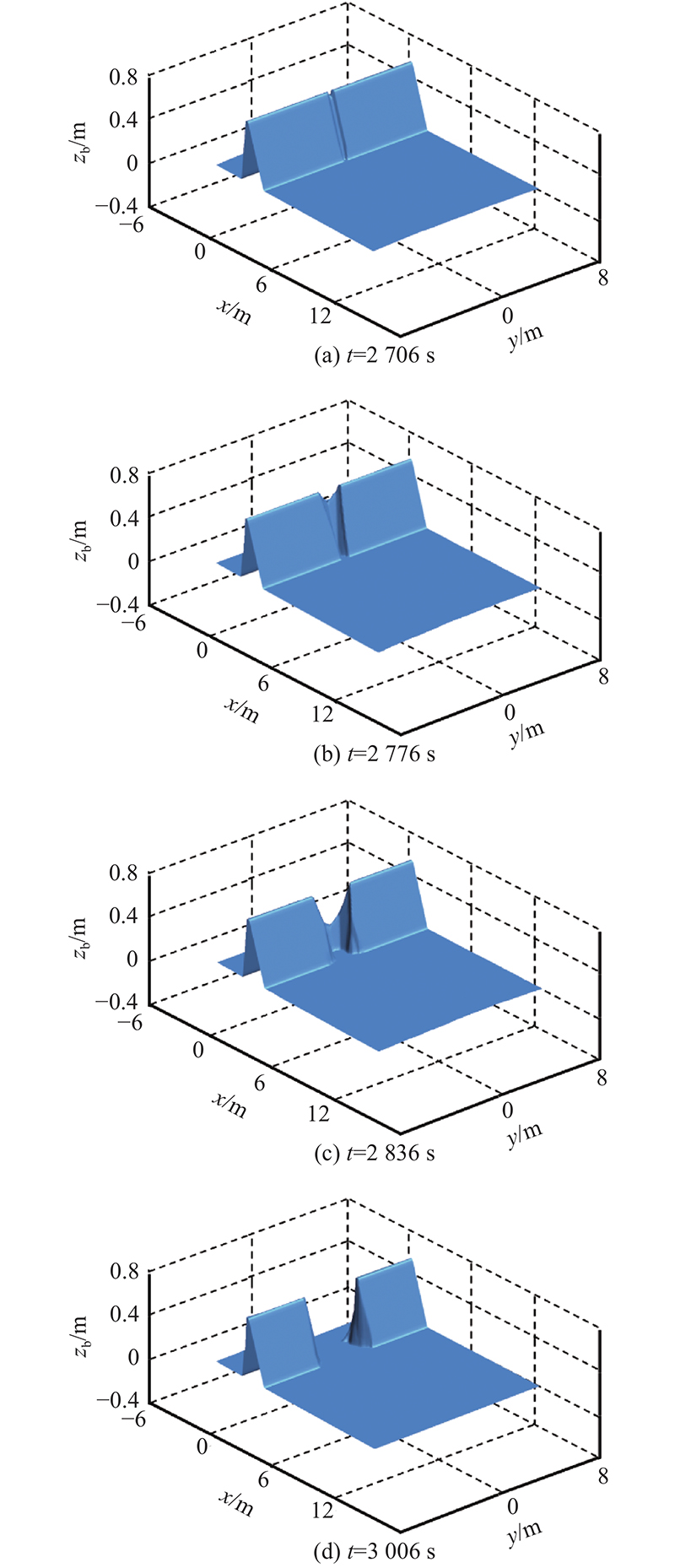
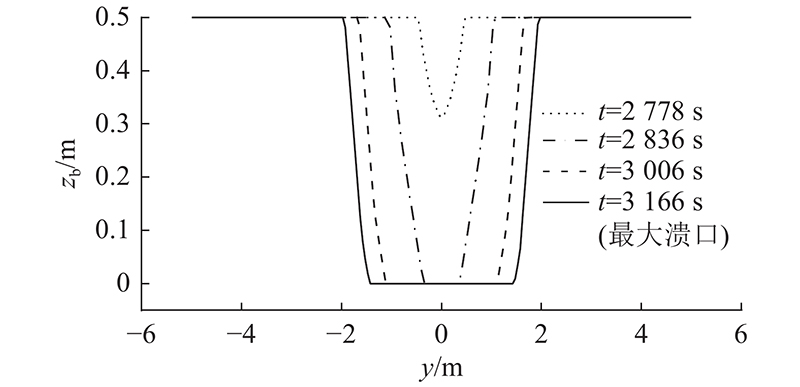
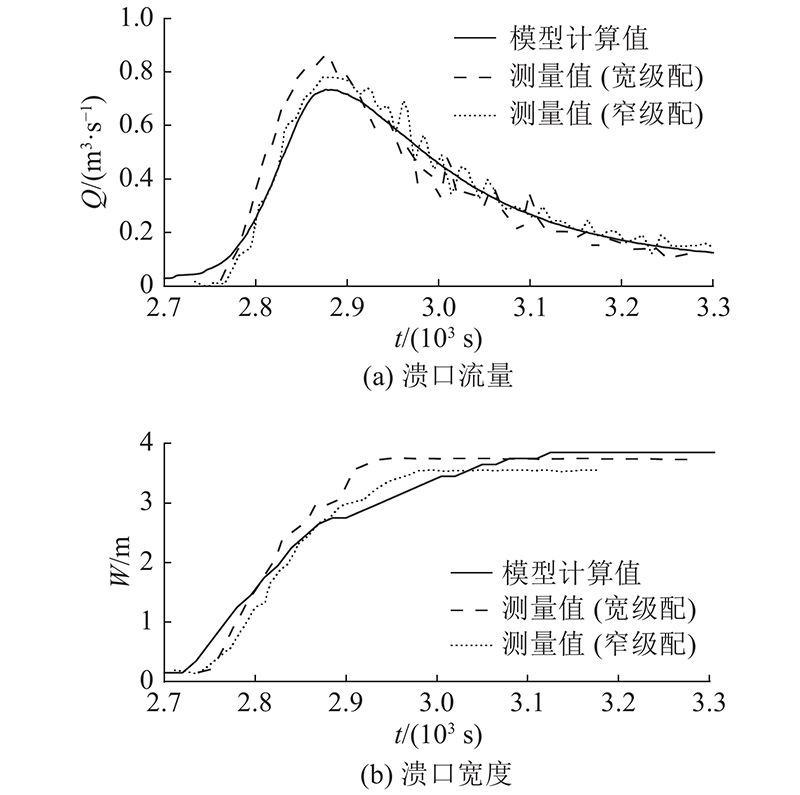
图11为不同时刻坝体高程计算结果，图12为不同时刻沿坝轴线方向高程剖面计算结果. 可知，溃决全程可以分为4个阶段. 1）漫顶水流冲刷坝体下游面，坝体下游面逐渐变陡. 2）坝顶泥沙被水流冲走，坝顶宽度逐渐减小并消失，溃口宽度增大. 3）坝体上游面被冲刷，溃口宽度继续增大. 阶段3）溃口宽度增大一方面是由于水流直接的冲刷作用，另一方面是由于边坡失稳引起的. 4）上游面泥沙被水流完全冲走，溃口宽度仍然增大. 阶段4）溃口增大的主要原因是溃口侧壁边坡角度大于休止角，导致边坡失稳，因此，阶段4）溃口宽度增大的速度比阶段3）慢. 如图13所示为溃口峰值流量时刻坝体高程和流矢计算结果. 可知，计算得到的坝体高程和流速分布对称性很好，与理论分析吻合. 如图14所示为不同参数的本开发模型计算值与测量值对比. 图中，W为溃口宽度，Q为溃口流量. 图14 (a)为溃口流量随时间变化的对比结果. 本模型没有考虑泥沙级配的影响，因此在对该算例宽、窄级配沙进行模拟时，采用相同的计算参数，最终的模拟结果只有1组. 可知，计算得到的流量过程线上升段与窄级配沙的测量值吻合良好，但小于宽级配沙的测量值. 流量过程线下降段与2种级配沙测量值吻合良好. 此外，峰值流量计算值低于2种级配沙测量结果，平均相对误差小于10%. 图14 (b)为溃口宽度随时间变化的对比结果. 可知，溃口宽度计算结果与2种级配沙测量值变化趋势总体一致. 在t=2900 s之前溃口宽度增大速度比之后溃口增大速度大，主要原因是2900 s以后，坝体溃决过程进入坝体溃决过程的阶段4）. 模型计算得到的最终溃口宽度略大于2种级配沙测量结果，平均相对误差小于5%.

为了进一步分析k_d、n_f、τ_c、φ_c,dry和φ_c,wet等关键模型参数对于计算结果的影响，开展敏感性分析. 以上文给定的参数取值及计算结果作为参考值，每个参数相对于参考值的改变量分别为参考值的20%、40%、−20%和−40%，计算得到对应的峰值流量及溃口最大宽度. 如图15所示为敏感性分析结果. 图中， $\varDelta $_r为各参数相对于参照值改变量， $\varDelta $_wr为溃口最大宽度相对于参照值改变量， $\varDelta $_Qr为溃口峰值流量相对于参照值改变量. 当干休止角和湿休止角改变量为参考值的−40%时，参数值太小，计算结果不收敛，因此图中没有给出相应的计算结果. 可知，最大溃口宽度和溃口峰值流量的计算值均与k_d、n_f成正相关关系，且与对k_d的敏感程度相比，二者均对n_f更为敏感. 最大溃口宽度和溃口峰值流量的计算值与φ_c,dry、φ_c,wet成负相关关系，当参数改变量为正时，最大溃口宽度对湿休止角敏感程度大于干休止角，改变量为负时则相反. 不管参数增大还是减小，峰值流量对干休止角都不敏感，对湿休止角则较为敏感. 与一维坝体溃决算例类似，τ_c对于计算结果没有影响.

采用二维漫顶溃坝算例，进一步验证本模型预测坝体溃口横向扩展过程的能力. 计算结果表明，该模型能够有效地模拟出土石坝溃口扩展的4个阶段，计算得到的峰值流量和最大溃口宽度与测量值的相对误差分别小于10%、5%，表明该模型能够适用于非黏性土石坝溃决计算分析.

（1）基于线性冲蚀公式建立二维非黏性土石坝溃决模型，该模型具有建模简单，计算效率高的优点.

（2）在棱柱形渠道断面和椭球形隆起边坡坍塌算例中，高程坡度的计算结果与设定休止角的最大误差小于0.5%，表明模型的边坡坍塌模块能够准确地模拟一维和二维边坡坍塌过程.

（3）一维和二维非黏性土石坝漫顶溃决实验计算结果表明，本模型对坝顶高程、最终溃口宽度及溃口峰值流量等关键参数的预测值与测量值吻合良好，能够有效地模拟出土石坝溃口扩展的4个阶段.

（4）模型关键参数敏感性分析发现，起动切应力对模拟计算结果影响很小；最大溃口宽度和峰值流量与干、湿休止角均成负相关，与曼宁系数、冲蚀系数均成正相关，且曼宁系数比冲蚀系数更为敏感. 此外，干休止角对于最大溃口宽度的影响大于其对峰值流量的影响.