在实际的优化问题中, 决策者往往要考虑许多互相冲突的目标,即多目标优化问题(multi-objective optimization problems, MOPs)[1]. 群智能算法[2-4]被证明是解决多目标优化问题的有效方法. 其中,粒子群优化算法(particle swarm optimization, PSO)[5]是著名的模拟鸟群捕食时互动的群智能算法. 由于机理简单、参数少、收敛速度快等优点,PSO已成功应用于求解MOPs,并拓展为多目标粒子群优化算法(multi-objective particle swarm optimization, MOPSO)[6]. 但MOPSO在求解MOPs时存在不足: 粒子群的收敛速度快,易导致早熟收敛从而陷入局部最优;粒子群单一的搜索模式,易导致收敛精度差、多样性差的问题.
许多学者试图通过选取最优粒子来提高MOPSO的性能. Liang等[7]引入竞赛选择机制, 利用所有其他粒子的历史最佳信息来更新粒子的速度, 并对粒子的每个维度选择不同的全局最优粒子进行独立更新,提高了算法的收敛性和多样性. 纪昌明等[8]优先选取存档中稀疏区域或边界区域的粒子作为全局最优粒子,通过树形结构存储迭代过程中搜索得到的最优粒子,进一步提高MOPSO的多样性. 然而,多数改进的粒子群算法没有考虑粒子本身的特性,在进化过程中往往使不同性能的粒子飞向同一个或同一类最优粒子,影响了算法的多样性. 此外, 粒子速度更新公式中参数的变化会调整粒子的探索和开发能力. 学者们试图通过调整参数来提高MOPSO的性能. Hu等[9]提出基于平行格坐标系统的自适应多目标粒子群算法, 通过Pareto熵动态监测种群的收敛状态, 并将此作为反馈信息自适应调整惯性权重和学习因子, 提升了算法的综合性能. 韩红桂等[10]提出自适应飞行参数调整机制, 根据粒子进化方向信息动态调整惯性权重和学习因子, 获得多样性较好的最优解. 除参数调整和最优粒子选取外, 学者们还试图从其他角度改进粒子群算法的性能. 张庆科等[11]将粒子的维度随机划分成多个子段,通过随机分配中心学习算子或离散学习算子实现对子段内维度的数值更新操作, 提高了算法在单峰函数、多峰函数求解的能力. 邱飞岳等[12]通过划分优化问题的决策变量, 保留变量间的关联性,在MOPSO中融合合作协同进化框架,使算法的多样性和收敛性得到提升. 刘彬等[13]根据速度交流机制将种群划分成多个子种群, 并在速度更新时互相分享子种群的信息, 以改善粒子的单一搜索模式, 提高了算法的收敛性和分布性. 但多数改进的多目标粒子群算法在迭代中没有考虑不同性能粒子搜索策略的差异, 可能会导致粒子泛化能力差, 以至于在面对复杂的MOPs时很难得到最优解集. 况且根据粒子性能赋予其不同搜索策略的算法大多局限在对单目标问题的研究.
本研究提出多角色多策略多目标粒子群优化算法(MOPSO_RS). 根据粒子的角色划分指标, 为不同性能的粒子赋予不同角色. 该算法针对粒子的不同角色制定多策略的全局最优粒子选取方法、多策略的参数调整方法和高斯变异方法, 改变种群的单一搜索模式, 提高粒子群算法在复杂的MOPs的求解能力.
1. 多角色多策略多目标粒子群算法
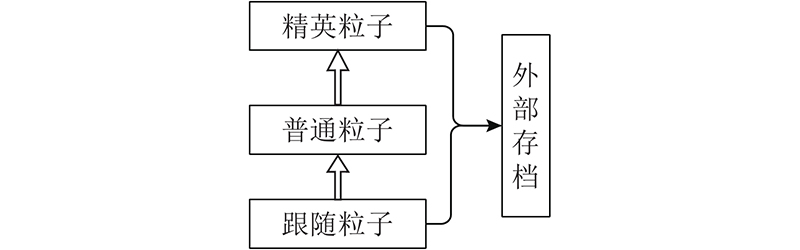
本研究算法结合质量指标和密度指标, 赋予粒子不同的角色: 精英粒子、普通粒子或跟随粒子. 结合粒子的角色, 提出多策略的全局最优粒子选取方法和多策略的参数调整方法, 使不同角色的粒子获得不同的搜索策略. 在算法中引入高斯变异方法, 使粒子向其全局最优粒子变异, 以增强粒子的搜索能力.
1.1. 角色划分
1.1.1. 角色划分指标
图 1
当采用非支配排序作为质量指标时, 这些极端粒子会影响判断粒子的质量. 为了减少这些极端粒子对质量指标的影响, 启发于离群点的思想[15], 通过计算每层中各粒子的局部离群因子Lf判断极端粒子, 计算公式为
式中:
在进化过程中, 位于目标空间中稀疏区域的粒子有利于维护种群多样性. 粒子
粒子的密度指标越小, 表示该粒子与其
式中:
1.1.2. 角色划分
受文献[16]的思想启发, 将多角色策略拓展到MOPSO. 将种群中粒子的角色划分指标
式中: 类别1、2、3分别表示精英粒子、普通粒子和跟随粒子,
在计算粒子角色划分指标时考虑个别极端粒子的影响, 因此在角色划分时将极端粒子分配成普通粒子或跟随粒子的角色, 保证精英粒子同时具备良好的收敛性和多样性的性能.
1.2. 基于多角色多策略的参数调整
对于不同角色的粒子, 如果采用单一的搜索策略, 粒子可能会无法找到更好的区域. 根据粒子的角色, 将粒子的个体认知部分的学习因子
1)精英粒子最贴合最优解, 无论向全局最优粒子发展, 还是注重自身的飞行信息, 所产生的下一步都具有极大可能性是非支配解. 因此精英粒子的学习因子
2)普通粒子较贴合最优解但多样性有待提升, 应重视向全局最优粒子的发展, 加大全局认知部分的学习因子
3)跟随粒子在种群中收敛性最差. 较小的学习因子
根据上述讨论, 第
式中:
1.3. 基于多角色多策略的全局最优粒子选取
在给不同角色的粒子制定搜索策略时, 除了调整粒子的学习参数外, 还应选取粒子最合适的全局最优粒子, 以增强粒子的搜索效率.将算法迭代过程分为前、后期共2个阶段, 迭代阶段
式中:
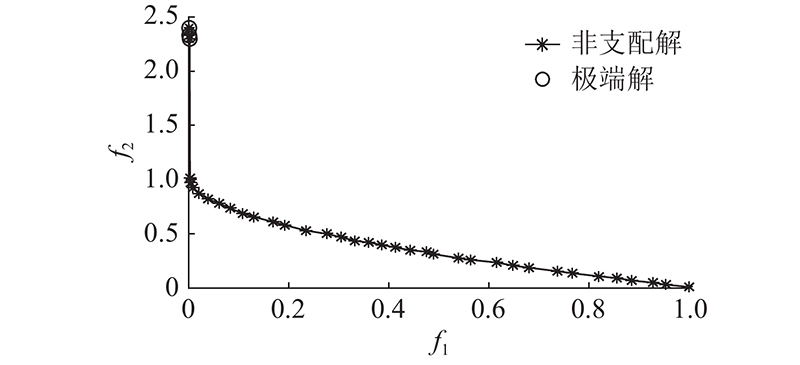
不同角色的粒子在迭代前、后期选取的全局最优粒子如图2所示. 图中,实心、空心箭头分别表示当IT= 1、2时不同角色的粒子选取的样本. 当IT= 1时, 种群的整体收敛性较差, 种群应增强全局搜索能力. 普通粒子和跟随粒子随机选择档案中最优解作为全局最优粒子, 以提高整体的收敛性. 精英粒子选取档案中密度指标
图 2
图 2 不同角色的粒子在迭代前、后期选取的全局最优粒子图
Fig.2 Global optimal particle graph selected by particles of different roles in before and after iteration
本研究的多策略全局最优选取方法, 可以使种群在最优解周围展开搜索的同时, 保证粒子在整个目标空间进行搜索, 提升种群的多样性和收敛性.
1.4. 基于多角色的高斯变异
为了避免种群过早收敛和陷入局部最优, 在粒子位置更新时, 利用高斯函数[17]对部分粒子进行扰动, 以增强粒子在目标空间的搜索能力. 根据不同角色, 使粒子朝向其相应的全局最优粒子方向变异. 粒子
式中:
当粒子与其全局最优粒子的位置较远时, 粒子通过较大幅度的变异, 增强粒子的搜索能力;当粒子与其全局最优粒子的位置近时, 粒子受到较小幅度的变异, 减少对粒子搜索行为的扰动. 精英粒子的全局最优粒子是外部归档集的最优解, 精英粒子与最优解的位置较近, 获得较小的变异幅度, 以避免对精英粒子的过多干扰;普通粒子和跟随粒子均与其全局最优粒子位置较远, 得到较大的变异幅度, 以探索更多区域. 随着迭代次数的增加, 粒子群整体的变异幅度越来越小, 保证了迭代后期粒子的开发能力.
1.5. 外部归档集维护
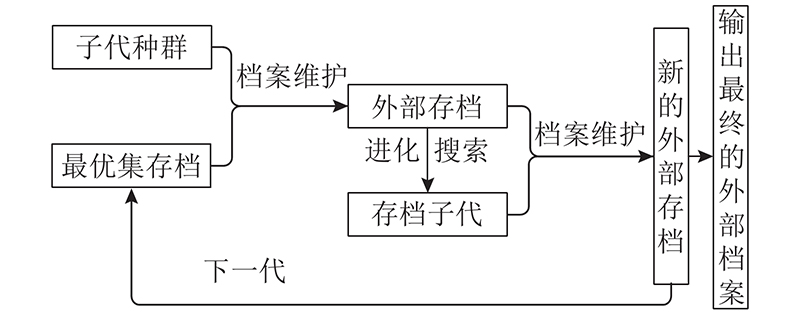
在选取全局最优粒子时, 将整个迭代过程分成前期和后期共2个部分. 前期种群处于探索阶段, 后期种群逐渐收敛稳定. 为了避免种群在迭代后期还处于整体收敛性差的阶段, 采用档案进化混合搜索方案, 即将模拟二进制交叉和多项式变异这2个进化算子用于位置更新公式, 以充分利用档案中非劣解的有效信息, 加快种群的收敛速度.
在每次迭代中, 种群经过更新变异生成子代种群OffSpring. OffSpring与最优解集存档进行档案维护后得到档案Ar. 为了充分利用非劣解集的信息, 档案进行进化搜索产生档案子代S. 对档案Ar与档案子代S进行档案维护得到新的外部存档, 并在下一代更新时替换最优解集存档. 直到满足总迭代次数或结束条件后, 循环结束, 输出最终的外部归档集. 外部归档集的更新示意图,如图3所示. 外部归档集的规模M设置为与种群规模N一致. 档案维护规则为将候选解集中角色划分指标RI<2的解集记为最优解集H. 当最优解的个数小于M时, 将角色划分指标RI较小的M个候选解存入档案Ar; 当最优解的个数超过外部存档的规模时, 循环删去剩余最优解集中具有最大D(1)的解, 直至满足规模要求. 档案Ar的表达式为
图 3
式中: |H|为集合H中最优解的个数, B为维护档案时的候选解集.
2. 算法流程
MOPSO_RS的总体框架如下.
1)初始化. 设置种群规模N、档案规模M和总迭代次数T; 初始化种群Pop; 初始化角色R; 定义个体最优位置p, 全局最优粒子g, 外部归档集Ar; 初始化权重w=0和学习因子c1=c2=0和当前迭代次数t=0.
2)档案更新. 根据外部归档集维护策略, 更新档案Ar, 同时得到档案子代S.
3)更新种群. 根据角色划分策略, 从
4)设置参数. 根据基于多角色多策略的参数调整策略, 设置各角色粒子的权重
5)迭代优化.
6)
7)更新个体最优位置
8)生成子种群. 更新种群粒子的速度和位置后, 根据高斯变异方法对粒子的位置进行变异, 得到子种群
9)档案更新. 根据外部归档集维护策略, 通过
10)更新种群. 对
11)重置参数. 根据角色
12)如果算法满足结束条件, 输出最终的外部归档集
在MOPSO_RS的执行过程中, 利用角色划分策略, 为不同性能的粒子赋予不同角色; 同时利用基于多角色多策略的全局最优粒子选取策略和基于多角色多策略的参数调整策略, 针对各角色选取不同的全局最优粒子, 引导粒子搜索整个目标空间, 获得处理不同复杂问题的智能.
3. 实验与结果分析
3.1. 实验设置
为了测试所提算法的性能, 对3目标的DTLZ1~DTLZ7、WFG2、WFG4、WFG9这10个基准问题[17]进行仿真实验. 对比的多目标优化算法有: 非支配排序遗传算法[18](NSGA-II)、协方差自适应进化策略的基于分解的多目标进化算法[19](MOEA/D with covariance matrix adaptation evolution strategy, MOEADCMA)、基于聚类的自适应多目标进化算法[20](clustering based adaptive multi-objective evolutionary algorithm, CAMOEA)、多搜索策略的多目标粒子群[21] (MOPSO with multiple search strategies, MMOPSO)和基于竞争机制的多目标粒子群算法[22] (competitive mechanism based multi-objective particle swarm optimizer, CMOPSO). 以上6种算法的种群规模均设为100.
为了进一步评估MOPSO_RS处理MOPs的性能, 将其与4种高维多目标算法在5、10、15个目标数的测试问题上进行比较. 对比的算法有: 基于参考点的非支配排序遗传算法[23] (NSGA-III)、基于径向空间划分的进化算法[24] (radial space division based evolutionary algorithm, RSEA)、新的多目标粒子群算法[25] (novel MOPSO, NMPSO)和参考向量引导的进化算法[26] (reference vector guided evolutionary algorithm, RVEA). 对应于5、10、15个目标维数[27], 5种算法的种群规模分别设为126、230、240. 为了使算法适用于可拓展的多目标测试问题, 在此实验上将本研究的密度指标替换成基于转移的多样性估计指标[28].
测试实验中, 根据目标维数, DTLZ1的决策变量维数设置为
3.2. 实验结果分析
为了定量评价多目标优化算法的性能, 采用反世代距离(inverted generational distance,
表 1 MOPSO_RS和其他5种多目标算法在不同测试问题得到的IGD结果
Tab.1
| 测试问题 | MOEADCMA | CAMOEA | NSGAII | MMOPSO | CMOPSO | MOPSO_RS |
| DTLZ1 | 2.068 6×10−2 (1.13×10−4) − | 2.136 4×10−2 (3.22×10−4) − | 2.739 6×10−2 (1.11×10−3) − | 1.157 7×10−1 (2.41×10−1) − | 7.869 8×10−1 (1.57×10+0) − | 2.026 2×10−2 (1.79×10−4) |
| DTLZ2 | 5.549 4×10−2 (3.97×10−4) + | 5.706 2×10−2 (7.67×10−4) − | 6.902 1×10−2 (2.77×10−3) − | 7.143 9×10−2 (2.00×10−3) − | 5.803 3×10−2 (1.15×10−3) − | 5.595 1×10−2 (8.06×10−4) |
| DTLZ3 | 1.810 6×10+0 (3.39×10+0) − | 5.838 6×10−2 (3.03×10−3) − | 6.947 4×10−2 (2.78×10−3) − | 2.371 7×10−1 (3.61×10−1) − | 3.773 6×10+1 (2.67×10+1) − | 5.471 1×10−2 (7.28×10−4) |
| DTLZ4 | 9.455 3×10−2 (6.45×10−2) − | 5.734 0×10−2 (9.37×10−4) − | 9.490 2×10−2 (1.58×10−1) − | 7.185 8×10−2 (2.92×10−3) − | 6.037 4×10−2 (1.24×10−3) − | 5.629 6×10−2 (1.02×10−3) |
| DTLZ5 | 2.277 5×10−2 (5.66×10−5) − | 5.073 2×10−3 (1.53×10−4) − | 5.854 1×10−3 (3.42×10−4) − | 6.532 5×10−3 (9.75×10−4) − | 5.909 7×10−3 (7.55×10−4) − | 4.360 3×10−3 (9.46×10−5) |
| DTLZ6 | 2.288 7×10−2 (2.19×10−5) − | 4.633 2×10−3 (1.28×10−4) − | 5.882 0×10−3 (3.01×10−4) − | 6.889 7×10−3 (6.76×10−4) − | 4.215 9×10−3 (4.69×10−5) − | 4.084 1×10−3 (2.39×10−5) |
| DTLZ7 | 1.512 8×10−1 (5.13×10−3) − | 6.190 9×10−2 (1.64×10−3) = | 7.584 4×10−2 (3.65×10−3) − | 1.206 6×10−1 (9.00×10−2) − | 1.554 6×10−1 (2.27×10−1) − | 6.176 5×10−2 (1.45×10−3) |
| WFG2 | 2.453 4×10−1 (1.67×10−2) − | 1.827 0×10−1 (7.41×10−3) − | 2.173 0×10−1 (9.22×10−3) − | 2.324 9×10−1 (1.28×10−2) − | 1.807 3×10−1 (6.13×10−3) − | 1.735 8×10−1 (4.34×10−3) |
| WFG4 | 3.312 3×10−1 (2.11×10−2) − | 2.329 7×10−1 (3.73×10−3) − | 2.788 7×10−1 (8.35×10−3) − | 3.113 3×10−1 (8.35×10−3) − | 2.670 6×10−1 (5.75×10−3) − | 2.275 9×10−1 (3.37×10−3) |
| WFG9 | 3.036 8×10−1 (2.52×10−2) − | 2.314 3×10−1 (4.11×10−3) − | 2.744 4×10−1 (1.20×10−2) − | 2.877 0×10−1 (2.18×10−2) − | 2.186 2×10−1 (3.26×10−3) = | 2.172 7×10−1 (3.62×10−3) |
| +/−/= | 1/9/0 | 0/9/1 | 0/10/0 | 0/10/0 | 0/9/1 |
表 2 MOPSO_RS和其他5种多目标算法在不同测试问题得到的HV结果
Tab.2
| 测试问题 | MOEADCMA | CAMOEA | NSGAII | MMOPSO | CMOPSO | MOPSO_RS |
| DTLZ1 | 8.403 8×10−1 (6.88×10−4) − | 8.385 4×10−1 (9.40×10−4) − | 8.242 1×10−1 (3.70×10−3) − | 6.980 3×10−1 (2.85×10−1) − | 3.535 1×10−1 (3.69×10−1) − | 8.422 1×10−1 (4.05×10−4) |
| DTLZ2 | 5.564 4×10−1 (4.67×10−4) + | 5.504 6×10−1 (2.22×10−3) + | 5.314 8×10−1 (4.80×10−3) − | 5.302 2×10−1 (4.38×10−3) − | 5.412 1×10−1 (3.11×10−3) − | 5.487 1×10−1 (2.39×10−3) |
| DTLZ3 | 3.407 1×10−1 (2.59×10−1) − | 5.485 8×10−1 (5.15×10−3) − | 5.293 7×10−1 (5.93×10−3) − | 4.370 4×10−1 (1.98×10−1) − | 0.000 0×10+0 (0.00×10+0) − | 5.574 0×10−1 (2.56×10−3) |
| DTLZ4 | 5.450 3×10−1 (2.37×10−2) − | 5.515 7×10−1 (1.82×10−3) + | 5.212 6×10−1 (8.00×10−2) − | 5.325 5×10−1 (5.42×10−3) − | 5.344 1×10−1 (2.78×10−3) − | 5.498 6×10−1 (2.70×10−3) |
| DTLZ5 | 1.904 1×10−1 (3.06×10−5) − | 1.991 7×10−1 (1.59×10−4) − | 1.991 4×10−1 (1.76×10−4) − | 1.991 9×10−1 (1.96×10−4) − | 1.981 3×10−1 (5.52×10−4) − | 1.996 5×10−1 (1.34×10−4) |
| DTLZ6 | 1.904 7×10−1 (9.91×10−6) − | 1.998 6×10−1 (1.22×10−4) − | 1.994 1×10−1 (1.52×10−4) − | 1.992 2×10−1 (1.63×10−4) − | 2.001 9×10−1 (3.10×10−5) + | 2.000 9×10−1 (3.36×10−5) |
| DTLZ7 | 2.588 5×10−1 (7.17×10−4) − | 2.736 0×10−1 (1.65×10−3) − | 2.682 5×10−1 (2.10×10−3) − | 2.632 6×10−1 (9.77×10−3) − | 2.603 7×10−1 (2.14×10−2) − | 2.751 3×10−1 (9.04×10−4) |
| WFG2 | 9.007 6×10−1 (1.65×10−2) − | 9.291 7×10−1 (1.78×10−3) = | 9.205 9×10−1 (2.43×10−3) − | 9.143 3×10−1 (3.78×10−3) − | 9.287 5×10−1 (1.41×10−3) = | 9.289 7×10−1 (1.34×10−3) |
| WFG4 | 5.062 5×10−1 (1.68×10−2) − | 5.361 2×10−1 (3.13×10−3) + | 5.023 6×10−1 (4.45×10−3) − | 4.811 8×10−1 (6.75×10−3) − | 4.840 6×10−1 (4.67×10−3) − | 5.253 2×10−1 (4.15×10−3) |
| WFG9 | 4.757 7×10−1 (2.81×10−2) − | 5.136 1×10−1 (4.23×10−3) = | 5.039 3×10−1 (6.93×10−3) − | 4.995 9×10−1 (1.94×10−2) − | 5.173 0×10−1 (2.72×10−3) + | 5.123 3×10−1 (5.13×10−3) |
| +/−/= | 1/10/0 | 3/5/2 | 0/10/0 | 0/10/0 | 2/7/1 |
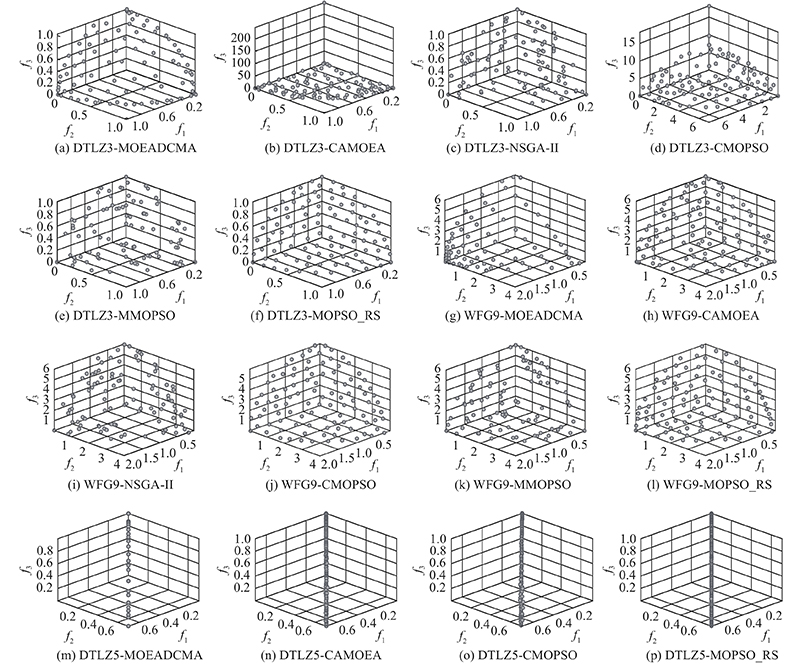
由表1可以看出, 在10个测试问题中MOPSO_RS获得9个 IGD 最优值, 1个次优值. MOEADCMA获得1个 IGD 最优值. 在DTLZ2测试问题上, MOPSO_RS稍逊于MOEADCMA, 优于其他4种算法. 结合图4可以看出, 在DTLZ3 (多模PF)问题上, MOEADCMA、NSGA-II和MMOPSO的多样性较差, CMOPSO没有收敛到真实PF附近, CAMOEA获得的PF中出现极端点, MOPSO_RS所获得的PF分布较均匀, 保持了较好的多样性和收敛性; 在DTLZ5(多峰PF)问题上, MOEADCMA分布性较差, 其他5种算法均具有较好的收敛性和多样性, 其中MOPSO_RS算法表现出最好的综合性能; 在WFG9 (不可分解的PF)问题上, MOEADCMA、NSGA-II、CAMOEA和MMOPSO分布不均匀, 具有较差的多样性, CMOPSO的综合性能较好, MOPSO_RS得到最好的综合性能. 由此可以看出, MOPSO_RS在处理不同的复杂多目标问题时均能获得较好的综合性能. 原因是MOPSO_RS针对不同角色粒子采用不同的搜索策略, 让种群既能在最优粒子周围展开搜索, 也能搜索整个目标空间. 本研究采用的角色划分指标能够有效避免极端点对算法的影响, 保证了算法的收敛性和多样性. 因此从结果上看, MOPSO_RS能够处理不同的MOPs问题. 在9个测试问题上, MOPSO_RS表现出的IGD均值都比其他算法好, 具有较优的收敛性和分布性.
从表2可以看出, 在10个测试问题中 MOPSO_RS获得4个
由表3可以看出, 在15个测试问题上, MOPSO_RS获得8个
图 4
图 4 各算法部分测试问题帕累托前沿图
Fig.4 Pareto front of some test problems of each algorithm
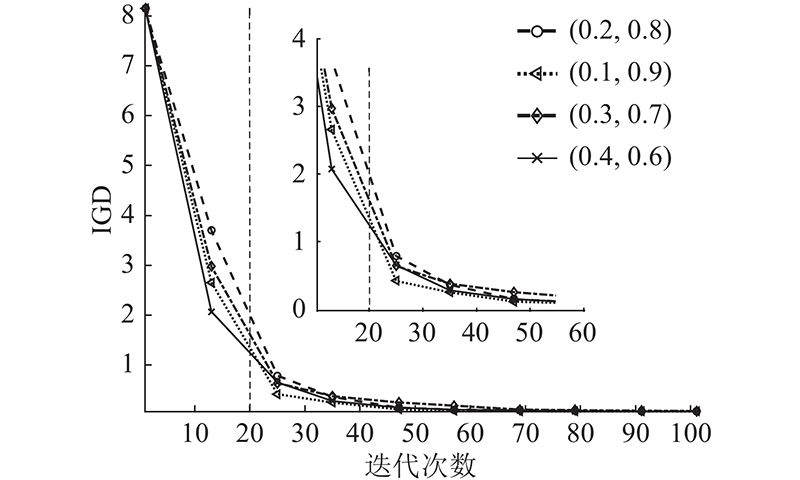
3.3. 角色划分指标阈值分析
MOPSO_RS根据粒子
图 5
3.4. 策略分析
为了验证所提策略的有效性, 对比全局最优粒子选取策略和高斯变异策略, 将MOPSO_R随机选取档案的最优解作为所有粒子的全局最优粒子. MOPSO_RS-OG中粒子采用未改进的高斯变异方法向其对应全局最优粒子方向变异. MOPSO_R-G中粒子均向档案中的最优解变异.这3种算法采用的其余策略均和MOPSO_RS相同. 如表4所示为以上4种算法在3目标测试问题上独立运行30次后的
表 3
MOPSO_RS和其他4种高维多目标算法在5、10、15个目标的测试函数上的
Tab.3
| 测试问题 | 目标数目 | NSGA-III | RSEA | RVEA | NMPSO | MOPSO_RS |
| DTLZ1 | 5 | 6.337 6×10−2 (8.48×10−5) − | 7.611 1×10−2 (2.16×10−3) − | 6.332 7×10−2 (7.81×10−5) − | 6.512 3×10−2 (1.99×10−3) − | 5.870 5×10−2 (5.15×10−4) |
| 10 | 1.493 3×10−1 (4.62×10−2) − | 1.524 3×10−1 (2.63×10−2) − | 1.334 2×10−1 (2.68×10−3) − | 1.687 7×10−1 (1.32×10−2) − | 1.100 4×10−1 (1.46×10−3) | |
| 15 | 2.030 2×10−1 (8.76×10−2) − | 2.009 3×10−1 (2.48×10−2) − | 1.334 4×10−1 (1.12×10−2) + | 1.169 0×10+0 (3.60×10+0) − | 1.351 8×10−1 (3.20×10−3) | |
| DTLZ2 | 5 | 1.949 0×10−1 (1.61×10−5) + | 2.455 6×10−1 (1.99×10−2) − | 1.948 9×10−1 (8.54×10−6) + | 2.162 3×10−1 (2.31×10−3) − | 2.099 2×10−1 (2.06×10−3) |
| 10 | 4.904 3×10−1 (5.93×10−2) − | 5.338 5×10−1 (3.17×10−2) − | 4.533 6×10−1 (3.46×10−4) − | 4.230 0×10−1 (2.20×10−3) − | 4.198 4×10−1 (2.21×10−3) | |
| 15 | 6.904 7×10−1 (8.99×10−2) − | 6.701 9×10−1 (2.53×10−2) − | 5.269 7×10−1 (6.76×10−4) + | 6.565 8×10−1 (7.27×10−2) − | 5.346 1×10−1 (3.80×10−3) | |
| WFG2 | 5 | 4.712 8×10−1 (1.79×10−3) + | 4.958 8×10−1 (1.39×10−2) + | 4.484 9×10−1 (8.61×10−3) + | 1.094 9×10+0 (2.08×10−1) − | 5.393 7×10−1 (2.20×10−2) |
| 10 | 1.447 3×10+0 (1.34×10−1) − | 1.099 6×10+0 (3.44×10−2) − | 1.133 8×10+0 (3.09×10−2) − | 1.956 8×10+0 (1.94×10−1) − | 1.022 4×10+0 (1.94×10−2) | |
| 15 | 2.036 9×10+0 (1.06×10−1) − | 1.953 8×10+0 (2.25×10−1) − | 1.722 4×10+0 (1.15×10−1) − | 2.729 8×10+0 (2.71×10−1) − | 1.525 0×10+0 (3.04×10−2) | |
| WFG4 | 5 | 1.176 6×10+0 (8.31×10−4) + | 1.298 9×10+0 (2.67×10−2) = | 1.177 3×10+0 (9.79×10−4) + | 1.265 5×10+0 (2.30×10−2) + | 1.292 6×10+0 (1.92×10−2) |
| 10 | 4.769 4×10+0 (3.99×10−2) − | 4.877 3×10+0 (1.06×10−1) − | 4.633 0×10+0 (5.26×10−2) − | 4.219 0×10+0 (2.93×10−2) = | 4.206 1×10+0 (3.27×10−2) | |
| 15 | 8.591 6×10+0 (5.17×10−1) − | 9.202 0×10+0 (2.42×10−1) − | 8.856 0×10+0 (1.90×10−1) − | 7.683 0×10+0 (5.87×10−2) = | 7.658 9×10+0 (5.89×10−2) | |
| WFG9 | 5 | 1.127 9×10+0 (6.02×10−3) + | 1.256 2×10+0 (4.88×10−2) − | 1.149 7×10+0 (2.73×10−3) + | 1.192 4×10+0 (1.66×10−2) + | 1.223 0×10+0 (2.14×10−2) |
| 10 | 4.521 1×10+0 (3.70×10−2) − | 4.808 5×10+0 (1.06×10−1) − | 4.467 2×10+0 (7.60×10−2) − | 4.147 5×10+0 (3.89×10−2) − | 4.100 5×10+0 (2.84×10−2) | |
| 15 | 8.127 9×10+0 (1.71×10−1) − | 9.053 4×10+0 (2.46×10−1) − | 7.460 2×10+0 (2.77×10−1) = | 7.665 7×10+0 (1.06×10−1) − | 7.484 3×10+0 (7.46×10−2) | |
| +/−/= | 4/11/0 | 1/13/1 | 6/8/1 | 2/11/2 | ||
表 4 不同策略对IGD的影响
Tab.4
| 测试问题 | MOPSO_RS-OG | MOPSO_R-G | MOPSO_R | MOPSO_RS |
| DTLZ3 | 5.437 4×10−2(1.86×10−3) + | 5.471 2×10−2 (7.02×10−4) = | 5.591 8×10−2 (2.65×10−3) − | 5.471 1×10−2 (7.28×10−4) |
| DTLZ4 | 5.793 9×10−2 (1.81×10−3) − | 5.746 1×10−2 (1.90×10−3) − | 5.690 1×10−2 (1.45×10−3) = | 5.629 6×10−2(1.02×10−3) |
| DTLZ5 | 4.454 9×10−3 (1.24×10−4) − | 4.368 3×10−3 (1.23×10−4) = | 4.423 6×10−3 (1.15×10−4) − | 4.360 3×10−3(9.46×10−5) |
| DTLZ6 | 4.107 9×10−3 (2.97×10−5) − | 4.120 2×10−3 (3.51×10−5) − | 4.125 3×10−3 (2.76×10−5) − | 4.084 1×10−3(2.39×10−5) |
| +/−/= | 1/3/2 | 0/3/3 | 0/5/1 |
MOPSO_RS-OG、MOPSO_RS的区别在于高斯变异的方法. 由表4可以看出, 除DTLZ3问题外, MOPSO_RS获得的
MOPSO_R、MOPSO_RS的区别在于是否针对粒子的角色选取不同的全局最优粒子. 相比于MOPSO_R, MOPSO_RS大多比MOPSO_R表现出的
4. 结 语
传统多目标粒子群的粒子都使用单一的搜索模式, 导致种群过早收敛和多样性差的同时使粒子的泛化能力差. 本研究提出多角色多策略多目标粒子群优化算法 (MOPSO_RS). 该算法采用角色划分方法赋予粒子角色, 结合各角色, 提出多策略的全局最优粒子方法和多策略的参数调整方法, 帮助种群执行各种搜索策略. 同时提出基于多角色的高斯变异, 使粒子根据其角色朝向不同的全局最优粒子变异, 增强粒子的搜索能力. MOPSO_RS在多目标、高维多目标测试问题上与其他几种改进算法的对比实验结果表明, MOPSO_RS在复杂问题上能够得到收敛性和多样性较好的Pareto解集以及其处理高维多目标问题的潜力. 策略分析实验证明了MOPSO_RS所提策略的有效性. 在多策略的全局最优粒子选取部分, 本研究简单地将整个迭代过程分成迭代前期和迭代后期共2个部分. 未来将在不降低算法性能的基础上研究如何融入检测种群迭代状态的方法. 随着目标数的上升, 个体在目标空间上往往难以互相确定支配关系. 未来也将研究处理高维多目标问题的粒子群优化算法.
参考文献
进化多目标优化算法研究
[J].DOI:10.3724/SP.J.1001.2009.00271 [本文引用: 1]
Research on evolutionary multi-objective optimization algorithms
[J].DOI:10.3724/SP.J.1001.2009.00271 [本文引用: 1]
求解多目标优化问题的改进布谷鸟搜索算法
[J].
Improved cuckoo search algorithm for multi-objective optimization problems
[J].
基于改进混合蛙跳算法的多约束车辆路径优化
[J].
Multi-constrained vehicle routing optimization based on improved hybrid shuffled frog leaping algorithm
[J].
Multi-objective particle swarm optimizers: a survey of the state-of-the-art
[J].
Comprehensive learning particle swarm optimizer for global optimization of multimodal functions
[J].DOI:10.1109/TEVC.2005.857610 [本文引用: 1]
基于树形结构无界存档的多目标粒子群算法
[J].
Multi-objective particle swarm optimization algorithm based on tree-structured unbounded archive
[J].
Adaptive multiobjective particle swarm optimization based on parallel cell coordinate system
[J].DOI:10.1109/TEVC.2013.2296151 [本文引用: 1]
自适应分解式多目标粒子群优化算法
[J].DOI:10.3969/j.issn.0372-2112.2020.07.001 [本文引用: 1]
Adaptive multiobjective particle swarm optimization based on decomposition archive
[J].DOI:10.3969/j.issn.0372-2112.2020.07.001 [本文引用: 1]
基于随机维度划分与学习的粒子群优化算法
[J].
Particle swarm optimization based on random vector partition and learning
[J].
基于大规模变量分解的多目标粒子群优化算法研究
[J].DOI:10.11897/SP.J.1016.2016.02598 [本文引用: 1]
Multi-objective particle swarm optimization algorithm using large scale variable decomposition
[J].DOI:10.11897/SP.J.1016.2016.02598 [本文引用: 1]
基于速度交流的多种群多目标粒子群算法研究
[J].DOI:10.3969/j.issn.1000-1158.2020.08.18 [本文引用: 1]
Research on multi-population multi-objective particle swarm optimization algorithm based on velocity communication
[J].DOI:10.3969/j.issn.1000-1158.2020.08.18 [本文引用: 1]
An efficient approach to nondominated sorting for evolutionary multiobjective
[J].
A fitness-based multi-role particle swarm optimization
[J].
基于高斯混沌变异和精英学习的自适应多目标粒子群算法
[J].
Adaptive multi-objective particle swarm optimization with Gaussian chaotic mutation and elite learning
[J].
A fast and elitist multiobjective genetic algorithm: NSGA-II
[J].DOI:10.1109/4235.996017 [本文引用: 1]
Biased multiobjective optimization and decomposition algorithm
[J].DOI:10.1109/TCYB.2015.2507366 [本文引用: 1]
A clustering-based adaptive evolutionary algorithm for multiobjective optimization with irregular pareto fronts
[J].DOI:10.1109/TCYB.2018.2834466 [本文引用: 1]
A novel multi-objective particle swarm optimization with multiple search strategies
[J].DOI:10.1016/j.ejor.2015.06.071 [本文引用: 1]
A competitive mechanism based multi-objective particle swarm optimizer with fast convergence
[J].DOI:10.1016/j.ins.2017.10.037 [本文引用: 1]
An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: solving problems with box constraints
[J].DOI:10.1109/TEVC.2013.2281535 [本文引用: 1]
A radial space division based evolutionary algorithm for many-objective optimization
[J].DOI:10.1016/j.asoc.2017.08.024 [本文引用: 1]
A reference vector guided evolutionary algorithm for many-objective optimization
[J].DOI:10.1109/TEVC.2016.2519378 [本文引用: 1]
A new many-objective evolutionary algorithm based on determinantal point processes
[J].
Shift-based density estimation for pareto-based algorithms in many-objective optimization
[J].DOI:10.1109/TEVC.2013.2262178 [本文引用: 1]
PlatEMO: a MATLAB platform for evolutionary multi-objective optimization
[J].DOI:10.1109/MCI.2017.2742868 [本文引用: 1]