随着通用飞机和无人机的推广应用,先进飞行器朝着智能化、多任务化的方向发展. 机翼是飞机升力的提供者,是决定飞机飞行能力的重要部件. 传统的刚性机翼已经不能满足应用要求,在这种情况下,能够适应各种飞行任务,达到最佳飞行性能的变形机翼(可以进行快速、连续、大尺度的主动变形)越来越受到研究者的重视. 根据飞机在实际飞行过程中不同的飞行任务、飞行条件,机翼的气动特性也有不同,改变机翼弯度是调整机翼气动特性最直接的方法[1].
美国20世纪80年代开始“多任务自适应变弯度机翼研究计划”(MAW)[2],光滑无缝隙的变形机翼通过液压系统驱动重叠式滑动机构改变机翼弯度,并完成多次飞行实验. 实验表明机翼升阻特性有明显提升,但是机翼的重量和复杂程度随之增加,这限制了该项技术的推广应用. Campanile等[3- 4]提出由内部刚性增强肋和外部柔性封闭壳体组成的柔性变形机翼,被称作“belt rib”. 柔性壳体在刚性增强肋的支撑作用下,可以承受大约335 KG的分布载荷,这种结构具有几何变化大、承载能力高、重量低的特点. Hasse等[5]在“belt rib”结构翼形的基础上,采用数值拓扑优化的方法定义内部加强结构,以实现机翼外形的变化. 该机翼能够实现翼形的整体改变,从NACA0012变为NACA2412翼形. Dayyani等[6-7]设计仿生式主动变弯度的鱼骨形机翼机构,采用缠绕滑轮带动钢丝束驱动,模拟鱼类的肌腱作用,变弯度实验表明,机翼具有较好的变形能力. 中国开展变弯度机翼相关研究有30多年的历史,在变形方案设计、气动设计方面仍处于探索阶段. Li等[8]从平面机构构型理论出发,设计平面连杆机构变弯度机翼,同时将机构间隙理论应用于该机翼的结构设计中,分析间隙对于变形精度的影响.
变弯度机翼设计的关键是解决轻质量、高形状适应性和高承载能力的内在冲突[9]. 本研究提出基于交叉簧片式铰链的柔性后缘机构与刚性连杆驱动机构组成的机翼变弯度方案,并对变弯度机翼展开如下研究. 1)针对机翼弦向大范围连续变弯度的要求,提出基于交叉簧片关节的弦向变弯度机翼机构方案. 基于链式梁约束建模方法,建立柔性后缘机构的理论静力学模型,分析其受力和变形的关系,与利用ANSYS所建立有限元建模的比较,验证理论模型的正确性. 2)基于柔性后缘机构的力学模型,提出系统的多目标机翼机构尺寸参数优化算法流程,使得机翼在巡航阶段和起降阶段设计点处的气动特性最优. 算法基于NSGA-II遗传算法,用XFOIL作为气动求解器,并考虑机翼在气动载荷的影响下的变形情况. 3)搭建机翼的实验平台,对机翼的变弯度精度、最大变弯度范围进行验证.
1. 变弯度机翼的机构设计
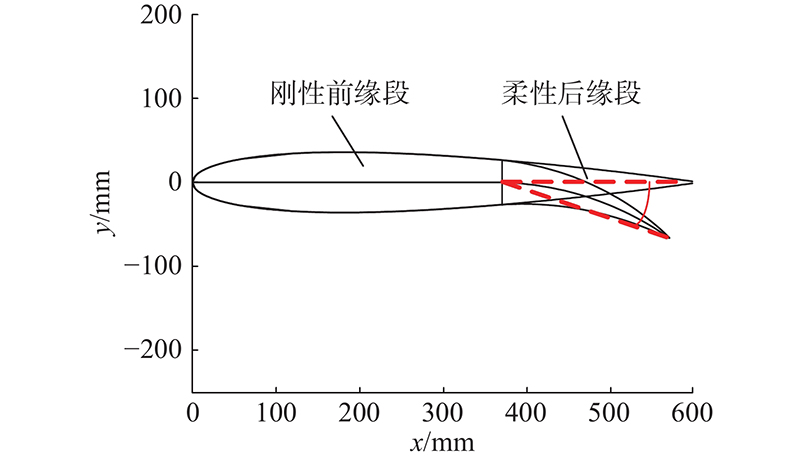
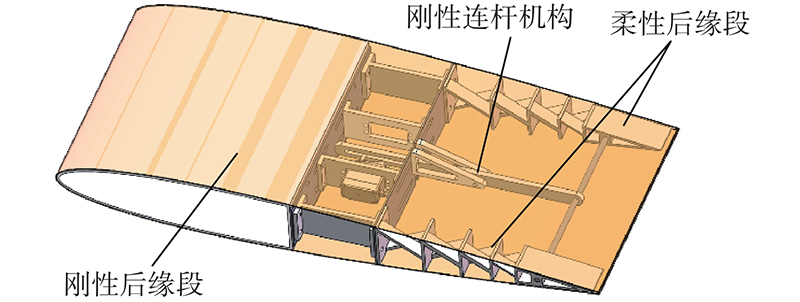
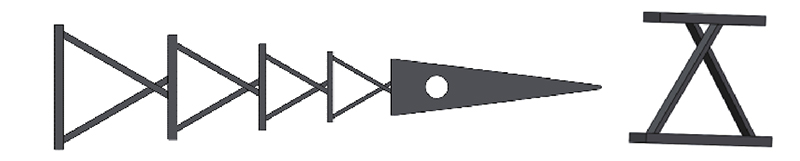
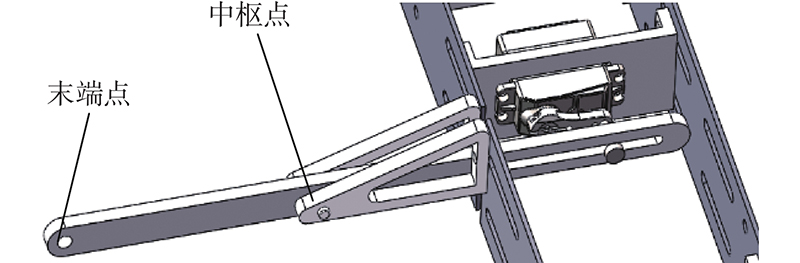
本研究设计的变弯度机翼拟应用于小型无人机,选择NACA0012翼型作为变弯度机翼的翼型. 其弦长为600 mm,变弯度后缘位于弦长的60%处,后缘弦向长度为240 mm,机翼变弯度的等效偏转角γ定义为尾缘点与变弯度后缘起偏点的连线所转过的角度,如图1所示. 为了实现机翼后缘整体的连续、大范围变形,提出变弯度机翼机构方案,由柔性后缘机构和刚性连杆驱动机构组成,如图2所示. 变弯度机翼的柔性后缘机构部分由4组形状相同,大小依次缩小的子单元构成,如图3所示. 当柔性后缘翼肋末端受到驱动力时,4组子单元会逐节向下弯曲,使得整体后缘实现连续、光滑变弯度的效果. 子单元为交叉簧片式柔性铰链,由1组柔性梁在空间中相互交错形成,具有免装配、免润滑、无间隙摩擦及良好的转动精度等优点,被广泛应用于柔性机构的设计中[10-11]. 变弯度机翼的驱动机构部分由伺服电机和摇杆构成,摇杆内有一滑槽,伺服电机的曲柄伸入摇杆的滑槽中. 摇杆在中枢点处铰接,摇杆末端通过连杆与柔性后缘尾缘处连接并可带动其运动,如图4所示. 驱动机构可看作摆动导杆机构. 其末端轨迹线为以中枢点为圆心的圆弧,导引与柔性后缘相连接的部分沿该轨迹线运动.
图 1
图 2
图 3
图 4
2. 柔性后缘力学模型的建立
建立柔性后缘力学模型的目的是得到柔性后缘机构受力与变形间的关系,柔性后缘视作由4组子单元首尾相接串联组成,每个柔性后缘子单元的弯度构成机翼后缘整体的大范围弯度. 因此,要研究整体后缘力学模型,要先建立柔性后缘子单元的力学模型.
2.1. 后缘子单元力学模型的建立
图 5
图 5 柔性后缘子单元参数定义
Fig.5 Parameter definition of flexible trailing edge sub element
式中所有的外载荷参数都根据梁的几何参数和材料参数进行归一化,小写字母代表归一化后的参数:
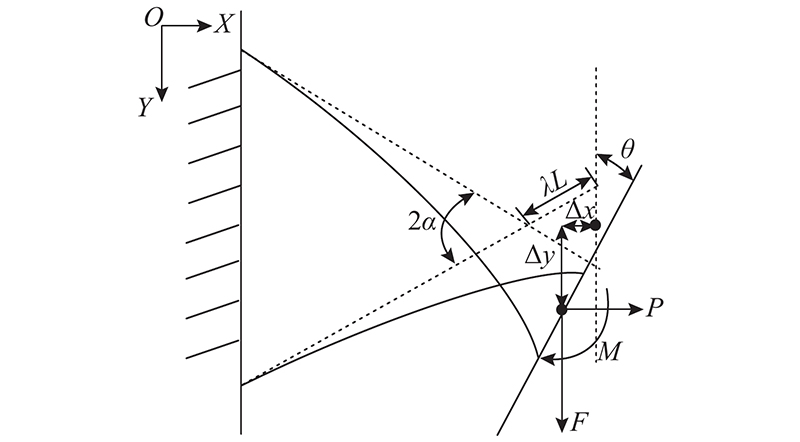
Wittrick[14]在研究交叉簧片式的柔性铰链时,得到结论:当交叉簧片柔性铰链的几何参数λ=87.3%或λ=12.7%时,铰链的轴漂最小,铰链右端活动刚体的运动最接近绕着交叉点的圆周运动. 本研究确定铰链的几何参数λ=12.7%,此时,将柔性铰链的轴漂忽略不计,则刚体中心点绕着交叉点做圆周运动,在X、Y轴上的位移Δx、Δy为转动角度θ的函数:
式(1)为子单元的受力与刚体旋转角度的静力学模型,式(2)为刚体中心点位移与旋转角度的几何方程,式(1)、(2)共同描述子单元受外力后与变形的关系.
2.2. 柔性后缘机构力学模型的建立
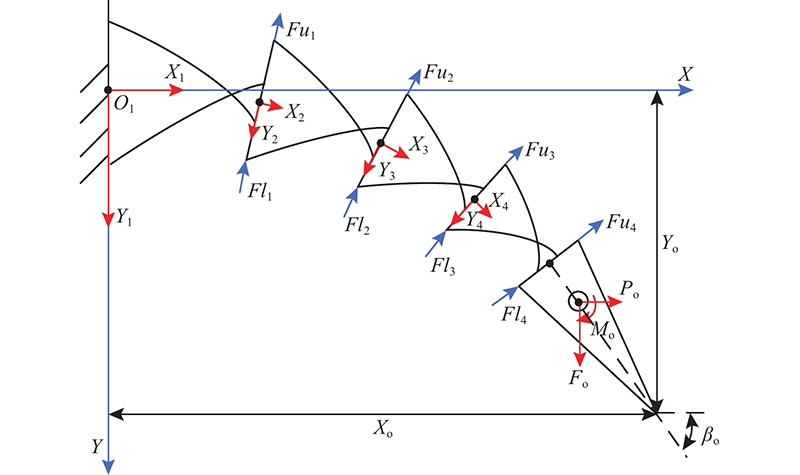
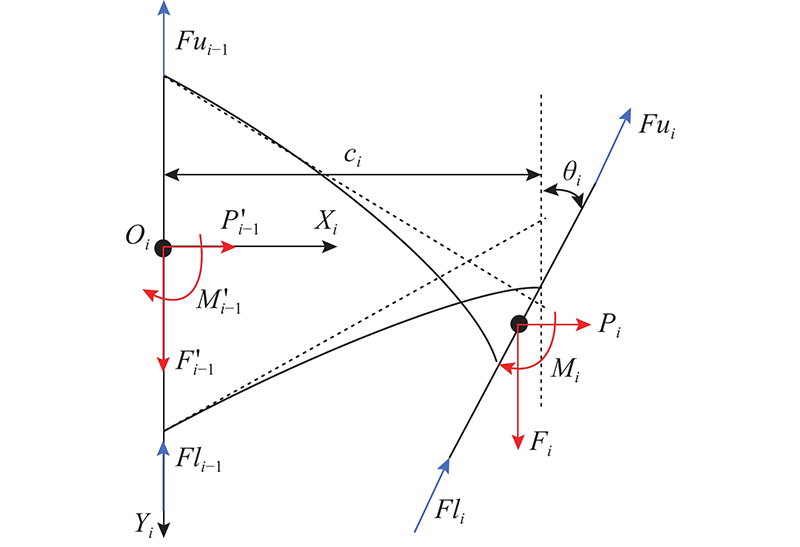
如图6所示为柔性后缘机构的受力示意图. 图中,Fo、Po和Mo分别为柔性后缘机构受到的驱动力和力矩,气动载荷会影响柔性后缘的变形,因此将上下表面蒙皮受到的气动载荷传递到柔性后缘的每个子单元上,设第i个子单元受到的上下表面气动载荷分别为Fui和Fli. Xo、Yo和βo分别为后缘末端的位置和末端刚体旋转角度. 柔性后缘机构的力学模型的建模方法借鉴链式梁约束模型[15]的思想,将整体柔性后缘机构离散为若干个子单元,每个子单元段符合子单元模型的受力及变形关系,在此基础上对每个离散子单元分别进行建模,再找出子单元间的受力平衡关系,将所有方程联立得到整体的受力和变形关系. 如图7所示, OiXiYi为第i个单元的左端刚体中心处的局部坐标系,Pi、Fi和Mi分别为第i个子单元在局部坐标系OiXiYi下受到的横向、轴向和弯矩的合力,Δxi、Δyi和θi分别为第i个子单元在局部坐标系OiXiYi下的横向位移、轴向位移和末端转角,ci为第i个子单元在未变形时所对应的弦向长度. 后缘力学模型可表示如下.
图 6
图 7
1)后缘子单元模型:
式中:
Li、Ii、λi、αi和E分别为第i个子单元所对应的结构几何参数和材料参数,每个子单元模型建立3个标量方程,一共有12个标量方程.
2)静力平衡方程. 对于第i个子单元,如图7所示,存在静力平衡关系:
式中:Pi−1
联立式(6)、(7)得到第i个单元的静力平衡方程
定义第i个单元坐标系OiXiYi对应全局坐标系OXY转动的角度为
最后一个子单元末端所受的轴向力、横向力和弯矩与驱动力的关系可以表示为
综上所述,前3个单元由式(8)建立9个标量方程和最后一个单元由式(9)建立3个标量方程,共为12个标量方程.
3)几何约束方程. 柔性后缘满足几何约束方程
式中:ctip为尾缘段刚体所对应的弦长. 综上所述,机翼后缘机构模型总计有27个标量方程,对于每个子单元,都有Pi、Fi、Mi、Δxi、Δyi和θi这6个未知参数,共24个未知参数,再加上驱动载荷Fo、Po、Mo和末端点位姿参数Xo、Yo、γ这6个参数,共有30个参数. 只要给定Fo、Po、Mo、Xo、Yo、γ中的任意3个,就可以求解出机翼后缘机构模型其余的未知参数.
将该模型推广到有任意数量子单元的情况,假设后缘由N个子单元构成,可以写出3N+3个方程,对应3N+6个参数,给定Fo、Po、Mo、Xo、Yo、γ中的任意3个,可以通过求解方程得出其余参数.
2.3. 柔性后缘机构模型的实例分析与验证
根据变弯度机翼弦长和翼型的要求,给定组成柔性后缘各个子单元形状几何参数如表1所示. 材料选用高性能尼龙材料,其弹性模量为1.3×109 Pa. 本研究不考虑气动载荷对后缘的影响,只计算在驱动力作用下的后缘变形情况.
表 1 柔性后缘子单元的形状几何参数
Tab.1
| 子单元编号 | L/mm | T/mm | W/mm | λ | α/(°) |
| 1 | 55.43 | 3.000 | 15 | 0.127 | 30 |
| 2 | 44.34 | 2.400 | 15 | 0.127 | 30 |
| 3 | 35.47 | 1.920 | 15 | 0.127 | 30 |
| 4 | 28.38 | 1.536 | 15 | 0.127 | 30 |
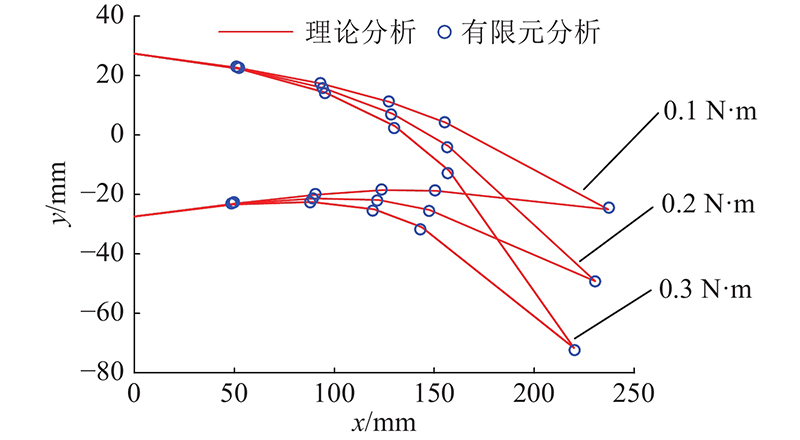
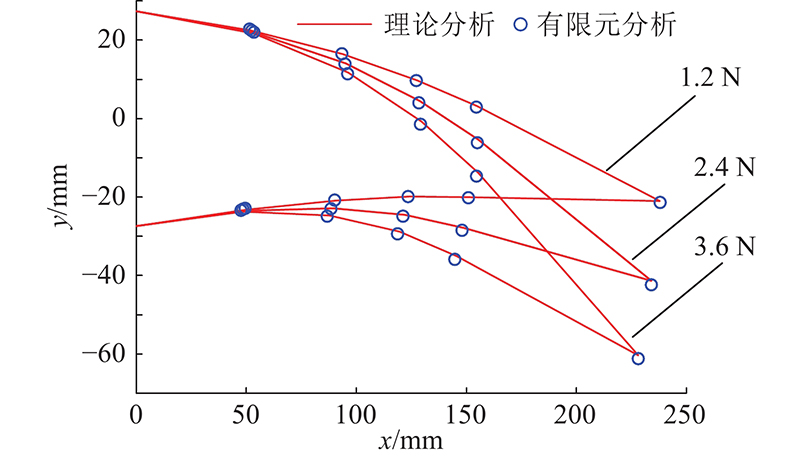
为了验证理论建模的正确性,比较理论模型分析结果与有限元模型,利用软件ANSYS Workbench,生成四面体网格单元,固定后缘左端,并在后缘右端施加驱动力和驱动力矩,计算在受力作用下的后缘变形情况. 选取翼面轮廓标志点,用有限元分析标志点坐标和理论分析标志点坐标的偏差之和SE(sum of error)作为评价指标,表达式为
式中:xi、yi为第i轮廓标志点的有限元分析横、纵坐标,
图 8
图 8 柔性后缘受弯矩时结果比较
Fig.8 Comparison of results when flexible trailing edge subjected to bending moment
图 9
图 9 柔性后缘受纵向载荷时结果比较
Fig.9 Comparison of results when flexible trailing edge subjected to longitudinal load
3. 变弯度机翼优化设计
3.1. 优化问题描述
机翼优化设计的目的是设计机翼最合理的结构参数,使飞机在给定的设计点处气动特性最优,机翼的优化设计与飞机的性能优劣有直接关系. 在力学模型中,对柔性后缘刚度影响最大的参数是后缘每个子单元的柔性梁厚度Ti,因此将Ti作为优化设计的设计变量.
选择飞机在2种设计状态的气动特性作为优化目标. 设计状态1)为马赫数Ma=0.2,雷诺数Re=6×106,攻角α=2°,后缘等效偏转角γ=5°,对应飞机的巡航阶段,要求机翼升阻比Cl/Cd最大;设计状态2)为Ma=0.1,Re=3×106,α=10°,后缘等效偏转角γ=10°,对应飞机的起降阶段,要求机翼升力系数Cl最大. 综上所述,该多目标优化问题可描述如下:目标函数为min(−Cl/Cd)1、min(−Cl)2,设计变量为T=[T1, T2, T3, T4],约束条件为2 mm≤Ti≤5 mm
3.2. 优化的流程
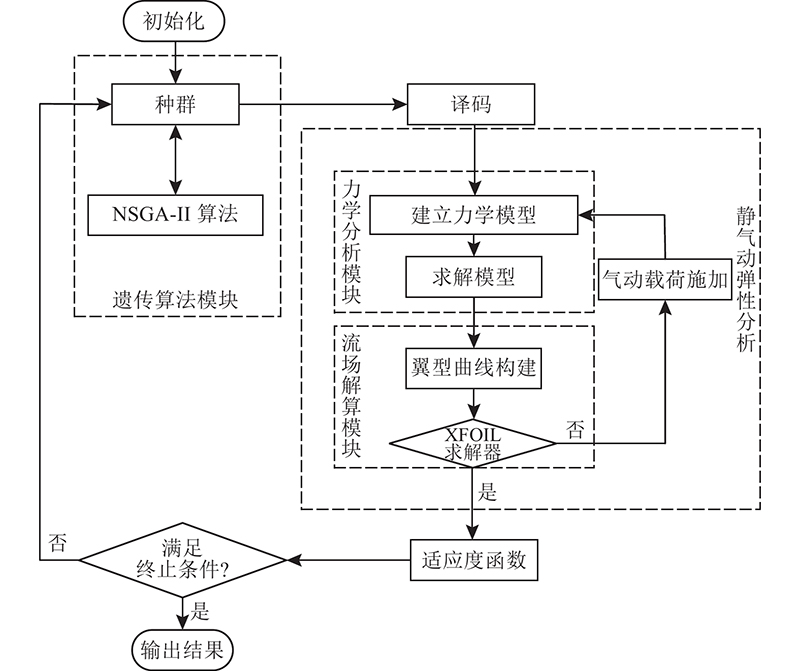
图 10
变弯度机翼算法的实现步骤如下。1)设定算法相关参数,初始化算法,得到遗传算法初始种群。2)对种群中的每个个体建立力学模型,计算出每个个体对应的机翼在驱动力作用下,达到所要求襟翼角时翼型的外轮廓标志点。3)将变形后的翼型外标志点采用NURBS(非均匀有理B样条)曲线拟合,构建出整体外形曲线。4)将参数化后的翼型曲线代入XFOIL气动力学求解器中,求解对应相应设计状态的边界条件,得到翼型的压力分布曲线。5)对翼型压力分布曲线进行分段积分处理,可得到施加在柔性后缘各个位置的气动力。6)计算在考虑气动载荷情况下的机翼后缘模型,在机翼后缘末端点位置不变的情况下求解模型,算得施加气动载荷后的翼型标志点,之后再次对翼型参数化。7)再次代入XFOIL中求解,计算出翼型的升力系数、阻力系数、升阻比等气动参数,得到适应度函数,并传递给遗传算法模块。 8)根据适应度函数值,对初始种群进行非劣排序,经过选择、交叉和变异后,得到下一代种群。9)判断是否满足终止条件。若满足,则优化算法结束,否则回到步骤2).
3.3. 优化结果分析
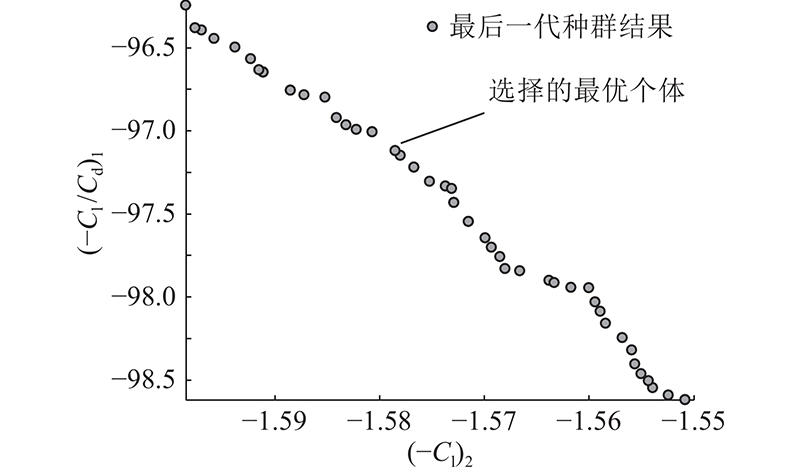
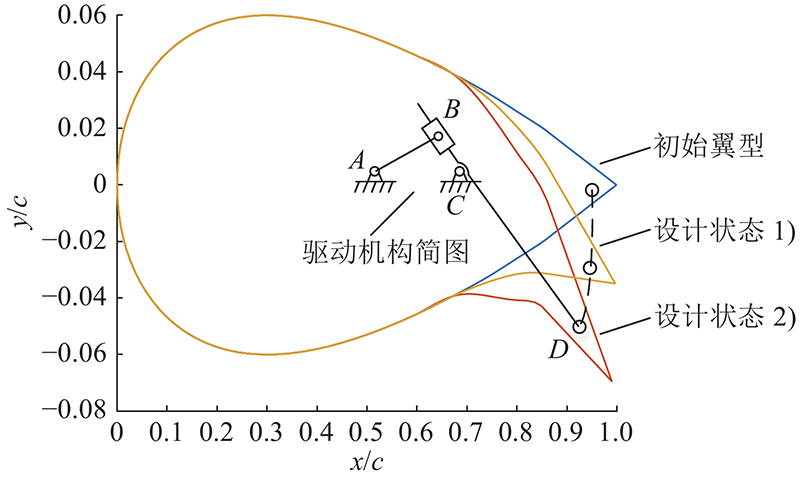
设定NSGA-II算法的种群所含个体数为50,同时遗传算法终止条件为遗传代数达到50代。经过优化算法解算后,优化问题的结果如图11所示。图中表现了最后一代种群各个个体的适应度函数值,其中纵坐标为设计状态1)对应的升阻比,横坐标为设计状态2)对应的升力系数。选择其中1个个体作为优化完成后的最优个体,该个体在Pareto前沿上,在2个优化目标间做了较好的折中。最优个体的对应设计变量的结果T=[5.00, 4.99, 3.66, 2.00]. 该结果对应的设计状态1)的升阻比和设计状态2)的升力系数分别为97.19、1.58.
图 11
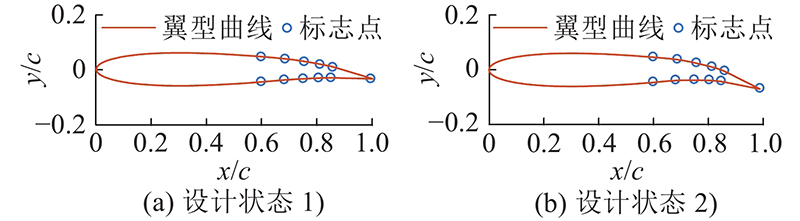
最优个体所对应的在设计状态1)、2)的翼型曲线和翼面轮廓标志点位置示意图如图12所示. 图中,c为翼型的弦长. 在设计状态1)处,交叉簧片式柔性铰链的最大转角为2.01°;在设计状态2)处,最大转角为4.76°。对应设计状态的驱动力和每个子单元偏转角度如表2所示. 表中,θi为各个子单元的偏转角,Fx、Fy为使柔性后缘变形的驱动力在x、y方向上的分力. 可知,气动载荷对每个子单元偏转角影响有限,但同时考虑气动载荷后驱动力明显变大. 由此可见,为了保证等效偏转角,机翼的气动载荷基本由驱动机构承担,对柔性后缘的变形影响较小. 将表1中的结构参数作为优化前的结构与优化后的结果相比较,可以算出,优化后的结构在设计状态1)中升阻比从96.14提升到97.19 ,提升1.09%;在设计状态2)中,升力系数从1.54提升到1.58,提升2.60%.
图 12
表 2 优化设计变量结果
Tab.2
| 飞行阶段 | θ1/(°) | θ2/(°) | θ3/(°) | θ4/(°) | Fx/N | Fy/N |
| 状态1)不考虑气动力 状态1)考虑气动力 状态2)不考虑气动力 状态2)考虑气动力 | 2.3 | 1.2 | 2.0 | 3.8 | 0 | 5.8 |
| 2.0 | 1.6 | 2.5 | 2.8 | −198 | 46.0 | |
| 4.6 | 2.5 | 4.0 | 7.5 | 0 | 12.0 | |
| 4.6 | 2.6 | 4.0 | 9.2 | −58 | 26.0 |
3.4. 驱动机构尺度优化
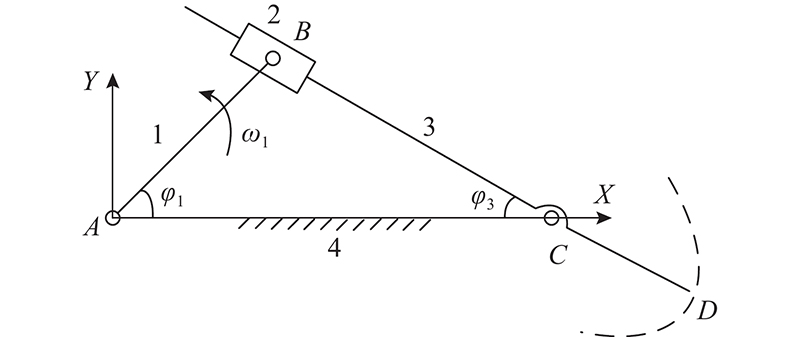
变弯度机翼的驱动机构可看作摆动导杆机构。如图13所示,驱动机构的原动件1为驱动机构中的舵机摇臂,其方位角为φ1,角速度为ω1;原动件3为驱动机构中的摇杆,其摆角为φ3. 机构末端点为D,末端点轨迹为绕着中枢点C的圆弧曲线.
图 13
建立直角坐标系,由机构中所含的封闭图形ABCA可以写出机构的封闭矢量方程:
用复数形式可以表示为
由式(14),解得
末端点D的坐标为
式中:lAB、lAC、lCD分别为AB、AC、CD的长度。由此得到驱动机构的原动件位置和各构件尺寸关于末端轨迹的关系.
驱动系统的末端轨迹为以中枢点C为圆心的圆弧曲线,如图14所示. 已知初始翼型、设计状态1)、2)的驱动机构末端点位置,由该3个位置可以确定驱动机构的末端轨迹圆弧线。根据末端轨迹线结合式(16)~(19),可以计算并确定驱动机构所有构件尺寸,保证末端轨迹线与该圆弧线重合. 经计算lAB=25.0 mm,lAC=101.0 mm,lCD=108.6 mm。结合机构的运动学模型以及各构件确定的尺寸. 计算得到当原动件摆动角度φ1=±76°时,驱动机构运动到上下极限位置;同时,计算得到当变弯度机翼达到设计状态1)、2)的位置时,其原动件摆动角度φ1=19°、44°.
图 14
4. 变弯度机翼样机实验
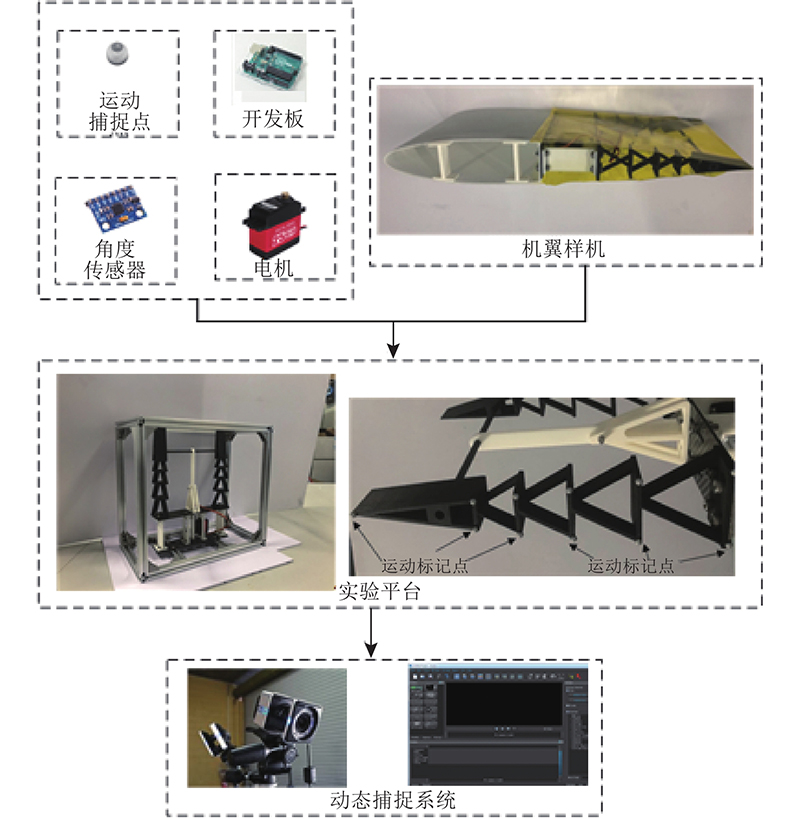
为了验证变弯度机翼的变弯度精度和变弯度能力,根据前述机翼结构建立三维模型,依据三维模型完成实物的制造和安装,并搭建实验平台如图15所示.
图 15
图 15 变弯度机翼实验平台
Fig.15 Parameter definition of flexible trailing edge sub element
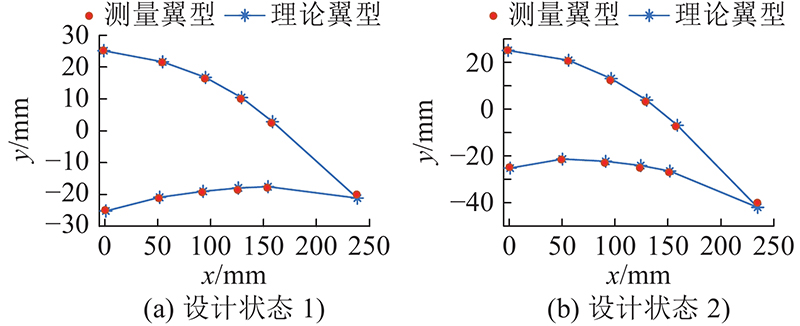
为了验证机翼的变形精度,当驱动机构原动件分别转动19 °、44 °时,驱动变弯度后缘到对应设计状态处,用动态捕捉系统对应数据处理软件Vicon Nexus读取运动标记点坐标. 将读取坐标经过坐标变换转移到机翼坐标系下,并与理论翼型相比较,如图16所示. 经计算,对于设计状态1),理论翼型所有标志点坐标和实验测得所有标志点坐标的偏差之和SE=5.9 mm;对于设计状态2),SE=9.6 mm. 偏差存在的原因,一方面是柔性后缘的力学模型存在一定误差,另一方面是驱动机构的运动副间隙. 考虑到机翼弦长为600 mm,偏差相对于机翼整体尺寸来讲较小.
图 16
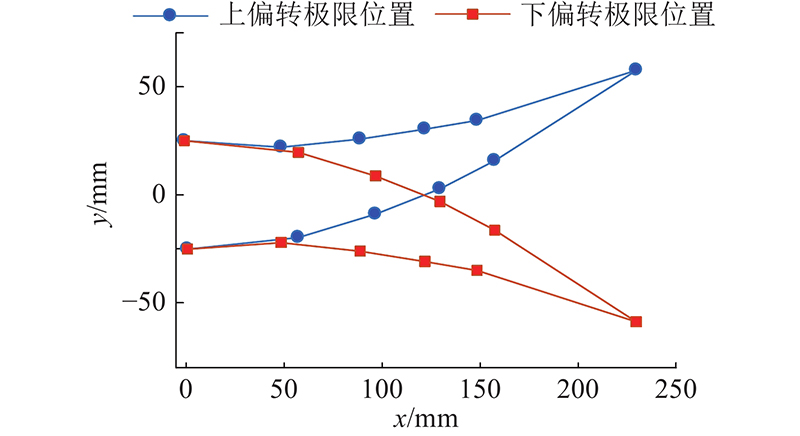
为了验证机翼变形范围,控制机翼从上极限位置运动到下极限位置,测得对应时刻的坐标数据. 机翼上、下极限位置如图17所示. 经过测量,当变弯度机翼在上、下极限位置时,y轴方向的末端坐标分别为57.7、−58.7 mm. 由此计算出变弯度机翼上、下极限位置等效偏转角分别为13.5°、−13.7°. 在达到上、下极限位置时,可测量得最大的交叉簧片柔性铰链转角为 10.08°,小于最大极限转角.
图 17
由实验结果可知,本研究所设计的变弯度机翼具有较好的变形能力,能够满足变弯度机翼的使用要求.
5. 结 论
(1)建立柔性后缘机构的力学模型,利用ANSYS对力学模型进行验证,柔性后缘标志点的位移相对误差可控制在2.15%.
(2)根据设计的机构方案和力学模型,开发基于NSGA-II遗传算法的机翼结构优化算法,经优化,机翼巡航阶段的升阻比提升1.09%,起降阶段的升力系数提高2.54%.
(3)搭建机翼实验平台,对机翼样机进行变形精度和变形范围实验。结果表明,机翼在2个设计状态处的外轮廓点坐标理论结果和实验结果的偏差之和分别为5.9、9.6 mm;变弯度机翼机构的等效偏转角为−13.5 °~13.7°,机翼具有较大的变形能力.
(4)在弦向柔性后缘变弯度机翼的研究方向,提出新颖的机构构型、系统的力学建模分析与设计方法,较好地协调了机翼变形能力与承载能力之间的矛盾,实现机翼弦向连续变弯度. 该机构可用于具有固定翼的无人机场景.
(5)本研究仅从翼型的角度出发,对提出的变弯度机翼机构进行了优化和气动仿真分析,对于分析结果,需要进一步进行风洞实验和飞行实验来验证其准确性.
参考文献
变弯度机翼技术发展研究
[J].
Research on variable camber wing technology development
[J].
Mission adaptive wing system for tactical aircraft
[J].
Modal synthesis of flexible mechanisms for airfoil shape control
[J].
Aerodynamic and aeroelastic amplification in adaptive belt-rib airfoils
[J].DOI:10.1016/j.ast.2004.07.007 [本文引用: 1]
Design of compliant mechanisms with selective compliance
[J].DOI:10.1088/0964-1726/18/11/115016 [本文引用: 1]
The design of a coated composite corrugated skin for the camber morphing airfoil
[J].DOI:10.1177/1045389X14544151 [本文引用: 1]
Fluid/structure-interaction analysis of the fish-bone-active-camber morphing concept
[J].DOI:10.2514/1.C032725 [本文引用: 1]
Type synthesis to design variable camber mechanisms
[J].
Variable stiffness material and structural concepts for morphing applications
[J].DOI:10.1016/j.paerosci.2013.07.001 [本文引用: 1]
柔性机构及其应用研究进展
[J].
State-of-art of compliant mechanisms and their applications
[J].
广义三交叉簧片柔性轴承的旋转刚度特性研究
[J].DOI:10.3901/JME.2015.13.189 [本文引用: 1]
Rotational stiffness characterization of generalized triple-cross-spring flexure pivots
[J].DOI:10.3901/JME.2015.13.189 [本文引用: 1]
Accuracy characteristics of the generalized cross-spring pivot
[J].DOI:10.1016/j.mechmachtheory.2010.05.004 [本文引用: 1]
Stiffness and stress characteristics of the generalized cross-spring pivot
[J].DOI:10.1016/j.mechmachtheory.2009.10.001 [本文引用: 1]
The properties of crossed flexure pivots, and the influence of the point at which the strips cross
[J].
Modeling large deflections of initially curved beams in compliant mechanisms using chained beam constraint model
[J].
A fast and elitist multiobjective genetic algorithm: NSGA-II
[J].DOI:10.1109/4235.996017 [本文引用: 1]
XFOIL: an analysis and design system for low Reynolds number airfoils
[J].