随着中国明确提出碳达峰、碳中和“3060”目标,以风能、光伏为代表的新能源发电形式将得到更为广泛的应用. 风电或光伏出力过程中的间歇性和随机性易造成电力系统震荡、频率稳定性破坏,甚至大规模切负荷,严重威胁电网的安全、稳定和经济运行[1-2]. 风电在短时间内受到极端天气影响导致输出功率大规模增加或减小称为风电爬坡[3]. 光伏爬坡主要由昼夜变换及短时气象条件突变素引起[4]. 探索可靠、高效的光伏或风电爬坡事件预测方法,有助于缓解电力系统调峰、调频的压力,增加电网中的风电和光伏发电消纳,降低后备电站的运营成本. 爬坡预测分为直接预测方法和间接预测方法[5-6]. 在直接预测方法中,Arias-castro等[7]建立结合云场模型的光伏爬坡预测模型,Zheng等[8]提出基于数据挖掘的风电爬坡率预测方法,实现风电爬坡的直接预测. 以上方法主要利用历史爬坡率数据进行特征识别,受制于爬坡事件数量,在数据缺乏的情况下难以有效预测小概率爬坡事件. 间接预测方法通过改进爬坡预测模型提高预测精度,是目前爬坡预测的主流方法,但对功率预测精度依赖较高. 在提升功率预测精度的研究中,Zhang等[9]建立了组合加权风电预测模型,有效提高了风电预测精度. 吴振威等[10]通过概率分布拟合得出不同时间尺度下光伏功率波动对应服从的分布,但缺乏对光伏发电波动性的定量考虑. 随着机器学习技术研究的不断深入,基于机器学习的功率预测方法不断涌现,如基于支持向量机(support vector machines, SVM)风电功率预测方法[11],基于长短期记忆(long short-term memory, LSTM)网络的风电场功率预测模型[12],基于人工神经网络(artificial neural network, ANN)和太阳辐射度的光伏爬坡预测方法[13],但该部分方法预测精度有待提升. 刘芳等[14]提出基于组合损失函数的反向传播(back propagation, BP)神经网络风力发电短期预测方法. Liu等[15]提出使用改进极限学习机(improved chicken swarm optimizer extreme learning machine, ICSOELM)预测光伏功率,效果优于传统的极限学习机与SVM模型. 上述方法虽然通过不同的途径提升了功率预测精度,但缺乏对功率时间特性的研究,该点在带有强烈间歇性和随机性的新能源预测中尤为重要. 与此同时,无论使用何种模型进行功率预测均存在不同程度的预测误差也是须考虑和研究的.
综上,本研究基于主成分分析(principal component analysis, PCA)、时序分解(seasonal-trend decomposition procedure based on loess, STL)和误差修正(error correction, EC)算法的风电功率爬坡事件预测模型. 主要贡献在于:1)提出主成分预测时序分解值(PCA-STL)模型,能够充分利用主成分特征和功率的时间特性提升预测准确度;2)在PCA-STL模型基础上提出LSTM-EC模型并应用在功率预测修正上,建立PCA-STL和LSTM-EC结合的风电或光伏功率预测模型,利用国内外真实数据集,验证模型的爬坡检测性能.
1. 爬坡事件定义
当出现雷雨与剧风极端天气条件时,风电功率显著增加,产生向上爬升事件;当风速大于切出风速时,部分风电机组会停止运行,风电功率急速下降,造成下爬坡事件. 在光伏发电中,短期的小气候变化,如瞬态云经过光伏板上空,易造成逆变器输出迅速下降,引发光伏输出功率陡降,触发光伏功率下爬坡事件[16]. Truewind[17]首次定义了新能源爬坡事件,且区分了上、下爬坡事件. Ferreira等[18]给出了与爬坡事件相关的表征量,如图1所示. 1)幅度变化,功率在爬坡事件开始和结束时间之间的变化值. 2)持续时间,功率爬坡事件开始时间和结束时间之差. 3)爬坡率,功率在爬坡时间的变化速率. 4)开始时间,爬坡事件发生的开始时间. 5)爬坡方向,根据爬坡变化方向分为上爬坡事件和下爬坡事件. 以上5个表征量反映了爬坡事件的变化程度、幅度、时间等参数.
图 1
该定义一方面体现了爬坡率的概念,另一方面清晰展示了爬坡速率的问题使检测率有所提高. 可以在对风电或光伏功率直接预测的基础上结合定义进行爬坡检测识别.
2. 爬坡事件预测模型
2.1. 模型描述
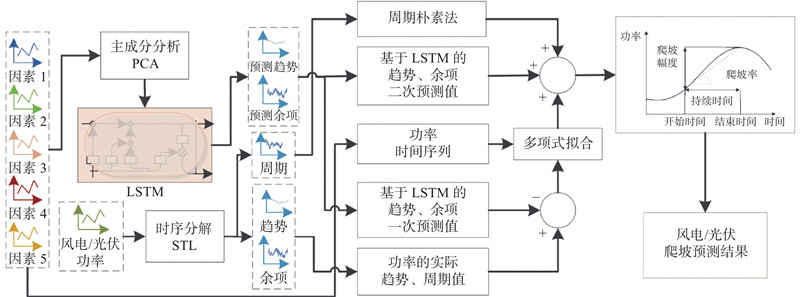
用于风电或光伏功率爬坡事件预测的模型如图2所示,由主成分预测时序分解值、预测误差修正和爬坡检测3部分组成. 对多个影响因素进行PCA降维,同时,对功率采取STL分解得到趋势、余项和周期,结合主成分建立基于LSTM的趋势和余项预测模型. LSTM是特殊的循环神经网络,解决了网络不能长期记忆的问题,相关原理见文献[20],PCA和STL分别实现了特征优化和时间特性表征. 分别计算趋势和余项的预测误差并在随后的2次预测中进行补偿,避免了系统误差累计;周期采用周期朴素法预测,与修正的趋势和余项预测值求和构成预测功率. 通过误差修正提升功率预测精度,高精度的功率预测能够增加后续爬坡事件检测准确性. 爬坡检测部分负责判断预测功率在规定时间内是否发生爬坡,具体参数根据实际环境进行调整,避免爬坡事件漏检或检测过于频繁.
图 2
2.2. PCA与STL分解
2.2.1. 基于PCA的数据降维
对风电或光伏功率产生影响的因素较多,导致风电或光伏预测中测试数据项多、样本矩阵稀疏,且个别数据噪声大、不易理解,应用风电或光伏预测模型后计算复杂,不利于测试数据的使用和显示. 为了解决以上问题,对数据降维处理. PCA多被用于解决多维数据的权属问题,降维详细流程如下.
1)构建风电或光伏数据样本矩阵,N组风电或光伏数据有m列特征,原始数据矩阵可以用N行m列的矩阵X表示,矩阵去中心化得到
2)构建风电或光伏数据样本协方差矩阵
3)对风电或光伏数据协方差阵C进行特征分解,计算协方差矩阵的特征值
4)确定风电或光伏数据主成分的个数q并构建主成分矩阵:
式中:
2.2.2. STL分解
STL分解法是时间序列分解模型,能够稳健地处理季节性数据,对异常值的包容性强,其原理参考文献[21]. 利用STL将某时刻的功率数据分解,在时间t内
式中:
STL分解主要由内循环和外循环组成,内循环更新功率的趋势分量和周期分量,外循环计算下一个内循环的鲁棒权重[22]. 利用STL方法对风电或光伏功率进行分解的流程如下. 1)去除功率趋势分量,得到去趋势序列为
经过上述流程后,风电或光伏功率时间序列能够被分解得到周期成分
在STL分解过程中须确定以下参数:循环中的观测值数量
2.2.3. 主成分与时序分解结果
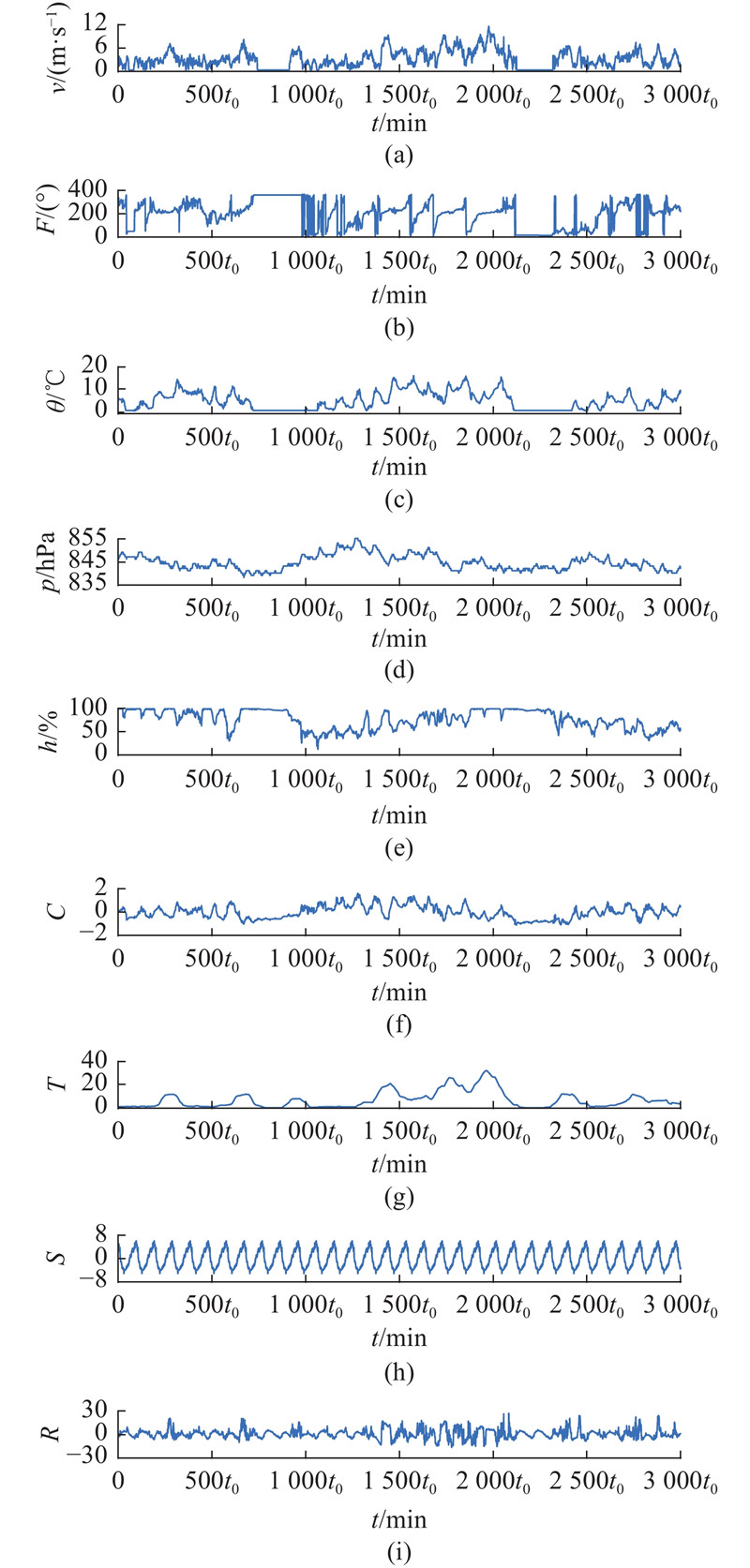
为了方便主成分预测时序分解值(PCA-STL),用PCA将风电实验数据由五维降到一维得到主成分数据.如图3(a)~(e)所示分别为风场环境中的风速v、风向F、温度θ、气压p、湿度h,如图3(f)所示为五维数据经过PCA得到的主成分信息C. 如图3(g)~(i)所示为通过STL方法分解风电功率数据得到的趋势T、周期S和余项R. 图中,t0=15 min. STL具体参数设定如下:数据采集频率为15 min,24 h共有96个点,
图 3
图 3 基于PCA与STL的风电分解结果
Fig.3 Wind power decomposition results based on PCA and STL
2.3. 功率预测修正算法
寻找系统多步预测的误差的变化规律,一方面,有助于提前发现提高模型预测精度的有益规律,以改进和修正模型;另一方面,有利于风电或光伏功率预测过程中的在线评估以及爬坡事件的及早风险发现. 在利用LSTM预测风电或光伏功率时存在一定的动态误差,当数据量较小时,模型参数更新不够充分导致误差较大. 本研究采用多项式拟合误差,参考图2的误差修正部分,风电或光伏功率实际值
在实际预测过程中,利用预测误差和时间序列建立回归拟合方程,获得误差系数ai(i = 2, 3, ··· ,m)和常数项
式中:
2.4. 整体预测步骤
基于前文的研究思路,为了完成风电和光伏爬坡事件预测,结合所提出的模型搭建步骤,给出新能源爬坡预测流程如下.
1)数据集预处理,对基于PCA的一维数据和利用STL分解功率得到的趋势
2)建立基于LSTM的风电或光伏时序值预测模型,调整LSTM神经元结构和参数,获得趋势预测值
3)再次使用LSTM模型预测风电或光伏的趋势值
4)根据爬坡定义检测风电或光伏功率
3. 实证分析
选取2个不同的数据集验证本研究所提模型.
1)国外某风电厂2018年2月1日—3月4日的运行数据,采集时间间隔为15 min,风电功率的数据特征包括风速、风向、温度、气压、湿度共5个影响因素,样本个数为3 000.
2)国内浙江省湖州市某光伏电站2018年1月1日—2月1日的运行数据,采集时间间隔为15 min,光伏功率的数据特征包括总辐射、组件温度、环境温度、气压、相对湿度共5个影响因素,样本个数为3000.
3.1. 评价指标
本研究模型测试用到的评价指标有直接预测指标和间接预测指标.
1)风电或光伏功率直接预测指标包括均方根误差(root-mean-square error,RMSE)、平均绝对误差(mean absolute error,MAE),计算式如下:
式中:N为数据量,P、
2)功率爬坡事件预测评价指标包括查准率
查准率
式中:
表 1 功率爬坡事件预测结果
Tab.1
| 风电功率爬坡事件预测结果 | 风电功率爬坡事件观测结果 | |
| 发生 | 不发生 | |
| 发生 | TP | FP |
| 不发生 | FN | TN |
3.2. 风电爬坡预测性能分析
3.2.1. 风电功率预测对比
为了验证所提模型在风电功率预测上的正确性,选择LSTM、PCA-LSTM、PS-LSTM(PCA-STL-LSTM)、文献[14]所提改进BP方法及PS-LSTM-EC(PCA-STL-LSTM-EC)进行比较. LSTM参数设置如下,隐藏单元的数量为65,求解器设置为Adam,Epoch=70,初始学习速率为0.005,以上参数保证了LSTM模型的损失收敛. 在PCA-LSTM中,数据由五维降至一维. 在PS-LSTM中,STL参数设定与2.2.3节中相同.
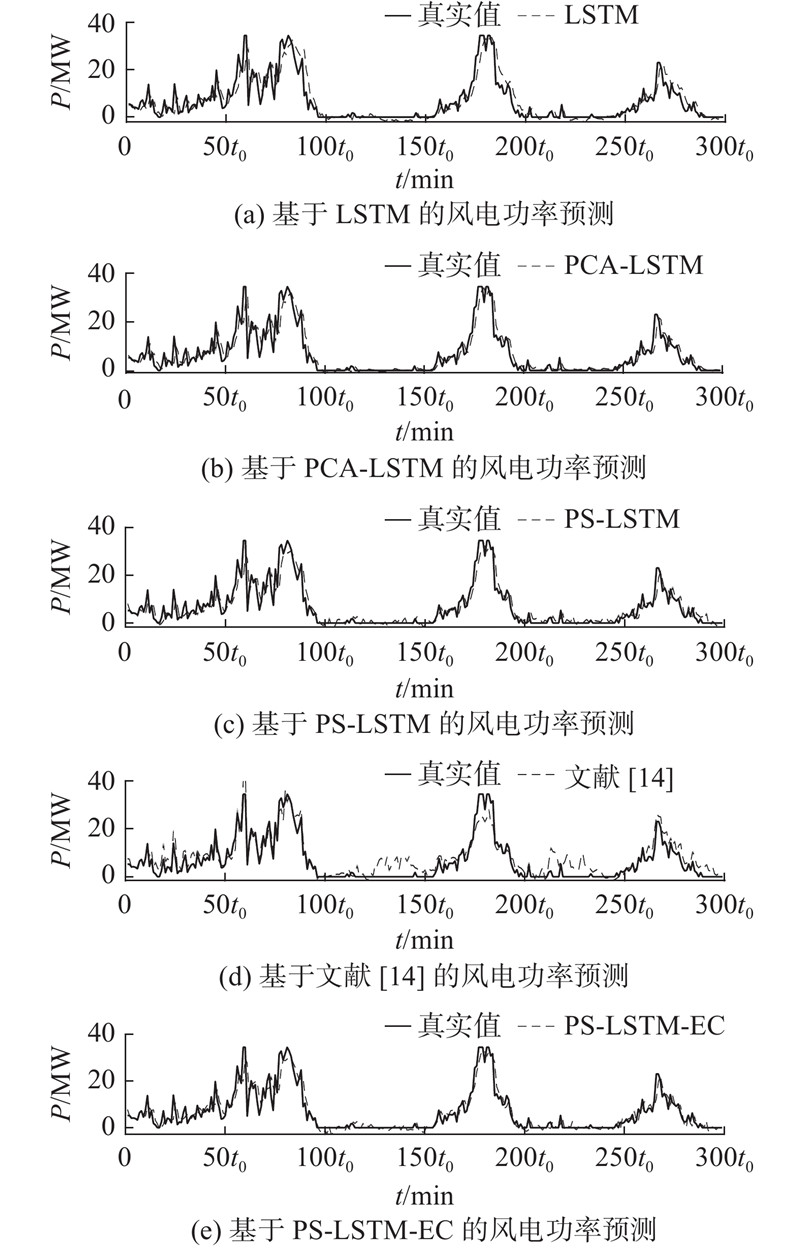
5种模型的风电功率直接预测结果如图4所示, 其中,
图 4
图 4 5种方法的风电功率预测结果与真实值的对比
Fig.4 Comparison of wind power prediction results of five methods and real values
表 2 5种方法的风电功率预测性能
Tab.2
| 模型 | RMSE/MW | MAE/MW |
| LSTM | 4.4315 | 2.8677 |
| PCA-LSTM | 4.0117 | 2.4402 |
| PS-LSTM | 3.7327 | 2.3899 |
| 文献[14] | 3.8943 | 3.0029 |
| PS-LSTM-EC | 3.6135 | 2.3206 |
3.2.2. 功率爬坡预测对比
使用预测得到的功率并基于爬坡定义对风电功率爬坡事件进行检测以验证模型爬坡的预测能力. 风电时空分布差异较大,目前对爬坡阈值尚未有统一标准,须结合实际情况确定合理阈值[23]. 在本研究中,风电装机容量
图 5
表 3 5种方法的风电爬坡预测准确性
Tab.3
| 模型 | TP | TN | FP | FN | | | |
| LSTM | 6 | 134 | 0 | 9 | 1.0000 | 0.4000 | 0.4000 |
| PCA-LSTM | 8 | 134 | 0 | 7 | 1.0000 | 0.5333 | 0.5333 |
| PS-LSTM | 9 | 134 | 0 | 5 | 1.0000 | 0.6000 | 0.6000 |
| 文献[14] | 3 | 127 | 7 | 9 | 0.3000 | 0.2500 | 0.1579 |
| PS-LSTM-EC | 10 | 134 | 0 | 5 | 1.0000 | 0.6667 | 0.6667 |
3.3. 光伏爬坡预测性能分析
3.3.1. 光伏功率预测对比
使用光伏数据集并选择LSTM、PCA-LSTM、PS-LSTM、文献[15]所提方法及PS-LSTM-EC方法进行实验比较. 由于光伏数据集与风电数据集存在差异,LSTM参数设置不同,具体参数设置如下,隐藏单元的数量为80,求解器设置为Adam,Epoch=50,初始学习速率为0.005,保证了LSTM模型的损失收敛. 在光伏预测中,PCA-LSTM和PS-LSTM中的PCA、STL参数与风电功率预测中的PCA、STL参数设置相同.
光伏功率直接预测结果图6所示. 图中,
图 6
图 6 5种方法的光伏功率预测结果与真实值的对比
Fig.6 Comparison of PV power prediction results of five methods and real values
表 4 5种方法的光伏功率预测性能
Tab.4
| 模型 | RMSE/MW | MAE/MW |
| LSTM | 7.4233 | 5.5645 |
| PCA-LSTM | 7.0877 | 4.9326 |
| PS-LSTM | 6.2524 | 4.3986 |
| 文献[15] | 17.9553 | 15.1483 |
| PS-LSTM-EC | 5.8476 | 3.8234 |
3.3.2. 功率爬坡预测对比
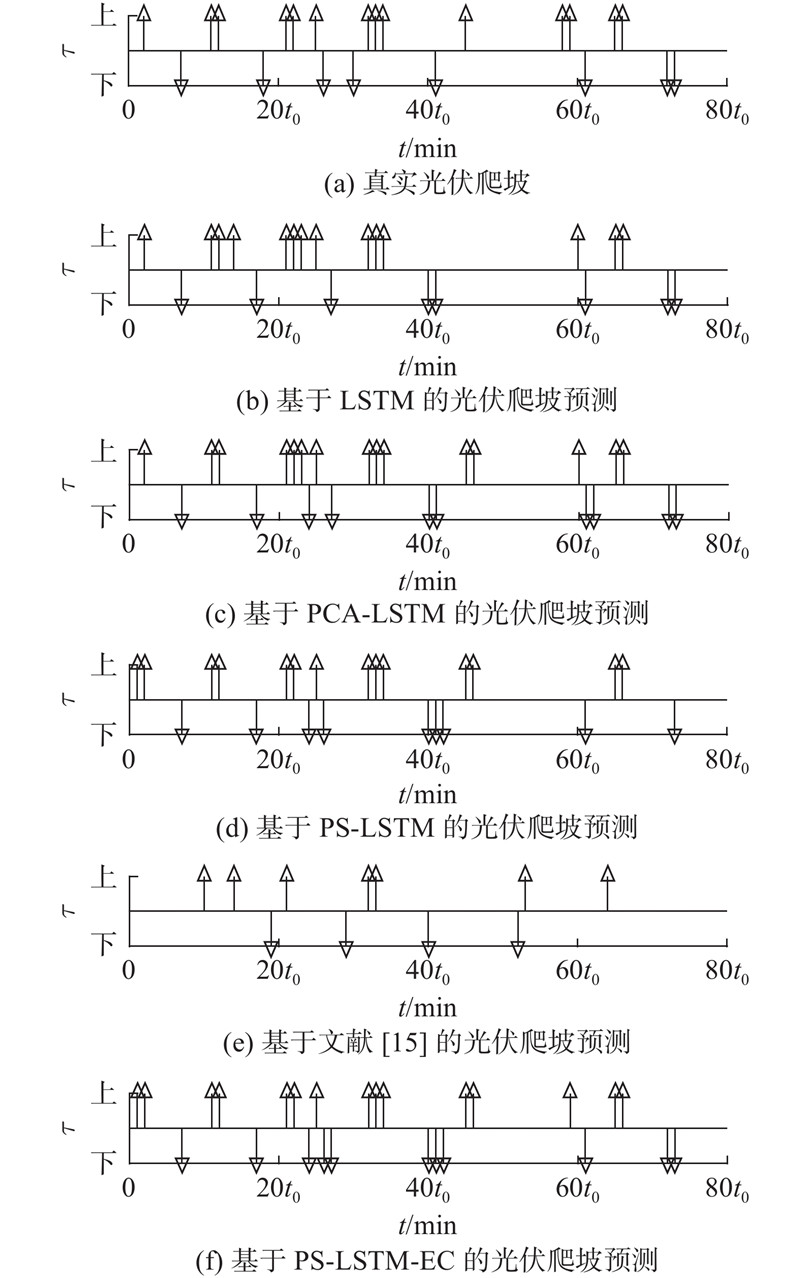
光伏装机容量
图 7
5种方法的光伏预测准确性对比如表5所示. 可以看到,PS-LSTM-EC方法的正确预报数目即TP和TN之和最高为64,误报数目FP=7,相比LSTM模型有所上升. 在PS-LSTM-EC方法的修正过程中,存在对个别值修正过度,影响了爬坡检测,漏报数目最低为3. 本研究所提模型的
表 5 5种方法的光伏爬坡预测准确性
Tab.5
| 模型 | TP | TN | FP | FN | | | |
| LSTM | 16 | 46 | 6 | 6 | 0.7273 | 0.7273 | 0.5714 |
| PCA-LSTM | 17 | 43 | 9 | 5 | 0.6538 | 0.7727 | 0.5484 |
| PS-LSTM | 17 | 45 | 7 | 5 | 0.7083 | 0.7727 | 0.5862 |
| 文献[15] | 5 | 44 | 8 | 14 | 0.3846 | 0.2632 | 0.1852 |
| PS-LSTM-EC | 19 | 45 | 7 | 3 | 0.7308 | 0.8636 | 0.6552 |
在光伏爬坡预测中,PS-LSTM-EC模型也取得了最佳的性能,表明模型能较好地预测光伏爬坡事件. 通过风电和光伏爬坡预测对比可知,无论是风电或光伏,本研究所提模型在功率直接预测和功率爬坡事件间接预测各个性能指标上均最佳,可以更准确地预测风电或光伏爬坡事件,为后续电网调度提供良好的保证,有助于风电或光伏系统的长期稳定运行.
4. 结 语
为了提高新能源爬坡事件预测精度,提出基于LSTM结合时序分解的新能源爬坡修正预测模型. 1)提出主成分预测时序分解值方法,优化LSTM网络的输入,提高功率数据的时间表征能力;2)在LSTM网络的输出部分添加误差修正算法,使得模型预测精度进一步提升,通过爬坡定义检测与匹配,完成风电或光伏爬坡事件的有效预测;3)以实际的风、光数据为例验证了模型的有效性. 本研究仍然存在一定的局限性,如缺乏对爬坡定义的优化,仅利用已有的爬坡定义直接进行爬坡事件预测,数据噪声会影响爬坡事件的检测率,可以考虑对定义及阈值模糊化处理,在光伏预测中,须进一步结合数值天气预报,提高模型预测性能.
参考文献
Development and calibration of an open source, low-cost power smart meter prototype for PV household-prosumers
[J].
基于风过程方法的风电功率预测结果不确定性估计
[J].
Uncertainty estimation of wind power prediction result based on wind process method
[J].
Identifying wind power ramp causes from multivariate datasets: a methodological proposal and its application to reanalysis data
[J].DOI:10.1049/iet-rpg.2014.0457 [本文引用: 1]
Sensitivity analysis of photovoltaic system design parameters to passively mitigate ramp rates
[J].DOI:10.1109/JPHOTOV.2020.3045679 [本文引用: 1]
A new hill climbing maximum power tracking control for wind turbines with inertial effect compensation
[J].DOI:10.1109/TIE.2019.2907510 [本文引用: 1]
Prediction of wind power ramp events based on residual correction
[J].DOI:10.1016/j.renene.2019.01.049 [本文引用: 1]
A poisson model for anisotropic solar ramp rate correlations
[J].DOI:10.1016/j.solener.2013.12.028 [本文引用: 1]
Prediction of wind farm power ramp rates: a data-mining approach
[J].DOI:10.1115/1.3142727 [本文引用: 2]
Wind power prediction based on variational mode decomposition multi-frequency combinations
[J].DOI:10.1007/s40565-018-0471-8 [本文引用: 1]
多时间尺度的光伏出力波动特性研究
[J].DOI:10.3969/j.issn.1007-2322.2014.01.011 [本文引用: 1]
Study on fluctuations characteristics of photovoltaic power output in different time scales
[J].DOI:10.3969/j.issn.1007-2322.2014.01.011 [本文引用: 1]
Forecasting model for wind power integrating least squares support vector machine, singular spectrum analysis, deep belief network, and locality-sensitive hashing
[J].
基于长短期记忆网络的风电场发电功率超短期预测
[J].
Short-term wind power forecasting based on LSTM
[J].
Real-time forecasting of solar irradiance ramps with smart image processing
[J].DOI:10.1016/j.solener.2015.01.024 [本文引用: 1]
基于组合损失函数的BP神经网络风力发电短期预测方法
[J].
Short-term forecasting method of wind power generation based on BP neural network with combined loss function
[J].
Prediction short-term photovoltaic power using improved chicken swarm optimizer-extreme learning machine model
[J].DOI:10.1016/j.jclepro.2019.119272 [本文引用: 5]
Solar power ramp event forewarning with limited historical observations
[J].DOI:10.1109/TIA.2019.2934935 [本文引用: 1]
新能源爬坡事件综述及展望
[J].
Review and prospect of renewable energy ramp events
[J].
基于双尺度长短期记忆网络的交通事故量预测模型
[J].
Traffic accident quantity prediction model based on dual-scale long short-term memory network
[J].
STL: a seasonal-trend decomposition procedure based on loess
[J].
基于季节分解和长短期记忆的北京市鸡蛋价格预测
[J].DOI:10.11975/j.issn.1002-6819.2020.09.038 [本文引用: 1]
Egg price forecasting in Beijing market using seasonal-trend decomposition procedures based on seasonal decomposition and long-short term memory
[J].DOI:10.11975/j.issn.1002-6819.2020.09.038 [本文引用: 1]