[2]
陈彦敏, 王皓, 马建辉, 等 基于层级注意力机制的互联网用户信用评估框架
[J]. 计算机研究与发展 , 2020 , 57 (8 ): 1755 - 1768
DOI:10.7544/issn1000-1239.2020.20200217
[本文引用: 1]
CHEN Yan-min, WANG Hao, MA Jian-hui, et al A hierarchical attention mechanism framework for internet credit evaluation
[J]. Journal of Computer Research and Development , 2020 , 57 (8 ): 1755 - 1768
DOI:10.7544/issn1000-1239.2020.20200217
[本文引用: 1]
[3]
GU Y, YANG X, PENG M, et al Robust weighted SVD-type latent factor models for rating prediction
[J]. Expert Systems with Applications , 2020 , 141 : 112885
DOI:10.1016/j.eswa.2019.112885
[本文引用: 2]
[4]
EKSTRAND M D, RIEDL J T, KONSTAN J A. Collaborative filtering recommender systems [M]. Boston: Now Publishers Inc, 2011.
[5]
黄璐, 林川杰, 何军, 等 融合主题模型和协同过滤的多样化移动应用推荐
[J]. 软件学报 , 2017 , 28 (3 ): 708 - 720
[本文引用: 1]
HUANG Lu, LIN Chuan-jie, HE Jun, et al Diversified mobile app recommendation combining topic model and collaborative filtering
[J]. Journal of Software , 2017 , 28 (3 ): 708 - 720
[本文引用: 1]
[6]
LIU D R, LAI C H, LEE W J A hybrid of sequential rules and collaborative filtering for product recommendation
[J]. Information Sciences , 2009 , 179 (20 ): 3505 - 3519
DOI:10.1016/j.ins.2009.06.004
[本文引用: 1]
[7]
JARBOUI F, GRUSON-DANIEL C, DURMUS A, et al. Markov decision process for MOOC users behavioral inference [C]// European MOOCs Stakeholders Summit . Naples: Springer, 2019: 70-80.
[本文引用: 1]
[8]
HIDASI B, KARATZOGLOU A, BALTRUNAS L, et al. Session-based recommendations with recurrent neural networks[EB/OL]. [2021-10-10]. https://arxiv.org/abs/1511.06939.
[本文引用: 4]
[9]
CHO K, VAN MERRIËNB B, GULCEHRE C, et al. Learning phrase representations using RNN encoder-decoder for statistical machine translation [EB/OL]. [2021-10-10]. https://arxiv.org/abs/1406.1078.
[本文引用: 2]
[10]
YU Z, LIAN J, MAHMOODY A, et al. Adaptive user modeling with long and short-term preferences for personalized recommendation [C]// Proceedings of the 28th International Joint Conference on Artificial Intelligence . Macao: AAAI Press, 2019: 4213-4219.
[本文引用: 1]
[11]
SHEIL H, RANA O. Classifying and recommending using gradient boosted machines and vector space models [C]// UK Workshop on Computational Intelligence . Nottingham: Springer, 2017: 214-221.
[本文引用: 1]
[12]
TANG J, WANG K. Personalized top-n sequential recommendation via convolutional sequence embedding [C]// Proceedings of the 11th ACM International Conference on Web Search and Data Mining . [S.l.] : ACM, 2018: 565-573.
[本文引用: 3]
[13]
刘浩翰, 吕鑫, 李建伏 考虑用户意图和时间间隔的会话型深度学习推荐系统
[J]. 计算机应用与软件 , 2021 , 38 (3 ): 190 - 195
[本文引用: 1]
LIU Hao-han, LV Xin, LI Jian-fu A session based deeplearning recommendation system considering userpurpose and time interval
[J]. Computer Applications and Software , 2021 , 38 (3 ): 190 - 195
[本文引用: 1]
[14]
CAO L, PHILIP S Y Behavior informatics: an informatics perspective for behavior studies
[J]. IEEE Intelligent Informatics Bulletin , 2009 , 10 (1 ): 6 - 11
[本文引用: 1]
[15]
WANG J, HUANG P, ZHAO H, et al. Billion-scale commodity embedding for e-commerce recommendation in Alibaba [C]// Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining . London: ACM, 2018: 839-848.
[本文引用: 2]
[16]
PEROZZI B, AL-RFOU R, SKIENA S. Deepwalk: online learning of social representations [C]// Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining . New York: ACM, 2014: 701-710.
[本文引用: 1]
[17]
MIKOLOV T, CHEN K, CORRADO G, et al. Efficient estimation of word representations in vector space [EB/OL]. [2021-10-10]. https://arxiv.org/abs/1301.3781.
[本文引用: 1]
[19]
岳希, 唐聃, 舒红平, 等 基于数据稀疏性的协同过滤推荐算法改进研究
[J]. 工程科学与技术 , 2020 , 52 (1 ): 198 - 202
[本文引用: 1]
YUE Xi, TANG Dan, SHU Hong-ping, et al Research on improvement of collaborative filtering recommendation algorithm based on data sparseness
[J]. Advanced Engineering Sciences , 2020 , 52 (1 ): 198 - 202
[本文引用: 1]
[20]
WARSHAW P R, DAVIS F D Disentangling behavioral intention and behavioral expectation
[J]. Journal of Experimental Social Psychology , 1985 , 21 (3 ): 213 - 228
DOI:10.1016/0022-1031(85)90017-4
[本文引用: 2]
[22]
HAN J, PEI J, MORTAZAVI-ASL B, et al. Prefixspan: mining sequential patterns efficiently by prefix-projected pattern growth [C]// Proceedings of the 17th International Conference on Data Engineering . Heidelberg: IEEE, 2001: 215-224.
[本文引用: 1]
[23]
MovieLens 1M dataset [DB/OL]. [2021-10-10]. https://grouplens.org/datasets/movielens/1m/.
[本文引用: 1]
[24]
HARPER F M, KONSTAN J A The movielens datasets: history and context
[J]. ACM Transactions on Interactive Intelligent Systems , 2015 , 5 (4 ): 1 - 19
[本文引用: 1]
[25]
RecSys2015 [DB/OL]. [2021-10-10]. https://recsys.acm.org/recs ys15/.
[本文引用: 1]
[26]
MCAULEY J. Amazon product data [DB/OL]. [2021-10-10]. http://jmcauley.ucsd.edu/data/amazon/.
[本文引用: 1]
[27]
MCAULEY J, TARGETT C, SHI Q, et al. Image-based recommendations on styles and substitutes [C]// Proceedings of the 38th International ACM SIGIR Conference on Research and Development in Information Retrieval . Santiago: ACM, 2015: 43-52.
[本文引用: 1]
[28]
YUAN Q, CONG G, SUN A. Graph-based point-of-interest recommendation with geographical and temporal influences [C]// Proceedings of the 23rd ACM International Conference on Conference on Information and Knowledge Management . Shanghai: ACM, 2014: 659-668.
[本文引用: 1]
[29]
ZHAO S L, ZHAO T, YANG H Q, et al. Stellar: spatial-temporal latent ranking for successive point-of-interest recommendation [C]// Proceedings of the 30th AAAI Conference on Artificial Intelligence . Phoenix: AAAI Press, 2016: 315–321.
[本文引用: 1]
[30]
LINDEN G, SMITH B, YORK J Amazon. com recommendations: item-to-item collaborative filtering
[J]. IEEE Internet Computing , 2003 , 7 (1 ): 76 - 80
DOI:10.1109/MIC.2003.1167344
[本文引用: 1]
[31]
RENDLE S, FREUDENTHALER C, GANTNER Z, et al. BPR: Bayesian personalized ranking from implicit feedback [EB/OL]. [2021-10-10]. https://arxiv.org/abs/1205.2618.
[本文引用: 1]
[32]
LI J, REN P, CHEN Z, et al. Neural attentive session-based recommendation [C]// Proceedings of the 2017 ACM on Conference on Information and Knowledge Management . Singapore: ACM, 2017: 1419–1428.
[本文引用: 2]
[33]
KINGMA D P, BA J. Adam: a method for stochastic optimization[EB/OL]. [2021-10-10]. https://arxiv.org/abs/1412.6980.
[本文引用: 1]
基于评分矩阵与评论文本的深度推荐模型
1
2020
... 互联网上沉淀了海量的用户行为数据,例如视频的观看和评分,商品的点击和购买,社交网站的发帖和点赞等. 这些数据蕴含丰富的行为信息,对其进行研究可以有效解决“信息过载”问题,提高需求匹配效率,给用户提供更好的服务. 在商业场景[1 ] 、社会治理[2 ] 领域具有巨大的应用前景,是当前的研究热点. ...
基于评分矩阵与评论文本的深度推荐模型
1
2020
... 互联网上沉淀了海量的用户行为数据,例如视频的观看和评分,商品的点击和购买,社交网站的发帖和点赞等. 这些数据蕴含丰富的行为信息,对其进行研究可以有效解决“信息过载”问题,提高需求匹配效率,给用户提供更好的服务. 在商业场景[1 ] 、社会治理[2 ] 领域具有巨大的应用前景,是当前的研究热点. ...
基于层级注意力机制的互联网用户信用评估框架
1
2020
... 互联网上沉淀了海量的用户行为数据,例如视频的观看和评分,商品的点击和购买,社交网站的发帖和点赞等. 这些数据蕴含丰富的行为信息,对其进行研究可以有效解决“信息过载”问题,提高需求匹配效率,给用户提供更好的服务. 在商业场景[1 ] 、社会治理[2 ] 领域具有巨大的应用前景,是当前的研究热点. ...
基于层级注意力机制的互联网用户信用评估框架
1
2020
... 互联网上沉淀了海量的用户行为数据,例如视频的观看和评分,商品的点击和购买,社交网站的发帖和点赞等. 这些数据蕴含丰富的行为信息,对其进行研究可以有效解决“信息过载”问题,提高需求匹配效率,给用户提供更好的服务. 在商业场景[1 ] 、社会治理[2 ] 领域具有巨大的应用前景,是当前的研究热点. ...
Robust weighted SVD-type latent factor models for rating prediction
2
2020
... 传统用户行为分析模型聚焦于用户历史行为中的静态行为模式挖掘,如基于矩阵分解的SVD算法[3 ] 将用户的单个行为当成独立的记录[3 -5 ] . 这类方法丢失了行为记录中的序列信息,忽视了用户行为模式的动态变化. 针对行为序列建模问题已经有不少研究. 在机器学习方面,Liu等[6 ] 通过基于统计的行为模式挖掘得到显式的关联规则,但忽略了不可观测的模式,也没有考虑行为的时间跨度和对行为进行更细粒度的研究. Jarboui等[7 ] 使用马尔科夫决策过程(Markov decision process, MDP)预测慕课用户的行为. 近年来,基于神经网络的深度学习方法也被广泛应用于序列行为建模. 如Hidasi等[8 ] 提出的GRU4Rec模型首次用门控循环单元(gated recurrent unit, GRU)[9 ] 进行序列行为预测. Yu等[10 ] 在长短期记忆神经网络(long short-term memory, LSTM)中加入时间感知控制器和内容感知控制器,使得状态更新时能充分考虑上下文信息. 以上方法考虑了行为的先后关系,但仍忽视行为的不确定性问题. 行为并不全是有意识的,其中可能存在很多的噪声[11 ] . L阶马尔可夫链或仅含有循环神经网络(recurrent neural networks, RNNs)的模型,均基于前一行为对紧邻的下一行为有直接影响的假设,因此无法表述行为模式的不确定性. Tang等[12 ] 提出基于卷积神经网络的Caser模型,根据序列的时间维度和行为表征的隐藏维度将近期若干行为作为二维矩阵数据,基于水平和垂直卷积,Caser模型可以学习到包含跳跃特点的行为模式,能在一定程度上解决行为不确定性问题,但Caser模型学习复杂不确定行为关系的能力受到卷积核大小的影响. 刘浩翰等[13 ] 则利用注意力机制来消除无目的点击行为对捕获主要意图的影响. ...
... [3 -5 ]. 这类方法丢失了行为记录中的序列信息,忽视了用户行为模式的动态变化. 针对行为序列建模问题已经有不少研究. 在机器学习方面,Liu等[6 ] 通过基于统计的行为模式挖掘得到显式的关联规则,但忽略了不可观测的模式,也没有考虑行为的时间跨度和对行为进行更细粒度的研究. Jarboui等[7 ] 使用马尔科夫决策过程(Markov decision process, MDP)预测慕课用户的行为. 近年来,基于神经网络的深度学习方法也被广泛应用于序列行为建模. 如Hidasi等[8 ] 提出的GRU4Rec模型首次用门控循环单元(gated recurrent unit, GRU)[9 ] 进行序列行为预测. Yu等[10 ] 在长短期记忆神经网络(long short-term memory, LSTM)中加入时间感知控制器和内容感知控制器,使得状态更新时能充分考虑上下文信息. 以上方法考虑了行为的先后关系,但仍忽视行为的不确定性问题. 行为并不全是有意识的,其中可能存在很多的噪声[11 ] . L阶马尔可夫链或仅含有循环神经网络(recurrent neural networks, RNNs)的模型,均基于前一行为对紧邻的下一行为有直接影响的假设,因此无法表述行为模式的不确定性. Tang等[12 ] 提出基于卷积神经网络的Caser模型,根据序列的时间维度和行为表征的隐藏维度将近期若干行为作为二维矩阵数据,基于水平和垂直卷积,Caser模型可以学习到包含跳跃特点的行为模式,能在一定程度上解决行为不确定性问题,但Caser模型学习复杂不确定行为关系的能力受到卷积核大小的影响. 刘浩翰等[13 ] 则利用注意力机制来消除无目的点击行为对捕获主要意图的影响. ...
融合主题模型和协同过滤的多样化移动应用推荐
1
2017
... 传统用户行为分析模型聚焦于用户历史行为中的静态行为模式挖掘,如基于矩阵分解的SVD算法[3 ] 将用户的单个行为当成独立的记录[3 -5 ] . 这类方法丢失了行为记录中的序列信息,忽视了用户行为模式的动态变化. 针对行为序列建模问题已经有不少研究. 在机器学习方面,Liu等[6 ] 通过基于统计的行为模式挖掘得到显式的关联规则,但忽略了不可观测的模式,也没有考虑行为的时间跨度和对行为进行更细粒度的研究. Jarboui等[7 ] 使用马尔科夫决策过程(Markov decision process, MDP)预测慕课用户的行为. 近年来,基于神经网络的深度学习方法也被广泛应用于序列行为建模. 如Hidasi等[8 ] 提出的GRU4Rec模型首次用门控循环单元(gated recurrent unit, GRU)[9 ] 进行序列行为预测. Yu等[10 ] 在长短期记忆神经网络(long short-term memory, LSTM)中加入时间感知控制器和内容感知控制器,使得状态更新时能充分考虑上下文信息. 以上方法考虑了行为的先后关系,但仍忽视行为的不确定性问题. 行为并不全是有意识的,其中可能存在很多的噪声[11 ] . L阶马尔可夫链或仅含有循环神经网络(recurrent neural networks, RNNs)的模型,均基于前一行为对紧邻的下一行为有直接影响的假设,因此无法表述行为模式的不确定性. Tang等[12 ] 提出基于卷积神经网络的Caser模型,根据序列的时间维度和行为表征的隐藏维度将近期若干行为作为二维矩阵数据,基于水平和垂直卷积,Caser模型可以学习到包含跳跃特点的行为模式,能在一定程度上解决行为不确定性问题,但Caser模型学习复杂不确定行为关系的能力受到卷积核大小的影响. 刘浩翰等[13 ] 则利用注意力机制来消除无目的点击行为对捕获主要意图的影响. ...
融合主题模型和协同过滤的多样化移动应用推荐
1
2017
... 传统用户行为分析模型聚焦于用户历史行为中的静态行为模式挖掘,如基于矩阵分解的SVD算法[3 ] 将用户的单个行为当成独立的记录[3 -5 ] . 这类方法丢失了行为记录中的序列信息,忽视了用户行为模式的动态变化. 针对行为序列建模问题已经有不少研究. 在机器学习方面,Liu等[6 ] 通过基于统计的行为模式挖掘得到显式的关联规则,但忽略了不可观测的模式,也没有考虑行为的时间跨度和对行为进行更细粒度的研究. Jarboui等[7 ] 使用马尔科夫决策过程(Markov decision process, MDP)预测慕课用户的行为. 近年来,基于神经网络的深度学习方法也被广泛应用于序列行为建模. 如Hidasi等[8 ] 提出的GRU4Rec模型首次用门控循环单元(gated recurrent unit, GRU)[9 ] 进行序列行为预测. Yu等[10 ] 在长短期记忆神经网络(long short-term memory, LSTM)中加入时间感知控制器和内容感知控制器,使得状态更新时能充分考虑上下文信息. 以上方法考虑了行为的先后关系,但仍忽视行为的不确定性问题. 行为并不全是有意识的,其中可能存在很多的噪声[11 ] . L阶马尔可夫链或仅含有循环神经网络(recurrent neural networks, RNNs)的模型,均基于前一行为对紧邻的下一行为有直接影响的假设,因此无法表述行为模式的不确定性. Tang等[12 ] 提出基于卷积神经网络的Caser模型,根据序列的时间维度和行为表征的隐藏维度将近期若干行为作为二维矩阵数据,基于水平和垂直卷积,Caser模型可以学习到包含跳跃特点的行为模式,能在一定程度上解决行为不确定性问题,但Caser模型学习复杂不确定行为关系的能力受到卷积核大小的影响. 刘浩翰等[13 ] 则利用注意力机制来消除无目的点击行为对捕获主要意图的影响. ...
A hybrid of sequential rules and collaborative filtering for product recommendation
1
2009
... 传统用户行为分析模型聚焦于用户历史行为中的静态行为模式挖掘,如基于矩阵分解的SVD算法[3 ] 将用户的单个行为当成独立的记录[3 -5 ] . 这类方法丢失了行为记录中的序列信息,忽视了用户行为模式的动态变化. 针对行为序列建模问题已经有不少研究. 在机器学习方面,Liu等[6 ] 通过基于统计的行为模式挖掘得到显式的关联规则,但忽略了不可观测的模式,也没有考虑行为的时间跨度和对行为进行更细粒度的研究. Jarboui等[7 ] 使用马尔科夫决策过程(Markov decision process, MDP)预测慕课用户的行为. 近年来,基于神经网络的深度学习方法也被广泛应用于序列行为建模. 如Hidasi等[8 ] 提出的GRU4Rec模型首次用门控循环单元(gated recurrent unit, GRU)[9 ] 进行序列行为预测. Yu等[10 ] 在长短期记忆神经网络(long short-term memory, LSTM)中加入时间感知控制器和内容感知控制器,使得状态更新时能充分考虑上下文信息. 以上方法考虑了行为的先后关系,但仍忽视行为的不确定性问题. 行为并不全是有意识的,其中可能存在很多的噪声[11 ] . L阶马尔可夫链或仅含有循环神经网络(recurrent neural networks, RNNs)的模型,均基于前一行为对紧邻的下一行为有直接影响的假设,因此无法表述行为模式的不确定性. Tang等[12 ] 提出基于卷积神经网络的Caser模型,根据序列的时间维度和行为表征的隐藏维度将近期若干行为作为二维矩阵数据,基于水平和垂直卷积,Caser模型可以学习到包含跳跃特点的行为模式,能在一定程度上解决行为不确定性问题,但Caser模型学习复杂不确定行为关系的能力受到卷积核大小的影响. 刘浩翰等[13 ] 则利用注意力机制来消除无目的点击行为对捕获主要意图的影响. ...
1
... 传统用户行为分析模型聚焦于用户历史行为中的静态行为模式挖掘,如基于矩阵分解的SVD算法[3 ] 将用户的单个行为当成独立的记录[3 -5 ] . 这类方法丢失了行为记录中的序列信息,忽视了用户行为模式的动态变化. 针对行为序列建模问题已经有不少研究. 在机器学习方面,Liu等[6 ] 通过基于统计的行为模式挖掘得到显式的关联规则,但忽略了不可观测的模式,也没有考虑行为的时间跨度和对行为进行更细粒度的研究. Jarboui等[7 ] 使用马尔科夫决策过程(Markov decision process, MDP)预测慕课用户的行为. 近年来,基于神经网络的深度学习方法也被广泛应用于序列行为建模. 如Hidasi等[8 ] 提出的GRU4Rec模型首次用门控循环单元(gated recurrent unit, GRU)[9 ] 进行序列行为预测. Yu等[10 ] 在长短期记忆神经网络(long short-term memory, LSTM)中加入时间感知控制器和内容感知控制器,使得状态更新时能充分考虑上下文信息. 以上方法考虑了行为的先后关系,但仍忽视行为的不确定性问题. 行为并不全是有意识的,其中可能存在很多的噪声[11 ] . L阶马尔可夫链或仅含有循环神经网络(recurrent neural networks, RNNs)的模型,均基于前一行为对紧邻的下一行为有直接影响的假设,因此无法表述行为模式的不确定性. Tang等[12 ] 提出基于卷积神经网络的Caser模型,根据序列的时间维度和行为表征的隐藏维度将近期若干行为作为二维矩阵数据,基于水平和垂直卷积,Caser模型可以学习到包含跳跃特点的行为模式,能在一定程度上解决行为不确定性问题,但Caser模型学习复杂不确定行为关系的能力受到卷积核大小的影响. 刘浩翰等[13 ] 则利用注意力机制来消除无目的点击行为对捕获主要意图的影响. ...
4
... 传统用户行为分析模型聚焦于用户历史行为中的静态行为模式挖掘,如基于矩阵分解的SVD算法[3 ] 将用户的单个行为当成独立的记录[3 -5 ] . 这类方法丢失了行为记录中的序列信息,忽视了用户行为模式的动态变化. 针对行为序列建模问题已经有不少研究. 在机器学习方面,Liu等[6 ] 通过基于统计的行为模式挖掘得到显式的关联规则,但忽略了不可观测的模式,也没有考虑行为的时间跨度和对行为进行更细粒度的研究. Jarboui等[7 ] 使用马尔科夫决策过程(Markov decision process, MDP)预测慕课用户的行为. 近年来,基于神经网络的深度学习方法也被广泛应用于序列行为建模. 如Hidasi等[8 ] 提出的GRU4Rec模型首次用门控循环单元(gated recurrent unit, GRU)[9 ] 进行序列行为预测. Yu等[10 ] 在长短期记忆神经网络(long short-term memory, LSTM)中加入时间感知控制器和内容感知控制器,使得状态更新时能充分考虑上下文信息. 以上方法考虑了行为的先后关系,但仍忽视行为的不确定性问题. 行为并不全是有意识的,其中可能存在很多的噪声[11 ] . L阶马尔可夫链或仅含有循环神经网络(recurrent neural networks, RNNs)的模型,均基于前一行为对紧邻的下一行为有直接影响的假设,因此无法表述行为模式的不确定性. Tang等[12 ] 提出基于卷积神经网络的Caser模型,根据序列的时间维度和行为表征的隐藏维度将近期若干行为作为二维矩阵数据,基于水平和垂直卷积,Caser模型可以学习到包含跳跃特点的行为模式,能在一定程度上解决行为不确定性问题,但Caser模型学习复杂不确定行为关系的能力受到卷积核大小的影响. 刘浩翰等[13 ] 则利用注意力机制来消除无目的点击行为对捕获主要意图的影响. ...
... 行为预测部分不是本研究的重点,因此,参考GRU4Rec[8 ] ,使用循环神经网络的变种门控循环单元GRU[9 ] 来进行预测. GRU使用更新门和重置门来决定如何更新每个单元的状态. 当前状态是过去状态和候选状态的线性插值: ...
... 预测用户下一个行为的任务可以看作分类任务,也可以看作基于相关度的排序任务,通常采用排序任务训练能取得更好的效果[8 ] . 因此,本研究采用基于pairwise的排序损失函数,通过比较正样本和负样本的预测概率来不断最小化损失函数L ,使正样本的排序不断靠前,负样本的排序不断靠后: ...
... 5) GRU4Rec② [8 ]−6 . ...
2
... 传统用户行为分析模型聚焦于用户历史行为中的静态行为模式挖掘,如基于矩阵分解的SVD算法[3 ] 将用户的单个行为当成独立的记录[3 -5 ] . 这类方法丢失了行为记录中的序列信息,忽视了用户行为模式的动态变化. 针对行为序列建模问题已经有不少研究. 在机器学习方面,Liu等[6 ] 通过基于统计的行为模式挖掘得到显式的关联规则,但忽略了不可观测的模式,也没有考虑行为的时间跨度和对行为进行更细粒度的研究. Jarboui等[7 ] 使用马尔科夫决策过程(Markov decision process, MDP)预测慕课用户的行为. 近年来,基于神经网络的深度学习方法也被广泛应用于序列行为建模. 如Hidasi等[8 ] 提出的GRU4Rec模型首次用门控循环单元(gated recurrent unit, GRU)[9 ] 进行序列行为预测. Yu等[10 ] 在长短期记忆神经网络(long short-term memory, LSTM)中加入时间感知控制器和内容感知控制器,使得状态更新时能充分考虑上下文信息. 以上方法考虑了行为的先后关系,但仍忽视行为的不确定性问题. 行为并不全是有意识的,其中可能存在很多的噪声[11 ] . L阶马尔可夫链或仅含有循环神经网络(recurrent neural networks, RNNs)的模型,均基于前一行为对紧邻的下一行为有直接影响的假设,因此无法表述行为模式的不确定性. Tang等[12 ] 提出基于卷积神经网络的Caser模型,根据序列的时间维度和行为表征的隐藏维度将近期若干行为作为二维矩阵数据,基于水平和垂直卷积,Caser模型可以学习到包含跳跃特点的行为模式,能在一定程度上解决行为不确定性问题,但Caser模型学习复杂不确定行为关系的能力受到卷积核大小的影响. 刘浩翰等[13 ] 则利用注意力机制来消除无目的点击行为对捕获主要意图的影响. ...
... 行为预测部分不是本研究的重点,因此,参考GRU4Rec[8 ] ,使用循环神经网络的变种门控循环单元GRU[9 ] 来进行预测. GRU使用更新门和重置门来决定如何更新每个单元的状态. 当前状态是过去状态和候选状态的线性插值: ...
1
... 传统用户行为分析模型聚焦于用户历史行为中的静态行为模式挖掘,如基于矩阵分解的SVD算法[3 ] 将用户的单个行为当成独立的记录[3 -5 ] . 这类方法丢失了行为记录中的序列信息,忽视了用户行为模式的动态变化. 针对行为序列建模问题已经有不少研究. 在机器学习方面,Liu等[6 ] 通过基于统计的行为模式挖掘得到显式的关联规则,但忽略了不可观测的模式,也没有考虑行为的时间跨度和对行为进行更细粒度的研究. Jarboui等[7 ] 使用马尔科夫决策过程(Markov decision process, MDP)预测慕课用户的行为. 近年来,基于神经网络的深度学习方法也被广泛应用于序列行为建模. 如Hidasi等[8 ] 提出的GRU4Rec模型首次用门控循环单元(gated recurrent unit, GRU)[9 ] 进行序列行为预测. Yu等[10 ] 在长短期记忆神经网络(long short-term memory, LSTM)中加入时间感知控制器和内容感知控制器,使得状态更新时能充分考虑上下文信息. 以上方法考虑了行为的先后关系,但仍忽视行为的不确定性问题. 行为并不全是有意识的,其中可能存在很多的噪声[11 ] . L阶马尔可夫链或仅含有循环神经网络(recurrent neural networks, RNNs)的模型,均基于前一行为对紧邻的下一行为有直接影响的假设,因此无法表述行为模式的不确定性. Tang等[12 ] 提出基于卷积神经网络的Caser模型,根据序列的时间维度和行为表征的隐藏维度将近期若干行为作为二维矩阵数据,基于水平和垂直卷积,Caser模型可以学习到包含跳跃特点的行为模式,能在一定程度上解决行为不确定性问题,但Caser模型学习复杂不确定行为关系的能力受到卷积核大小的影响. 刘浩翰等[13 ] 则利用注意力机制来消除无目的点击行为对捕获主要意图的影响. ...
1
... 传统用户行为分析模型聚焦于用户历史行为中的静态行为模式挖掘,如基于矩阵分解的SVD算法[3 ] 将用户的单个行为当成独立的记录[3 -5 ] . 这类方法丢失了行为记录中的序列信息,忽视了用户行为模式的动态变化. 针对行为序列建模问题已经有不少研究. 在机器学习方面,Liu等[6 ] 通过基于统计的行为模式挖掘得到显式的关联规则,但忽略了不可观测的模式,也没有考虑行为的时间跨度和对行为进行更细粒度的研究. Jarboui等[7 ] 使用马尔科夫决策过程(Markov decision process, MDP)预测慕课用户的行为. 近年来,基于神经网络的深度学习方法也被广泛应用于序列行为建模. 如Hidasi等[8 ] 提出的GRU4Rec模型首次用门控循环单元(gated recurrent unit, GRU)[9 ] 进行序列行为预测. Yu等[10 ] 在长短期记忆神经网络(long short-term memory, LSTM)中加入时间感知控制器和内容感知控制器,使得状态更新时能充分考虑上下文信息. 以上方法考虑了行为的先后关系,但仍忽视行为的不确定性问题. 行为并不全是有意识的,其中可能存在很多的噪声[11 ] . L阶马尔可夫链或仅含有循环神经网络(recurrent neural networks, RNNs)的模型,均基于前一行为对紧邻的下一行为有直接影响的假设,因此无法表述行为模式的不确定性. Tang等[12 ] 提出基于卷积神经网络的Caser模型,根据序列的时间维度和行为表征的隐藏维度将近期若干行为作为二维矩阵数据,基于水平和垂直卷积,Caser模型可以学习到包含跳跃特点的行为模式,能在一定程度上解决行为不确定性问题,但Caser模型学习复杂不确定行为关系的能力受到卷积核大小的影响. 刘浩翰等[13 ] 则利用注意力机制来消除无目的点击行为对捕获主要意图的影响. ...
3
... 传统用户行为分析模型聚焦于用户历史行为中的静态行为模式挖掘,如基于矩阵分解的SVD算法[3 ] 将用户的单个行为当成独立的记录[3 -5 ] . 这类方法丢失了行为记录中的序列信息,忽视了用户行为模式的动态变化. 针对行为序列建模问题已经有不少研究. 在机器学习方面,Liu等[6 ] 通过基于统计的行为模式挖掘得到显式的关联规则,但忽略了不可观测的模式,也没有考虑行为的时间跨度和对行为进行更细粒度的研究. Jarboui等[7 ] 使用马尔科夫决策过程(Markov decision process, MDP)预测慕课用户的行为. 近年来,基于神经网络的深度学习方法也被广泛应用于序列行为建模. 如Hidasi等[8 ] 提出的GRU4Rec模型首次用门控循环单元(gated recurrent unit, GRU)[9 ] 进行序列行为预测. Yu等[10 ] 在长短期记忆神经网络(long short-term memory, LSTM)中加入时间感知控制器和内容感知控制器,使得状态更新时能充分考虑上下文信息. 以上方法考虑了行为的先后关系,但仍忽视行为的不确定性问题. 行为并不全是有意识的,其中可能存在很多的噪声[11 ] . L阶马尔可夫链或仅含有循环神经网络(recurrent neural networks, RNNs)的模型,均基于前一行为对紧邻的下一行为有直接影响的假设,因此无法表述行为模式的不确定性. Tang等[12 ] 提出基于卷积神经网络的Caser模型,根据序列的时间维度和行为表征的隐藏维度将近期若干行为作为二维矩阵数据,基于水平和垂直卷积,Caser模型可以学习到包含跳跃特点的行为模式,能在一定程度上解决行为不确定性问题,但Caser模型学习复杂不确定行为关系的能力受到卷积核大小的影响. 刘浩翰等[13 ] 则利用注意力机制来消除无目的点击行为对捕获主要意图的影响. ...
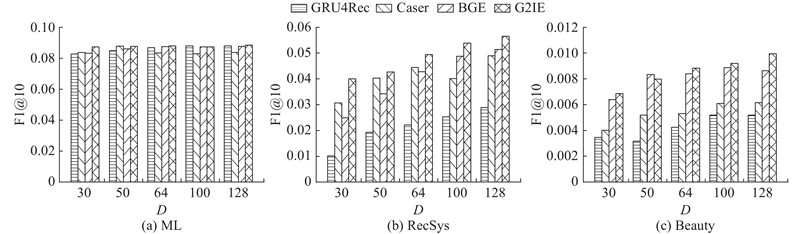
... 将G2IE方法与另外8个方法进行比较,从而验证G2IE方法的有效性. 类似文献[12 ],研究不同方法的嵌入表征维度对性能的影响. ...
... 6) Caser③ [12 ]32 ],在预测未来行为时忽略用户的隐藏表征. 该方法的参数设置如下:隐藏空间维度为128,水平卷积的输出通道维度为16,水平卷积核大小为(i ,128), $i$ $\{ 1, \cdots ,5\} $ −6 ,负采样数量为10. ...
考虑用户意图和时间间隔的会话型深度学习推荐系统
1
2021
... 传统用户行为分析模型聚焦于用户历史行为中的静态行为模式挖掘,如基于矩阵分解的SVD算法[3 ] 将用户的单个行为当成独立的记录[3 -5 ] . 这类方法丢失了行为记录中的序列信息,忽视了用户行为模式的动态变化. 针对行为序列建模问题已经有不少研究. 在机器学习方面,Liu等[6 ] 通过基于统计的行为模式挖掘得到显式的关联规则,但忽略了不可观测的模式,也没有考虑行为的时间跨度和对行为进行更细粒度的研究. Jarboui等[7 ] 使用马尔科夫决策过程(Markov decision process, MDP)预测慕课用户的行为. 近年来,基于神经网络的深度学习方法也被广泛应用于序列行为建模. 如Hidasi等[8 ] 提出的GRU4Rec模型首次用门控循环单元(gated recurrent unit, GRU)[9 ] 进行序列行为预测. Yu等[10 ] 在长短期记忆神经网络(long short-term memory, LSTM)中加入时间感知控制器和内容感知控制器,使得状态更新时能充分考虑上下文信息. 以上方法考虑了行为的先后关系,但仍忽视行为的不确定性问题. 行为并不全是有意识的,其中可能存在很多的噪声[11 ] . L阶马尔可夫链或仅含有循环神经网络(recurrent neural networks, RNNs)的模型,均基于前一行为对紧邻的下一行为有直接影响的假设,因此无法表述行为模式的不确定性. Tang等[12 ] 提出基于卷积神经网络的Caser模型,根据序列的时间维度和行为表征的隐藏维度将近期若干行为作为二维矩阵数据,基于水平和垂直卷积,Caser模型可以学习到包含跳跃特点的行为模式,能在一定程度上解决行为不确定性问题,但Caser模型学习复杂不确定行为关系的能力受到卷积核大小的影响. 刘浩翰等[13 ] 则利用注意力机制来消除无目的点击行为对捕获主要意图的影响. ...
考虑用户意图和时间间隔的会话型深度学习推荐系统
1
2021
... 传统用户行为分析模型聚焦于用户历史行为中的静态行为模式挖掘,如基于矩阵分解的SVD算法[3 ] 将用户的单个行为当成独立的记录[3 -5 ] . 这类方法丢失了行为记录中的序列信息,忽视了用户行为模式的动态变化. 针对行为序列建模问题已经有不少研究. 在机器学习方面,Liu等[6 ] 通过基于统计的行为模式挖掘得到显式的关联规则,但忽略了不可观测的模式,也没有考虑行为的时间跨度和对行为进行更细粒度的研究. Jarboui等[7 ] 使用马尔科夫决策过程(Markov decision process, MDP)预测慕课用户的行为. 近年来,基于神经网络的深度学习方法也被广泛应用于序列行为建模. 如Hidasi等[8 ] 提出的GRU4Rec模型首次用门控循环单元(gated recurrent unit, GRU)[9 ] 进行序列行为预测. Yu等[10 ] 在长短期记忆神经网络(long short-term memory, LSTM)中加入时间感知控制器和内容感知控制器,使得状态更新时能充分考虑上下文信息. 以上方法考虑了行为的先后关系,但仍忽视行为的不确定性问题. 行为并不全是有意识的,其中可能存在很多的噪声[11 ] . L阶马尔可夫链或仅含有循环神经网络(recurrent neural networks, RNNs)的模型,均基于前一行为对紧邻的下一行为有直接影响的假设,因此无法表述行为模式的不确定性. Tang等[12 ] 提出基于卷积神经网络的Caser模型,根据序列的时间维度和行为表征的隐藏维度将近期若干行为作为二维矩阵数据,基于水平和垂直卷积,Caser模型可以学习到包含跳跃特点的行为模式,能在一定程度上解决行为不确定性问题,但Caser模型学习复杂不确定行为关系的能力受到卷积核大小的影响. 刘浩翰等[13 ] 则利用注意力机制来消除无目的点击行为对捕获主要意图的影响. ...
Behavior informatics: an informatics perspective for behavior studies
1
2009
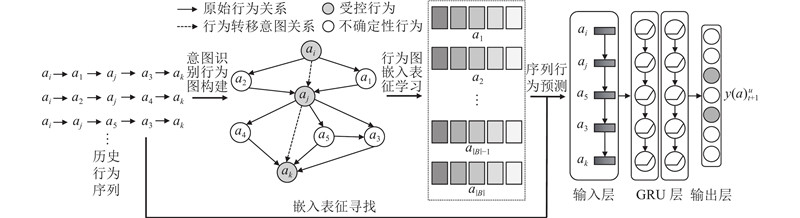
... 行为信息学认为,图论有助于呈现行为的进化和行为模式[14 ] . 为了表达更加复杂的行为关系,基于图神经网络的方法被用来学习行为表征. Wang等[15 ] 提出BGE模型,根据历史行为序列构建行为图,再基于DeepWalk[16 ] 和Skip-Gram[17 ] 在图结构上学习得到行为嵌入表征. 但是由于行为种类众多,每个用户的行为记录可能只占所有可能行为的一小部分,构建的行为图较稀疏. 解决数据稀疏问题,一方面可以利用外部信息增强行为间的关系,如Wang等[15 ] 在BGE的基础上,依赖行为的辅助信息(例如行为类别),提出EGES模型. 王永贵等[18 ] 用项目评分矩阵以及项目类型矩阵构造用户类别偏好矩阵,更好地反映用户的兴趣偏好;另一方面,也可以从自身行为数据中挖掘更多关系解决数据稀疏问题,如岳希等[19 ] 先根据用户之间的相似度初步预测空缺值,再结合平均值和预测值进行填补. 但以上方法都未能同时考虑行为不确定性和数据稀疏问题. ...
2
... 行为信息学认为,图论有助于呈现行为的进化和行为模式[14 ] . 为了表达更加复杂的行为关系,基于图神经网络的方法被用来学习行为表征. Wang等[15 ] 提出BGE模型,根据历史行为序列构建行为图,再基于DeepWalk[16 ] 和Skip-Gram[17 ] 在图结构上学习得到行为嵌入表征. 但是由于行为种类众多,每个用户的行为记录可能只占所有可能行为的一小部分,构建的行为图较稀疏. 解决数据稀疏问题,一方面可以利用外部信息增强行为间的关系,如Wang等[15 ] 在BGE的基础上,依赖行为的辅助信息(例如行为类别),提出EGES模型. 王永贵等[18 ] 用项目评分矩阵以及项目类型矩阵构造用户类别偏好矩阵,更好地反映用户的兴趣偏好;另一方面,也可以从自身行为数据中挖掘更多关系解决数据稀疏问题,如岳希等[19 ] 先根据用户之间的相似度初步预测空缺值,再结合平均值和预测值进行填补. 但以上方法都未能同时考虑行为不确定性和数据稀疏问题. ...
... [15 ]在BGE的基础上,依赖行为的辅助信息(例如行为类别),提出EGES模型. 王永贵等[18 ] 用项目评分矩阵以及项目类型矩阵构造用户类别偏好矩阵,更好地反映用户的兴趣偏好;另一方面,也可以从自身行为数据中挖掘更多关系解决数据稀疏问题,如岳希等[19 ] 先根据用户之间的相似度初步预测空缺值,再结合平均值和预测值进行填补. 但以上方法都未能同时考虑行为不确定性和数据稀疏问题. ...
1
... 行为信息学认为,图论有助于呈现行为的进化和行为模式[14 ] . 为了表达更加复杂的行为关系,基于图神经网络的方法被用来学习行为表征. Wang等[15 ] 提出BGE模型,根据历史行为序列构建行为图,再基于DeepWalk[16 ] 和Skip-Gram[17 ] 在图结构上学习得到行为嵌入表征. 但是由于行为种类众多,每个用户的行为记录可能只占所有可能行为的一小部分,构建的行为图较稀疏. 解决数据稀疏问题,一方面可以利用外部信息增强行为间的关系,如Wang等[15 ] 在BGE的基础上,依赖行为的辅助信息(例如行为类别),提出EGES模型. 王永贵等[18 ] 用项目评分矩阵以及项目类型矩阵构造用户类别偏好矩阵,更好地反映用户的兴趣偏好;另一方面,也可以从自身行为数据中挖掘更多关系解决数据稀疏问题,如岳希等[19 ] 先根据用户之间的相似度初步预测空缺值,再结合平均值和预测值进行填补. 但以上方法都未能同时考虑行为不确定性和数据稀疏问题. ...
1
... 行为信息学认为,图论有助于呈现行为的进化和行为模式[14 ] . 为了表达更加复杂的行为关系,基于图神经网络的方法被用来学习行为表征. Wang等[15 ] 提出BGE模型,根据历史行为序列构建行为图,再基于DeepWalk[16 ] 和Skip-Gram[17 ] 在图结构上学习得到行为嵌入表征. 但是由于行为种类众多,每个用户的行为记录可能只占所有可能行为的一小部分,构建的行为图较稀疏. 解决数据稀疏问题,一方面可以利用外部信息增强行为间的关系,如Wang等[15 ] 在BGE的基础上,依赖行为的辅助信息(例如行为类别),提出EGES模型. 王永贵等[18 ] 用项目评分矩阵以及项目类型矩阵构造用户类别偏好矩阵,更好地反映用户的兴趣偏好;另一方面,也可以从自身行为数据中挖掘更多关系解决数据稀疏问题,如岳希等[19 ] 先根据用户之间的相似度初步预测空缺值,再结合平均值和预测值进行填补. 但以上方法都未能同时考虑行为不确定性和数据稀疏问题. ...
一种优化聚类的协同过滤推荐算法
1
2020
... 行为信息学认为,图论有助于呈现行为的进化和行为模式[14 ] . 为了表达更加复杂的行为关系,基于图神经网络的方法被用来学习行为表征. Wang等[15 ] 提出BGE模型,根据历史行为序列构建行为图,再基于DeepWalk[16 ] 和Skip-Gram[17 ] 在图结构上学习得到行为嵌入表征. 但是由于行为种类众多,每个用户的行为记录可能只占所有可能行为的一小部分,构建的行为图较稀疏. 解决数据稀疏问题,一方面可以利用外部信息增强行为间的关系,如Wang等[15 ] 在BGE的基础上,依赖行为的辅助信息(例如行为类别),提出EGES模型. 王永贵等[18 ] 用项目评分矩阵以及项目类型矩阵构造用户类别偏好矩阵,更好地反映用户的兴趣偏好;另一方面,也可以从自身行为数据中挖掘更多关系解决数据稀疏问题,如岳希等[19 ] 先根据用户之间的相似度初步预测空缺值,再结合平均值和预测值进行填补. 但以上方法都未能同时考虑行为不确定性和数据稀疏问题. ...
一种优化聚类的协同过滤推荐算法
1
2020
... 行为信息学认为,图论有助于呈现行为的进化和行为模式[14 ] . 为了表达更加复杂的行为关系,基于图神经网络的方法被用来学习行为表征. Wang等[15 ] 提出BGE模型,根据历史行为序列构建行为图,再基于DeepWalk[16 ] 和Skip-Gram[17 ] 在图结构上学习得到行为嵌入表征. 但是由于行为种类众多,每个用户的行为记录可能只占所有可能行为的一小部分,构建的行为图较稀疏. 解决数据稀疏问题,一方面可以利用外部信息增强行为间的关系,如Wang等[15 ] 在BGE的基础上,依赖行为的辅助信息(例如行为类别),提出EGES模型. 王永贵等[18 ] 用项目评分矩阵以及项目类型矩阵构造用户类别偏好矩阵,更好地反映用户的兴趣偏好;另一方面,也可以从自身行为数据中挖掘更多关系解决数据稀疏问题,如岳希等[19 ] 先根据用户之间的相似度初步预测空缺值,再结合平均值和预测值进行填补. 但以上方法都未能同时考虑行为不确定性和数据稀疏问题. ...
基于数据稀疏性的协同过滤推荐算法改进研究
1
2020
... 行为信息学认为,图论有助于呈现行为的进化和行为模式[14 ] . 为了表达更加复杂的行为关系,基于图神经网络的方法被用来学习行为表征. Wang等[15 ] 提出BGE模型,根据历史行为序列构建行为图,再基于DeepWalk[16 ] 和Skip-Gram[17 ] 在图结构上学习得到行为嵌入表征. 但是由于行为种类众多,每个用户的行为记录可能只占所有可能行为的一小部分,构建的行为图较稀疏. 解决数据稀疏问题,一方面可以利用外部信息增强行为间的关系,如Wang等[15 ] 在BGE的基础上,依赖行为的辅助信息(例如行为类别),提出EGES模型. 王永贵等[18 ] 用项目评分矩阵以及项目类型矩阵构造用户类别偏好矩阵,更好地反映用户的兴趣偏好;另一方面,也可以从自身行为数据中挖掘更多关系解决数据稀疏问题,如岳希等[19 ] 先根据用户之间的相似度初步预测空缺值,再结合平均值和预测值进行填补. 但以上方法都未能同时考虑行为不确定性和数据稀疏问题. ...
基于数据稀疏性的协同过滤推荐算法改进研究
1
2020
... 行为信息学认为,图论有助于呈现行为的进化和行为模式[14 ] . 为了表达更加复杂的行为关系,基于图神经网络的方法被用来学习行为表征. Wang等[15 ] 提出BGE模型,根据历史行为序列构建行为图,再基于DeepWalk[16 ] 和Skip-Gram[17 ] 在图结构上学习得到行为嵌入表征. 但是由于行为种类众多,每个用户的行为记录可能只占所有可能行为的一小部分,构建的行为图较稀疏. 解决数据稀疏问题,一方面可以利用外部信息增强行为间的关系,如Wang等[15 ] 在BGE的基础上,依赖行为的辅助信息(例如行为类别),提出EGES模型. 王永贵等[18 ] 用项目评分矩阵以及项目类型矩阵构造用户类别偏好矩阵,更好地反映用户的兴趣偏好;另一方面,也可以从自身行为数据中挖掘更多关系解决数据稀疏问题,如岳希等[19 ] 先根据用户之间的相似度初步预测空缺值,再结合平均值和预测值进行填补. 但以上方法都未能同时考虑行为不确定性和数据稀疏问题. ...
Disentangling behavioral intention and behavioral expectation
2
1985
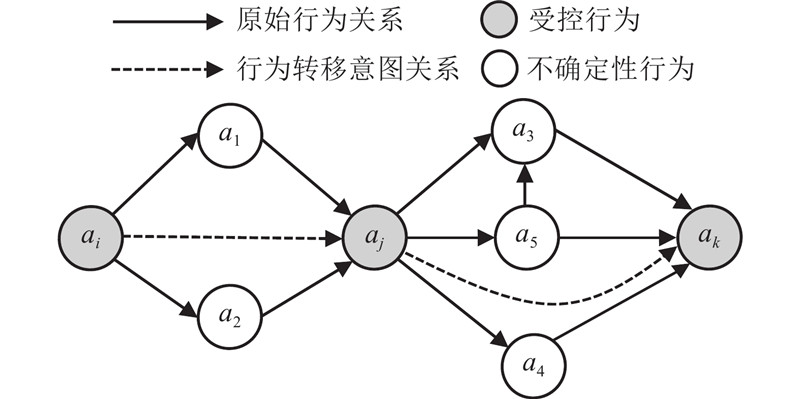
... 定义3 行为转移意图. 行为意图是指个体制定有意识的计划来执行或不执行某些特定的未来行为的程度[20 ] . 计划行为理论(theory of planned behavior, TPB)[21 ] 认为行为意图是行为的直接前提,并且只有当某个行为受个体的意志控制时,行为意图才能通过此行为表达. 参考Warshaw等[20 ] 对行为意图的定义,可以把行为间的转移意图形式化为在行为集合 $B$
... [20 ]对行为意图的定义,可以把行为间的转移意图形式化为在行为集合 $B$
The theory of planned behavior
1
1991
... 定义3 行为转移意图. 行为意图是指个体制定有意识的计划来执行或不执行某些特定的未来行为的程度[20 ] . 计划行为理论(theory of planned behavior, TPB)[21 ] 认为行为意图是行为的直接前提,并且只有当某个行为受个体的意志控制时,行为意图才能通过此行为表达. 参考Warshaw等[20 ] 对行为意图的定义,可以把行为间的转移意图形式化为在行为集合 $B$
1
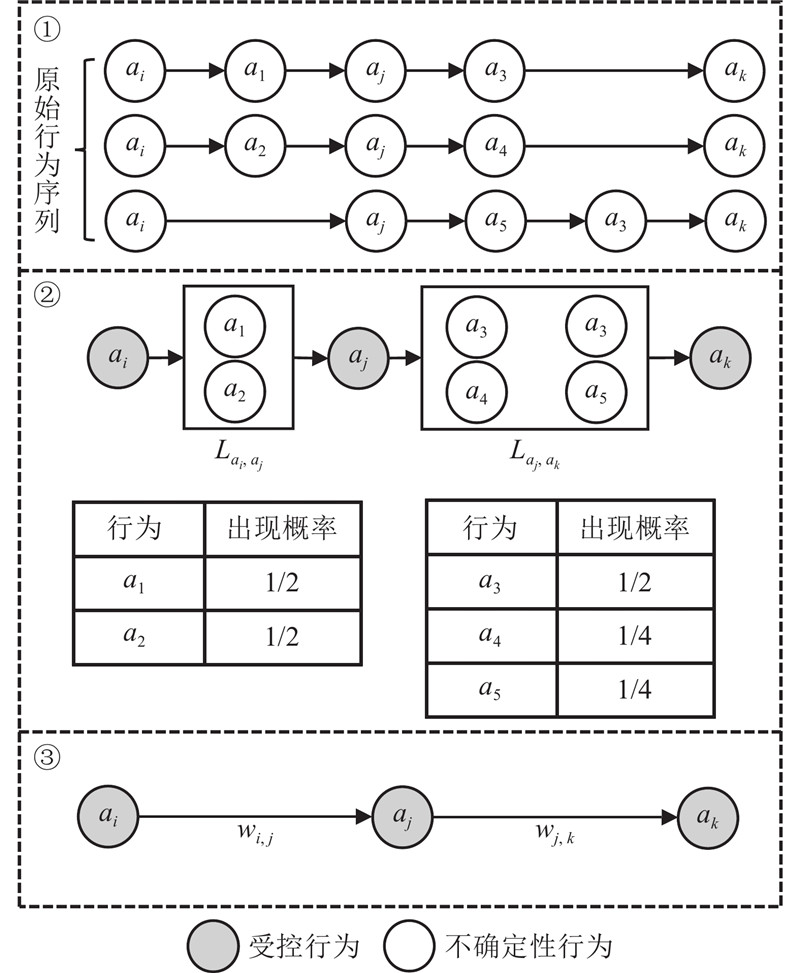
... 用 $p = \left\langle {{a_i},{a_j}, \cdots ,{a_k}} \right\rangle $ $P = {\{ {p_i}\}}$ $ \left( {{a_i},{a_j}} \right) $ $p$ $ {a_i},{a_j} \in p $ $A = {\{ {({a_i},{a_j})_m}\} }$ $p$ $ {L_{{a_i},{a_j}}} $ $ \left( {{a_i},{a_j}} \right) $ [22 ] 中加入行为时间跨度限制,并在每次挖掘得到受控行为模式 $p$ $ {L_{{a_i},{a_j}}} $
1
... 本研究基于3个不同领域的公开数据集验证模型的有效性. 1)MovieLens 1M (ML)[23 -24 ] :包含用户对电影的评分行为. 2)RecSys15-Buy(RecSys)[25 ] :来自RecSys2015年的竞赛数据,包含用户在电商网站上的点击行为和购买行为,本研究使用其中的购买数据. 3)Amazon Beauty(Beauty)[26 -27 ] :包含用户对商品评价的行为数据. ...
The movielens datasets: history and context
1
2015
... 本研究基于3个不同领域的公开数据集验证模型的有效性. 1)MovieLens 1M (ML)[23 -24 ] :包含用户对电影的评分行为. 2)RecSys15-Buy(RecSys)[25 ] :来自RecSys2015年的竞赛数据,包含用户在电商网站上的点击行为和购买行为,本研究使用其中的购买数据. 3)Amazon Beauty(Beauty)[26 -27 ] :包含用户对商品评价的行为数据. ...
1
... 本研究基于3个不同领域的公开数据集验证模型的有效性. 1)MovieLens 1M (ML)[23 -24 ] :包含用户对电影的评分行为. 2)RecSys15-Buy(RecSys)[25 ] :来自RecSys2015年的竞赛数据,包含用户在电商网站上的点击行为和购买行为,本研究使用其中的购买数据. 3)Amazon Beauty(Beauty)[26 -27 ] :包含用户对商品评价的行为数据. ...
1
... 本研究基于3个不同领域的公开数据集验证模型的有效性. 1)MovieLens 1M (ML)[23 -24 ] :包含用户对电影的评分行为. 2)RecSys15-Buy(RecSys)[25 ] :来自RecSys2015年的竞赛数据,包含用户在电商网站上的点击行为和购买行为,本研究使用其中的购买数据. 3)Amazon Beauty(Beauty)[26 -27 ] :包含用户对商品评价的行为数据. ...
1
... 本研究基于3个不同领域的公开数据集验证模型的有效性. 1)MovieLens 1M (ML)[23 -24 ] :包含用户对电影的评分行为. 2)RecSys15-Buy(RecSys)[25 ] :来自RecSys2015年的竞赛数据,包含用户在电商网站上的点击行为和购买行为,本研究使用其中的购买数据. 3)Amazon Beauty(Beauty)[26 -27 ] :包含用户对商品评价的行为数据. ...
1
... 按照文献[28 -29 ] 中的常规做法,数据集保留至少有5个行为的用户,把数据集中每位用户前70%的行为序列作为训练集,即用户的历史行为序列,后30%的行为序列作为测试集,即用户未来发生的行为. 稀疏性是用户-行为交互矩阵的稀疏性,其计算方式为 ${\rm{SI}} = 1 - {n'}\big/{{(|U|\times |B|)}}$ $n'$ 表1 所示, ${{\rm{len}}}_{{\text{a}}}$
1
... 按照文献[28 -29 ] 中的常规做法,数据集保留至少有5个行为的用户,把数据集中每位用户前70%的行为序列作为训练集,即用户的历史行为序列,后30%的行为序列作为测试集,即用户未来发生的行为. 稀疏性是用户-行为交互矩阵的稀疏性,其计算方式为 ${\rm{SI}} = 1 - {n'}\big/{{(|U|\times |B|)}}$ $n'$ 表1 所示, ${{\rm{len}}}_{{\text{a}}}$
Amazon. com recommendations: item-to-item collaborative filtering
1
2003
... 3) ItemKNN① [30 ]
1
... 4) BPRMF① [31 ]32 ],使用行为隐藏表征的平均值来表示序列. 该方法的参数设置如下:因子数量为10,L2正则化为0.0025,学习率为0.05. ...
2
... 4) BPRMF① [31 ]32 ],使用行为隐藏表征的平均值来表示序列. 该方法的参数设置如下:因子数量为10,L2正则化为0.0025,学习率为0.05. ...
... 6) Caser③ [12 ]32 ],在预测未来行为时忽略用户的隐藏表征. 该方法的参数设置如下:隐藏空间维度为128,水平卷积的输出通道维度为16,水平卷积核大小为(i ,128), $i$ $\{ 1, \cdots ,5\} $ −6 ,负采样数量为10. ...
1
... 本研究提出的G2IE模型参数设置如下:在ML、RecSys和Beauty数据集上,频繁序列模式挖掘的最大时间跨度分别为20 min、1 h、7 d. 最小频繁序列模式长度分别设置为10、10、2,无最大长度限制. 行为图嵌入表征学习模块的表征维度d =128,采用Adam[33 ] 优化器最小化目标函数,学习率为0.001. 在序列行为预测模块,基于滑动窗口将数据处理为时间步为5的序列,输入层维度为5×128,用行为图嵌入表征学习模块的结果初始化,2层GRU,隐藏状态均为128维,取最后一层最后一个时刻的隐藏状态为序列表征,输出层权重参数维度为 $|B|$ $|B|$ −6 ,学习率为0.001. ...