在Gauss伪谱法的开区间 $ \left( { - 1,1} \right) $ N 个离散点(LG配点),即 $ \left\{ {{\tau _1},{\tau _2}, \cdot \cdot \cdot ,{\tau _i}, \cdot \cdot \cdot ,{\tau _N}} \right\} $ $ \left( {i = } \right. $ $ \left. {1,2, \cdot \cdot \cdot ,N} \right) $ N 阶Legendre多项式 $ {G_N}\left( \tau \right) $
(17) $ \begin{split} & J = \varPhi \left( {X\left( {{\tau _0}} \right),{t_0},X\left( {{\tau _{\rm{f}}}} \right),{t_{\rm{f}}}} \right) + \frac{{{t_k} - {t_{k - 1}}}}{2}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \times \hfill \\ & \sum\limits_{k = 1}^K {\sum\limits_{i = 1}^N {\omega _i^{\left( k \right)}} L\left[ {{X^{\left( k \right)}}\left( {\tau _i^{}} \right),{U^{\left( k \right)}}\left( {\tau _i^{}} \right),\tau ;\;{t_{k - 1}},{t_k}} \right]} . \end{split} $
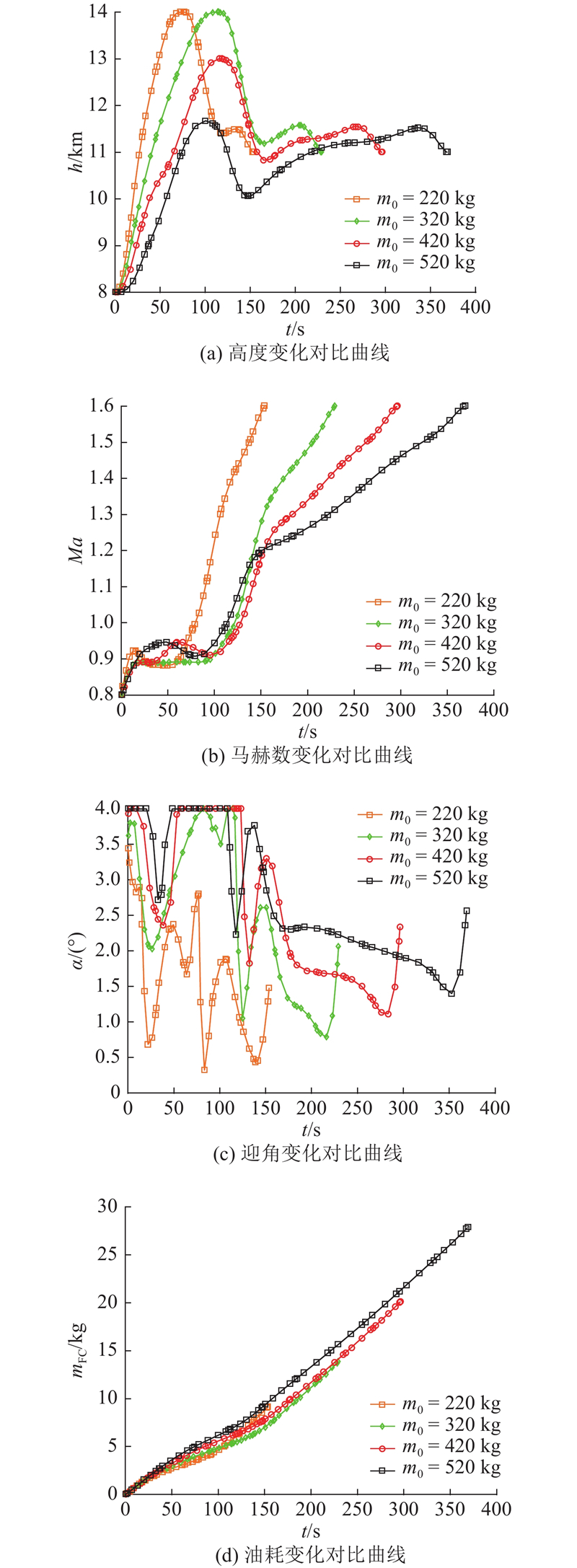
以某小型超音速无人机为研究对象,结合实际飞行情况,该型无人机的参数设定为: $ {m_0} = $ $420{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{kg}}, S = $ $ 1.33{\kern 1pt} {\kern 1pt} {{\rm{m}}^2}$ . 将初始约束条件设定为: ${x_0} = 0,{h_0} = 8{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 000{\kern 1pt} {\kern 1pt} {\rm{m}}, $ $ M{a_0} = 0.8,{\gamma _0} = 0$ . 将终端约束条件设定为: ${h_{\rm{f}}} = $ $ 11{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 000{\kern 1pt} {\kern 1pt} {\rm{m}},M{a_{\rm{f}}} = 1.6$ $\;{\gamma _{\rm{f}}} = 0,{m_{\rm{f}}} \geqslant 300{\kern 1pt} {\kern 1pt} {\rm{kg}}$ . 将控制约束条件设定为: $ \left| \alpha \right| \leqslant {4^ \circ } $ . 将实时路径约束条件设定为: $ \left| \gamma \right| \leqslant {40^ \circ }$ $8{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 000{\kern 1pt} {\kern 1pt} {\rm{m}} \leqslant h\left( t \right) \leqslant 14{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 000{\kern 1pt} {\kern 1pt} {\rm{m}}$ $ 0.8Ma \leqslant Ma\left( t \right) \leqslant $ $1.6{\kern 1pt} {\kern 1pt} Ma, \;\left| {{n_y}} \right| \leqslant 2$ .
[1]
明超, 孙瑞胜, 白宏阳, 等 吸气式超声速导弹爬升段多约束轨迹优化
[J]. 宇航学报 , 2016 , 37 (9 ): 1063 - 1071
DOI:10.3873/j.issn.1000-1328.2016.09.005
[本文引用: 1]
MING Chao, SUN Rui-sheng, BAI Hong-yang, et al Climb trajectory optimization with multiple constraints for air-breathing supersonic missile
[J]. Journal of Astronautics , 2016 , 37 (9 ): 1063 - 1071
DOI:10.3873/j.issn.1000-1328.2016.09.005
[本文引用: 1]
[4]
WALTER S, STARKEY R. GoJett: design and optimization of a supersonic unmanned aerial flight system [C]// 12th AIAA Aviation Technology , Integration and Operations Conference . Indiana: AIAA, 2012.
[本文引用: 1]
[5]
Japan Aerospace Exploration Agency (JAXA). Demonstration of aerodynamic design technologies on supersonic experimental airplane (NEXST-1) by flight test [R]. Alexandria: U. S. Department of Commerce National Technical Information Service, 2007.
[本文引用: 1]
[6]
BRAVO-MOSQUERA P D, ABDALLA A M, CERO NMUNOZ H D, et al Integration assessment of conceptual design and intake aerodynamics of a non-conventional air-to-ground fighter aircraft
[J]. Aerospace Science and Technology , 2019 , 86 (3 ): 497 - 519
[本文引用: 1]
[7]
SCHAMHORST R. An overview of military aircraft supersonic inlet aerodynamics [C]// 50th AIAA Aerospace Sciences Meeting . Tennessee: AIAA, 20 12.
[8]
FENG X Q, LI Z K, SONG B F Research of low boom and low drag supersonic aircraft design
[J]. Chinese Journal of Aeronautics , 2014 , 27 (3 ): 531 - 541
DOI:10.1016/j.cja.2014.04.004
[9]
王钢林, 郑遂 跨声速面积律的近场机理研究
[J]. 实验流体力学 , 2016 , 30 (4 ): 1 - 6
URL
[本文引用: 1]
WANG Gang-lin, ZHENG Sui Research on mechanism of transonic area rule in near field
[J]. Journal of Experiments in Fluid Mechanics , 2016 , 30 (4 ): 1 - 6
URL
[本文引用: 1]
[10]
YAN X D, LYU S, TANG S Analysis of optimal initial glide conditions for hypersonic glide vehicles
[J]. Chinese Journal of Aeronautics , 2014 , 27 (2 ): 217 - 225
DOI:10.1016/j.cja.2014.02.019
[本文引用: 1]
[11]
罗淑贞, 孙青林, 檀盼龙, 等 基于高斯伪谱法的翼伞系统复杂多约束轨迹规划
[J]. 航空学报 , 2017 , 38 (3 ): 220 - 230
URL
[本文引用: 2]
LUO Shu-zhen, SUN Qing-lin, TAN Pan-long, et al Trajectory planning of parafoil system with intricate constraints based on Gauss pseudo-spectral method
[J]. Acta Aeronautica et Astronautica Sinica , 2017 , 38 (3 ): 220 - 230
URL
[本文引用: 2]
[12]
杨希祥, 杨慧欣, 王鹏 伪谱法及其在飞行器轨迹优化设计领域的应用综述
[J]. 国防科技大学学报 , 2015 , 37 (4 ): 1 - 8
DOI:10.11887/j.cn.201504001
[本文引用: 1]
YANG Xi-xiang, YANG Hui-xin, WANG Peng Overview of pseudo-spectral method and its application in trajectory optimum design for flight vehicles
[J]. Journal of National University of Defense Technology , 2015 , 37 (4 ): 1 - 8
DOI:10.11887/j.cn.201504001
[本文引用: 1]
[13]
刘超越, 张成 基于高斯伪谱法的二级助推战术火箭多阶段轨迹优化
[J]. 兵工学报 , 2019 , 40 (2 ): 292 - 302
URL
LIU Chao-yue, ZHANG Cheng Multi-stage trajectory optimization of tactical two-stage booster rocket based on Gauss Pseudo-spectral method
[J]. Acta Armamentarii , 2019 , 40 (2 ): 292 - 302
URL
[14]
王少奇, 马东立, 杨穆清, 等 高空太阳能无人机三维航迹优化
[J]. 北京航空航天大学学报 , 2019 , 45 (5 ): 936 - 943
URL
WANG Shao-qi, MA Dong-li, YANG Mu-qing, et al Three dimensional optimal path planning for high altitude solar powered UAV
[J]. Journal of Beijing University of Aeronautics and Astronautics , 2019 , 45 (5 ): 936 - 943
URL
[15]
HONG S M, SEO M G, SHIM S W, et al Sensitivity analysis on weight and trajectory optimization results for multistage guided missile
[J]. IFAC PapersOn -Line , 2016 , 49 (17 ): 23 - 27
DOI:10.1016/j.ifacol.2016.09.005
[本文引用: 1]
[17]
DARBY C L. Hp pseudo-spectral method for solving continuous-time nonlinear optimal control problems [D]. Gainesville: University of Florida, 2011.
[本文引用: 1]
[18]
邱文杰, 孟秀云 基于hp自适应伪谱法的飞行器多阶段轨迹优化
[J]. 北京理工大学学报 , 2017 , 37 (4 ): 412 - 417
URL
[本文引用: 1]
QIU Wen-jie, MENG Xiu-yun Multi-phase trajectory optimization of vehicle based on hp adaptive pseudo-spectral method
[J]. Journal of Beijing Institute of Technology , 2017 , 37 (4 ): 412 - 417
URL
[本文引用: 1]
[19]
COTS O, GERGAUD J, GOUBINAT D Direct and indirect methods in optimal control with state constraints and the climbing trajectory of an aircraft
[J]. Optimal Control Applications and Methods , 2018 , 39 (1 ): 281 - 301
DOI:10.1002/oca.2347
[本文引用: 1]
[20]
YANG S B, CUI T, HAO X Y, et al Trajectory optimization for a ramjet-powered vehicle in ascent phase via the Gauss pseudo-spectral method
[J]. Aerospace Science and Technology , 2017 , 67 (8 ): 88 - 95
[本文引用: 1]
[21]
明超, 孙瑞胜, 白宏阳, 等. 基于hp自适应伪谱法的多脉冲导弹弹道优化设计[J]. 固体火箭技术, 2015, 38(2): 151-155.
[本文引用: 1]
MING Chao, SUN Rui-sheng, BAI Hong-yang, et al. Optimizing design of trajectory for multiple-pulse missiles based on hp-adaptive pseudo-spectral method [J]. Journal of Solid Rocket Technology , 2015, 38(2): 151-155.
[本文引用: 1]
[22]
HUNTINGTON G T, BENSON D A, RAO A V. A comparison of accuracy and computational efficiency of three pseudo-spectral methods [C]// AIAA Guidance, Navigation and Control Conference and Exhibit . South Carolina: AIAA, 2007.
[本文引用: 1]
[23]
RAO A V, GARG D, HAGER W W Pseudo-spectral method for solving infinite horizon optimal control problems
[J]. Automatica , 2011 , 47 (4 ): 829 - 837
DOI:10.1016/j.automatica.2011.01.085
[本文引用: 1]
吸气式超声速导弹爬升段多约束轨迹优化
1
2016
... 在未来军事作战环境中,超音速无人机拥有出色的机动性能及突防能力,可以替代有人战斗机快速执行对地攻击和目标侦查的高风险任务,得到了国内外许多研究者的关注[1 -3 ] . 随着军事和科学应用研究的深入,将超音速飞机小型化,作为低成本的飞行试验系统变得至关重要[4 -5 ] . 对于小型的超音速无人机而言,由于机身空间结构的限制并兼顾良好的经济性能,对气动外形设计与推进系统的要求极高. 当接近声速时,激波阻力急剧增加,涡喷发动机推力有限,跨音速加速性能较差,则通过规划在该飞行阶段的合适航迹,将在很大程度上缓解对推进系统严苛要求的挑战[6 -9 ] . 从经济性能角度来看,选择合适推力且不配备加力燃烧室的涡喷发动机是低成本小型超音速无人机的较优方案. 本文提出配置高推重比的无加力涡喷发动机,利用马赫俯冲机动实现跨音速飞行从而突破音障的方案,可以有效降低发动机成本,提高该型无人机的经济性能. 在既定先进的气动外形构型下,研究无人机可靠且快速突破音障的航迹具有现实工程意义与广泛应用价值. ...
吸气式超声速导弹爬升段多约束轨迹优化
1
2016
... 在未来军事作战环境中,超音速无人机拥有出色的机动性能及突防能力,可以替代有人战斗机快速执行对地攻击和目标侦查的高风险任务,得到了国内外许多研究者的关注[1 -3 ] . 随着军事和科学应用研究的深入,将超音速飞机小型化,作为低成本的飞行试验系统变得至关重要[4 -5 ] . 对于小型的超音速无人机而言,由于机身空间结构的限制并兼顾良好的经济性能,对气动外形设计与推进系统的要求极高. 当接近声速时,激波阻力急剧增加,涡喷发动机推力有限,跨音速加速性能较差,则通过规划在该飞行阶段的合适航迹,将在很大程度上缓解对推进系统严苛要求的挑战[6 -9 ] . 从经济性能角度来看,选择合适推力且不配备加力燃烧室的涡喷发动机是低成本小型超音速无人机的较优方案. 本文提出配置高推重比的无加力涡喷发动机,利用马赫俯冲机动实现跨音速飞行从而突破音障的方案,可以有效降低发动机成本,提高该型无人机的经济性能. 在既定先进的气动外形构型下,研究无人机可靠且快速突破音障的航迹具有现实工程意义与广泛应用价值. ...
基于NSGA-II的超音速飞机最快爬升轨迹分析
2
2011
... 在未来军事作战环境中,超音速无人机拥有出色的机动性能及突防能力,可以替代有人战斗机快速执行对地攻击和目标侦查的高风险任务,得到了国内外许多研究者的关注[1 -3 ] . 随着军事和科学应用研究的深入,将超音速飞机小型化,作为低成本的飞行试验系统变得至关重要[4 -5 ] . 对于小型的超音速无人机而言,由于机身空间结构的限制并兼顾良好的经济性能,对气动外形设计与推进系统的要求极高. 当接近声速时,激波阻力急剧增加,涡喷发动机推力有限,跨音速加速性能较差,则通过规划在该飞行阶段的合适航迹,将在很大程度上缓解对推进系统严苛要求的挑战[6 -9 ] . 从经济性能角度来看,选择合适推力且不配备加力燃烧室的涡喷发动机是低成本小型超音速无人机的较优方案. 本文提出配置高推重比的无加力涡喷发动机,利用马赫俯冲机动实现跨音速飞行从而突破音障的方案,可以有效降低发动机成本,提高该型无人机的经济性能. 在既定先进的气动外形构型下,研究无人机可靠且快速突破音障的航迹具有现实工程意义与广泛应用价值. ...
... 目前,轨迹规划方法主要有最优控制法和智能优化算法,其中最优控制法包括间接法和直接法[10 -11 ] . 间接法收敛半径小,难以估计共轭变量的初值,且超音速无人机轨迹优化问题存在多个复杂约束,将会使推导求解十分困难,故利用参数化方法将连续空间的最优控制问题转化为非线性规划问题(nonlinear program,NLP)的直接法被广泛应用于飞行器轨迹优化领域[12 -15 ] . 另一类研究方法是利用传统的分而治之模型与智能优化算法进行求解. 陈晓等[16 ] 用能量法建立爬升、平飞和下滑段轨迹优化模型,利用再开始FR(Fletcher-Revees)共轭梯度法求解最优轨迹. 安兵辉等[3 ] 用能量高度法构建超音速飞机进入俯冲、俯冲直线段和改出俯冲3段俯冲段模型,使用遗传算法进行轨迹规划. 运用传统分而治之模型,仅是在各段分别寻优,且这类智能优化算法在求解复杂约束问题时局部搜索能力不足,易发生早熟收敛[11 ] . 近年来,结合伪谱法与hp型有限元法的hp自适应伪谱法受到广泛关注,该算法由Darby[17 ] 提出,在优化过程中对区间网格密度h (配点数)和多项式阶数p 进行自适应调整,相较于其他伪谱法,对状态与控制变量的近似程度更高,适用于状态或控制变量变化较快的优化问题,表现出很高的效率及计算精度[18 ] . ...
基于NSGA-II的超音速飞机最快爬升轨迹分析
2
2011
... 在未来军事作战环境中,超音速无人机拥有出色的机动性能及突防能力,可以替代有人战斗机快速执行对地攻击和目标侦查的高风险任务,得到了国内外许多研究者的关注[1 -3 ] . 随着军事和科学应用研究的深入,将超音速飞机小型化,作为低成本的飞行试验系统变得至关重要[4 -5 ] . 对于小型的超音速无人机而言,由于机身空间结构的限制并兼顾良好的经济性能,对气动外形设计与推进系统的要求极高. 当接近声速时,激波阻力急剧增加,涡喷发动机推力有限,跨音速加速性能较差,则通过规划在该飞行阶段的合适航迹,将在很大程度上缓解对推进系统严苛要求的挑战[6 -9 ] . 从经济性能角度来看,选择合适推力且不配备加力燃烧室的涡喷发动机是低成本小型超音速无人机的较优方案. 本文提出配置高推重比的无加力涡喷发动机,利用马赫俯冲机动实现跨音速飞行从而突破音障的方案,可以有效降低发动机成本,提高该型无人机的经济性能. 在既定先进的气动外形构型下,研究无人机可靠且快速突破音障的航迹具有现实工程意义与广泛应用价值. ...
... 目前,轨迹规划方法主要有最优控制法和智能优化算法,其中最优控制法包括间接法和直接法[10 -11 ] . 间接法收敛半径小,难以估计共轭变量的初值,且超音速无人机轨迹优化问题存在多个复杂约束,将会使推导求解十分困难,故利用参数化方法将连续空间的最优控制问题转化为非线性规划问题(nonlinear program,NLP)的直接法被广泛应用于飞行器轨迹优化领域[12 -15 ] . 另一类研究方法是利用传统的分而治之模型与智能优化算法进行求解. 陈晓等[16 ] 用能量法建立爬升、平飞和下滑段轨迹优化模型,利用再开始FR(Fletcher-Revees)共轭梯度法求解最优轨迹. 安兵辉等[3 ] 用能量高度法构建超音速飞机进入俯冲、俯冲直线段和改出俯冲3段俯冲段模型,使用遗传算法进行轨迹规划. 运用传统分而治之模型,仅是在各段分别寻优,且这类智能优化算法在求解复杂约束问题时局部搜索能力不足,易发生早熟收敛[11 ] . 近年来,结合伪谱法与hp型有限元法的hp自适应伪谱法受到广泛关注,该算法由Darby[17 ] 提出,在优化过程中对区间网格密度h (配点数)和多项式阶数p 进行自适应调整,相较于其他伪谱法,对状态与控制变量的近似程度更高,适用于状态或控制变量变化较快的优化问题,表现出很高的效率及计算精度[18 ] . ...
1
... 在未来军事作战环境中,超音速无人机拥有出色的机动性能及突防能力,可以替代有人战斗机快速执行对地攻击和目标侦查的高风险任务,得到了国内外许多研究者的关注[1 -3 ] . 随着军事和科学应用研究的深入,将超音速飞机小型化,作为低成本的飞行试验系统变得至关重要[4 -5 ] . 对于小型的超音速无人机而言,由于机身空间结构的限制并兼顾良好的经济性能,对气动外形设计与推进系统的要求极高. 当接近声速时,激波阻力急剧增加,涡喷发动机推力有限,跨音速加速性能较差,则通过规划在该飞行阶段的合适航迹,将在很大程度上缓解对推进系统严苛要求的挑战[6 -9 ] . 从经济性能角度来看,选择合适推力且不配备加力燃烧室的涡喷发动机是低成本小型超音速无人机的较优方案. 本文提出配置高推重比的无加力涡喷发动机,利用马赫俯冲机动实现跨音速飞行从而突破音障的方案,可以有效降低发动机成本,提高该型无人机的经济性能. 在既定先进的气动外形构型下,研究无人机可靠且快速突破音障的航迹具有现实工程意义与广泛应用价值. ...
1
... 在未来军事作战环境中,超音速无人机拥有出色的机动性能及突防能力,可以替代有人战斗机快速执行对地攻击和目标侦查的高风险任务,得到了国内外许多研究者的关注[1 -3 ] . 随着军事和科学应用研究的深入,将超音速飞机小型化,作为低成本的飞行试验系统变得至关重要[4 -5 ] . 对于小型的超音速无人机而言,由于机身空间结构的限制并兼顾良好的经济性能,对气动外形设计与推进系统的要求极高. 当接近声速时,激波阻力急剧增加,涡喷发动机推力有限,跨音速加速性能较差,则通过规划在该飞行阶段的合适航迹,将在很大程度上缓解对推进系统严苛要求的挑战[6 -9 ] . 从经济性能角度来看,选择合适推力且不配备加力燃烧室的涡喷发动机是低成本小型超音速无人机的较优方案. 本文提出配置高推重比的无加力涡喷发动机,利用马赫俯冲机动实现跨音速飞行从而突破音障的方案,可以有效降低发动机成本,提高该型无人机的经济性能. 在既定先进的气动外形构型下,研究无人机可靠且快速突破音障的航迹具有现实工程意义与广泛应用价值. ...
Integration assessment of conceptual design and intake aerodynamics of a non-conventional air-to-ground fighter aircraft
1
2019
... 在未来军事作战环境中,超音速无人机拥有出色的机动性能及突防能力,可以替代有人战斗机快速执行对地攻击和目标侦查的高风险任务,得到了国内外许多研究者的关注[1 -3 ] . 随着军事和科学应用研究的深入,将超音速飞机小型化,作为低成本的飞行试验系统变得至关重要[4 -5 ] . 对于小型的超音速无人机而言,由于机身空间结构的限制并兼顾良好的经济性能,对气动外形设计与推进系统的要求极高. 当接近声速时,激波阻力急剧增加,涡喷发动机推力有限,跨音速加速性能较差,则通过规划在该飞行阶段的合适航迹,将在很大程度上缓解对推进系统严苛要求的挑战[6 -9 ] . 从经济性能角度来看,选择合适推力且不配备加力燃烧室的涡喷发动机是低成本小型超音速无人机的较优方案. 本文提出配置高推重比的无加力涡喷发动机,利用马赫俯冲机动实现跨音速飞行从而突破音障的方案,可以有效降低发动机成本,提高该型无人机的经济性能. 在既定先进的气动外形构型下,研究无人机可靠且快速突破音障的航迹具有现实工程意义与广泛应用价值. ...
Research of low boom and low drag supersonic aircraft design
0
2014
跨声速面积律的近场机理研究
1
2016
... 在未来军事作战环境中,超音速无人机拥有出色的机动性能及突防能力,可以替代有人战斗机快速执行对地攻击和目标侦查的高风险任务,得到了国内外许多研究者的关注[1 -3 ] . 随着军事和科学应用研究的深入,将超音速飞机小型化,作为低成本的飞行试验系统变得至关重要[4 -5 ] . 对于小型的超音速无人机而言,由于机身空间结构的限制并兼顾良好的经济性能,对气动外形设计与推进系统的要求极高. 当接近声速时,激波阻力急剧增加,涡喷发动机推力有限,跨音速加速性能较差,则通过规划在该飞行阶段的合适航迹,将在很大程度上缓解对推进系统严苛要求的挑战[6 -9 ] . 从经济性能角度来看,选择合适推力且不配备加力燃烧室的涡喷发动机是低成本小型超音速无人机的较优方案. 本文提出配置高推重比的无加力涡喷发动机,利用马赫俯冲机动实现跨音速飞行从而突破音障的方案,可以有效降低发动机成本,提高该型无人机的经济性能. 在既定先进的气动外形构型下,研究无人机可靠且快速突破音障的航迹具有现实工程意义与广泛应用价值. ...
跨声速面积律的近场机理研究
1
2016
... 在未来军事作战环境中,超音速无人机拥有出色的机动性能及突防能力,可以替代有人战斗机快速执行对地攻击和目标侦查的高风险任务,得到了国内外许多研究者的关注[1 -3 ] . 随着军事和科学应用研究的深入,将超音速飞机小型化,作为低成本的飞行试验系统变得至关重要[4 -5 ] . 对于小型的超音速无人机而言,由于机身空间结构的限制并兼顾良好的经济性能,对气动外形设计与推进系统的要求极高. 当接近声速时,激波阻力急剧增加,涡喷发动机推力有限,跨音速加速性能较差,则通过规划在该飞行阶段的合适航迹,将在很大程度上缓解对推进系统严苛要求的挑战[6 -9 ] . 从经济性能角度来看,选择合适推力且不配备加力燃烧室的涡喷发动机是低成本小型超音速无人机的较优方案. 本文提出配置高推重比的无加力涡喷发动机,利用马赫俯冲机动实现跨音速飞行从而突破音障的方案,可以有效降低发动机成本,提高该型无人机的经济性能. 在既定先进的气动外形构型下,研究无人机可靠且快速突破音障的航迹具有现实工程意义与广泛应用价值. ...
Analysis of optimal initial glide conditions for hypersonic glide vehicles
1
2014
... 目前,轨迹规划方法主要有最优控制法和智能优化算法,其中最优控制法包括间接法和直接法[10 -11 ] . 间接法收敛半径小,难以估计共轭变量的初值,且超音速无人机轨迹优化问题存在多个复杂约束,将会使推导求解十分困难,故利用参数化方法将连续空间的最优控制问题转化为非线性规划问题(nonlinear program,NLP)的直接法被广泛应用于飞行器轨迹优化领域[12 -15 ] . 另一类研究方法是利用传统的分而治之模型与智能优化算法进行求解. 陈晓等[16 ] 用能量法建立爬升、平飞和下滑段轨迹优化模型,利用再开始FR(Fletcher-Revees)共轭梯度法求解最优轨迹. 安兵辉等[3 ] 用能量高度法构建超音速飞机进入俯冲、俯冲直线段和改出俯冲3段俯冲段模型,使用遗传算法进行轨迹规划. 运用传统分而治之模型,仅是在各段分别寻优,且这类智能优化算法在求解复杂约束问题时局部搜索能力不足,易发生早熟收敛[11 ] . 近年来,结合伪谱法与hp型有限元法的hp自适应伪谱法受到广泛关注,该算法由Darby[17 ] 提出,在优化过程中对区间网格密度h (配点数)和多项式阶数p 进行自适应调整,相较于其他伪谱法,对状态与控制变量的近似程度更高,适用于状态或控制变量变化较快的优化问题,表现出很高的效率及计算精度[18 ] . ...
基于高斯伪谱法的翼伞系统复杂多约束轨迹规划
2
2017
... 目前,轨迹规划方法主要有最优控制法和智能优化算法,其中最优控制法包括间接法和直接法[10 -11 ] . 间接法收敛半径小,难以估计共轭变量的初值,且超音速无人机轨迹优化问题存在多个复杂约束,将会使推导求解十分困难,故利用参数化方法将连续空间的最优控制问题转化为非线性规划问题(nonlinear program,NLP)的直接法被广泛应用于飞行器轨迹优化领域[12 -15 ] . 另一类研究方法是利用传统的分而治之模型与智能优化算法进行求解. 陈晓等[16 ] 用能量法建立爬升、平飞和下滑段轨迹优化模型,利用再开始FR(Fletcher-Revees)共轭梯度法求解最优轨迹. 安兵辉等[3 ] 用能量高度法构建超音速飞机进入俯冲、俯冲直线段和改出俯冲3段俯冲段模型,使用遗传算法进行轨迹规划. 运用传统分而治之模型,仅是在各段分别寻优,且这类智能优化算法在求解复杂约束问题时局部搜索能力不足,易发生早熟收敛[11 ] . 近年来,结合伪谱法与hp型有限元法的hp自适应伪谱法受到广泛关注,该算法由Darby[17 ] 提出,在优化过程中对区间网格密度h (配点数)和多项式阶数p 进行自适应调整,相较于其他伪谱法,对状态与控制变量的近似程度更高,适用于状态或控制变量变化较快的优化问题,表现出很高的效率及计算精度[18 ] . ...
... [11 ]. 近年来,结合伪谱法与hp型有限元法的hp自适应伪谱法受到广泛关注,该算法由Darby[17 ] 提出,在优化过程中对区间网格密度h (配点数)和多项式阶数p 进行自适应调整,相较于其他伪谱法,对状态与控制变量的近似程度更高,适用于状态或控制变量变化较快的优化问题,表现出很高的效率及计算精度[18 ] . ...
基于高斯伪谱法的翼伞系统复杂多约束轨迹规划
2
2017
... 目前,轨迹规划方法主要有最优控制法和智能优化算法,其中最优控制法包括间接法和直接法[10 -11 ] . 间接法收敛半径小,难以估计共轭变量的初值,且超音速无人机轨迹优化问题存在多个复杂约束,将会使推导求解十分困难,故利用参数化方法将连续空间的最优控制问题转化为非线性规划问题(nonlinear program,NLP)的直接法被广泛应用于飞行器轨迹优化领域[12 -15 ] . 另一类研究方法是利用传统的分而治之模型与智能优化算法进行求解. 陈晓等[16 ] 用能量法建立爬升、平飞和下滑段轨迹优化模型,利用再开始FR(Fletcher-Revees)共轭梯度法求解最优轨迹. 安兵辉等[3 ] 用能量高度法构建超音速飞机进入俯冲、俯冲直线段和改出俯冲3段俯冲段模型,使用遗传算法进行轨迹规划. 运用传统分而治之模型,仅是在各段分别寻优,且这类智能优化算法在求解复杂约束问题时局部搜索能力不足,易发生早熟收敛[11 ] . 近年来,结合伪谱法与hp型有限元法的hp自适应伪谱法受到广泛关注,该算法由Darby[17 ] 提出,在优化过程中对区间网格密度h (配点数)和多项式阶数p 进行自适应调整,相较于其他伪谱法,对状态与控制变量的近似程度更高,适用于状态或控制变量变化较快的优化问题,表现出很高的效率及计算精度[18 ] . ...
... [11 ]. 近年来,结合伪谱法与hp型有限元法的hp自适应伪谱法受到广泛关注,该算法由Darby[17 ] 提出,在优化过程中对区间网格密度h (配点数)和多项式阶数p 进行自适应调整,相较于其他伪谱法,对状态与控制变量的近似程度更高,适用于状态或控制变量变化较快的优化问题,表现出很高的效率及计算精度[18 ] . ...
伪谱法及其在飞行器轨迹优化设计领域的应用综述
1
2015
... 目前,轨迹规划方法主要有最优控制法和智能优化算法,其中最优控制法包括间接法和直接法[10 -11 ] . 间接法收敛半径小,难以估计共轭变量的初值,且超音速无人机轨迹优化问题存在多个复杂约束,将会使推导求解十分困难,故利用参数化方法将连续空间的最优控制问题转化为非线性规划问题(nonlinear program,NLP)的直接法被广泛应用于飞行器轨迹优化领域[12 -15 ] . 另一类研究方法是利用传统的分而治之模型与智能优化算法进行求解. 陈晓等[16 ] 用能量法建立爬升、平飞和下滑段轨迹优化模型,利用再开始FR(Fletcher-Revees)共轭梯度法求解最优轨迹. 安兵辉等[3 ] 用能量高度法构建超音速飞机进入俯冲、俯冲直线段和改出俯冲3段俯冲段模型,使用遗传算法进行轨迹规划. 运用传统分而治之模型,仅是在各段分别寻优,且这类智能优化算法在求解复杂约束问题时局部搜索能力不足,易发生早熟收敛[11 ] . 近年来,结合伪谱法与hp型有限元法的hp自适应伪谱法受到广泛关注,该算法由Darby[17 ] 提出,在优化过程中对区间网格密度h (配点数)和多项式阶数p 进行自适应调整,相较于其他伪谱法,对状态与控制变量的近似程度更高,适用于状态或控制变量变化较快的优化问题,表现出很高的效率及计算精度[18 ] . ...
伪谱法及其在飞行器轨迹优化设计领域的应用综述
1
2015
... 目前,轨迹规划方法主要有最优控制法和智能优化算法,其中最优控制法包括间接法和直接法[10 -11 ] . 间接法收敛半径小,难以估计共轭变量的初值,且超音速无人机轨迹优化问题存在多个复杂约束,将会使推导求解十分困难,故利用参数化方法将连续空间的最优控制问题转化为非线性规划问题(nonlinear program,NLP)的直接法被广泛应用于飞行器轨迹优化领域[12 -15 ] . 另一类研究方法是利用传统的分而治之模型与智能优化算法进行求解. 陈晓等[16 ] 用能量法建立爬升、平飞和下滑段轨迹优化模型,利用再开始FR(Fletcher-Revees)共轭梯度法求解最优轨迹. 安兵辉等[3 ] 用能量高度法构建超音速飞机进入俯冲、俯冲直线段和改出俯冲3段俯冲段模型,使用遗传算法进行轨迹规划. 运用传统分而治之模型,仅是在各段分别寻优,且这类智能优化算法在求解复杂约束问题时局部搜索能力不足,易发生早熟收敛[11 ] . 近年来,结合伪谱法与hp型有限元法的hp自适应伪谱法受到广泛关注,该算法由Darby[17 ] 提出,在优化过程中对区间网格密度h (配点数)和多项式阶数p 进行自适应调整,相较于其他伪谱法,对状态与控制变量的近似程度更高,适用于状态或控制变量变化较快的优化问题,表现出很高的效率及计算精度[18 ] . ...
基于高斯伪谱法的二级助推战术火箭多阶段轨迹优化
0
2019
基于高斯伪谱法的二级助推战术火箭多阶段轨迹优化
0
2019
Sensitivity analysis on weight and trajectory optimization results for multistage guided missile
1
2016
... 目前,轨迹规划方法主要有最优控制法和智能优化算法,其中最优控制法包括间接法和直接法[10 -11 ] . 间接法收敛半径小,难以估计共轭变量的初值,且超音速无人机轨迹优化问题存在多个复杂约束,将会使推导求解十分困难,故利用参数化方法将连续空间的最优控制问题转化为非线性规划问题(nonlinear program,NLP)的直接法被广泛应用于飞行器轨迹优化领域[12 -15 ] . 另一类研究方法是利用传统的分而治之模型与智能优化算法进行求解. 陈晓等[16 ] 用能量法建立爬升、平飞和下滑段轨迹优化模型,利用再开始FR(Fletcher-Revees)共轭梯度法求解最优轨迹. 安兵辉等[3 ] 用能量高度法构建超音速飞机进入俯冲、俯冲直线段和改出俯冲3段俯冲段模型,使用遗传算法进行轨迹规划. 运用传统分而治之模型,仅是在各段分别寻优,且这类智能优化算法在求解复杂约束问题时局部搜索能力不足,易发生早熟收敛[11 ] . 近年来,结合伪谱法与hp型有限元法的hp自适应伪谱法受到广泛关注,该算法由Darby[17 ] 提出,在优化过程中对区间网格密度h (配点数)和多项式阶数p 进行自适应调整,相较于其他伪谱法,对状态与控制变量的近似程度更高,适用于状态或控制变量变化较快的优化问题,表现出很高的效率及计算精度[18 ] . ...
无人飞行器纵向剖面轨迹优化
1
2013
... 目前,轨迹规划方法主要有最优控制法和智能优化算法,其中最优控制法包括间接法和直接法[10 -11 ] . 间接法收敛半径小,难以估计共轭变量的初值,且超音速无人机轨迹优化问题存在多个复杂约束,将会使推导求解十分困难,故利用参数化方法将连续空间的最优控制问题转化为非线性规划问题(nonlinear program,NLP)的直接法被广泛应用于飞行器轨迹优化领域[12 -15 ] . 另一类研究方法是利用传统的分而治之模型与智能优化算法进行求解. 陈晓等[16 ] 用能量法建立爬升、平飞和下滑段轨迹优化模型,利用再开始FR(Fletcher-Revees)共轭梯度法求解最优轨迹. 安兵辉等[3 ] 用能量高度法构建超音速飞机进入俯冲、俯冲直线段和改出俯冲3段俯冲段模型,使用遗传算法进行轨迹规划. 运用传统分而治之模型,仅是在各段分别寻优,且这类智能优化算法在求解复杂约束问题时局部搜索能力不足,易发生早熟收敛[11 ] . 近年来,结合伪谱法与hp型有限元法的hp自适应伪谱法受到广泛关注,该算法由Darby[17 ] 提出,在优化过程中对区间网格密度h (配点数)和多项式阶数p 进行自适应调整,相较于其他伪谱法,对状态与控制变量的近似程度更高,适用于状态或控制变量变化较快的优化问题,表现出很高的效率及计算精度[18 ] . ...
无人飞行器纵向剖面轨迹优化
1
2013
... 目前,轨迹规划方法主要有最优控制法和智能优化算法,其中最优控制法包括间接法和直接法[10 -11 ] . 间接法收敛半径小,难以估计共轭变量的初值,且超音速无人机轨迹优化问题存在多个复杂约束,将会使推导求解十分困难,故利用参数化方法将连续空间的最优控制问题转化为非线性规划问题(nonlinear program,NLP)的直接法被广泛应用于飞行器轨迹优化领域[12 -15 ] . 另一类研究方法是利用传统的分而治之模型与智能优化算法进行求解. 陈晓等[16 ] 用能量法建立爬升、平飞和下滑段轨迹优化模型,利用再开始FR(Fletcher-Revees)共轭梯度法求解最优轨迹. 安兵辉等[3 ] 用能量高度法构建超音速飞机进入俯冲、俯冲直线段和改出俯冲3段俯冲段模型,使用遗传算法进行轨迹规划. 运用传统分而治之模型,仅是在各段分别寻优,且这类智能优化算法在求解复杂约束问题时局部搜索能力不足,易发生早熟收敛[11 ] . 近年来,结合伪谱法与hp型有限元法的hp自适应伪谱法受到广泛关注,该算法由Darby[17 ] 提出,在优化过程中对区间网格密度h (配点数)和多项式阶数p 进行自适应调整,相较于其他伪谱法,对状态与控制变量的近似程度更高,适用于状态或控制变量变化较快的优化问题,表现出很高的效率及计算精度[18 ] . ...
1
... 目前,轨迹规划方法主要有最优控制法和智能优化算法,其中最优控制法包括间接法和直接法[10 -11 ] . 间接法收敛半径小,难以估计共轭变量的初值,且超音速无人机轨迹优化问题存在多个复杂约束,将会使推导求解十分困难,故利用参数化方法将连续空间的最优控制问题转化为非线性规划问题(nonlinear program,NLP)的直接法被广泛应用于飞行器轨迹优化领域[12 -15 ] . 另一类研究方法是利用传统的分而治之模型与智能优化算法进行求解. 陈晓等[16 ] 用能量法建立爬升、平飞和下滑段轨迹优化模型,利用再开始FR(Fletcher-Revees)共轭梯度法求解最优轨迹. 安兵辉等[3 ] 用能量高度法构建超音速飞机进入俯冲、俯冲直线段和改出俯冲3段俯冲段模型,使用遗传算法进行轨迹规划. 运用传统分而治之模型,仅是在各段分别寻优,且这类智能优化算法在求解复杂约束问题时局部搜索能力不足,易发生早熟收敛[11 ] . 近年来,结合伪谱法与hp型有限元法的hp自适应伪谱法受到广泛关注,该算法由Darby[17 ] 提出,在优化过程中对区间网格密度h (配点数)和多项式阶数p 进行自适应调整,相较于其他伪谱法,对状态与控制变量的近似程度更高,适用于状态或控制变量变化较快的优化问题,表现出很高的效率及计算精度[18 ] . ...
基于hp自适应伪谱法的飞行器多阶段轨迹优化
1
2017
... 目前,轨迹规划方法主要有最优控制法和智能优化算法,其中最优控制法包括间接法和直接法[10 -11 ] . 间接法收敛半径小,难以估计共轭变量的初值,且超音速无人机轨迹优化问题存在多个复杂约束,将会使推导求解十分困难,故利用参数化方法将连续空间的最优控制问题转化为非线性规划问题(nonlinear program,NLP)的直接法被广泛应用于飞行器轨迹优化领域[12 -15 ] . 另一类研究方法是利用传统的分而治之模型与智能优化算法进行求解. 陈晓等[16 ] 用能量法建立爬升、平飞和下滑段轨迹优化模型,利用再开始FR(Fletcher-Revees)共轭梯度法求解最优轨迹. 安兵辉等[3 ] 用能量高度法构建超音速飞机进入俯冲、俯冲直线段和改出俯冲3段俯冲段模型,使用遗传算法进行轨迹规划. 运用传统分而治之模型,仅是在各段分别寻优,且这类智能优化算法在求解复杂约束问题时局部搜索能力不足,易发生早熟收敛[11 ] . 近年来,结合伪谱法与hp型有限元法的hp自适应伪谱法受到广泛关注,该算法由Darby[17 ] 提出,在优化过程中对区间网格密度h (配点数)和多项式阶数p 进行自适应调整,相较于其他伪谱法,对状态与控制变量的近似程度更高,适用于状态或控制变量变化较快的优化问题,表现出很高的效率及计算精度[18 ] . ...
基于hp自适应伪谱法的飞行器多阶段轨迹优化
1
2017
... 目前,轨迹规划方法主要有最优控制法和智能优化算法,其中最优控制法包括间接法和直接法[10 -11 ] . 间接法收敛半径小,难以估计共轭变量的初值,且超音速无人机轨迹优化问题存在多个复杂约束,将会使推导求解十分困难,故利用参数化方法将连续空间的最优控制问题转化为非线性规划问题(nonlinear program,NLP)的直接法被广泛应用于飞行器轨迹优化领域[12 -15 ] . 另一类研究方法是利用传统的分而治之模型与智能优化算法进行求解. 陈晓等[16 ] 用能量法建立爬升、平飞和下滑段轨迹优化模型,利用再开始FR(Fletcher-Revees)共轭梯度法求解最优轨迹. 安兵辉等[3 ] 用能量高度法构建超音速飞机进入俯冲、俯冲直线段和改出俯冲3段俯冲段模型,使用遗传算法进行轨迹规划. 运用传统分而治之模型,仅是在各段分别寻优,且这类智能优化算法在求解复杂约束问题时局部搜索能力不足,易发生早熟收敛[11 ] . 近年来,结合伪谱法与hp型有限元法的hp自适应伪谱法受到广泛关注,该算法由Darby[17 ] 提出,在优化过程中对区间网格密度h (配点数)和多项式阶数p 进行自适应调整,相较于其他伪谱法,对状态与控制变量的近似程度更高,适用于状态或控制变量变化较快的优化问题,表现出很高的效率及计算精度[18 ] . ...
Direct and indirect methods in optimal control with state constraints and the climbing trajectory of an aircraft
1
2018
... 无人机加速从高亚音速到超音速的飞行过程,一般限制在铅垂平面内,可以将无人机作为质点处理,超音速无人机在地面坐标系下的动力学模型[19 ] 为 ...
Trajectory optimization for a ramjet-powered vehicle in ascent phase via the Gauss pseudo-spectral method
1
2017
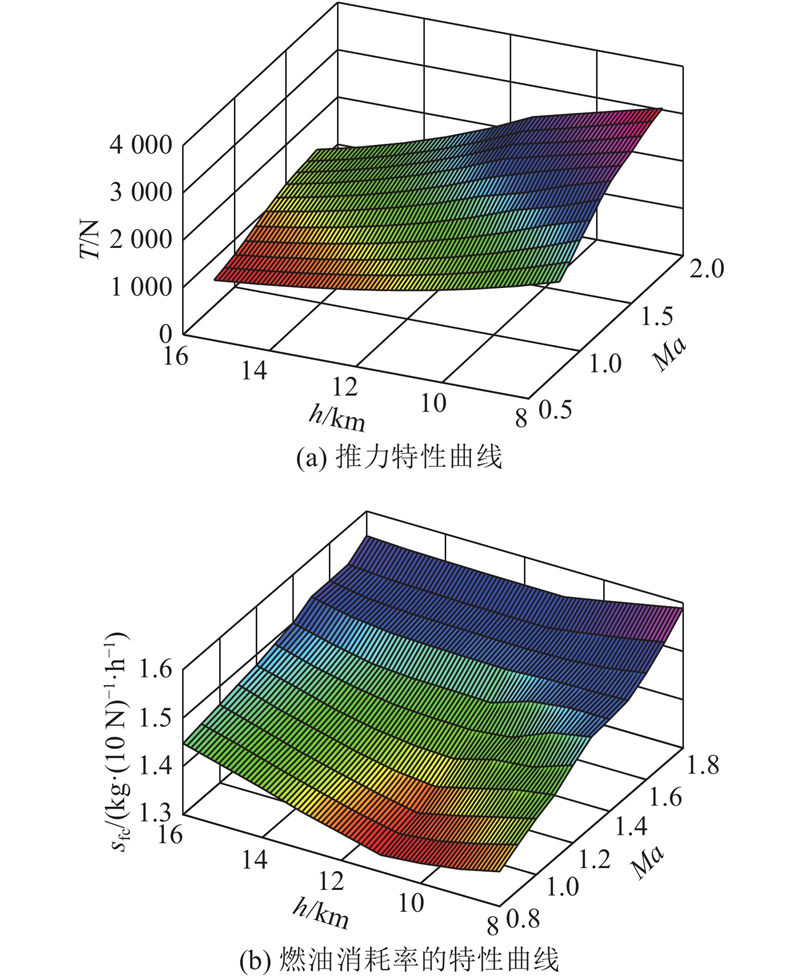
... 发动机推力、燃油消耗率与飞行高度、飞行速度、转速等密切相关,模型较复杂[20 ] . 在高亚音速到超音速阶段,为了使无人机能够顺利突破音障,该阶段发动机均应处于最大转速状态. 根据发动机参数,最大转速下推力、燃油消耗率与 $ h $ Ma 之间的关系如图1 所示. ...
1
... 4)实时路径约束条件.无人机作马赫俯冲机动必须严格满足实时路径约束,否则生成的轨迹不可行,甚至可能会影响机体的结构与操纵安全[21 ] . ...
1
... 4)实时路径约束条件.无人机作马赫俯冲机动必须严格满足实时路径约束,否则生成的轨迹不可行,甚至可能会影响机体的结构与操纵安全[21 ] . ...
1
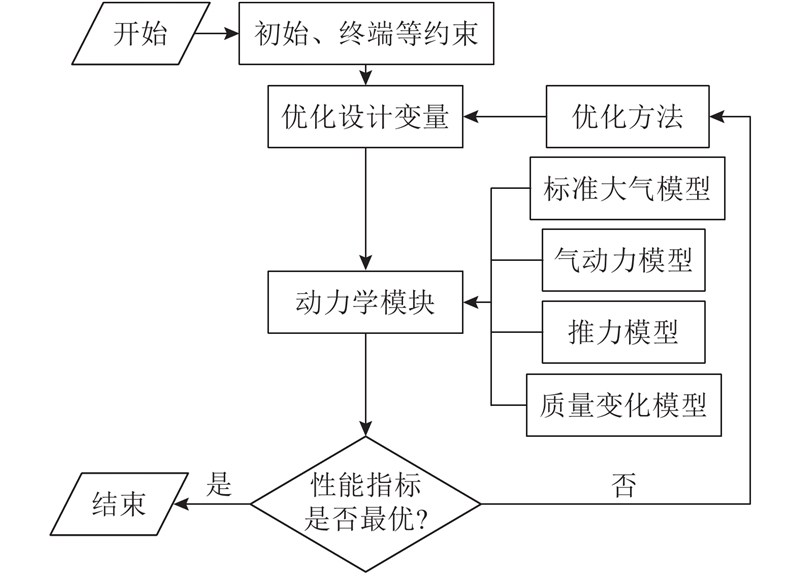
... 采用的hp自适应伪谱法是融合Gauss伪谱法与hp型有限元法,将状态变量与控制变量在Legendre-Gauss(LG)点上离散,以这些离散点为节点构造全局插值多项式,从而近似状态变量与控制变量,对插值多项式进行求导得到微分矩阵. 利用微分矩阵将动力学微分方程约束转化为代数约束,将小型超音速无人机连续时间最优控制问题转换为非线性规划问题. 设e 为离散化动力学约束和路径约束的最大容许误差,若某一离散区间的容许误差高于e ,则对区间网格密度h 和全局插值多项式的阶次p 进行自适应调整. 相比于其他伪谱法,如Legendre伪谱法、Radau伪谱法,Gauss伪谱法具有更高的求解精度和收敛速度,在处理含初始和终端约束的问题上更具优势[22 -23 ] . ...
Pseudo-spectral method for solving infinite horizon optimal control problems
1
2011
... 采用的hp自适应伪谱法是融合Gauss伪谱法与hp型有限元法,将状态变量与控制变量在Legendre-Gauss(LG)点上离散,以这些离散点为节点构造全局插值多项式,从而近似状态变量与控制变量,对插值多项式进行求导得到微分矩阵. 利用微分矩阵将动力学微分方程约束转化为代数约束,将小型超音速无人机连续时间最优控制问题转换为非线性规划问题. 设e 为离散化动力学约束和路径约束的最大容许误差,若某一离散区间的容许误差高于e ,则对区间网格密度h 和全局插值多项式的阶次p 进行自适应调整. 相比于其他伪谱法,如Legendre伪谱法、Radau伪谱法,Gauss伪谱法具有更高的求解精度和收敛速度,在处理含初始和终端约束的问题上更具优势[22 -23 ] . ...