人体姿态识别在早期的研究中通过采集作业姿态图像、视频数据,借助ImageJ与PS软件人工标记、测量姿态的肢体角度数据[3]. 人工标记方法的过程繁琐,尤其是在识别大量的姿态图像数据上容易产生人为失误[4],但是为后续研究打开了思路,奠定了方法论基础. 随着技术的革新,人体姿态识别方法不断优化. 朱德慰等[5]面向人机协作安全问题,基于Kinect摄像机识别人体骨架特征,实现人机协作过程中人的姿态特征识别与异常行为监测,为企业安全生产奠定基础. Kinect摄像机实现了机器设备辅助下的智能化人体作业姿态识别与分析,但是目前kinect内置算法较复杂,识别精度较差[6-7]. 动作捕捉系统具有更高的稳定性与准确性. 该系统使用多个摄像头或传感器,捕捉安装在作业人员关键肢体部位上的特定标记点,以图像帧系列的方法记录标记点的位置信息,使用配套软件分析标记点的变化情况并反馈构建人体骨架,分析作业姿态[8]. 在识别过程中,被识别者需要穿戴配套带有标记点的服装,测量精度较高,但该方法整体规模较大,难以深入现场进行识别[9].
随着人工智能与计算机视觉技术的发展,直接使用人体作业姿态RGB图像进行人体姿态识别,成为了目前领域内的热点研究方向[10-11]. 相关的姿态识别算法从经典的树状结构模型发展到顺序卷积结构[12-13],其中以卷积神经网络(convolutional neural network, CNN)为代表,图像特征提取能力显著优于其他深度学习算法[14]. CNN可以直接输入二维图像,从图像数据中学习图像纹理和空间特征,避免了扩展后图像结构的损失. CNN网络复杂程度低、训练参数少,易于训练和优化,具有良好的鲁棒性[13]. Wei等[15]提出的卷积姿势机(convolutional pose machine, CPM)融合CNN与姿势机(pose machine, PM),形成端到端的级联体系,使其同时具备CNN与PM的优势,有效解决了结构化人体姿态识别的问题.
本文基于CPM,提出潜航员作业姿态识别与分析的方法. 该方法以潜航员作业姿态二维图像、视频数据为基础,学习人体姿态特征到肢体部位与关节点位置的映射. 通过算法识别得到特征关节点坐标,利用骨架映射模型计算与判断肢体角度数据以及肢体特殊状态. 以“蛟龙号”载人潜水器为例,采集潜航员作业姿态库,对所提方法进行应用验证.
1. 人体姿态特征结构化编码
1.1. 人体姿态特征骨架模型
表 1 人体姿态关节点编码
Tab.1
| 编码 | 含义 | 编码 | 含义 | |
| 1 | 头部 | 9 | 左手腕 | |
| 2 | 颈部 | 10 | 左手指 | |
| 3 | 右肩 | 11 | 右髋 | |
| 4 | 右手肘 | 12 | 右膝 | |
| 5 | 右手腕 | 13 | 右踝 | |
| 6 | 右手指 | 14 | 左髋 | |
| 7 | 左肩 | 15 | 左膝 | |
| 8 | 左手肘 | 16 | 左踝 |
1.2. 人体姿态的肢体角度计算
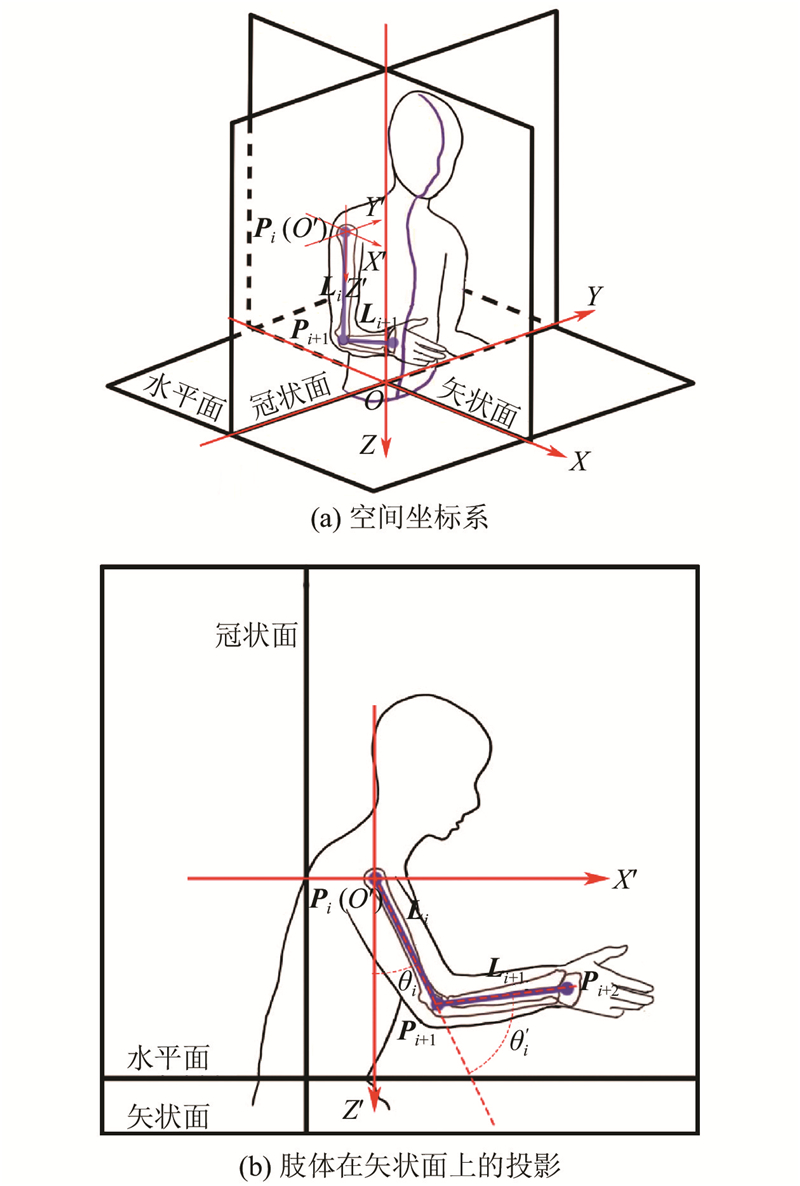
以解剖学为基础,定义矢状面、冠状面及水平面为基准面,构建人体作业姿态
图 1
图 1 空间坐标系与矢状面投影定义
Fig.1 Spatial and sagittal projection coordinate system definition
表 2 人体肢体编码
Tab.2
| 编码 | 含义 | 编码 | 含义 | |
| 1-2 | 颈部 | 2-9-12 | 腰部 | |
| 2-3-4 | 右大臂 | 3-4-5 | 右小臂 | |
| 4-5-6 | 右手腕 | 2-7-8 | 左大臂 | |
| 7-8-9 | 左小臂 | 8-9-10 | 左手腕 | |
| 11-12-13 | 右腿 | 14-15-16 | 左腿 |
为了分析具体的肢体部位,将坐标系偏移至肢体根关节点
构建偏移矩阵,计算肢体关节点的偏移坐标:
如图1(b)所示,将肢体
肢体
在两点法的基础上,定义肢体在矢状面上的投影长度:
当作业姿势图像为二维图像时,无法直接从图像中计算肢体的实际长度,需要额外引入肢体实际测量长度T. 反推肢体在二维图像中缺失的深度坐标
当作业姿势图像为三维图像时,可以直接计算肢体的空间长度:
利用两点法、投影规则,计算肢体在冠状面上投影的偏转角度
根据欧拉旋转矩阵与齐次变换,可以调整肢体角度坐标轴参考关系及肢体相对关系. 定义肢体在3个维度上的旋转角为
一次齐次变换表达式为
式中:t为对应关节点之间的空间距离. 多次变化可以递归转换肢体相对角度的关系.
1.3. 人体姿态的肢体特殊状态判断
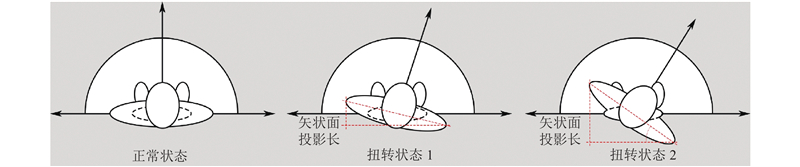
在作业姿态分析中,需要确定各肢体在作业过程中是否呈现特殊危险状态,如肢体躯干和颈部是否处于扭转状态、腿部处于单腿支撑状态还是双腿支撑状态、手腕是否处于扭转或外展状态以及大臂自然下垂状态等.
图 2
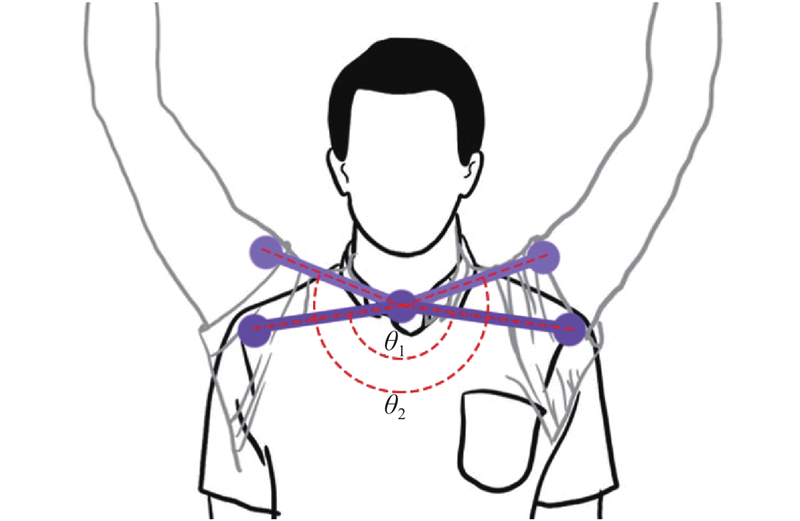
在人体姿态分析中,手臂特殊状态的判断包括大臂是否处于自然下垂状态、手臂是否处于外展或内收状态以及双肩是否处于抬高状态. 大臂自然下垂状态定义为人体腰部与大臂夹角较大(> 45°),但大臂相对于竖直参考系的弯曲夹角较小(< 20°). 通过计算并对比腰部与大臂的夹角和大臂弯曲角度之间的差值进行判断. 手臂外展或内收状态定义为大臂与小臂构成的工作平面与矢状面不平行,可以通过计算大臂与小臂在冠状面上投影的偏转角度进行判断. 若大臂与小臂的偏转角度均接近90°,则可以判断手臂在正常工作平面中. 双肩抬高状态定义为左、右肩关节点过高. 计算颈部关节点与左、右肩关节点连线的相对角度[6],如图3所示. 若该角度小于180°,则判断双肩处于正常状态.
图 3
腿部的特殊状态判断包括单腿受力支撑、 双腿受力支撑、跪姿等腿部支撑情况. 当人体两腿部肢体弯曲角度之间的差值达到30°时,或当某一腿部弯曲肢体角度大于90°时[16],均可以判断腿部状态为单腿支撑状态或跪姿状态,其余情况判定为双腿支撑.
2. 基于卷积姿态机的人体作业姿态识别分析算法
2.1. 算法原理
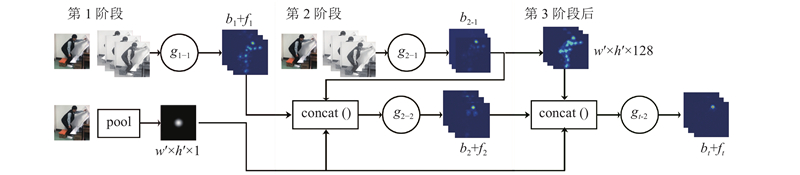
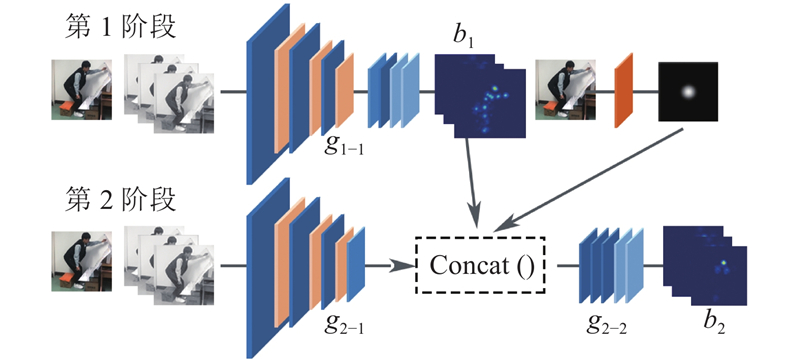
基于CPM构建本文的潜航员作业姿态识别算法,开展作业姿态特征关节点二维坐标的提取、肢体角度的计算、特殊姿态状态的判断. 算法原理如图4所示,算法的主体框架由多个卷积组g1-1, g2-1, g2-2, ···, gt-2分阶段串联所构成.
图 4
图 4 潜航员作业姿态识别算法的原理
Fig.4 Principles of submariner's operation posture recognition algorithm
算法中每个阶段都可以独立完成肢体特征提取工作. 在第1阶段中,算法将输入的原始图像处理为RGB三层图像,将RGB三层图像作为g1-1的输入,经过全卷积层产生P+1个特征图b1与损失值f1. 此时生成的特征图识别精度较低,但是经过全卷积的处理具有更大的感受野,可以识别更全局、深层次的特征,定义为深层特征或空间特征. 算法的后续阶段均由2个卷积组构成,如第2阶段由g2-1、g2-2 2个卷积组构成,g2-1以原始图像的RGB三层图像为输入,输出部分特征图b2-1. g2-1卷积组未经过全卷积,此时的卷积感受野较小,可以更好地识别局部、细节特征即纹理特征,因此g2-1生成的特征图b2-1被定义为浅层特征或纹理特征. 将g1-1生成的特征图b1、g2-1生成的特征图b2-1以及原图经过高斯模糊处理的中心约束图像A采用concat()函数串联起来后,作为g2-2的输入. 经过g2-2的处理后,算法完成第2阶段的工作,生成精度较高的特征图b2与损失值f1,作为后续阶段的部分输入.
第3阶段往后与第2阶段完全一致,但为了提高算法网络的运行效率,原图不再作为直接输入,而是将原图经g2-2后生成的深度为128的图像、中心约束图像A以及前一阶段产生的bt-1与ft-1串联输入到当前的gt-2卷积组中,生成精度更高的第t阶段特征图bt. 通常网络在运行4~6个阶段后达到相对的稳定状态,准确率较高.
2.2. 算法网络结构
2.2.1. 算法结构
图 5
图 5 潜航员作业姿态识别算法的结构
Fig.5 Structure of submariner’s operation posture recognition algorithm
表 3 算法g1-1卷积组的参数
Tab.3
| 序号 | 输入 | 运算 | 参数 | 输出 |
| 1 | 原始图像 | — | — | 368×368×3 |
| 2 | 368×368×3 | Conv.+ReLU | k = 9, n = 128, s = 1 | 368×368×128 |
| 3 | 368×368×128 | max_pool | 2×2, s = 2 | 184×184×128 |
| 4 | 184×184×128 | Conv.+ReLU | k = 9, n = 128, s = 1 | 184×184×128 |
| 5 | 184×184×128 | max_pool | 2×2, s =2 | 92×92×128 |
| 6 | 92×92×128 | Conv.+ReLU | k = 9, n = 128, s = 1 | 92×92×128 |
| 7 | 92×92×128 | max_pool | 2×2, s = 2 | 46×46×128 |
| 8 | 46×46×128 | Conv.+ReLU | k = 5, n = 32, s = 1 | 46×46×32 |
| 9 | 46×46×32 | Conv.+ReLU | k = 9, n = 512, s = 1 | 46×46×512 |
| 10 | 46×46×512 | Conv.+ReLU | k = 1, n = 512, s = 1 | 46×46×512 |
| 11 | 46×46×512 | Conv.+ReLU | k = 1, n = 15, s = 1 | 46×46×15 |
表 4 算法g2-1与g2-2卷积组的参数
Tab.4
| 序号 | 输入 | 运算 | 参数 | 输出 |
| 1 | 原始图像 | — | — | 368×368×3 |
| 2 | 368×368×3 | Conv.+ReLU | k = 9, n = 128, s = 1 | 368×368×128 |
| 3 | 368×368×128 | max_pool | 2×2, s = 2 | 184×184×128 |
| 4 | 184×184×128 | Conv.+ReLU | k = 9, n = 128, s = 1 | 184×184×128 |
| 5 | 184×184×128 | max_pool | 2×2, s = 2 | 92×92×128 |
| 6 | 92×92×128 | Conv.+ReLU | k = 9, n = 128, s = 1 | 92×92×128 |
| 7 | 92×92×128 | max_pool | 2×2, s = 2 | 46×46×128 |
| 8 | 46×46×128 | Conv.+ReLU | k = 5, n = 32, s = 1 | 46×46×32 |
| 9 | 46×46×32+ 46×46×15+ 46×46×1 | Concat ( ) | — | 46×46×48 |
| 10 | 46×46×48 | Conv.+ReLU | k = 11, n = 128, s = 1 | 46×46×128 |
| 11 | 46×46×128 | Conv.+ReLU | k = 11, n = 128, s = 1 | 46×46×128 |
| 12 | 46×46×128 | Conv.+ReLU | k = 11, n = 128, s = 1 | 46×46×128 |
| 13 | 46×46×128 | Conv.+ReLU | k = 1, n = 128, s = 1 | 46×46×128 |
| 14 | 46×46×128 | Conv.+ReLU | k = 1, n = 15, s = 1 | 46×46×15 |
2.2.2. 算法训练
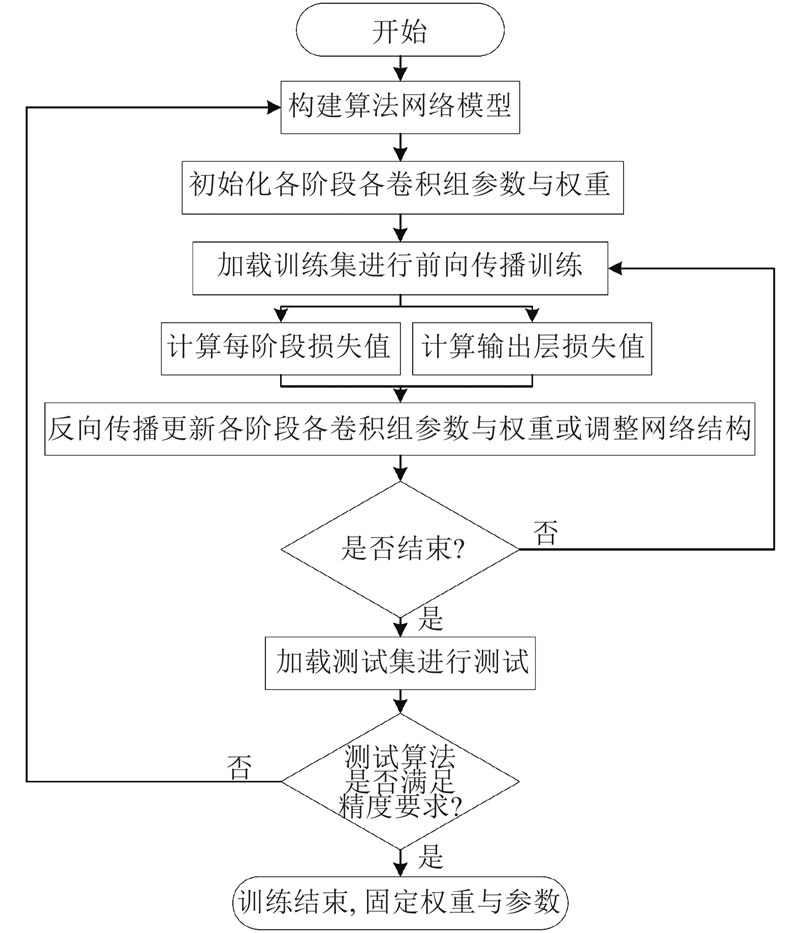
本文算法是分阶段级联的网络结构,因此采取中继监督优化的学习方式. 利用各阶段计算的损失值计算输出层总误差,将误差进行反向传播,更新各阶段各层参数与权重. 训练流程如图6所示,配套安装MPII人体姿态数据集,该数据集包含28 000多个人体姿态训练样本. 构建网络模型,基于随机函数设置网络的参数与权重,从训练集中选取静态图像并通过向前传播的方式对网络进行训练,计算各阶段的损失值并计算输出层总误差. 基于反向传播算法、梯度下降原则,更新各个阶段网络层中的参数与权重,使得输出损失误差最小. 将上述步骤重复迭代,直至所有训练集中的样本图像训练完成且模型精度达到要求,结束并完成算法的训练.
图 6
图 6 潜航员作业姿态识别算法的训练流程
Fig.6 Training process of submariner's operation posture recognition algorithm
2.2.3. 算法测试
在网络训练完成后,作业姿态图像经过算法识别后输出的6个阶段人体关节点特征图如图7所示. 根据结果可知,在网络运行的前2个阶段中,图像可视效果较好的关节点被准确地识别,如头部、颈部、右肩及右手肘等关节点,但例如左肩、左膝关节点的识别效果较发散甚至缺失. 随着网络后续阶段的运行,关节点及其之间更多的空间特征与纹理特征被提取,这些关节点特征的识别逐渐收敛,得到较高精度的识别效果. 关节点特征图中的高斯函数峰值点对应的坐标数据为该关节点的坐标值.
图 7
图 7 6个阶段的人体关节点特征图
Fig.7 Characteristic diagram of human joint points in six stages
使用关节点正确估计比例(percentage of correct keypoints,PCK)作为评价指标. PCK是评价人体姿态识别算法性能的主流评价指标,第i个关节点部位的
式中:
在所有测试图像识别完成后,计算所有肢体部位的PCK指标,如表5所示,本文算法PCK平均值为81.2 %,优于4类经典算法. 与国际较先进的算法相比较一致,其中头部、肩部与肘部等上半身关节部位的准确度最优,腕部、踝部易被遮挡的关节点的准确度较优.
表 5 不同算法的PCK指标对比
Tab.5
| 方法 | 头部 | 颈部 | 肩部 | 肘部 | 腕部 | 臀部 | 膝部 | 踝部 | 平均 |
| FC[19] | 75.8 | 71.3 | 67.3 | 64.3 | 60.4 | 63.7 | 60.1 | 55.7 | 64.8 |
| DC[20] | 83.6 | 74.6 | 73.9 | 71.1 | 66.0 | 70.9 | 64.1 | 59.4 | 70.5 |
| CPN[21] | 85.4 | 77.1 | 79.6 | 74.5 | 69.9 | 73.6 | 70.9 | 64.8 | 74.5 |
| PAF[13] | 82.6 | 75.8 | 75.9 | 71.3 | 68.5 | 68.9 | 65.9 | 60.9 | 71.2 |
| 文献[17] | 91.8 | 82.1 | 80.6 | 70.9 | 82.1 | 81.9 | 74.6 | 80.2 | 80.5 |
| 文献[18] | 90.6 | 84.3 | 84.5 | 75.0 | 78.0 | 83.8 | 78.9 | 79.2 | 81.8 |
| 本文方法 | 93.6 | 83.2 | 90.5 | 83.2 | 73.6 | 77.9 | 76.2 | 71.7 | 81.2 |
3. 潜航员作业姿态识别分析应用验证
3.1. 潜航员作业姿态图像数据获取
3.1.1. 实验设计
以蛟龙号载人潜水器中的潜航员作业姿态识别分析为例,对所提算法进行进一步的应用与验证. 基于现有蛟龙号载人潜水器操作界面布局,采用PVC板材搭建载人潜水器操作界面模拟实验平台,如图8所示. 完整的操作界面由4块操作面板组成,为了便于描述,由下至上依次命名为面板1~4.
根据潜航员配置及载人潜水器环境的特殊性,招募了5名受试者参与实验,其中4名男性、1名女性,年龄平均值为25岁,标准差为0.71,身高为168~180 cm,体重为50~70 kg. 所有受试者无明显身体缺陷,具有独立完成操作潜航员操作作业的能力.
图 8
图 8 载人潜水器模拟操作界面布局
Fig.8 Manned submersible simulation operation interface layout
3.1.2. 潜航员作业姿态识别数据集
根据潜航员的作业任务,将潜航员的作业姿态划分为操作姿态、观察姿态、操作与观察姿态,具体包括各操作面板点击操作、双手同时操作操纵杆、观察显示屏或观察窗等观察作业以及观察与操作并行等作业姿态. 采集到的潜航员作业姿态部分样本数据集如图9所示(无骨架). 在实验过程中,受试者完成相应的作业姿态,实验人员利用手机对作业姿态图像进行采集,基于给定作业任务完整记录受试者作业过程中的动态作业视频. 每位受试者采集到作业姿态图像15张,作业过程视频2个,5名受试者共计75张作业姿态静态图像数据,共收集10个帧率为30帧/s的作业,单个视频时长为6.0~7.0 s.
图 9
图 9 利用潜航员作业姿态识别算法所生成的人体骨架
Fig.9 Human skeleton generated by submariner’s operation posture recognition algorithm
3.2. 潜航员作业姿态图像数据获取
将采集到的潜航员作业姿态识别数据集分为作业姿态图像与视频数据2类. 作业姿态图像用来分析静态关键姿态,视频数据引入时间序列分析整个作业任务中作业姿态的动态过程变化,例如颈部角度在时间维度的变化情况、手臂角度变化情况等. 利用潜航员作业姿态识别算法识别的潜航员作业姿态骨架如图9所示. 可以看出,算法所识别的人体骨架模型基本完整,无关节点或肢体缺失. 除存在较大遮挡的左侧肘部与脚踝肢体有轻微偏移外,算法的整体识别效果较好.
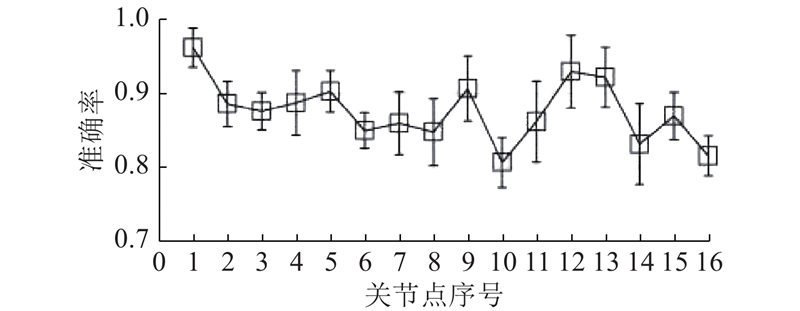
提取作业姿态识别算法中生成的关节点坐标准确性得分数据,计算每个关节点识别准确率的平均值和标准差,结果如图10所示. 关节点识别准确率的平均值达到0.877,其中头部关节点的准确率最高为0.963,左手指关节点的准确率最低为0.801. 右手腕、左手腕、右膝及右踝关节点的准确率均大于0.9.
图 10
肢体右侧关节点准确率的平均值略高于肢体左侧关节点平均值(右侧:0.890;左侧:0.849). 准确率的结果表明,本文作业姿态识别算法在潜航员作业姿态识别上是可靠的,较好地完成了潜航员作业姿态智能识别的工作,可以为后续作业姿态危险因素分析提供可靠的数据来源. 图10中,误差棒为该关节点识别准确率的标准差,即该关节点准确率的波动范围.
根据1.2节提出的角度计算公式与关节点坐标值数据,计算作业姿态各肢体角度,共计750个肢体角度样本数据. 将所有样本数据输入至SPSS 25.0软件中进行数据分析,计算重复实验中10组肢体角度的平均值
表 6 潜航员作业姿态识别的肢体角度平均值(标准差)与ICC结果
Tab.6
| 作业姿态 | | ICC | |||||||||
| 颈部 | 腰部 | 右大臂 | 右小臂 | 右手腕 | 左大臂 | 左小臂 | 左手腕 | 右腿 | 左腿 | ||
| 1 | 1.2(1.3) | 2.2(2.9) | 14.5(10.7) | 72.5(9.8) | 1.8(1.2) | 14.8(12.3) | 70.0(5.8) | 1.7(1.7) | 105(8.0) | 107.2(11.5) | 0.966 |
| 2 | 8.6(6.8) | 6.9(1.7) | 29.4(9.7) | 42.2(14.0) | 6.3(4.5) | 19.4(10.0) | 65.0(4.3) | 1.7(1.5) | 103.1(10.1) | 105.4(10.2) | 0.951 |
| 3 | −6.7(3.9) | 8.2(1.9) | 39.3(7.4) | 30.7(13.1) | 7.7(5.9) | 22.6(9.2) | 67.7(10.2) | 1.9(1.5) | 104.4(10.5) | 105.2(11.6) | 0.953 |
| 4 | −17.9(10.0) | 28.2(3.7) | −9.9(33.2) | 74.4(32.0) | 2.2(2.0) | 77.7(11.2) | 18.5(6.8) | 8.4(4.5) | 101.8(10.8) | 104.6(10.3) | 0.879 |
| 5 | −19.7(8.1) | 35.9(6.1) | −11.4(4.4) | 21.5(11.4) | 16.6(4.5) | 82.8(8.9) | 18.1(9.0) | 12.5(4.5) | 67.3(21.9) | 68.9(24.9) | 0.888 |
| 6 | 7.7(1.5) | 5.6(0.2) | 21.2(7.6) | 40.5(19.3) | 22.2(2.0) | 23.6(7.1) | 34.7(10.5) | 22.0(0.5) | 108.2(12.7) | 106.4(10.5) | 0.944 |
| 7 | 20.4(10.0) | 30.5(14.0) | −19.6(10.5) | 119.5(22.9) | 2.2(1.2) | −14.1(13.4) | 112.6(18.3) | 2.0(1.8) | 106.1(9.2) | 109.3(11.3) | 0.950 |
| 8 | −4.9(9.6) | 19.5(13.9) | −10.5(9.5) | 91.4(9.7) | 2.0(1.0) | −5.0(8.1) | 87.6(9.4) | 1.9(1.6) | 104.8(2.4) | 107.1(4.7) | 0.971 |
| 9 | −16.9(9.9) | 16.0(10.9) | 8.1(9.4) | 82.6(12.2) | 3.3(2.0) | 10.3(7.5) | 82.1(8.6) | 1.4(0.7) | 104.2(1.0) | 104.5(3.0) | 0.976 |
| 10 | −6.3(3.2) | 16.6(8.4) | 17.0(17.7) | 61.7(27.6) | 9.5(3.1) | 8.9(2.5) | 76.9(11.9) | 1.8(1.1) | 108.4(4.9) | 107.6(7.2) | 0.921 |
| 11 | −17.4(3.9) | 15.9(7.1) | 16.8(15.4) | 65.1(24.2) | 10.7(5.7) | 8.8(4.9) | 71.6(15.6) | 1.9(1.6) | 106.2(5.4) | 107.1(3.5) | 0.933 |
| 12 | −14.8(5.3) | 26.2(5.6) | −10.0(6.8) | 82.8(15.2) | 1.7(1.7) | 75.6(11.1) | 20.0(6.5) | 9.1(3.7) | 108.9(11.7) | 109.4(12.7) | 0.963 |
| 13 | −23.4(6.3) | 24.1(6.8) | −10.4(4.4) | 90.9(13.3) | 1.9(1.8) | 78.4(10.8) | 16.8(8.2) | 8.3(3.4) | 103.7(10.2) | 107.4(12.3) | 0.965 |
| 14 | −14.0(11.1) | 39.2(7.7) | 10.7(10.2) | 19(6.6) | 16.7(5.3) | 79.8(13.6) | 23.1(14.3) | 12.7(5.4) | 65.0(26.0) | 67.7(28.7) | 0.832 |
| 15 | −24.9(9.0) | 37.3(6.3) | 10.3(4.6) | 21(5.3) | 16.1(4.7) | 81.2(10.8) | 21.2(11.1) | 12.2(4.7) | 68.0(27.9) | 69.8(27.8) | 0.874 |
| ICC | 0.935 | 0.923 | 0.976 | 0.974 | 0.853 | 0.881 | 0.956 | 0.887 | 0.852 | 0.819 | — |
表6的肢体角度数据表明,作业姿态4、5、11、13、15等作业姿态的颈部肢体角度接近甚至大于−20°,颈部出现较大程度的后仰状态. 在腰部肢体角度上整体较小,腰部呈现向前微弯. 作业姿态5、12、13、14、15等作业姿态的大臂肢体角度约为80°,即手臂与双肩处于抬高状态,甚至个别受试者出现手过头现象. 在腿部肢体的角度上,大部分角度接近110°,与正常坐姿相比,潜航员坐姿腿部弯曲角度偏大. 在作业姿态5、14、15上,腿部肢体状态由坐姿转变为双腿弯曲.
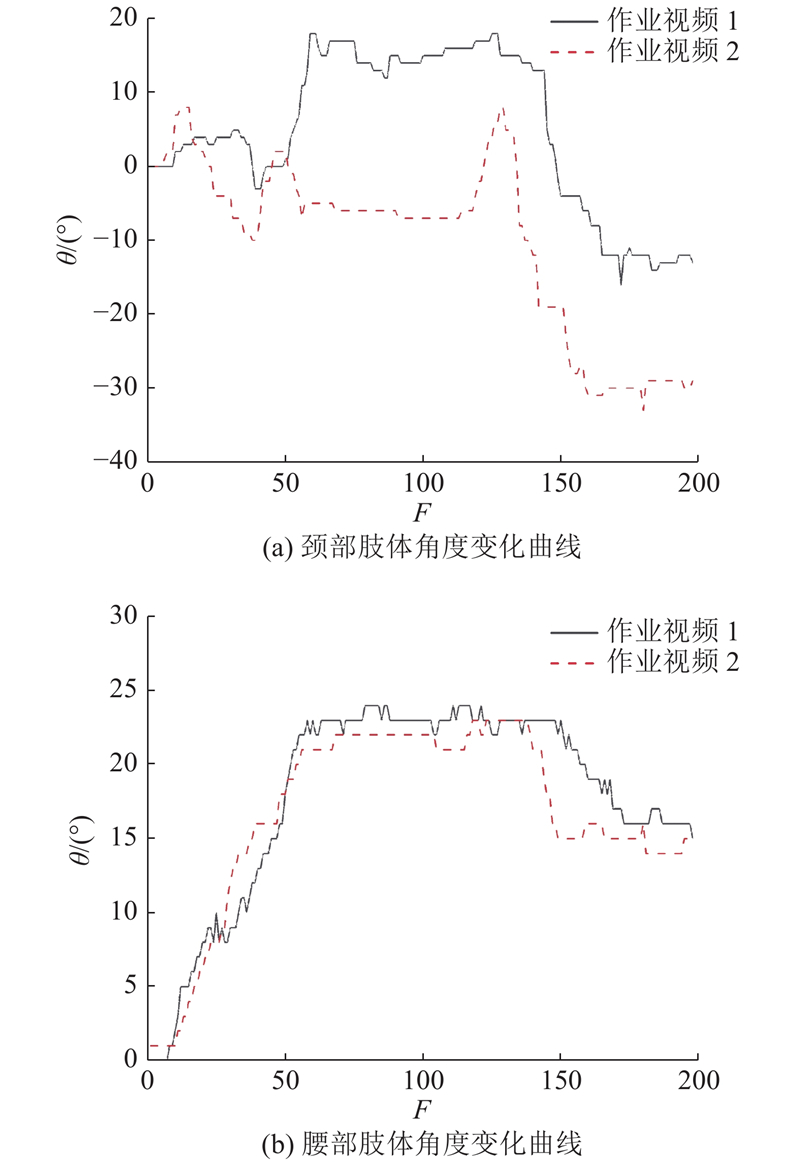
图 11
经过分析发现,在载人潜水器操作界面作业姿态中,作业姿态5、作业姿态14和作业姿态15均为操作远端面板,作业人员姿态扭曲较严重,需要较大的弯腰伸手操作;臀部的抬高导致了作业人员的下肢支撑点减少,引起腿部不舒适性的增加. 作业姿态 13 和作业视频2在头颈部的角度变化较大且处于后仰状态,头颈部风险较大. 整体来看,腿部角度均较大,大腿与小腿收缩较大;腿部空间较小,难以完成弯腰起立的远端操作. 在操作远端面板时,腰部与头部后仰角度过大,因此建议在载人潜水器操作界面设计时考虑操作频率问题,减少作业人员远端操作频率,指导作业人员在作业时注意头颈部与腰背部的姿态配合,降低肢体的后仰弯曲角度.
4. 结 语
本文提出基于卷积姿态机的潜航员作业姿态识别分析方法,构建用于分析潜航员作业姿态的人体姿态骨架模型. 算法部分结合卷积神经网络与姿态机架构,使用中继监督优化的方式完成了算法的训练工作. 在算法的测试中,关节点识别的准确率较CPN、PAF经典算法有较大提升,算法性能较先进. 通过将潜航员作业姿态图像输入本文算法中进行应用验证,证明了算法识别的准确性与稳定性;分析潜航员作业姿态,提出较危险的不良因素,相关性系数高于Plantard等[7]的研究结果.
本文算法解决了潜航员作业姿态识别分析繁杂、准确度低的问题,输出的潜航员作业姿态关节点坐标、肢体角度及肢体状态等数据可以用于后续的潜航员作业姿态分析与评估,提高了该类方法的应用价值. 在后续研究中,应用本文算法输出的数据对潜航员作业姿态进行风险评估,降低潜航员在作业时发生损伤的可能性.
参考文献
Human reliability prediction in deep-sea sampling process of the manned submersible
[J].
载人潜水器舱室空间舒适性复合评估方法
[J].DOI:10.11918/j.issn.0367-6234.201810148 [本文引用: 1]
Compound evaluation method for the space comfort of manned submersible
[J].DOI:10.11918/j.issn.0367-6234.201810148 [本文引用: 1]
面向老年俯身作业的人机工程舒适性设计
[J].
Man-machine comfortable designing for bending operations of elderly
[J].
Observer variability in posture assessment from video recordings: The effect of partly visible periods
[J].
Real time RULA assessment using Kinect v2 sensor
[J].
Validation of an ergonomic assessment method using kinect data in real workplace conditions
[J].
A comparison of currently available optoelectronic motion capture systems
[J].
Wearable IMU-based real-time motion warning system for construction workers' musculoskeletal disorders prevention
[J].
Image representation of pose-transition feature for 3D skeleton-based action recognition
[J].
基于深度卷积神经网络的车型识别方法
[J].
Vehicle category recognition based on deep convolutional neural network
[J].
Hands deep in deep learning for hand pose estimation
[J].
How does lower limb dominance influence postural control movements during single leg stance?
[J].
Janitor ergonomics and injuries in the safe workload ergonomic exposure project (SWEEP) study
[J].