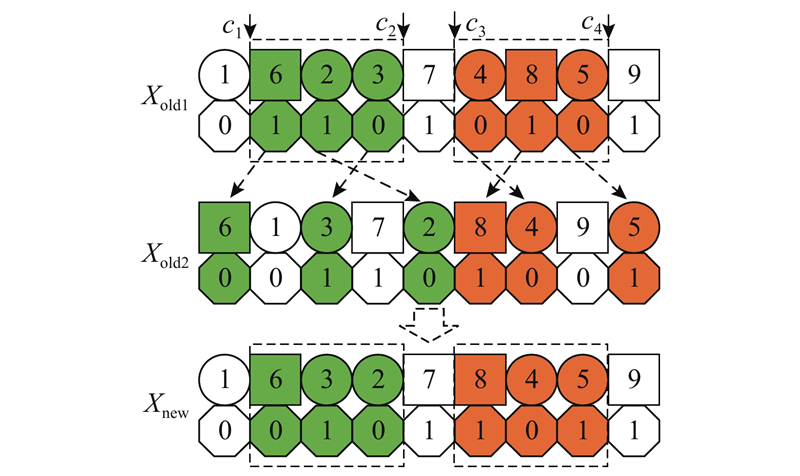
式中:C T 为节拍时间;i 为拆卸任务编号;I l l 上任务编号集合,拆卸线Ⅰ任务集为 ${{{I}}_1} = $ $ \left\{ {1,2,\cdots,{n_1}} \right\}$ ${{{I}}_2} = \{ {n_1} + 1, {n_1} + 2,\cdots, $ $ {n_1} + {n_2} \}$ W 为工作站编号集合, ${{W}} = \{ 1,2,\cdots, {n_1} + {n_2} \}$ w 为工作站编号,其中 $w \in {{W}}$ K 为操作者编号集合, ${{K}} = \left\{ {1,2} \right\}$ k =1为工人拆卸,k =2为机器拆卸,其中 $k \in {{K}}$ t ik i 由操作者k 拆卸所需的时间;C w 1C w 2C r 为投入一个机器人所需的成本;C rt 为机器人拆卸时的单位时间成本;C pt 为工人拆卸时的单位时间成本;S w w 开启则S w x iwk i 分配给工作站w 中的操作者k, 则x iwk r kw k 分配给工作站w, 则r kw
(16) $ \left.{\begin{array}{*{20}{c}} {{f_i}\left( {{x^1}} \right) \leqslant {f_i}\left( {{x^2}} \right),\; i \in \left\{ {1,2,\cdots,M} \right\}}; \\ {{f_j}\left( {{x^1}} \right) < {f_j}\left( {{x^2}} \right),\; j \in \left\{ {1,2,\cdots,M} \right\}}. \end{array}} \right\}$
式中:d 为非劣解的个数, $d \in \left\{ {2,3,\cdots,D - 1} \right\}$ m 为目标函数的个数, $m \in \left\{ {1,2,\cdots,M} \right\}$ $f_m^{d - 1}$ $f_m^{d + 1}$ d −1个和第d +1个非劣解的第m 个目标函数值; $f_m^{\min }$ $f_m^{\max }$ m 个目标函数的最小值与最大值.
[1]
GUNGOR A, GUPTA S M, POCHAMPALLY K, et al. Complications in disassembly line balancing [C]// Proceedings of SPIE International Conference on Environmentally Conscious Manufacturing. Bellingham: SPIE, 2001: 289-298.
[本文引用: 3]
[2]
AVIKAL S, JAIN R, YADAV H, et al. A new heuristic for disassembly line balancing problems with AND/OR precedence relation [C]// Proceedings of the 2nd International Conference on Soft Computing for Problem Solving . Lakshmipat: Advances in Intelligent Systems and Computing, 2014: 519-525.
[本文引用: 1]
[3]
KOC A, SABUNCUOGLU I, EREL E Two exact formulations for disassembly line balancing problems with task precedence diagram construction using an AND/OR graph
[J]. IIE Transactions , 2009 , 41 (10 ): 866 - 881
DOI:10.1080/07408170802510390
[本文引用: 1]
[4]
REN Y, YU D, ZHANG C, et al An improved gravitational search algorithm for profit-oriented partial disassembly line balancing problem
[J]. International Journal of Production Research , 2017 , 55 (24 ): 7302 - 7316
DOI:10.1080/00207543.2017.1341066
[本文引用: 1]
[5]
丁力平, 谭建荣, 冯毅雄, 等 基于Pareto蚁群算法的拆卸线平衡多目标优化
[J]. 计算机集成制造系统 , 2009 , 15 (7 ): 1406 - 1413
URL
[本文引用: 2]
DING Li-ping, TAN Jian-rong, FENG Yi-xiong, et al Multi-objective optimization for disassembly line balancing based on Pareto ant colony algorithm
[J]. Computer Integrated Manufacturing Systems , 2009 , 15 (7 ): 1406 - 1413
URL
[本文引用: 2]
[6]
郭磊, 张秀芬 多重故障驱动的再制造并行拆卸序列规划方法
[J]. 浙江大学学报: 工学版 , 2020 , 54 (11 ): 2233 - 2246
URL
[本文引用: 1]
GUO Lei, ZHANG Xiu-fen Remanufacturing parallel disassembly sequence planning method driven by multiple failures
[J]. Journal of Zhejiang University: Engineering Science , 2020 , 54 (11 ): 2233 - 2246
URL
[本文引用: 1]
[7]
徐进, 张树有, 费少梅 基于自适应粒子群的产品再制造拆卸规划
[J]. 浙江大学学报: 工学版 , 2011 , 45 (10 ): 1746 - 1752
DOI:10.3785/j.issn.1008-973X.2011.10.008
XU Jin, ZHANG Shu-you, FEI Shao-mei Product remanufacture disassembly planning based on adaptive particle swarm optimization algorithm
[J]. Journal of Zhejiang University: Engineering Science , 2011 , 45 (10 ): 1746 - 1752
DOI:10.3785/j.issn.1008-973X.2011.10.008
[8]
朱卓悦, 徐志刚, 沈卫东, 等 基于遗传蝙蝠算法的选择性拆卸序列规划
[J]. 浙江大学学报(工学版) , 2018 , 52 (11 ): 2120 - 2127
DOI:10.3785/j.issn.1008-973X.2018.11.010
[本文引用: 1]
ZHU Zhuo-yue, XU Zhi-gang, SHEN Wei-dong, et al Selective-disassembly sequence planning based on genetic-bat algorithm
[J]. Journal of Zhejiang University: Engineering Science , 2018 , 52 (11 ): 2120 - 2127
DOI:10.3785/j.issn.1008-973X.2018.11.010
[本文引用: 1]
[9]
鲁建厦, 翟文倩, 李嘉丰, 等 基于改进混合蛙跳算法的多约束车辆路径优化
[J]. 浙江大学学报(工学版) , 2021 , 55 (2 ): 259 - 270
URL
[本文引用: 1]
LU Jian-xia, ZHAI Wen-qian, LI Jia-feng, et al Multi-constrained vehicle routing optimization based on improved hybrid shuffled frog leaping algorithm
[J]. Journal of Zhejiang University: Engineering Science , 2021 , 55 (2 ): 259 - 270
URL
[本文引用: 1]
[10]
王云, 冯毅雄, 谭建荣, 等 柔性作业车间分批调度多目标优化方法
[J]. 浙江大学学报: 工学版 , 2011 , 45 (4 ): 719 - 726
DOI:10.3785/j.issn.1008-973X.2011.04.022
[本文引用: 1]
WANG Yun, FENG Yi-xiong, TAN Jian-rong, et al Multi-objective optimization method of flexible job-shop lot-splitting scheduling
[J]. Journal of Zhejiang University: Engineering Science , 2011 , 45 (4 ): 719 - 726
DOI:10.3785/j.issn.1008-973X.2011.04.022
[本文引用: 1]
[11]
任彩乐, 张超勇, 孟磊磊, 等 基于改进候鸟优化算法的混合流水车间调度问题
[J]. 计算机集成制造系统 , 2019 , 25 (3 ): 643 - 653
URL
[本文引用: 1]
REN Cai-yue, ZHANG Chao-yong, MENG Lei-lei, et al Hybrid flow-shop scheduling problems based on improved migrating birds optimization algorithm
[J]. Computer Integrated Manufacturing Systems , 2019 , 25 (3 ): 643 - 653
URL
[本文引用: 1]
[12]
OZCEYLAN E, KALAYCI C, GUNGOR A, et al Disassembly line balancing problem a review of the state of the art and future directions
[J]. International Journal of Production Research , 2019 , 57 (15/16 ): 4805 - 4827
DOI:10.1080/00207543.2018.1428775
[本文引用: 1]
[13]
GAO K, HE Z, HUANG Y, et al A survey on meta-heuristics for solving disassembly line balancing, planning and scheduling problems in remanufacturing
[J]. Swarm and Evolutionary Computation , 2020 , 57 : 100719
DOI:10.1016/j.swevo.2020.100719
[14]
LAILI Y, LI Y, FANG Y, et al Model review and algorithm comparison on multi-objective disassembly line balancing
[J]. Journal of Manufacturing Systems , 2020 , 56 : 484 - 500
DOI:10.1016/j.jmsy.2020.07.015
[本文引用: 1]
[15]
HEZER S, KARA Y A network-based shortest route model for parallel disassembly line balancing problem
[J]. International Journal of Production Research , 2015 , 53 (6 ): 1849 - 1865
DOI:10.1080/00207543.2014.965348
[本文引用: 2]
[16]
GUO J, PU A P, DU B G, et al. Multi-objective optimization of stochastic hybrid production line balancing including assembly and disassembly tasks [EB/OL]. (2021-04-05). https://www.tandfonline.com/doi/full/10.1080/00207543.2021.1905902.
[本文引用: 1]
[17]
ZHU L, ZHANG Z, GUAN C Multi-objective partial parallel disassembly line balancing problem using hybrid group neighbourhood search algorithm
[J]. Journal of Manufacturing Systems , 2020 , 56 : 252 - 269
DOI:10.1016/j.jmsy.2020.06.013
[本文引用: 3]
[18]
SHI Y Brain storm optimization algorithm
[J]. Lecture Notes in Computer Science , 2011 , 3 (4 ): 303 - 309
[本文引用: 1]
[20]
吴秀丽, 张志强, 李俊青 求解离散调度问题的双机制头脑风暴优化算法
[J]. 控制与决策 , 2017 , 32 (9 ): 1583 - 1590
URL
[本文引用: 1]
WU Xiu-li, ZHANG Zhi-qiang, LI Jun-qing A brain storm optimization algorithm integrating diversity and discussion mechanism for solving discrete production scheduling problem
[J]. Control and Decision , 2017 , 32 (9 ): 1583 - 1590
URL
[本文引用: 1]
[21]
DEK K, PRATAP A, AGARWAL S, et al A fast and elitist multiobjective genetic algorithm: NSGA-II
[J]. IEEE Transactions on Evolutionary Computation , 2002 , 6 (2 ): 182 - 197
DOI:10.1109/4235.996017
[本文引用: 2]
[22]
BADER J, ZITALER E HypE: an algorithm for fast hypervolume-based many-objective optimization
[J]. Evolutionary Computation , 2011 , 19 (1 ): 45 - 76
DOI:10.1162/EVCO_a_00009
[本文引用: 1]
[23]
KALAYCI C B, GUPTA S M Artificial bee colony algorithm for solving sequence-dependent disassembly line balancing problem
[J]. Expert Systems with Applications , 2013 , 40 (18 ): 7231 - 7241
DOI:10.1016/j.eswa.2013.06.067
[本文引用: 5]
[24]
GUPTA S M, MCGOVERN S M. Disassembly sequencing problem: a case study of a cell phone [C]// 4th International Conference on Environmentally Conscious Manufacturing . Philadelphia: SPIE, 2004: 43-52.
[本文引用: 1]
[25]
KALAYCI C, GUPTA S. A particle swarm optimization algorithm for solving disassembly line balancing problem [C]// Proceedings of Northeast Decision Sciences Institute 2012 Annual Conference . Newport, Rhode Island: Northeast Decision Sciences Institute, 2012: 347-357.
[本文引用: 4]
[26]
KALAYCI C B, POLAT O, GUPTA S M A variable neighbourhood search algorithm for disassembly lines
[J]. Journal of Manufacturing Technology Management , 2015 , 26 (2 ): 182 - 194
DOI:10.1108/JMTM-11-2013-0168
[本文引用: 1]
[27]
TUNCEL E, ZEID A, KAMARTHI S Solving large scale disassembly line balancing problem with uncertainty using reinforcement learning
[J]. Journal of Intelligent Manufacturing , 2014 , 25 (4 ): 647 - 659
DOI:10.1007/s10845-012-0711-0
[本文引用: 1]
[28]
汪开普, 张则强, 朱立夏, 等 多目标拆卸线平衡问题的Pareto遗传模拟退火算法
[J]. 计算机集成制造系统 , 2017 , 23 (6 ): 1277 - 1285
URL
[本文引用: 4]
WANG Kai-pu, ZHANG Ze-qiang, ZHU Li-xia, et al Pareto genetic simulated annealing algorithm for multi-objective disassembly line balancing problem
[J]. Computer Integrated Manufacturing Systems , 2017 , 23 (6 ): 1277 - 1285
URL
[本文引用: 4]
[29]
ZHU L, ZHANG Z, WANG Y, et al On the end-of-life state oriented multi-objective disassembly line balancing problem
[J]. Journal of Intelligent Manufacturing , 2020 , 31 (6 ): 1403 - 1428
DOI:10.1007/s10845-019-01519-3
[本文引用: 1]
[30]
KALAYCI C B, POLAT O, GUPTA S M A hybrid genetic algorithm for sequence-dependent disassembly line balancing problem
[J]. Annals of Operations Research , 2016 , 242 (2 ): 321 - 354
DOI:10.1007/s10479-014-1641-3
[本文引用: 1]
3
... 时代的快速发展和人民生活的水平不断提高,使得电器电子产品的更新换代速率加快. 大量废旧的电器电子产品中含有许多可再利用的资源和危害材料,若大量闲置或随意丢弃,会对环境造成污染和带来资源的浪费. 为了有效地解决废旧电器电子产品的拆卸问题,Gungor等[1 ] 提出拆卸线平衡问题(disassembly line balancing problem, DLBP). ...
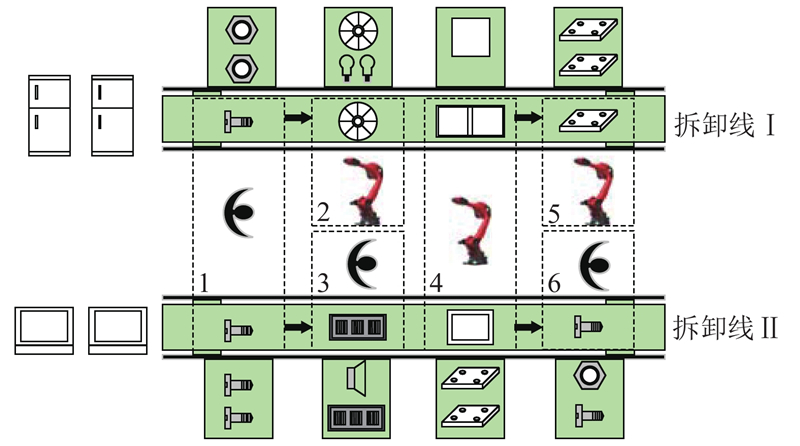
... 拆卸线布局的研究主要集中于直线型[1 -5 , 12 -14 ] . 与直线型拆卸线相比,并行拆卸线是将2条及以上的拆卸线平行放置,可同步拆卸多种不同的产品,有效地提高拆卸效率和生产线柔性. Hezer等[15 ] 提出并行拆线平衡问题(parallel disassembly line balancing problem, PDLBP),采用基于最短路径的网络模型求解. Guo等[16 ] 设计可同时拆卸和装配的并行生产线,构建以拆卸成本和平滑度指标为优化目标的数学模型,应用变邻域和非支配排序遗传算法的混合算法求解. Zhu等[17 ] 构建并行不完全拆卸线平衡问题的数学模型,设计混合群邻域算法求解. Hezer等[15 -17 ] 分别构建不同问题的PDLBP数学模型,但存在一定的不足,所建模型均属于概念模型,无法精确求解,即无法验证所有约束对于优化目标的正确性. 存在对2条拆卸线任务定义不明确的情况,例如提到并行线上具有相同编号任务时无法确定是哪条线上的任务. 本文考虑当前劳动力短缺的国情,拆卸线属于劳动密集型工作,需要大量的劳动. 替换部分工作站操作者由机器人拆卸,即在站间操作者不同的基础上与PDLBP结合,构建以工作站数目、机器人数、拆卸成本和空闲时间均衡指标为优化目标的PDLBP数学模型,应用CPLEX和LINGO对模型进行精确求解,验证该模型的正确性. ...
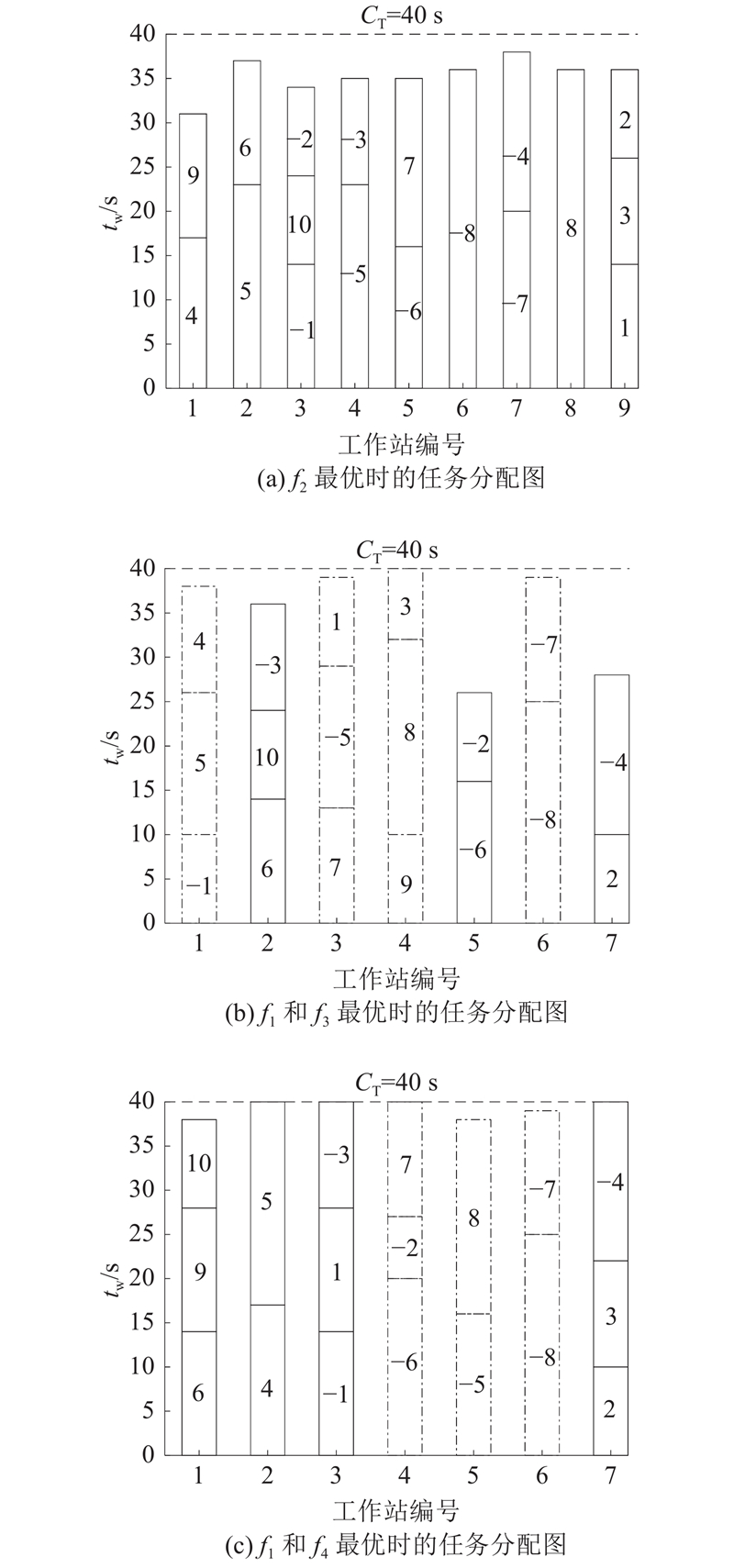
... 为了验证所建的PDLBP模型的正确性,采用CPLEX和LINGO精确解求解器,对1.3节所建模型开发相关程序,求解P10和P8算例. 算例中,基础拆卸时间和各零件优先关系等信息均来自文献[1 , 23 ],具体的拆卸信息如表1 所示. 表中,t ip 为工人拆卸时间,t ir 为机器人拆卸时间,c ost 为成本. 应用数学规划的方法对所提各优化目标求解时,各目标类型均不同,例如f 1 为混合整数线性规划(mixed integer linear programming, MILP)问题,f 2 和f 3 为混合整数二次规划(mixed integer quadratic programming, MIQP)问题,上述目标均可用CPLEX求解,但是f 4 为混合整数非线性规划(mixed integer nonlinear programming, MINLP)问题,无法应用CPLEX求解,应用LINGO对f 4 进行精确求解. 为了验证IBSO算法的有效性,应用MATLAB运行IBSO算法求解该算例,与精确解对比. IBSO参数为:C n =120,M gen =200,p 1 =0.2,p 2 =0.5,p 3 =0.5,p 4 =0.6,精确解与IBSO算法的对比结果如表2 所示. 表中,t s 为求解时间. 各目标最优值的任务分配图如图7 所示. 图中,t w 为工作站工作时间;任务前为“−”的是拆卸线Ⅱ任务;工作站中为点划线,表示该工作站由机器人拆卸,拆卸线Ⅰ拆卸P10产品即n 1 =10,拆卸线Ⅱ拆卸P8产品即n 2 =8. ...
1
... DLBP经过20年的发展,学者们从求解方法和拆卸布局方面不断深入研究. 求解方法主要包括启发式方法[2 ] 、数学规划法[3 ] 和智能算法等,而启发式方法过于依赖启发式规则,数学规划方法不适合求解大规模DLBP. 智能算法已广泛应用于求解DLBP,Ren等[4 ] 以拆卸利润最大为目标,提出重力搜索算法求解. 丁力平等[5 ] 结合Pareto解集思想与智能算法,更好地平衡多个优化目标,提出基于Pareto的蚁群算法求解多目标DLBP. 智能算法以其诸多优势已广泛应用于求解拆卸序列规划[6 -8 ] 、车辆路径规划[9 ] 和车间调度[10 -11 ] 等问题,均取得了良好的成果. ...
Two exact formulations for disassembly line balancing problems with task precedence diagram construction using an AND/OR graph
1
2009
... DLBP经过20年的发展,学者们从求解方法和拆卸布局方面不断深入研究. 求解方法主要包括启发式方法[2 ] 、数学规划法[3 ] 和智能算法等,而启发式方法过于依赖启发式规则,数学规划方法不适合求解大规模DLBP. 智能算法已广泛应用于求解DLBP,Ren等[4 ] 以拆卸利润最大为目标,提出重力搜索算法求解. 丁力平等[5 ] 结合Pareto解集思想与智能算法,更好地平衡多个优化目标,提出基于Pareto的蚁群算法求解多目标DLBP. 智能算法以其诸多优势已广泛应用于求解拆卸序列规划[6 -8 ] 、车辆路径规划[9 ] 和车间调度[10 -11 ] 等问题,均取得了良好的成果. ...
An improved gravitational search algorithm for profit-oriented partial disassembly line balancing problem
1
2017
... DLBP经过20年的发展,学者们从求解方法和拆卸布局方面不断深入研究. 求解方法主要包括启发式方法[2 ] 、数学规划法[3 ] 和智能算法等,而启发式方法过于依赖启发式规则,数学规划方法不适合求解大规模DLBP. 智能算法已广泛应用于求解DLBP,Ren等[4 ] 以拆卸利润最大为目标,提出重力搜索算法求解. 丁力平等[5 ] 结合Pareto解集思想与智能算法,更好地平衡多个优化目标,提出基于Pareto的蚁群算法求解多目标DLBP. 智能算法以其诸多优势已广泛应用于求解拆卸序列规划[6 -8 ] 、车辆路径规划[9 ] 和车间调度[10 -11 ] 等问题,均取得了良好的成果. ...
基于Pareto蚁群算法的拆卸线平衡多目标优化
2
2009
... DLBP经过20年的发展,学者们从求解方法和拆卸布局方面不断深入研究. 求解方法主要包括启发式方法[2 ] 、数学规划法[3 ] 和智能算法等,而启发式方法过于依赖启发式规则,数学规划方法不适合求解大规模DLBP. 智能算法已广泛应用于求解DLBP,Ren等[4 ] 以拆卸利润最大为目标,提出重力搜索算法求解. 丁力平等[5 ] 结合Pareto解集思想与智能算法,更好地平衡多个优化目标,提出基于Pareto的蚁群算法求解多目标DLBP. 智能算法以其诸多优势已广泛应用于求解拆卸序列规划[6 -8 ] 、车辆路径规划[9 ] 和车间调度[10 -11 ] 等问题,均取得了良好的成果. ...
... 拆卸线布局的研究主要集中于直线型[1 -5 , 12 -14 ] . 与直线型拆卸线相比,并行拆卸线是将2条及以上的拆卸线平行放置,可同步拆卸多种不同的产品,有效地提高拆卸效率和生产线柔性. Hezer等[15 ] 提出并行拆线平衡问题(parallel disassembly line balancing problem, PDLBP),采用基于最短路径的网络模型求解. Guo等[16 ] 设计可同时拆卸和装配的并行生产线,构建以拆卸成本和平滑度指标为优化目标的数学模型,应用变邻域和非支配排序遗传算法的混合算法求解. Zhu等[17 ] 构建并行不完全拆卸线平衡问题的数学模型,设计混合群邻域算法求解. Hezer等[15 -17 ] 分别构建不同问题的PDLBP数学模型,但存在一定的不足,所建模型均属于概念模型,无法精确求解,即无法验证所有约束对于优化目标的正确性. 存在对2条拆卸线任务定义不明确的情况,例如提到并行线上具有相同编号任务时无法确定是哪条线上的任务. 本文考虑当前劳动力短缺的国情,拆卸线属于劳动密集型工作,需要大量的劳动. 替换部分工作站操作者由机器人拆卸,即在站间操作者不同的基础上与PDLBP结合,构建以工作站数目、机器人数、拆卸成本和空闲时间均衡指标为优化目标的PDLBP数学模型,应用CPLEX和LINGO对模型进行精确求解,验证该模型的正确性. ...
基于Pareto蚁群算法的拆卸线平衡多目标优化
2
2009
... DLBP经过20年的发展,学者们从求解方法和拆卸布局方面不断深入研究. 求解方法主要包括启发式方法[2 ] 、数学规划法[3 ] 和智能算法等,而启发式方法过于依赖启发式规则,数学规划方法不适合求解大规模DLBP. 智能算法已广泛应用于求解DLBP,Ren等[4 ] 以拆卸利润最大为目标,提出重力搜索算法求解. 丁力平等[5 ] 结合Pareto解集思想与智能算法,更好地平衡多个优化目标,提出基于Pareto的蚁群算法求解多目标DLBP. 智能算法以其诸多优势已广泛应用于求解拆卸序列规划[6 -8 ] 、车辆路径规划[9 ] 和车间调度[10 -11 ] 等问题,均取得了良好的成果. ...
... 拆卸线布局的研究主要集中于直线型[1 -5 , 12 -14 ] . 与直线型拆卸线相比,并行拆卸线是将2条及以上的拆卸线平行放置,可同步拆卸多种不同的产品,有效地提高拆卸效率和生产线柔性. Hezer等[15 ] 提出并行拆线平衡问题(parallel disassembly line balancing problem, PDLBP),采用基于最短路径的网络模型求解. Guo等[16 ] 设计可同时拆卸和装配的并行生产线,构建以拆卸成本和平滑度指标为优化目标的数学模型,应用变邻域和非支配排序遗传算法的混合算法求解. Zhu等[17 ] 构建并行不完全拆卸线平衡问题的数学模型,设计混合群邻域算法求解. Hezer等[15 -17 ] 分别构建不同问题的PDLBP数学模型,但存在一定的不足,所建模型均属于概念模型,无法精确求解,即无法验证所有约束对于优化目标的正确性. 存在对2条拆卸线任务定义不明确的情况,例如提到并行线上具有相同编号任务时无法确定是哪条线上的任务. 本文考虑当前劳动力短缺的国情,拆卸线属于劳动密集型工作,需要大量的劳动. 替换部分工作站操作者由机器人拆卸,即在站间操作者不同的基础上与PDLBP结合,构建以工作站数目、机器人数、拆卸成本和空闲时间均衡指标为优化目标的PDLBP数学模型,应用CPLEX和LINGO对模型进行精确求解,验证该模型的正确性. ...
多重故障驱动的再制造并行拆卸序列规划方法
1
2020
... DLBP经过20年的发展,学者们从求解方法和拆卸布局方面不断深入研究. 求解方法主要包括启发式方法[2 ] 、数学规划法[3 ] 和智能算法等,而启发式方法过于依赖启发式规则,数学规划方法不适合求解大规模DLBP. 智能算法已广泛应用于求解DLBP,Ren等[4 ] 以拆卸利润最大为目标,提出重力搜索算法求解. 丁力平等[5 ] 结合Pareto解集思想与智能算法,更好地平衡多个优化目标,提出基于Pareto的蚁群算法求解多目标DLBP. 智能算法以其诸多优势已广泛应用于求解拆卸序列规划[6 -8 ] 、车辆路径规划[9 ] 和车间调度[10 -11 ] 等问题,均取得了良好的成果. ...
多重故障驱动的再制造并行拆卸序列规划方法
1
2020
... DLBP经过20年的发展,学者们从求解方法和拆卸布局方面不断深入研究. 求解方法主要包括启发式方法[2 ] 、数学规划法[3 ] 和智能算法等,而启发式方法过于依赖启发式规则,数学规划方法不适合求解大规模DLBP. 智能算法已广泛应用于求解DLBP,Ren等[4 ] 以拆卸利润最大为目标,提出重力搜索算法求解. 丁力平等[5 ] 结合Pareto解集思想与智能算法,更好地平衡多个优化目标,提出基于Pareto的蚁群算法求解多目标DLBP. 智能算法以其诸多优势已广泛应用于求解拆卸序列规划[6 -8 ] 、车辆路径规划[9 ] 和车间调度[10 -11 ] 等问题,均取得了良好的成果. ...
基于自适应粒子群的产品再制造拆卸规划
0
2011
基于自适应粒子群的产品再制造拆卸规划
0
2011
基于遗传蝙蝠算法的选择性拆卸序列规划
1
2018
... DLBP经过20年的发展,学者们从求解方法和拆卸布局方面不断深入研究. 求解方法主要包括启发式方法[2 ] 、数学规划法[3 ] 和智能算法等,而启发式方法过于依赖启发式规则,数学规划方法不适合求解大规模DLBP. 智能算法已广泛应用于求解DLBP,Ren等[4 ] 以拆卸利润最大为目标,提出重力搜索算法求解. 丁力平等[5 ] 结合Pareto解集思想与智能算法,更好地平衡多个优化目标,提出基于Pareto的蚁群算法求解多目标DLBP. 智能算法以其诸多优势已广泛应用于求解拆卸序列规划[6 -8 ] 、车辆路径规划[9 ] 和车间调度[10 -11 ] 等问题,均取得了良好的成果. ...
基于遗传蝙蝠算法的选择性拆卸序列规划
1
2018
... DLBP经过20年的发展,学者们从求解方法和拆卸布局方面不断深入研究. 求解方法主要包括启发式方法[2 ] 、数学规划法[3 ] 和智能算法等,而启发式方法过于依赖启发式规则,数学规划方法不适合求解大规模DLBP. 智能算法已广泛应用于求解DLBP,Ren等[4 ] 以拆卸利润最大为目标,提出重力搜索算法求解. 丁力平等[5 ] 结合Pareto解集思想与智能算法,更好地平衡多个优化目标,提出基于Pareto的蚁群算法求解多目标DLBP. 智能算法以其诸多优势已广泛应用于求解拆卸序列规划[6 -8 ] 、车辆路径规划[9 ] 和车间调度[10 -11 ] 等问题,均取得了良好的成果. ...
基于改进混合蛙跳算法的多约束车辆路径优化
1
2021
... DLBP经过20年的发展,学者们从求解方法和拆卸布局方面不断深入研究. 求解方法主要包括启发式方法[2 ] 、数学规划法[3 ] 和智能算法等,而启发式方法过于依赖启发式规则,数学规划方法不适合求解大规模DLBP. 智能算法已广泛应用于求解DLBP,Ren等[4 ] 以拆卸利润最大为目标,提出重力搜索算法求解. 丁力平等[5 ] 结合Pareto解集思想与智能算法,更好地平衡多个优化目标,提出基于Pareto的蚁群算法求解多目标DLBP. 智能算法以其诸多优势已广泛应用于求解拆卸序列规划[6 -8 ] 、车辆路径规划[9 ] 和车间调度[10 -11 ] 等问题,均取得了良好的成果. ...
基于改进混合蛙跳算法的多约束车辆路径优化
1
2021
... DLBP经过20年的发展,学者们从求解方法和拆卸布局方面不断深入研究. 求解方法主要包括启发式方法[2 ] 、数学规划法[3 ] 和智能算法等,而启发式方法过于依赖启发式规则,数学规划方法不适合求解大规模DLBP. 智能算法已广泛应用于求解DLBP,Ren等[4 ] 以拆卸利润最大为目标,提出重力搜索算法求解. 丁力平等[5 ] 结合Pareto解集思想与智能算法,更好地平衡多个优化目标,提出基于Pareto的蚁群算法求解多目标DLBP. 智能算法以其诸多优势已广泛应用于求解拆卸序列规划[6 -8 ] 、车辆路径规划[9 ] 和车间调度[10 -11 ] 等问题,均取得了良好的成果. ...
柔性作业车间分批调度多目标优化方法
1
2011
... DLBP经过20年的发展,学者们从求解方法和拆卸布局方面不断深入研究. 求解方法主要包括启发式方法[2 ] 、数学规划法[3 ] 和智能算法等,而启发式方法过于依赖启发式规则,数学规划方法不适合求解大规模DLBP. 智能算法已广泛应用于求解DLBP,Ren等[4 ] 以拆卸利润最大为目标,提出重力搜索算法求解. 丁力平等[5 ] 结合Pareto解集思想与智能算法,更好地平衡多个优化目标,提出基于Pareto的蚁群算法求解多目标DLBP. 智能算法以其诸多优势已广泛应用于求解拆卸序列规划[6 -8 ] 、车辆路径规划[9 ] 和车间调度[10 -11 ] 等问题,均取得了良好的成果. ...
柔性作业车间分批调度多目标优化方法
1
2011
... DLBP经过20年的发展,学者们从求解方法和拆卸布局方面不断深入研究. 求解方法主要包括启发式方法[2 ] 、数学规划法[3 ] 和智能算法等,而启发式方法过于依赖启发式规则,数学规划方法不适合求解大规模DLBP. 智能算法已广泛应用于求解DLBP,Ren等[4 ] 以拆卸利润最大为目标,提出重力搜索算法求解. 丁力平等[5 ] 结合Pareto解集思想与智能算法,更好地平衡多个优化目标,提出基于Pareto的蚁群算法求解多目标DLBP. 智能算法以其诸多优势已广泛应用于求解拆卸序列规划[6 -8 ] 、车辆路径规划[9 ] 和车间调度[10 -11 ] 等问题,均取得了良好的成果. ...
基于改进候鸟优化算法的混合流水车间调度问题
1
2019
... DLBP经过20年的发展,学者们从求解方法和拆卸布局方面不断深入研究. 求解方法主要包括启发式方法[2 ] 、数学规划法[3 ] 和智能算法等,而启发式方法过于依赖启发式规则,数学规划方法不适合求解大规模DLBP. 智能算法已广泛应用于求解DLBP,Ren等[4 ] 以拆卸利润最大为目标,提出重力搜索算法求解. 丁力平等[5 ] 结合Pareto解集思想与智能算法,更好地平衡多个优化目标,提出基于Pareto的蚁群算法求解多目标DLBP. 智能算法以其诸多优势已广泛应用于求解拆卸序列规划[6 -8 ] 、车辆路径规划[9 ] 和车间调度[10 -11 ] 等问题,均取得了良好的成果. ...
基于改进候鸟优化算法的混合流水车间调度问题
1
2019
... DLBP经过20年的发展,学者们从求解方法和拆卸布局方面不断深入研究. 求解方法主要包括启发式方法[2 ] 、数学规划法[3 ] 和智能算法等,而启发式方法过于依赖启发式规则,数学规划方法不适合求解大规模DLBP. 智能算法已广泛应用于求解DLBP,Ren等[4 ] 以拆卸利润最大为目标,提出重力搜索算法求解. 丁力平等[5 ] 结合Pareto解集思想与智能算法,更好地平衡多个优化目标,提出基于Pareto的蚁群算法求解多目标DLBP. 智能算法以其诸多优势已广泛应用于求解拆卸序列规划[6 -8 ] 、车辆路径规划[9 ] 和车间调度[10 -11 ] 等问题,均取得了良好的成果. ...
Disassembly line balancing problem a review of the state of the art and future directions
1
2019
... 拆卸线布局的研究主要集中于直线型[1 -5 , 12 -14 ] . 与直线型拆卸线相比,并行拆卸线是将2条及以上的拆卸线平行放置,可同步拆卸多种不同的产品,有效地提高拆卸效率和生产线柔性. Hezer等[15 ] 提出并行拆线平衡问题(parallel disassembly line balancing problem, PDLBP),采用基于最短路径的网络模型求解. Guo等[16 ] 设计可同时拆卸和装配的并行生产线,构建以拆卸成本和平滑度指标为优化目标的数学模型,应用变邻域和非支配排序遗传算法的混合算法求解. Zhu等[17 ] 构建并行不完全拆卸线平衡问题的数学模型,设计混合群邻域算法求解. Hezer等[15 -17 ] 分别构建不同问题的PDLBP数学模型,但存在一定的不足,所建模型均属于概念模型,无法精确求解,即无法验证所有约束对于优化目标的正确性. 存在对2条拆卸线任务定义不明确的情况,例如提到并行线上具有相同编号任务时无法确定是哪条线上的任务. 本文考虑当前劳动力短缺的国情,拆卸线属于劳动密集型工作,需要大量的劳动. 替换部分工作站操作者由机器人拆卸,即在站间操作者不同的基础上与PDLBP结合,构建以工作站数目、机器人数、拆卸成本和空闲时间均衡指标为优化目标的PDLBP数学模型,应用CPLEX和LINGO对模型进行精确求解,验证该模型的正确性. ...
A survey on meta-heuristics for solving disassembly line balancing, planning and scheduling problems in remanufacturing
0
2020
Model review and algorithm comparison on multi-objective disassembly line balancing
1
2020
... 拆卸线布局的研究主要集中于直线型[1 -5 , 12 -14 ] . 与直线型拆卸线相比,并行拆卸线是将2条及以上的拆卸线平行放置,可同步拆卸多种不同的产品,有效地提高拆卸效率和生产线柔性. Hezer等[15 ] 提出并行拆线平衡问题(parallel disassembly line balancing problem, PDLBP),采用基于最短路径的网络模型求解. Guo等[16 ] 设计可同时拆卸和装配的并行生产线,构建以拆卸成本和平滑度指标为优化目标的数学模型,应用变邻域和非支配排序遗传算法的混合算法求解. Zhu等[17 ] 构建并行不完全拆卸线平衡问题的数学模型,设计混合群邻域算法求解. Hezer等[15 -17 ] 分别构建不同问题的PDLBP数学模型,但存在一定的不足,所建模型均属于概念模型,无法精确求解,即无法验证所有约束对于优化目标的正确性. 存在对2条拆卸线任务定义不明确的情况,例如提到并行线上具有相同编号任务时无法确定是哪条线上的任务. 本文考虑当前劳动力短缺的国情,拆卸线属于劳动密集型工作,需要大量的劳动. 替换部分工作站操作者由机器人拆卸,即在站间操作者不同的基础上与PDLBP结合,构建以工作站数目、机器人数、拆卸成本和空闲时间均衡指标为优化目标的PDLBP数学模型,应用CPLEX和LINGO对模型进行精确求解,验证该模型的正确性. ...
A network-based shortest route model for parallel disassembly line balancing problem
2
2015
... 拆卸线布局的研究主要集中于直线型[1 -5 , 12 -14 ] . 与直线型拆卸线相比,并行拆卸线是将2条及以上的拆卸线平行放置,可同步拆卸多种不同的产品,有效地提高拆卸效率和生产线柔性. Hezer等[15 ] 提出并行拆线平衡问题(parallel disassembly line balancing problem, PDLBP),采用基于最短路径的网络模型求解. Guo等[16 ] 设计可同时拆卸和装配的并行生产线,构建以拆卸成本和平滑度指标为优化目标的数学模型,应用变邻域和非支配排序遗传算法的混合算法求解. Zhu等[17 ] 构建并行不完全拆卸线平衡问题的数学模型,设计混合群邻域算法求解. Hezer等[15 -17 ] 分别构建不同问题的PDLBP数学模型,但存在一定的不足,所建模型均属于概念模型,无法精确求解,即无法验证所有约束对于优化目标的正确性. 存在对2条拆卸线任务定义不明确的情况,例如提到并行线上具有相同编号任务时无法确定是哪条线上的任务. 本文考虑当前劳动力短缺的国情,拆卸线属于劳动密集型工作,需要大量的劳动. 替换部分工作站操作者由机器人拆卸,即在站间操作者不同的基础上与PDLBP结合,构建以工作站数目、机器人数、拆卸成本和空闲时间均衡指标为优化目标的PDLBP数学模型,应用CPLEX和LINGO对模型进行精确求解,验证该模型的正确性. ...
... [15 -17 ]分别构建不同问题的PDLBP数学模型,但存在一定的不足,所建模型均属于概念模型,无法精确求解,即无法验证所有约束对于优化目标的正确性. 存在对2条拆卸线任务定义不明确的情况,例如提到并行线上具有相同编号任务时无法确定是哪条线上的任务. 本文考虑当前劳动力短缺的国情,拆卸线属于劳动密集型工作,需要大量的劳动. 替换部分工作站操作者由机器人拆卸,即在站间操作者不同的基础上与PDLBP结合,构建以工作站数目、机器人数、拆卸成本和空闲时间均衡指标为优化目标的PDLBP数学模型,应用CPLEX和LINGO对模型进行精确求解,验证该模型的正确性. ...
1
... 拆卸线布局的研究主要集中于直线型[1 -5 , 12 -14 ] . 与直线型拆卸线相比,并行拆卸线是将2条及以上的拆卸线平行放置,可同步拆卸多种不同的产品,有效地提高拆卸效率和生产线柔性. Hezer等[15 ] 提出并行拆线平衡问题(parallel disassembly line balancing problem, PDLBP),采用基于最短路径的网络模型求解. Guo等[16 ] 设计可同时拆卸和装配的并行生产线,构建以拆卸成本和平滑度指标为优化目标的数学模型,应用变邻域和非支配排序遗传算法的混合算法求解. Zhu等[17 ] 构建并行不完全拆卸线平衡问题的数学模型,设计混合群邻域算法求解. Hezer等[15 -17 ] 分别构建不同问题的PDLBP数学模型,但存在一定的不足,所建模型均属于概念模型,无法精确求解,即无法验证所有约束对于优化目标的正确性. 存在对2条拆卸线任务定义不明确的情况,例如提到并行线上具有相同编号任务时无法确定是哪条线上的任务. 本文考虑当前劳动力短缺的国情,拆卸线属于劳动密集型工作,需要大量的劳动. 替换部分工作站操作者由机器人拆卸,即在站间操作者不同的基础上与PDLBP结合,构建以工作站数目、机器人数、拆卸成本和空闲时间均衡指标为优化目标的PDLBP数学模型,应用CPLEX和LINGO对模型进行精确求解,验证该模型的正确性. ...
Multi-objective partial parallel disassembly line balancing problem using hybrid group neighbourhood search algorithm
3
2020
... 拆卸线布局的研究主要集中于直线型[1 -5 , 12 -14 ] . 与直线型拆卸线相比,并行拆卸线是将2条及以上的拆卸线平行放置,可同步拆卸多种不同的产品,有效地提高拆卸效率和生产线柔性. Hezer等[15 ] 提出并行拆线平衡问题(parallel disassembly line balancing problem, PDLBP),采用基于最短路径的网络模型求解. Guo等[16 ] 设计可同时拆卸和装配的并行生产线,构建以拆卸成本和平滑度指标为优化目标的数学模型,应用变邻域和非支配排序遗传算法的混合算法求解. Zhu等[17 ] 构建并行不完全拆卸线平衡问题的数学模型,设计混合群邻域算法求解. Hezer等[15 -17 ] 分别构建不同问题的PDLBP数学模型,但存在一定的不足,所建模型均属于概念模型,无法精确求解,即无法验证所有约束对于优化目标的正确性. 存在对2条拆卸线任务定义不明确的情况,例如提到并行线上具有相同编号任务时无法确定是哪条线上的任务. 本文考虑当前劳动力短缺的国情,拆卸线属于劳动密集型工作,需要大量的劳动. 替换部分工作站操作者由机器人拆卸,即在站间操作者不同的基础上与PDLBP结合,构建以工作站数目、机器人数、拆卸成本和空闲时间均衡指标为优化目标的PDLBP数学模型,应用CPLEX和LINGO对模型进行精确求解,验证该模型的正确性. ...
... -17 ]分别构建不同问题的PDLBP数学模型,但存在一定的不足,所建模型均属于概念模型,无法精确求解,即无法验证所有约束对于优化目标的正确性. 存在对2条拆卸线任务定义不明确的情况,例如提到并行线上具有相同编号任务时无法确定是哪条线上的任务. 本文考虑当前劳动力短缺的国情,拆卸线属于劳动密集型工作,需要大量的劳动. 替换部分工作站操作者由机器人拆卸,即在站间操作者不同的基础上与PDLBP结合,构建以工作站数目、机器人数、拆卸成本和空闲时间均衡指标为优化目标的PDLBP数学模型,应用CPLEX和LINGO对模型进行精确求解,验证该模型的正确性. ...
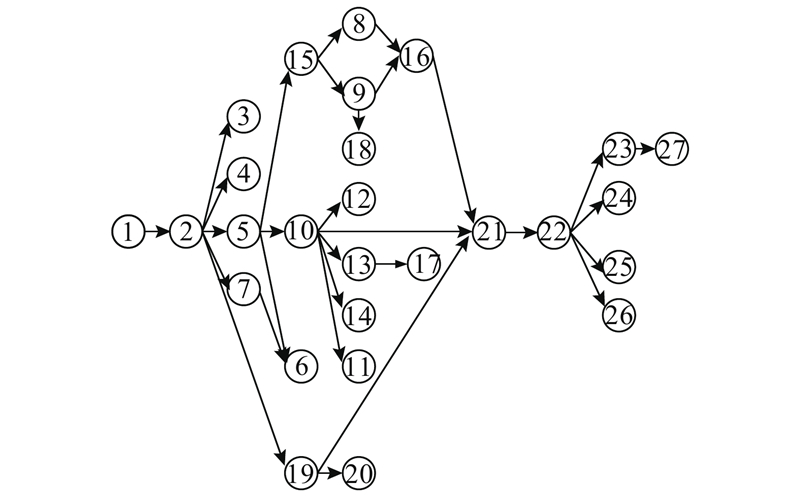
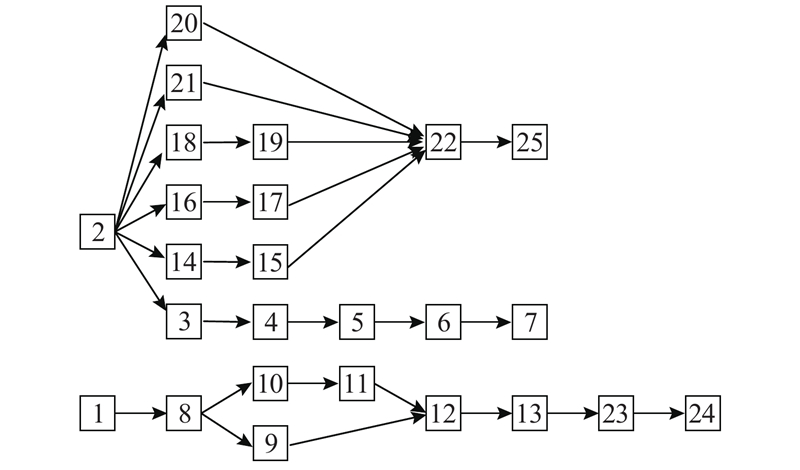
... 为了验证IBSO算法求解本文问题的求解性能,应用27规模的电视机[29 ] 和25规模的电冰箱[17 ] 拆卸实例,构建2条并行拆卸线;运用所建模型和所提算法对2种废旧电器分配工人或机器人进行拆卸,应用2种经典算法GA[30 ] 和NSGA-Ⅱ[21 ] 和BSO求解实例与IBSO算法进行对比. 电视机和电冰箱的拆卸信息如表4 所示,电视机和电冰箱的优先关系分别如图8 、9 所示. ...
Brain storm optimization algorithm
1
2011
... 头脑风暴优化算法(brain strom optimization, BSO)[18 ] 是受头脑风暴会议中思维碰撞过程的启发而提出的群智能优化算法,现已成功应用于电动车路径优化[19 ] 和离散调度问题[20 ] 等离散型组合优化问题中,表现出优越的求解性能. DLBP属于离散型组合优化问题,为了解决本文的多目标PDLBP,提出改进头脑风暴优化算法(improved brain storm optimization, IBSO). 在算法中,将原始连续操作进行离散化处理,分别设计变异交叉操作,分别对应算法中的单个个体产生机制和2个个体产生机制,设计四点交叉操作策略. 引入Pareto解集思想和NSGA-Ⅱ拥挤距离[21 ] 的双精英策略,筛选非劣解. ...
基于头脑风暴算法的电动货车路径优化问题
1
2020
... 头脑风暴优化算法(brain strom optimization, BSO)[18 ] 是受头脑风暴会议中思维碰撞过程的启发而提出的群智能优化算法,现已成功应用于电动车路径优化[19 ] 和离散调度问题[20 ] 等离散型组合优化问题中,表现出优越的求解性能. DLBP属于离散型组合优化问题,为了解决本文的多目标PDLBP,提出改进头脑风暴优化算法(improved brain storm optimization, IBSO). 在算法中,将原始连续操作进行离散化处理,分别设计变异交叉操作,分别对应算法中的单个个体产生机制和2个个体产生机制,设计四点交叉操作策略. 引入Pareto解集思想和NSGA-Ⅱ拥挤距离[21 ] 的双精英策略,筛选非劣解. ...
基于头脑风暴算法的电动货车路径优化问题
1
2020
... 头脑风暴优化算法(brain strom optimization, BSO)[18 ] 是受头脑风暴会议中思维碰撞过程的启发而提出的群智能优化算法,现已成功应用于电动车路径优化[19 ] 和离散调度问题[20 ] 等离散型组合优化问题中,表现出优越的求解性能. DLBP属于离散型组合优化问题,为了解决本文的多目标PDLBP,提出改进头脑风暴优化算法(improved brain storm optimization, IBSO). 在算法中,将原始连续操作进行离散化处理,分别设计变异交叉操作,分别对应算法中的单个个体产生机制和2个个体产生机制,设计四点交叉操作策略. 引入Pareto解集思想和NSGA-Ⅱ拥挤距离[21 ] 的双精英策略,筛选非劣解. ...
求解离散调度问题的双机制头脑风暴优化算法
1
2017
... 头脑风暴优化算法(brain strom optimization, BSO)[18 ] 是受头脑风暴会议中思维碰撞过程的启发而提出的群智能优化算法,现已成功应用于电动车路径优化[19 ] 和离散调度问题[20 ] 等离散型组合优化问题中,表现出优越的求解性能. DLBP属于离散型组合优化问题,为了解决本文的多目标PDLBP,提出改进头脑风暴优化算法(improved brain storm optimization, IBSO). 在算法中,将原始连续操作进行离散化处理,分别设计变异交叉操作,分别对应算法中的单个个体产生机制和2个个体产生机制,设计四点交叉操作策略. 引入Pareto解集思想和NSGA-Ⅱ拥挤距离[21 ] 的双精英策略,筛选非劣解. ...
求解离散调度问题的双机制头脑风暴优化算法
1
2017
... 头脑风暴优化算法(brain strom optimization, BSO)[18 ] 是受头脑风暴会议中思维碰撞过程的启发而提出的群智能优化算法,现已成功应用于电动车路径优化[19 ] 和离散调度问题[20 ] 等离散型组合优化问题中,表现出优越的求解性能. DLBP属于离散型组合优化问题,为了解决本文的多目标PDLBP,提出改进头脑风暴优化算法(improved brain storm optimization, IBSO). 在算法中,将原始连续操作进行离散化处理,分别设计变异交叉操作,分别对应算法中的单个个体产生机制和2个个体产生机制,设计四点交叉操作策略. 引入Pareto解集思想和NSGA-Ⅱ拥挤距离[21 ] 的双精英策略,筛选非劣解. ...
A fast and elitist multiobjective genetic algorithm: NSGA-II
2
2002
... 头脑风暴优化算法(brain strom optimization, BSO)[18 ] 是受头脑风暴会议中思维碰撞过程的启发而提出的群智能优化算法,现已成功应用于电动车路径优化[19 ] 和离散调度问题[20 ] 等离散型组合优化问题中,表现出优越的求解性能. DLBP属于离散型组合优化问题,为了解决本文的多目标PDLBP,提出改进头脑风暴优化算法(improved brain storm optimization, IBSO). 在算法中,将原始连续操作进行离散化处理,分别设计变异交叉操作,分别对应算法中的单个个体产生机制和2个个体产生机制,设计四点交叉操作策略. 引入Pareto解集思想和NSGA-Ⅱ拥挤距离[21 ] 的双精英策略,筛选非劣解. ...
... 为了验证IBSO算法求解本文问题的求解性能,应用27规模的电视机[29 ] 和25规模的电冰箱[17 ] 拆卸实例,构建2条并行拆卸线;运用所建模型和所提算法对2种废旧电器分配工人或机器人进行拆卸,应用2种经典算法GA[30 ] 和NSGA-Ⅱ[21 ] 和BSO求解实例与IBSO算法进行对比. 电视机和电冰箱的拆卸信息如表4 所示,电视机和电冰箱的优先关系分别如图8 、9 所示. ...
HypE: an algorithm for fast hypervolume-based many-objective optimization
1
2011
... Pareto解集评价:超体积指标[22 ] (hyper-volume)简称HV指标,表示算法运行求得的Pareto解集与参考点即各目标最差值所围成的目标空间中区域的超体积. 如图6 所示,在最小化的双目标优化问题中,求解出包含5个非劣解的Pareto解集{x 1 ,x 2 ,x 3 ,x 4 ,x 5 },f 1 和f 2 的最差值构成参考点R 的坐标点(a ,b ),HV指标的值即为坐标点(a ,b )与非劣解x 1 、x 2 、x 3 、x 4 、x 5 坐标点在二维空间所围成的超体积,即为阴影部分面积. HV指标越大,说明该算法的综合性能越好. 引用该指标,评价对比实例应用中IBSO算法与GA、NSGA-Ⅱ算法求解实例的性能. 具体公式如下: ...
Artificial bee colony algorithm for solving sequence-dependent disassembly line balancing problem
5
2013
... 为了验证所建的PDLBP模型的正确性,采用CPLEX和LINGO精确解求解器,对1.3节所建模型开发相关程序,求解P10和P8算例. 算例中,基础拆卸时间和各零件优先关系等信息均来自文献[1 , 23 ],具体的拆卸信息如表1 所示. 表中,t ip 为工人拆卸时间,t ir 为机器人拆卸时间,c ost 为成本. 应用数学规划的方法对所提各优化目标求解时,各目标类型均不同,例如f 1 为混合整数线性规划(mixed integer linear programming, MILP)问题,f 2 和f 3 为混合整数二次规划(mixed integer quadratic programming, MIQP)问题,上述目标均可用CPLEX求解,但是f 4 为混合整数非线性规划(mixed integer nonlinear programming, MINLP)问题,无法应用CPLEX求解,应用LINGO对f 4 进行精确求解. 为了验证IBSO算法的有效性,应用MATLAB运行IBSO算法求解该算例,与精确解对比. IBSO参数为:C n =120,M gen =200,p 1 =0.2,p 2 =0.5,p 3 =0.5,p 4 =0.6,精确解与IBSO算法的对比结果如表2 所示. 表中,t s 为求解时间. 各目标最优值的任务分配图如图7 所示. 图中,t w 为工作站工作时间;任务前为“−”的是拆卸线Ⅱ任务;工作站中为点划线,表示该工作站由机器人拆卸,拆卸线Ⅰ拆卸P10产品即n 1 =10,拆卸线Ⅱ拆卸P8产品即n 2 =8. ...
... 为了验证IBSO算法求解性能的优越性,应用该算法求解包含25项拆卸任务的移动电话[24 ] 经典算例问题,与文献[23 , 25 ~28 ]的求解结果进行对比. 利用IBSO算法求解P25经典算例问题时,根据问题的特征对解码操作进行修改,以适合求解该问题,但编码思想相同且算法主体结构和核心操作均未改变,因此应用P25经典算例问题验证IBSO算法的性能. P25问题的4个优化目标分别为:最小化工作站开启数f 1 、空闲时间均衡指标f 2 、危害指标f 3 和需求指标f 4 . IBSO求解P25问题的参数为:C n =150,M gen =300,p 1 =0.2,p 2 =0.4,p 3 =0.5,p 4 =0.6. ...
... 如表3 所示为IBSO算法与文献[23 , 25 ~28 ]的求解结果对比. 多目标角度如下:将所有算法结果进行一次Pareto筛选,筛选共得到12个Pareto前沿解,其中包含IBSO算法求解结果的有10个,可见IBSO所得的非劣解集更逼近真实Pareto前沿. 单目标角度如下:虽然所有对比算法的前2个目标值均求解为9,但对于目标f 3 和f 4 的最优值分别为73和811,均劣于IBSO算法所求的最优值70和802. 根据式(18)分别计算各算法所求结果的HV. 从表3 可以看出,利用IBSO算法所求结果的HV最大为5.033×108 . 求解经典算例的HV指标参考点为[25,4 291,106,1 015]. 综上所述,以上对比有效验证了IBSO算法的求解性能. ...
... Results of solving P25 problem by each algorithm
Tab.3 算法 f 1 f 2 f 3 f 4 HV/108 算法 f 1 f 2 f 3 f 4 HV/108 ABC[23 ] 9 9 81 853 2.774 IBSO 9 9 76 825 5.033 PSO[25 ] 9 9 80 857 2.814 9 9 77 823 VNS[26 ] 9 9 76 825 3.905 9 11 75 821 RL[27 ] 9 9 97 862 0.943 9 15 74 817 9 9 76 825 4.276 9 15 75 815 9 11 75 821 10 157 71 876 GASA[28 ] 9 15 75 815 11 395 70 870 10 141 73 814 12 559 71 804 10 195 74 811 12 523 73 802 − − − − − − 12 559 72 802
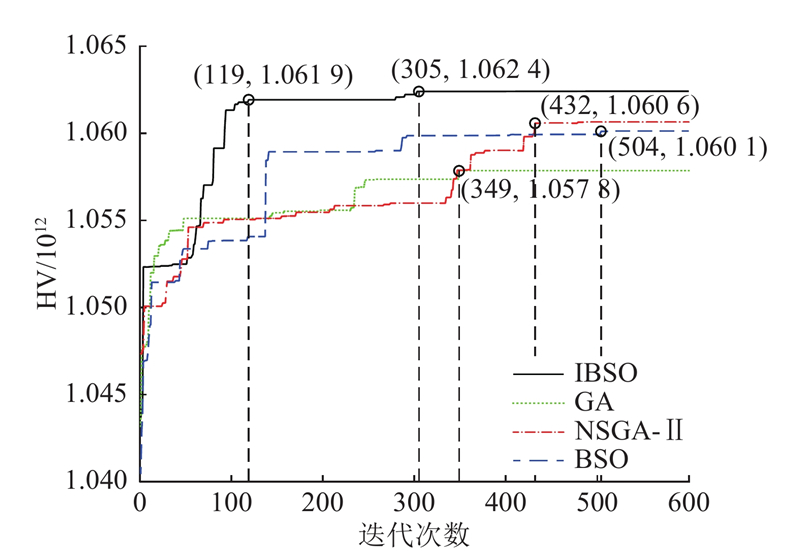
4. 大规模实例对比 为了验证IBSO算法求解本文问题的求解性能,应用27规模的电视机[29 ] 和25规模的电冰箱[17 ] 拆卸实例,构建2条并行拆卸线;运用所建模型和所提算法对2种废旧电器分配工人或机器人进行拆卸,应用2种经典算法GA[30 ] 和NSGA-Ⅱ[21 ] 和BSO求解实例与IBSO算法进行对比. 电视机和电冰箱的拆卸信息如表4 所示,电视机和电冰箱的优先关系分别如图8 、9 所示. ...
... (3)应用IBSO算法求解25规模基准算例,与文献[23 , 25 ~28 ]的求解结果进行对比,验证了IBSO算法的优越性. 将该算法引入电视机与电冰箱的大规模拆卸实例中,通过与GA、NSGA-Ⅱ和BSO算法求解结果和HV指标对比,验证了IBSO算法的求解性能. ...
1
... 为了验证IBSO算法求解性能的优越性,应用该算法求解包含25项拆卸任务的移动电话[24 ] 经典算例问题,与文献[23 , 25 ~28 ]的求解结果进行对比. 利用IBSO算法求解P25经典算例问题时,根据问题的特征对解码操作进行修改,以适合求解该问题,但编码思想相同且算法主体结构和核心操作均未改变,因此应用P25经典算例问题验证IBSO算法的性能. P25问题的4个优化目标分别为:最小化工作站开启数f 1 、空闲时间均衡指标f 2 、危害指标f 3 和需求指标f 4 . IBSO求解P25问题的参数为:C n =150,M gen =300,p 1 =0.2,p 2 =0.4,p 3 =0.5,p 4 =0.6. ...
4
... 为了验证IBSO算法求解性能的优越性,应用该算法求解包含25项拆卸任务的移动电话[24 ] 经典算例问题,与文献[23 , 25 ~28 ]的求解结果进行对比. 利用IBSO算法求解P25经典算例问题时,根据问题的特征对解码操作进行修改,以适合求解该问题,但编码思想相同且算法主体结构和核心操作均未改变,因此应用P25经典算例问题验证IBSO算法的性能. P25问题的4个优化目标分别为:最小化工作站开启数f 1 、空闲时间均衡指标f 2 、危害指标f 3 和需求指标f 4 . IBSO求解P25问题的参数为:C n =150,M gen =300,p 1 =0.2,p 2 =0.4,p 3 =0.5,p 4 =0.6. ...
... 如表3 所示为IBSO算法与文献[23 , 25 ~28 ]的求解结果对比. 多目标角度如下:将所有算法结果进行一次Pareto筛选,筛选共得到12个Pareto前沿解,其中包含IBSO算法求解结果的有10个,可见IBSO所得的非劣解集更逼近真实Pareto前沿. 单目标角度如下:虽然所有对比算法的前2个目标值均求解为9,但对于目标f 3 和f 4 的最优值分别为73和811,均劣于IBSO算法所求的最优值70和802. 根据式(18)分别计算各算法所求结果的HV. 从表3 可以看出,利用IBSO算法所求结果的HV最大为5.033×108 . 求解经典算例的HV指标参考点为[25,4 291,106,1 015]. 综上所述,以上对比有效验证了IBSO算法的求解性能. ...
... Results of solving P25 problem by each algorithm
Tab.3 算法 f 1 f 2 f 3 f 4 HV/108 算法 f 1 f 2 f 3 f 4 HV/108 ABC[23 ] 9 9 81 853 2.774 IBSO 9 9 76 825 5.033 PSO[25 ] 9 9 80 857 2.814 9 9 77 823 VNS[26 ] 9 9 76 825 3.905 9 11 75 821 RL[27 ] 9 9 97 862 0.943 9 15 74 817 9 9 76 825 4.276 9 15 75 815 9 11 75 821 10 157 71 876 GASA[28 ] 9 15 75 815 11 395 70 870 10 141 73 814 12 559 71 804 10 195 74 811 12 523 73 802 − − − − − − 12 559 72 802
4. 大规模实例对比 为了验证IBSO算法求解本文问题的求解性能,应用27规模的电视机[29 ] 和25规模的电冰箱[17 ] 拆卸实例,构建2条并行拆卸线;运用所建模型和所提算法对2种废旧电器分配工人或机器人进行拆卸,应用2种经典算法GA[30 ] 和NSGA-Ⅱ[21 ] 和BSO求解实例与IBSO算法进行对比. 电视机和电冰箱的拆卸信息如表4 所示,电视机和电冰箱的优先关系分别如图8 、9 所示. ...
... (3)应用IBSO算法求解25规模基准算例,与文献[23 , 25 ~28 ]的求解结果进行对比,验证了IBSO算法的优越性. 将该算法引入电视机与电冰箱的大规模拆卸实例中,通过与GA、NSGA-Ⅱ和BSO算法求解结果和HV指标对比,验证了IBSO算法的求解性能. ...
A variable neighbourhood search algorithm for disassembly lines
1
2015
... Results of solving P25 problem by each algorithm
Tab.3 算法 f 1 f 2 f 3 f 4 HV/108 算法 f 1 f 2 f 3 f 4 HV/108 ABC[23 ] 9 9 81 853 2.774 IBSO 9 9 76 825 5.033 PSO[25 ] 9 9 80 857 2.814 9 9 77 823 VNS[26 ] 9 9 76 825 3.905 9 11 75 821 RL[27 ] 9 9 97 862 0.943 9 15 74 817 9 9 76 825 4.276 9 15 75 815 9 11 75 821 10 157 71 876 GASA[28 ] 9 15 75 815 11 395 70 870 10 141 73 814 12 559 71 804 10 195 74 811 12 523 73 802 − − − − − − 12 559 72 802
4. 大规模实例对比 为了验证IBSO算法求解本文问题的求解性能,应用27规模的电视机[29 ] 和25规模的电冰箱[17 ] 拆卸实例,构建2条并行拆卸线;运用所建模型和所提算法对2种废旧电器分配工人或机器人进行拆卸,应用2种经典算法GA[30 ] 和NSGA-Ⅱ[21 ] 和BSO求解实例与IBSO算法进行对比. 电视机和电冰箱的拆卸信息如表4 所示,电视机和电冰箱的优先关系分别如图8 、9 所示. ...
Solving large scale disassembly line balancing problem with uncertainty using reinforcement learning
1
2014
... Results of solving P25 problem by each algorithm
Tab.3 算法 f 1 f 2 f 3 f 4 HV/108 算法 f 1 f 2 f 3 f 4 HV/108 ABC[23 ] 9 9 81 853 2.774 IBSO 9 9 76 825 5.033 PSO[25 ] 9 9 80 857 2.814 9 9 77 823 VNS[26 ] 9 9 76 825 3.905 9 11 75 821 RL[27 ] 9 9 97 862 0.943 9 15 74 817 9 9 76 825 4.276 9 15 75 815 9 11 75 821 10 157 71 876 GASA[28 ] 9 15 75 815 11 395 70 870 10 141 73 814 12 559 71 804 10 195 74 811 12 523 73 802 − − − − − − 12 559 72 802
4. 大规模实例对比 为了验证IBSO算法求解本文问题的求解性能,应用27规模的电视机[29 ] 和25规模的电冰箱[17 ] 拆卸实例,构建2条并行拆卸线;运用所建模型和所提算法对2种废旧电器分配工人或机器人进行拆卸,应用2种经典算法GA[30 ] 和NSGA-Ⅱ[21 ] 和BSO求解实例与IBSO算法进行对比. 电视机和电冰箱的拆卸信息如表4 所示,电视机和电冰箱的优先关系分别如图8 、9 所示. ...
多目标拆卸线平衡问题的Pareto遗传模拟退火算法
4
2017
... 为了验证IBSO算法求解性能的优越性,应用该算法求解包含25项拆卸任务的移动电话[24 ] 经典算例问题,与文献[23 , 25 ~28 ]的求解结果进行对比. 利用IBSO算法求解P25经典算例问题时,根据问题的特征对解码操作进行修改,以适合求解该问题,但编码思想相同且算法主体结构和核心操作均未改变,因此应用P25经典算例问题验证IBSO算法的性能. P25问题的4个优化目标分别为:最小化工作站开启数f 1 、空闲时间均衡指标f 2 、危害指标f 3 和需求指标f 4 . IBSO求解P25问题的参数为:C n =150,M gen =300,p 1 =0.2,p 2 =0.4,p 3 =0.5,p 4 =0.6. ...
... 如表3 所示为IBSO算法与文献[23 , 25 ~28 ]的求解结果对比. 多目标角度如下:将所有算法结果进行一次Pareto筛选,筛选共得到12个Pareto前沿解,其中包含IBSO算法求解结果的有10个,可见IBSO所得的非劣解集更逼近真实Pareto前沿. 单目标角度如下:虽然所有对比算法的前2个目标值均求解为9,但对于目标f 3 和f 4 的最优值分别为73和811,均劣于IBSO算法所求的最优值70和802. 根据式(18)分别计算各算法所求结果的HV. 从表3 可以看出,利用IBSO算法所求结果的HV最大为5.033×108 . 求解经典算例的HV指标参考点为[25,4 291,106,1 015]. 综上所述,以上对比有效验证了IBSO算法的求解性能. ...
... Results of solving P25 problem by each algorithm
Tab.3 算法 f 1 f 2 f 3 f 4 HV/108 算法 f 1 f 2 f 3 f 4 HV/108 ABC[23 ] 9 9 81 853 2.774 IBSO 9 9 76 825 5.033 PSO[25 ] 9 9 80 857 2.814 9 9 77 823 VNS[26 ] 9 9 76 825 3.905 9 11 75 821 RL[27 ] 9 9 97 862 0.943 9 15 74 817 9 9 76 825 4.276 9 15 75 815 9 11 75 821 10 157 71 876 GASA[28 ] 9 15 75 815 11 395 70 870 10 141 73 814 12 559 71 804 10 195 74 811 12 523 73 802 − − − − − − 12 559 72 802
4. 大规模实例对比 为了验证IBSO算法求解本文问题的求解性能,应用27规模的电视机[29 ] 和25规模的电冰箱[17 ] 拆卸实例,构建2条并行拆卸线;运用所建模型和所提算法对2种废旧电器分配工人或机器人进行拆卸,应用2种经典算法GA[30 ] 和NSGA-Ⅱ[21 ] 和BSO求解实例与IBSO算法进行对比. 电视机和电冰箱的拆卸信息如表4 所示,电视机和电冰箱的优先关系分别如图8 、9 所示. ...
... (3)应用IBSO算法求解25规模基准算例,与文献[23 , 25 ~28 ]的求解结果进行对比,验证了IBSO算法的优越性. 将该算法引入电视机与电冰箱的大规模拆卸实例中,通过与GA、NSGA-Ⅱ和BSO算法求解结果和HV指标对比,验证了IBSO算法的求解性能. ...
多目标拆卸线平衡问题的Pareto遗传模拟退火算法
4
2017
... 为了验证IBSO算法求解性能的优越性,应用该算法求解包含25项拆卸任务的移动电话[24 ] 经典算例问题,与文献[23 , 25 ~28 ]的求解结果进行对比. 利用IBSO算法求解P25经典算例问题时,根据问题的特征对解码操作进行修改,以适合求解该问题,但编码思想相同且算法主体结构和核心操作均未改变,因此应用P25经典算例问题验证IBSO算法的性能. P25问题的4个优化目标分别为:最小化工作站开启数f 1 、空闲时间均衡指标f 2 、危害指标f 3 和需求指标f 4 . IBSO求解P25问题的参数为:C n =150,M gen =300,p 1 =0.2,p 2 =0.4,p 3 =0.5,p 4 =0.6. ...
... 如表3 所示为IBSO算法与文献[23 , 25 ~28 ]的求解结果对比. 多目标角度如下:将所有算法结果进行一次Pareto筛选,筛选共得到12个Pareto前沿解,其中包含IBSO算法求解结果的有10个,可见IBSO所得的非劣解集更逼近真实Pareto前沿. 单目标角度如下:虽然所有对比算法的前2个目标值均求解为9,但对于目标f 3 和f 4 的最优值分别为73和811,均劣于IBSO算法所求的最优值70和802. 根据式(18)分别计算各算法所求结果的HV. 从表3 可以看出,利用IBSO算法所求结果的HV最大为5.033×108 . 求解经典算例的HV指标参考点为[25,4 291,106,1 015]. 综上所述,以上对比有效验证了IBSO算法的求解性能. ...
... Results of solving P25 problem by each algorithm
Tab.3 算法 f 1 f 2 f 3 f 4 HV/108 算法 f 1 f 2 f 3 f 4 HV/108 ABC[23 ] 9 9 81 853 2.774 IBSO 9 9 76 825 5.033 PSO[25 ] 9 9 80 857 2.814 9 9 77 823 VNS[26 ] 9 9 76 825 3.905 9 11 75 821 RL[27 ] 9 9 97 862 0.943 9 15 74 817 9 9 76 825 4.276 9 15 75 815 9 11 75 821 10 157 71 876 GASA[28 ] 9 15 75 815 11 395 70 870 10 141 73 814 12 559 71 804 10 195 74 811 12 523 73 802 − − − − − − 12 559 72 802
4. 大规模实例对比 为了验证IBSO算法求解本文问题的求解性能,应用27规模的电视机[29 ] 和25规模的电冰箱[17 ] 拆卸实例,构建2条并行拆卸线;运用所建模型和所提算法对2种废旧电器分配工人或机器人进行拆卸,应用2种经典算法GA[30 ] 和NSGA-Ⅱ[21 ] 和BSO求解实例与IBSO算法进行对比. 电视机和电冰箱的拆卸信息如表4 所示,电视机和电冰箱的优先关系分别如图8 、9 所示. ...
... (3)应用IBSO算法求解25规模基准算例,与文献[23 , 25 ~28 ]的求解结果进行对比,验证了IBSO算法的优越性. 将该算法引入电视机与电冰箱的大规模拆卸实例中,通过与GA、NSGA-Ⅱ和BSO算法求解结果和HV指标对比,验证了IBSO算法的求解性能. ...
On the end-of-life state oriented multi-objective disassembly line balancing problem
1
2020
... 为了验证IBSO算法求解本文问题的求解性能,应用27规模的电视机[29 ] 和25规模的电冰箱[17 ] 拆卸实例,构建2条并行拆卸线;运用所建模型和所提算法对2种废旧电器分配工人或机器人进行拆卸,应用2种经典算法GA[30 ] 和NSGA-Ⅱ[21 ] 和BSO求解实例与IBSO算法进行对比. 电视机和电冰箱的拆卸信息如表4 所示,电视机和电冰箱的优先关系分别如图8 、9 所示. ...
A hybrid genetic algorithm for sequence-dependent disassembly line balancing problem
1
2016
... 为了验证IBSO算法求解本文问题的求解性能,应用27规模的电视机[29 ] 和25规模的电冰箱[17 ] 拆卸实例,构建2条并行拆卸线;运用所建模型和所提算法对2种废旧电器分配工人或机器人进行拆卸,应用2种经典算法GA[30 ] 和NSGA-Ⅱ[21 ] 和BSO求解实例与IBSO算法进行对比. 电视机和电冰箱的拆卸信息如表4 所示,电视机和电冰箱的优先关系分别如图8 、9 所示. ...