Musser于1955年基于薄壳弹性理论提出谐波齿轮传动[1],因其具有体积小、高精度、高效率、重合度大、承载能力强的特点,被广泛应用于精度要求较高的航空航天、精密机床、工业机器人等领域[2]. 柔轮为谐波齿轮传动三大核心部件之一,利用其可控变形与刚轮进行啮合运动,从而实现速度变化与传递动力的功能,因此柔轮是研究重点. 在柔轮结构优化和应力方面,王迪[3]基于有限元法对所提出的3种新型结构柔轮进行参数优化分析. Sahoo等[4]通过有限元法(finite element method, FEM)估算空载条件下渐开线齿廓的柔轮筒体应力、应变和初始转矩,并采用实验法予以验证. Wang等[5]基于力学分析和有限元法提出基于力学分析的短筒柔轮的快速应力计算方法. 高海波等[6]探究柔轮结构参数对柔轮应力的敏感程度. 董慧敏等[7]将正交实验法与有限元法相结合,分析柔轮各结构参数与等效应力之间的关系,并优化柔轮结构. 在齿廓设计方面,辛洪兵[8]首先用数值方法验证了圆弧齿廓的可行性和有效性,同时还推导出了双圆弧齿廓的设计求解过程. 沈允文[9]通过对比几种谐波齿廓的性能,得出双圆弧齿廓相比其他齿廓,在传动精度和啮合性能方面都更加优良. 王家序等[10]在此基础上进一步提出具有更宽啮合区间、更高重合度的存在“双共轭”现象的公切线双圆弧齿廓. 在空间啮合方面,Ishikawa等[11]基于齿条近似法设计不同类型的三维齿廓,王家序等[12]提出双圆弧谐波传动的三维齿廓设计方法. 现有的双圆弧齿廓设计和三维齿廓修形都是在线性假设径向变形量的基础上进行设计的[13-14]. 但在实际的谐波传动中,由于柔轮齿圈结构的存在,柔轮沿轴向的径向变形是非线性变化的[15],柔轮的实际径向变形不能使柔轮轮齿运动到理论设计的位置,且柔轮长短轴径向变形也不同,从而导致柔轮与刚轮齿廓干涉,磨损严重,不能满足传动要求.
本研究以无公切线双圆弧齿廓为研究对象,利用有限元法分析柔轮的齿宽、壁厚、筒长、波发生器与柔轮杯底距离等结构参数对柔轮长短轴处径向变形的影响规律、线性假设径向变形与有限元径向变形的差异变化情况以及柔轮径向变形对各个参数的敏感度,探究柔轮结构与柔轮变形内在联系. 基于有限元径向变形对双圆弧齿廓进行设计和三维齿廓修形,并对比分析线性假设法设计修形与有限元法设计修形的柔轮应力情况. 结合有限元进一步完善谐波双圆弧齿廓的设计和修形,为实际的谐波齿廓的齿廓设计和修形提供参考.
1. 双圆弧齿廓设计及修形
1.1. 双圆弧齿廓设计
1.1.1. 柔轮齿廓
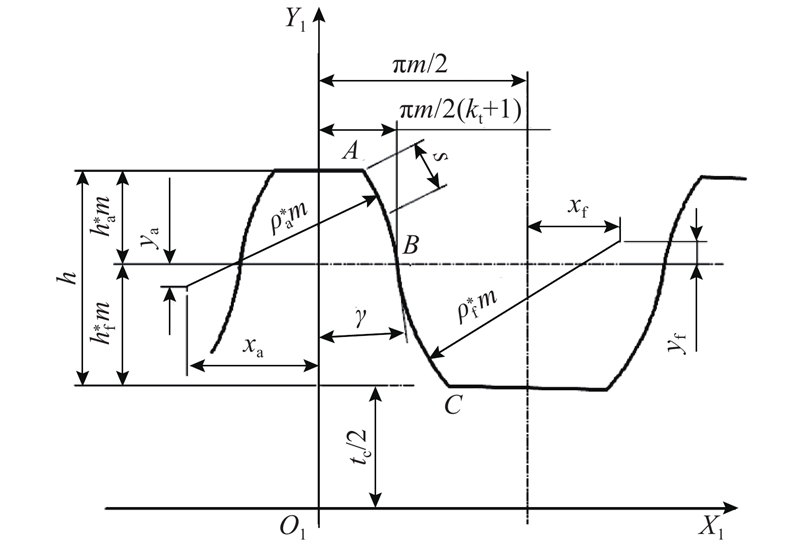
无公切线双圆弧齿廓主要由2段相切圆弧AB和BC以及其他过渡圆弧组成,具体齿形如图1所示. 图中,ha *为齿顶高系数,hf *为齿根高系数,m为齿形模数,xa为凸齿圆心横坐标的偏移量,ya为凸齿圆心纵坐标的移距量,xf为凹齿圆心横坐标的偏移量,yf为凹齿圆心纵坐标的移距量,h为全齿高,γ为双圆弧倾角,kt为齿厚比,tc为齿根壁厚,ρa *为凸圆弧齿廓半径系数,ρf *为凹圆弧齿廓半径系数.
图 1
为了表达柔轮双圆弧齿廓,建立柔轮局部坐标系S1{O1X1Y1},如图1所示,坐标系Y1轴与柔轮轮齿对称轴线重合,坐标原点O1为Y1轴与柔轮中性层曲线的交点,从齿廓齿顶A处起以弧长s为参数分段表示圆弧AB和BC.
凸圆弧齿廓AB段为
式中:s为从齿廓齿顶A处起的弧长参数,
凹圆弧齿廓BC段为
式中:
1.1.2. 柔轮变形和转角关系
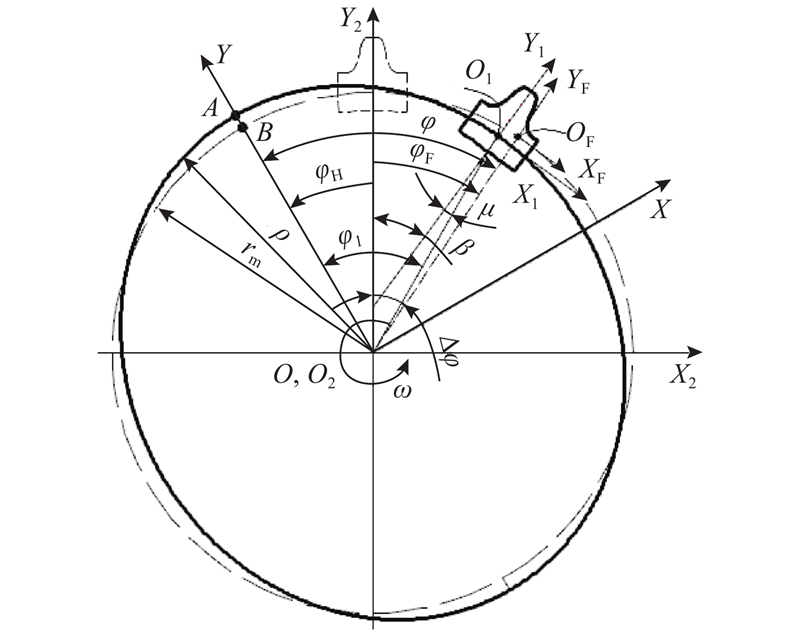
为了使研究的问题不失普遍性,选用的形式为波发生器输入,刚轮固定,柔轮输出. 建立谐波传动坐标系如图2所示,在波发生器上建立坐标系S{OXY},其坐标原点O位于波发生器的圆心,X轴与波发生器短轴重合. 以水平方向为X2轴,原点O2与刚轮圆心重合,建立刚轮坐标系S2{O2X2Y2}. 以柔轮任意一个齿代替柔轮所有齿的运动,并将坐标系S1{O1X1Y1}置于该齿上,原点O1位于啮合端的中线上,Y1轴与轮齿的对称轴重合. 坐标系S{OFXFYF}位于柔轮输出端,投影到XOY平面,OF在柔轮输出端的中线上,YF与柔轮变形前的轮齿对称轴重合.
图 2
在波发生器的作用下,柔轮变形可以表现为3个方向的位移,分别为径向位移ω、切向位移v以及转角位移μ. 变形方程如下:
式中:rm为柔轮未变形时中性层曲线半径,
波发生器选用标准椭圆凸轮波发生器,因此原始波发生曲线矢径为
式中:a、b分别为标准椭圆的长半轴半径与短半轴半径.
根据柔轮中性层曲线长度不变可知,柔轮中性层曲线总长在变形前、后不会发生变化,则有
式中:
根据谐波传动装配后各构件的空间运动关系,可以得到柔轮精确转角关系为
式中:β为柔轮轴Y1相对于刚轮轴Y2的转角,
1.1.3. 基于改进运动学法的刚轮齿廓的求解
基于包络法的谐波啮合理论相比其他啮合理论最为完善,但由于其理论公式太多,运用起来较复杂. 基于改进运动学的谐波啮合理论发展时间较短,但由于其啮合矩阵具有不随共轭曲面形式改变的唯一性,这种理论计算过程简单,编制程序容易,还适用于变速比、空间啮合的情况[16]. 因此,选用基于改进运动学的共轭理论来推导刚轮的齿廓.
根据齿廓啮合的基本定理可知,2个相对运动的曲面要实现共轭运动,须满足基本共轭方程:
式中:n、v(12)分别为两曲面在接触点的法向矢量和相对速度矢量.
在柔轮齿廓坐标系S1{O1X1Y1}中,柔轮齿廓的径矢和法向量分别为
在刚轮坐标系S2{O2X2Y2}中应满足共轭方程,其相应的矩阵形式为
将柔轮齿廓坐标系S1{O1X1Y1}中的柔轮齿廓坐标的矢径r1和法向量n1转换到刚轮坐标系S2{O2X2Y2}中,可以得到
式中:M21为柔轮坐标系S1到刚轮坐标系S2的坐标变换矩阵;
矢径与时间的微分就是相对速度:
将式(10)、(11)代入共轭方程式(9),可以得到
令
可以得到基于改进运动学法的谐波啮合方程:
将式(3)、(5)、(8)代入式(13)中,可以求解出不同弧长参数s所对应的{
1.2. 三维齿廓的修型
图 3
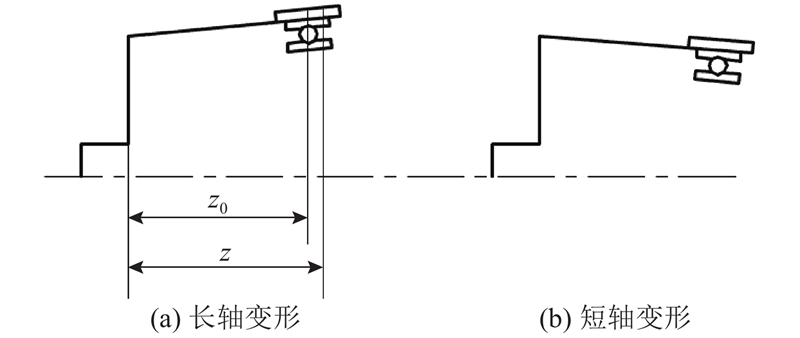
忽略杯底和齿圈的影响,假设波发生器与柔轮内壁是线接触状态. 在波发生器的作用下,柔轮在长轴附近会外张一定的角度,在短轴附近会内倾一定的角度,如图4所示,且外扩角和内倾角在轴向方向呈线性变化,因此柔轮会在轴向产生线性变化的线性假设径向变形.
图 4
在柔轮轴向上距筒底为z的任意截面的线性假设径向变形为
式中:
在实际工作中,由于柔轮齿圈作用以及波发生器与柔轮内壁接触复杂,线性计算的径向变形与实际变形有较大差异,并不能满足使用要求. 因此,通过有限元法计算柔轮长短轴的径向变形就尤为重要.
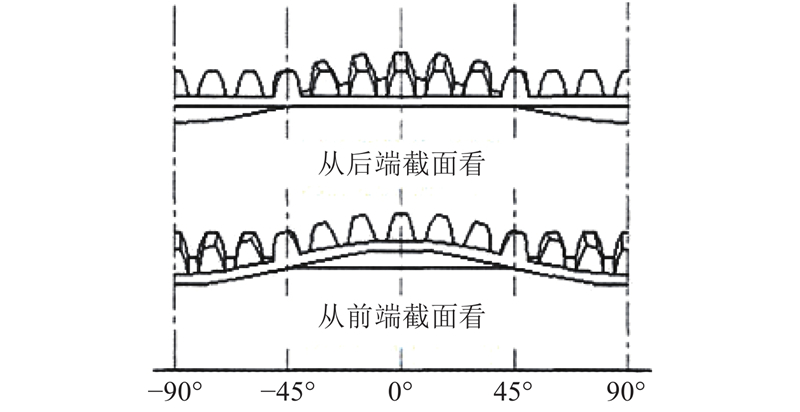
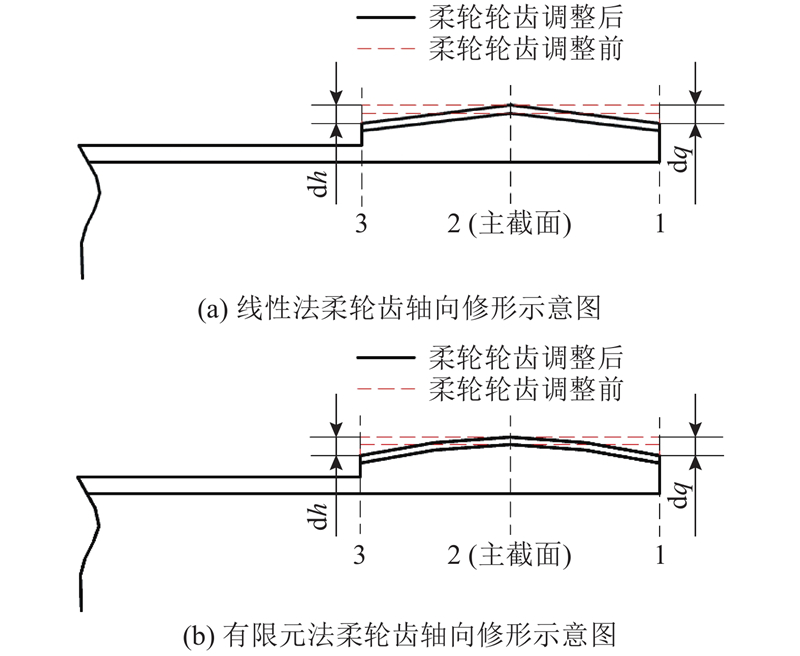
为了避免柔轮在不同径向变形的作用下与刚轮啮合时产生干涉或没有啮合的现象,选取柔轮齿宽中间截面2为主截面,截面1为前端截面,截面3为后端截面. 为了减少实际加工工序,在不改变任意截面的齿廓形状的条件下,利用改进运动学法的啮合理论以及MATLAB仿真分析,通过合理调整各截面柔轮齿廓的径向位置,使柔轮齿廓在任意转角下都位于刚轮齿廓内部,从而实现柔轮和刚轮的无干涉啮合. 线性法修形、有限元法修形后的齿形如图5所示. 图中,dq、dh分别为前、后端修形.
图 5
由于齿廓三维修形的主要目的是调整柔轮齿的齿根壁厚,可以得到修形公式为
式中:tx为修形后齿根壁厚,tc为修形前齿根壁厚,d为修形量.
由于线性法的修形是根据柔轮轴向线性假设径向变形进行壁厚调整的,线性假设变形是线性变化的,根据式(15)可知线性法修形后柔轮轮齿在轴向呈线性三角. 根据有限元得到的径向变形为曲线变化,因此将根据有限元径向变形得到的修形量代入式(15),可以得到柔轮轮齿在轴向呈曲线三角.
2. 结构参数对柔轮径向变形的影响
2.1. 结构参数分析
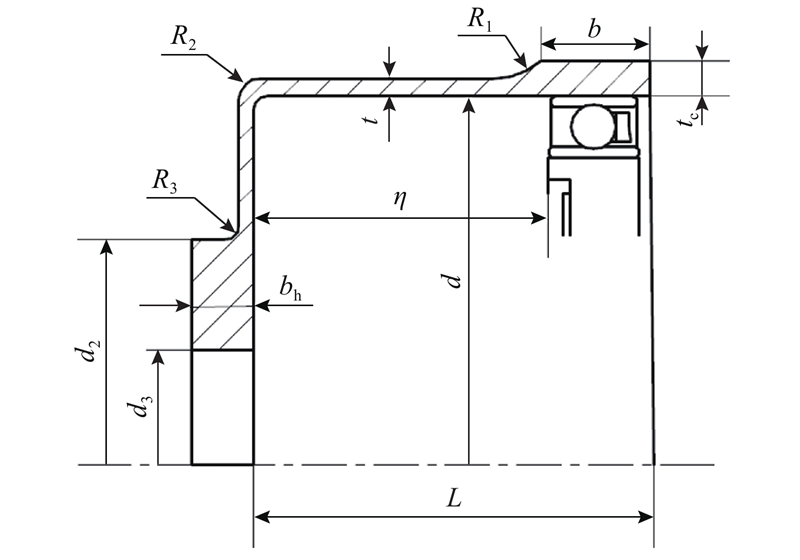
径向变形是谐波齿廓的设计和三维修形中的重要参数,实际变形与线性假设变形的差异程度会直接影响谐波齿廓的啮合、润滑性能,严重的可能导致噪声、振动加剧. 为了进一步研究柔轮结构和柔轮变形之间的关系,在柔轮主要的几何结构参数中初选与柔轮变形相关度较大的柔轮齿宽b、筒底壁厚t、筒长L以及波发生器与柔轮杯底的距离η等参数,研究对柔轮长短轴处有限元径向变形的影响规律. 柔轮结构如图6所示.
图 6
2.2. 齿宽对柔轮径向变形的影响
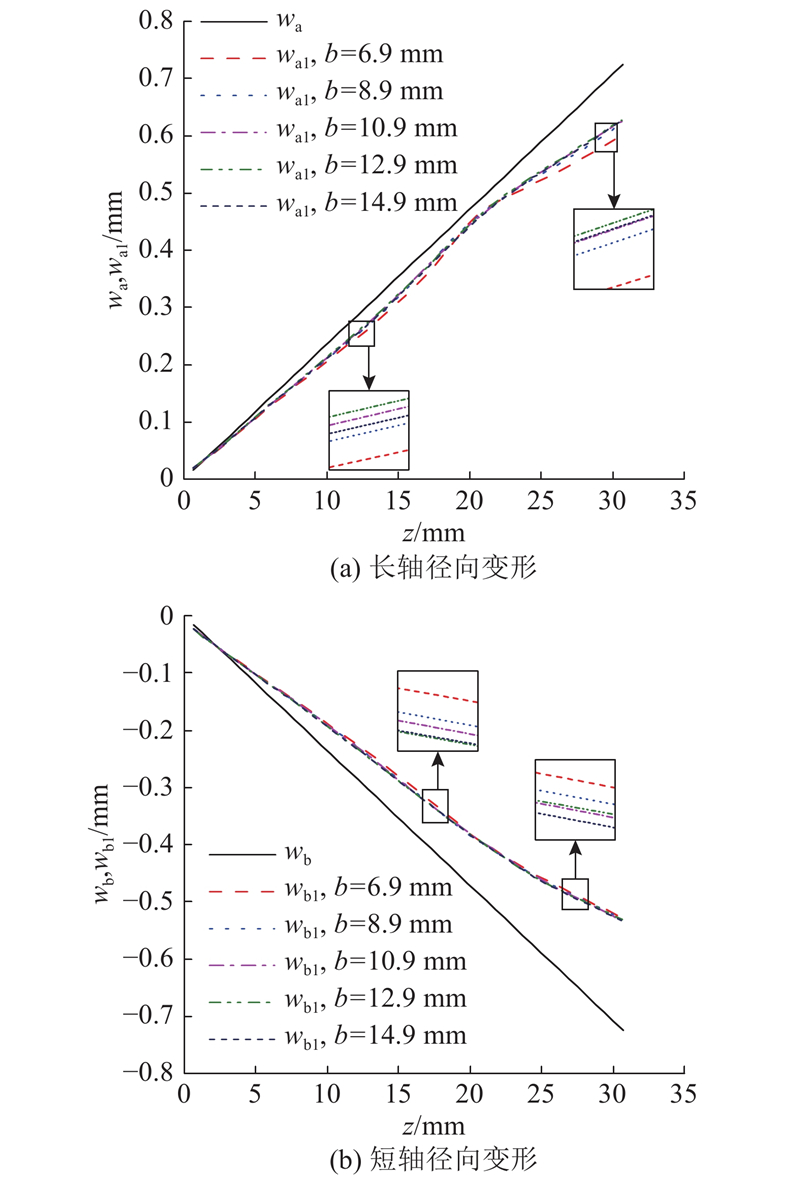
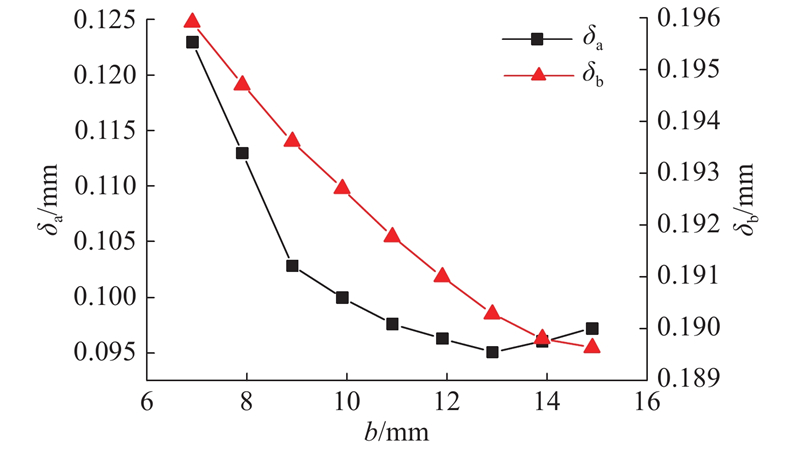
齿圈部分是整个柔轮啮合中最重要的一部分,而齿圈的存在也对柔轮的径向变形有较大影响,因此探究齿圈的宽度对柔轮径向变形很有必要. 选取齿宽b∈[6.9,14.9],柔轮在长短轴的线性假设径向变形和有限元径向变形如图7所示. 图中,wa为长轴处线性假设径向变形,wa1为长轴处有限元径向变形,wb为短轴处线性假设径向变形,wb1为短轴处有限元径向变形. 可以看出,柔轮轴向的径向变形无法呈线性变化,特别是在齿圈部分,由于齿圈的挠性作用,与线性假设径向变形有一定的偏差. 相比长轴,短轴处的径向变形与线性假设径向变形偏差更大. 如图8所示为齿宽对wa与wa1最大差异δa、wb与wb1最大差异δb的影响. 可以看出,随着齿宽的增加,长短轴处的径向变形与线性假设径向变形的最大差异都有所减小.
图 7
图 7 不同齿宽的柔轮长短轴径向变形
Fig.7 Radial deformation diagram of long and short axis of flexspline with different tooth widths
图 8
图 8 齿宽对柔轮有限元径向变形与线性假设径向变形差异的影响
Fig.8 Influence of tooth width on difference between finite element and linear assumed radial deformation of flexspline
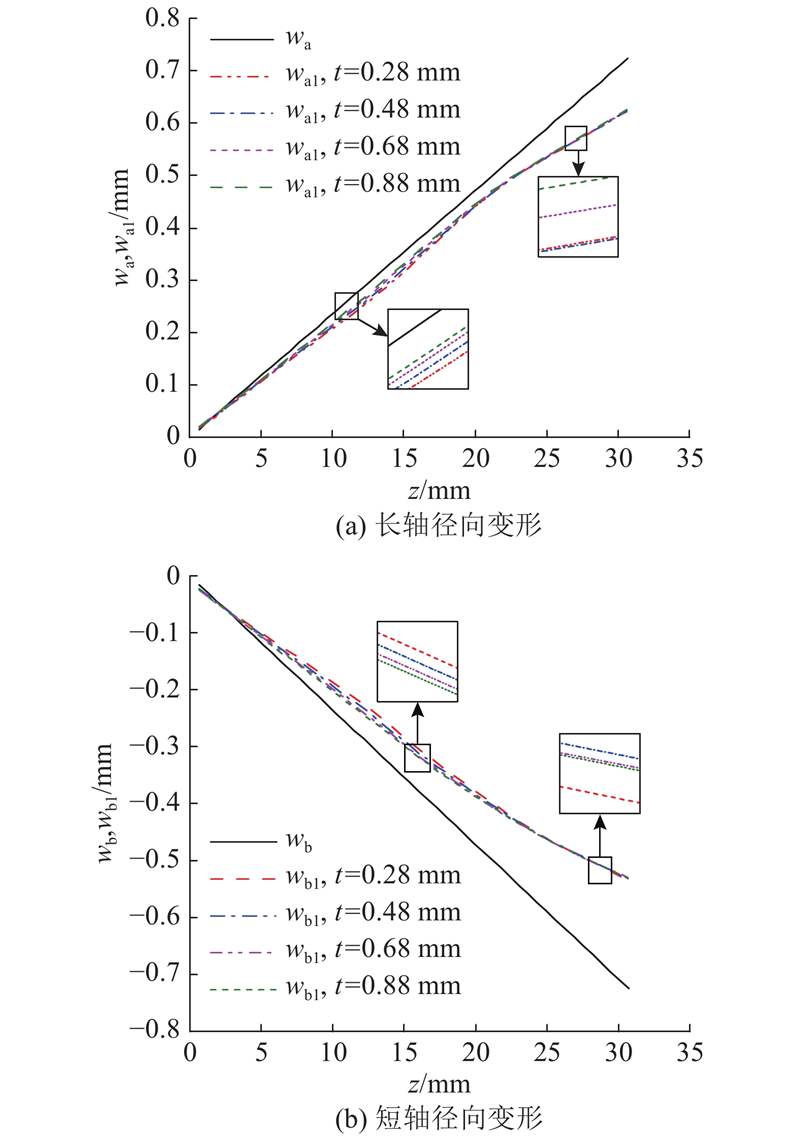
2.3. 筒体壁厚对柔轮径向变形的影响
图 9
图 9 不同壁厚的柔轮长短轴径向变形图
Fig.9 Radial deformation diagram of long and short axis of flexspline with different thicknesses
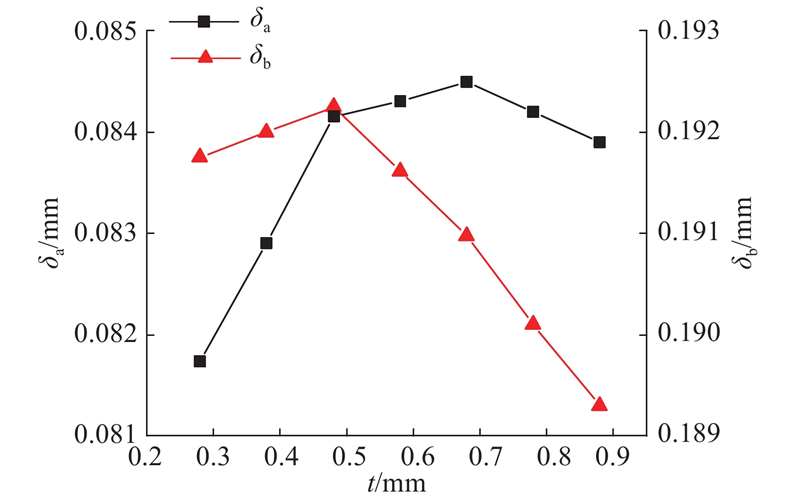
图 10
图 10 壁厚对柔轮有限元径向变形与线性假设径向变形差异的影响
Fig.10 Influence of thickness on difference between finite element and linear assumed radial deformation of flexspline
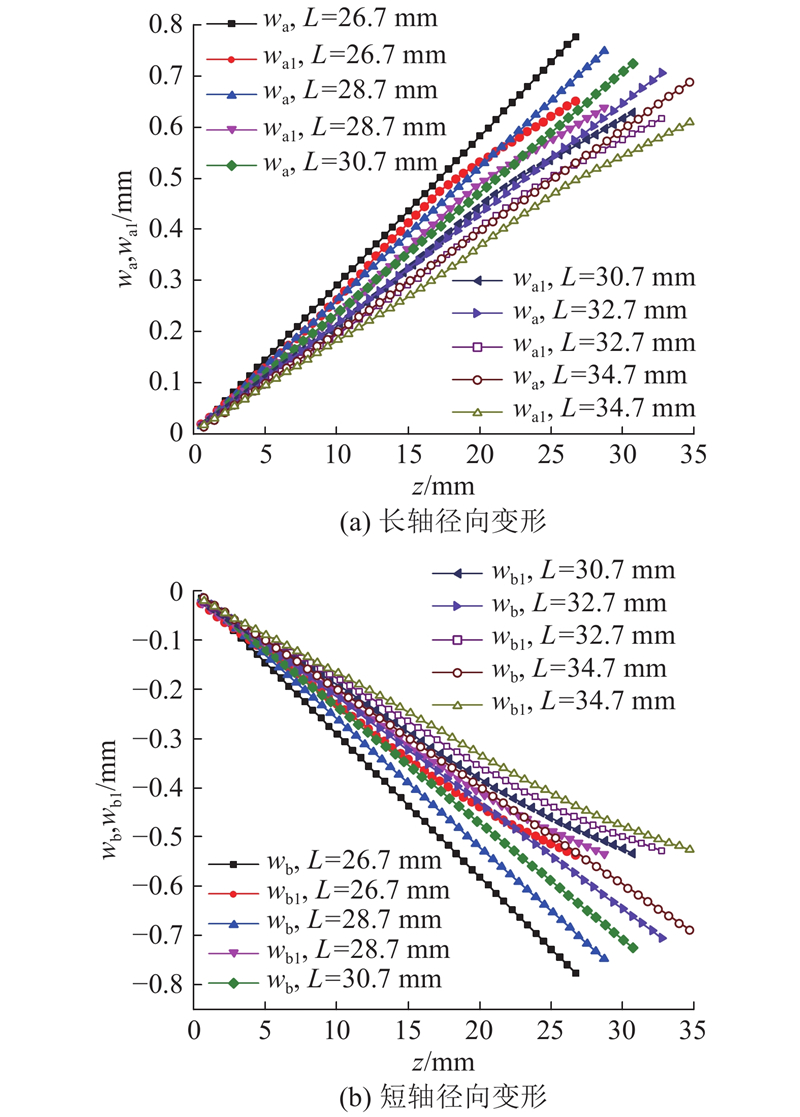
2.4. 筒长对柔轮径向变形的影响
图 11
图 11 不同筒长的柔轮长短轴径向变形
Fig.11 Radial deformation of long and short axis of flexspline with different lengths
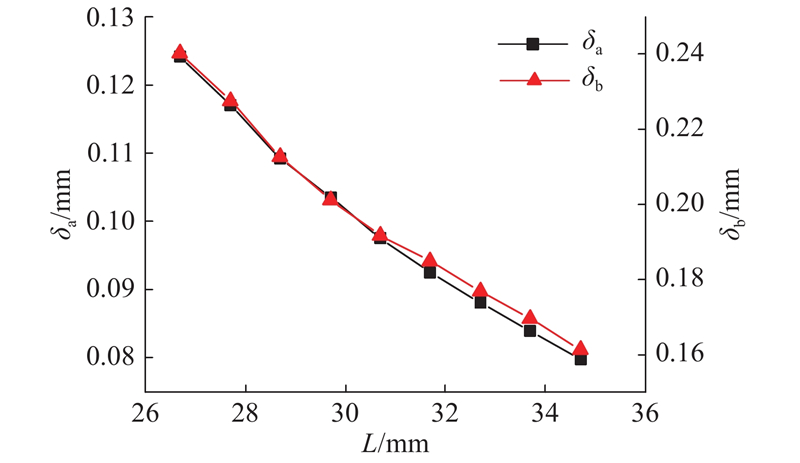
图 12
图 12 筒长对柔轮有限元径向变形与线性假设径向变形差异的影响
Fig.12 Influence of length on difference between finite element and linear assumed radial deformation of flexspline
2.5. 波发生器与杯底的距离对柔轮径向变形的影响
图 13
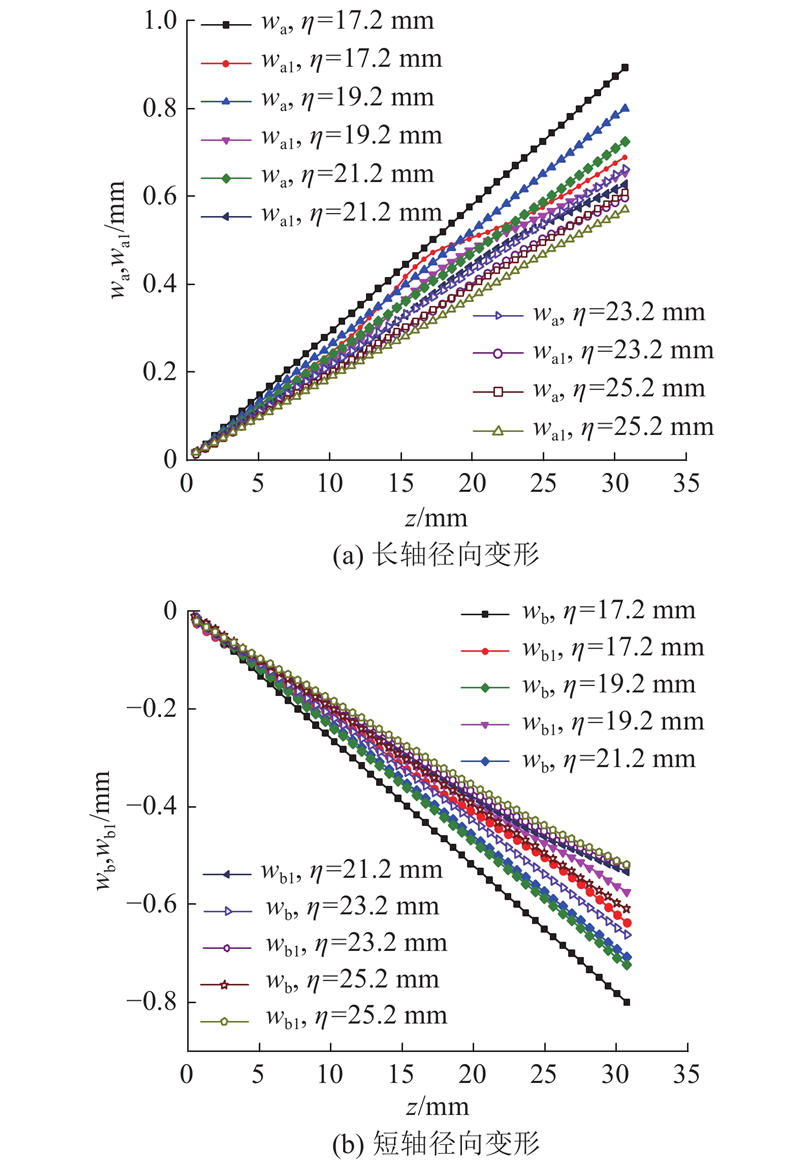
图 13 不同η的柔轮长短轴径向变形
Fig.13 Radial deformation of long and short axis of flexspline with different locations of wave generator
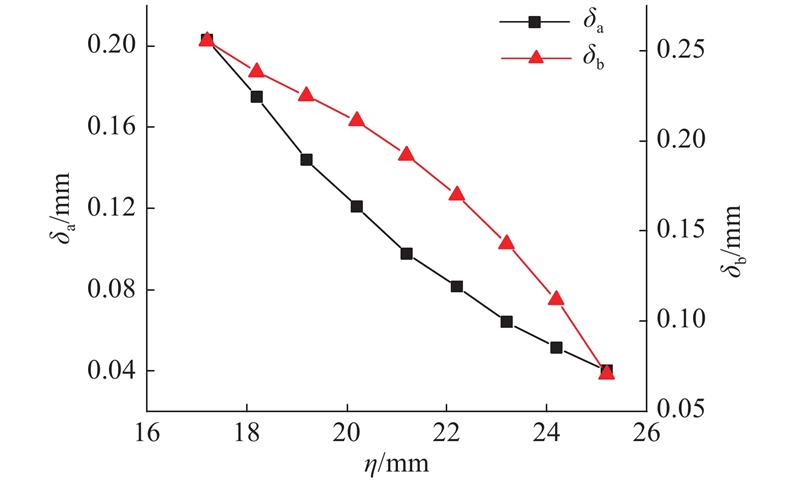
图 14
图 14 η对柔轮有限元径向变形与线性假设径向变形差异的影响
Fig.14 Influence of location of wave generator on difference between finite element and linear assumed radial deformation of flexspline
综合分析以上4个参数对柔轮有限元径向变形的影响规律,可以看出,各个参数对径向变形的影响程度各不相同. 其中波发生器与杯底的距离对柔轮径向变形影响程度最大,敏感度最高,其次是齿宽和筒长,壁厚对柔轮径向变形的影响程度最小.
3. 谐波传动的有限元分析
3.1. 共轭齿廓设计实例
表 1 柔轮关键结构参数
Tab.1
| 参数 | 符号 | 数值/mm | 参数 | 符号 | 数值/mm | |
| 齿宽 | b | 10.8 | 柔轮内壁直径 | d | 61.32 | |
| 筒长 | L | 30.7 | 筒体壁厚 | t | 0.38 | |
| 齿根壁厚 | tc | 0.66 | 波发生器距离杯底的距离 | η | 21.2 |
表 2 理论法齿廓参数
Tab.2
| 参数 | 柔轮齿廓参数 | 刚轮齿廓参数 | |||||||||||||||||
| ha*/mm | hf*/mm | xa/mm | ya/mm | ρa/mm | t1/mm | γ/(°) | xf/mm | yf/mm | ρf/mm | ha*/mm | hf*/mm | xa/mm | ya/mm | ρa/mm | ρf/mm | xf/mm | yf/mm | ||
| 数值/mm | 0.7 | 0.9 | 0.396 3 | 0.608 4 | 0.63 | 0.653 6 | 6 | 0.876 7 | 0.742 2 | 0.65 | 0.65 | 0.90 | 0.871 9 | 1.154 4 | 0.644 9 | 0.631 9 | 0.397 9 | 1.021 7 | |
表 3 有限元法齿廓参数
Tab.3
| 参数 | 柔轮齿廓参数 | 刚轮齿廓参数 | |||||||||||||||||
| ha*/mm | hf*/mm | xa/mm | ya/mm | ρa/mm | t1/mm | γ/(°) | xf/mm | yf/mm | ρf/mm | ha*/mm | hf*/mm | xa/mm | ya/mm | ρa/mm | ρf/mm | xf/mm | yf/mm | ||
| 数值/mm | 0.7 | 0.9 | 0.396 3 | 0.608 4 | 0.63 | 0.653 6 | 6 | 0.876 7 | 0.742 2 | 0.65 | 0.65 | 0.90 | 0.874 8 | 1.181 7 | 0.647 3 | 0.639 5 | 0.404 6 | 1.044 | |
3.2. 三维齿廓修形
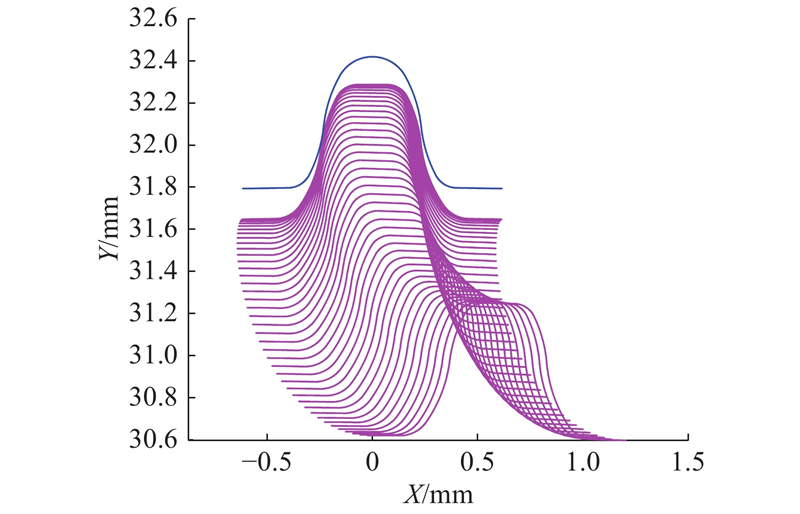
图 15
图 15 修形前柔轮齿运动轨迹图
Fig.15 Track diagram of tooth movement of flexspline before modification
图 16
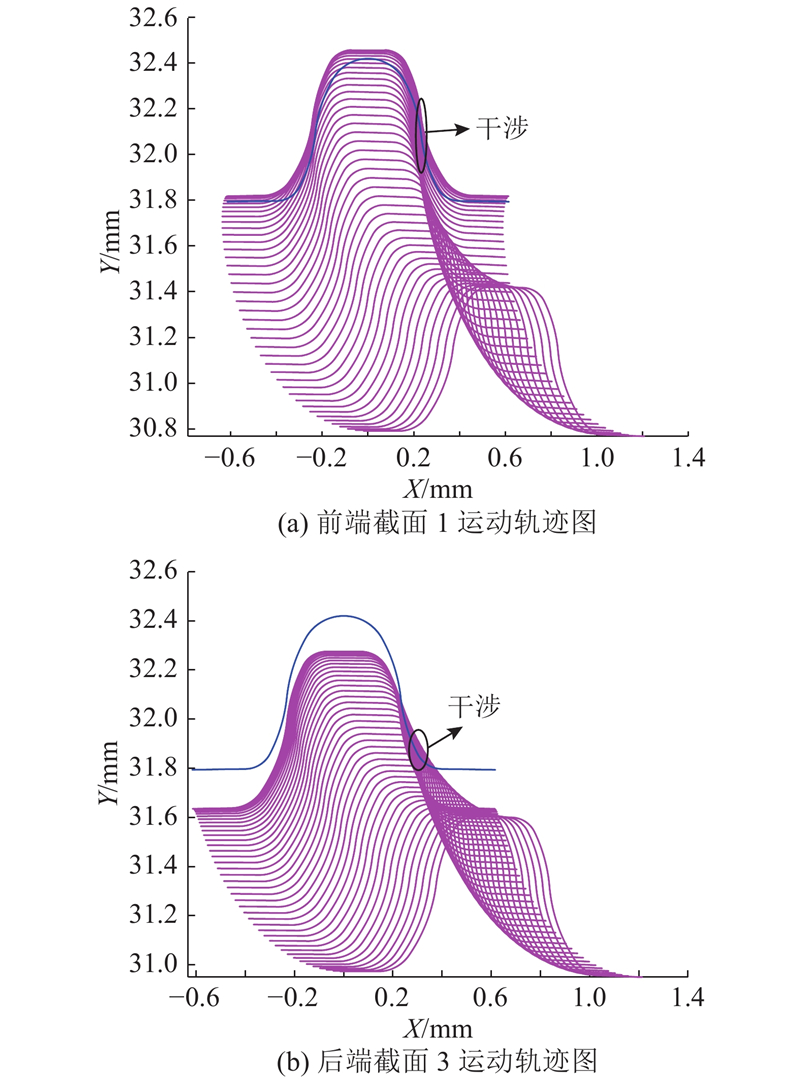
图 16 修形后前端截面1运动轨迹图
Fig.16 Track diagram of tooth movement of front section 1 after modification
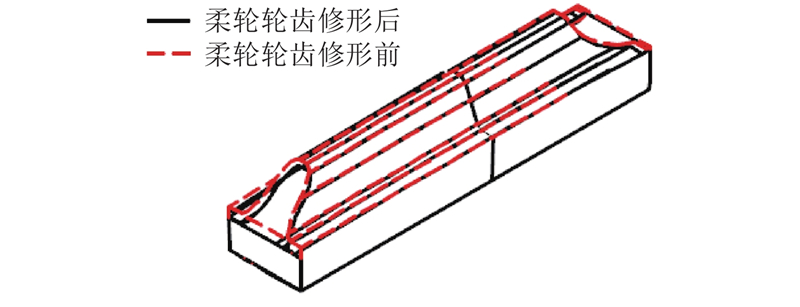
修形后的柔轮齿廓三维图如图17所示,线性法修形是根据柔轮齿前后端的壁厚调整量与齿宽的线性关系,来确定其余各截面的壁厚调整量. 有限元法修形是根据各截面的有限元径向变形和柔轮与刚轮的啮合状态来确定壁厚调整量.
图 17
图 17 柔轮齿廓修形后的三维图
Fig.17 3D view of tooth profile of flexspline after modification
图 18
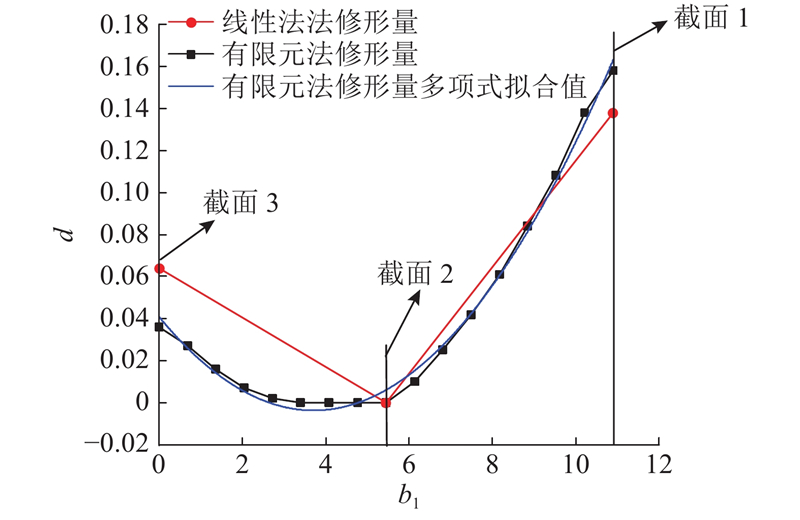
图 18 柔轮齿三维轴向修形量对比图
Fig.18 Comparison chart of 3D axial modification amount of flexspline tooth
将柔轮齿三维轴向修形量代入式(15),可以确定相应的柔轮齿轴向截面齿根壁厚. 修形后的柔轮齿可以在不采用轮齿磨削、切削或修形等二次加工方法的前提下,通过滚齿加工实现. 刀具在沿柔轮轴向进给的同时根据柔轮齿轴向截面的齿根壁厚来调整径向进给量,从而完成对修形后的柔轮齿的加工.
3.3. 仿真实体模型建立
建立波发生器、柔轮、刚轮的三维模型,其中为了减少工作量并缩短计算时间,将波发生器简化为椭圆刚体、刚轮简化为内圆柱齿圈. 有限元分析主要是柔轮变形和柔轮应力两部分,在变形分析中,在建模中对b、t、L、η进行参数变化. 在应力分析中,主要是柔轮齿廓变化以及三维修形变化. 将建立的三维实体利用ANSA进行网格划分,为了保证计算的精确和收敛,采用八节点六面体网格C3D8R. 对刚轮与柔轮轮齿部分进行细化处理. 在ANSYS中对网格模型进行材料属性赋予,如表4所示. 表中,E为弹性模量,μ为泊松比,ρ为密度. 考虑柔轮弹性变形的特点,设置“面-面”接触,柔轮内壁为接触面(contact),波发生器外表面为目标面(target),摩擦系数为0.15. 设置3个分析步骤:1)将波发生器椭圆分为两半进行位移约束,使波发生器外表面与柔轮内壁接触,并将其撑开;2)对刚轮添加位移约束,使刚轮与柔轮装配,刚轮齿廓与柔轮齿廓接触;3)释放柔轮绕轴向的旋转约束,在柔轮输出端施加额定扭矩T=63 N·m.
表 4 谐波齿轮材料性能参数
Tab.4
| 部件 | 材料 | E/GPa | μ | ρ/(kg·m−3) |
| 柔轮 | 30CrMnSiA | 196 | 0.300 | 775 0 |
| 刚轮 | 45 | 210 | 0.269 | 785 0 |
| 波发生器 | 45 | 210 | 0.269 | 785 0 |
3.4. 柔轮应力分析
利用ANSYS Workbench分别对线性法、有限元法的仿真模型进行有限元分析. 如图19所示为不同设计修形方法的柔轮应力对比. 可以发现,当未修形时(平齿)柔轮的最大应力为1 335 MPa,线性法设计修形后的柔轮的最大应力为554 MPa,有限元设计修形的柔轮最大应力为410 MPa. 在未修形时,柔轮齿宽方向的最大应力在柔轮齿的前后端,同时柔轮齿圆周方向的应力分布不均. 修形后的柔轮齿宽方向的最大应力主要集中在中间截面附近,且圆周方向呈区域性均匀分布. 相比线性法设计修形,有限元法设计修形的柔轮最大应力减少约144 MPa.
图 19
图 19 不同设计修形方法柔轮应力对比
Fig.19 Stress comparison of flexspline with different design and modification methods
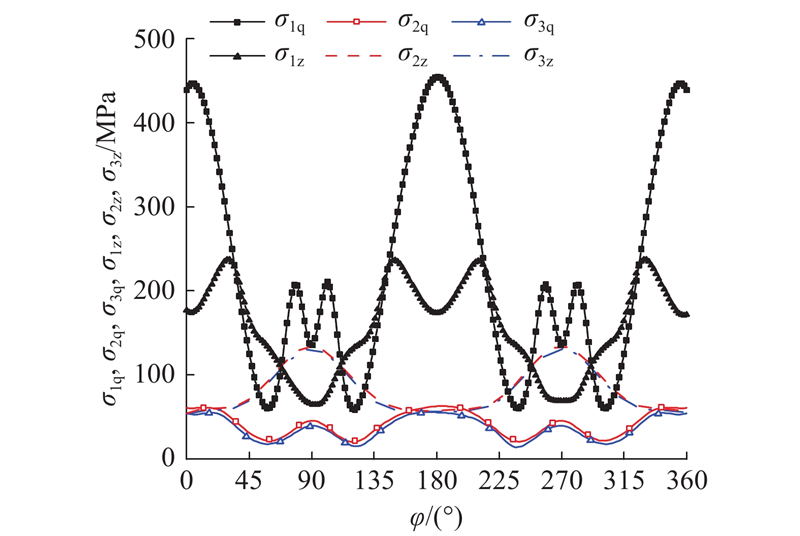
如图20所示为柔轮齿中间截面和前端截面的周向应力曲线图. 图中,σ1q为线性法设计未修形时柔轮齿前端截面应力,σ2q为线性法设计修形时柔轮齿前端截面应力,σ3q为有限元法设计修形时柔轮齿前端截面应力,σ1z为线性法设计未修形时柔轮齿中间截面应力,σ2z为线性法设计修形时柔轮齿中间截面应力,σ3z为有限元法设计修形时柔轮齿中间截面应力. 未修形时的柔轮齿宽方向的应力主要在前段,柔轮齿周向应力曲线波动较大,且最大应力主要发生在柔轮和刚轮的啮入区和啮出区,说明未修形的齿廓在啮合过程中存在一定的干涉情况. 修形后的柔轮齿的应力主要在齿宽的中间截面附近,周向应力波动相比较小,且最大应力在柔轮长轴处,主要是在波发生器的作用下所产生的,相比线性法设计修行,有限元法设计修形的柔轮整体周向应力和最大应力都更小. 表明利用有限元法对谐波齿廓进行设计和修形,能降低柔轮应力,提高柔轮的承载能力.
图 20
图 20 柔轮周向应力分布图
Fig.20 Circumferential stress distribution diagram of flexspline
4. 结 论
(1)柔轮在实际工作中,其径向变形与理论变形具有明显的差异,特别是在齿圈部分. 柔轮的长短轴径向变形也不一致,且短轴处的变形明显小于长轴处.
(2)柔轮结构参数柔轮齿宽、筒底壁厚、筒长以及波发生器与柔轮杯底的距离等参数会对柔轮实际变形产生一定的影响,其中适当增大齿宽、筒长以及波发生器与筒底的距离,能减小柔轮径向变形与线性假设变形的差异,而壁厚对柔轮径向变形的影响程度较小.
(3)对线性法设计修形和有限元法设计修形的仿真模型进行有限元分析,结果表明有限元法设计修形的柔轮最大应力比未修形的减小925 MPa,比线性法设计修形的减少144 MPa,有限元法设计修形的柔轮齿各截面的周向应力也低于线性法设计修形的. 说明基于有限元法的谐波齿廓设计和修形能有效弥补线性法设计修形未考虑到的柔轮变形差异,降低柔轮应力,提高谐波传动的啮合性能和承载能力.
(4)本研究针对谐波齿轮传动提出有限元法齿廓设计与修形方法,但是在工程实际中,柔轮的有限元变形与实际变形会存在一定的出入,后续将针对实际变形偏差利用样机实验结果对有限元法进行修正和改进,从而使得本研究更具有工程实际价值.
参考文献
Load sharing by tooth pairs in involute toothed harmonic drive with conventional wave generator cam
[J].
A rapid stress calculation method for short flexspline harmonic drive
[J].DOI:10.1108/EC-08-2018-0364 [本文引用: 1]
基于ANSYS的杯形柔轮结构参数对柔轮应力的敏感度分析
[J].DOI:10.3901/JME.2010.05.001 [本文引用: 1]
Sensitivity analysis of cup-shaped flexible wheel structure parameters to flexible wheel stress based on ANSYS
[J].DOI:10.3901/JME.2010.05.001 [本文引用: 1]
基于正交试验和有限元分析的谐波传动柔轮杯体结构优化
[J].
Optimization of cup body structure of harmonic drive flexspline based on orthogonal experiment and finite element analysis
[J].
双圆弧谐波齿轮传动基本齿廓设计
[J].
Design for basic rack of harmonic drive with double-circular-arc tooth profile
[J].
论谐波齿轮传动的齿形
[J].
On the tooth profile of harmonic gear transmission
[J].
公切线式双圆弧齿廓谐波齿轮传动设计
[J].
Design of common tangent double circular arc tooth profile harmonic gear transmission
[J].
杯形柔轮谐波传动三维双圆弧齿廓设计
[J].
Three -dimensional double arc tooth profile design of cup-shaped flexible wheel harmonic drive
[J].
径向变形量对谐波减速器啮合特性及柔轮应力的影响分析
[J].
Analysis of the influence of radial deformation on the meshing characteristics and flexspline stress of harmonic reducer
[J].
谐波传动柔轮空间齿廓设计与制造工艺
[J].
Design and manufacturing technology of flexspline's spatial tooth profile in harmonic drive
[J].
谐波传动中凸轮径向变形量对齿廓修形的影响
[J].
The influence of cam radial deformation on tooth profile modification in harmonic drive
[J].
The parametric design of double-circular-arc tooth profile and its influence on the functional backlash of harmonic drive
[J].