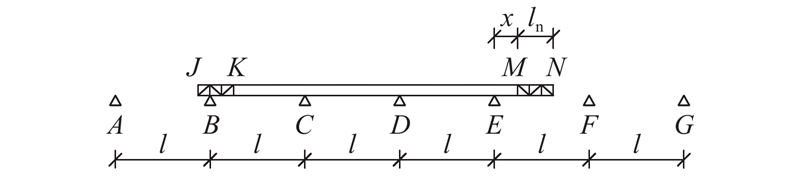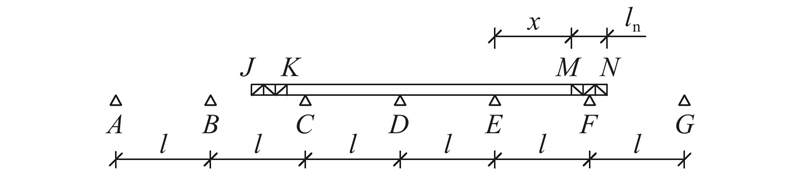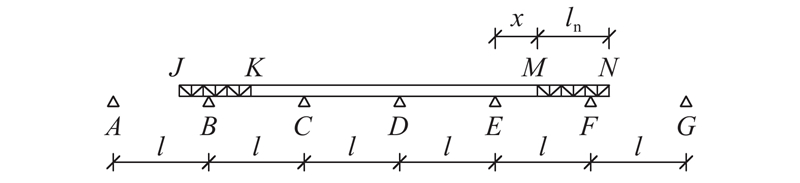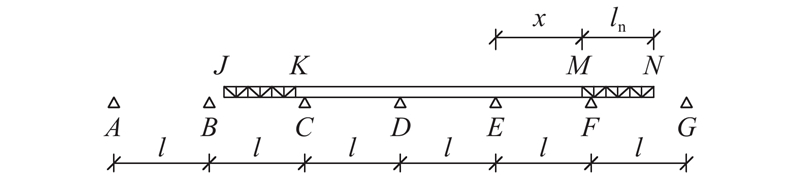1959年，桥梁顶推法施工首次成功运用到奥地利Ager桥中，此后，顶推法施工在桥梁建设中得到迅速的发展^[1-5]. 顶推法施工在伴随着桥梁事业快速发展的同时，对顶推跨径提出了更高的要求.1967年，西德维纳河桥采用顶推施工法时的最大顶推跨径为31.5 m，到了2005年米约大桥的最大顶推跨径达到了171 m. 随着顶推跨径的增大，主梁前端支点处的负弯矩相应地增大，且在顶推施工中主梁截面要承受不断交替循环的正负弯矩^[5-6]，对于这种情况，顶推法中使用导梁能够有效地改善主梁的受力特性. 导梁的第一次运用是在1963年的卡罗尼桥中，该导梁长度为17 m，成功减少了混凝土主梁在最大悬臂状态时支点的负弯矩，取得了很好的效果. 随后导梁逐渐成为桥梁顶推施工的技术标准^[7-8]. 桥梁顶推施工中导梁的长度、自重荷载集度及抗弯刚度等参数对主梁的受力特性有较大的影响^[9]，合理选择导梁的参数能够有效地改善主梁在顶推施工中的内力，可以节约成本^[10-11].

目前，普遍采用基于力法的连续梁三弯矩方程和基于位移法的直接平衡方程，分析导梁参数在桥梁顶推过程中对主梁内力变化的影响规律，推导出合理的导梁参数计算方法. Rosignoli^[12]基于位移法推导导梁和主梁的相互接触平衡方程，分析导梁长度和刚度对支点负弯矩的影响. Lee等^[13]研究变截面导梁的自重荷载集度，分析在顶推施工中不同自重荷载集度对主梁内力的影响. Arturo等^[14]研究3种最优导梁参数的计算方法，使用数值优化方法获得最优导梁的参数解. Mohammad等^[15]提出半无限梁的导梁与主梁的系统简化模型，开展数值优化设计. 王卫锋等^[16]基于位移法推导主梁在顶推过程中支点负弯矩的变化规律，以支点负弯矩为控制内力进行优化. 董创文等^[17]基于力法和一次落架法思想建立三弯矩方程组，推导导梁最优长度的计算公式. 谢福君等^[18]基于三弯矩方程，研究钢箱梁导梁顶推参数的影响.

虽然国内外学者在连续梁桥顶推施工导梁参数优化中取得了一定的成果，但都是基于连续顶推的单导梁研究. 本文以三跨等跨混凝土连续梁桥为例，构建主梁-双导梁的计算简化模型，利用位移法推导顶推过程中主梁内力的解析表达式，揭示了在不同导梁参数下主梁内力的变化规律. 针对桥梁不同的截面形式，提出合理、严谨的导梁参数优化计算方法. 基于不同长度的前、后导梁，分析不等跨连续梁桥的内力变化规律.

以三跨混凝土连续梁桥为例进行计算，为了简化计算，基本假定如下. 1）主梁和导梁的截面形式为等截面，即主梁和导梁的自重荷载集度和抗弯刚度均为常数；2）顶推过程中荷载仅考虑主梁和导梁的自重；3）各跨跨径的长度相同；4）在顶推过程中，忽略顶推设备对梁体的动力冲击效应；5）不考虑支座沉降和混凝土收缩徐变的影响.

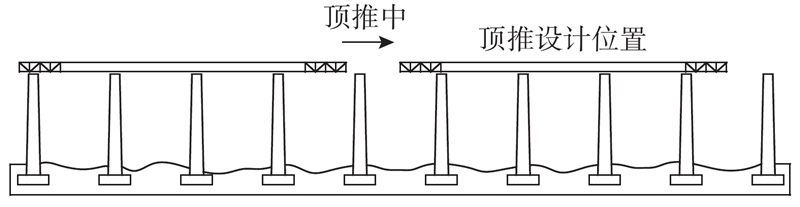
混凝土桥梁通常在桥岸侧的临时建造场浇筑或者某墩处支架现浇，逐步顶推至设计位置，如图1所示. 在顶推过程中，主梁前端在某个时刻会经历最大悬臂状态，导梁的作用是减小主梁前端的最大悬臂长度. 随着顶推的进行，主梁后端会经历最大悬臂状态，若仅设置前导梁，则为了减小主梁后端的最大悬臂长度，需要在主梁后端设置辅助墩，这会增加工期和施工成本，尤其是当顶推距离较大时，工程上一般会设置前、后2个导梁. 由于假定中各跨跨径长度相同，前、后导梁需要设置成相同的长度. 这是因为如果前、后导梁的长度不一致，那么主梁的最大悬臂长度取决于较短导梁的长度，造成主梁前、后端在各自最大悬臂状态时承受的内力不同. 当较短导梁一端处的主梁内力为控制内力时，另一端的导梁长度会显得太长，不经济. 当较长导梁一端处的主梁内力为控制内力时，另一端的导梁长度会显得太短，不安全. 在本文的三跨混凝土连续梁桥顶推中，导梁采用长度相同的前、后双导梁.

桥梁顶推计算简图如图2所示. 假设前、后导梁的长度均为l_n，各跨跨径的长度均为l，使用无量纲的参数α表示导梁长度与各跨跨径长度的比值，即α = l_n/l. 前、后导梁的自重荷载集度均为q_n，主梁的自重荷载集度为q，使用无量纲的参数β表示导梁的自重荷载集度与主梁的自重荷载集度的比值，即β = q_n/q. 前、后导梁的抗弯刚度均为E_nI_n，主梁的抗弯刚度为EI，使用无量纲的参数γ表示导梁的抗弯刚度与主梁的抗弯刚度的比值，即γ = E_nI_n/（EI）. 导梁的长度、自重荷载集度和抗弯刚度等性质可以通过α、β和γ这3个参数表示，则将桥梁顶推施工中导梁优化分析问题转化为α、β和γ这3个参数的最优组合问题.

从图1可知，在顶推过程中，桥梁从顶推起点开始会重复经历若干个阶段直至到达顶推终点，即设计位置，因此可以将桥梁在整个顶推过程中的受力分析简化为对这若干个顶推阶段的受力分析. 研究发现，α对顶推阶段有影响，故顶推阶段如下表示.

1）当0 < α ≤ 0.5时，可以分为2个顶推阶段，设主梁前端M与E支点的距离为x，令λ = x/l.

第1阶段：0≤ λ <1 – α. 该阶段起点定义为主梁前端M处于E支点时，终点定义为前导梁前端N即将到达F支点时（此时桥梁前端处于最大悬臂状态，悬臂长度为l），计算简图如图2所示.

根据图2可以得到第1阶段E支点处混凝土主梁的弯矩 $M_{E{\rm{1}}}^{\rm{I}}$（上标I表示当0 < α ≤ 0.5时，下标E1表示E支点处和顶推第1阶段）. 由于该阶段前导梁前端N并未到达前方桥墩F支点，始终处于悬臂状态，可以直接列出此时E支点位置处的弯矩表达式：

第2阶段：1−α ≤ λ ≤ 1.0. 该阶段起点定义为前导梁前端N处于F支点时（此时前导梁不是完全悬臂状态而是支承于F支点，这样相对于第1阶段存在体系转换），终点定义为主梁前端M到达F支点时，计算简图如图3所示.

根据位移法^[19]中的直接平衡法建立各个节点的平衡方程，其中θ_F、θ_M、θ_E、θ_D、θ_C为节点角位移，Δ_M为节点线位移.

节点F的角位移平衡方程为

节点M的角位移平衡方程为

节点M的线位移平衡方程为

节点E的角位移平衡方程为

节点D的角位移平衡方程为

节点C的角位移平衡方程为

联立式（2）~（7），可得第2阶段E支点处混凝土主梁弯矩 $M_{E2}^{\rm{I}}$的表达式：

式中：

2）当0.5 < α < 1.0时，可以分为3个顶推阶段.

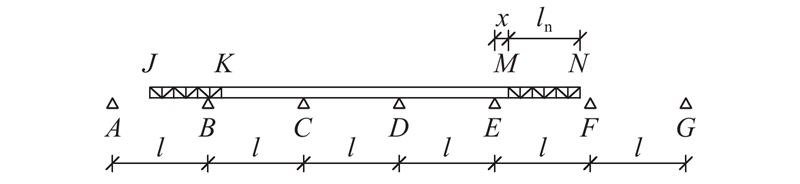
第1阶段：0 ≤ λ < 1− α. 该阶段起点定义为主梁前端M处于E支点时，终点定义为前导梁前端N即将到达F支点时，计算简图如图4所示.

该阶段E支点处混凝土主梁弯矩 $M_{E{\rm{1}}}^{{\rm{II}}}$的推导过程及结果与 $M_{E1}^{\rm{I}}$相同.

第2阶段：1−α ≤ λ ≤ α. 该阶段起点定义为前导梁前端N处于F支点时，终点定义为后导梁后端J到达B支点时，计算简图如图5所示.

根据位移法建立各个节点的平衡方程，可得第2阶段E支点处混凝土主梁弯矩 $M_{E{\rm{2}}}^{{\rm{II}}}$的表达式，限于篇幅，省略推导过程及结果.

第3阶段：α < λ ≤ 1.0. 该阶段起点定义为后导梁后端J刚好离开B支点时，终点定义为主梁前端M到达F支点时，计算简图如图6所示.

该阶段E支点处混凝土主梁弯矩 $M_{E{\rm{3}}}^{{\rm{II}}}$的推导过程及结果与 $M_{E2}^{\rm{I}}$相同.

桥梁顶推过程中主梁的受力特性、导梁参数的改变对主梁第一跨内的内力影响较大，对主梁后面跨的内力影响较小^[20]. 对主梁第一跨内EF跨中的E支点最大负弯矩及EF跨内的最大正弯矩进行基于导梁参数的内力分析.

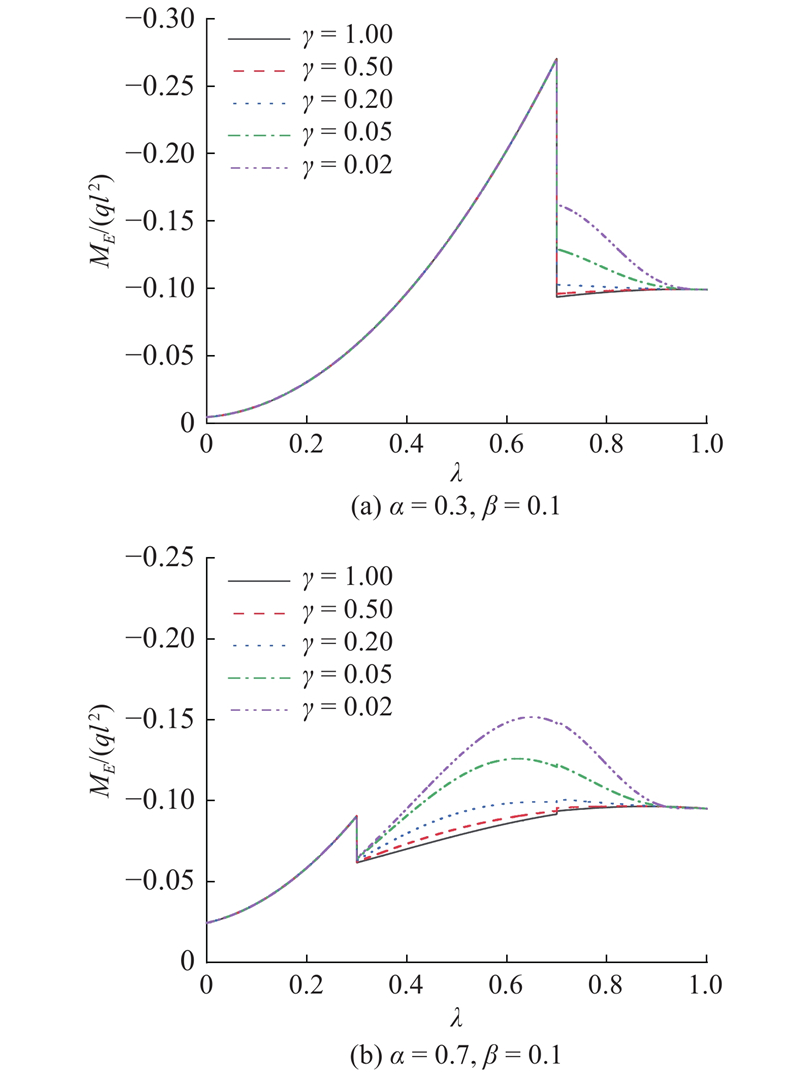
为了分析α、β和γ这3个参数在顶推过程中对E支点处混凝土主梁负弯矩的影响，假设α和β为常数，研究不同γ条件下在顶推过程中E支点处混凝土主梁负弯矩M_E的变化. 假设α = 0.3、β = 0.1和α = 0.7、β = 0.1 2种情况，不同γ的取值分别为1、0.5、0.2、0.05、0.02，如图7所示.

由图7（a）可得，当0 < α ≤ 0.5时M_E在第1阶段末与第2阶段初有一个突变，这是因为第1阶段E支点前的主梁及前导梁处于悬臂状态，第2阶段前导梁上F支点后发生了体系转换，降低了E支点处的负弯矩M_E. 第1阶段的M_E与γ无关，第2阶段内M_E与γ有关，且γ越小，第2阶段内的最大负弯矩越大. 在第2阶段末不同γ的M_E相同，说明第2阶段末的M_E与γ无关.

由图7（b）可知，当0.5 < α < 1.0时 M_E具有上述相同的性质. 不同的是，顶推过程有3个阶段，除了在第1阶段末与第2阶段初有一个突变，在第2阶段末与第3阶段初也有一个突变. 不同范围的α会影响顶推过程中桥梁结构的体系转换.

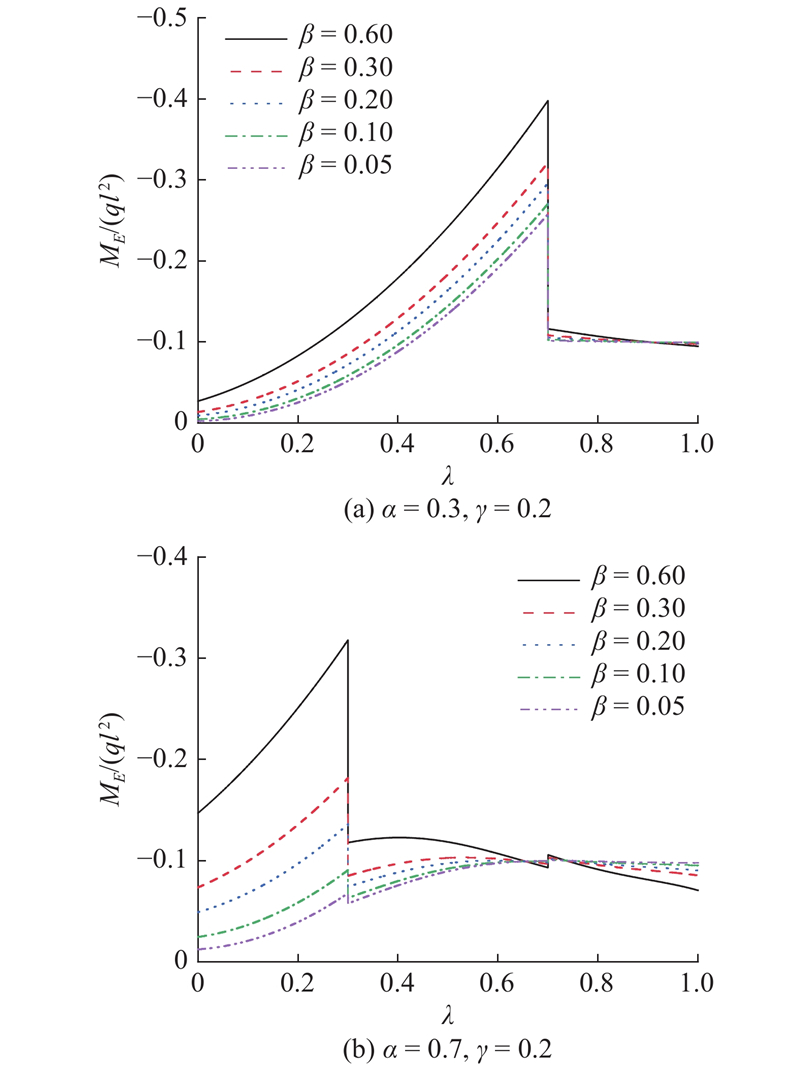
假设α和γ为常数，研究不同β条件下在顶推过程中M_E的变化. 假设α = 0.3、γ = 0.2和α = 0.7、γ = 0.2 2种情况，不同β的取值分别为0.6、0.3、0.2、0.1、0.05，如图8所示.

由图8可得，β会直接影响M_E，且随着β的增大，第1阶段末的M_E相应增大，顶推结束阶段时的M_E相应减小. 第1阶段末M_E增大的幅度明显大于顶推结束阶段时M_E减小的幅度.

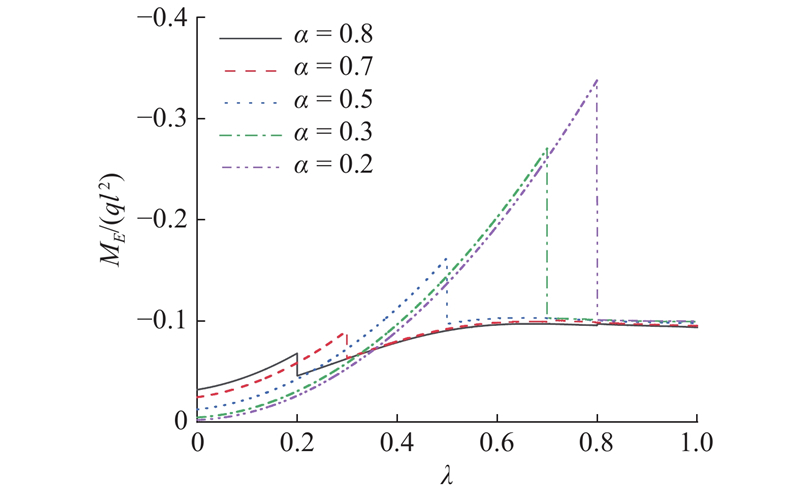
假设β和γ为常数，研究在顶推过程中不同α条件下M_E的变化. 假设β = 0.1，γ = 0.2，不同α的取值分别为0.8、0.7、0.5、0.3、0.2，如图9所示.

由图9可知，α主要影响顶推过程中第1阶段末的负弯矩，随着α的增大，第1阶段末的负弯矩减小. α会影响顶推结束阶段时的弯矩，不过影响程度非常小.

综合上述对E支点最大负弯矩的分析可知，第1阶段的最大负弯矩在第1阶段末，主要由α和β决定，与γ无关，且α和β的影响程度较高，α越小、β越大，第1阶段末的最大负弯矩越大. 第2阶段初到顶推阶段结束前的最大负弯矩在中间阶段，主要由γ决定，γ越小，第2阶段初到顶推阶段结束前的最大负弯矩越大. 顶推阶段结束时的负弯矩主要由α和β决定，与γ无关，但α和β的影响程度较低.

前导梁N上F支点后，随着顶推的开展（1 − α ≤ λ ≤ 1.0），EF跨内最大正弯矩的大小及位置都是随时变化的，无法直接求得. 由于EF跨内荷载是主梁及导梁的自重（竖直向下），顶推任意时刻从E点到F点的剪力都是单调递减的. 根据弯矩与剪力的微分关系可知，顶推任意时刻EF跨内剪力为零的点均为该时刻EF跨内的最大正弯矩点^[21].

假设β和γ为常数，研究不同α条件下在顶推过程中EF跨内最大正弯矩M_EFmax的变化. 假设β = 0.1，γ = 0.4，不同α的取值分别为0.8、0.6、0.5、0.4、0.2，如图10所示.

从图10可知，不同α对M_EFmax有一定的影响. α越小，顶推过程中M_EFmax的最大值越大，且该最大值越靠近顶推结束阶段. 在顶推结束阶段，α越大，M_EFmax越小. 这是因为在顶推结束阶段，导梁越长，F支点的负弯矩越大，能够越大程度地减轻EF跨内的最大正弯矩. 相较于M_E，α对M_EFmax的影响程度较小.

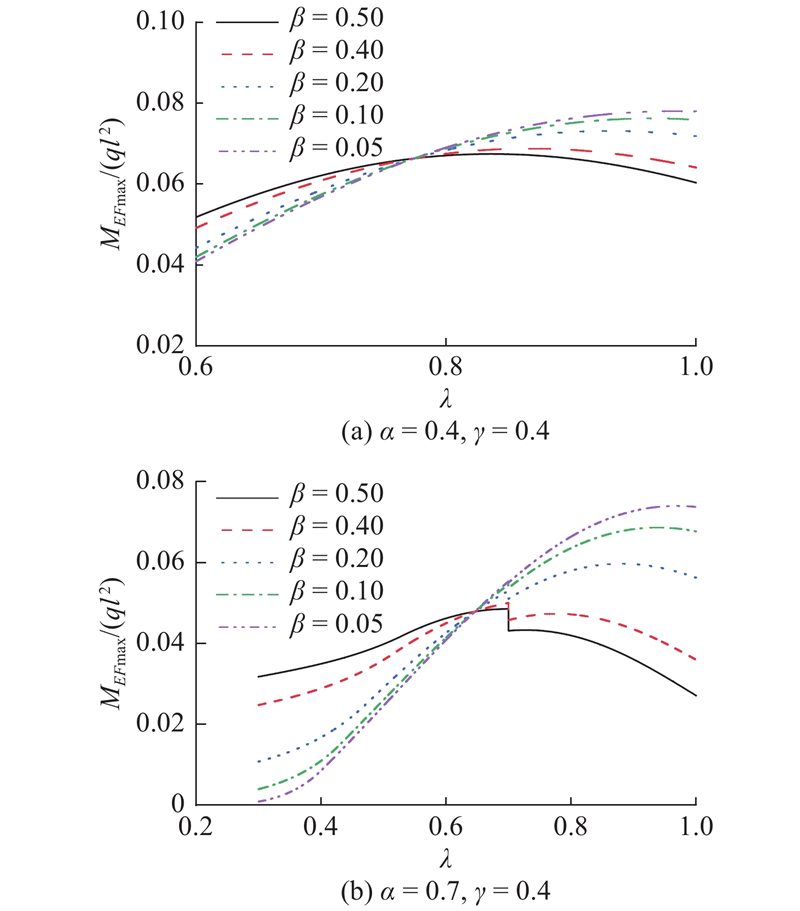
当α和γ为常数时，研究不同β对顶推过程中M_EFmax的影响. 假设α = 0.4、γ = 0.4和α = 0.7、γ = 0.4 2种情况，不同β的取值分别为0.5、0.4、0.2、0.1、0.05，如图11所示.

从图11可知，顶推过程中M_EFmax的最大值变化规律与图10相似. β越小，则顶推过程中M_EFmax的最大值越大，该最大值越靠近顶推结束阶段. 在顶推结束阶段，β越大，M_EFmax越小. 这是因为导梁自重荷载集度越大，F支点的负弯矩越大，能够越大程度地减轻EF跨内的最大正弯矩. 从图11（b）可知，M_EFmax在λ = α时会发生突变，突变大小会随着β的减小而减小. 当β < 0.2时，相较于 M_EFmax的最大值可以忽略突变处的值.

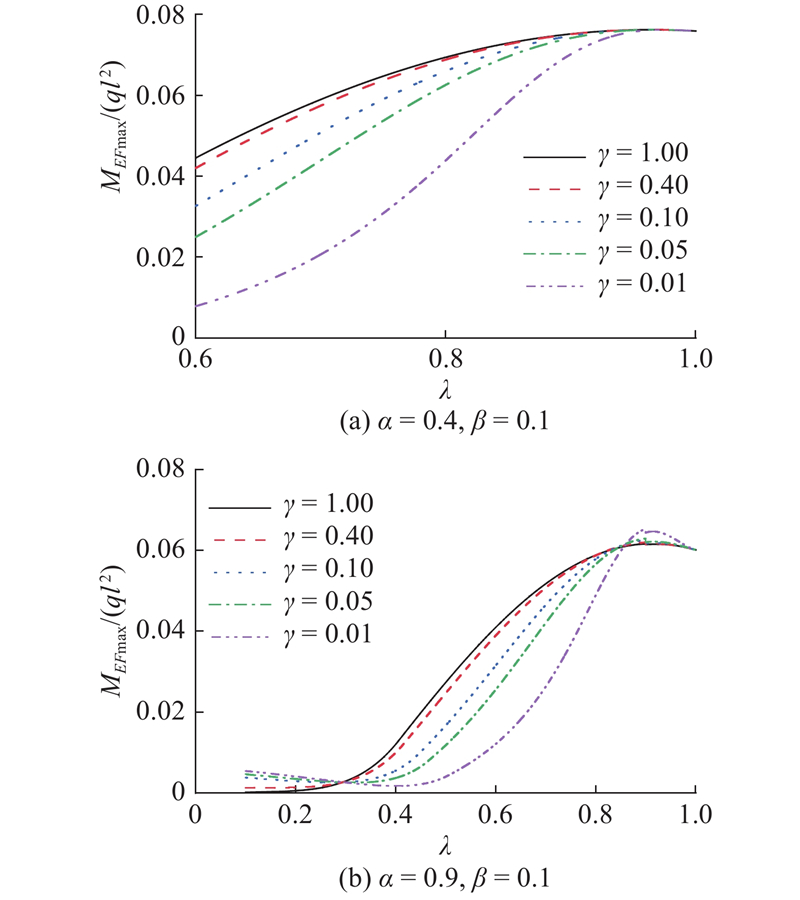
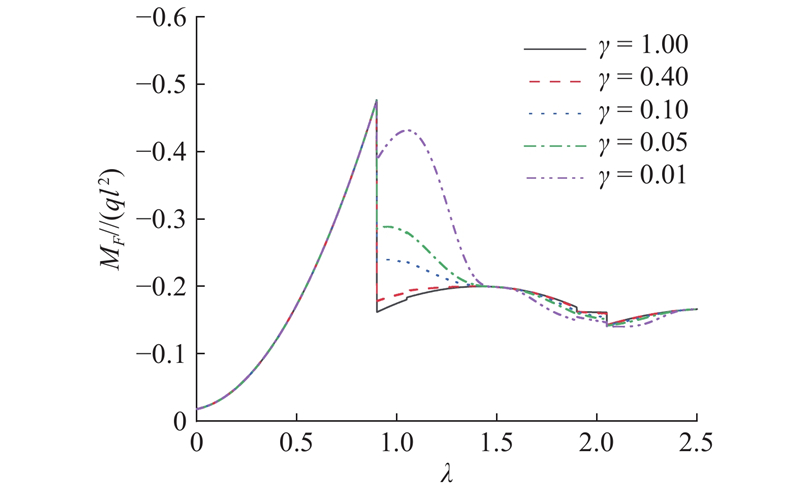
当α和β为常数时，研究不同γ在顶推过程中M_EFmax的变化. 假设α=0.4、β=0.1和α=0.9、β = 0.1 2种情况，不同β的取值分别为1、0.4、0.1、0.05、0.01，如图12所示.

从图12可知，不同γ对顶推过程中的M_EFmax有较大影响，但对顶推结束阶段的M_EFmax几乎没有影响. 顶推过程中M_EFmax的最大值总是发生在顶推结束阶段附近.

综合对EF跨内最大正弯矩的分析发现，M_EFmax的最大值总是发生在顶推结束阶段附近，且β越小，M_EFmax的最大值越接近顶推结束阶段，α与γ略有影响，可以忽略不计. 顶推结束阶段的M_EFmax主要由α与β决定，与γ关系不大.

基于导梁参数（α、β、γ）对E支点最大负弯矩和EF跨内最大正弯矩的内力分析研究可知，相对于EF跨内最大正弯矩，导梁参数对E支点最大负弯矩的影响更加显著. EF跨内最大正弯矩主要由主梁本身的材料、尺寸等性质决定，导梁参数对EF跨内最大正弯矩的影响相对较小^[16]. 在导梁优化中，将E支点最大负弯矩作为主要控制内力，EF跨内最大正弯矩为次要控制内力，开展优化分析.

基于导梁参数对E支点最大负弯矩的分析发现，当α较小时，第1阶段末的负弯矩大于顶推结束阶段的负弯矩，这说明导梁长度设置得过短，没有有效地减小最大悬臂状态时的负弯矩，如图7（a）所示. 当α较大时，第1阶段末的负弯矩小于顶推结束阶段的负弯矩. 这说明导梁长度设置得过长，此时的最大负弯矩是在第2阶段初到顶推结束阶段之间，不经济，如图7（b）所示. 文献[16]表明，最优的导梁参数是通过平衡最前墩（即E支点）上顶板的负弯矩得到的，即最优的α和β是使得顶推第1阶段末的负弯矩等于顶推结束阶段的负弯矩，最优的γ是使得在第2阶段初到顶推结束阶段之间的最大负弯矩等于第1阶段末及顶推结束阶段的负弯矩.

在本文的顶推计算模型中，当0 < α ≤ 0.5时和当0.5 < α < 1.0时的顶推阶段不同，分别进行计算. 当0 < α ≤ 0.5时， $M_{E{\rm{1}}}^{\rm{I}}{\rm{(}}\lambda = 1 - \alpha {\rm{)}} = M_{E{\rm{2}}}^{\rm{I}}{\rm{(}}\lambda = 1{\rm{)}}$. 当0.5 < α < 1.0时， $M_{E{\rm{1}}}^{{\rm{II}}}{\rm{(}}\lambda = 1 - \alpha {\rm{)}} = M_{E{\rm{3}}}^{{\rm{II}}}{\rm{(}}\lambda = 1{\rm{)}}$. $M_{E{\rm{1}}}^{\rm{I}} = M_{E{\rm{1}}}^{{\rm{II}}}$， $M_{E{\rm{2}}}^{\rm{I}} = M_{E{\rm{3}}}^{{\rm{II}}}$，故2种情况的结果相同，方程隐式解如下：

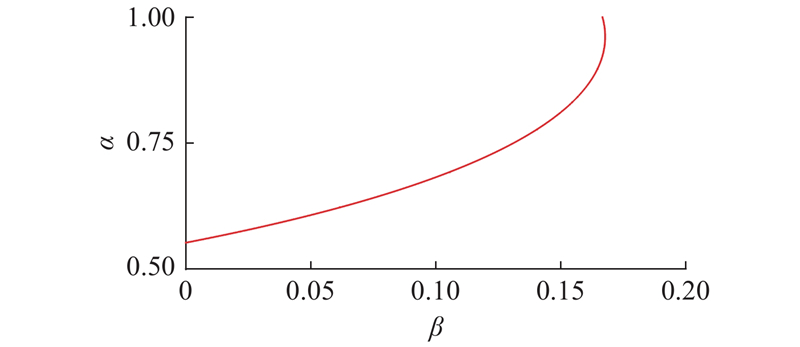
根据式（11），可得在该导梁参数优化中α与β的关系，如图13所示.

从图13可知，要满足最优导梁参数，β的取值为0~0.2，相应的α为0.5~1.0，所以最优导梁参数α > 0.5. 以0.5 < α < 1.0时的顶推阶段进行数值优化.

在获得最优导梁参数α和β的关系后，通过确定β来计算相应的α，获得一组最优的导梁参数α和β. 通过这组最优的α和β来确定γ，所以β的选取显得尤为重要. 传统的β的选取是依据工程经验选定的，但是对于具体的桥梁工程，这种选取方法是不严谨的. 因为不同桥梁的材料、截面形式有所差异，这些因素对跨内最大正弯矩的影响较大，除了考虑E支点最大负弯矩，还必须考虑EF跨内最大正弯矩的影响，通过实桥数值算例进行研究分析.

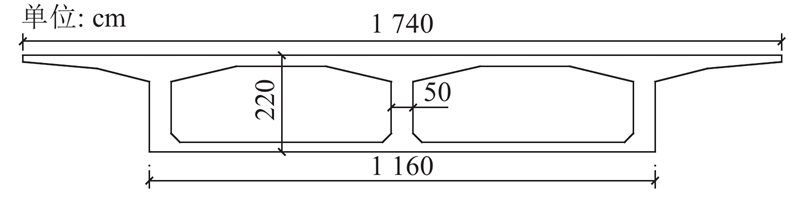
该数值算例的截面形式如图14所示. 在实际的顶推过程中，桥梁截面总是承受反复循环的正、负弯矩，不考虑顶推过程中预应力的影响，混凝土截面的最大拉应力出现在2个地方：一个是在最大负弯矩下的混凝土顶板上缘，另一个是在最大正弯矩下的混凝土底板下缘. 为了防止混凝土截面最大拉应力超过拉应力设计值，最大负弯矩下混凝土顶板上缘的最大拉应力应满足

最大正弯矩下混凝土底板下缘的最大拉应力应满足

式中： $M_{{\rm{max}}}^{\rm{N}}$、 $M_{{\rm{max}}}^{\rm{P}}$分别为截面最大负弯矩和最大正弯矩， ${W_{\rm{t}}}$、 ${W_{\rm{b}}}$分别为截面顶板上缘和底板下缘的弹性截面模量， ${\sigma _{\rm{t}}}$为拉应力设计值.

由式（12）、（13）可知，即使 $M_{{\rm{max}}}^{\rm{N}}$大于 $M_{{\rm{max}}}^{\rm{P}}$，由于桥梁截面形式的差异将直接影响 ${W_{\rm{t}}}$和 ${W_{\rm{b}}}$，进而影响截面的最大拉应力，使得截面的最大拉应力有可能出现在最大正弯矩下混凝土底板下缘，必须同时考虑在最大负弯矩和最大正弯矩下截面的应力状态.

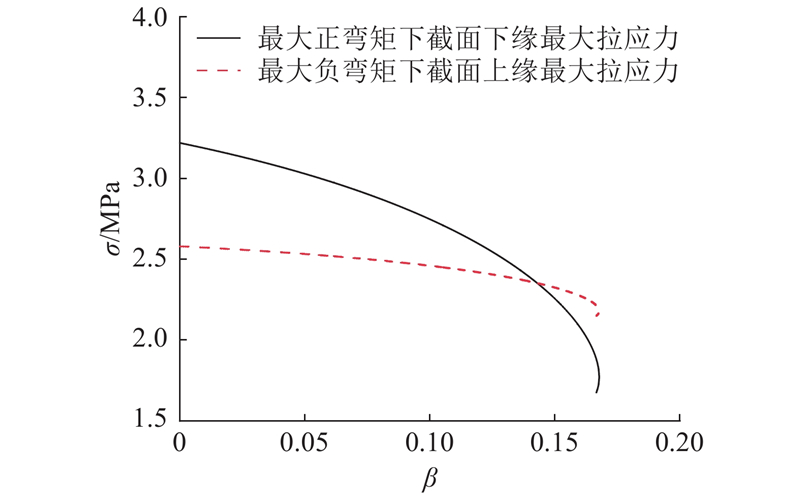
在式（11）的前提下，以 $M_{E{\rm{1}}}^{{\rm{II}}}{\rm{(}}\lambda = 1 - \alpha {\rm{)}}$作为最大负弯矩 $M_{{\rm{max}}}^{\rm{N}}$. 从图12可知，β越小， $M_{{\rm{max}}}^{\rm{P}}$越靠近顶推结束阶段. 由于β的取值为0~0.2，相对较小，为了方便计算，可以近似认为 $M_{{\rm{max}}}^{\rm{P}}$在顶推结束阶段取得. 在该数值算例中， ${W_{\rm{t}}}$、 ${W_{\rm{b}}}$分别为8.72 m³和5.59 m³，q和l分别为250 kN/m和30 m. 通过式（11）~（13），可得在最大负弯矩和最大正弯矩下截面最大拉应力与β的关系，如图15所示.

从图15可知，无论是在最大负弯矩下的截面上缘最大拉应力还是在最大正弯矩下的截面下缘最大拉应力，都随着β的增大而减小. β对最大正弯矩下的截面下缘最大拉应力的影响更大，拉应力减小得更快. 理论上，β的取值越大越好，能够使得截面上、下缘的最大拉应力都有不同程度的减小. 从图13可知，β越大，α越大，导梁变得又重又长，使得经济成本大大增加，此时可以根据导梁优化时侧重的方向去平衡安全与经济之间的关系. 建议β的取值为最大负弯矩下截面拉应力与最大正弯矩下截面拉应力的交点处的β，此处β所对应的最大负弯矩与最大正弯矩下的截面最大拉应力相等，充分利用截面. β为0.14，故相应的α为0.78.

得到最优的导梁参数α和β后，为了使得在第2阶段初到顶推结束阶段之间的最大负弯矩等于第1阶段末及顶推结束阶段时的负弯矩，将α=0.78、β=0.14代入到 $M_{E{\rm{1}}}^{{\rm{II}}}{\rm{(}}\lambda = 1 - \alpha {\rm{)}}$、 $M_{E{\rm{2}}}^{{\rm{II}}}{\rm{(}}1 - $ $ \alpha \leqslant \lambda \leqslant \alpha {\rm{)}}$及 $M_{E{\rm{3}}}^{{\rm{II}}}{\rm{(}}\alpha < \lambda \leqslant 1{\rm{)}}$中，经过计算可知，最优的γ为0.39，即导梁数值优化完成.

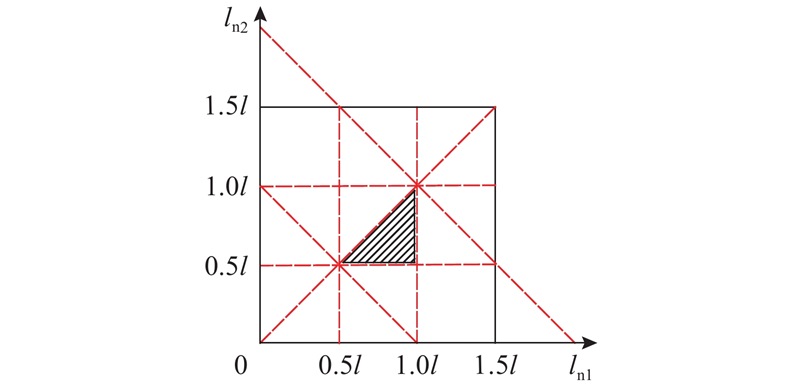
为了拓展研究理论，开展基于导梁参数的不等跨连续梁桥的内力分析，其中主跨与边跨的比值假设为1.5∶1. 在不等跨连续梁桥中，前导梁和后导梁的最优长度不一定相同，故假设前导梁和后导梁的长度分别为l_n1和l_n2，使用无量纲的参数α₁表示前导梁长度与边跨长度的比值，即α₁=l_n1/l. 使用无量纲的参数α₂表示后导梁长度与边跨长度的比值，即α₂=l_n2/l，假设前、后导梁的自重荷载集度和抗弯刚度相同. 不同的l_n1和l_n2对顶推阶段有影响，选取部分工况进行分析，即0 < l_n2 < l_n1，0.5l < l_n1 < l，0.5l < l_n2 < l，l < l_n1+l_n2 < 2 l，如图16所示.

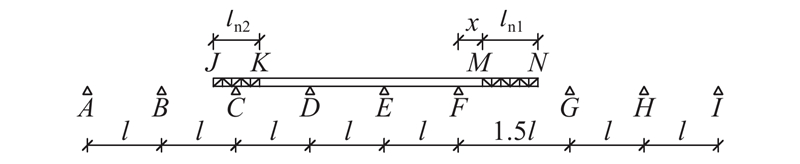
不等跨连续梁桥顶推计算简图如图17所示. 该工况起点定义为主梁前端M处于F支点时，终点定义为主梁前端M到达H支点时，可以细分为6种不同的顶推阶段，限于篇幅，省略推导过程.

为了分析α₁、α₂、β和γ这4个参数在顶推过程中对F支点处混凝土主梁负弯矩M_F的影响，假设α₁、α₂和β为常数，研究不同γ条件下M_F的变化. 假设α₁ = 0.6、α₂ = 0.55和β = 0.1，不同γ的取值分别为1、0.4、0.1、0.05、0.01，如图18所示.

从图18可知，不等跨连续梁桥顶推与等跨连续梁桥顶推具有类似的受力特性，但是不等跨连续梁桥具有更多的顶推阶段，更加复杂. 第1阶段内的M_F与γ无关，第2阶段内的M_E与γ有关，且γ越小，第2阶段内的最大负弯矩越大. 随着顶推的进行，从第3阶段开始，γ对M_F的影响变得非常小，可以忽略不计.

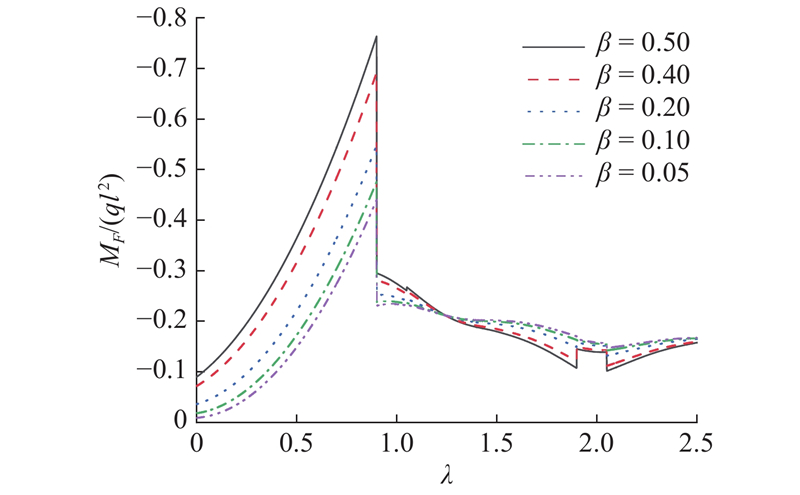
假设α₁、α₂和γ为常数，研究不同β条件下M_F的变化. 假设α₁ = 0.6，α₂ = 0.55，γ = 0.1，不同β的取值分别为0.5、0.4、0.2、0.1、0.05，如图19所示.

从图19可知，β主要影响顶推过程中第1阶段的M_F，且随着β的增大，第1阶段的M_F相应增大，对后面顶推阶段M_F的影响较小.

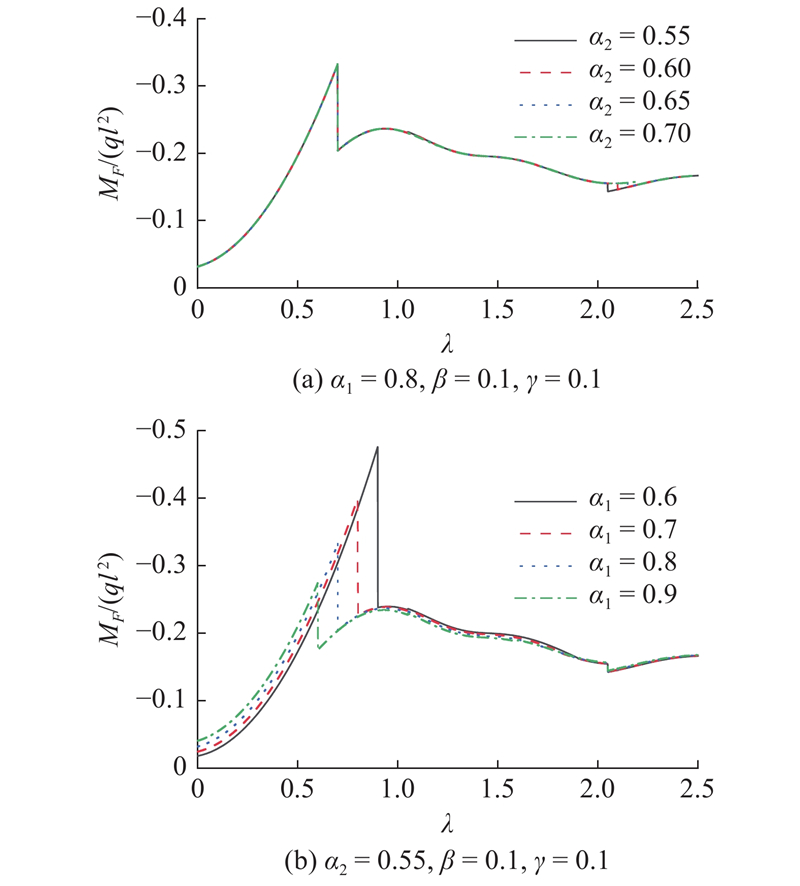
假设β和γ为常数，研究不同的α₁和α₂条件下M_F的变化. 假设β = 0.1，γ = 0.1，设置2种情况. 当α₁ = 0.8时，α₂的取值分别为0.55、0.6、0.5和0.7；当α₂ = 0.55时，α₁的取值分别为0.6、0.7、0.8和0.9，如图20所示.

从图20可知，后导梁的长度对M_F的影响较小，前导梁的长度对M_F的影响较大，且主要影响顶推第1阶段的M_F.

（1）对于等跨连续梁桥，建议前、后导梁的长度及其他参数设置相同；对于不等跨连续梁桥，前、后导梁的长度不一定相同.

（2）对于等跨连续梁桥，α对顶推阶段有影响，不同范围的α会在顶推过程中影响桥梁的结构体系转换. 对于不等跨连续梁桥，情况更加复杂，不同前、后导梁的长度相互影响桥梁顶推阶段.

（3）在实桥的数值算例中，最优导梁参数α、β、γ分别为0.78、0.14及0.39.

（4）对于不等跨连续桥，后导梁的长度对主梁支点的最大负弯矩影响较小，前导梁的长度对主梁支点的最大负弯矩影响较大，且主要影响顶推第1阶段.