(11) $\left. \begin{array}{l} {P_{\rm{a}}} = \{ w \in W|{\rm{AD}}_{\min }^3(w) < s\}; \\ {P_{\rm{b}}} = \{ w/({2^k} \pm 1)|w \in W,k \in {N_0}\} \cap N\backslash \{ w\}; \\ {P_{\rm{c}}} = \mathop \cup \limits_{\mathop {w \in W}\limits_{p' \in P} } \{ p = A_q^2(w,p')|q\;{\rm{valid}},{\rm{AD}}_{\min }^3(p) < s\} ;\\ {P_{\rm{d}}} = \{ w/({2^k} \pm {2^l} \pm 1)|w \in W,k,l \in {N_0}\} \cap N\backslash {P_{\rm{a}}};\\ {P_{\rm{e}}} = \mathop \cup \limits_{\mathop {w \in W}\limits_{p' \in P} } \{ p = A_q^2(w,p')/({2^k} \pm 1)|q\;{\rm{valid}},\\ \qquad {\rm{AD}}_{\min }^3(p) <s,k \in {N_0}\} \cap N\backslash {P_{\rm{a}}};\\ {P_{\rm{f}}} = \mathop \cup \limits_{\mathop {w \in W}\limits_{p',p'' \in P} } \{ p = A_q^3(w,p',p'')|q\;{\rm{valid}},\\ \qquad {\rm{AD}}_{\min }^3(p) < s,k \in {N_0}\} \backslash {P_{\rm{a}}}. \end{array} \right\}$
[1]
GROGINSKY H L, WORKS G A A pipeline fast Fourier transform
[J]. IEEE Transactions on Computers , 1970 , 19 (11 ): 1015 - 1019
[本文引用: 1]
[2]
HE S, TORKELSON M. A new approach to pipeline FFT processor[C]// International Parallel Processing Symposium . Hawaii: IEEE, 1996: 766-770.
[本文引用: 1]
[3]
GARRIDO M, QURESHI F, TAKALA J, et al. Hardware architectures for the fast Fourier transform[M]//SHUVRA S, LEUPERS R, TAKALA J, et al. Handbook of signal processing systems . Switzerland: Springer, 2018: 613-648.
[本文引用: 1]
[4]
QURESHI F. Optimization of rotations in FFTs[D]. Linköping: Linköping University, 2012.
[本文引用: 1]
[5]
GARRIDO M, HUANG S, CHEN S, et al The serial commutator FFT
[J]. IEEE Transactions on Circuits and Systems II: Express Briefs , 2016 , 63 (10 ): 974 - 978
DOI:10.1109/TCSII.2016.2538119
[本文引用: 1]
[6]
INGEMARSSON C, KALLSTROM P, GUSTAFSSON O. Using DSP block pre-adders in pipeline SDF FFT implementations in contemporary FPGAs[C]// 22nd International Conference on Field Programmable Logic and Applications . Oslo: IEEE, 2012: 71-74.
[本文引用: 2]
[7]
INGEMARSSON C, GUSTAFSSON O SFF: the single-stream FPGA-optimized feedforward FFT hardware architecture
[J]. Journal of Signal Processing Systems , 2018 , 90 (11 ): 1583 - 1592
DOI:10.1007/s11265-018-1370-y
[本文引用: 2]
[8]
MA Z G, YIN X B, YU F A novel memory-based FFT architecture for real-valued signals based on a radix-2 decimation-in-frequency algorithm
[J]. IEEE Transactions on Circuits and Systems II: Express Briefs , 2015 , 62 (9 ): 876 - 880
DOI:10.1109/TCSII.2015.2435522
[本文引用: 1]
[9]
TANG A M, YU L, HAN F J, et al. CORDIC-based FFT real-time processing design and FPGA implementation[C]// 12th International Colloquium on Signal Processing and its Applications . Malacca: IEEE, 2016: 233-236.
[本文引用: 1]
[10]
SHI J Y, TIAN Y H, WANG M X, et al. A novel design of 1024-point pipelined FFT processor based on Cordic algorithm[C]// 2nd International Conference on Intelligent System Design and Engineering Application . Sanya: IEEE, 2012: 80-83.
[本文引用: 1]
[11]
MANKAR A, PRASAD N, DAS A D, et al Multiplier: less VLSI architectures for radix‐22 folded pipelined complex FFT core
[J]. International Journal of Circuit Theory and Applications , 2015 , 43 (11 ): 1743 - 1758
DOI:10.1002/cta.2038
[本文引用: 1]
[12]
ZHANG J F, LIU H Z, CHEN T, et al Enhanced hardware efficient FFT processor based on adaptive recoding CORDIC
[J]. Electronics and Electrical Engineering , 2013 , 19 (4 ): 97 - 103
[本文引用: 1]
[13]
MAHDAVI H, TIMARCHI S Area-time-power efficient FFT architectures based on binary-signed-digit CORDIC
[J]. IEEE Transactions on Circuits and Systems I: Regular Papers , 2019 , 66 (10 ): 3874 - 3881
DOI:10.1109/TCSI.2019.2922988
[本文引用: 1]
[14]
MEYER-BASE U, MEYER-BASE A, HILBERG W. Coordinate rotation digital computer (CORDIC) synthesis for FPGA[C]// International Workshop on Field-programmable Logic . Berlin: Springer, 1994: 397–408.
[本文引用: 1]
[15]
VORONENKO Y, PUSCHEL M Multiplierless multiple constant multiplication
[J]. ACM Transactions on Algorithms , 2007 , 3 (2 ): 11 - 49
DOI:10.1145/1240233.1240234
[本文引用: 1]
[16]
KUMM M, HARDIECK M, WILLKOMM J, et al. Multiple constant multiplication with ternary adders[C]// 23rd International Conference on Field Programmable Logic and Applications . Porto: IEEE, 2013: 1-8.
[本文引用: 1]
[17]
KUMM M. Multiple constant multiplication optimizations for programmable gate arrays [M]. Wiesbaden: Springer, 2016.
[本文引用: 1]
[18]
EHLIAR A. Optimizing Xilinx designs through primitive instantiation[C]// 7th FPGA World Conference . Copenhagen: ACM, 2010: 20-27.
[本文引用: 1]
[19]
MA Y K, LIANG H H. Implementation of a pipeline large-FFT processor based on the FPGA[C]// International Conference in Communications, Signal Processing and Systems. Harbin: Springer, 2017: 638-644.
[本文引用: 1]
[20]
NGUYEN H N, KHAN S A, KIM C H, et al A high-performance, resource-efficient, reconfigurable parallel-pipelined FFT processor for FPGA platforms
[J]. Microprocessors and Microsystems , 2018 , 60 : 96 - 106
DOI:10.1016/j.micpro.2018.04.003
[本文引用: 5]
[21]
VALENCIA D, ALIMOHAMMAD A Compact and high-throughput parameterizable architectures for memory-based FFT algorithms
[J]. IET Circuits, Devices and Systems , 2019 , 13 (5 ): 696 - 703
DOI:10.1049/iet-cds.2018.5556
[本文引用: 3]
[22]
WANG Z, LIU X, HE B, et al A combined SDC-SDF architecture for normal I/O pipelined radix-2 FFT
[J]. IEEE Transactions on Very Large Scale Integration Systems , 2015 , 23 (5 ): 973 - 977
DOI:10.1109/TVLSI.2014.2319335
[本文引用: 2]
[23]
NGUYEN H N, KHAN S A, KIM C H, et al A pipelined FFT processor using an optimal hybrid rotation scheme for complex multiplication: design, FPGA implementation and analysis
[J]. Electronics , 2018 , 7 (8 ): 137
DOI:10.3390/electronics7080137
[本文引用: 4]
[24]
VINAY K M, DAVID S A, SOBHA P M. Area and frequency optimized 1024 point radix-2 FFT processor on FPGA[C]// 2015 International Conference on VLSI Systems, Architecture, Technology and Applications . Bengaluru: IEEE, 2015: 1-6.
[本文引用: 1]
A pipeline fast Fourier transform
1
1970
... 基2单路延迟反馈架构(single-path delay feedback,SDF)是Groginsky等[1 ] 提出的单路流水线FFT架构. He等[2 ] 提出基22 算法,结合基2与基4算法的优势,以资源占用少、控制简单、运算量小等优势,得到了广泛的应用. 近年来,Garrido等[3 -4 ] 对FFT的硬件实现进行了大量研究. 在蝶形单元架构的改进方面,Garrido等[5 ] 提出串行架构,将蝶形单元数量减少一半,利用率提高到了100%,但计算速度降低了一半. Ingemarsson等[6 ] 将传统SDF架构中的加法器和选择器换位,LUT资源占用减少了近1/3. Ingemarsson等[7 ] 指出,若将小点数FFT架构中的一个加法器置换为短移位寄存器,则LUT资源占用减少了近43%. 目前对蝶形单元的改进已趋于完善,可以从占用资源很多的旋转因子乘法器模块继续进行改进,进一步改善FFT硬件架构的性能,研究方向主要有基于内存的架构和采用坐标旋转数字计算方法(coordinate rotation digital computer,CORDIC)的架构. Ma等[8 ] 提出基于内存的FFT架构,将旋转因子存储于ROM中,用DSP完成复数乘法器运算. 这种基于内存的架构,对于大点数的FFT,需要大量的内存单元和DSP资源,设计更加复杂,硬件成本更高,因此采用CORDIC的架构逐渐得到更多的研究. Tang等[9 ] 将旋转角度存储于ROM中,利用CORDIC计算旋转因子. Shi等[10 ] 提前计算出每种旋转角度在各级旋转时的方向系数并存储在ROM中,计算时只需寻址读出相应的方向系数. Mankar等[11 ] 提出基于CORDIC-新分布式算法(new distributed arithmetic,NEDA)的折叠FFT架构. Zhang等[12 ] 提出自适应编码CORDIC(adaptive recoding CORDIC, ARC)FFT架构. Mahdavi等[13 ] 提出基于二进制符号数编码(binary-signed-digit, BSD)CORDIC的FFT架构. 目前的研究主要是用CORDIC实现全部的旋转因子并着重于硬件实现方面的改进,鲜少将其他常数乘法器应用于FFT架构中. ...
1
... 基2单路延迟反馈架构(single-path delay feedback,SDF)是Groginsky等[1 ] 提出的单路流水线FFT架构. He等[2 ] 提出基22 算法,结合基2与基4算法的优势,以资源占用少、控制简单、运算量小等优势,得到了广泛的应用. 近年来,Garrido等[3 -4 ] 对FFT的硬件实现进行了大量研究. 在蝶形单元架构的改进方面,Garrido等[5 ] 提出串行架构,将蝶形单元数量减少一半,利用率提高到了100%,但计算速度降低了一半. Ingemarsson等[6 ] 将传统SDF架构中的加法器和选择器换位,LUT资源占用减少了近1/3. Ingemarsson等[7 ] 指出,若将小点数FFT架构中的一个加法器置换为短移位寄存器,则LUT资源占用减少了近43%. 目前对蝶形单元的改进已趋于完善,可以从占用资源很多的旋转因子乘法器模块继续进行改进,进一步改善FFT硬件架构的性能,研究方向主要有基于内存的架构和采用坐标旋转数字计算方法(coordinate rotation digital computer,CORDIC)的架构. Ma等[8 ] 提出基于内存的FFT架构,将旋转因子存储于ROM中,用DSP完成复数乘法器运算. 这种基于内存的架构,对于大点数的FFT,需要大量的内存单元和DSP资源,设计更加复杂,硬件成本更高,因此采用CORDIC的架构逐渐得到更多的研究. Tang等[9 ] 将旋转角度存储于ROM中,利用CORDIC计算旋转因子. Shi等[10 ] 提前计算出每种旋转角度在各级旋转时的方向系数并存储在ROM中,计算时只需寻址读出相应的方向系数. Mankar等[11 ] 提出基于CORDIC-新分布式算法(new distributed arithmetic,NEDA)的折叠FFT架构. Zhang等[12 ] 提出自适应编码CORDIC(adaptive recoding CORDIC, ARC)FFT架构. Mahdavi等[13 ] 提出基于二进制符号数编码(binary-signed-digit, BSD)CORDIC的FFT架构. 目前的研究主要是用CORDIC实现全部的旋转因子并着重于硬件实现方面的改进,鲜少将其他常数乘法器应用于FFT架构中. ...
1
... 基2单路延迟反馈架构(single-path delay feedback,SDF)是Groginsky等[1 ] 提出的单路流水线FFT架构. He等[2 ] 提出基22 算法,结合基2与基4算法的优势,以资源占用少、控制简单、运算量小等优势,得到了广泛的应用. 近年来,Garrido等[3 -4 ] 对FFT的硬件实现进行了大量研究. 在蝶形单元架构的改进方面,Garrido等[5 ] 提出串行架构,将蝶形单元数量减少一半,利用率提高到了100%,但计算速度降低了一半. Ingemarsson等[6 ] 将传统SDF架构中的加法器和选择器换位,LUT资源占用减少了近1/3. Ingemarsson等[7 ] 指出,若将小点数FFT架构中的一个加法器置换为短移位寄存器,则LUT资源占用减少了近43%. 目前对蝶形单元的改进已趋于完善,可以从占用资源很多的旋转因子乘法器模块继续进行改进,进一步改善FFT硬件架构的性能,研究方向主要有基于内存的架构和采用坐标旋转数字计算方法(coordinate rotation digital computer,CORDIC)的架构. Ma等[8 ] 提出基于内存的FFT架构,将旋转因子存储于ROM中,用DSP完成复数乘法器运算. 这种基于内存的架构,对于大点数的FFT,需要大量的内存单元和DSP资源,设计更加复杂,硬件成本更高,因此采用CORDIC的架构逐渐得到更多的研究. Tang等[9 ] 将旋转角度存储于ROM中,利用CORDIC计算旋转因子. Shi等[10 ] 提前计算出每种旋转角度在各级旋转时的方向系数并存储在ROM中,计算时只需寻址读出相应的方向系数. Mankar等[11 ] 提出基于CORDIC-新分布式算法(new distributed arithmetic,NEDA)的折叠FFT架构. Zhang等[12 ] 提出自适应编码CORDIC(adaptive recoding CORDIC, ARC)FFT架构. Mahdavi等[13 ] 提出基于二进制符号数编码(binary-signed-digit, BSD)CORDIC的FFT架构. 目前的研究主要是用CORDIC实现全部的旋转因子并着重于硬件实现方面的改进,鲜少将其他常数乘法器应用于FFT架构中. ...
1
... 基2单路延迟反馈架构(single-path delay feedback,SDF)是Groginsky等[1 ] 提出的单路流水线FFT架构. He等[2 ] 提出基22 算法,结合基2与基4算法的优势,以资源占用少、控制简单、运算量小等优势,得到了广泛的应用. 近年来,Garrido等[3 -4 ] 对FFT的硬件实现进行了大量研究. 在蝶形单元架构的改进方面,Garrido等[5 ] 提出串行架构,将蝶形单元数量减少一半,利用率提高到了100%,但计算速度降低了一半. Ingemarsson等[6 ] 将传统SDF架构中的加法器和选择器换位,LUT资源占用减少了近1/3. Ingemarsson等[7 ] 指出,若将小点数FFT架构中的一个加法器置换为短移位寄存器,则LUT资源占用减少了近43%. 目前对蝶形单元的改进已趋于完善,可以从占用资源很多的旋转因子乘法器模块继续进行改进,进一步改善FFT硬件架构的性能,研究方向主要有基于内存的架构和采用坐标旋转数字计算方法(coordinate rotation digital computer,CORDIC)的架构. Ma等[8 ] 提出基于内存的FFT架构,将旋转因子存储于ROM中,用DSP完成复数乘法器运算. 这种基于内存的架构,对于大点数的FFT,需要大量的内存单元和DSP资源,设计更加复杂,硬件成本更高,因此采用CORDIC的架构逐渐得到更多的研究. Tang等[9 ] 将旋转角度存储于ROM中,利用CORDIC计算旋转因子. Shi等[10 ] 提前计算出每种旋转角度在各级旋转时的方向系数并存储在ROM中,计算时只需寻址读出相应的方向系数. Mankar等[11 ] 提出基于CORDIC-新分布式算法(new distributed arithmetic,NEDA)的折叠FFT架构. Zhang等[12 ] 提出自适应编码CORDIC(adaptive recoding CORDIC, ARC)FFT架构. Mahdavi等[13 ] 提出基于二进制符号数编码(binary-signed-digit, BSD)CORDIC的FFT架构. 目前的研究主要是用CORDIC实现全部的旋转因子并着重于硬件实现方面的改进,鲜少将其他常数乘法器应用于FFT架构中. ...
The serial commutator FFT
1
2016
... 基2单路延迟反馈架构(single-path delay feedback,SDF)是Groginsky等[1 ] 提出的单路流水线FFT架构. He等[2 ] 提出基22 算法,结合基2与基4算法的优势,以资源占用少、控制简单、运算量小等优势,得到了广泛的应用. 近年来,Garrido等[3 -4 ] 对FFT的硬件实现进行了大量研究. 在蝶形单元架构的改进方面,Garrido等[5 ] 提出串行架构,将蝶形单元数量减少一半,利用率提高到了100%,但计算速度降低了一半. Ingemarsson等[6 ] 将传统SDF架构中的加法器和选择器换位,LUT资源占用减少了近1/3. Ingemarsson等[7 ] 指出,若将小点数FFT架构中的一个加法器置换为短移位寄存器,则LUT资源占用减少了近43%. 目前对蝶形单元的改进已趋于完善,可以从占用资源很多的旋转因子乘法器模块继续进行改进,进一步改善FFT硬件架构的性能,研究方向主要有基于内存的架构和采用坐标旋转数字计算方法(coordinate rotation digital computer,CORDIC)的架构. Ma等[8 ] 提出基于内存的FFT架构,将旋转因子存储于ROM中,用DSP完成复数乘法器运算. 这种基于内存的架构,对于大点数的FFT,需要大量的内存单元和DSP资源,设计更加复杂,硬件成本更高,因此采用CORDIC的架构逐渐得到更多的研究. Tang等[9 ] 将旋转角度存储于ROM中,利用CORDIC计算旋转因子. Shi等[10 ] 提前计算出每种旋转角度在各级旋转时的方向系数并存储在ROM中,计算时只需寻址读出相应的方向系数. Mankar等[11 ] 提出基于CORDIC-新分布式算法(new distributed arithmetic,NEDA)的折叠FFT架构. Zhang等[12 ] 提出自适应编码CORDIC(adaptive recoding CORDIC, ARC)FFT架构. Mahdavi等[13 ] 提出基于二进制符号数编码(binary-signed-digit, BSD)CORDIC的FFT架构. 目前的研究主要是用CORDIC实现全部的旋转因子并着重于硬件实现方面的改进,鲜少将其他常数乘法器应用于FFT架构中. ...
2
... 基2单路延迟反馈架构(single-path delay feedback,SDF)是Groginsky等[1 ] 提出的单路流水线FFT架构. He等[2 ] 提出基22 算法,结合基2与基4算法的优势,以资源占用少、控制简单、运算量小等优势,得到了广泛的应用. 近年来,Garrido等[3 -4 ] 对FFT的硬件实现进行了大量研究. 在蝶形单元架构的改进方面,Garrido等[5 ] 提出串行架构,将蝶形单元数量减少一半,利用率提高到了100%,但计算速度降低了一半. Ingemarsson等[6 ] 将传统SDF架构中的加法器和选择器换位,LUT资源占用减少了近1/3. Ingemarsson等[7 ] 指出,若将小点数FFT架构中的一个加法器置换为短移位寄存器,则LUT资源占用减少了近43%. 目前对蝶形单元的改进已趋于完善,可以从占用资源很多的旋转因子乘法器模块继续进行改进,进一步改善FFT硬件架构的性能,研究方向主要有基于内存的架构和采用坐标旋转数字计算方法(coordinate rotation digital computer,CORDIC)的架构. Ma等[8 ] 提出基于内存的FFT架构,将旋转因子存储于ROM中,用DSP完成复数乘法器运算. 这种基于内存的架构,对于大点数的FFT,需要大量的内存单元和DSP资源,设计更加复杂,硬件成本更高,因此采用CORDIC的架构逐渐得到更多的研究. Tang等[9 ] 将旋转角度存储于ROM中,利用CORDIC计算旋转因子. Shi等[10 ] 提前计算出每种旋转角度在各级旋转时的方向系数并存储在ROM中,计算时只需寻址读出相应的方向系数. Mankar等[11 ] 提出基于CORDIC-新分布式算法(new distributed arithmetic,NEDA)的折叠FFT架构. Zhang等[12 ] 提出自适应编码CORDIC(adaptive recoding CORDIC, ARC)FFT架构. Mahdavi等[13 ] 提出基于二进制符号数编码(binary-signed-digit, BSD)CORDIC的FFT架构. 目前的研究主要是用CORDIC实现全部的旋转因子并着重于硬件实现方面的改进,鲜少将其他常数乘法器应用于FFT架构中. ...
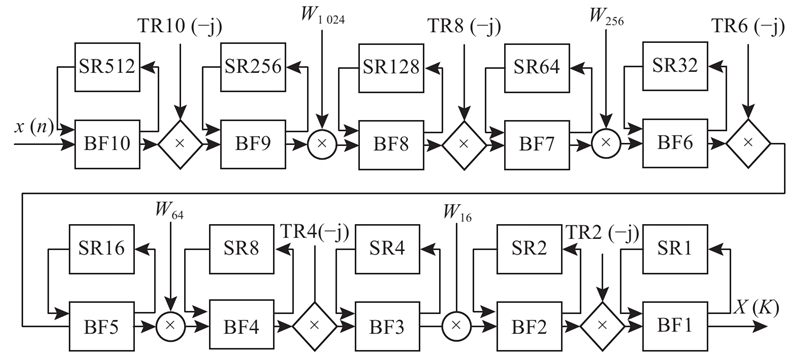
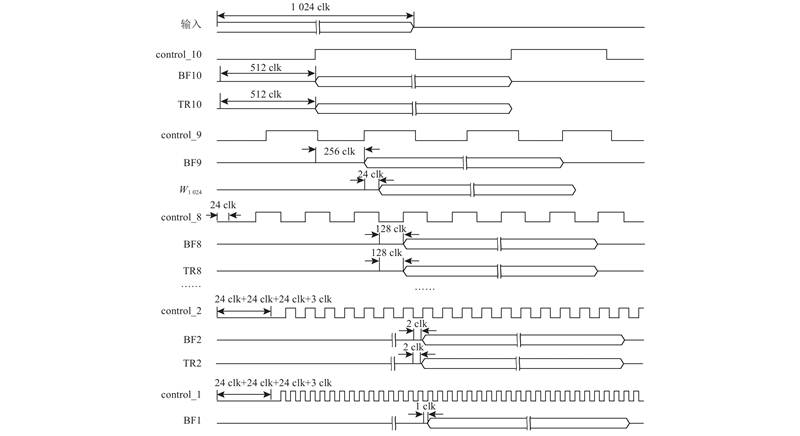
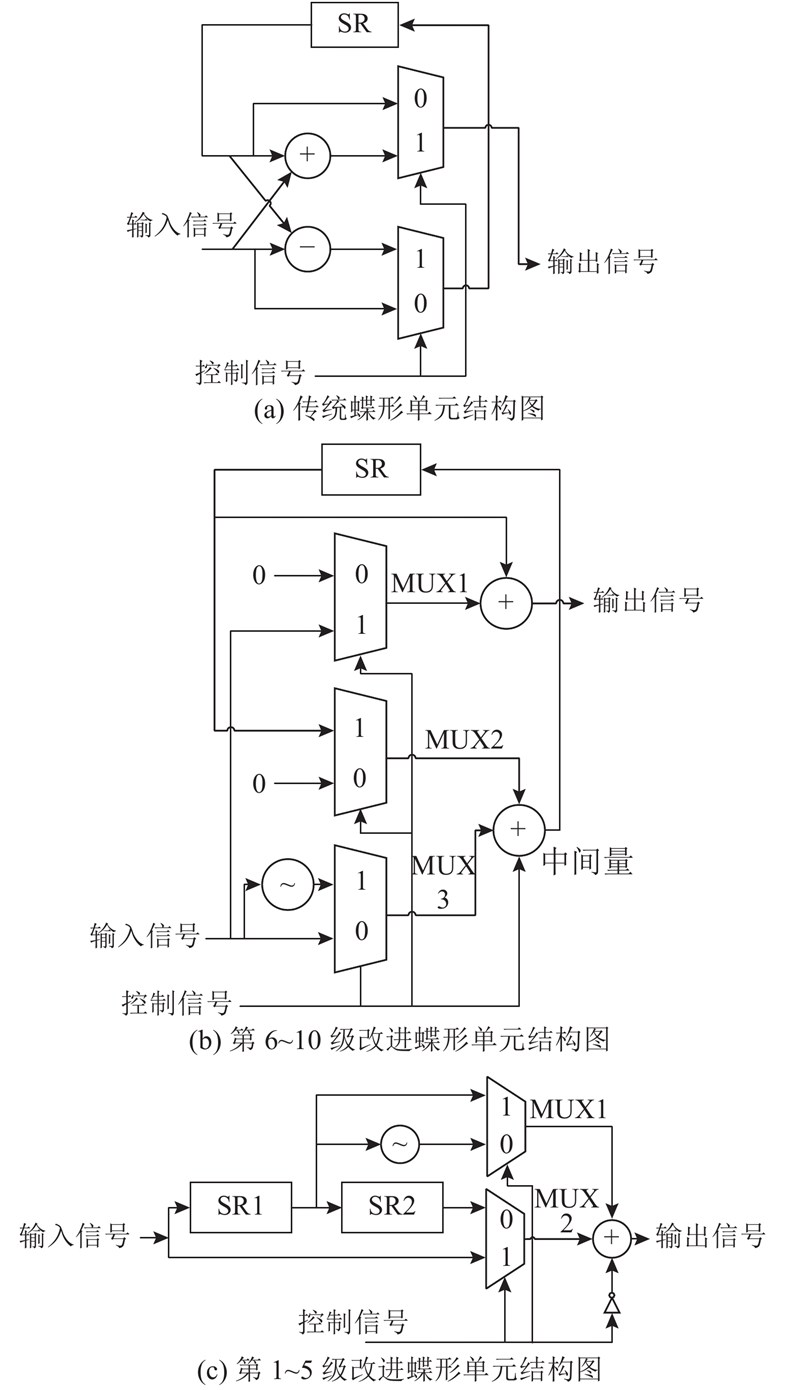
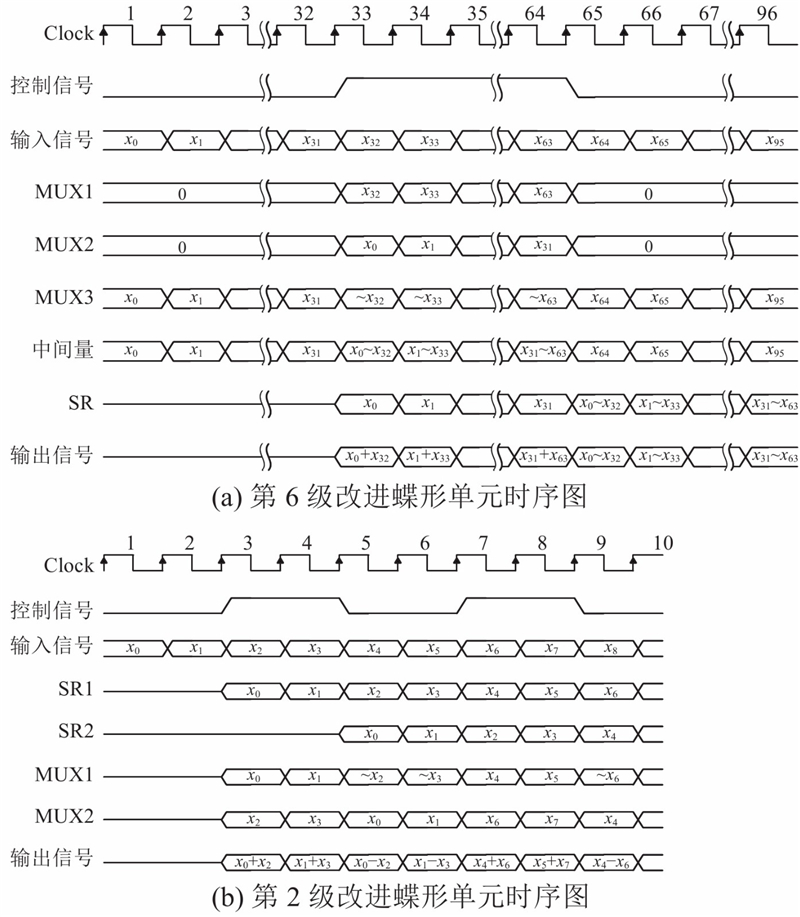
... 传统的SDF蝶形结构如图3(a) 所示. 当使用N 输入的LUT进行2个数的加法运算时,只会占用2个输入端口,其他几个端口会闲置. 若将加法器输入端一侧的其他逻辑输入合并到该LUT的闲置端口,则可以更加充分地利用LUT资源[18 ] . 将传统蝶形结构中的加法器和选择器交换位置,使得选择器位于加法器输入端一侧,就可以将选择器和加法器综合进同一个 LUT单元中,从而节省硬件资源. 改进后的碟形单元结构如图3(b) 所示[6 ] . 现代Xilinx FPGA具有6输入LUT,允许将2个长度相同且长度≤16的1 bit位宽短移位寄存器映射到同一个LUT6资源中,输出为1 bit位宽的加法器需要映射到一个完整的LUT6资源中. 这意味着短移位寄存器的LUT成本是加法器的一半. 对于所需移位寄存器长度≤16的情况,将传统蝶形结构中的一个加法器换成一个短移位寄存器,可以减少硬件资源占用. 改进后的碟形单元结构如图3(c) 所示[7 ] . 基于上述2种思想,第6~10级蝶形单元采用图3(b) 的改进结构,第1~5级蝶形单元采用图3(c) 的改进结构,可以减少硬件资源占用,且这2种改进结构具有相同的数据顺序和控制结构,因此组合起来控制时序很简单. 分别以第6级和第2级蝶形单元为例说明工作时序,如图4 所示. ...
SFF: the single-stream FPGA-optimized feedforward FFT hardware architecture
2
2018
... 基2单路延迟反馈架构(single-path delay feedback,SDF)是Groginsky等[1 ] 提出的单路流水线FFT架构. He等[2 ] 提出基22 算法,结合基2与基4算法的优势,以资源占用少、控制简单、运算量小等优势,得到了广泛的应用. 近年来,Garrido等[3 -4 ] 对FFT的硬件实现进行了大量研究. 在蝶形单元架构的改进方面,Garrido等[5 ] 提出串行架构,将蝶形单元数量减少一半,利用率提高到了100%,但计算速度降低了一半. Ingemarsson等[6 ] 将传统SDF架构中的加法器和选择器换位,LUT资源占用减少了近1/3. Ingemarsson等[7 ] 指出,若将小点数FFT架构中的一个加法器置换为短移位寄存器,则LUT资源占用减少了近43%. 目前对蝶形单元的改进已趋于完善,可以从占用资源很多的旋转因子乘法器模块继续进行改进,进一步改善FFT硬件架构的性能,研究方向主要有基于内存的架构和采用坐标旋转数字计算方法(coordinate rotation digital computer,CORDIC)的架构. Ma等[8 ] 提出基于内存的FFT架构,将旋转因子存储于ROM中,用DSP完成复数乘法器运算. 这种基于内存的架构,对于大点数的FFT,需要大量的内存单元和DSP资源,设计更加复杂,硬件成本更高,因此采用CORDIC的架构逐渐得到更多的研究. Tang等[9 ] 将旋转角度存储于ROM中,利用CORDIC计算旋转因子. Shi等[10 ] 提前计算出每种旋转角度在各级旋转时的方向系数并存储在ROM中,计算时只需寻址读出相应的方向系数. Mankar等[11 ] 提出基于CORDIC-新分布式算法(new distributed arithmetic,NEDA)的折叠FFT架构. Zhang等[12 ] 提出自适应编码CORDIC(adaptive recoding CORDIC, ARC)FFT架构. Mahdavi等[13 ] 提出基于二进制符号数编码(binary-signed-digit, BSD)CORDIC的FFT架构. 目前的研究主要是用CORDIC实现全部的旋转因子并着重于硬件实现方面的改进,鲜少将其他常数乘法器应用于FFT架构中. ...
... 传统的SDF蝶形结构如图3(a) 所示. 当使用N 输入的LUT进行2个数的加法运算时,只会占用2个输入端口,其他几个端口会闲置. 若将加法器输入端一侧的其他逻辑输入合并到该LUT的闲置端口,则可以更加充分地利用LUT资源[18 ] . 将传统蝶形结构中的加法器和选择器交换位置,使得选择器位于加法器输入端一侧,就可以将选择器和加法器综合进同一个 LUT单元中,从而节省硬件资源. 改进后的碟形单元结构如图3(b) 所示[6 ] . 现代Xilinx FPGA具有6输入LUT,允许将2个长度相同且长度≤16的1 bit位宽短移位寄存器映射到同一个LUT6资源中,输出为1 bit位宽的加法器需要映射到一个完整的LUT6资源中. 这意味着短移位寄存器的LUT成本是加法器的一半. 对于所需移位寄存器长度≤16的情况,将传统蝶形结构中的一个加法器换成一个短移位寄存器,可以减少硬件资源占用. 改进后的碟形单元结构如图3(c) 所示[7 ] . 基于上述2种思想,第6~10级蝶形单元采用图3(b) 的改进结构,第1~5级蝶形单元采用图3(c) 的改进结构,可以减少硬件资源占用,且这2种改进结构具有相同的数据顺序和控制结构,因此组合起来控制时序很简单. 分别以第6级和第2级蝶形单元为例说明工作时序,如图4 所示. ...
A novel memory-based FFT architecture for real-valued signals based on a radix-2 decimation-in-frequency algorithm
1
2015
... 基2单路延迟反馈架构(single-path delay feedback,SDF)是Groginsky等[1 ] 提出的单路流水线FFT架构. He等[2 ] 提出基22 算法,结合基2与基4算法的优势,以资源占用少、控制简单、运算量小等优势,得到了广泛的应用. 近年来,Garrido等[3 -4 ] 对FFT的硬件实现进行了大量研究. 在蝶形单元架构的改进方面,Garrido等[5 ] 提出串行架构,将蝶形单元数量减少一半,利用率提高到了100%,但计算速度降低了一半. Ingemarsson等[6 ] 将传统SDF架构中的加法器和选择器换位,LUT资源占用减少了近1/3. Ingemarsson等[7 ] 指出,若将小点数FFT架构中的一个加法器置换为短移位寄存器,则LUT资源占用减少了近43%. 目前对蝶形单元的改进已趋于完善,可以从占用资源很多的旋转因子乘法器模块继续进行改进,进一步改善FFT硬件架构的性能,研究方向主要有基于内存的架构和采用坐标旋转数字计算方法(coordinate rotation digital computer,CORDIC)的架构. Ma等[8 ] 提出基于内存的FFT架构,将旋转因子存储于ROM中,用DSP完成复数乘法器运算. 这种基于内存的架构,对于大点数的FFT,需要大量的内存单元和DSP资源,设计更加复杂,硬件成本更高,因此采用CORDIC的架构逐渐得到更多的研究. Tang等[9 ] 将旋转角度存储于ROM中,利用CORDIC计算旋转因子. Shi等[10 ] 提前计算出每种旋转角度在各级旋转时的方向系数并存储在ROM中,计算时只需寻址读出相应的方向系数. Mankar等[11 ] 提出基于CORDIC-新分布式算法(new distributed arithmetic,NEDA)的折叠FFT架构. Zhang等[12 ] 提出自适应编码CORDIC(adaptive recoding CORDIC, ARC)FFT架构. Mahdavi等[13 ] 提出基于二进制符号数编码(binary-signed-digit, BSD)CORDIC的FFT架构. 目前的研究主要是用CORDIC实现全部的旋转因子并着重于硬件实现方面的改进,鲜少将其他常数乘法器应用于FFT架构中. ...
1
... 基2单路延迟反馈架构(single-path delay feedback,SDF)是Groginsky等[1 ] 提出的单路流水线FFT架构. He等[2 ] 提出基22 算法,结合基2与基4算法的优势,以资源占用少、控制简单、运算量小等优势,得到了广泛的应用. 近年来,Garrido等[3 -4 ] 对FFT的硬件实现进行了大量研究. 在蝶形单元架构的改进方面,Garrido等[5 ] 提出串行架构,将蝶形单元数量减少一半,利用率提高到了100%,但计算速度降低了一半. Ingemarsson等[6 ] 将传统SDF架构中的加法器和选择器换位,LUT资源占用减少了近1/3. Ingemarsson等[7 ] 指出,若将小点数FFT架构中的一个加法器置换为短移位寄存器,则LUT资源占用减少了近43%. 目前对蝶形单元的改进已趋于完善,可以从占用资源很多的旋转因子乘法器模块继续进行改进,进一步改善FFT硬件架构的性能,研究方向主要有基于内存的架构和采用坐标旋转数字计算方法(coordinate rotation digital computer,CORDIC)的架构. Ma等[8 ] 提出基于内存的FFT架构,将旋转因子存储于ROM中,用DSP完成复数乘法器运算. 这种基于内存的架构,对于大点数的FFT,需要大量的内存单元和DSP资源,设计更加复杂,硬件成本更高,因此采用CORDIC的架构逐渐得到更多的研究. Tang等[9 ] 将旋转角度存储于ROM中,利用CORDIC计算旋转因子. Shi等[10 ] 提前计算出每种旋转角度在各级旋转时的方向系数并存储在ROM中,计算时只需寻址读出相应的方向系数. Mankar等[11 ] 提出基于CORDIC-新分布式算法(new distributed arithmetic,NEDA)的折叠FFT架构. Zhang等[12 ] 提出自适应编码CORDIC(adaptive recoding CORDIC, ARC)FFT架构. Mahdavi等[13 ] 提出基于二进制符号数编码(binary-signed-digit, BSD)CORDIC的FFT架构. 目前的研究主要是用CORDIC实现全部的旋转因子并着重于硬件实现方面的改进,鲜少将其他常数乘法器应用于FFT架构中. ...
1
... 基2单路延迟反馈架构(single-path delay feedback,SDF)是Groginsky等[1 ] 提出的单路流水线FFT架构. He等[2 ] 提出基22 算法,结合基2与基4算法的优势,以资源占用少、控制简单、运算量小等优势,得到了广泛的应用. 近年来,Garrido等[3 -4 ] 对FFT的硬件实现进行了大量研究. 在蝶形单元架构的改进方面,Garrido等[5 ] 提出串行架构,将蝶形单元数量减少一半,利用率提高到了100%,但计算速度降低了一半. Ingemarsson等[6 ] 将传统SDF架构中的加法器和选择器换位,LUT资源占用减少了近1/3. Ingemarsson等[7 ] 指出,若将小点数FFT架构中的一个加法器置换为短移位寄存器,则LUT资源占用减少了近43%. 目前对蝶形单元的改进已趋于完善,可以从占用资源很多的旋转因子乘法器模块继续进行改进,进一步改善FFT硬件架构的性能,研究方向主要有基于内存的架构和采用坐标旋转数字计算方法(coordinate rotation digital computer,CORDIC)的架构. Ma等[8 ] 提出基于内存的FFT架构,将旋转因子存储于ROM中,用DSP完成复数乘法器运算. 这种基于内存的架构,对于大点数的FFT,需要大量的内存单元和DSP资源,设计更加复杂,硬件成本更高,因此采用CORDIC的架构逐渐得到更多的研究. Tang等[9 ] 将旋转角度存储于ROM中,利用CORDIC计算旋转因子. Shi等[10 ] 提前计算出每种旋转角度在各级旋转时的方向系数并存储在ROM中,计算时只需寻址读出相应的方向系数. Mankar等[11 ] 提出基于CORDIC-新分布式算法(new distributed arithmetic,NEDA)的折叠FFT架构. Zhang等[12 ] 提出自适应编码CORDIC(adaptive recoding CORDIC, ARC)FFT架构. Mahdavi等[13 ] 提出基于二进制符号数编码(binary-signed-digit, BSD)CORDIC的FFT架构. 目前的研究主要是用CORDIC实现全部的旋转因子并着重于硬件实现方面的改进,鲜少将其他常数乘法器应用于FFT架构中. ...
Multiplier: less VLSI architectures for radix‐22 folded pipelined complex FFT core
1
2015
... 基2单路延迟反馈架构(single-path delay feedback,SDF)是Groginsky等[1 ] 提出的单路流水线FFT架构. He等[2 ] 提出基22 算法,结合基2与基4算法的优势,以资源占用少、控制简单、运算量小等优势,得到了广泛的应用. 近年来,Garrido等[3 -4 ] 对FFT的硬件实现进行了大量研究. 在蝶形单元架构的改进方面,Garrido等[5 ] 提出串行架构,将蝶形单元数量减少一半,利用率提高到了100%,但计算速度降低了一半. Ingemarsson等[6 ] 将传统SDF架构中的加法器和选择器换位,LUT资源占用减少了近1/3. Ingemarsson等[7 ] 指出,若将小点数FFT架构中的一个加法器置换为短移位寄存器,则LUT资源占用减少了近43%. 目前对蝶形单元的改进已趋于完善,可以从占用资源很多的旋转因子乘法器模块继续进行改进,进一步改善FFT硬件架构的性能,研究方向主要有基于内存的架构和采用坐标旋转数字计算方法(coordinate rotation digital computer,CORDIC)的架构. Ma等[8 ] 提出基于内存的FFT架构,将旋转因子存储于ROM中,用DSP完成复数乘法器运算. 这种基于内存的架构,对于大点数的FFT,需要大量的内存单元和DSP资源,设计更加复杂,硬件成本更高,因此采用CORDIC的架构逐渐得到更多的研究. Tang等[9 ] 将旋转角度存储于ROM中,利用CORDIC计算旋转因子. Shi等[10 ] 提前计算出每种旋转角度在各级旋转时的方向系数并存储在ROM中,计算时只需寻址读出相应的方向系数. Mankar等[11 ] 提出基于CORDIC-新分布式算法(new distributed arithmetic,NEDA)的折叠FFT架构. Zhang等[12 ] 提出自适应编码CORDIC(adaptive recoding CORDIC, ARC)FFT架构. Mahdavi等[13 ] 提出基于二进制符号数编码(binary-signed-digit, BSD)CORDIC的FFT架构. 目前的研究主要是用CORDIC实现全部的旋转因子并着重于硬件实现方面的改进,鲜少将其他常数乘法器应用于FFT架构中. ...
Enhanced hardware efficient FFT processor based on adaptive recoding CORDIC
1
2013
... 基2单路延迟反馈架构(single-path delay feedback,SDF)是Groginsky等[1 ] 提出的单路流水线FFT架构. He等[2 ] 提出基22 算法,结合基2与基4算法的优势,以资源占用少、控制简单、运算量小等优势,得到了广泛的应用. 近年来,Garrido等[3 -4 ] 对FFT的硬件实现进行了大量研究. 在蝶形单元架构的改进方面,Garrido等[5 ] 提出串行架构,将蝶形单元数量减少一半,利用率提高到了100%,但计算速度降低了一半. Ingemarsson等[6 ] 将传统SDF架构中的加法器和选择器换位,LUT资源占用减少了近1/3. Ingemarsson等[7 ] 指出,若将小点数FFT架构中的一个加法器置换为短移位寄存器,则LUT资源占用减少了近43%. 目前对蝶形单元的改进已趋于完善,可以从占用资源很多的旋转因子乘法器模块继续进行改进,进一步改善FFT硬件架构的性能,研究方向主要有基于内存的架构和采用坐标旋转数字计算方法(coordinate rotation digital computer,CORDIC)的架构. Ma等[8 ] 提出基于内存的FFT架构,将旋转因子存储于ROM中,用DSP完成复数乘法器运算. 这种基于内存的架构,对于大点数的FFT,需要大量的内存单元和DSP资源,设计更加复杂,硬件成本更高,因此采用CORDIC的架构逐渐得到更多的研究. Tang等[9 ] 将旋转角度存储于ROM中,利用CORDIC计算旋转因子. Shi等[10 ] 提前计算出每种旋转角度在各级旋转时的方向系数并存储在ROM中,计算时只需寻址读出相应的方向系数. Mankar等[11 ] 提出基于CORDIC-新分布式算法(new distributed arithmetic,NEDA)的折叠FFT架构. Zhang等[12 ] 提出自适应编码CORDIC(adaptive recoding CORDIC, ARC)FFT架构. Mahdavi等[13 ] 提出基于二进制符号数编码(binary-signed-digit, BSD)CORDIC的FFT架构. 目前的研究主要是用CORDIC实现全部的旋转因子并着重于硬件实现方面的改进,鲜少将其他常数乘法器应用于FFT架构中. ...
Area-time-power efficient FFT architectures based on binary-signed-digit CORDIC
1
2019
... 基2单路延迟反馈架构(single-path delay feedback,SDF)是Groginsky等[1 ] 提出的单路流水线FFT架构. He等[2 ] 提出基22 算法,结合基2与基4算法的优势,以资源占用少、控制简单、运算量小等优势,得到了广泛的应用. 近年来,Garrido等[3 -4 ] 对FFT的硬件实现进行了大量研究. 在蝶形单元架构的改进方面,Garrido等[5 ] 提出串行架构,将蝶形单元数量减少一半,利用率提高到了100%,但计算速度降低了一半. Ingemarsson等[6 ] 将传统SDF架构中的加法器和选择器换位,LUT资源占用减少了近1/3. Ingemarsson等[7 ] 指出,若将小点数FFT架构中的一个加法器置换为短移位寄存器,则LUT资源占用减少了近43%. 目前对蝶形单元的改进已趋于完善,可以从占用资源很多的旋转因子乘法器模块继续进行改进,进一步改善FFT硬件架构的性能,研究方向主要有基于内存的架构和采用坐标旋转数字计算方法(coordinate rotation digital computer,CORDIC)的架构. Ma等[8 ] 提出基于内存的FFT架构,将旋转因子存储于ROM中,用DSP完成复数乘法器运算. 这种基于内存的架构,对于大点数的FFT,需要大量的内存单元和DSP资源,设计更加复杂,硬件成本更高,因此采用CORDIC的架构逐渐得到更多的研究. Tang等[9 ] 将旋转角度存储于ROM中,利用CORDIC计算旋转因子. Shi等[10 ] 提前计算出每种旋转角度在各级旋转时的方向系数并存储在ROM中,计算时只需寻址读出相应的方向系数. Mankar等[11 ] 提出基于CORDIC-新分布式算法(new distributed arithmetic,NEDA)的折叠FFT架构. Zhang等[12 ] 提出自适应编码CORDIC(adaptive recoding CORDIC, ARC)FFT架构. Mahdavi等[13 ] 提出基于二进制符号数编码(binary-signed-digit, BSD)CORDIC的FFT架构. 目前的研究主要是用CORDIC实现全部的旋转因子并着重于硬件实现方面的改进,鲜少将其他常数乘法器应用于FFT架构中. ...
1
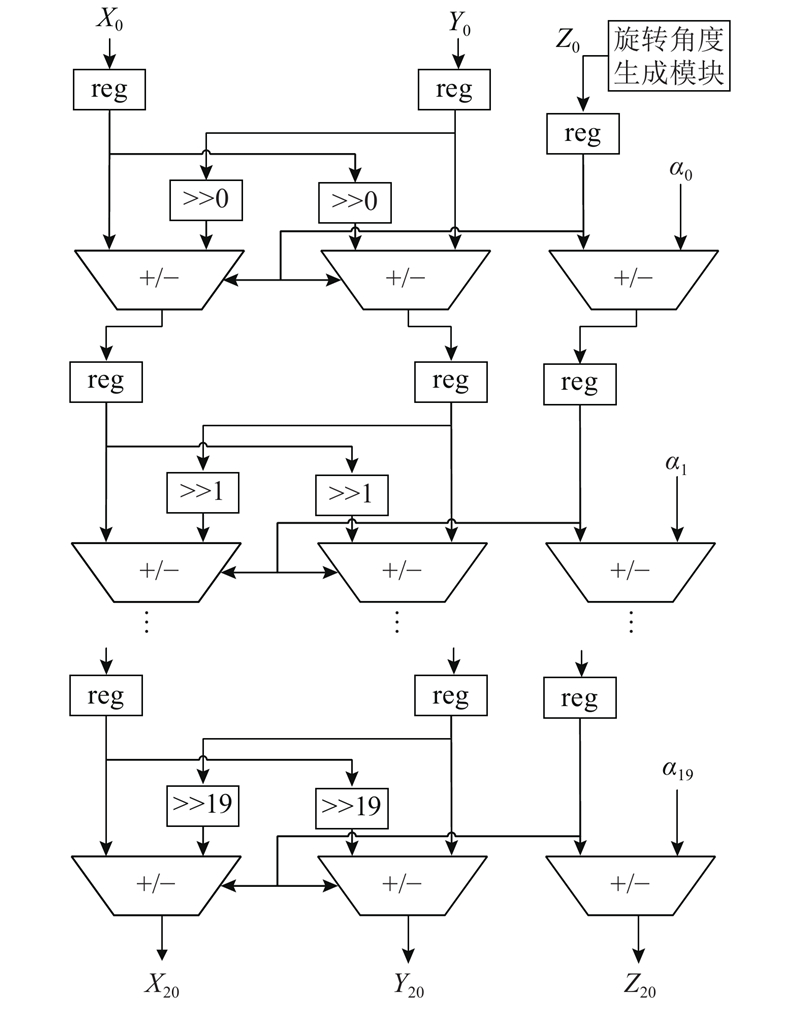
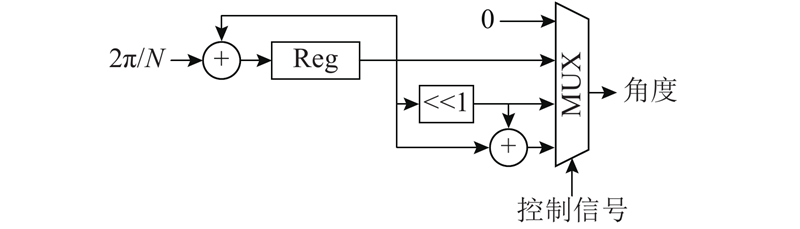
... CORDIC算法通过一系列固定的、与运算基数有关的角度不断偏转,以逼近所需的旋转角度[14 ] . 只需要移位和加减运算,就可以完成矢量的旋转,即三角函数的乘法. 设总共需要n 次旋转,其中第i 次旋转角度为θi ,且tanθi =s i − i si 取值为±1,+1表示逆时针旋转,−1表示顺时针旋转. 第i 次旋转的表达式为 ...
Multiplierless multiple constant multiplication
1
2007
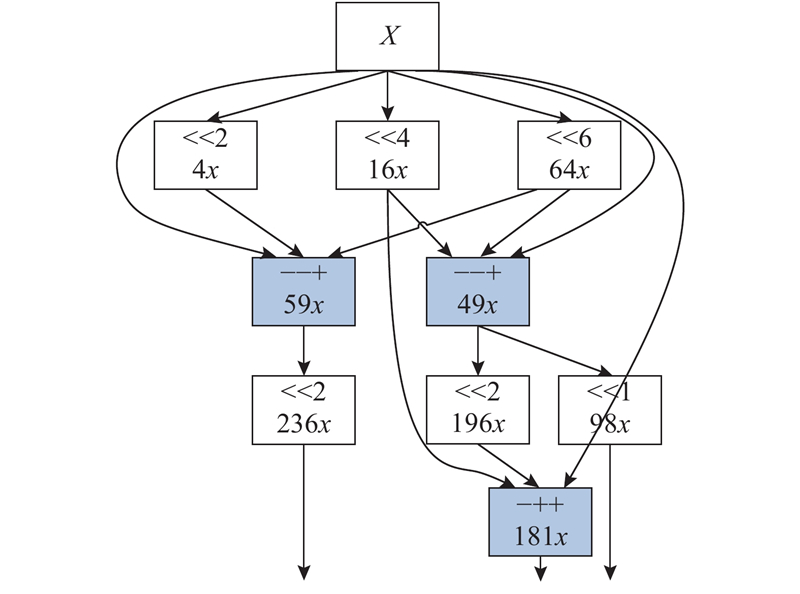
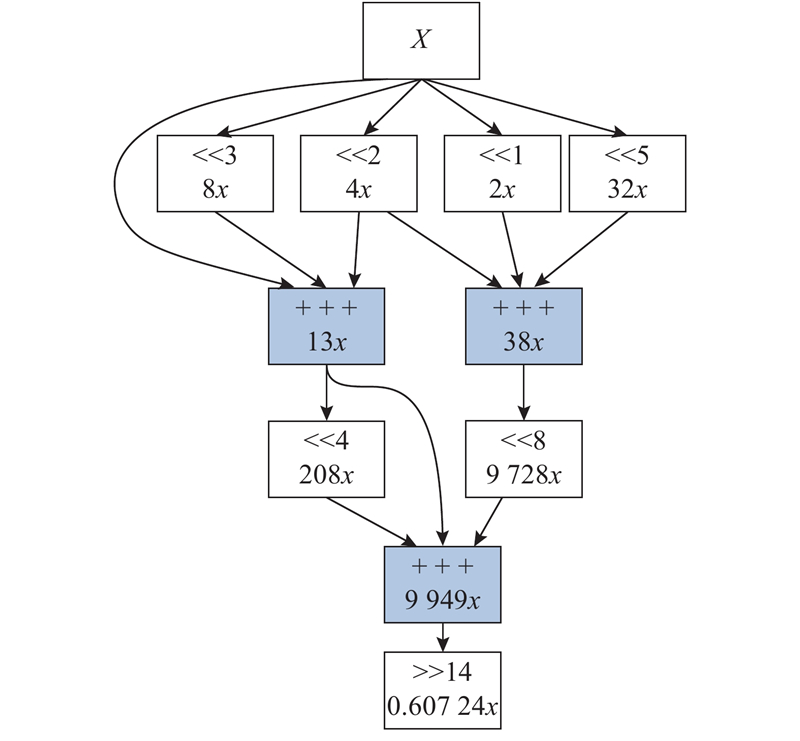
... 在信号处理中,MCM可以将常数乘法分解为加减法和移位操作,用来实现一个变量与多个常数相乘. 移位操作可以通过硬件连接实现,资源消耗忽略不计,因此MCM的硬件资源消耗取决于加减法器的数量[15 ] ,RPAGT(reduced pipelined adder graph)算法是目前资源消耗较少的求解方法之一. 现代FPGA(Virtex 5-7、Spartan 6、Kintex 7和Artix 7)可以实现三输入加法器,使用三输入加法器的流水线MCM架构相比于传统二输入加法器实现的架构平均可以减少27%的运算量和15%的slice[16 ] ,因此将常数分解为三输入加法,可以进一步减小硬件资源占用和流水线级数. 算法流程[17 ] 如下. ...
1
... 在信号处理中,MCM可以将常数乘法分解为加减法和移位操作,用来实现一个变量与多个常数相乘. 移位操作可以通过硬件连接实现,资源消耗忽略不计,因此MCM的硬件资源消耗取决于加减法器的数量[15 ] ,RPAGT(reduced pipelined adder graph)算法是目前资源消耗较少的求解方法之一. 现代FPGA(Virtex 5-7、Spartan 6、Kintex 7和Artix 7)可以实现三输入加法器,使用三输入加法器的流水线MCM架构相比于传统二输入加法器实现的架构平均可以减少27%的运算量和15%的slice[16 ] ,因此将常数分解为三输入加法,可以进一步减小硬件资源占用和流水线级数. 算法流程[17 ] 如下. ...
1
... 在信号处理中,MCM可以将常数乘法分解为加减法和移位操作,用来实现一个变量与多个常数相乘. 移位操作可以通过硬件连接实现,资源消耗忽略不计,因此MCM的硬件资源消耗取决于加减法器的数量[15 ] ,RPAGT(reduced pipelined adder graph)算法是目前资源消耗较少的求解方法之一. 现代FPGA(Virtex 5-7、Spartan 6、Kintex 7和Artix 7)可以实现三输入加法器,使用三输入加法器的流水线MCM架构相比于传统二输入加法器实现的架构平均可以减少27%的运算量和15%的slice[16 ] ,因此将常数分解为三输入加法,可以进一步减小硬件资源占用和流水线级数. 算法流程[17 ] 如下. ...
1
... 传统的SDF蝶形结构如图3(a) 所示. 当使用N 输入的LUT进行2个数的加法运算时,只会占用2个输入端口,其他几个端口会闲置. 若将加法器输入端一侧的其他逻辑输入合并到该LUT的闲置端口,则可以更加充分地利用LUT资源[18 ] . 将传统蝶形结构中的加法器和选择器交换位置,使得选择器位于加法器输入端一侧,就可以将选择器和加法器综合进同一个 LUT单元中,从而节省硬件资源. 改进后的碟形单元结构如图3(b) 所示[6 ] . 现代Xilinx FPGA具有6输入LUT,允许将2个长度相同且长度≤16的1 bit位宽短移位寄存器映射到同一个LUT6资源中,输出为1 bit位宽的加法器需要映射到一个完整的LUT6资源中. 这意味着短移位寄存器的LUT成本是加法器的一半. 对于所需移位寄存器长度≤16的情况,将传统蝶形结构中的一个加法器换成一个短移位寄存器,可以减少硬件资源占用. 改进后的碟形单元结构如图3(c) 所示[7 ] . 基于上述2种思想,第6~10级蝶形单元采用图3(b) 的改进结构,第1~5级蝶形单元采用图3(c) 的改进结构,可以减少硬件资源占用,且这2种改进结构具有相同的数据顺序和控制结构,因此组合起来控制时序很简单. 分别以第6级和第2级蝶形单元为例说明工作时序,如图4 所示. ...
1
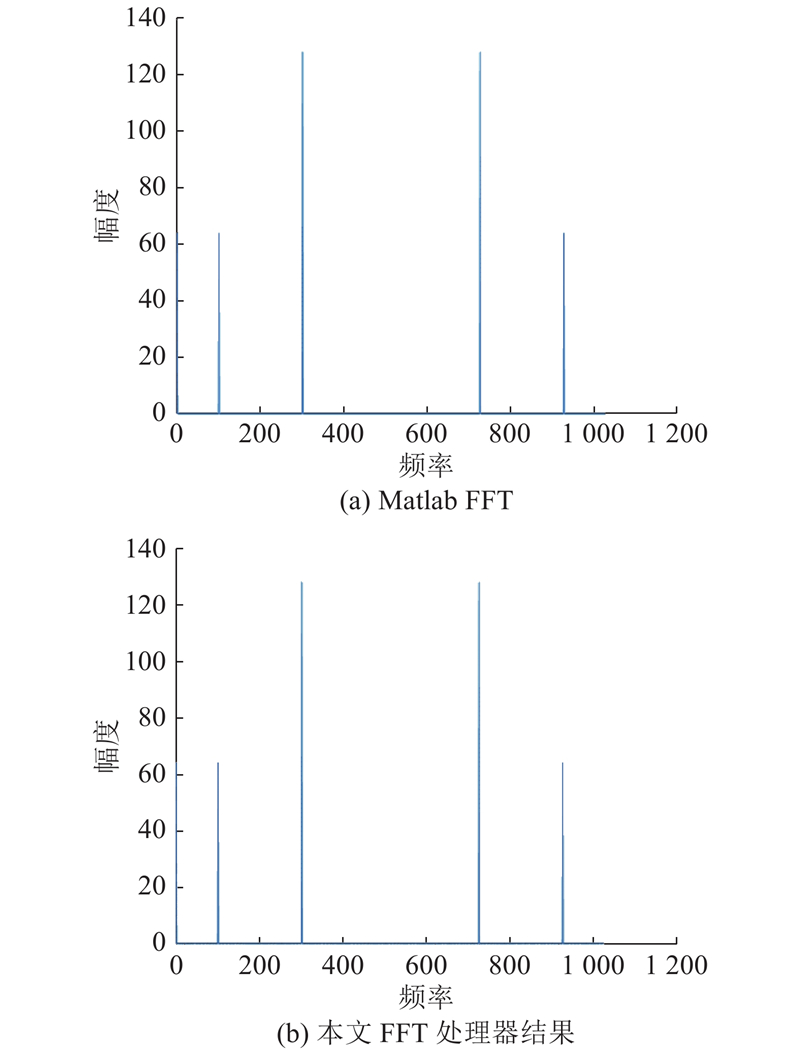
... 测试数据形式如式(15)所示,采用常见的直流分量与余弦分量叠加的信号形式作为输入数据[19 ] . 如图11 所示为Matlab和本文的FFT处理器的结果,测试数据如表5 所示. 将FFT处理器的结果与信号的频域特性对比可知,相对误差均小于0.2%. 设计的FFT处理器可以正确地提取信号的频域特性,实现FFT的功能. ...
A high-performance, resource-efficient, reconfigurable parallel-pipelined FFT processor for FPGA platforms
5
2018
... 本文实现了数据位宽为16 bit的64点、256点和1 024点基22 SDF FFT架构,得到在Virtex-5、Virtex-7 FPGA芯片上的电路性能. 该设计没有使用DSP48E资源,因此在比较硬件性能时,采用文献[20 ]的方法,将slice regs、LUTs、DSP48E都转换为slice数量进行统一度量. 在Xilinx Virtex-5和Virtex-7 FPGA中,每个DSP48E相当于占用大约500个slice. 电路性能和硬件资源的对比情况如表6 所示. 表中,N 为计算点数,f 为频率,T p 为吞吐率,T p,u 为单位slice吞吐率. Valencia等[21 ] 将旋转因子储存到ROM中,通过状态机控制读取旋转因子的地址,实现了紧凑的基2/4 FFT架构. 本文设计的64点、1 024点FFT架构吞吐率虽然仅提升10%,但因为硬件资源占用更少,单位面积吞吐率分别提高了35.20%和66.29%. Wang等[22 ] 提出组合SDC-SDF FFT架构,通过共享算术资源,减少了近50%的复数乘法器,但需要使用DSP48E资源,提高了控制时序的复杂度;本文设计的256点FFT单位面积吞吐率提高了30.37%. Nguyen等[23 ] 使用优化的CORDIC算法,通过设置误差阈值来减少CORDIC模块的迭代次数,但吞吐率较低;本文设计的单位面积吞吐率提高了115%. Nguyen等[20 ] 提出基于CORDIC算法的并行双路延迟换向结构FFT处理器,提升了吞吐率且不占用BRAM资源,但整序换向模块会占用较多的LUT资源;本文设计的FFT架构单位面积吞吐率提高了25.38%. ...
... [20 ]提出基于CORDIC算法的并行双路延迟换向结构FFT处理器,提升了吞吐率且不占用BRAM资源,但整序换向模块会占用较多的LUT资源;本文设计的FFT架构单位面积吞吐率提高了25.38%. ...
... FPGA implementation results of circuit performance and hardware resources for different architectures
Tab.6 方法 FPGA型号 N Slices LUTs Regs DSP48Es slice总量 f /MHz T p /(MS·s−1 ) T p,u /(kS·s−1 ) 实际数 等效slice数 文献[21 ]方法 V7 64 − 848 626 8 4 000 5 474 335 335 61.20 本文方法 V7 64 667 2 423 1 924 0 0 4 347 359.69 359.69 82.74 文献[22 ]方法 V5 256 − 1 733 1 073 12 6 000 8 806 297 297 33.72 本文方法 V5 256 1 093 3 925 3 258 0 0 7 183 315.77 315.77 43.96 文献[23 ]方法 V7 1 024 − 11 865 1 393 0 0 13 258 200 200 15.08 文献[21 ]方法 V7 1 024 − 1 671 2 065 25 12 500 16 236 317 317 19.52 文献[20 ]方法 V7 1 024 − 12 737 2 715 0 0 15 452 200 400 25.89 本文方法 V7 1 024 1 645 6 098 4 785 0 0 10 883 353.21 353.21 32.46
3.3. 误差分析 FFT处理器的精度通过测量1 024个点的平均相对误差(mean relative error, MRE)来评估,如下所示: ...
... 传统的基于内存的FFT处理器MRE为0.52%,文献[20 ]的MRE为0.81%,文献[23 ]的MRE为0.72%,文献[24 ] 的MRE为0.314%. 虽然本文的MRE略高于上述文献的架构,但相对误差小于1%,且硬件性能更具优势,以较少的硬件资源消耗得到了较好的计算结果. ...
... 本文针对FFT硬件实现中旋转因子乘法器消耗硬件资源较多的问题,采用CORDIC与MCM混合的方法,实现了无需常规乘法器的FFT架构,不必占用DSP48E资源. 利用现代FPGA可以实现三输入加法器的特点,设计旋转角度数量较少的W 16 旋转因子模块,减少了硬件资源占用. 对于旋转角度数量较多的模块,采用流水线CORDIC架构实现,且旋转角度实时生成,避免了存储单元的使用. 蝶形单元中的存储模块均使用移位寄存器实现,整体架构只占用分布式逻辑资源,不需要BRAM资源. 本文提出的FFT架构可以应用于处理数据较多、计算较复杂的雷达成像处理领域,因为它可以把节省下来的硬件资源和ROM、DSP48E用于实现其他功能模块,以减少整体系统的资源消耗. 通过与Nguyen等[20 -23 ] 提出的FFT架构对比可知,利用本文的设计方法大大提高了硬件效率. ...
Compact and high-throughput parameterizable architectures for memory-based FFT algorithms
3
2019
... 本文实现了数据位宽为16 bit的64点、256点和1 024点基22 SDF FFT架构,得到在Virtex-5、Virtex-7 FPGA芯片上的电路性能. 该设计没有使用DSP48E资源,因此在比较硬件性能时,采用文献[20 ]的方法,将slice regs、LUTs、DSP48E都转换为slice数量进行统一度量. 在Xilinx Virtex-5和Virtex-7 FPGA中,每个DSP48E相当于占用大约500个slice. 电路性能和硬件资源的对比情况如表6 所示. 表中,N 为计算点数,f 为频率,T p 为吞吐率,T p,u 为单位slice吞吐率. Valencia等[21 ] 将旋转因子储存到ROM中,通过状态机控制读取旋转因子的地址,实现了紧凑的基2/4 FFT架构. 本文设计的64点、1 024点FFT架构吞吐率虽然仅提升10%,但因为硬件资源占用更少,单位面积吞吐率分别提高了35.20%和66.29%. Wang等[22 ] 提出组合SDC-SDF FFT架构,通过共享算术资源,减少了近50%的复数乘法器,但需要使用DSP48E资源,提高了控制时序的复杂度;本文设计的256点FFT单位面积吞吐率提高了30.37%. Nguyen等[23 ] 使用优化的CORDIC算法,通过设置误差阈值来减少CORDIC模块的迭代次数,但吞吐率较低;本文设计的单位面积吞吐率提高了115%. Nguyen等[20 ] 提出基于CORDIC算法的并行双路延迟换向结构FFT处理器,提升了吞吐率且不占用BRAM资源,但整序换向模块会占用较多的LUT资源;本文设计的FFT架构单位面积吞吐率提高了25.38%. ...
... FPGA implementation results of circuit performance and hardware resources for different architectures
Tab.6 方法 FPGA型号 N Slices LUTs Regs DSP48Es slice总量 f /MHz T p /(MS·s−1 ) T p,u /(kS·s−1 ) 实际数 等效slice数 文献[21 ]方法 V7 64 − 848 626 8 4 000 5 474 335 335 61.20 本文方法 V7 64 667 2 423 1 924 0 0 4 347 359.69 359.69 82.74 文献[22 ]方法 V5 256 − 1 733 1 073 12 6 000 8 806 297 297 33.72 本文方法 V5 256 1 093 3 925 3 258 0 0 7 183 315.77 315.77 43.96 文献[23 ]方法 V7 1 024 − 11 865 1 393 0 0 13 258 200 200 15.08 文献[21 ]方法 V7 1 024 − 1 671 2 065 25 12 500 16 236 317 317 19.52 文献[20 ]方法 V7 1 024 − 12 737 2 715 0 0 15 452 200 400 25.89 本文方法 V7 1 024 1 645 6 098 4 785 0 0 10 883 353.21 353.21 32.46
3.3. 误差分析 FFT处理器的精度通过测量1 024个点的平均相对误差(mean relative error, MRE)来评估,如下所示: ...
... 文献[
21 ]方法
V7 1 024 − 1 671 2 065 25 12 500 16 236 317 317 19.52 文献[20 ]方法 V7 1 024 − 12 737 2 715 0 0 15 452 200 400 25.89 本文方法 V7 1 024 1 645 6 098 4 785 0 0 10 883 353.21 353.21 32.46 3.3. 误差分析 FFT处理器的精度通过测量1 024个点的平均相对误差(mean relative error, MRE)来评估,如下所示: ...
A combined SDC-SDF architecture for normal I/O pipelined radix-2 FFT
2
2015
... 本文实现了数据位宽为16 bit的64点、256点和1 024点基22 SDF FFT架构,得到在Virtex-5、Virtex-7 FPGA芯片上的电路性能. 该设计没有使用DSP48E资源,因此在比较硬件性能时,采用文献[20 ]的方法,将slice regs、LUTs、DSP48E都转换为slice数量进行统一度量. 在Xilinx Virtex-5和Virtex-7 FPGA中,每个DSP48E相当于占用大约500个slice. 电路性能和硬件资源的对比情况如表6 所示. 表中,N 为计算点数,f 为频率,T p 为吞吐率,T p,u 为单位slice吞吐率. Valencia等[21 ] 将旋转因子储存到ROM中,通过状态机控制读取旋转因子的地址,实现了紧凑的基2/4 FFT架构. 本文设计的64点、1 024点FFT架构吞吐率虽然仅提升10%,但因为硬件资源占用更少,单位面积吞吐率分别提高了35.20%和66.29%. Wang等[22 ] 提出组合SDC-SDF FFT架构,通过共享算术资源,减少了近50%的复数乘法器,但需要使用DSP48E资源,提高了控制时序的复杂度;本文设计的256点FFT单位面积吞吐率提高了30.37%. Nguyen等[23 ] 使用优化的CORDIC算法,通过设置误差阈值来减少CORDIC模块的迭代次数,但吞吐率较低;本文设计的单位面积吞吐率提高了115%. Nguyen等[20 ] 提出基于CORDIC算法的并行双路延迟换向结构FFT处理器,提升了吞吐率且不占用BRAM资源,但整序换向模块会占用较多的LUT资源;本文设计的FFT架构单位面积吞吐率提高了25.38%. ...
... FPGA implementation results of circuit performance and hardware resources for different architectures
Tab.6 方法 FPGA型号 N Slices LUTs Regs DSP48Es slice总量 f /MHz T p /(MS·s−1 ) T p,u /(kS·s−1 ) 实际数 等效slice数 文献[21 ]方法 V7 64 − 848 626 8 4 000 5 474 335 335 61.20 本文方法 V7 64 667 2 423 1 924 0 0 4 347 359.69 359.69 82.74 文献[22 ]方法 V5 256 − 1 733 1 073 12 6 000 8 806 297 297 33.72 本文方法 V5 256 1 093 3 925 3 258 0 0 7 183 315.77 315.77 43.96 文献[23 ]方法 V7 1 024 − 11 865 1 393 0 0 13 258 200 200 15.08 文献[21 ]方法 V7 1 024 − 1 671 2 065 25 12 500 16 236 317 317 19.52 文献[20 ]方法 V7 1 024 − 12 737 2 715 0 0 15 452 200 400 25.89 本文方法 V7 1 024 1 645 6 098 4 785 0 0 10 883 353.21 353.21 32.46
3.3. 误差分析 FFT处理器的精度通过测量1 024个点的平均相对误差(mean relative error, MRE)来评估,如下所示: ...
A pipelined FFT processor using an optimal hybrid rotation scheme for complex multiplication: design, FPGA implementation and analysis
4
2018
... 本文实现了数据位宽为16 bit的64点、256点和1 024点基22 SDF FFT架构,得到在Virtex-5、Virtex-7 FPGA芯片上的电路性能. 该设计没有使用DSP48E资源,因此在比较硬件性能时,采用文献[20 ]的方法,将slice regs、LUTs、DSP48E都转换为slice数量进行统一度量. 在Xilinx Virtex-5和Virtex-7 FPGA中,每个DSP48E相当于占用大约500个slice. 电路性能和硬件资源的对比情况如表6 所示. 表中,N 为计算点数,f 为频率,T p 为吞吐率,T p,u 为单位slice吞吐率. Valencia等[21 ] 将旋转因子储存到ROM中,通过状态机控制读取旋转因子的地址,实现了紧凑的基2/4 FFT架构. 本文设计的64点、1 024点FFT架构吞吐率虽然仅提升10%,但因为硬件资源占用更少,单位面积吞吐率分别提高了35.20%和66.29%. Wang等[22 ] 提出组合SDC-SDF FFT架构,通过共享算术资源,减少了近50%的复数乘法器,但需要使用DSP48E资源,提高了控制时序的复杂度;本文设计的256点FFT单位面积吞吐率提高了30.37%. Nguyen等[23 ] 使用优化的CORDIC算法,通过设置误差阈值来减少CORDIC模块的迭代次数,但吞吐率较低;本文设计的单位面积吞吐率提高了115%. Nguyen等[20 ] 提出基于CORDIC算法的并行双路延迟换向结构FFT处理器,提升了吞吐率且不占用BRAM资源,但整序换向模块会占用较多的LUT资源;本文设计的FFT架构单位面积吞吐率提高了25.38%. ...
... FPGA implementation results of circuit performance and hardware resources for different architectures
Tab.6 方法 FPGA型号 N Slices LUTs Regs DSP48Es slice总量 f /MHz T p /(MS·s−1 ) T p,u /(kS·s−1 ) 实际数 等效slice数 文献[21 ]方法 V7 64 − 848 626 8 4 000 5 474 335 335 61.20 本文方法 V7 64 667 2 423 1 924 0 0 4 347 359.69 359.69 82.74 文献[22 ]方法 V5 256 − 1 733 1 073 12 6 000 8 806 297 297 33.72 本文方法 V5 256 1 093 3 925 3 258 0 0 7 183 315.77 315.77 43.96 文献[23 ]方法 V7 1 024 − 11 865 1 393 0 0 13 258 200 200 15.08 文献[21 ]方法 V7 1 024 − 1 671 2 065 25 12 500 16 236 317 317 19.52 文献[20 ]方法 V7 1 024 − 12 737 2 715 0 0 15 452 200 400 25.89 本文方法 V7 1 024 1 645 6 098 4 785 0 0 10 883 353.21 353.21 32.46
3.3. 误差分析 FFT处理器的精度通过测量1 024个点的平均相对误差(mean relative error, MRE)来评估,如下所示: ...
... 传统的基于内存的FFT处理器MRE为0.52%,文献[20 ]的MRE为0.81%,文献[23 ]的MRE为0.72%,文献[24 ] 的MRE为0.314%. 虽然本文的MRE略高于上述文献的架构,但相对误差小于1%,且硬件性能更具优势,以较少的硬件资源消耗得到了较好的计算结果. ...
... 本文针对FFT硬件实现中旋转因子乘法器消耗硬件资源较多的问题,采用CORDIC与MCM混合的方法,实现了无需常规乘法器的FFT架构,不必占用DSP48E资源. 利用现代FPGA可以实现三输入加法器的特点,设计旋转角度数量较少的W 16 旋转因子模块,减少了硬件资源占用. 对于旋转角度数量较多的模块,采用流水线CORDIC架构实现,且旋转角度实时生成,避免了存储单元的使用. 蝶形单元中的存储模块均使用移位寄存器实现,整体架构只占用分布式逻辑资源,不需要BRAM资源. 本文提出的FFT架构可以应用于处理数据较多、计算较复杂的雷达成像处理领域,因为它可以把节省下来的硬件资源和ROM、DSP48E用于实现其他功能模块,以减少整体系统的资源消耗. 通过与Nguyen等[20 -23 ] 提出的FFT架构对比可知,利用本文的设计方法大大提高了硬件效率. ...
1
... 传统的基于内存的FFT处理器MRE为0.52%,文献[20 ]的MRE为0.81%,文献[23 ]的MRE为0.72%,文献[24 ] 的MRE为0.314%. 虽然本文的MRE略高于上述文献的架构,但相对误差小于1%,且硬件性能更具优势,以较少的硬件资源消耗得到了较好的计算结果. ...