路况预测是智能交通系统(intelligent traffic system,ITS)中重要的一部分,原理是根据交通流中过去、现在、未来的交通路况评价参数来推测未来路况的变化趋势. 由于交通流的随机性,如何提高路况预测的准确率一直是ITS的研究难点[1].
第二类是由数据驱动,通过支持向量机(support vector machine,SVM)、循环神经网络(recurrent neural network,RNN)、相关向量机(relevance vector machine,RVM)等机器学习和深度学习算法构建预测模型. Cao等[5]提出基于粒子群算法(particle swarm algorithm,PSO)优化SVM的车流量预测方法. 温峻峰等[6]使用均值滤波和PSO优化SVM,预测车道饱和度. Fu等[7]利用多个基于RNN的算法预测车流量,实验结果表明,门控循环单元(gated recurrent unit,GRU)的性能优于LSTM,并显著优于ARIMA. 近年来,对交通流信息进行特征提取和预测的深层模型逐渐被学者们重视. Liu等[8]通过卷积层提取交通流时空信息和周期性特征,生成新的特征数据集,利用LSTM进行车速预测,提出CNN-LSTM. Liu等[9]根据该思想设计CNN-Bi-LSTM,将CNN-LSTM中的LSTM改进为双向LSTM(Bi-LSTM). CNN-Bi-LSTM具有更高的预测精度,但仍有提高的空间.
RVM是基于贝叶斯框架的稀疏概率模型. RVM具有极高的测试速度,且预测准确率与SVM、LSTM和GRU等算法近似,因此RVM被引入到交通路况评价参数预测中,但未经参数优化的RVM准确率不高. 针对该问题,Xin等[10]采用遗传算法(genetic algorithm,GA)优化RVM,证明利用智能算法可以提高RVM的准确率. Shen等[11-12]提出利用混沌模拟退火算法优化RVM的交通流量预测方法,与模型驱动的方法相比,该方法具有更高的预测精度. 他们只利用了RVM的测试速度优势,没有考虑参数寻优算法的效率问题. 在任何规模的数据集下,机器学习算法参数寻优的耗时会占整体耗时的80%~95%. 参数寻优的效率会影响整体算法的效率.
在如何评价路况的问题上,王璐媛等[13]指出交通路况评价参数可以分为3类:基于道路服务水平的评价参数[14]、基于时间比的评价参数[15]、基于经济学的评价参数[16]. 在过去的研究中,路况判别的标准往往是车速、占有率等单一指标. 目前,国内外学者多数采用多个基于道路服务水平的评价参数描述路况. 宋顶利等[17]提出基于改进PSO优化K最邻近算法(k-nearest neighbor,KNN)的交通路况预测模型. 通过预测车流量、平均车速和道路占有率3个特征参数评价路况. 晏雨婵等[18]提出预测未来交通路况的方法. 利用PSO优化SVM,预测交通流和平均车速,计算平均速度、交通流密度等拥堵评价指标,采用综合评价的方式分析未来交通拥堵级别.
本文的主要贡献如下.
1)本文利用RVM对车流量和车速进行预测,为RVM的组合核核函数构建基于GA算法和PSO算法的参数寻优算法. 利用Spark平台对参数寻优算法进行并行化以提高模型训练效率,提出交通路况评价参数预测算法SPGAPSO-CKRVM. 其中,“SP”表示基于Spark并行化,“CK”表示组合核.
2)利用SPGAPSO-CKRVM的预测结果,计算平均车速、路段饱和度和交通流密度. 通过多指标模糊综合评价方法分析路况,利用熵值法确定各个指标的权重系数,将路况划分为6个等级.
3)利用加拿大Whitemud Drive公路的真实数据,验证了预测模型的准确率和效率.
1. 相关技术和原理
1.1. 相关向量机
RVM是由Tipping[19]提出的有监督学习算法. RVM具有SVM的一切优点,克服了支持向量个数多、测试时间长、核函数必须满足Mercer定理等缺点. RVM实现了模型的稀疏化,体现了数据最核心的特征,减少了模型测试时的计算量.
RVM与SVM拥有相同的函数形式,利用核技巧处理非线性问题. RVM更稀疏的模型决定了测试时间更短,且准确率与SVM相近,更适合于预测交通路况评价参数.
1.2. 模糊综合评价
模糊综合评价是基于模糊数学的评价方法,根据隶属度理论,将定性评价转化为定量评价,能够解决模糊的、难以量化的、非确定性的问题.
模糊综合评价的一般步骤如下. 1)确定评价结果的因素集
1.3. 熵值法
2. 基于模糊综合评价的路况预测模型
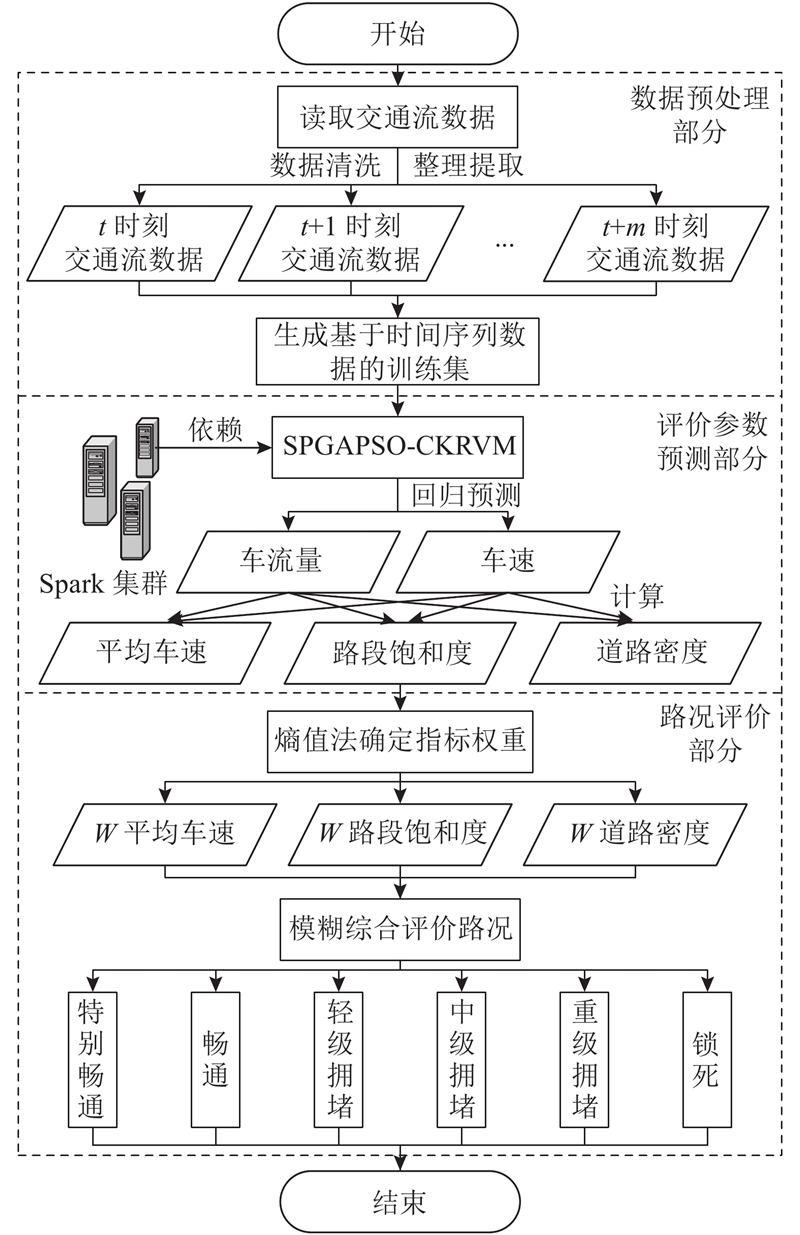
提出的路况预测模型分为数据预处理、评价参数预测和路况评价3部分,如图1所示.
图 1
2.1. 数据预处理部分
数据预处理部分负责从原始交通流数据中提取各个时刻的车流量和车速信息,对因采集设备故障而缺失的数据采用历史趋势法和指数平滑法进行数据修补. 将处理后数据转变为时间序列数据,作为评价参数预测部分的输入. 目前的研究多将数据处理为时间间隔为30、10、5 min的时间序列数据. 越短的时间间隔越有实际应用价值,数据的稀疏性和预测难度越大[21]. 过短的时间间隔会导致决策者来不及下达合理的决策. 综合考虑,以5 min为时间间隔处理交通流数据. 以车流量为例,设计的模型输入如下:
式中:
2.2. 评价参数预测部分
评价参数预测部分负责利用Spark集群高效地训练预测模型,预测未来时刻的车流量和车速信息,基于预测结果计算未来时刻的平均车速、路段饱和度和道路密度. 路段饱和度是指该路段实际交通流量与最大通行车流量的比值,反映道路的实际负荷能力. 路段饱和度的计算方法如下:
式中:
交通流密度是指在单位时间内该条道路单位长度内的车辆数,计算方法如下:
式中:
2.3. 路况评价部分
路况评价部分负责通过熵值法和模糊综合评价法来评价未来时刻的路况. 考虑《道路通行能力手册》,将路况划分为6个级别:特别畅通、畅通、轻级拥堵、中级拥堵、重级拥堵和锁死.
设评价参数预测部分的结果为
式(4)的含义是对每个因素
图 2
利用熵值法求出平均车速、路段饱和度和道路密度的权重系数
使用
3. SPGAPSO-CKRVM算法
3.1. RVM的组合核函数
传统的RVM大多采用单一的核函数完成特征空间的映射过程,包括线性核、多项式核、RBF核、Sigmoid核和Laplacian核. 其中,线性核和多项式核在单维和低维数据中的效果更好. RBF核和Sigmoid核在高维数据和分类问题中被广泛使用. 单一核函数在样本规模较大或样本在高维空间中分布不平坦时效果不佳[22]. 针对该问题,将常用核函数进行组合,构建组合核函数,如下所示:
式中:
3.2. 组合核RVM的参数寻优算法
组合核RVM的参数寻优问题和一般的RVM参数寻优问题不同,如式(9)、(10)中的
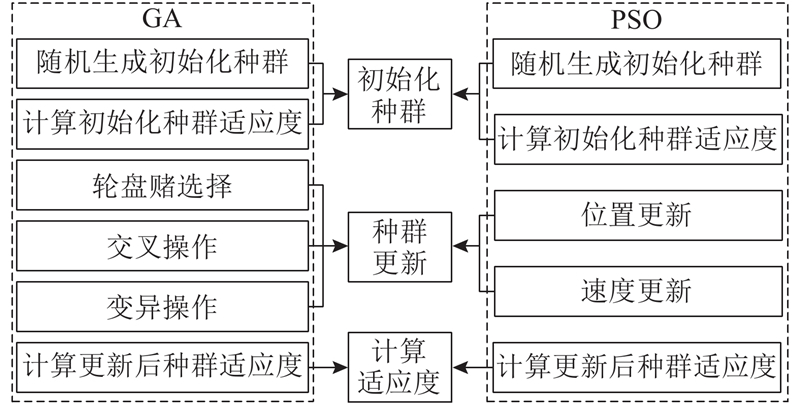
基于GA和PSO,构建参数寻优算法. 随机初始化2个种群,分别进行GA操作和PSO操作. 在每次迭代中,通过计算个体适应度的方式来比较出两者中的较优值,将该较优值作为该次迭代的结果进入下次迭代.
式中:
式中:
3.3. 参数寻优算法耗时分析
参数寻优算法中的GA和PSO均可以分为初始化种群、种群更新、计算适应度3部分,如图3所示.
图 3
如图3所示,初始化种群部分包括随机生成初始化种群和计算初始化种群适应度. 种群更新部分包括选择、交叉、变异、速度更新、位置更新和种群更新. 计算适应度部分负责遍历种群中的所有个体并计算个体适应度.
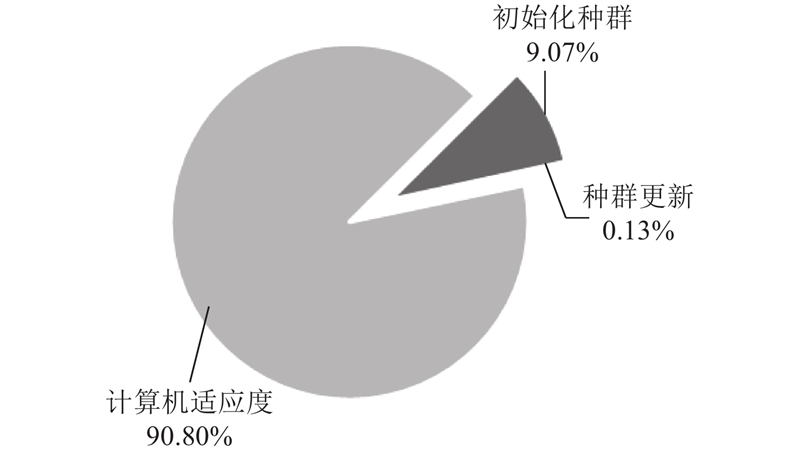
为了研究算法的各部分耗时,运行参数寻优算法20次,其中
图 4
图 4 参数寻优算法各部分耗时
Fig.4 Time consumed by each part in parameter optimization algorithm
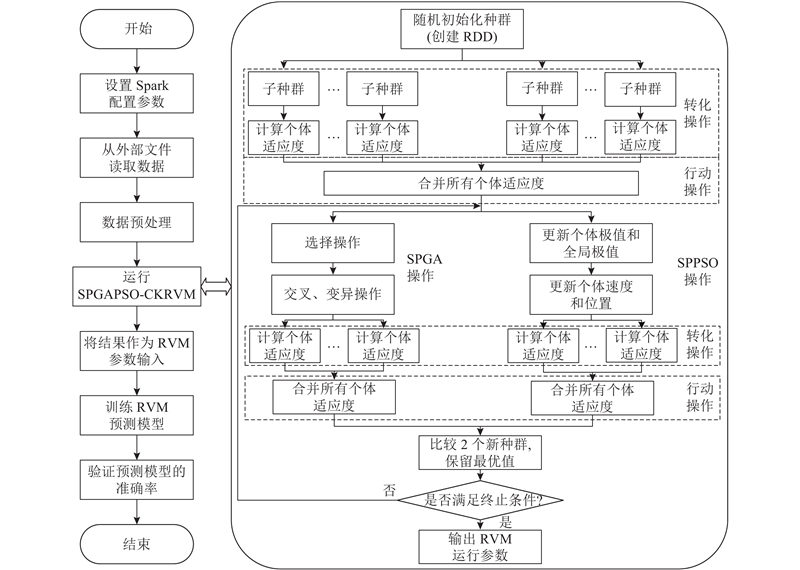
3.4. 基于Spark的并行化设计
图 5
1)初始化.
初始化Spark运行参数,关键的参数包括default.parallelism、executor.cores和num-executors,分别对应RDD默认并行度、每个executor占用CPU cores的数量和executors的总数. 从外部文件中读取实验数据,根据下式进行基于极值的归一化处理,将数据压缩至(0,1).
式中:
2)计算个体适应度.
将初始种群划分为
3)种群更新.
在SPGA操作中,根据个体适应度的计算结果和轮盘赌思想进行选择操作,即越优秀的个体被选中的概率越大. 对选择出的个体进行交叉操作和变异操作,以产生下一代种群. 在SPPSO操作中更新各粒子的速度及位置,以产生下一代种群. 重新计算个体适应度,比较2个下一代种群的个体适应度,保留最优值.
4)验证准确率.
将3)得到的结果解码为
4. 相关实验及结果分析
4.1. 实验数据
使用从加拿大Whitemud Drive公路1027号、1036号和1042号监测点的地感磁线圈收集到的交通流数据作为实验数据. 数据由加拿大阿尔伯塔大学智慧交通研究中心提供. 数据集中含有2015年8月6号到8月28号的交通流数据,收集频率为20 s/次. 其中8月28号的数据为测试集. 实验数据对应的监测点信息如表1所示.
表 1 Whitemud Drive公路实验数据信息
Tab.1
| 数据集编号 | 道路 | 方向 | 监测点编号 |
| 数据集1 | Whitemud Drive | 向东 | 1027 |
| 数据集2 | Whitemud Drive | 向西 | 1036 |
| 数据集3 | Whitemud Drive匝道 | 向西 | 1042 |
4.2. 实验环境及参数设置
通过虚拟机,搭建8个节点的Spark集群来验证SPGAPSO-CKRVM算法的性能. 集群的详细配置如下:CentOS-6.10-x64、Spark-2.1.1-bin-hadoop2.7、hadoop-2.7.2.tar、pyspark-2.3.2、py4j-0.10.8.1. SPGAPSO-CKRVM算法的参数设置如表2所示.
表 2 SPGAPSO-CKRVM算法的参数设置
Tab.2
| 参数 | 参数值 |
| 种群大小 | 10 |
| 最大迭代次数 | 20 |
| 最小适应度 | 0.000 1 |
| 交叉概率 | 0.6 |
| 变异概率 | 0.2 |
| 粒子群学习因子 | 1.5 |
| 粒子速度 | [−0.2,0.2] |
| 粒子位置 | [−8,8] |
在大量实验中发现,针对本文的应用和数据集,种群大小为10的GA和PSO经常在16~18代停止收敛. 将
4.3. 实验结果分析
4.3.1. RVM核函数的性能实验
在RVM核函数的性能实验中,使用准确率(1−MAPE)作为标准,评价核函数的性能. 实验结果如表3所示.
表 3 不同核函数的性能对比结果
Tab.3
| 编号 | 核函数 | 准确率 | ||
| 数据集1 | 数据集2 | 数据集3 | ||
| 1 | | 0.8084 | 0.7964 | 0.7131 |
| 2 | | 0.8520 | 0.8355 | 0.7452 |
| 3 | | 0.8529 | 0.8310 | 0.7472 |
| 4 | | 0.8514 | 0.8367 | 0.7544 |
| 5 | | 0.8529 | 0.8368 | 0.7554 |
| 6 | | 0.8503 | 0.8387 | 0.7555 |
从表3可知,所有核函数在数据集1和数据集2上的准确率都高于数据集3. 这是因为数据集3对应的匝道车流量随机性更强,预测难度更大. 编号为5和6的组合核函数性能普遍优于编号为1~4的单一核函数. 除了在数据集1中,编号为6的组合核函数准确率高于编号为5的组合核函数. 使用编号为6的组合核函数作为RVM的核函数,开展后续实验.
4.3.2. 评价参数预测实验
在评价参数预测实验中,利用RMSE、MAE 和MAPE作为评价指标,将提出的SPGAPSO-CKRVM与现有的机器学习和深度学习算法进行对比. 车流量预测的结果如表4所示.
表 4 不同算法模型预测车流量的对比
Tab.4
| 算法模型 | 数据集1 | 数据集2 | 数据集3 | ||||||||
| MSE | RMSE | MAPE | MSE | RMSE | MAPE | MSE | RMSE | MAPE | |||
| PSO-SVM | 564.06 | 23.75 | 0.1624 | 251.54 | 15.86 | 0.1724 | 48.86 | 6.99 | 0.2701 | ||
| LSTM | 493.13 | 22.21 | 0.1435 | 234.37 | 15.31 | 0.1689 | 82.88 | 9.10 | 0.2702 | ||
| GRU | 495.68 | 22.26 | 0.1432 | 233.978 | 15.29 | 0.1676 | 83.10 | 9.12 | 0.2733 | ||
| CNN-LSTM | 483.18 | 21.92 | 0.1438 | 235.89 | 15.36 | 0.1663 | 82.43 | 9.08 | 0.2659 | ||
| CNN-GRU[26] | 487.46 | 22.07 | 0.1429 | 229.62 | 15.15 | 0.1648 | 82.44 | 9.08 | 0.2640 | ||
| Bi-LSTM[27] | 481.34 | 21.94 | 0.1545 | 223.13 | 14.94 | 0.1811 | 81.58 | 9.03 | 0.2703 | ||
| GA-CKRVM[28] | 433.53 | 20.82 | 0.1412 | 161.56 | 12.71 | 0.1616 | 62.24 | 7.76 | 0.2347 | ||
| CNN-Bi-LSTM | 477.35 | 21.84 | 0.1396 | 227.11 | 15.07 | 0.1622 | 81.79 | 9.04 | 0.2578 | ||
| SPGAPSO-CKRVM | 392.43 | 19.81 | 0.1383 | 161.1 | 12.69 | 0.1589 | 41.09 | 6.41 | 0.2232 | ||
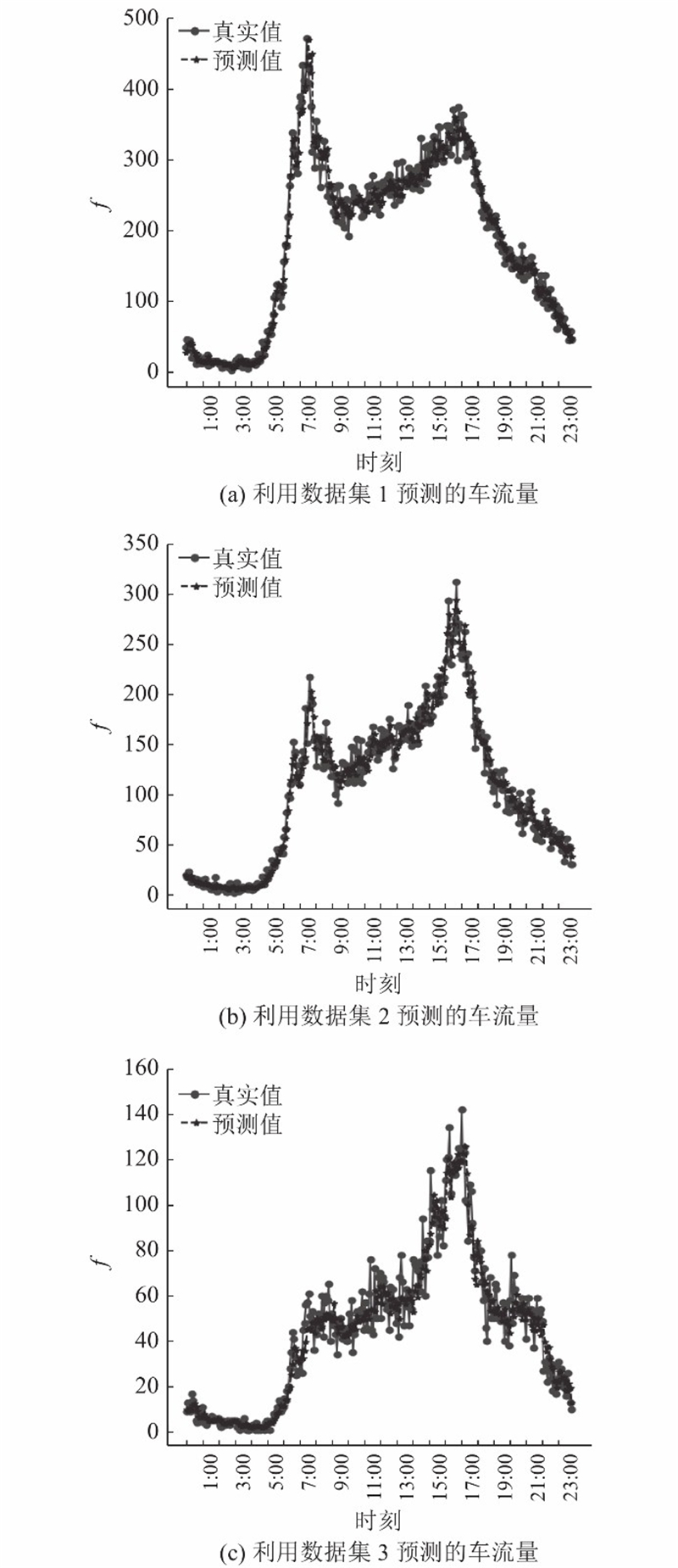
图 6
图 6 利用SPGAPSO-CKRVM预测3个路段的车流量结果
Fig.6 Traffic flow prediction results in three stations by SPGAPSO-CKRVM
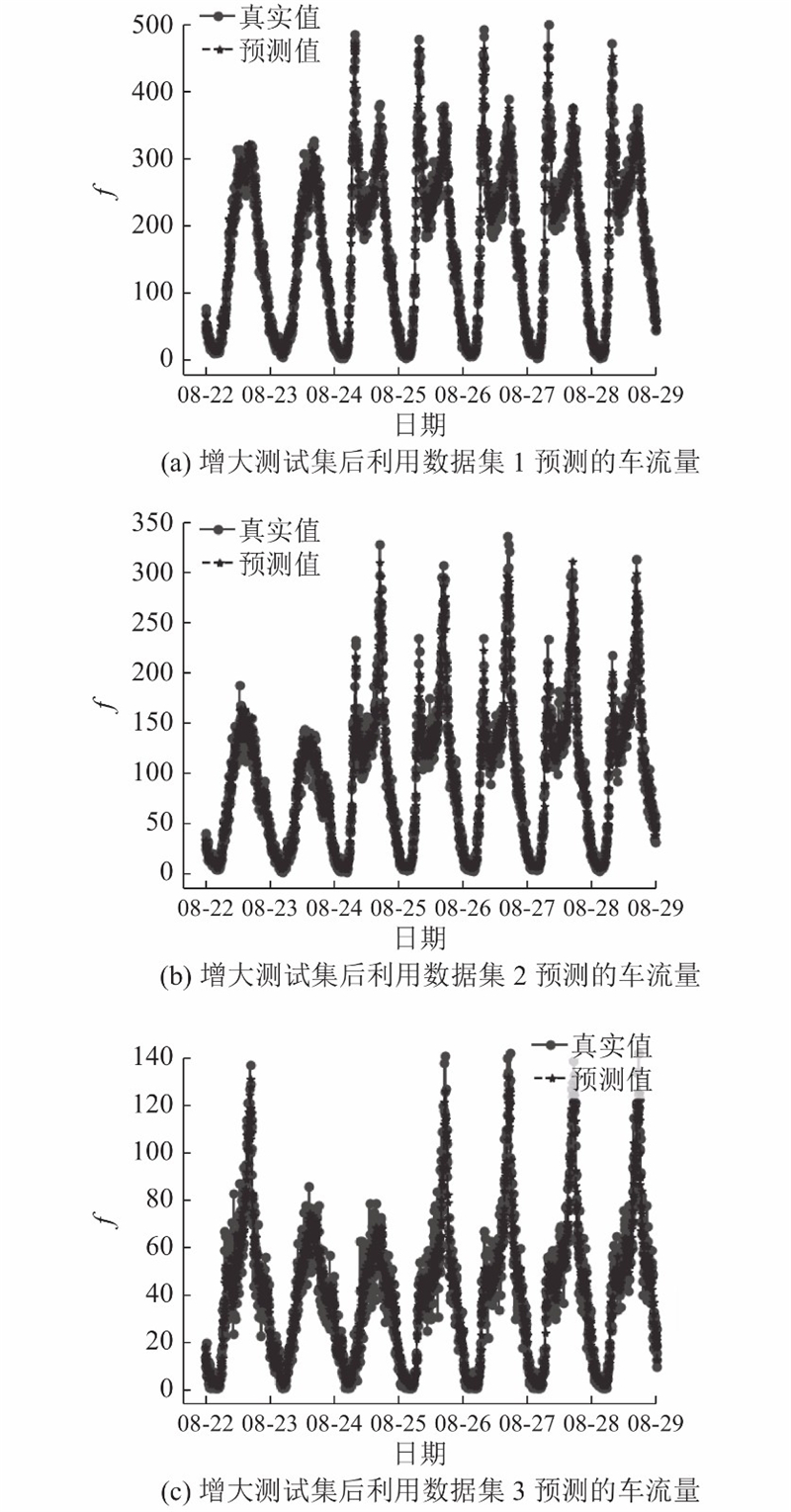
为了展现模型在处理数据纵向周期性和横向周期性方面的优势,增大了测试集,将最后一周的数据作为测试集. 预测结果如图7所示.
图 7
图 7 增大测试集后利用SPGAPSO-CKRVM预测3个路段的车流量结果
Fig.7 Traffic flow prediction results in three stations after increasing test set
为了开展路况预测的实验,利用SPGAPSO-CKRVM对车速数据进行预测. 车速的预测结果如表5所示.
表 5 不同算法模型预测车速的对比
Tab.5
| 算法模型 | 数据集1 | 数据集2 | 数据集3 | ||||||||
| MSE | RMSE | MAPE | MSE | RMSE | MAPE | MSE | RMSE | MAPE | |||
| PSO-SVM | 6.0762 | 2.4650 | 0.0738 | 7.2539 | 2.6933 | 0.0768 | 7.1888 | 2.6812 | 0.0754 | ||
| LSTM | 5.1940 | 2.2790 | 0.0596 | 5.6122 | 2.3690 | 0.0625 | 5.5984 | 2.3661 | 0.0629 | ||
| GRU | 5.1532 | 2.2701 | 0.0583 | 5.6074 | 2.3681 | 0.0628 | 5.6164 | 2.3699 | 0.0632 | ||
| CNN-LSTM | 5.1726 | 2.2740 | 0.0582 | 5.3024 | 2.3027 | 0.0613 | 5.5418 | 2.3541 | 0.0622 | ||
| CNN-GRU | 5.0687 | 2.2514 | 0.0576 | 5.2964 | 2.3014 | 0.0612 | 5.5469 | 2.3552 | 0.0621 | ||
| Bi-LSTM | 5.1557 | 2.2706 | 0.0579 | 5.4228 | 2.3287 | 0.0627 | 5.5691 | 2.3599 | 0.0625 | ||
| GA-CKRVM | 4.8118 | 2.1936 | 0.0581 | 5.0895 | 2.2560 | 0.0603 | 5.5145 | 2.3483 | 0.0597 | ||
| CNN-Bi-LSTM | 5.0794 | 2.2538 | 0.0572 | 5.1734 | 2.2745 | 0.0599 | 5.5286 | 2.3513 | 0.0603 | ||
| SPGAPSO-CKRVM | 4.6656 | 2.1601 | 0.0570 | 4.9809 | 2.2318 | 0.0586 | 5.4214 | 2.3284 | 0.0589 | ||
从表5可以看出,车速预测和车流量预测的对比结果类似. 增大车速预测的测试集后,SPGAPSO-CKRVM在3个数据集中对应的MAPE为0.060 6、0.058 9和0.059 1,RMSE为2.187 2、2.248 2和2.317 4. SPGAPSO-CKRVM的表现均优于其他算法或模型,预测准确率可以满足路况预测的要求.
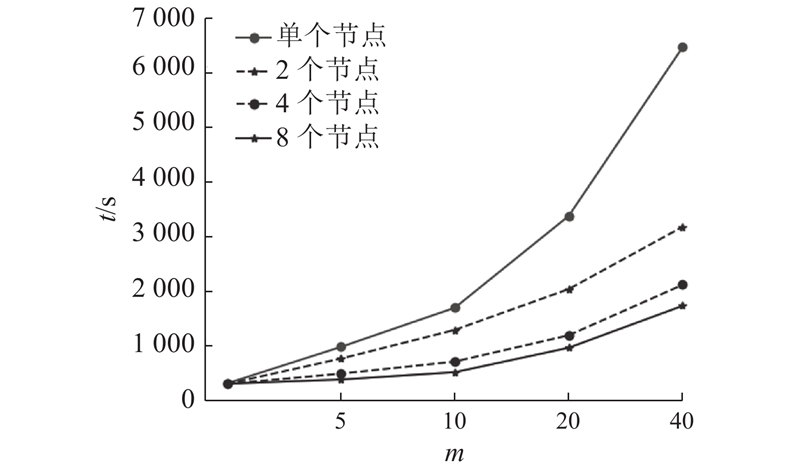
4.3.3. 算法可扩展性实验
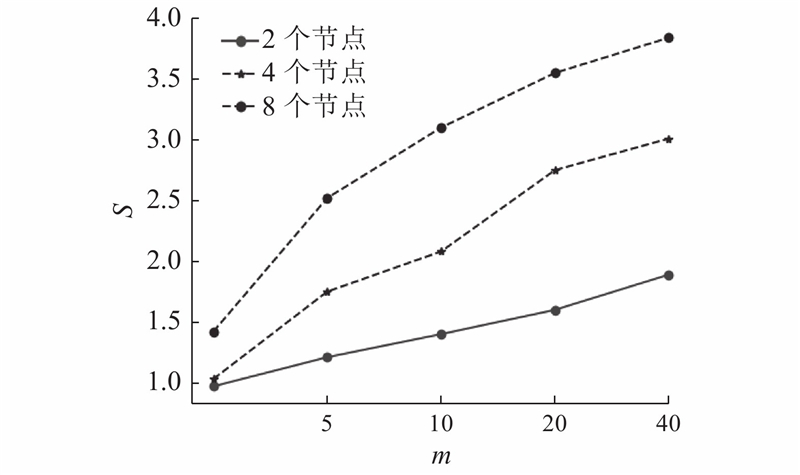
算法可扩展性实验用于测试是否可以通过增加节点来提高算法运行速度,通过计算加速比来衡量并行化效果. 该实验基于单个节点、2个节点、4个节点和8个节点,运行SPGAPSO-CKRVM算法10次,记录实验结果并计算加速比. 加速比的计算方式如下:
图 8
图 9
种群大小决定SPGAPSO-CKRVM的计算量. 从图8可以看出,随着计算量的逐步增大,运行时间呈线性增长. 当计算量小时,算法在单个节点、2个节点、4个节点和8个节点上的训练时间差别较小. 随着计算量的增大,8个节点的运行时间远远低于4个节点、2个节点和单个节点. 这是因为节点数越多,每个计算节点负责处理的计算量越小.
从图9可以看出,在计算量小的情况下,加速效果不明显. 这是因为集群的启动作业、划分任务和分配资源等基础操作的消耗时间较多,集群尚未发挥到理想的效果. 随着计算量的增大,并行计算的优势越来越明显,加速比呈增长趋势并逐渐趋于理想值. 实验结果验证了提出的SPGAPSO-CKRVM算法具有较好的可扩展性.
4.3.4. 路况预测结果
由于在进行车速预测时使用的数据为平均车速,不需进行平均车速的计算. 根据美国发行的《道路通行能力手册》计算出Whitemud Drive的最大道路通行能力约为单车道180 PCH,根据式(2)、(3)计算ID1027路段未来时刻的路段饱和度和交通流密度.
利用Matlab计算得到
图 10
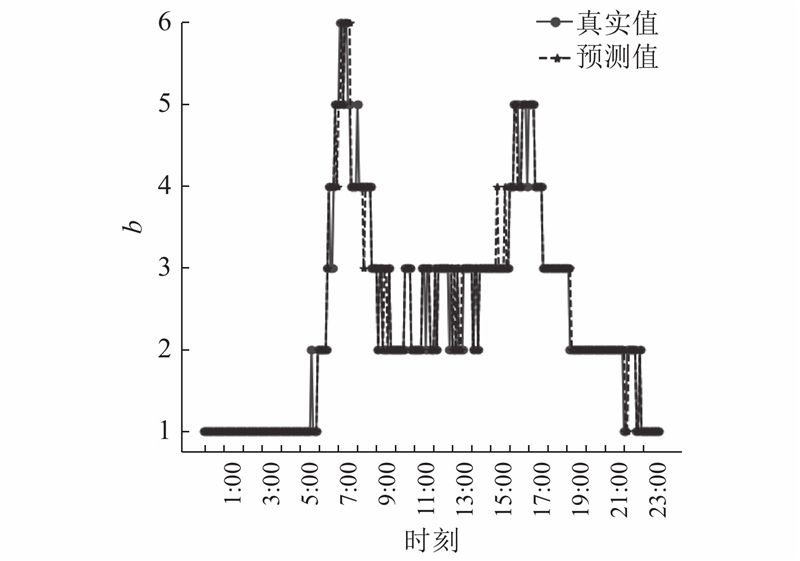
从图10可知,早高峰比晚高峰更拥堵,甚至已出现锁死路况. 晚高峰路况比早高峰路况缓和一些. 路况预测结果与实际路况基本吻合,共28个时刻存在误差,路况预测准确率为90.28%,证明了模糊综合评价路况的合理性.
5. 结 语
本文结合RVM、智能算法、Spark并行化技术和模糊综合评价,构建准确的路况预测模型. 利用加拿大Whitemud Drive公路的真实数据进行实验后可知,提出的模型在预测精度上优于其他方法,有效缩短了参数寻优的时间,能够准确地预测未来路况,准确率可以达到90.28%. 进一步的研究方向如下. 1)考虑更多的可能影响车流量的因素,例如平均车速、车道占用率和临近道路中的车流量情况等. 针对车速预测问题,设计针对性模型,利用图神经网络提高车速预测的准确率. 2)优化参数寻优算法. 大多数智能算法会在RVM的参数寻优中出现迭代前期收敛速度过快、迭代后期种群多样性降低的问题. 在后续的研究中,应尝试将RVM结合复杂的智能算法,如自适应遗传算法(adaptive genetic algorithm)和量子粒子群算法(quantum particle swarm algorithm). 3)尝试将RVM结合深度学习. 利用LSTM、DBN、CNN等深度学习算法提取交通数据特征,利用RVM进行预测,构成深层预测模型. 4)尝试结合因果科学. 研究挖掘路况成因,结合更多的交通专业知识,构建路况因果图,将数据驱动的模型转变为因果驱动模型.
参考文献
支持向量机在智能交通系统中的研究应用综述
[J].DOI:10.3778/j.issn.1673-9418.2001029 [本文引用: 1]
Survey on research and application of support vector machines in intelligent transportation system
[J].DOI:10.3778/j.issn.1673-9418.2001029 [本文引用: 1]
An aggregation approach to short-term traffic flow prediction
[J].
Detection and estimation for the traffic flow based on Kalman filter
[J].
基于粒子群优化的支持向量回归车道饱和度预测
[J].
Traffic lane saturation prediction with the support vector regression based on particle swarm optimization
[J].
Short-term traffic speed forecasting based on attention convolutional neural network for arterials
[J].DOI:10.1111/mice.12417 [本文引用: 1]
Financial assets price prediction based on relevance vector machine with genetic algorithm
[J].DOI:10.4156/jcit.vol7.issue5.12 [本文引用: 1]
Hybrid CSA optimization with seasonal RVR in traffic flow forecasting
[J].
A novel learning method for multi-intersections aware traffic flow forecasting
[J].
交通运行指数的研究与应用综述
[J].DOI:10.3963/j.issn1674-4861.2016.03.001 [本文引用: 1]
An overview of studies and applications on traffic performance index
[J].DOI:10.3963/j.issn1674-4861.2016.03.001 [本文引用: 1]
Development of highway congestion index with fuzzy set models
[J].
Developing a travel time congestion index
[J].DOI:10.1177/0361198196156400101 [本文引用: 1]
并行优化KNN算法的交通运输路况预测模型
[J].DOI:10.3969/j.issn.1001-7119.2016.09.040 [本文引用: 1]
Forecasting model of road transportation based on parallel optimized KNN algorithm
[J].DOI:10.3969/j.issn.1001-7119.2016.09.040 [本文引用: 1]
基于多指标模糊综合评价的交通拥堵预测与评估
[J].
Traffic congestion prediction and assessment based on multi-index fuzzy comprehensive evaluation
[J].
Sparse Bayesian learning and the relevance vector machine
[J].
综合评价中确定权重向量的几种方法比较
[J].DOI:10.3969/j.issn.1007-2373.2001.02.012 [本文引用: 2]
Comparing several methods of assuring weight vector in synthetical evaluation
[J].DOI:10.3969/j.issn.1007-2373.2001.02.012 [本文引用: 2]
Short-term traffic speed prediction under different data collection time intervals using a SARIMA-SDGM hybrid prediction model
[J].
A novel hybrid kernel function relevance vector machine for multi-task motor imagery EEG classification
[J].
基于MapReduce的层叠分组并行SVM算法研究
[J].DOI:10.3969/j.issn.1000-386x.2015.03.040 [本文引用: 1]
Research on cascade-grouping parallel SVM algorithm based on mapreduce
[J].DOI:10.3969/j.issn.1000-386x.2015.03.040 [本文引用: 1]
基于Spark的并行SVM算法研究
[J].
Research on parallel SVM algorithm based on Spark
[J].
A hybrid method for traffic flow forecasting using multimodal deep learning
[J].
基于Bi-LSTM模型的高速公路交通量预测
[J].
Highway traffic volume prediction based on Bi-LSTM model
[J].
一种组合核相关向量机的短时交通流局域预测方法
[J].DOI:10.11918/j.issn.0367-6234.2017.03.023 [本文引用: 1]
A short-term traffic flow local prediction method of combined kernel function relevance vector machine
[J].DOI:10.11918/j.issn.0367-6234.2017.03.023 [本文引用: 1]