目前,安全、智能和环保汽车已经成为现阶段国内外汽车厂商的主要发展目标之一,连续、快速和稳定的车轮滑移率跟踪控制是汽车实现智能安全避障、制动能量回收等先进控制技术的重要基础,因此深入研究连续、快速和稳定的车轮滑移率跟踪控制方法具有重要的工程实用价值.
车轮滑移率跟踪控制早期多应用于汽车的防抱死制动系统(anti-lock braking system,ABS)中,通过控制车轮滑移率使轮胎-地面附着系数最大,进而提高汽车制动稳定性和缩短汽车制动距离. 由于车轮滑移率动态在汽车制动过程中呈现出复杂的非线性特点,早期多采用逻辑切换规则的控制方式实现车轮滑移率的强鲁棒跟踪控制[1-5]. Kuo等[1]利用车轮滑移率、角加速度和车轮制动力矩信息,设计ABS工作模式的逻辑切换控制规则,将轮胎-地面附着系数控制到最大值. Tanelli等[2]将车轮制动力矩和车轮滑移率等信息作为切换控制信号,实现ABS工作模式的切换控制. 马付雷[4]基于车轮角加速度辅助车轮滑移率等信息设计逻辑切换规则,实现ABS工作模式的平滑切换控制. 上述基于逻辑切换规则的控制方式难以对任意目标滑移率进行高精度的稳定跟踪控制,无法满足安全、智能和环保汽车对车轮滑移率跟踪控制的需求.
基于动态模型的控制方式更容易实现连续目标滑移率的跟踪控制,易满足安全、智能和环保汽车对车轮滑移率跟踪控制的需求. Pasillas-Lepine等[6]采用Backstepping方法,设计车轮滑移率跟踪控制律. Shim等[7]基于滑模控制理论,设计车轮滑移率跟踪控制律. Yu等[8]采用最小化目标滑移率跟踪误差准则,设计车轮滑移率跟踪控制律. Mirzaei等[9]采用最优预测控制方法,设计车轮滑移率跟踪控制律. Amodeo等[10]采用二阶滑模控制方法,设计车轮滑移律跟踪控制律. Tanelli等[11]基于李雅普诺夫稳定性理论,推导出可智能区分车轮滑移率稳定和非稳定区域的车轮滑移率跟踪控制律. Johansen等[12]采用线性二次最优控制方法,设计具有实时调度特性的车轮滑移率跟踪控制律. Zhang等[13]设计干扰观测器,在线补偿车轮滑移率闭环系统的不确定性. Zhang等[14]基于耗散性理论,设计车轮滑移率跟踪控制律. He等[15]利用障碍李雅普诺夫函数,设计车轮滑移率跟踪控制律. He等[16]利用时变非对称障碍函数,设计车轮滑移率跟踪控制律. 上述基于动态模型的控制方式通常需要依靠简化的控制模型才能得到有效的控制方案,简化后的控制模型无法精确地表征车轮滑移率状态在汽车制动过程中呈现出的复杂非线性. 在基于动态模型的控制方式中,采用简化的控制模型设计控制方案之前需要解决简化的控制模型无法精确表征系统状态的问题.
本文基于Burckhardt轮胎模型建立车轮滑移率跟踪控制模型,将模型简化过程中的不确定性考虑成系统的复合干扰项,同时将轮胎侧向力对纵向力的影响考虑成未知参数,从而解耦控制模型中的轮胎纵向力和侧向力. 利用双曲正切函数和终端吸引因子设计改进的跟踪微分器,平滑车轮滑移率跟踪误差和估计车轮滑移率跟踪误差的一阶导数,分别基于自适应快速终端滑模控制理论和投影算子理论设计车轮滑移率跟踪控制律和未知参数的自适应律. 仿真结果表明,所设计的车轮滑移率跟踪控制律具有控制精度高、鲁棒性强的优点,可以有效地抑制滑模控制固有的“抖振”现象.
1. 车轮滑移率跟踪控制模型
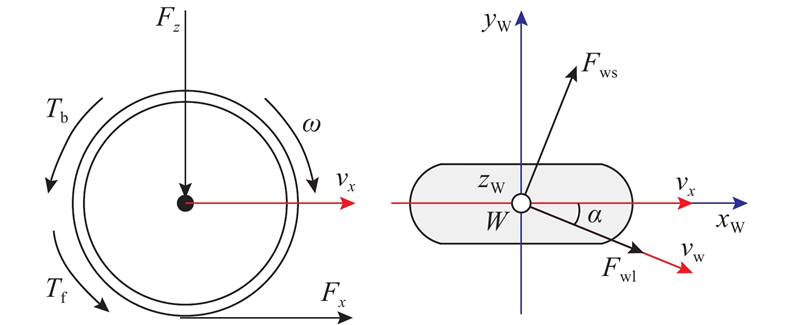
如图1所示的车轮滑移率动态模型,基于Burckhardt轮胎模型,建立关于车轮角速度和汽车纵向速度的动力学方程:
图 1
式中:
为了简化式(1)描述的关于车轮角速度和汽车纵向速度的动力学方程,将包含轮胎侧向力的因子与轮胎滚动阻力矩和机械摩擦阻力矩之和考虑成式(1)的扰动项,则式(1)修正为
式中:
Burckhardt轮胎模型描述的轮胎纵向力可以表示为
式中:
其中
若用未知参数描述车轮侧向滑移率对轮胎纵向力的影响,则式(3)修正为
假设
Burckhardt轮胎模型在制动工况下定义的车轮滑移率可以简化为
对式(7)求二阶微分运算,可得
对式(6)求一阶微分运算,可得
由于车身惯量远大于车轮惯量,车轮滑移率的变化快于车身运动状态的变化. 将式(6)、(9)代入式(8),令
式中:
2. 车轮滑移率跟踪控制器
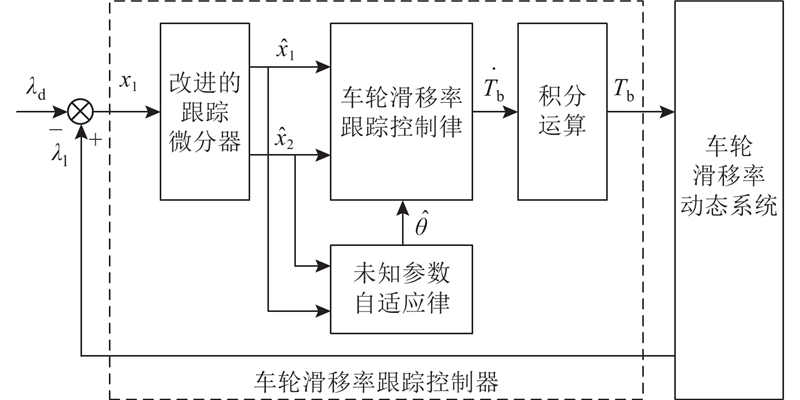
考虑式(10)描述的车轮滑移率跟踪控制模型,目标是设计改进的跟踪微分器、车轮滑移率跟踪控制律和未知参数自适应律,使得闭环系统可以高精度地跟踪车轮目标滑移率,对系统的复合干扰项具有较强的鲁棒性. 系统的总体架构如图2所示,改进的跟踪微分器用于平滑车轮滑移率跟踪误差,估计车轮滑移率跟踪误差的一阶导数. 车轮滑移率跟踪控制律基于改进的跟踪微分器的输出,计算车轮滑移率动态系统高精度的跟踪车轮目标滑移率所需要的车轮制动力矩变化率;利用未知参数自适应律实时估计和补偿车轮滑移率跟踪控制律中的未知参数,以提高车轮滑移率跟踪控制律对未建模动态的自适应能力. 车轮滑移率跟踪控制律的输出通过积分运算后作用于车轮滑移率动态系统,可以抑制系统的“抖振”现象.
图 2
2.1. 改进的跟踪微分器
利用跟踪微分器可以准确地计算信号的一阶导数,为全状态反馈控制律设计奠定基础. 申帅等[18]利用跟踪微分器计算航空光电稳定平台的加速度信号,实现航空光电稳定平台的高增益加速度反馈控制. 谭诗利等[19]利用跟踪微分器计算高超声速飞行器反演控制律中的虚拟控制量,有效解决了高超声速飞行器反演控制律的微分膨胀问题. 为了提高跟踪微分器的收敛速度,利用双曲正切函数和终端吸引因子设计改进的跟踪微分器来平滑车轮滑移率跟踪误差,估计车轮滑移率跟踪误差的一阶导数,以避免利用传统的一阶惯性环节求解信号微分过程中产生的噪声放大效应. 基于双曲正切函数和终端吸引子,设计定理1描述的具有渐近稳定平衡原点的动态系统. 基于该动态系统,构建改进的跟踪微分器.
定理1 假设原点
式中:
证明:定义Lyapunov候选函数为
由双曲正切函数为奇函数,且
对式(12)求导,可得
将式(11)代入式(13),可得
定义集合
由式(11)可知,当
根据文献[21]可知,基于式(11)构建改进的跟踪微分器为
式中:W为改进跟踪微分器的匹配参数,
2.2. 车轮滑移率跟踪控制律
基于改进跟踪微分器的输出,将式(10)描述的车轮滑移率跟踪控制模型转化为
以式(18)为基础,设计车轮滑移率跟踪控制律,使得闭环系统可以高精度地跟踪车轮目标滑移率,且对系统的复合干扰项具有较强的鲁棒性. 定义车轮滑移率跟踪误差滑模面为
式中:
基于式(19),定义如下快速终端滑模面:
式中:
由文献[22]可知,式(20)描述的快速终端滑模面可以在有限时间收敛到平衡点,收敛时间可以表示为
式中:
定理2 考虑式(18)描述的车轮滑移率跟踪控制模型,设计如下控制律:
式中:η1、η2为设计参数,
式中:
若设计参数
证明:定义Lyapunov候选函数为
式中:
对式(25)求导,可得
将式(22)代入式(26),可得
将式(23)代入式(27),可得
由投影算子的性质[24],可知
若设计参数
将式(29)、(30)代入式(28),可得
由式(30)可以定义如下不变集:
当
因此,当
当
综上所述,由LaSalle不变性原理[20]可知,闭环系统是渐近稳定的.
注1:在系统的复合干扰存在条件下,车轮滑移率跟踪闭环系统的状态轨迹可以渐近收敛到平衡原点,特别是在快速终端滑模面上的状态轨迹可以在有限时间内收敛到
注2:由式(22)可知,利用高阶滑模控制思想,将引起的“抖振”现象的不连续控制输入项包含于控制指令的一阶导数中;通过积分运算求解控制指令,从而有效抑制不连续控制输入项对系统性能的影响.
3. 仿真结果及分析
基于车辆动力学仿真软件CarSim,对设计的车轮滑移率跟踪控制律进行仿真验证,选择车辆前左轮和后右轮的仿真结果进行分析. 设计的改进跟踪微分器参数设置如下:
3.1. 斜坡信号工况
图 3
图 3 斜坡信号工况的跟踪误差及误差变化率
Fig.3 Tracking error and its rate of ramp signal maneuver
图 4
3.2. 正弦信号工况
图 5
图 5 正弦信号工况的跟踪误差及误差变化率
Fig.5 Tracking error and its rate of sine signal maneuver
图 6
4. 结 论
(1)基于Burckhardt轮胎模型建立车轮滑移率跟踪控制模型,将模型简化过程中的不确定性考虑成系统复合干扰项,将轮胎侧向力对纵向力的影响考虑成未知参数,解耦控制模型中的轮胎纵向力和侧向力.
(2)利用双曲正切函数和终端吸引因子设计改进的跟踪微分器,平滑车轮滑移率跟踪误差和估计车轮滑移率跟踪误差的一阶导数. 以车轮滑移率跟踪控制模型和改进的跟踪微分器输出为基础,基于自适应快速终端滑模控制理论和投影算子理论推导出未知参数自适应律,对系统复合干扰项具有强鲁棒性的车轮滑移率跟踪控制律;利用LaSalle不变性原理,证明了闭环系统的渐近稳定性.
(3)利用车辆动力学软件仿真,验证所提出的控制律的可行性和有效性. 结果表明,设计的改进跟踪微分器可以较好地平滑车轮滑移率跟踪误差,且可以无噪声地估计车轮滑移率跟踪误差变化率;提出的车轮滑移率跟踪控制律具有良好的控制品质,可以有效地抑制滑模控制中固有的“抖振”现象.
参考文献
A four-phase control scheme of an anti-skid brake system for all road conditions
[J].
Existence, stability and robustness analysis of limit cycles in hybrid anti-lock braking systems
[J].DOI:10.1080/00207170802203598 [本文引用: 1]
A switched control strategy for antilock braking system with on/off valves
[J].
ABS逻辑门限值自调整控制方法研究与试验验证
[J].DOI:10.3901/JME.2010.22.090 [本文引用: 1]
Research and verification of the logic threshold self-adjusting control method for ABS
[J].DOI:10.3901/JME.2010.22.090 [本文引用: 1]
Design and experimental validation of a nonlinear wheel slip control algorithm
[J].DOI:10.1016/j.automatica.2012.05.073 [本文引用: 1]
Investigation of sliding-surface design on the performance of sliding mode controller in antilock braking systems
[J].DOI:10.1109/TVT.2007.905391 [本文引用: 1]
Multiple model adaptive backstepping control for antilock braking system based on LuGre dynamic tyre model
[J].
Optimal design of a non-linear controller for anti-lock braking system
[J].DOI:10.1016/j.trc.2012.01.008 [本文引用: 1]
Wheel slip control via second-order sliding-mode generation
[J].DOI:10.1109/TITS.2009.2035438 [本文引用: 1]
Robust nonlinear output feedback control for brake by wire control systems
[J].DOI:10.1016/j.automatica.2007.08.020 [本文引用: 1]
Gain-scheduled wheel slip control in automotive brake systems
[J].DOI:10.1109/TCST.2003.815607 [本文引用: 1]
Adaptive backstepping sliding mode control for wheel slip tracking of vehicle with uncertainty observer
[J].
Robust backstepping sliding mode control with L2-gain performance for reference input wheel slip tracking of vehicle
[J].
Design and analysis of output feedback constraint control for antilock braking system with time-varying slip ratio
[J].
Design and analysis of output feedback constraint control for antilock braking system based on Burckhardt's model
[J].DOI:10.1108/AA-08-2018-0119 [本文引用: 1]
基于跟踪微分器的加速度反馈控制
[J].
Acceleration feedback control based on tracking differentiator
[J].
应用跟踪微分器的高超声速飞行器的反演控制
[J].
Backstepping control for hypersonic vehicle with a novel tracking differentiator
[J].
Nonlinear tracking differentiator
[J].
Nonsingular fast terminal sliding-mode control for nonlinear dynamical systems
[J].DOI:10.1002/rnc.1666 [本文引用: 1]
Adaptive robust control of MIMO nonlinear systems in semi-strict feedback form
[J].DOI:10.1016/S0005-1098(01)00082-6 [本文引用: 1]