[1]
CAO X, WEI Y, WEN F, et al Face alignment by explicit shape regression
[J]. International Journal of Computer Vision , 2014 , 107 (2 ): 177 - 190
DOI:10.1007/s11263-013-0667-3
[本文引用: 1]
[2]
ZHANG K, ZHANG Z, LI Z, et al Joint face detection and alignment using multitask cascaded convolutional networks
[J]. IEEE Signal Processing Letters , 2016 , 23 (10 ): 1499 - 1503
DOI:10.1109/LSP.2016.2603342
[本文引用: 1]
[3]
CHEN D, REN S, WEI Y, et al. Joint cascade face detection and alignment [C] // European Conference on Computer Vision . Switzerland: Springer, 2014: 109-122.
[本文引用: 1]
[4]
LIAO S, JAIN A K, LI S Z Partial face recognition: alignment-free approach
[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2013 , 35 (5 ): 1193 - 1205
DOI:10.1109/TPAMI.2012.191
[本文引用: 1]
[5]
MCNEILL G, VIJAYAKUMAR S. Hierarchical procrustes matching for shape retrieval [C] // 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition . New York: IEEE, 2006: 885-894.
[本文引用: 1]
[6]
LIN C, ZHANG T, LV C, et al. Improved explicit shape regression face alignment algorithm[C] // 2018 Chinese Control and Decision Conference . Shenyang: IEEE, 2018: 1166-1169.
[本文引用: 4]
[7]
DANTONE M, GALL J, FANELLI G, et al. Realtime facial feature detection using conditional regression forests [C] // IEEE Conference on Computer Vision and Pattern Recognition . Providence: IEEE, 2012: 2578-2585.
[本文引用: 4]
[8]
LI Q, SUN Z, HE R. Fast multi-view face alignment via multi-task auto-encoders [C] // 2017 IEEE International Joint Conference on Biometrics . Denver: IEEE, 2017: 538-545.
[本文引用: 4]
[9]
TZIMIROPOULOS G. Project-out cascaded regression with an application to face alignment [C] // IEEE Conference on Computer Vision and Pattern Recognition . Boston: IEEE, 2015: 3659-3667.
[本文引用: 2]
[10]
XIONG X, TORRE F D L. Supervised descent method and its applications to face alignment [C] // IEEE Conference on Computer Vision and Pattern Recognition . Portland: IEEE, 2013: 532-539.
[本文引用: 5]
[11]
LIU X Y An empirical study of boosting methods on severely imbalanced data
[J]. Applied Mechanics and Materials , 2014 , 513 (2 ): 2510 - 2513
[本文引用: 1]
[12]
DING C, SONG B, AKSHAY M, et al Collaborative sensing in a distributed PTZ camera network
[J]. IEEE Transactions on Image Processing , 2012 , 21 (7 ): 3282 - 3295
DOI:10.1109/TIP.2012.2188806
[本文引用: 1]
[13]
BERNARDIN K, CAMP F V D, STIEFELHAGEN R. Automatic person detection and tracking using fuzzy controlled active cameras [C] // IEEE Conference on Computer Vision and Pattern Recognition . Minneapolis: IEEE, 2007: 1-8.
[本文引用: 1]
[14]
SCOTTI G, MARCENARO L, COELHO C, et al Dual camera intelligent sensor for high definition 360 degrees surveillance
[J]. IEE Proceedings of Vision Image and Signal Processing , 2005 , 152 (2 ): 250 - 257
DOI:10.1049/ip-vis:20041302
[本文引用: 1]
[15]
KIM S, CHOI J. Face recognition method based on fixed and PTZ camera control for moving humans [C] // 2019 11th International Conference on Ubiquitous and Future Networks. Zagreb: IEEE, 2019: 561-563.
[本文引用: 1]
[16]
张文靖. 人脸-摄像机主动位姿协同[D]. 昆明: 昆明理工大学, 2019.
[本文引用: 1]
ZHANG Wen-jing. Face-camera active pose cooperation [D]. Kunming: Kunming University of Science and Technology, 2019.
[本文引用: 1]
[17]
曾慧, 穆志纯, 袁立 基于三维模型的人脸姿态估计方法
[J]. 计算机工程 , 2011 , 37 (9 ): 1 - 3
[本文引用: 1]
ZENG Hui, MU Zhi-chun, YUAN li Face pose estimation method based on 3D model
[J]. Computer Engineering , 2011 , 37 (9 ): 1 - 3
[本文引用: 1]
[18]
LEE D, YANG M H, OH S. Fast and accurate head pose estimation via random projection forests [C] // IEEE Proceedings of the International Conference on Computer Vision. Santiago: IEEE, 2015: 1958-1966.
[本文引用: 1]
[19]
MURPHY C E, TRIVEDI M M Head pose estimation in computer: a survey
[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2009 , 31 (4 ): 607 - 626
DOI:10.1109/TPAMI.2008.106
[本文引用: 1]
[20]
王世宙. 双目立体测量系统中数控平台的设计与标定 [D]. 南京: 南京航空航天大学, 2011.
[本文引用: 2]
WANG Shi-zhou. The design and calibration of the NC platform in binocular stereo measurement [D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2011.
[本文引用: 2]
[21]
邵杰, 张爱武, 王书民, 等 交替误差补偿的无人飞艇位姿估计
[J]. 计算机辅助设计与图形学学报 , 2013 , 25 (9 ): 1361 - 1367
[本文引用: 1]
SHAO Jie, ZHANG Ai-wu, WANG Shu-min, et al Pose estimation of unmanned airship of alternating error compensation
[J]. Journal of Computer-Aided Design and Computer Graphics , 2013 , 25 (9 ): 1361 - 1367
[本文引用: 1]
[22]
龚健雅, 季顺平 从摄影测量到计算机视觉
[J]. 武汉大学学报: 信息科学版 , 2017 , 42 (11 ): 1518 - 1522
[本文引用: 1]
GONG Jian-ya, JI Shun-ping Form photogrammetry to computer vision
[J]. Geomatics and Information Science of Wuhan University , 2017 , 42 (11 ): 1518 - 1522
[本文引用: 1]
[23]
龚健雅, 季顺平 摄影测量与深度学习
[J]. 测绘学报 , 2018 , 47 (6 ): 693 - 704
GONG Jian-ya, JI Shun-ping Photogrammetry and deep learning
[J]. Acta Geodaetica et Cartographica Sinica , 2018 , 47 (6 ): 693 - 704
[24]
DROUARD V, HORAUD R, DELEFORGE A, et al Robust head-pose estimation based on partially-latent mixture of linear regressions
[J]. IEEE Transactions on Image Processing , 2017 , 26 (3 ): 1428 - 1440
DOI:10.1109/TIP.2017.2654165
[本文引用: 1]
[25]
李成龙, 钟凡, 马昕, 等 基于卡尔曼滤波和随机回归森林的实时头部姿态估计
[J]. 计算机辅助设计与图形学学报 , 2017 , 29 (12 ): 2309 - 2316
DOI:10.3724/SP.J.1089.2017.16521
[本文引用: 1]
LI Cheng-long, ZHONG Fan, MA Xin, et al Real-time head pose estimation based on Kalman and random regression forest
[J]. Journal of Computer-Aided Design and Computer Graphics , 2017 , 29 (12 ): 2309 - 2316
DOI:10.3724/SP.J.1089.2017.16521
[本文引用: 1]
Face alignment by explicit shape regression
1
2014
... 人脸纠正是将倾斜、偏转的人脸变换为正视人脸图像的过程,是人脸检测、表情识别与人脸识别等技术的关键步骤. 在像方空间下,纠正人脸图像主要采用人脸对齐的方法[1 -2 ] . ...
Joint face detection and alignment using multitask cascaded convolutional networks
1
2016
... 人脸纠正是将倾斜、偏转的人脸变换为正视人脸图像的过程,是人脸检测、表情识别与人脸识别等技术的关键步骤. 在像方空间下,纠正人脸图像主要采用人脸对齐的方法[1 -2 ] . ...
1
... 人脸对齐是根据输入的人脸图像,定位出面部关键特征点,将非正视人脸相似变换至正视人脸[3 -4 ] . 对齐方法主要有手动标定对齐、局部对齐、整体对齐. Mcneill等[5 ] 采用基于分段的形状匹配算法(HPM),在基准形状检索测试中表现良好. Lin等[6 ] 提出基于级联回归的显式形状回归算法(ESR),使用矢量回归函数完成人脸面部形状推断,在面部形状定位中准确度较高. 手动标定对齐适用于构建人脸正视图像样本库. Dantone等[7 ] 采用回归森林方法分类人脸特征点,该方法对于低质量图像具有良好的估算能力.Li等[8 ] 提出两级多任务自动编码框架,通过引入头部姿态信息处理大视点的变化,从而实现脸部快速对准. 局部对齐方法是以先验知识为基础的局部似然估计,当特征点数量增加时,计算代价较高. Tzimiropoulos[9 ] 采用Hand-crafted类型的Sift特征进行无监督学习,建立精确的人脸对齐系统. Xiong等[10 ] 利用线性最小二乘函数的监督下降法,在面部特征检测问题上达到较好的性能. 整体对齐相较于局部对齐表现出较强的鲁棒性与实时性. 当人脸偏转角度较大时,人脸图像变形较大、信息缺失较严重,人脸对齐的累积误差呈现明显的增大趋势,难以纠正人脸图像[11 ] . ...
Partial face recognition: alignment-free approach
1
2013
... 人脸对齐是根据输入的人脸图像,定位出面部关键特征点,将非正视人脸相似变换至正视人脸[3 -4 ] . 对齐方法主要有手动标定对齐、局部对齐、整体对齐. Mcneill等[5 ] 采用基于分段的形状匹配算法(HPM),在基准形状检索测试中表现良好. Lin等[6 ] 提出基于级联回归的显式形状回归算法(ESR),使用矢量回归函数完成人脸面部形状推断,在面部形状定位中准确度较高. 手动标定对齐适用于构建人脸正视图像样本库. Dantone等[7 ] 采用回归森林方法分类人脸特征点,该方法对于低质量图像具有良好的估算能力.Li等[8 ] 提出两级多任务自动编码框架,通过引入头部姿态信息处理大视点的变化,从而实现脸部快速对准. 局部对齐方法是以先验知识为基础的局部似然估计,当特征点数量增加时,计算代价较高. Tzimiropoulos[9 ] 采用Hand-crafted类型的Sift特征进行无监督学习,建立精确的人脸对齐系统. Xiong等[10 ] 利用线性最小二乘函数的监督下降法,在面部特征检测问题上达到较好的性能. 整体对齐相较于局部对齐表现出较强的鲁棒性与实时性. 当人脸偏转角度较大时,人脸图像变形较大、信息缺失较严重,人脸对齐的累积误差呈现明显的增大趋势,难以纠正人脸图像[11 ] . ...
1
... 人脸对齐是根据输入的人脸图像,定位出面部关键特征点,将非正视人脸相似变换至正视人脸[3 -4 ] . 对齐方法主要有手动标定对齐、局部对齐、整体对齐. Mcneill等[5 ] 采用基于分段的形状匹配算法(HPM),在基准形状检索测试中表现良好. Lin等[6 ] 提出基于级联回归的显式形状回归算法(ESR),使用矢量回归函数完成人脸面部形状推断,在面部形状定位中准确度较高. 手动标定对齐适用于构建人脸正视图像样本库. Dantone等[7 ] 采用回归森林方法分类人脸特征点,该方法对于低质量图像具有良好的估算能力.Li等[8 ] 提出两级多任务自动编码框架,通过引入头部姿态信息处理大视点的变化,从而实现脸部快速对准. 局部对齐方法是以先验知识为基础的局部似然估计,当特征点数量增加时,计算代价较高. Tzimiropoulos[9 ] 采用Hand-crafted类型的Sift特征进行无监督学习,建立精确的人脸对齐系统. Xiong等[10 ] 利用线性最小二乘函数的监督下降法,在面部特征检测问题上达到较好的性能. 整体对齐相较于局部对齐表现出较强的鲁棒性与实时性. 当人脸偏转角度较大时,人脸图像变形较大、信息缺失较严重,人脸对齐的累积误差呈现明显的增大趋势,难以纠正人脸图像[11 ] . ...
4
... 人脸对齐是根据输入的人脸图像,定位出面部关键特征点,将非正视人脸相似变换至正视人脸[3 -4 ] . 对齐方法主要有手动标定对齐、局部对齐、整体对齐. Mcneill等[5 ] 采用基于分段的形状匹配算法(HPM),在基准形状检索测试中表现良好. Lin等[6 ] 提出基于级联回归的显式形状回归算法(ESR),使用矢量回归函数完成人脸面部形状推断,在面部形状定位中准确度较高. 手动标定对齐适用于构建人脸正视图像样本库. Dantone等[7 ] 采用回归森林方法分类人脸特征点,该方法对于低质量图像具有良好的估算能力.Li等[8 ] 提出两级多任务自动编码框架,通过引入头部姿态信息处理大视点的变化,从而实现脸部快速对准. 局部对齐方法是以先验知识为基础的局部似然估计,当特征点数量增加时,计算代价较高. Tzimiropoulos[9 ] 采用Hand-crafted类型的Sift特征进行无监督学习,建立精确的人脸对齐系统. Xiong等[10 ] 利用线性最小二乘函数的监督下降法,在面部特征检测问题上达到较好的性能. 整体对齐相较于局部对齐表现出较强的鲁棒性与实时性. 当人脸偏转角度较大时,人脸图像变形较大、信息缺失较严重,人脸对齐的累积误差呈现明显的增大趋势,难以纠正人脸图像[11 ] . ...
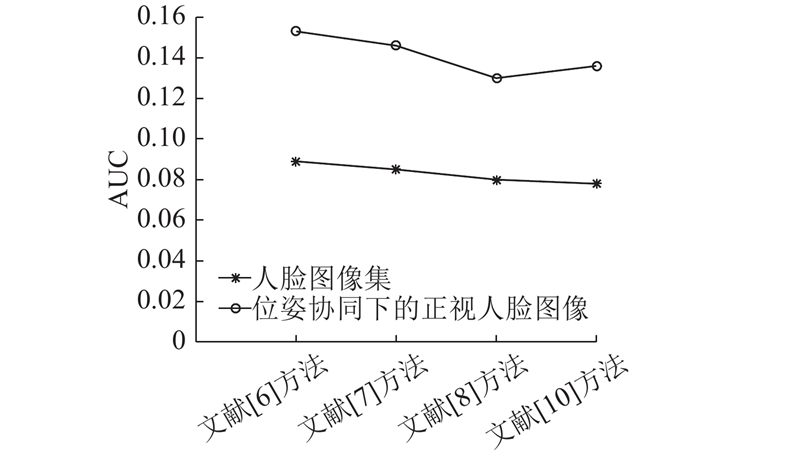
... 将摄像机静止下所拍摄的人脸图像集与位姿协同下所拍摄的人脸正视图像集分别利用手动标定对齐[6 ] 、局部对齐[7 -8 ] 、整体对齐[10 ] 的方法进行人脸对齐和误差评定,如图8 所示. 人脸对齐的评价标准参考文献[9 ],模型评估指标受试者工作特征曲线下面积(area under curve,AUC)越大,人脸对齐的累积误差越小,人脸对齐精度越高. 利用位姿协同所拍摄的人脸正视图像集,相较于摄像机静止所拍摄的人脸图像集,AUC较大,人脸对齐的准确度更高. ...
... 定量对比分析摄像机静止和位姿协同下所拍摄的人脸图像对人脸对齐的影响. 以人脸正对摄像机为起始状态,绕Y 轴缓慢逆时针旋转. 分别控制摄像机静止和作位姿协同运动,拍摄不同角度下的人脸图像,利用手动标定对齐[6 ] 、局部对齐[7 -8 ] 、整体对齐[10 ] 的方法进行人脸对齐的效果如图10 所示. 图中,c 为人脸偏转角度. ...
... 对于摄像机静止下所拍摄的人脸图像,文献[6 ]、[7 ]、[8 ]、[10 ]方法分别在人脸偏转角大于6°、6°、9°、14°时,AUC逐渐减小,人脸对齐的累积误差逐渐增大,人脸对齐逐渐失准. 对于位姿协同下所拍摄的人脸图像,这4种方法在同样的人脸偏转角度时,AUC较高,人脸对齐的累积误差较小,人脸对齐的准确度保持在良好稳定水平. 可知,位姿协同下获取的人脸正视图像,减缓因人脸偏转角度大而引起的人脸图像的形变和信息缺失,降低人脸对齐精度对人脸偏转角度的敏感度,提高人脸对齐的鲁棒性. ...
4
... 人脸对齐是根据输入的人脸图像,定位出面部关键特征点,将非正视人脸相似变换至正视人脸[3 -4 ] . 对齐方法主要有手动标定对齐、局部对齐、整体对齐. Mcneill等[5 ] 采用基于分段的形状匹配算法(HPM),在基准形状检索测试中表现良好. Lin等[6 ] 提出基于级联回归的显式形状回归算法(ESR),使用矢量回归函数完成人脸面部形状推断,在面部形状定位中准确度较高. 手动标定对齐适用于构建人脸正视图像样本库. Dantone等[7 ] 采用回归森林方法分类人脸特征点,该方法对于低质量图像具有良好的估算能力.Li等[8 ] 提出两级多任务自动编码框架,通过引入头部姿态信息处理大视点的变化,从而实现脸部快速对准. 局部对齐方法是以先验知识为基础的局部似然估计,当特征点数量增加时,计算代价较高. Tzimiropoulos[9 ] 采用Hand-crafted类型的Sift特征进行无监督学习,建立精确的人脸对齐系统. Xiong等[10 ] 利用线性最小二乘函数的监督下降法,在面部特征检测问题上达到较好的性能. 整体对齐相较于局部对齐表现出较强的鲁棒性与实时性. 当人脸偏转角度较大时,人脸图像变形较大、信息缺失较严重,人脸对齐的累积误差呈现明显的增大趋势,难以纠正人脸图像[11 ] . ...
... 将摄像机静止下所拍摄的人脸图像集与位姿协同下所拍摄的人脸正视图像集分别利用手动标定对齐[6 ] 、局部对齐[7 -8 ] 、整体对齐[10 ] 的方法进行人脸对齐和误差评定,如图8 所示. 人脸对齐的评价标准参考文献[9 ],模型评估指标受试者工作特征曲线下面积(area under curve,AUC)越大,人脸对齐的累积误差越小,人脸对齐精度越高. 利用位姿协同所拍摄的人脸正视图像集,相较于摄像机静止所拍摄的人脸图像集,AUC较大,人脸对齐的准确度更高. ...
... 定量对比分析摄像机静止和位姿协同下所拍摄的人脸图像对人脸对齐的影响. 以人脸正对摄像机为起始状态,绕Y 轴缓慢逆时针旋转. 分别控制摄像机静止和作位姿协同运动,拍摄不同角度下的人脸图像,利用手动标定对齐[6 ] 、局部对齐[7 -8 ] 、整体对齐[10 ] 的方法进行人脸对齐的效果如图10 所示. 图中,c 为人脸偏转角度. ...
... 对于摄像机静止下所拍摄的人脸图像,文献[6 ]、[7 ]、[8 ]、[10 ]方法分别在人脸偏转角大于6°、6°、9°、14°时,AUC逐渐减小,人脸对齐的累积误差逐渐增大,人脸对齐逐渐失准. 对于位姿协同下所拍摄的人脸图像,这4种方法在同样的人脸偏转角度时,AUC较高,人脸对齐的累积误差较小,人脸对齐的准确度保持在良好稳定水平. 可知,位姿协同下获取的人脸正视图像,减缓因人脸偏转角度大而引起的人脸图像的形变和信息缺失,降低人脸对齐精度对人脸偏转角度的敏感度,提高人脸对齐的鲁棒性. ...
4
... 人脸对齐是根据输入的人脸图像,定位出面部关键特征点,将非正视人脸相似变换至正视人脸[3 -4 ] . 对齐方法主要有手动标定对齐、局部对齐、整体对齐. Mcneill等[5 ] 采用基于分段的形状匹配算法(HPM),在基准形状检索测试中表现良好. Lin等[6 ] 提出基于级联回归的显式形状回归算法(ESR),使用矢量回归函数完成人脸面部形状推断,在面部形状定位中准确度较高. 手动标定对齐适用于构建人脸正视图像样本库. Dantone等[7 ] 采用回归森林方法分类人脸特征点,该方法对于低质量图像具有良好的估算能力.Li等[8 ] 提出两级多任务自动编码框架,通过引入头部姿态信息处理大视点的变化,从而实现脸部快速对准. 局部对齐方法是以先验知识为基础的局部似然估计,当特征点数量增加时,计算代价较高. Tzimiropoulos[9 ] 采用Hand-crafted类型的Sift特征进行无监督学习,建立精确的人脸对齐系统. Xiong等[10 ] 利用线性最小二乘函数的监督下降法,在面部特征检测问题上达到较好的性能. 整体对齐相较于局部对齐表现出较强的鲁棒性与实时性. 当人脸偏转角度较大时,人脸图像变形较大、信息缺失较严重,人脸对齐的累积误差呈现明显的增大趋势,难以纠正人脸图像[11 ] . ...
... 将摄像机静止下所拍摄的人脸图像集与位姿协同下所拍摄的人脸正视图像集分别利用手动标定对齐[6 ] 、局部对齐[7 -8 ] 、整体对齐[10 ] 的方法进行人脸对齐和误差评定,如图8 所示. 人脸对齐的评价标准参考文献[9 ],模型评估指标受试者工作特征曲线下面积(area under curve,AUC)越大,人脸对齐的累积误差越小,人脸对齐精度越高. 利用位姿协同所拍摄的人脸正视图像集,相较于摄像机静止所拍摄的人脸图像集,AUC较大,人脸对齐的准确度更高. ...
... 定量对比分析摄像机静止和位姿协同下所拍摄的人脸图像对人脸对齐的影响. 以人脸正对摄像机为起始状态,绕Y 轴缓慢逆时针旋转. 分别控制摄像机静止和作位姿协同运动,拍摄不同角度下的人脸图像,利用手动标定对齐[6 ] 、局部对齐[7 -8 ] 、整体对齐[10 ] 的方法进行人脸对齐的效果如图10 所示. 图中,c 为人脸偏转角度. ...
... 对于摄像机静止下所拍摄的人脸图像,文献[6 ]、[7 ]、[8 ]、[10 ]方法分别在人脸偏转角大于6°、6°、9°、14°时,AUC逐渐减小,人脸对齐的累积误差逐渐增大,人脸对齐逐渐失准. 对于位姿协同下所拍摄的人脸图像,这4种方法在同样的人脸偏转角度时,AUC较高,人脸对齐的累积误差较小,人脸对齐的准确度保持在良好稳定水平. 可知,位姿协同下获取的人脸正视图像,减缓因人脸偏转角度大而引起的人脸图像的形变和信息缺失,降低人脸对齐精度对人脸偏转角度的敏感度,提高人脸对齐的鲁棒性. ...
2
... 人脸对齐是根据输入的人脸图像,定位出面部关键特征点,将非正视人脸相似变换至正视人脸[3 -4 ] . 对齐方法主要有手动标定对齐、局部对齐、整体对齐. Mcneill等[5 ] 采用基于分段的形状匹配算法(HPM),在基准形状检索测试中表现良好. Lin等[6 ] 提出基于级联回归的显式形状回归算法(ESR),使用矢量回归函数完成人脸面部形状推断,在面部形状定位中准确度较高. 手动标定对齐适用于构建人脸正视图像样本库. Dantone等[7 ] 采用回归森林方法分类人脸特征点,该方法对于低质量图像具有良好的估算能力.Li等[8 ] 提出两级多任务自动编码框架,通过引入头部姿态信息处理大视点的变化,从而实现脸部快速对准. 局部对齐方法是以先验知识为基础的局部似然估计,当特征点数量增加时,计算代价较高. Tzimiropoulos[9 ] 采用Hand-crafted类型的Sift特征进行无监督学习,建立精确的人脸对齐系统. Xiong等[10 ] 利用线性最小二乘函数的监督下降法,在面部特征检测问题上达到较好的性能. 整体对齐相较于局部对齐表现出较强的鲁棒性与实时性. 当人脸偏转角度较大时,人脸图像变形较大、信息缺失较严重,人脸对齐的累积误差呈现明显的增大趋势,难以纠正人脸图像[11 ] . ...
... 将摄像机静止下所拍摄的人脸图像集与位姿协同下所拍摄的人脸正视图像集分别利用手动标定对齐[6 ] 、局部对齐[7 -8 ] 、整体对齐[10 ] 的方法进行人脸对齐和误差评定,如图8 所示. 人脸对齐的评价标准参考文献[9 ],模型评估指标受试者工作特征曲线下面积(area under curve,AUC)越大,人脸对齐的累积误差越小,人脸对齐精度越高. 利用位姿协同所拍摄的人脸正视图像集,相较于摄像机静止所拍摄的人脸图像集,AUC较大,人脸对齐的准确度更高. ...
5
... 人脸对齐是根据输入的人脸图像,定位出面部关键特征点,将非正视人脸相似变换至正视人脸[3 -4 ] . 对齐方法主要有手动标定对齐、局部对齐、整体对齐. Mcneill等[5 ] 采用基于分段的形状匹配算法(HPM),在基准形状检索测试中表现良好. Lin等[6 ] 提出基于级联回归的显式形状回归算法(ESR),使用矢量回归函数完成人脸面部形状推断,在面部形状定位中准确度较高. 手动标定对齐适用于构建人脸正视图像样本库. Dantone等[7 ] 采用回归森林方法分类人脸特征点,该方法对于低质量图像具有良好的估算能力.Li等[8 ] 提出两级多任务自动编码框架,通过引入头部姿态信息处理大视点的变化,从而实现脸部快速对准. 局部对齐方法是以先验知识为基础的局部似然估计,当特征点数量增加时,计算代价较高. Tzimiropoulos[9 ] 采用Hand-crafted类型的Sift特征进行无监督学习,建立精确的人脸对齐系统. Xiong等[10 ] 利用线性最小二乘函数的监督下降法,在面部特征检测问题上达到较好的性能. 整体对齐相较于局部对齐表现出较强的鲁棒性与实时性. 当人脸偏转角度较大时,人脸图像变形较大、信息缺失较严重,人脸对齐的累积误差呈现明显的增大趋势,难以纠正人脸图像[11 ] . ...
... 将摄像机静止下所拍摄的人脸图像集与位姿协同下所拍摄的人脸正视图像集分别利用手动标定对齐[6 ] 、局部对齐[7 -8 ] 、整体对齐[10 ] 的方法进行人脸对齐和误差评定,如图8 所示. 人脸对齐的评价标准参考文献[9 ],模型评估指标受试者工作特征曲线下面积(area under curve,AUC)越大,人脸对齐的累积误差越小,人脸对齐精度越高. 利用位姿协同所拍摄的人脸正视图像集,相较于摄像机静止所拍摄的人脸图像集,AUC较大,人脸对齐的准确度更高. ...
... 当人脸偏转角度分别为5°、15°、25°、35°、45°、55°时,利用文献[10 ]的方法分别对摄像机静止时所拍摄的人脸图像与位姿协同下所拍摄的人脸图像进行人脸对齐,以纠正人脸. 如图9(a) ~(f) 所示为摄像机静止时所拍摄的人脸进行纠正后的图像,如图9(g) ~(l) 所示为对应人脸偏转角度下摄像机进行位姿协同所拍摄的人脸进行纠正后的图像. ...
... 定量对比分析摄像机静止和位姿协同下所拍摄的人脸图像对人脸对齐的影响. 以人脸正对摄像机为起始状态,绕Y 轴缓慢逆时针旋转. 分别控制摄像机静止和作位姿协同运动,拍摄不同角度下的人脸图像,利用手动标定对齐[6 ] 、局部对齐[7 -8 ] 、整体对齐[10 ] 的方法进行人脸对齐的效果如图10 所示. 图中,c 为人脸偏转角度. ...
... 对于摄像机静止下所拍摄的人脸图像,文献[6 ]、[7 ]、[8 ]、[10 ]方法分别在人脸偏转角大于6°、6°、9°、14°时,AUC逐渐减小,人脸对齐的累积误差逐渐增大,人脸对齐逐渐失准. 对于位姿协同下所拍摄的人脸图像,这4种方法在同样的人脸偏转角度时,AUC较高,人脸对齐的累积误差较小,人脸对齐的准确度保持在良好稳定水平. 可知,位姿协同下获取的人脸正视图像,减缓因人脸偏转角度大而引起的人脸图像的形变和信息缺失,降低人脸对齐精度对人脸偏转角度的敏感度,提高人脸对齐的鲁棒性. ...
An empirical study of boosting methods on severely imbalanced data
1
2014
... 人脸对齐是根据输入的人脸图像,定位出面部关键特征点,将非正视人脸相似变换至正视人脸[3 -4 ] . 对齐方法主要有手动标定对齐、局部对齐、整体对齐. Mcneill等[5 ] 采用基于分段的形状匹配算法(HPM),在基准形状检索测试中表现良好. Lin等[6 ] 提出基于级联回归的显式形状回归算法(ESR),使用矢量回归函数完成人脸面部形状推断,在面部形状定位中准确度较高. 手动标定对齐适用于构建人脸正视图像样本库. Dantone等[7 ] 采用回归森林方法分类人脸特征点,该方法对于低质量图像具有良好的估算能力.Li等[8 ] 提出两级多任务自动编码框架,通过引入头部姿态信息处理大视点的变化,从而实现脸部快速对准. 局部对齐方法是以先验知识为基础的局部似然估计,当特征点数量增加时,计算代价较高. Tzimiropoulos[9 ] 采用Hand-crafted类型的Sift特征进行无监督学习,建立精确的人脸对齐系统. Xiong等[10 ] 利用线性最小二乘函数的监督下降法,在面部特征检测问题上达到较好的性能. 整体对齐相较于局部对齐表现出较强的鲁棒性与实时性. 当人脸偏转角度较大时,人脸图像变形较大、信息缺失较严重,人脸对齐的累积误差呈现明显的增大趋势,难以纠正人脸图像[11 ] . ...
Collaborative sensing in a distributed PTZ camera network
1
2012
... 运动目标的实时、自动跟踪是计算机视觉、目标识别和安全监控的关键技术之一,为了扩大监视范围,许多监控系统采用摄像机机位主动调整方法[12 ] . Bernardin等[13 ] 介绍利用平移式可缩放相机对室内环境进行自动监测的系统,表现出较高的自然度、灵活性和鲁棒性. Scotti等[14 ] 提出新型集成多摄像机视频传感器全景场景分析系统,开发了全向成像设备与PTZ相机协同操作的策略. Kim等[15 ] 使用线性判别分析(LDA)特征提取算法和内核相关过滤器(KCF)跟踪算法,主动调整摄像机机位,达到了跟踪监测效果,但需要搭建固定摄像机和PTZ摄像机的多相机协同环境. ...
1
... 运动目标的实时、自动跟踪是计算机视觉、目标识别和安全监控的关键技术之一,为了扩大监视范围,许多监控系统采用摄像机机位主动调整方法[12 ] . Bernardin等[13 ] 介绍利用平移式可缩放相机对室内环境进行自动监测的系统,表现出较高的自然度、灵活性和鲁棒性. Scotti等[14 ] 提出新型集成多摄像机视频传感器全景场景分析系统,开发了全向成像设备与PTZ相机协同操作的策略. Kim等[15 ] 使用线性判别分析(LDA)特征提取算法和内核相关过滤器(KCF)跟踪算法,主动调整摄像机机位,达到了跟踪监测效果,但需要搭建固定摄像机和PTZ摄像机的多相机协同环境. ...
Dual camera intelligent sensor for high definition 360 degrees surveillance
1
2005
... 运动目标的实时、自动跟踪是计算机视觉、目标识别和安全监控的关键技术之一,为了扩大监视范围,许多监控系统采用摄像机机位主动调整方法[12 ] . Bernardin等[13 ] 介绍利用平移式可缩放相机对室内环境进行自动监测的系统,表现出较高的自然度、灵活性和鲁棒性. Scotti等[14 ] 提出新型集成多摄像机视频传感器全景场景分析系统,开发了全向成像设备与PTZ相机协同操作的策略. Kim等[15 ] 使用线性判别分析(LDA)特征提取算法和内核相关过滤器(KCF)跟踪算法,主动调整摄像机机位,达到了跟踪监测效果,但需要搭建固定摄像机和PTZ摄像机的多相机协同环境. ...
1
... 运动目标的实时、自动跟踪是计算机视觉、目标识别和安全监控的关键技术之一,为了扩大监视范围,许多监控系统采用摄像机机位主动调整方法[12 ] . Bernardin等[13 ] 介绍利用平移式可缩放相机对室内环境进行自动监测的系统,表现出较高的自然度、灵活性和鲁棒性. Scotti等[14 ] 提出新型集成多摄像机视频传感器全景场景分析系统,开发了全向成像设备与PTZ相机协同操作的策略. Kim等[15 ] 使用线性判别分析(LDA)特征提取算法和内核相关过滤器(KCF)跟踪算法,主动调整摄像机机位,达到了跟踪监测效果,但需要搭建固定摄像机和PTZ摄像机的多相机协同环境. ...
1
... 本文建立人脸-摄像机位姿协同系统,映射相邻采样时刻的人脸姿态变化量到摄像机所在的运动控制器坐标系中,计算摄像机协同位姿[16 ] . 将协同位姿信号转换为PCI-1240U4轴运动控制卡控制的步进电机的脉冲信号,实现摄像机位姿的调整,在物方空间降低人脸旋转时的信息丢失,实时获取人脸正视图像,纠正人脸. ...
1
... 本文建立人脸-摄像机位姿协同系统,映射相邻采样时刻的人脸姿态变化量到摄像机所在的运动控制器坐标系中,计算摄像机协同位姿[16 ] . 将协同位姿信号转换为PCI-1240U4轴运动控制卡控制的步进电机的脉冲信号,实现摄像机位姿的调整,在物方空间降低人脸旋转时的信息丢失,实时获取人脸正视图像,纠正人脸. ...
基于三维模型的人脸姿态估计方法
1
2011
... 主动位姿协同需要计算人脸姿态角,现有的人脸姿态角计算方法可以分为基于外观的方法和基于模型的方法[17 ] . 基于外观的方法是假设人脸运动姿态与人脸特征[18 ] 之间存在某种特定关系,在二维人脸图像中得到特征向量,建立特征向量与人脸运动姿态之间的映射关系来进行姿态计算. 基于模型的方法主要思路是通过构建三维人脸标准模型,利用二维人脸图像特征和三维人脸模型特征间的对应关系来计算人脸姿态. 基于外观的方法关键是所建立映射关系的准确性[19 ] ,局限性是过度依赖训练样本数量. 与基于外观的方法相比,基于模型的方法计算简单、精度更高[20 -21 ] ,因此采用基于模型的方法进行人脸姿态计算. ...
基于三维模型的人脸姿态估计方法
1
2011
... 主动位姿协同需要计算人脸姿态角,现有的人脸姿态角计算方法可以分为基于外观的方法和基于模型的方法[17 ] . 基于外观的方法是假设人脸运动姿态与人脸特征[18 ] 之间存在某种特定关系,在二维人脸图像中得到特征向量,建立特征向量与人脸运动姿态之间的映射关系来进行姿态计算. 基于模型的方法主要思路是通过构建三维人脸标准模型,利用二维人脸图像特征和三维人脸模型特征间的对应关系来计算人脸姿态. 基于外观的方法关键是所建立映射关系的准确性[19 ] ,局限性是过度依赖训练样本数量. 与基于外观的方法相比,基于模型的方法计算简单、精度更高[20 -21 ] ,因此采用基于模型的方法进行人脸姿态计算. ...
1
... 主动位姿协同需要计算人脸姿态角,现有的人脸姿态角计算方法可以分为基于外观的方法和基于模型的方法[17 ] . 基于外观的方法是假设人脸运动姿态与人脸特征[18 ] 之间存在某种特定关系,在二维人脸图像中得到特征向量,建立特征向量与人脸运动姿态之间的映射关系来进行姿态计算. 基于模型的方法主要思路是通过构建三维人脸标准模型,利用二维人脸图像特征和三维人脸模型特征间的对应关系来计算人脸姿态. 基于外观的方法关键是所建立映射关系的准确性[19 ] ,局限性是过度依赖训练样本数量. 与基于外观的方法相比,基于模型的方法计算简单、精度更高[20 -21 ] ,因此采用基于模型的方法进行人脸姿态计算. ...
Head pose estimation in computer: a survey
1
2009
... 主动位姿协同需要计算人脸姿态角,现有的人脸姿态角计算方法可以分为基于外观的方法和基于模型的方法[17 ] . 基于外观的方法是假设人脸运动姿态与人脸特征[18 ] 之间存在某种特定关系,在二维人脸图像中得到特征向量,建立特征向量与人脸运动姿态之间的映射关系来进行姿态计算. 基于模型的方法主要思路是通过构建三维人脸标准模型,利用二维人脸图像特征和三维人脸模型特征间的对应关系来计算人脸姿态. 基于外观的方法关键是所建立映射关系的准确性[19 ] ,局限性是过度依赖训练样本数量. 与基于外观的方法相比,基于模型的方法计算简单、精度更高[20 -21 ] ,因此采用基于模型的方法进行人脸姿态计算. ...
2
... 主动位姿协同需要计算人脸姿态角,现有的人脸姿态角计算方法可以分为基于外观的方法和基于模型的方法[17 ] . 基于外观的方法是假设人脸运动姿态与人脸特征[18 ] 之间存在某种特定关系,在二维人脸图像中得到特征向量,建立特征向量与人脸运动姿态之间的映射关系来进行姿态计算. 基于模型的方法主要思路是通过构建三维人脸标准模型,利用二维人脸图像特征和三维人脸模型特征间的对应关系来计算人脸姿态. 基于外观的方法关键是所建立映射关系的准确性[19 ] ,局限性是过度依赖训练样本数量. 与基于外观的方法相比,基于模型的方法计算简单、精度更高[20 -21 ] ,因此采用基于模型的方法进行人脸姿态计算. ...
... 求解人脸姿态时,对标准人脸模型进行旋转、平移、缩放,以使标准人脸模型的特征点在像平面的投影与相应待测图像中的人脸特征点最佳拟合[20 ] . 利用最小二乘法,将标准人脸特征点与待测人脸特征点进行拟合: ...
2
... 主动位姿协同需要计算人脸姿态角,现有的人脸姿态角计算方法可以分为基于外观的方法和基于模型的方法[17 ] . 基于外观的方法是假设人脸运动姿态与人脸特征[18 ] 之间存在某种特定关系,在二维人脸图像中得到特征向量,建立特征向量与人脸运动姿态之间的映射关系来进行姿态计算. 基于模型的方法主要思路是通过构建三维人脸标准模型,利用二维人脸图像特征和三维人脸模型特征间的对应关系来计算人脸姿态. 基于外观的方法关键是所建立映射关系的准确性[19 ] ,局限性是过度依赖训练样本数量. 与基于外观的方法相比,基于模型的方法计算简单、精度更高[20 -21 ] ,因此采用基于模型的方法进行人脸姿态计算. ...
... 求解人脸姿态时,对标准人脸模型进行旋转、平移、缩放,以使标准人脸模型的特征点在像平面的投影与相应待测图像中的人脸特征点最佳拟合[20 ] . 利用最小二乘法,将标准人脸特征点与待测人脸特征点进行拟合: ...
交替误差补偿的无人飞艇位姿估计
1
2013
... 主动位姿协同需要计算人脸姿态角,现有的人脸姿态角计算方法可以分为基于外观的方法和基于模型的方法[17 ] . 基于外观的方法是假设人脸运动姿态与人脸特征[18 ] 之间存在某种特定关系,在二维人脸图像中得到特征向量,建立特征向量与人脸运动姿态之间的映射关系来进行姿态计算. 基于模型的方法主要思路是通过构建三维人脸标准模型,利用二维人脸图像特征和三维人脸模型特征间的对应关系来计算人脸姿态. 基于外观的方法关键是所建立映射关系的准确性[19 ] ,局限性是过度依赖训练样本数量. 与基于外观的方法相比,基于模型的方法计算简单、精度更高[20 -21 ] ,因此采用基于模型的方法进行人脸姿态计算. ...
交替误差补偿的无人飞艇位姿估计
1
2013
... 主动位姿协同需要计算人脸姿态角,现有的人脸姿态角计算方法可以分为基于外观的方法和基于模型的方法[17 ] . 基于外观的方法是假设人脸运动姿态与人脸特征[18 ] 之间存在某种特定关系,在二维人脸图像中得到特征向量,建立特征向量与人脸运动姿态之间的映射关系来进行姿态计算. 基于模型的方法主要思路是通过构建三维人脸标准模型,利用二维人脸图像特征和三维人脸模型特征间的对应关系来计算人脸姿态. 基于外观的方法关键是所建立映射关系的准确性[19 ] ,局限性是过度依赖训练样本数量. 与基于外观的方法相比,基于模型的方法计算简单、精度更高[20 -21 ] ,因此采用基于模型的方法进行人脸姿态计算. ...
从摄影测量到计算机视觉
1
2017
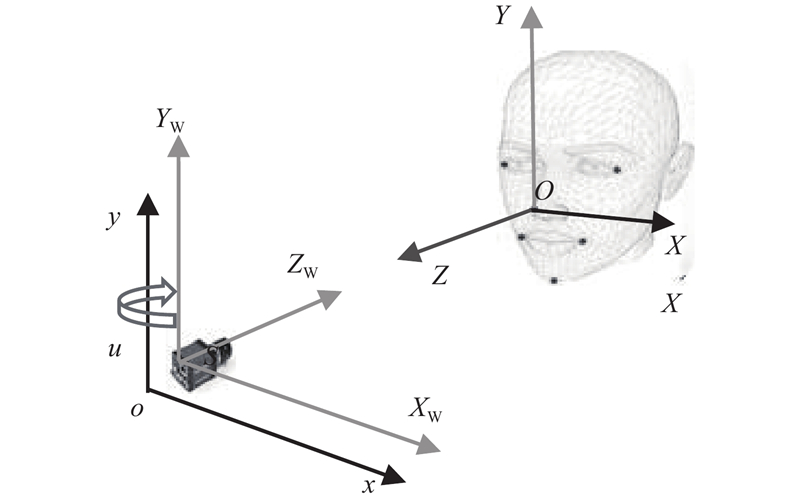
... 人脸姿态可以理解为摄影测量领域的相片外方位元素[22 -24 ] . 人脸姿态求解模型的坐标系关系如图1 所示. 图中,S-X K Y K Z K 为摄像机坐标系;O-X W Y W Z W 为世界坐标系;o 1 -x'y' 为像平面坐标系;o-u'v' 为像素坐标系. x' 、y' 轴分别平行于X S 、Y S 轴,且摄像机坐标系中每个像点的Z K 坐标均为−f (f 为相片主距). ...
从摄影测量到计算机视觉
1
2017
... 人脸姿态可以理解为摄影测量领域的相片外方位元素[22 -24 ] . 人脸姿态求解模型的坐标系关系如图1 所示. 图中,S-X K Y K Z K 为摄像机坐标系;O-X W Y W Z W 为世界坐标系;o 1 -x'y' 为像平面坐标系;o-u'v' 为像素坐标系. x' 、y' 轴分别平行于X S 、Y S 轴,且摄像机坐标系中每个像点的Z K 坐标均为−f (f 为相片主距). ...
Robust head-pose estimation based on partially-latent mixture of linear regressions
1
2017
... 人脸姿态可以理解为摄影测量领域的相片外方位元素[22 -24 ] . 人脸姿态求解模型的坐标系关系如图1 所示. 图中,S-X K Y K Z K 为摄像机坐标系;O-X W Y W Z W 为世界坐标系;o 1 -x'y' 为像平面坐标系;o-u'v' 为像素坐标系. x' 、y' 轴分别平行于X S 、Y S 轴,且摄像机坐标系中每个像点的Z K 坐标均为−f (f 为相片主距). ...
基于卡尔曼滤波和随机回归森林的实时头部姿态估计
1
2017
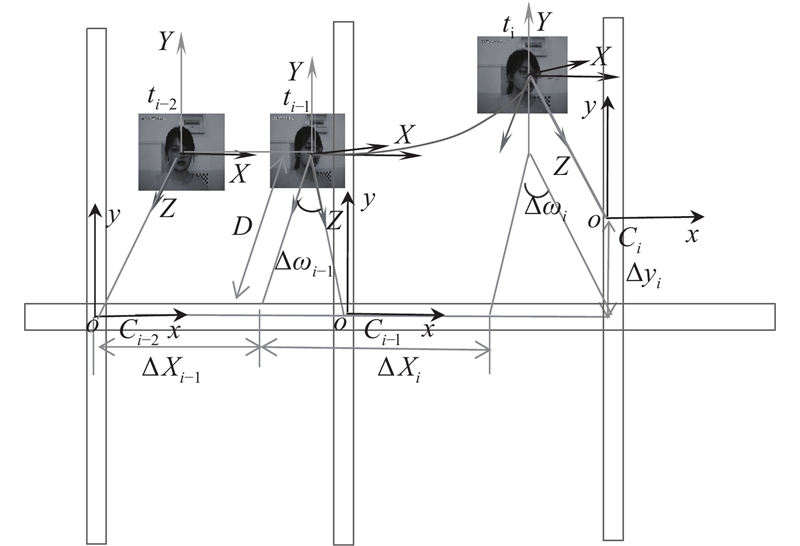
... 摄像机协同位姿为M T x T y R ω T . 摄像机协同位姿计算的关键是将人脸运动中姿态角变化而导致的摄像机在x 、y 轴产生的平移分量补偿到摄像机协同位姿中[25 ] . ...
基于卡尔曼滤波和随机回归森林的实时头部姿态估计
1
2017
... 摄像机协同位姿为M T x T y R ω T . 摄像机协同位姿计算的关键是将人脸运动中姿态角变化而导致的摄像机在x 、y 轴产生的平移分量补偿到摄像机协同位姿中[25 ] . ...