在仿人机器人-地面-环境系统中存在各种非理想因素,如建模误差和外力扰动. 从步行策略上看,人类可以通过实时调整落脚点以保持稳定[5]. Diedam等[6]考虑机器人质心(center of mass,CoM)状态变化,利用线性模型预测控制(model predictive control,MPC)策略实现落脚点调整. Fu[7]通过外力冲击估计与可捕捉区域检验,实时计算机器人落脚点. 张继文等[8]通过感知躯干倾斜角度,利用比例-微分控制器调整机器人落脚点. Zhang等[9]通过分析摆动腿动力学特性,提出能耗最优控制策略. Yu等[10]通过检测质心速度和加速度,将测量零力矩点(zero moment point,ZMP)和名义ZMP的误差映射为落脚点调整量. 此外,通过步行状态机切换,Ding等[11]实现了落脚点序列调整,但是仅调整落脚点对于机器人抗扰稳定性的提升有限.
实际上,步态优化面临结构尺寸、驱动能力、ZMP支撑范围等方面的约束. 从本质上讲,仿人机器人步态规划是约束优化问题. MPC采用滚动优化机制且能够求解多约束优化问题,在该问题求解上得到了越来越多的应用[16]. Aftab等[17]采用飞轮倒立摆模型(inverted pendulum plus flywheel model,IPFM),考虑躯干转动角度范围、足部支撑范围、腿长限制等可行性约束,提出线性MPC策略,实现落脚点和躯干旋转的同步优化. Lack等[18-19]从旋转角动量优化出发,实现了外力扰动下的稳定行走. 以上方法的目标函数中均只优化躯干旋转角速度或角加速度而没有考虑旋转角度,在外力消失后不能保证躯干恢复竖直状态.
本文提出基于MPC的机器人步态实时生成与优化策略. 考虑足部稳定支撑区域、躯干旋转角度范围和躯干旋转力矩范围等可行性约束,将该问题建模成为二次规划(quadratic programming,QP)问题. 基于CoM状态和躯干倾斜状态,通过在目标函数中引入足部落脚点和躯干摆动角度跟踪惩罚项,实时生成最优的CoM参考轨迹、足部落脚点和躯干旋转角度. 该方法既能够在无外力推动情况下生成变步行参数步态,也能够在有外力推动时调整足部落脚点和躯干旋转角度.
1. 问题描述
1.1. 行走动力学模型-IPFM
图 1
基于该模型,ZMP可以计算如下:
式中:
其中,
图 2
图 2 双足步行足部支撑多边形与ZMP、CoM轨迹
Fig.2 Foot support polygon, ZMP trajectory and CoM trajectory for bipedal walking
将步态规划问题转化为:给定落脚点参考位置和躯干转动参考角度,实时优化CoM轨迹、足部落脚点和躯干旋转角度,以保证ZMP位于足部支撑多边形以内.
1.2. 系统状态方程
基于IPFM模型和MPC理论[23],以CoM前向、侧向位置和躯干横滚角和俯仰角的3阶导数为控制输入,假设在每个采样时间间隔dt内的控制输入保持恒定,则第k个采样时刻,系统状态方程为
式中:
利用上述状态模型,给定当前状态,在预测时域(包含未来Nh个采样时长)内各参量的位置、速度、加速度可以由控制输入序列计算:
式中:
式(5)中,各系数矩阵
式中:
2. 二次规划问题建模
考虑可行性约束,建立能够调整足部落脚点和躯干倾斜姿态的步态规划约束优化模型. 该问题可以表示成下列QP模型:
式中:
2.1. 多目标惩罚函数
预先给定参考的足部落脚点位置和步行周期(本文中各周期时长为定值T),为了实现CoM轨迹生成并且能够在线调整足部落脚点和躯干摆动角度,在优化目标中引入CoM跟踪误差惩罚、躯干摆动角度跟踪误差惩罚以及足部落脚点跟踪误差惩罚. 考虑机器人驱动能力和系统控制能耗,引入CoM速度惩罚、躯干摆动角速度惩罚和控制输入惩罚,最终提出如下多目标惩罚函数:
式中:
利用该目标函数,式(7)中优化矢量
因此,优化变量数目
式(7)中的Hessian矩阵G推导如下:
式中:diag函数以各矩阵为对角元素生成对角矩阵;
其中,I为单位矩阵.
式(7)中的目标函数一次项矩阵g计算如下:
2.2. 参考轨迹生成
在目标函数(8)中,需要给定预测时域内参考的足部落脚点位置、CoM位置和躯干转动角度.
2.2.1. 参考落脚点位置
不同周期的足部落脚点,可以通过预先指定参考步长和步宽等步行参数求出. 通过坐标切换,求得参考落脚点的水平位置如下:
式中:
2.2.2. 参考CoM位置
式中:
给定步行周期时长和预测时长,预测时域内将会利用Nf个未来周期的落脚点信息. 此外,对于实际机器人而言,当前已落下的支撑脚应该保持不动. 需要将当前周期足部落脚点和预先指定的未来Nf周期落脚点映射成整个预测时域的参考落脚点.
在每个周期内,不考虑双足支撑阶段,参考足部支撑位置应保持不变. 预测时域内参考足部落脚点(以前向落脚点为例)可由下式计算:
式中:
其中,各行对应采样时刻,各列对应支撑周期.
2.2.3. 参考躯干旋转角度
在正常模式下,人类趋向于保持躯干竖直,以减少能量消耗. 本文将预测时域内的躯干参考横滚角和俯仰角设置为0,
式中:0为零元素矩阵.
2.3. 可行性约束
为了保证生成步态的可行性,需要考虑ZMP稳定性约束、足部落脚点变动范围限制、髋关节力矩限制等可行性约束.
2.3.1. ZMP稳定性约束
根据ZMP稳定性理论,机器人在行走过程中应保证ZMP在足部支撑多边形内. 由于单足支撑阶段支撑多边形稳定区域最小,且当采样时间较大时可以忽略双足支撑过程,本文只考虑单足支撑阶段以简化约束形式. 以前向运动为例,在预测时域内ZMP位置面临以下约束:
式中:
2.3.2. 足部落脚点变动范围约束
由目标函数(8)可知,实际足部落脚点会根据当前状态发生变化. 该变化受到腿长、关节角速度、自碰撞等约束,需要予以考虑. 从以下2个方面进行讨论.
1)由于机器人结构尺寸和驱动能力的限制,机器人步行参数如步长和步宽将会受到限制. 以前向足部落脚点为例,使用如下约束:
式中:
2)由于预测时域内足部落脚点在每次循环中都被重新计算,可能导致不同循环生成的未来某一周期的足部落脚点发生变动. 由于驱动能力的限制,摆动腿的摆动位置和速度(跟每个周期的足部落脚点直接相关)不能任意变化. 本文不直接约束摆动腿轨迹,而是限制由不同的控制循环计算生成的同一周期的落脚点位置变化. 由于该约束在每个循环均生效,本文只限制预测时域内未来下一个周期的落脚点变化. 提出如下约束:
式中:
2.3.3. 躯干转动约束
躯干旋转范围受到结构尺寸、驱动能力等限制,以躯干绕x轴转动(横滚角变化)为例,使用如下约束:
式中:
髋关节输出力矩存在以下约束:
式中:
使用IPFM模型,以上可行性约束条件均为线性约束,可以转化为式(7)中线性约束函数的表达形式,因此该优化问题是二次规划问题.
3. 动力学仿真
3.1. 仿真环境与参数设置
使用由意大利技术研究所(Italiatan Institution of Technology,IIT)仿人机器人课题组开发的基于开放式动力学引擎(open dynamics engine,ODE)的动力学仿真平台和IIT研发的COMAN[26]机器人,如图3所示. 机器人总高度为1.2 m,总质量为31 kg,每条腿各有6个自由度(髋关节3个、膝关节1个、踝关节2个),直立状态下髋关节高0.467 m. 机器人模型和控制器模型参数如表1所示,式(18)~(22)所列的约束条件参数如表2所示. 在仿真过程中,默认的步行周期为0.8 s,参考步长为10 cm,参考步宽为14.5 cm,摆动腿最大摆动高度为8 cm,双足支撑相占步行周期的比例为20%. 在行走过程中,摆动腿轨迹通过5次多项式插值获得. 仿真器底层的通讯频率为200 Hz.
图 3
图 3 COMAN机器人虚拟样机与ODE仿真环境
Fig.3 Virtual prototype of “COMAN” humanoid robot and ODE-based simulation environment
表 1 机器人与控制器的模型参数设置
Tab.1
| 参数 | 数值 | 参数 | 数值 | |
| | 2×105 | | 105 | |
| | 5×109 | | 106 | |
| | 10 | | 10 | |
| | 105 | | 103 | |
| | 1 | | 1 | |
| | 10 | | 10 | |
| | 5×107 | | 5×107 | |
| Nh | 31 | Nf | 2 | |
| Nc | 415 | dt/s | 0.05 | |
| T/s | 0.8 | m/kg | 30 | |
| Ix(Iy)/(kg·m2) | 0.3 | g/(m·s−2) | 9.8 |
表 2 二次规划约束条件参数设置
Tab.2
| 参数 | 数值 | 参数 | 数值 | |
| | −0.03 | | 0.07 | |
| | −0.05 | | 0.05 | |
| | −0.2 | | 0.3 | |
| | −0.1 | | 0.2 | |
| | −2 | | 3 | |
| | −2 | | 2 | |
| | −5 | | 10 | |
| | −10 | | 10 | |
| | −60 | | 80 | |
| | −80 | | 80 |
3.2. 无干扰变参数行走
由于存在动力学模型简化、机器人-地面接触模型不精确、多刚体系统姿态估计算法不准确等不确定性,机器人的实际状态与理想状态必然存在偏差. 改变步行参数将导致步态的非周期,进一步放大这种偏差,甚至可能导致失稳. 因此,需要机器人能够实时调整自身状态,以完成预定的行走目标. 首先验证该算法在使用实时反馈数据的情况下实现变参数稳定行走的能力.
表 3 变步行参数设置
Tab.3
| 周期 | 步长/cm | 步宽/cm | 周期 | 步长/cm | 步宽/cm | |
| 5 | 5 | − | 9 | −5 | 14 | |
| 6 | 15 | − | 10 | 0 | 14 | |
| 7 | 5 | 16 | 11 | −5 | 0 | |
| 8 | 15 | 16 | 12 | 5 | 0 |
仿真结果表明,只利用足部调整,由于实际反馈状态的不理想,机器人在行走过程中发生倾覆. 从图4可见,机器人上半身从6 s后开始剧烈晃动,最终失稳. 在集成躯干转动优化后,机器人可以顺利完成行走.
图 4
图 4 变步行参数行走躯干转动角度
Fig.4 Trunk rotation angles when walking with variant step parameters
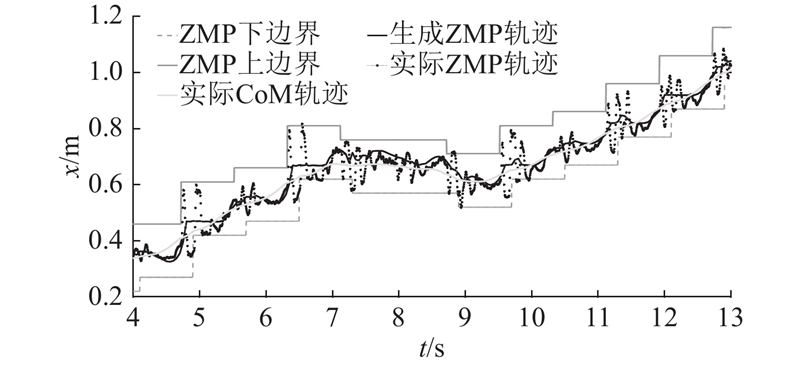
图 5
图 5 变步行参数行走前向足部支撑区域和ZMP、CoM轨迹
Fig.5 Forward support region,ZMP trajectories and CoM trajectory when walking with variant step parameters
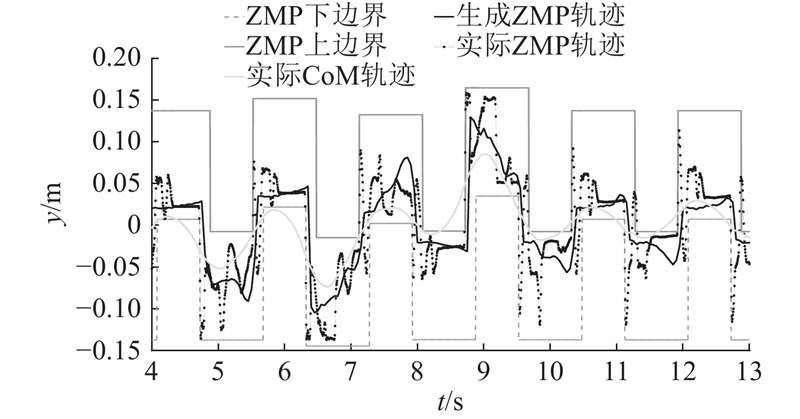
图 6
图 6 变步行参数行走侧向足部支撑区域和ZMP、CoM轨迹
Fig.6 Lateral support region,ZMP trajectories and CoM trajectory when walking with variant step parameters
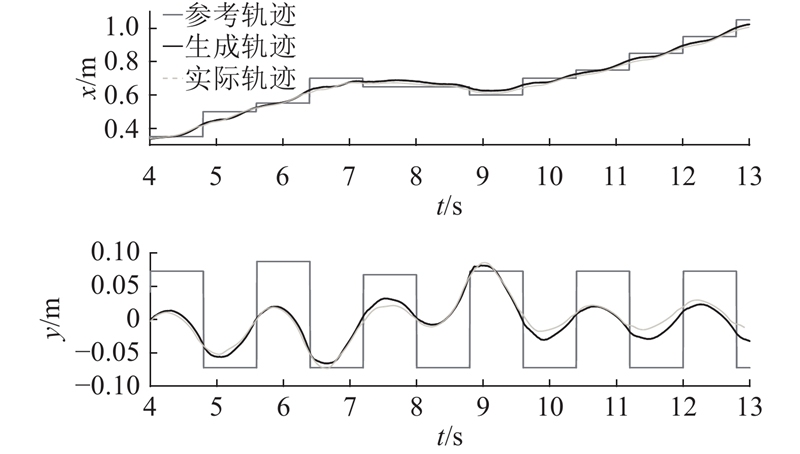
图5~7分别给出集成躯干转动后机器人其他重要状态参数的优化生成与实际测量结果. 图5、6表明,机器人在行走过程中能够较好地跟踪预定的足部落脚点. 不需要指定参考ZMP轨迹,由于足部落脚点的微调和躯干的转动,机器人能够保持生成ZMP轨迹和实际ZMP轨迹始终在足部支撑区域以内. 结合图4~7可以看出,在第6~14周期内,机器人利用躯干转动(图4中6~13 s内俯仰角的调整),在矢状面内的前进方向较准确地跟踪参考落脚点行走. 从图7可以看出,机器人侧向质心在第8周期(6 s左右)不能及时向左支撑脚靠近,导致后续周期CoM轨迹发生较明显的振荡. 由于足部落脚点调整(图6中8~10 s内侧向落脚点的调整)以及躯干转动(图4中8~10 s内算法生成横滚角的调整),保证机器人在侧向稳定.
图 7
图 7 变步行参数行走CoM轨迹
Fig.7 CoM trajectories when walking with variant step parameters
3.3. 行走过程中抗扰恢复
仿真中,在3.6 s时刻(此刻左脚支撑,且右脚摆动高度达到最高)对髋关节中心施加持续0.1 s的不同方向水平外力,观察机器人能否保持稳定.
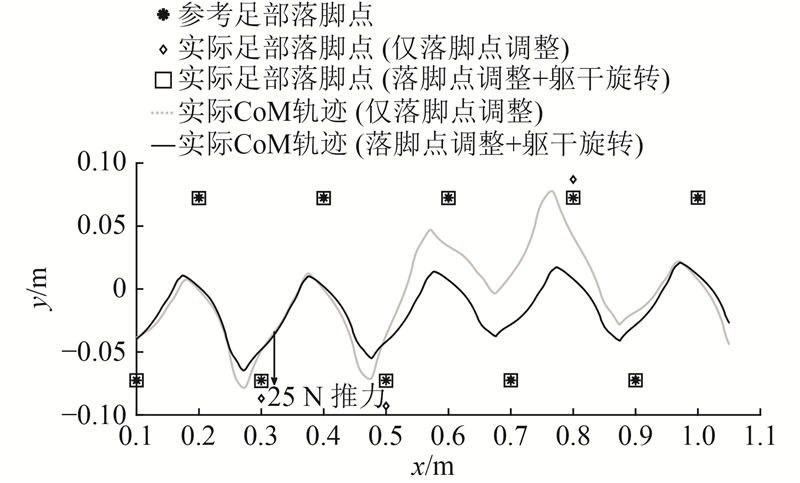
图 8
图 8 沿y轴负方向25 N外力作用下不同策略对应的实际落脚点和实际CoM轨迹
Fig.8 Actual step locations and CoM trajectories when using different strategies under external force(25 N along − y axis)
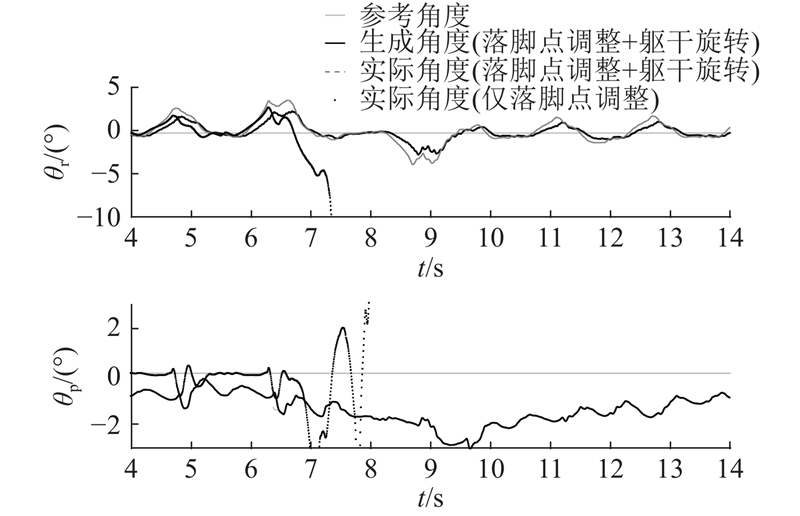
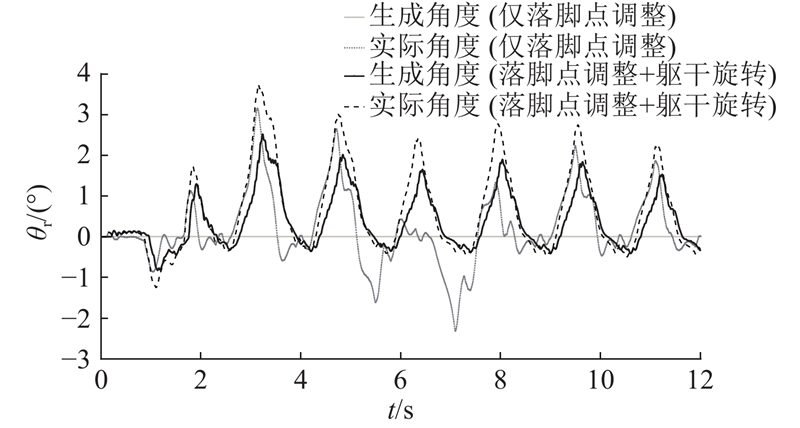
通过引入躯干转动,机器人在遇到外力干扰时能够及时调整躯干转动角度以保持平衡. 如图9所示,当沿y轴负方向外力出现时,机器人能够主动增大横滚角以减少落脚点的调整量. 与仅利用落脚点调整时躯干横滚角会发生正、反两个方向较大的变动不同,在目标函数中引入躯干转动角度惩罚项,能够让机器人减轻躯干的左、右摆动,利用更少的周期恢复正常的摆动姿态.
图 9
图 9 沿y轴负方向25 N外力作用下不同策略生成的横滚角度和实际横滚角度
Fig.9 Generated and actual roll angles when using different strategies under external force(25 N along − y axis)
表4给出不同策略能够抵抗的不同方向的最大外力. 可以看出,在各个方向上,集成躯干转动优化,机器人能够抵抗更大的外力干扰而保持稳定.
表 4 不同方向的最大抵抗外力
Tab.4
| N | ||||
| 策略 | x轴正向 | x轴负向 | y轴正向 | y轴负向 |
| 仅落脚点调整 | 240 | 165 | 167 | 30 |
| 落脚点调整+躯干转动 | 308 | 185 | 202 | 65 |
数值分析表明,在矢状面沿x轴方向,对外力的抵抗能力提高了10%以上;在冠状面沿y轴方向,对外力的抵抗能力提高了20%以上. 特别地,机器人对沿x轴正向的外界推力抵抗能力最强,是由于足部沿该方向的长度最长,单足相可以利用的支撑区域最大. 机器人对沿y轴负方向外力的抵抗能力比其他几个方向均低很多. 原因是推动力出现时机器人处于左腿支撑且质心已经朝y轴负方向开始移动. 机器人足部宽度明显比长度窄,y轴负向的推力将加速摆动腿落地,从而缩短落脚点调整和躯干转动的反应时间.
3.4. 算法执行效率
该算法及仿真程序使用C++语言编程实现. 在Ubuntu16.04系统中,使用开源优化求解库QuadProg++,求解该QP问题. 该求解器利用对偶法求解约束优化问题,通过代码优化,在主频3.0 GHz 的四核Intel CPU上每个控制循环耗时小于2 ms. 考虑到该算法属于规划层,底层可以以更高的频率进行通讯(实际上,以往的试验表明,500 Hz通讯频率能够满足多数任务的需求). 该算法能够满足未来硬件试验的要求.
4. 结 论
(1)提出可在线生成质心轨迹、调整落脚点和优化躯干转动角度的优化目标. 通过简化可行性约束,建立二次规划求解模型. 数值求解表明,每个循环在2 ms以内完成,能够满足实时控制的需求.
(2)通过多刚体动力学仿真,验证了该算法的可行性. 面对模型不精确对机器人状态产生的干扰,实现了变参数行走任务. 结果表明,利用躯干转动,可以实现更大范围的变参数步态在线生成.
(3)利用躯干转动,提高了机器人对外界推力的抵抗能力. 结果表明,通过引入躯干旋转优化,在同样大小和方向的外力推动下,所需要的落脚点调整量明显减少. 与只进行落脚点调整相比,在矢状面沿x轴方向,对外力的抵抗能力提高了10%以上;在冠状面沿y轴方向,对外力的抵抗能力提高了20%以上.
以后将在IIT开发的新一代仿人机器人样机COMAN+上进行验证试验. 未来一方面考虑将目标函数从落脚点位置跟踪变成速度跟踪,提高对外力干扰的抵抗能力. 另一方面,考虑集成实时变高度求解,开展更加鲁棒的多任务步行算法研究.
参考文献
仿人服务机器人发展与研究现状
[J].
Development and research status of humanoid service robots
[J].
面向全方位双足步行跟随的路径规划
[J].
Omni-directional bipedal walking path planning
[J].
仿人足底肌电特征的机器人行走规划
[J].
Humanoid walking planning based on EMG from human foot-bottom
[J].
基于最优控制的仿人机器人行走振动抑制
[J].
Walking vibration suppression for humanoid robot based on optimal control
[J].
The organization of human postural movements: a formal basis and experimental synthesis
[J].DOI:10.1017/S0140525X00020008 [本文引用: 1]
基于AHRS反馈的仿人机器人步行稳定控制
[J].
Stabilizing control of humanoids' walking based on AHRS feedback
[J].
Predicting foot placement for balance through a simple model with swing leg dynamics
[J].
Disturbance rejection for biped walking using zero-moment point variation based on body acceleration
[J].
Walking stabilization control for humanoid robots on unknown slope based on walking sequences adjustment
[J].
Postural feedback responses scale with biomechanical constraints in human standing
[J].DOI:10.1007/s00221-003-1674-3 [本文引用: 1]
Bioinspired control of walking with toe-off, heel-strike, and disturbance rejection for a biped robot
[J].DOI:10.1109/TIE.2017.2698361 [本文引用: 1]
Push recovery for the standing under-actuated bipedal robot using the hip strategy
[J].DOI:10.1631/FITEE.14a0230 [本文引用: 1]
模型预测控制: 现状与挑战
[J].
Model predictive control: status and challenges
[J].
Zero-moment point-thirty five years of its life
[J].DOI:10.1142/S0219843604000083 [本文引用: 1]
A reactive walking pattern generator based on nonlinear model predictive control
[J].DOI:10.1109/LRA.2016.2518739 [本文引用: 1]