根据材料力学特点,众多学者将微凸体接触变形过程划分为3个阶段:纯弹性、弹塑性和全塑性,其中微凸体的弹塑性变形机理尤为复杂. 早在20世纪初,Abbott等[4]就建立了大变形下微凸体塑性接触模型(简称AF模型). 随后,Greenwood等[5]首次将Hertz点接触通过高度分布函数扩展到整个粗糙表面接触,提出了开创性的GW模型. 由于Hertz点接触和AF模型分别仅适用于外载荷极小和极大场合,Chang等[6]基于塑性变形时体积守恒建立了伪弹塑性接触模型(简称CEB模型),但是其预测的平均接触压力存在跳跃式突变. 由于弹塑性变形阶段微凸体中塑性流的出现和弹性变形的截止具有瞬态性,该变形区间中的接触行为极其复杂,如何准确表述该区间中的变形机制一直是研究的热点问题之一.
1)插值多项式类模型. Zhao等[7]采用三次样板函数将弹塑性区间内的接触面积表示为变形量的四次插值多项式,同时基于Francis[15]的研究工作将该区间内的平均接触压力表示为变形量的对数多项式,提出了弹塑性接触模型(简称ZMC模型). 赵永武等[8]认为ZMC模型中对数关系描述的平均接触压力在接触变形临界点处不光滑,并采用该模型中提出的样板函数描述了弹塑性变形区间内的平均接触压力(简称Zhao模型). Brake[9]采用Hermit插值多项式表示弹塑性变形时的接触面积和平均接触压力(简称Brake模型). 徐超等[10]针对Zhao模型和Brake模型预测的平均接触压力的非单调性变化,采用椭圆曲线方程描述了弹塑性变形区间内的平均接触压力(简称Xu模型). 李玲等[11]采用以接触变形量为自变量的多项式描述弹塑性变形区间内的接触面积(简称Li模型),但该模型过于复杂. 由于采用的插值方法不同,采用插值多项式构建微接触模型时存在不唯一性,ZMC模型、Xu模型和Li模型都能连续且光滑地描述弹塑性变形阶段内的接触状态.
2)幂指函数类模型. Kogut等[12]采用有限元分析方法研究了弹塑性球体和刚性平面间的无摩擦接触变形,将弹塑性变形阶段分成2个区间(弹塑性区间Ⅰ和弹塑性区间Ⅱ),并通过曲线拟合有限元结果将弹塑性变形区间内接触特征表示为关于无量纲变形量的幂指函数(简称KE模型). Lin等[13]认为KE模型在弹塑性接触区间的起始点处预测接触面积和接触压力时存在不连续性,并采用材料屈服强度对平均接触压力进行归一化,建立了关于无量纲接触变形的幂指表达式(简称Lin模型). 王东等[14]采用幂指函数描述了弹塑性阶段内的无量纲接触面积和接触载荷与无量纲接触变形间的关系(简称Wang模型). 然而,KE模型、Lin模型和Wang模型都尚未研究微凸体接触刚度与接触变形间的关系,且仅适用于描述泊松比
本文针对插值多项式类和幂指函数类微接触模型存在的不足,利用量纲归一化优点,采用幂指函数建立考虑材料属性的弹塑性微接触解析模型,并且考虑材料泊松比对最大接触压力因子的影响,可连续性且光滑性地描述
1. 纯弹性和全塑性接触模型
图 1
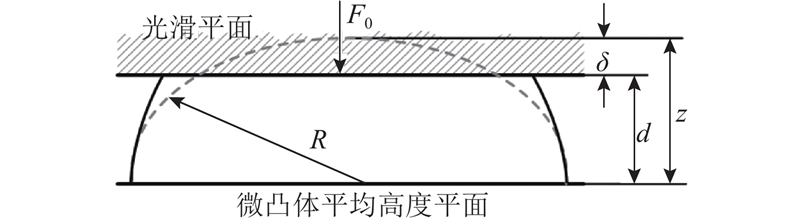
图 1 单微凸体与刚性光滑平面接触示意图
Fig.1 Diagram for contact between asperity and rigid smooth plane
当外载荷极小时,微凸体仅发生纯弹性接触变形,其微接触特性(接触面积A、平均接触压力p、接触载荷F和接触刚度K)可以用Hertz接触理论求解,表示为
式中:E为两接触材料的等效弹性模量;
将式(2)代入式(1),得到屈服临界点处的接触特性:
当外载荷足够大时,微凸体与刚性光滑平面间发生完全塑性变形接触,其接触特性可采用全塑性接触理论[4](简称AF模型)求解:
2. 弹塑性接触模型
2.1. 量纲归一化处理
由于不同量纲单位会使评价指标不同,量纲归一化使不同模型数据间具有可比性,利用屈服临界点处的接触特性(式(3)),对纯弹性变形阶段的接触特性进行归一化处理,可得
式中:
由式(5)和(6)可以看出,纯弹性和全塑性变形区间内微凸体的无量纲接触特性和无量纲接触变形间存在幂指关系.
2.2. 考虑材料属性的弹塑性微接触模型构建
为使所建立的弹塑性微接触模型更加符合实际情况,利用量纲归一化的优点,采用幂指形式的函数描述弹塑性区间内量纲归一化的微接触特性(简称本文模型),微凸体的接触面积、平均接触压力、接触载荷和接触刚度分别表示为
由连续介质力学理论[16]可知,量纲归一化后微凸体接触特性在整个变形阶段仍然是连续、光滑和单调的. 因此,微凸体在无量纲屈服临界点
1)接触面积:
2)平均接触压力:
3)接触载荷:
4)接触刚度:
依据边界条件式(8)~(11),可得式(7)中的参数:
式(12)采用KE模型中的全塑性临界点
3. 分析与讨论
3.1. 插值多项式类模型的唯一性分析
表 1 插值多项式类微接触模型比较
Tab.1
| 模型 | 微凸体接触特性 | 临界点 | ||||
| 接触面积 | 平均接触压力 | 接触载荷 | 屈服 | 全塑性 | ||
| ZMC[7] | 4次多项式 | 对数多项式 | 接触面积和 平均接触压力的乘积 | | | |
| Zhao[8] | ZMC模型 | 3.5次多项式 | | |||
| Brake[9] | 3次多项式 | 3次多项式 | | |||
| Xu[10] | Brake模型 | 椭圆曲线 | | |||
| Li[11] | 3次多项式 | ZMC模型 | | |||
ZMC模型和Zhao模型都采用了式(13)中的3次样板函数,本文仅枚举2次~6次的整数次样板函数:
根据连续和光滑性将
其中,
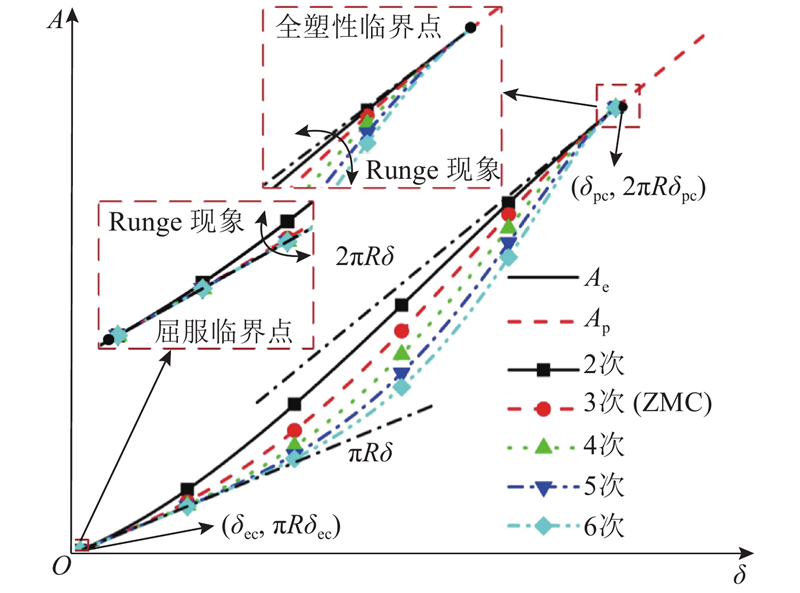
根据式(13)和(14),将基于不同样板函数得到的接触面积表示在图2中. 可以看出,所有在曲线临界点
图 2
图 2 不同样板函数预测接触面积的比较
Fig.2 Comparison of contact area predicted different template functions
图 3
图 3 不同模型预测接触特性的比较
Fig.3 Comparison of contact characteristics predicteddifferent models
3.2. 幂指函数类模型的连续性分析
表 2 幂指函数类模型中系数和指数比较
Tab.2
| 幂指表达式 | KE模型[12] | Lin模型[13] | Wang模型[14] | |||||
| α | β | α | β | α | β | |||
| 注:KE 模型有 2 个弹塑性变形区间(弹塑性区间Ⅰ: | ||||||||
| | 0.93 | 1.136 | 1.00 | 1.159 7 | 1.00 | 1.158 1 | ||
| 0.94 | 1.146 | |||||||
| | 1.19 | 0.289 | 1.08 | 0.220 4 | 1.00 | 0.209 1 | ||
| 1.61 | 0.117 | |||||||
| | 1.03 | 1.425 | 1.00 | 1.380 1 | 1.00 | 1.367 3 | ||
| 1.40 | 1.263 | |||||||
| 全塑性临界点 | | | | |||||
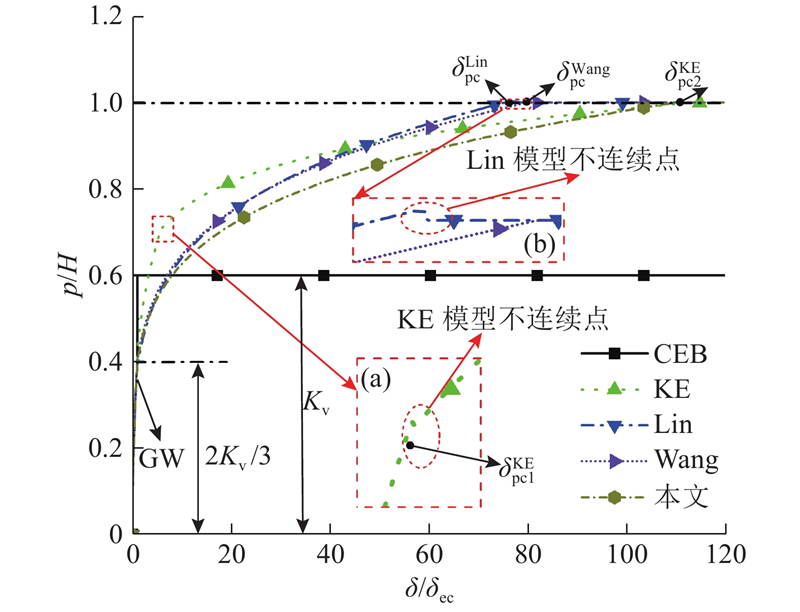
仅以平均接触压力为例,说明幂指函数类模型的不连续性. 如图4所示,同时将CEB模型和本文模型的预测值绘制于图中,并分别将GW模型和PW模型预测的接触压力用点划线在
图 4
图 4 无量纲平均接触压力随无量纲变形的变化
Fig.4 Change of dimensionless average contact pressure with dimensionless deformation
3.3. 材料属性对接触特性的影响
大多数金属材料的泊松比
图 5
图 5 最大接触压力因子随泊松比的变化
Fig.5 Change of maximum contact pressure factor withPoisson's ratio
图 6
图 6 无量纲接触载荷随无量纲变形的变化
Fig.6 Change of dimensionless contact load with dimensionless deformation
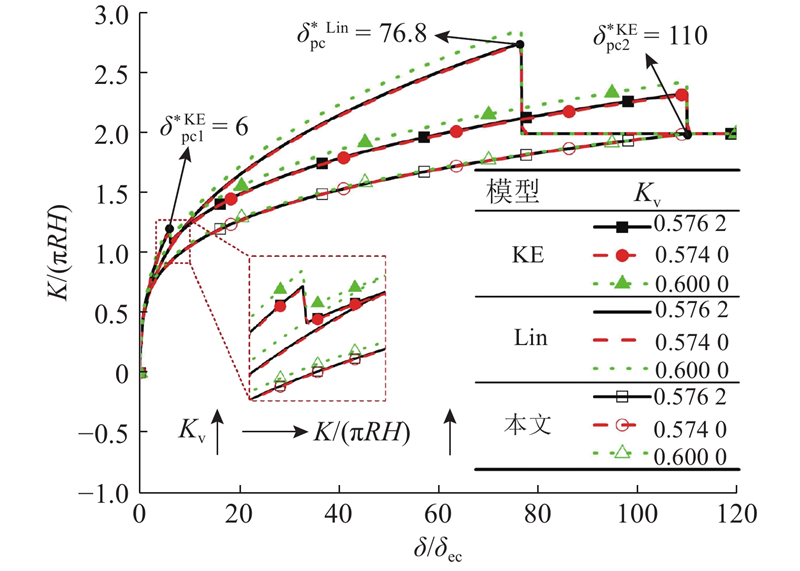
图 7
图 7 无量纲接触刚度随无量纲变形的变化
Fig.7 Change of dimensionless contact stiffness with dimensionless deformation
图6中KE模型、Lin模型和本文模型预测的
由图7可得,
4. 结 论
(1)KE模型、Lin模型和Wang模型仅考虑了特定泊松比
(2)较经典的KE模型和Lin模型,本模型的优势如下:考虑了材料泊松比的影响,可用于描述
(3)微凸体接触面积不受最大接触压力因子
参考文献
一种机床固定结合部的动力学参数化建模方法
[J].
Dynamic and parameterized modeling of fixed joints in machine tools using surface response method
[J].
一种考虑侧接触的微凸体弹塑性接触力学模型
[J].
Elastic-plastic model for contact of two asperities considering shoulder-shoulder contact
[J].
机械结合面切向接触阻尼能量耗散弹塑性分形模型
[J].
Elastoplastic fractal model for tangential contact damping energy dissipation of machine joint interfaces
[J].
Specifying surface quality: a method based on accurate measurement and comparison
[J].
Contact of nominally flat surfaces
[J].
An elastic-plastic model for the contact of rough surfaces
[J].DOI:10.1115/1.3261348 [本文引用: 3]
An asperity microcontact model incorporating the transition from elastic deformation to fully plastic flow
[J].DOI:10.1115/1.555332 [本文引用: 3]
新的粗糙表面弹塑性接触模型
[J].DOI:10.3321/j.issn:0577-6686.2007.03.016 [本文引用: 2]
New elastic-plastic model for the contact of rough surface
[J].DOI:10.3321/j.issn:0577-6686.2007.03.016 [本文引用: 2]
An analytical elastic-perfectly plastic contact model
[J].DOI:10.1016/j.ijsolstr.2012.06.013 [本文引用: 2]
一种改进的粗糙表面法向弹塑性接触解析模型
[J].
An improved analytical model for normal elastic-plastic contact of rough surfaces
[J].
螺栓结合面微观接触模型
[J].
Micro-contact model of bolted-joint interface
[J].
Elastic-plastic contact analysis of a sphere and a rigid flat
[J].DOI:10.1115/1.1490373 [本文引用: 4]
An elastoplastic microasperity contact model for metallic materials
[J].DOI:10.1115/1.1843830 [本文引用: 3]
一种考虑微凸体法向弹塑性接触的粗糙面力学模型
[J].
A normal mechanical model for elastic-plastic contact of rough surface
[J].
Phenomenological analysis of plastic spherical indentation
[J].DOI:10.1115/1.3443378 [本文引用: 1]
The effect of contact conditions and material properties on elastic-plastic spherical contact
[J].