自动钻铆系统在实际铆接时受到大载荷的循环施加,钻铆系统的结构会出现一定的弹性形变,导致加工精度下降. 自动钻铆系统需要具有较强的刚度以抵抗这种弹性形变,这就需要定量地分析钻铆系统末端的变形,研究其末端刚度,为其后的控制反馈提供一定的数据支持. Kim等[8]研究了多体系统中工作空间内的刚度矩阵、Salgado等[9]将机床刀具、夹具、压紧机构等机床部件的刚度矩阵合成为系统整体刚度矩阵加以分析、闫蓉等[10]提出了一种多轴加工系统刚度场半解析方法,用以分析工作空间中的刚度特性分布规律、Gao等[11]通过解析法建立了机床工作空间内的刚度模型,并利用该模型对不同位姿下的加工误差进行了分析、吴石等[12]利用多体小变形理论建立了机床的综合刚度模型,并通过力椭球分析了加工各要素对加工系统综合刚度性能的影响.
以往对机床刚度的研究大多采用多体运动学的方法进行分析,很少全面地考虑机床变形的所有来源、对于本研究卧式双机联合钻铆系统,需要综合考虑机床变形的各个来源建立其末端刚度模型. 针对这一情况,本文运用机器人学相关理论建立其运动学模型,并使用雅克比矩阵法、点传递法、有限元分析法逐一对其柔性运动轴、运动关节、末端执行器等关键部件建立刚度矩阵,在此基础上基于弹性小变形原理建立多轴机床的末端综合刚度模型. 这种末端综合刚度模型可分析不同位姿下系统所产生的变形,以便优化结构设计,必要时通过控制系统给出补偿量,提高铆接精度.
1. 钻铆系统组成及工作流程
图 1
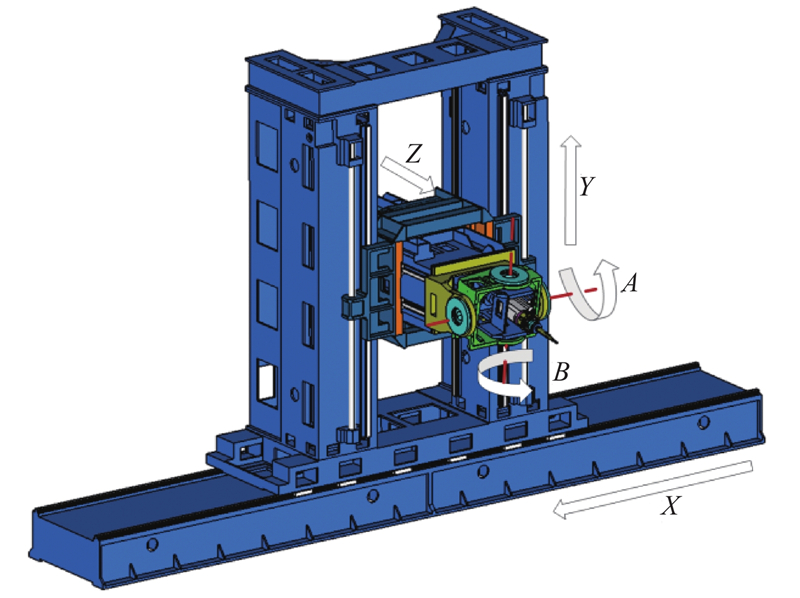
图 1 卧式双机联合自动钻铆系统布局
1-带外铆接头的多轴机床;2-飞机壁板工装;3-带内铆接头的多轴机床;4-内铆接头;5-AGV车;6-外铆接头 Layout of automatic horizontal dual-machine cooperative drilling and riveting system
卧式双机联合钻铆系统的刚度主要取决于两侧多轴机床中刚度较差的一个. 由于带内铆接头的多轴机床受载时变形更为明显,本文主要以带内铆接头的多轴机床作为分析对象,并视其末端刚度为卧式双机联合钻铆系统的刚度. 带内铆接头的多轴机床运动轴分布图如图2所示,该多轴机床包含X、Y、Z三个直角坐标移动轴和A、B两个正交转动轴,理论上能够以任意姿态达到加工空间内的任意位置,可满足在飞机壁板复杂曲面上的加工需求.
图 2
图 2 带内铆接头的多轴机床运动轴分布
Fig.2 Distribution of flexible links in multi-axis machine tool with inner riveting head
根据设计要求,多轴机床在工作时需承受高达5 t的压铆力,其运动关节、末端执行器(铆接头)以及柔性运动轴均会产生不同程度的变形,以往对末端坐标系的机器人刚度研究通常仅考虑运动关节变形对末端刚度的影响,运动轴及末端执行器的变形相对于传动机构的变形往往因为数值过小而不加考虑. 对于多轴机床来说,其Z轴和A轴悬伸较长,在加工时会形成悬臂结构导致其变形量较大,因此Z、A两运动轴的变形是末端变形的重要来源之一,不可忽略. 为了提高计算精度,需综合考虑运动轴、传动机构以及末端执行器的变形来建立该多轴机床的末端刚度矩阵.
2. 多轴机床运动学建模
多轴机床可以看作由3个棱柱联轴节以及2个转动关节所组成的五轴机械臂,因此,可以按照Denavit-Hartenberg方法建立其连杆坐标系[15-16]. 所建立运动学模型如图3所示,图中的坐标系从参考坐标系到末端坐标系分别为Or、OX、OY、OZ、OA、OB、Ot. 多轴机床的连杆参数如表1所示。表中,
图 3
表 1 多轴机床的连杆参数
Tab.1
| 连杆 | θi/(°) | αi−1/(°) | ai−1/mm | di/mm | 关节范围 |
| 1 | 0 | 0 | 0 | dX | 0~4 500 mm |
| 2 | 90 | −90 | 0 | dY | 0~2 500 mm |
| 3 | 90 | −90 | 0 | dZ | −800 −La ~ − La mm |
| 4 | θA | −90 | 0 | 0 | −30°~30° |
| 5 | θB | −90 | 0 | 0 | −15°~15° |
根据机器人学相关理论,相邻坐标系之间的坐标变换可根据下式进行计算:
式中:
根据如表1所示的连杆参数以及式(1),可得多轴机床从参考坐标系到坐标系的坐标变换为
式(2)描述了从参考坐标系到末端执行器坐标系之间的变换关系. 对于任意两坐标系之间的变换关系,仍可采用类似式(2)的连乘方式得到.
3. 各环节刚度辨识
多轴机床在实际工作时需要承受大载荷的循环施加,其运动传递的各个环节都会产生相应的变形. 根据理论推导以及相关的实验数据,多轴机床末端变形主要由结构变形和传动变形所产生,实际表现为加工时末端执行器、柔性连杆和运动关节刚性的不足. 针对这一情况,需要首先确定末端执行器、柔性连杆和运动关节这3个环节的刚度矩阵,为计算整机的末端刚度矩阵提供必要的基础数据支持.
3.1. 末端执行器刚度辨识
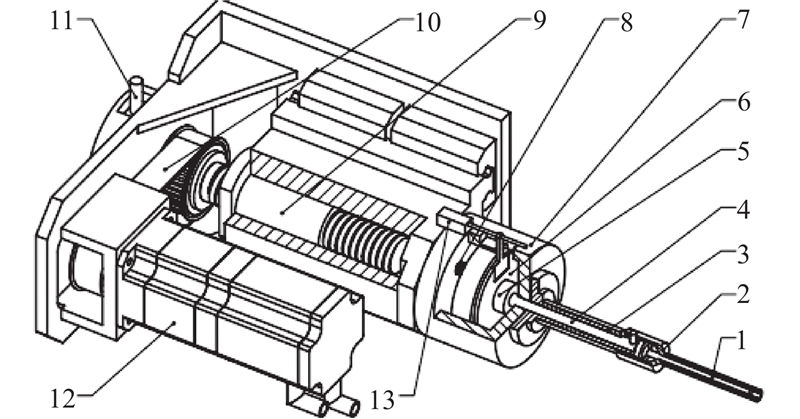
多轴机床中的末端执行器即为布置在该机床末端的铆接头,如图4所示为该铆接头的结构简化图. 为了减少和壁板的干涉,铆接头被设计成细长的杆状结构,在重载的情况下极易产生较大的结构变形. 铆接头的变形主要来源于铆杆、套筒和衬套的组合体,可利用有限元分析的方法对该组合体进行静力分析,得到该铆接头的刚度矩阵. 选择铆接头末端的参考点作为末端坐标系的原点,并以该参考点变形作为铆接头的变形. 运用有限元分析法,在给铆接头各个方向施加30 000 N的载荷及1 000 N·m的转矩后,即可得到铆接头各个方向上受载后的变形.
图 4
图 4 铆接头结构原理图
1-铆接头;2-衬套;3-套筒;4-导柱;5-衬套力传感器;6-活塞;7-外筒;8-支撑弹簧;9-滚珠丝杆;10-同步带轮;11-镦紧力传感器;12-伺服电机;13-长度计 Theory and structure of riveting head
铆接头的柔度矩阵为其刚度矩阵的逆矩阵,为6×6阶矩阵. 柔度矩阵的每一列分别代表在对应方向上单位力作用下所产生的变形. 基于这个特性,可利用有限元方法对各个方向施加力得到末端参考点各个方向上的变形,依据式(3)可得到柔度矩阵上的对应列:
式中:
依照式(3)求取柔度矩阵各列后,考虑到铆接头在工作时不会受到转矩,同时忽略高阶微量即可得到铆接头的柔度矩阵,求取其逆后,得到刚度对角矩阵:
式中:主对角线上的前3个数值单位为N/m,后3个数值单位为N·m/rad,以下不作特殊说明均采用该单位.
3.2. 柔性运动轴刚度辨识
图 5
图 6
3.3. 运动关节刚度辨识
多轴机床包含3个移动关节和2个转动关节,串联布置在整个机器上. 在多轴机床受载时,各个关节均会沿其运动方向产生不同程度的偏移. 所谓关节刚度,即为各个关节抵抗这种位置偏移的能力.
图 7
图 8
式中:L为转动关节受载后转动的弧长;R为测量点到转动中心的半径;
各个关节的关节广义力可由经典机器人理论得到,即
式中:
多轴机床的关节刚度矩阵为一个五阶对角矩阵,如下式所示:
式中:
各个关节的关节刚度可由下式求取:
式中:
经由试验测量及计算,在多轴机床末端加载10 000 N的情况下,得到各个关节的位移及广义力如表2所示. 根据之前求取的位移与广义力,可得到多轴机床的关节刚度矩阵为
表 2 各关节位移及关节广义力
Tab.2
| 关节 | Dji/mm | τji/N | 关节 | Dji/rad | τji/(N·m) | |
| X轴 | 0.01 | 9 697.5 | A轴 | 0.015 | 572.7 | |
| Y轴 | 0.015 | 9 699.8 | B轴 | 0.007 | 300.4 | |
| Z轴 | 0.03 | 1 796.5 | − | − | − |
4. 钻铆系统末端刚度建模
4.1. 基于弹性小变形理论的末端刚度模型
在实际工作时,多轴机床运动传递的各个环节均会产生不同程度上的弹性变形,同时这些变形均符合弹性小变形原理,因此多轴机床末端的变形可视为各个环节变形的叠加. 这些产生弹性变形的主要环节包括运动关节的变形、柔性运动轴的变形、末端执行器的变形. 由此,总体的变形在末端坐标
式中:
对于任意微小位移,存在如下的映射关系:
式中:
联立式(12)、(13),可得
式中:
根据式(14),分别求出柔性运动轴柔度矩阵
另一侧的多轴机床组成结构与带内铆接头的多轴机床类似,同为五轴结构且变形环节,也包含运动关节、末端执行器及柔性运动轴,也可由该方法得到其柔度矩阵,此处不再赘述.
4.2. 运动关节刚度矩阵建模
对于大部分机械臂来说,运动关节在其运动方向上的变形是整个机械臂末端变形的主要来源,其刚度矩阵建立的精度对末端刚度矩阵的影响最大. 经典的关节刚度矩阵忽略了受力所产生的变形对雅克比矩阵的影响,仅适用于小载荷的情况. 本文所述的多轴机床在加工时最大会承受接近50 000 N的大载荷,使用经典的刚度矩阵会产生较大的误差. 针对这种情况,本文采用了种更为精确的算法来建立关节刚度矩阵[17].
根据虚功原理,关节空间内的广义力做的虚功等于末端坐标系内广义力所做的虚功,即
式中:
根据机器人学经典理论,可得
式中:
联立式(15)、(16),可得广义力的关系为
同时,各个广义力满足以下等式:
式中:
式中:
对于静态未加载的多轴机床,式(21)中等式右边的第一项为0,在这种情况下,可得到经典理论中的关节刚度矩阵:
大多数情况下,关节变形所带来的雅克比矩阵的变化对于计算的影响较小,因此式(23)适用于绝大部分机械臂的刚度场建立. 对于本文分析的多轴机床,应当遵循式(21)来建立关节刚度场.
令式(21)中等式右边第一项为
结合式(21)、(24),可得机床关节的刚度矩阵:
4.3. 柔性运动轴刚度矩阵建模
在多轴机床中,由于Z轴和A轴悬伸较长,产生的变形对于末端的变形来说不可忽略,将Z轴和A轴视为柔性运动轴,建立其相应的刚度矩阵.
由于各个运动轴变形属于弹性小变形,可忽略单个运动轴变形对坐标变换矩阵的影响,将运动轴变形所产生的机器人末端变形等效为各个运动轴变形的线性叠加[18]. 基于这个假设,以柔性运动轴Z轴为例,其末端刚度矩阵推导如下.
如图9所示,考虑固连在柔性轴Z轴末端的坐标系
图 9
式中:
在基坐标系
式中:
由式(27)可得到坐标系
根据机器人学相关理论,存在以下公式成立:
式中:
联立式(28)、(29),可得到坐标系
在坐标系
联立式(26)、(30)(31)即可得到如下公式:
根据式(32)即可得到末端坐标系内的Z轴刚度矩阵为
采用类似的解法可得到A轴在末端坐标系内的刚度矩阵为
式中:
由式(33)、(34),可得到柔性运动轴的在末端坐标系内的刚度矩阵为
4.4. 末端执行器刚度矩阵建模
铆接头末端坐标系即为整个机床的末端坐标系,因此如式(4)所示的刚度矩阵无需变换,即为末端执行器在末端坐标系内的刚度矩阵.
5. 钻铆系统末端变形测试
5.1. 试验测试原理
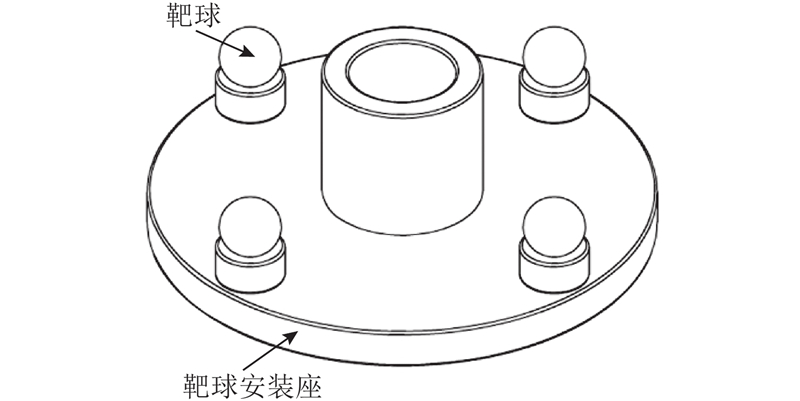
为验证多轴机床总柔度矩阵的准确性,对不同位姿下的多轴机床的末端变形进行试验求取,如图10所示为末端变形测量试验现场. 该实验主要需要卧式双机联合钻铆系统、末端变形实验装置及激光跟踪仪这3个设备来完成. 在具体操作时,卧式双机联合钻铆系统中带内铆接头的多轴机床保持位姿不变,带外铆接头的多轴机床进行加载;末端变形试验装置安装在内铆接头的末端,其结构如图11所示. 该装置上的4个凸起内安装有磁铁,用以固定激光跟踪仪的测量球;激光跟踪仪放置在带内铆接头的多轴机床一侧,并且在合适位置完成找准工作后,需要保持该位置在整个实验过程中不变. 激光跟踪仪作为本试验的测量设备,其测量精度和距离测量球的长度有关,其精度公式如下:
图 10
图 11
式中:
5.2. 试验测试结果
实际试验时,首先卧式双机联合钻铆系统的位姿参数经由其自带的控制台调整到实验所需数值,然后外铆接头一侧的多轴机床进行加载. 在保持一定压铆力的情况下,利用激光跟踪仪分别测量4个测量球在加载前及加载后的空间坐标,经计算后得到多轴机床的末端变形.
试验测得的结果与计算得到的结果如表3所示,
表 3 试验、计算所得末端变形对比
Tab.3
| 位姿 | Fe / N | Dc / mm | De / mm | η / % | ||||
| X轴 | Y轴 | Z轴 | A轴 | B轴 | ||||
| 1 000 | 900 | −300 | 0 | 0 | 10 000 | 0.129 | 0.139 | 7.19 |
| 2 000 | 400 | −500 | 0 | 0 | 10 000 | 0.120 | 0.127 | 5.51 |
| 3 000 | 1 400 | −500 | 10 | 10 | 10 000 | 0.159 | 0.175 | 9.14 |
| 3 000 | 1 400 | −100 | 0 | 0 | 10 000 | 0.140 | 0.155 | 9.68 |
| 1 000 | 900 | −100 | 10 | 0 | 15 000 | 0.194 | 0.206 | 5.82 |
| 2 000 | 1 400 | −500 | 10 | 10 | 15 000 | 0.223 | 0.241 | 7.47 |
| 3 000 | 400 | −300 | 0 | 0 | 20 000 | 0.205 | 0.221 | 7.24 |
| 1 000 | 900 | −100 | 10 | 0 | 20 000 | 0.237 | 0.253 | 6.32 |
6. 结 论
(1)在其余位置参数不变时,变换X轴位置参数对末端变形量的影响并不大;变换Y轴或者Z轴位置参数时,末端变形量变化较为明显. 因此,后续的结构优化工作可重点关注Y轴与Z轴,以提高自动钻铆设备的末端刚度.
(2)在钻铆力一定时,试验所得的末端变形量最大值与最小值的差异约为32%,表明该多轴机床具有良好的整体刚度,其末端刚度对位姿变化的影响不太敏感.
(3)利用本文所述末端综合柔度矩阵所得到的机床末端变形量与实际实验所得结果误差不超过10%,说明该末端综合柔度矩阵具有相当高的精度,并且在钻铆系统受重载的情况下仍适用. 这对于卧式双机联合钻铆系统的设计与后续的改进具有重要的参考意义.
参考文献
机器人钻铆系统研究现状及发展趋势
[J].
Research status and development trends of robot drilling and riveting system
[J].
飞机结构件的自动化精密制孔技术
[J].DOI:10.3969/j.issn.1671-833X.2009.24.011 [本文引用: 1]
Automatic precision drilling technology of aircraft structural part
[J].DOI:10.3969/j.issn.1671-833X.2009.24.011 [本文引用: 1]
飞机装配设备及供应商一览
[J].DOI:10.3969/j.issn.1671-833X.2008.11.014 [本文引用: 1]
Introduction of aircraft assembly equipment and suppliers
[J].DOI:10.3969/j.issn.1671-833X.2008.11.014 [本文引用: 1]
E7000 ARJ-manual flexible tooling for horizontal riveting system
[J].DOI:10.4271/2014-01-2250 [本文引用: 1]
飞机数字化自动钻铆系统及其关键技术
[J].
Lightweight automatic drilling system and key technology for aircraft
[J].
飞机自动钻铆技术研究现状及其关键技术
[J].
Research status of aircraft automatic drilling and riveting system and its key technology
[J].
Non-dimensionalized performance indices based optimal grasping for multi-fingered hands
[J].DOI:10.1016/S0957-4158(03)00039-4 [本文引用: 1]
Evaluation of the stiffness chain on the deflection of end-mills under cutting forces
[J].
多轴加工系统闭链刚度场建模与刚度性能分析
[J].
Closed-loop stiffness modeling and stiffness index analysis for multi-axis machining system
[J].
Stiffness modeling of ma-chine tools based on machining space analysis
[J].
复杂曲面模具加工系统综合刚度场建模与分析
[J].
The Modeling and analysis about comprehensive stiffness field of complex curved surface mould processing system
[J].
Enhanced stiffness modeling, identification and characterization for robot manipulators
[J].DOI:10.1109/TRO.2004.842347 [本文引用: 1]