随着机器人技术的飞速发展,软体机器人作为该领域的新兴分支,凭借独特的柔顺性和适应性而备受关注。软体机器人的设计灵感大多来源于自然界中的生物(尺蠖、蠕虫和蛇等),其结构大部分或全部采用柔性材料,如硅橡胶、尼龙、形状记忆合金等,因而能够在非结构化环境中安全、高效地作业,展现出传统刚性机器人难以比拟的优势[1]。软体爬行机器人因自身柔软且易变形的结构特性,具有可适应非结构化环境的优点,被广泛应用于医疗、救援和侦察等领域。
近年来,为了增强软体爬行机器人对非结构化环境的适应能力,学者们设计了多种具备不同运动模式的软体爬行机器人。Guo等[2]通过形状记忆编程来调整驱动器条带的形状,使得软体爬行机器人的前后摩擦结构在与表面接触时产生不同的摩擦力,进而使机器人在无需额外传感控制的前提下即可实现定向运动。Duhr等[3]研发了一种基于软磁性材料的爬行机器人,该机器人通过Kirigami切割、各向异性摩擦和磁场控制,可实现双向爬行、转弯和S形轨迹运动等。Ta等[4]设计了一种具有二维各向异性摩擦特性的表面,通过配置不同摩擦系数的材料来产生各向异性摩擦,进而为可打印软体机器人的蠕动运动提供驱动力。综上,通过优化摩擦表面微结构的几何形状、排列方式和材料特性,可实现软体爬行机器人运动的高效控制和能量优化。
研究表明[12-14],在剪切力作用下,弹性体的几何形状会发生显著变化,导致其实际接触面积与初始表征面积之间存在显著差异。随着对弹性体摩擦特性研究的不断深入,许多学者开始利用弹性体变形量与实际接触面积之间的关系来设计和优化各向异性摩擦特性,以提升摩擦性能和运动效率。Xue等[15]受壁虎脚趾垫的启发,设计了一种PDMS(polydimethylsiloxane,聚二甲基硅氧烷)微柱,这些微柱的末端带有不对称勺形悬垂结构,摩擦力在悬垂结构末端方向上及其反方向上表现出明显的各向异性。Wang等[16]研制了一种仿尺蠖软体机器人,其足部结构采用形状记忆合金,可在通电后产生变形,从而改变与地面的接触面积,以形成不同的摩擦系数,实现锚定和滑动运动。尹宏飞等[17]设计了一种气压驱动的仿尺蠖软体爬行机器人,通过向各组气囊充气来改变机器人的变形量,以调整其与地面之间的接触面积,进而改变摩擦力,实现周期性运动。Nojiri等[18]提出了一种新型的摩擦可变表面,通过结构变形来改变接触面积,从而改变摩擦力。该表面能够在轻触时提供低摩擦力,而在重压时提供高摩擦力。Zhao等[19]仿照昆虫的角质层结构研制了一种仿生垫,该仿生垫具有曲率均匀的半球形接触表面和均匀分布的弹性柱阵列。通过调整曲率和弹性柱刚度等结构参数,可改变仿生垫弹性柱阵列与接触底面的接触面积,从而实现对摩擦力的精确调控。
现阶段,许多学者通过在摩擦接触表面制备规则排列的几何凸起结构来提升各向异性摩擦性能,但关于几何凸起结构在偏转过程中因接触面积改变而导致摩擦差异的作用机制仍鲜有报道。基于此,受动物脚掌表面纹理的启发,本文设计了一种具有各向异性摩擦特性的三角形表面织构,并基于该设计研制了一种仿尺蠖软体爬行机器人。该机器人通过波纹致动器的伸缩变形单元和三角形各向异性摩擦单元的协同工作,来实现前进运动与转向运动。本文研究工作如下:首先,采用超弹性本构模型表征硅胶的材料特性,并构建波纹致动器的运动学模型;然后,搭建摩擦力测试实验平台,对机器人摩擦足在不同粗糙度接触基面上的各向异性摩擦性能进行测试;最后,通过实验展示机器人的前进和转向运动性能。本文旨在为仿生摩擦学、仿生软体机器人等领域[20-21]的发展提供一定的理论依据与技术指导。
1 软体爬行机器人的设计与建模
1.1 波纹致动器与各向异性摩擦足的设计与建模
在软体爬行机器人的运动中,可变形主体与各向异性摩擦结构发挥着关键作用。因此,在设计时须协同调控机器人主体的变形量与其摩擦结构的各向异性摩擦特性,以实现预期的运动功能。
图1
图1
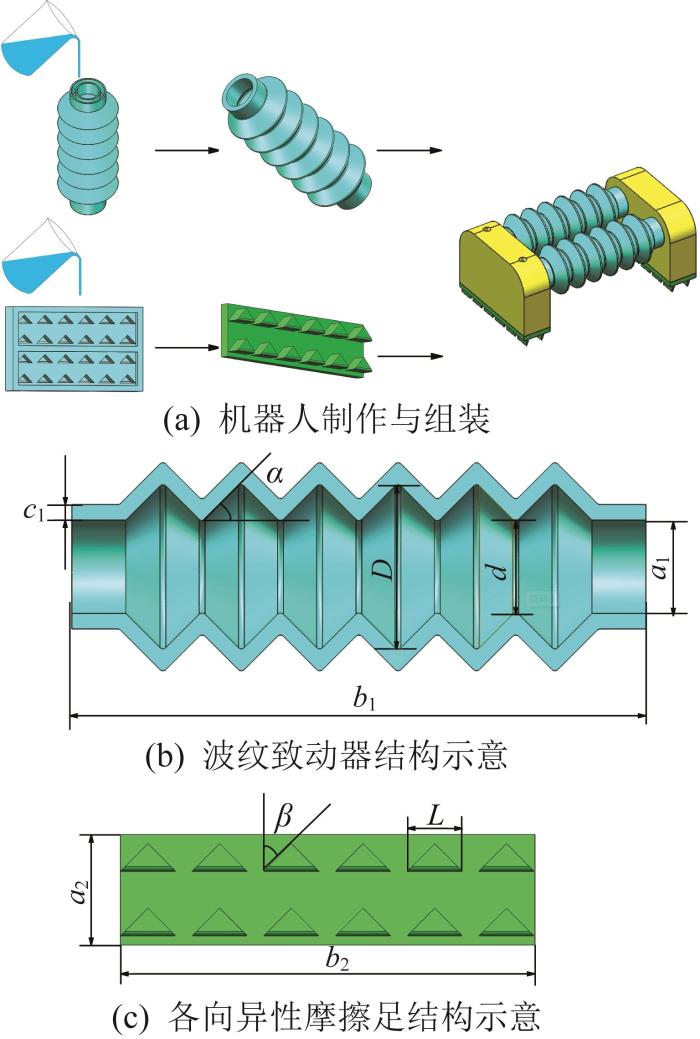
软体爬行机器人的制作流程及其关键部件结构
Fig.1
Fabrication process of soft crawling robot and the structure of its key components
在制备微型气动波纹致动器时,若采用“先对半剖分再黏合”的传统工艺,则会因壁面过薄、尺寸过小而难以精准对位与可靠粘接,易在连接处引入缺陷,导致波纹致动器收缩不均甚至失效。为了解决这一问题,本文采用双薄壳式模具法。具体步骤如下:先设计并制作双薄壳式模具,随后将符合硬度要求的硅胶灌注至模具中,待硅胶完全固化后,利用工具去除2层薄壳,即可得到完整且质量优异的波纹致动器。
波纹致动器和各向异性摩擦足的关键尺寸和材料设置如下:波纹致动器的管口直径a1=9 mm,管长b1=55 mm,壁厚c1=1.5 mm,大径D=15.8 mm,小径d=9 mm,倾角α=45°,采用30A硅胶(DPSGJ0,普斯顿)制作;各向异性摩擦足背衬层的宽度a2=12 mm,长度b2=45 mm,厚度c2=2 mm,表面阵列的等腰三角形凸起织构的底边长度L=6 mm,底角β=45°,排成2排6列,共计12个三角形凸起织构,采用5A硅胶制造。组装完成后,机器人的2个波纹致动器中心线之间的距离为25 mm,即联合致动器中心弧线到单个致动器中心弧线的距离m=12.5 mm。采用硅胶黏合剂(3680强力胶)对软体爬行机器人的连接部分进行粘接。在组装过程中,严格按照顺序依次粘接各个部件,确保连接牢固可靠,从而保障整个机器人的结构稳定性和运动协调性。
1.2 超弹性本构模型的确定
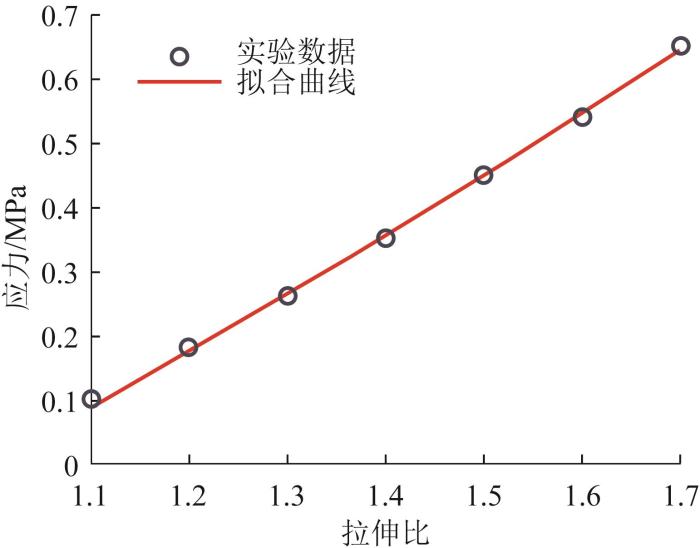
软体致动器采用的柔性材料具有非线性力学特性,在外力的作用下会产生大幅度的变形。对于柔性材料的描述,国内外学者提出了多个超弹性本构模型。常见的模型包括Neo-Hookean模型、Mooney-Rivlin模型、Ogden模型和Yeoh模型等。这些模型可以通过实验数据来拟合,用于描述柔性材料在不同应变条件下的力学响应。为了简化预测模型,本文选择Yeoh模型来描述硅胶材料的应变能密度函数[23]。
对于各向同性超弹性材料,其应变能密度可表示为应变不变量的函数。根据唯象理论,应变能密度函数可写成以主伸长率表示的偶次幂形式。定义一阶、二阶、三阶应变不变量分别为:
式中:I1、I2、I3分别为一阶、二阶、三阶应变不变量,
则应变能密度函数可表示为:
为便于计算,通常将应变能密度函数在参考状态附近展开。取二阶Yeoh模型(又称二参数模型,对应阶数N=2),得到应变能密度函数的最简形式:
式中:C10、C20为材料常数。
图2
1.3 波纹致动器运动学建模
为了获取单个波纹致动器在弹性阶段的弹性模量(即材料在受力时产生弹性变形的能力),搭建了图3所示的压缩实验平台,以测量波纹致动器在不同压缩位移下的弹性力。
图3
通过压缩实验可得:波纹致动器的最大压缩位移为24 mm,此时产生的弹性力约为4.2 N。
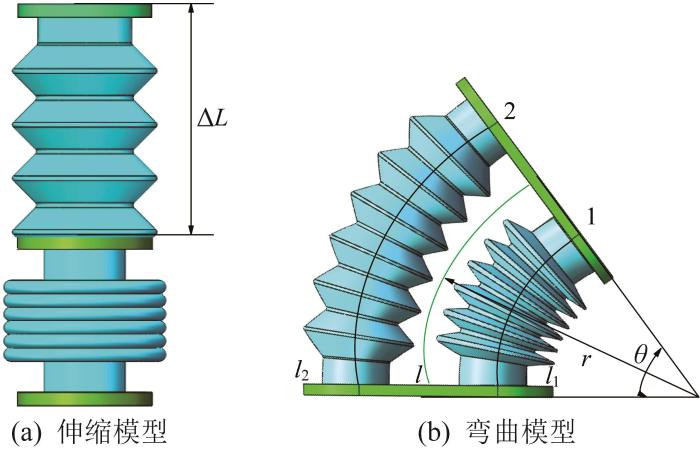
当对双波纹联合致动器中的2个波纹致动器同时施加相同负压时,2个波纹致动器会产生相同的压缩位移,此时联合致动器仅发生伸缩运动,因此可只对单个波纹致动器进行运动学建模。然而,当2个波纹致动器所受的负压不同时,其压缩位移会出现差异,从而导致联合致动器产生弯曲现象,此时须分别对每个波纹致动器进行运动学建模。波纹致动器的变形模型如图4所示。其中:定义右侧波纹致动器为1号,其弯曲后的中心弧长为l1;左侧波纹致动器为2号,其弯曲后的中心弧长为l2;联合致动器的中心弧长为l。
图4
图4
双波纹联合致动器的变形模型
Fig.4
Deformation model of double-corrugated combined actuator
由图4(a)所示的伸缩模型可知:当双波纹联合致动器的弯曲角度θ=0°时,2个波纹致动器的位移变化量相同,则联合致动器的中心弧长与各波纹致动器的中心弧长均相等,即有:
假设双波纹联合致动器在弯曲过程中满足常曲率假设,根据图4(b)所示的弯曲模型,通过弧长关系可以推导出任意弯曲状态下各波纹致动器的中心弧长li :
式中:ri 为波纹致动器i对应的曲率半径,i=1, 2。
结合2个波纹致动器之间的位置关系,可知:
假设波纹致动器均匀变形,对联合致动器中心弧长l作如下限制:
根据
在波纹致动器因受到压力作用而产生伸缩运动时,定义弹性系数Kt来表征其在伸缩过程中的刚度。波纹致动器的弹性系数Kt可表示为其所受的应力与应变的比值,计算式如下:
式中:
由
式中:P为作用在波纹致动器内壁上的压强,Sh为波纹致动器的平均横截面积。
气体作用在波纹致动器上的平均横截面积为波纹致动器凸起部分的外壁横截面积和凹陷部分的内壁横截面积的平均值。波纹致动器外壁截面的直径为大径D加上两侧壁厚,则波纹致动器的理论有效横截面积Sh可表示为:
其中:
式中:D1为波纹致动器的外直径。
根据上文的波纹致动器压缩实验数据,可得Kt≈4.2 N/24 mm=0.175 N/mm。
联立
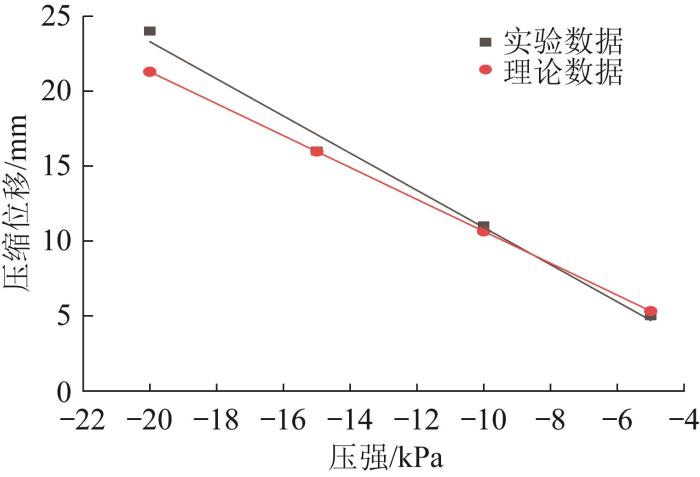
图5所示为单个波纹致动器在-20~-5 kPa负压作用下伸缩变形的理论结果与实验结果对比。
图5
图5
波纹致动器压缩位移与压强的关系
Fig.5
Relationship between compression displacement and pressure for corrugated actuator
当只对一侧的波纹致动器施加负压时,假定另一侧波纹致动器的中心弧长l2保持不变,结合
将整个联合致动器的弯曲变形视作单侧波纹致动器进行伸缩运动。联立
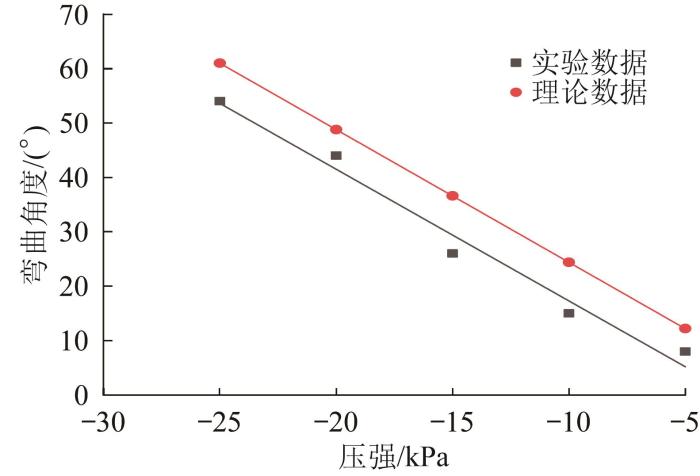
图6所示为双波纹联合致动器在-25~-5 kPa负压作用下弯曲变形的理论结果与实验结果对比。
图6
图6
波纹致动器弯曲角度与压强的关系
Fig.6
Relationship between bending angle and pressure for corrugated actuator
1.4 摩擦实验
为测试各向异性摩擦足的摩擦力,搭建了图7所示的实验平台,主要由接触基面、基面滑动模块、竖直加载模块、力传感器和硅胶试件等组成。所采用的力传感器为六轴力传感器(M3813B,南宁宇立仪器有限公司),可输出3个方向的力和3个方向的扭矩。接触基面固定在水平滑动导轨上;基面滑动模块通过电机驱动直线运动单元,使接触基面以恒定速度水平滑动。竖直加载模块用于对硅胶试件施加载荷,以改变试件与亚克力和木质基面之间的接触力。通过在加载平台上放置相应质量的砝码,以对硅胶试件施加预定的法向载荷。加载平台下方依次连接力传感器与加载头,加载头直接与待测试件相连。加载平台通过竖直滑动导轨实现上下移动,根据试件的变形量移动对应的距离,以实现恒力加载。
图7
在实验开始前,使用酒精擦洗硅胶试件与接触基面,以去除试件和接触基面表面的污渍。具体的摩擦力测试流程如下:首先,在加载平台上方放置相应的砝码,对硅胶试件施加预设的法向载荷。然后,维持法向载荷不变,使基面滑动模块作水平运动,通过改变驱动电机的转速将水平加载速度设定为1 mm/s;在竖直方向上,因软体爬行机器人质量为87.3 g,其每只摩擦足所需承受的质量为43.65 g,故对硅胶试件施加0.5 N载荷。水平滑动导轨的加载行程为180 mm,加载的初始位置为导轨左端距加载头最左端65 mm处,如此可在水平运动时使加载头的中间位置与接触基面的中间位置重合,即整个加载过程对称[25]。
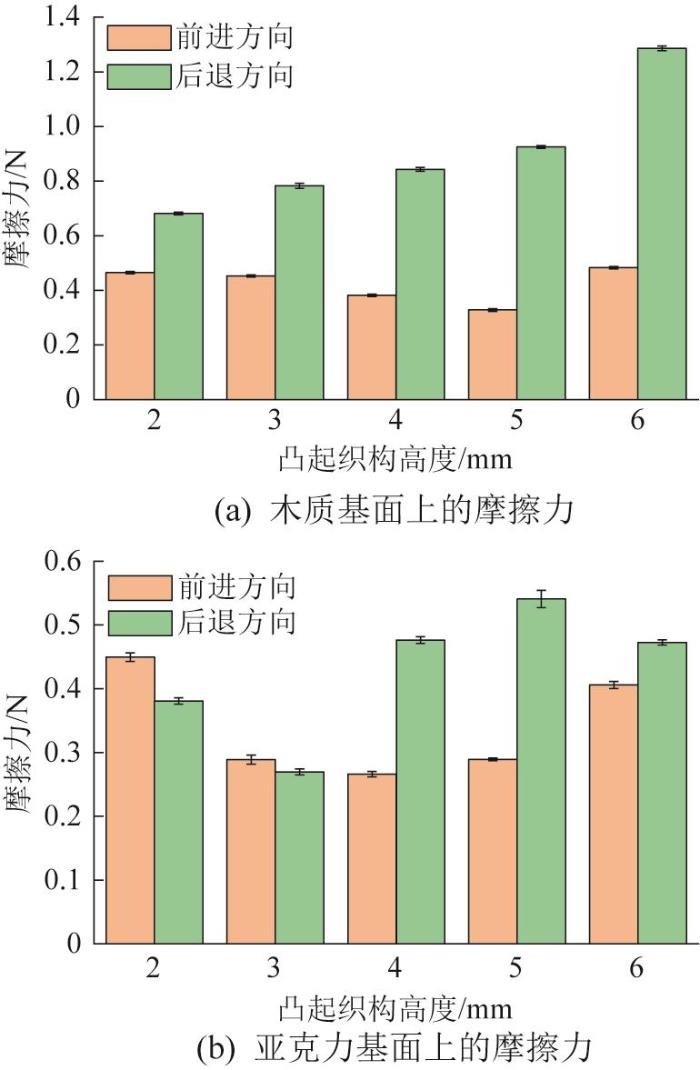
通过摩擦力测试实验测得三角形凸起织构高度不同时摩擦足在木质基面和亚克力基面上沿前进、后退方向的摩擦力,如图8所示。
图8
图8
摩擦足在不同接触基面上的摩擦力
Fig.8
Friction force of friction foot on different contact surfaces
由图8可得:当凸起织构高度为5 mm时,摩擦足的各向异性摩擦性能最佳,其在木质基面和亚克力基面上的各向异性摩擦性能指标(即前进与后退方向上的摩擦力比值)分别为2.82和1.87。基于此,在软体爬行机器人运动实验中,采用凸起织构高度为5 mm的各向异性摩擦足作为支撑结构,利用其摩擦特性为机器人提供定向驱动力。
2 软体爬行机器人的控制与运动分析
2.1 机器人控制分析
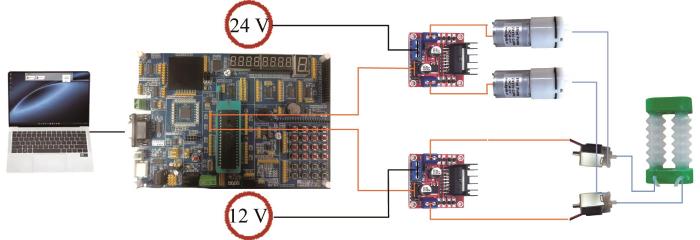
为精准操控软体爬行机器人,选用单片机作为核心控制单元。鉴于气动波纹致动器由30A硅胶制成,具备出色的回弹性能,其与大气接触时能迅速复原,无需气泵额外充气,本文实验采用微型气泵搭配三通微型气动电磁阀,由单片机调控波纹致动器的抽气与放气过程。借助L298驱动模块控制气泵及电磁阀,通过调整阀门激活时长与次序,改变气流持续时间,从而驱动波纹致动器完成多种运动模式。软体爬行机器人系统中各部件(单片机、驱动模块、气泵及两位三通电磁阀)的电气连接布局如图9所示。各功能模块采用独立供电设计,每个阀门单独控制一个波纹致动器的抽/放气循环。图9中:黑线表示电源与驱动模块的电流连接路径;橙线表示单片机向驱动模块、阀门传输脉冲调制信号的线路;蓝线表示气泵、电磁阀与机器人之间的气动连接。
图9
2.2 机器人运动分析
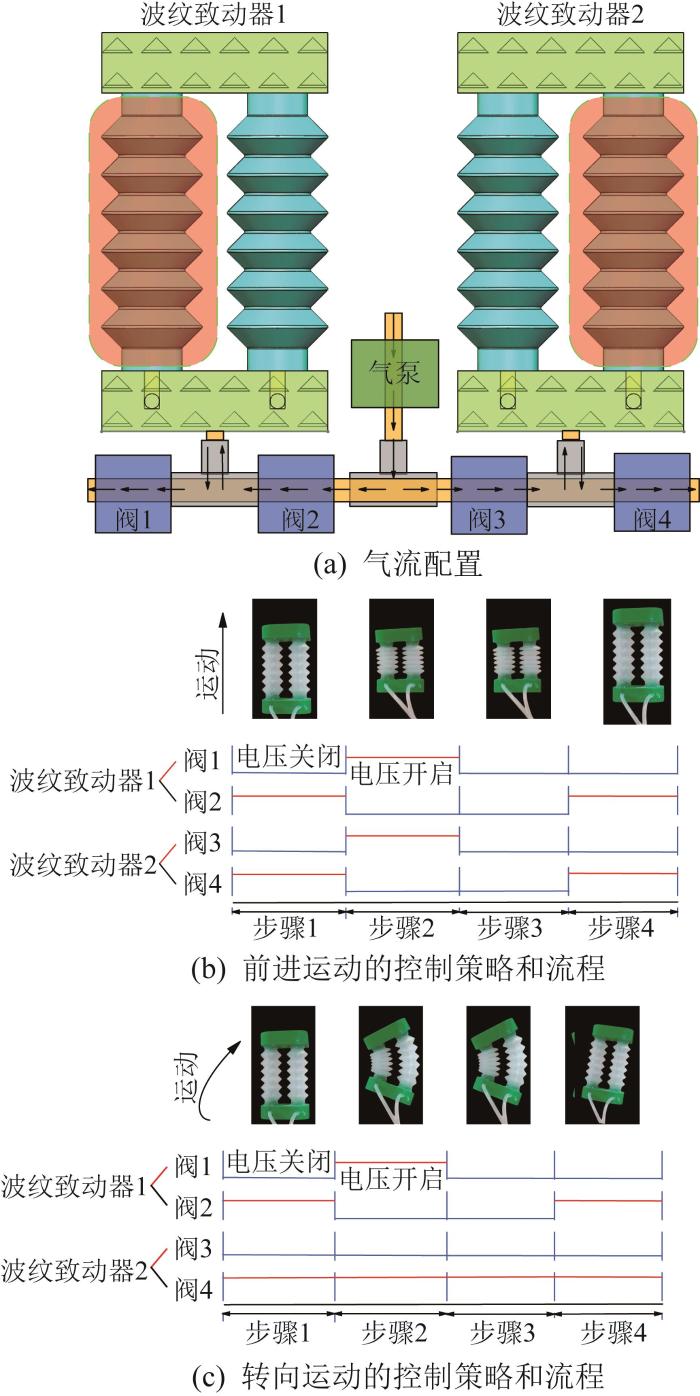
本文所研制的软体爬行机器人两侧的气动波纹致动器由独立气泵调控气压,通过变换对2个波纹致动器施加负压的次序,可精准实现前进与转向运动。该机器人仿照尺蠖锚定运动模式设计,图10展示了机器人的气流配置及前进、转向控制策略与流程。前进运动原理如下:当同步对2个波纹致动器施加负压以使其同时压缩时,后摩擦足的三角形凸起织构尖端与基面接触,摩擦力较小;前摩擦足的三角形凸起织构大端与基面接触,摩擦力较大。此时,后摩擦足移动,前摩擦足静止锚定。当2个波纹致动器同时放气复原时,摩擦状态互换,即后摩擦足锚定,前摩擦足移动,至此完成一个运动周期,机器人向前爬行。由此可知,软体爬行机器人实现锚定运动的关键在于波纹致动器两侧摩擦足的摩擦力差异,以此驱动机器人向前移动。
图10
软体爬行机器人的转向运动原理与前进运动相似,区别在于:转向时仅对一侧波纹致动器进行抽/放气操作。当运动侧的波纹致动器压缩时,其后端的各向异性摩擦足在该侧的移动幅度大于静止侧,带动机器人单侧向前移动,从而实现转向。若要控制机器人的转向方向,则只需操控远离预期运动方向一侧的波纹致动器按前进运动的步骤进行即可。
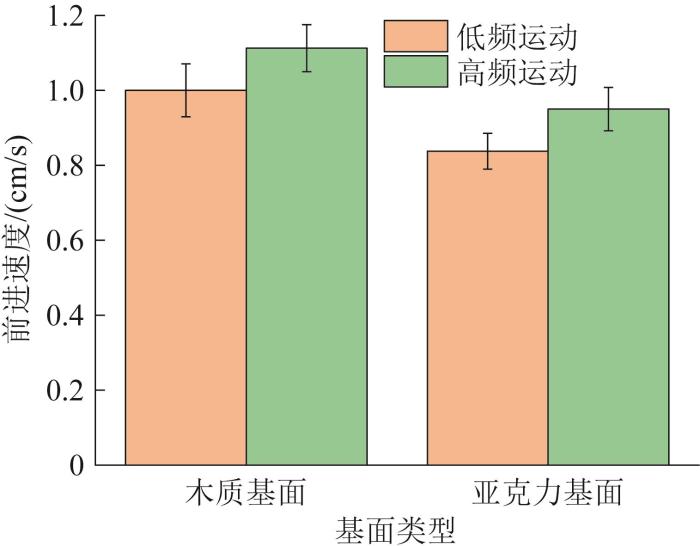
通过实验测试机器人在水平木质基面和亚克力基面上的运动性能,包括前进运动和转向运动。同时,改变气泵在一个周期内的抽气时间,将气泵对波纹致动器完全抽气所需的时间定义为低频抽气时间Tlow;高频抽气时间定义为抽气时间缩减为原来的一半,即Thigh=Tlow/2。通过实验可得,波纹致动器完全抽气所需的时间为0.350 s,即Tlow=0.350 s,Thigh=0.175 s。假设采用低频抽气时机器人作低频运动,采用高频抽气时机器人作高频运动。
图11
图12
图13
表1 机器人的转向运动数据
Table 1
| 基面 | 转向角度/(°) | 时间/s | 转向速度/[(°)/s] |
|---|---|---|---|
| 木质基面 | 90 | 26 | 3.46 |
| 95 | 28 | 3.39 | |
| 90 | 25 | 3.60 | |
| 亚克力基面 | 90 | 28 | 3.21 |
| 85 | 28 | 3.04 | |
| 90 | 30 | 3.00 |
3 结 论
本文设计了一种由采用三角形表面织构的各向异性摩擦足与气动波纹致动器组成的软体爬行机器人。首先,建立了波纹致动器的运动学模型,以分析其弹性变形与压强的关系,并通过实验验证了所构建运动学模型的正确性。然后,搭建了摩擦力测试实验平台,得到了各向异性摩擦足的摩擦力,并通过实验获得了凸起织构高度和接触基面粗糙度对各向异性摩擦性能的影响,确定了性能最佳的摩擦足结构。最后,制作了一个可实现锚定运动的软体爬行机器人样机,并开展了运动实验。实验结果表明,所设计的机器人可在不同材质的接触基面上实现良好的运动效果,但仅限于平坦地形。由于足部结构设计的局限性,机器人在更大范围的地形上(如草地、天然土壤、沙子)的运动能力受限。未来,可针对更高效的锚定机构进行深入研究,以进一步提高机器人的运动能力和地形适应性。
参考文献
软体智能机器人的系统设计与力学建模
[J].
System design and mechanical modeling of soft smart robots
[J].
Hydrogen-bonded liquid crystal elastomers combining shape memory programming and reversible actuation
[J].
Kirigami makes a soft magnetic sheet crawl
[J].
Design of frictional 2D-anisotropy surface for wriggle locomotion of printable soft-bodied robots
[C]//
仿生取向结构表界面及其摩擦各向异性研究进展
[J].
Research advances in biomimetic surfaces with oriented structures and its frictional anisotropy
[J].
Internally architectured materials with directionally asymmetric friction
[J].
Sticking/climbing ability and morphology studies of the toe pads of Chinese fire belly newt
[J].
Marine drag reduction of shark skin inspired riblet surfaces
[J].
Insect aquaplaning: Nepenthes pitcher plants capture prey with the peristome, a fully wettable water-lubricated anisotropic surface
[J].
Anisotropic friction in biological systems
[M]//
Nanoscale friction and adhesion of tree frog toe pads
[J].
Evolution of real contact area under shear and the value of static friction of soft materials
[J].
An experimental study on the relation between friction force and real contact area
[J].
Finite deformations govern the anisotropic shear-induced area reduction of soft elastic contacts
[J].
Bioinspired orientation-dependent friction
[J].
Locomotion of inchworm-inspired robot made of smart soft composite (SSC)
[J].
仿尺蠖软体爬行机器人的设计与分析
[J].
Design and analysis of inchworm-like software crawling robot
[J].
Development of contact area variable surface for manipulation requiring sliding
[C]//
Insect-inspired design strategy for flexible attachments with strong frictional force and weak pull-off force
[J].
软体仿尺蠖机器人综述与研制
[J].
Overview and research of software inching robot
[J].
环氧树脂-水凝胶软硬复合表界面各向异性摩擦研究
[J].
Anisotropic friction of epoxy-bydrogel based surfaces with soft-hard combination
[J].
3腔道仿生软体爬行机器人设计
[J].
Research of three-cavity bionic soft crawling robot
[J].
一种多运动模式的软体爬行机器人
[J].
A soft crawling robot with multi-motion modes
[J].