随着城市化进程的加速和地下空间开发的规模化发展，盾构法隧道施工技术因具有安全性高、环境影响小和地层适应性强等优势，已成为地铁、公路隧道及综合管廊等工程建设中的核心方法^[1]。作为盾构施工的关键环节，管片拼装的质量与效率直接影响隧道结构的稳定性、施工进度及工程成本。传统的管片拼装依赖人工操作或半自动化机械辅助，存在拼装精度低、施工效率不足及工人劳动强度大等问题^[2-3]。尤其是在地质条件复杂或施工空间狭小的环境下，人工操作的局限性凸显，亟须开发智能化技术以实现管片拼装的自动化与高精度控制。

盾构管片拼装位姿的精确检测是实现自动化拼装的前提和基础^[4]。在国外，日本是较早开展管片自动拼装技术研究的国家。早在20世纪90年代，日本学者Tanaka等^[5]提出了基于光切测量技术的管片位姿检测方法，通过计算高度差与间距确定了管片拼装姿态。德国海瑞克公司^[6]和美国罗宾斯公司^[7]根据自身盾构拼装设备的结构特点，制定了适用于矩形、六边形、菱形等不同形状管片的自动化粗定位流程，并在实际工程中推广应用，显著提高了施工效率。在国内，相关研究也取得了显著进展。高翔等^[8]提出了基于3个线激光传感器的管片位姿检测方法，通过扫描管片边缘获取特征点坐标，进而推导出待安装管片抓取位姿与安装位姿的表达式，并通过仿真验证了该检测方法的可行性。在此基础上，王红梅等^[9]针对K形盾构管片，设计了基于4组线激光传感器的管片位姿检测方案：结合管片边缘点坐标测量值和管片几何参数理论值，计算得到管片位姿。这类基于线激光传感器的检测方法虽在应对深度信息缺失、图像处理复杂度高等问题上具有一定优势，但高度依赖管片几何参数，导致其在实际应用中面临由几何误差引起的定位不准确问题。为此，吴志洋等^[10]提出了将激光位移传感器与视觉系统相融合的管片位姿检测方法，通过视觉系统获取管片的平面位姿，结合激光位移传感器采集的深度信息，最终实现对管片完整位姿的融合计算。虽然该方法在测量精度与适应性方面有所提升，但在传感器失效或部分信息缺失的情况下，其测量精度与稳定性仍难以保障，影响系统的鲁棒性。

目前，国内外在盾构管片自动拼装定位领域虽已取得一定成果，但在传感器协同、数据融合以及系统鲁棒性提升等方面仍面临诸多挑战，尤其是针对多传感器融合方案的鲁棒性与精度的系统性研究相对不足。因此，本文聚焦于基于多传感器融合的盾构管片自动拼装定位方法研究，旨在通过融合不同传感器的测量数据，提升管片位姿检测的准确性与鲁棒性，从而为管片的高精度、高可靠性自动拼装提供理论支持与实践经验。

线激光测量技术不仅具备较高的测量精度，而且在多尘、潮湿等复杂恶劣环境下依然表现出良好的稳定性^[11]，因而特别适用于盾构管片自动拼装过程中目标位姿的检测。然而，线激光传感器的测量范围有限，其输出通常为二维点云数据。若要实现对管片拼装位姿的准确检测，则需要结合管片的构型特征，合理部署多个线激光传感器，以提高空间信息获取的完整性与准确性。

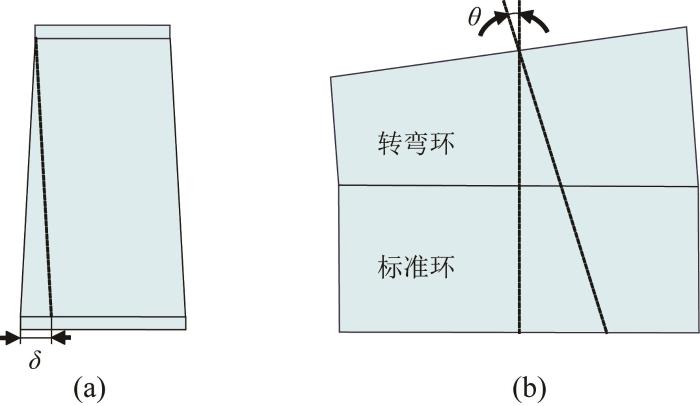
管片的构型取决于隧道的衬砌方式。在地铁隧道施工中，常见的衬砌方式包括3种^[12]：通用型楔形衬砌、转弯环相互组合型衬砌以及标准环与转弯环组合型衬砌。不同衬砌方式对应着管片在形状、组合逻辑等构型上的差异，以适配不同的隧道线形控制需求。其中：标准环与转弯环之间的几何关系如图1所示。图中：δ表示管片的楔形量，θ表示转弯偏转角。盾构隧道通过管片自身的楔形量来控制隧道线形，并根据设计需要选择不同位置的封顶块。

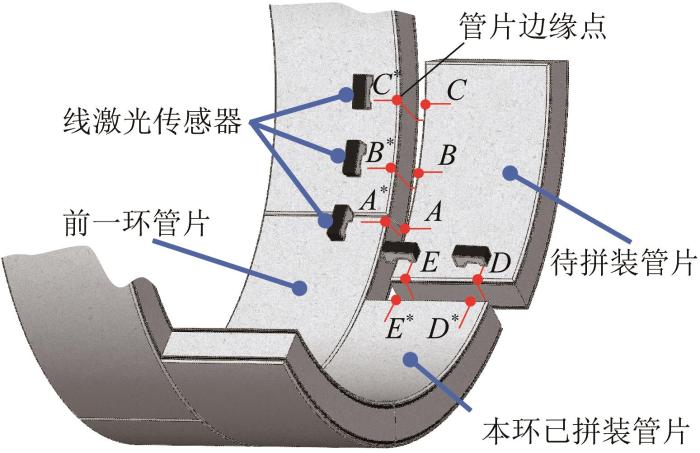
在实际工程应用中，隧道衬砌方式的选择取决于设计单位的施工习惯以及隧道线路的曲线布设特征，这种差异导致盾构管片类型多样。尽管如此，各类楔形管片普遍具有弧边与直边的几何特征。基于此，本文提出了一种基于5个线激光传感器的盾构管片拼装位姿检测方法。如图2所示，将5个线激光传感器分别布置在管片的弧边、直边以及连接缝等关键边界位置处，以实现对任意楔形管片的位姿检测。

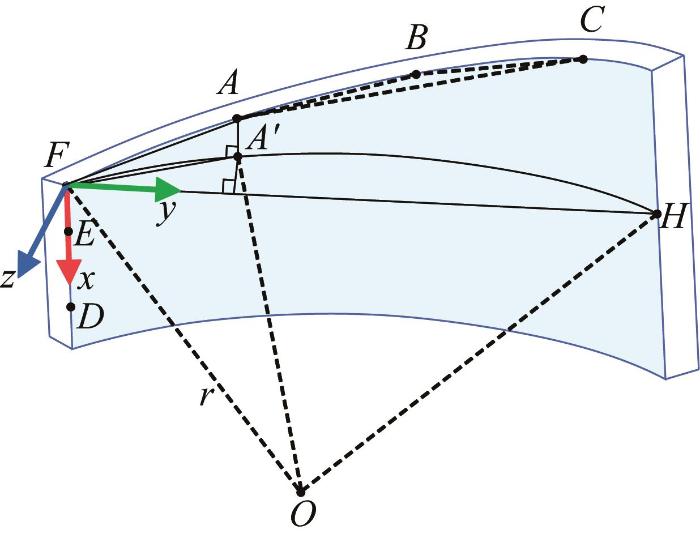
在管片拼装过程中，5个线激光传感器固定安装在拼装机器人的末端执行器上，用于实时检测管片的拼装位姿。具体而言，传感器s₁、s₂、s₃用于检测管片的弧边，其激光线分别与待拼装管片的弧边产生随机交点A、B、C，与对应已拼装管片弧边的交点记为A^∗、B^∗、C^∗，传感器s₄、s₅用于检测管片的直边，其激光线分别与待拼装管片的直边产生交点D、E，与对应已拼装管片直边的交点记为D^∗、E^∗。通过采集上述5组激光偏折点的三维坐标，结合管片几何模型，可计算得到待拼装管片相对于拼装机器人末端执行器坐标系（简称末端执行器坐标系）的位姿。在此基础上，控制系统引导拼装机器人进行精确的位姿调整，进而实现盾构管片的高精度自动化拼装。待拼装管片的位姿计算模型如图3所示。

设各线激光传感器的坐标系为{s _h }（h=1, 2, …, 5）。点A、B、C、D、E在对应传感器坐标系{s _h }中的坐标可由线激光传感器测得。以矢量形式表示各点在传感器坐标系{s _h }中的位置，分别记为 A_s1、 B_s2、 C_s3、 D_s4、 E_s5，可表示为：

设末端执行器坐标系为{t}，传感器s₁、s₂、s₃、s₄、s₅的坐标系至末端执行器坐标系{t}的齐次变换矩阵为Ts1t、Ts2t、Ts3t、Ts4t、Ts5t，则点A、B、C、D、E在末端执行器坐标系{t}中的位置At、Bt、Ct、Dt、 E_t分别表示为：

根据式(1)和式(2)，由坐标的齐次变换可得：

在末端执行器坐标系{t}下，可由At、Bt、Ct计算出由点A、B、C确定的平面（简称平面ABC）的参数方程，设所求平面的参数方程为ax+by+cz+d=0；由Dt、Et可求出直线DE的参数方程，可表示为：

式中：(m₁, n₁, p₁)为直线DE的方向向量。

点F为管片弧边与直边的交点，即直线DE与平面ABC的交点。联立直线DE和平面ABC的参数方程，即可求出点F在末端执行器坐标系{t}下的位置矢量Ft=xFtyFtzFtT。

设圆O为管片的内接圆，与管片两直边的交点分别为点F和点H。设圆O半径为r，内接圆的弦FH长l，r和l均为管片的固有几何参数，可直接由设计参数确定。过A点作直线DE的平行线，与圆O交于点A'，分别连接点A和点F以及点A'和点F。由于直线FD平行于圆O的轴线，因此可得AA'⊥AF。以点F为原点建立管片坐标系{seg}，其中x轴沿向量FD⃗方向，y轴沿向量FH⃗方向，z轴由右手定则确定。设点A在管片坐标系{seg}下的位置矢量Aseg=xAsegyAsegzAsegT，则根据几何关系，可得：

由于向量DE⃗和向量FA⃗的夹角与∠FAA'相等，因此有：

其中：

线段A'F与线段FH均为圆O的弦，而弦的垂直平分线与圆心O相交，则有：

根据图3所示的几何关系，还可得：

将式(6)至(8)代入式(5)，便可求得点A在管片坐标系{seg}下的位置矢量xAsegyAsegzAsegT。此外，在管片坐标系{seg}中，点D、F的位置矢量 D_seg、F_seg可表示为：

其中：

基于此，可求得点A、D、F在管片坐标系{seg}下的坐标。

设管片坐标系{seg}到末端执行器坐标系{t}的齐次变换矩阵为Tsegt，可表示为：

式中：Rsegt为旋转矩阵，tsegt为平移向量。

则根据位姿的齐次变换，可得：

由于平移向量tsegt中各元素的值为管片坐标系{seg}的原点F在末端执行器坐标系{t}中的坐标，则有：

由此可知，齐次变换矩阵Tsegt中仅旋转矩阵Rsegt为待求量。为便于求解Rsegt，进而得到Tsegt，先分别求解由点D、F、A所构成的三角形的几何中心坐标，该几何中心在末端执行器坐标系{t}和管片坐标系{seg}中的位置矢量 P_ct和 P_cseg可表示为：

再对Dt、Ft、At和Dseg、Fseg、Aseg进行中心化处理，可得：

旋转矩阵Rsegt可分解为：

其中：

式中：I为单位矩阵，S为反对称矩阵，Ωx、Ωy、Ωz为罗德里格参数。

则式(11)可改写为：

将式(14)和式(15)代入式(17)，并利用最小二乘法求得Ωx、Ωy、Ωz的值，将其代入式(16)即可求得Rsegt，进而可得管片坐标系{seg}到末端执行器坐标系{t}的齐次变换矩阵Tsegt。至此，完成了基于线激光传感器的待拼装管片位姿检测与计算。

RGB-D相机作为3D视觉传感器，可同步获取待检测目标的彩色图像和深度信息。先利用图像信息进行目标检测，再结合配准后的深度信息，即可得到目标点在相机坐标系下的三维坐标。通过对布置在管片特定位置处的靶标进行测量，可间接解算得到管片的拼装位姿。

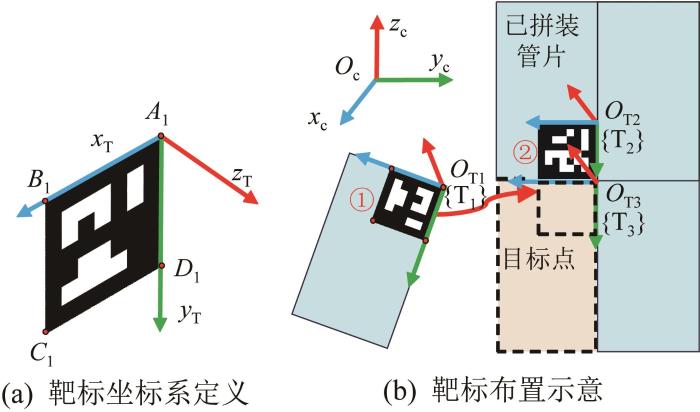
以靶标右上角点A₁为原点建立靶标坐标系，其中：x_T轴沿边A₁B₁方向，y_T轴沿边A₁D₁方向，z_T轴由右手定则确定，如图4(a)所示；靶标在管片上的布置如图4(b)所示。为便于描述，图4(b)中的管片以俯视图形式绘制。设{c}为相机坐标系；{T₁}和{T₂}分别为靶标1和靶标2的坐标系，{T₁}和{T₂}相对于{c}的位姿可由相机直接检测获得；{T₃}为待拼装管片目标拼装点坐标系（简称目标坐标系）。

设目标坐标系{T₃}至靶标2坐标系{T₂}的旋转矩阵为RT3T2，平移向量为tT3T2，则两坐标系间的齐次变换矩阵TT3T2可表示为：

管片拼装过程可视作靶标1坐标系{T₁}与目标坐标系{T₃}重合的过程。因此，仅需将靶标2坐标系{T₂}的原点OT2沿yT2轴的正方向平移至OT3，再绕xT2轴旋转α_c，即可得到目标坐标系{T₃}。通过相机测量可以获得靶标2的角点OT2和OT3在相机坐标系{c}下的坐标，则目标坐标系{T₃}至靶标2坐标系{T₂}的平移向量tT3T2可表示为：

式中：OT2c和OT3c分别为角点OT2和OT3在相机坐标系{c}中的位置矢量。

设管片内接圆半径为r，则旋转角α_c可表示为：

根据旋转变换关系，可得出目标坐标系{T₃}至靶标2坐标系{T₂}的旋转矩阵RT3T2与旋转角αc存在以下关系：

将式(19)至(21)代入式(18)，即可求得齐次变换矩阵TT3T2。设TT2c为靶标2坐标系{T₂}至相机坐标系{c}的齐次变换矩阵，则可通过相机对靶标2的实时识别和定位确定TT2c，进而获得目标坐标系{T₃}至相机坐标系{c}的齐次变换矩阵TT3c：

线激光传感器具有测量精度高和响应快速的优势，在盾构管片拼装位姿检测中得到了广泛应用。然而，线激光传感器在实际测量过程中易受管片边缘缺损的影响。对于轻微的边缘缺损，可通过点云滤波与插值方法进行补偿，但当缺损范围较大时，边缘坐标的提取可能完全失效。此外，线激光传感器受限于其有限的测量范围，在初始定位阶段通常需要人工粗定位辅助，从而影响位姿检测系统的自动化程度。相比之下，基于相机的视觉系统通过识别管片表面布设的靶标，能够有效规避边缘缺损对位姿检测的影响，并提供更广阔的测量视场。但单目相机依赖图像深度估计，其三维重建精度和实时性均存在一定局限。而RGB-D相机能够直接获取场景的深度信息，具备良好的实时性能，但其测量精度通常为毫米级，明显低于线激光传感器所能达到的微米级精度。

为充分发挥不同类型传感器的优势，本文基于自适应加权融合（adaptive weighted fusion, AWF）算法，动态融合线激光传感器与RGB-D相机的位姿测量数据。AWF算法能够自动调整各传感器的权重，实现对精度与测量范围的有效互补，从而提升复杂环境下位姿检测的稳定性与鲁棒性。

设位姿检测系统由n个不同类型的传感器构成，对同一目标参数X_M进行测量，其测量模型可表示为zi(k)=XM+vi(k)，i=1,2,⋯,n。其中：zi(k)表示第i个传感器在k时刻的观测值；vi(k)表示第i个传感器在k时刻的测量噪声，vi的期望E(vi)和方差D(vi)均未知。当zi(k)与zj(k)的差值较大时，说明2个传感器的观测值之间支持程度较低，甚至可能相互背离；反之，若zi(k)与zj(k)的差值较小，则表明这2个传感器的观测值之间支持程度较高，传感器所测数据具有较高的真实性^[13]。将多传感器观测值间的支持程度定义为观测支持度^[14]。

为了对同一时刻各传感器间的观测支持度进行量化，引入指数衰减函数定义k时刻下2个传感器间的观测支持度sij(k)：

式中：μ为度量尺度参数，且μ>0，可通过调整μ的大小改变观测支持度。

为了衡量k时刻下所有传感器间的观测支持度，通过计算两两传感器之间的观测支持度sij(k)，构建观测支持度矩阵 S_k ：

在观测支持度矩阵 S_k 中，sij(k)仅表示k时刻下传感器i与传感器j之间的观测支持度，而传感器i受其他传感器的综合支持程度由第i行元素体现。为衡量传感器i受其他传感器的综合支持程度，定义 S_k 中第i行元素的加权和为k时刻下传感器i的综合观测支持度S_i(k)，即：

式中：aj(k)为k时刻下两传感器间观测支持度的加权系数，且aj(k)≥0。

综合观测支持度Si(k)反映了k时刻下传感器i与其他大多数传感器间观测值的接近程度。Si(k)的值越大，表明该时刻下传感器i的观测值越接近其他大多数传感器的观测值，即传感器的测量结果越可靠；反之，Si(k)的值越小，表明该时刻下传感器i的观测值越偏离其他大多数传感器的观测值，即传感器的观测结果越不可靠。在实际应用中，可针对每个传感器分别设置一个较小的综合观测支持度阈值δi≥0，当传感器的综合观测支持度Si(k)≤δi时，说明该传感器的观测值偏离其他传感器观测值的程度较高，可认为该传感器出现异常，测量结果不可靠，需要进一步对其进行故障隔离或恢复处理。

综合观测支持度Si(k)直观反映了传感器测量结果的可靠性，故利用Si(k)作为传感器观测值的权重，以实现多传感器的加权融合。Si(k)应满足以下条件：

根据式(25)，所有传感器的权重应满足以下关系：

其中：

由于 S_k 是一个正矩阵，则根据Perron-Frobenius定理，该矩阵存在最大实特征值λ（λ>0），且λ对应一个正特征向量，该特征向量的所有分量均大于0^[15]。令A为该特征向量，则有：

求出 S_k 的最大实特征值λ和对应的正特征向量A后，可得：

展开式(29)，可得：

为使Si(k)满足式(26)中的归一化条件，对Si(k)进行归一化处理，即：

由此可计算得到各传感器的权重。根据式(31)中求出的权重，可得到多传感器加权融合后的最终估计值z^i(k)：

基于观测支持度的多传感器自适应融合算法虽具有不依赖系统模型和噪声统计特性的优势，仅需计算传感器间的观测支持度即可实现权重的自适应分配，但在实际应用中仍存在一定局限性。具体而言，由于测量误差和异常值的干扰，某一时刻下传感器的观测支持度可能无法准确反映其真实的测量可靠性。这种观测支持度与可靠性之间的偏差会导致权重分配失准，造成融合结果出现显著误差。为解决上述问题，提出了一种改进的AWF（improved AWF, IAWF）算法。IAWF算法在观测支持度的基础上，通过引入传感器测量方差来对传感器的可靠性进行度量，在充分利用AWF算法对较大测量异常值抑制能力的同时有效提升了可靠性评估的准确性，解决了AWF算法可能会出现的权重分配紊乱问题。

在融合过程中，若传感器的观测支持度大且测量方差小，则表示该传感器的状态较好，应该赋予较大的权重；反之，权重应减小。由此可知，传感器的权重与观测支持度呈正相关，与测量方差呈负相关，则结合式(31)可得新的传感器权重Wi(k)：

式中：σi2(k)为k时刻下传感器i的测量方差估计值。

则最终的融合估计可表示为：

在融合过程中，σi2(k)采用估计的方式进行计算。设z¯(k)为k时刻下所有传感器观测值的算术平均值，则有：

则k时刻下传感器i的测量误差估计值ei(k)及其均值e¯i(k)可表示为：

联立式(36)和式(37)，可求得传感器i在k时刻的测量方差估计值：

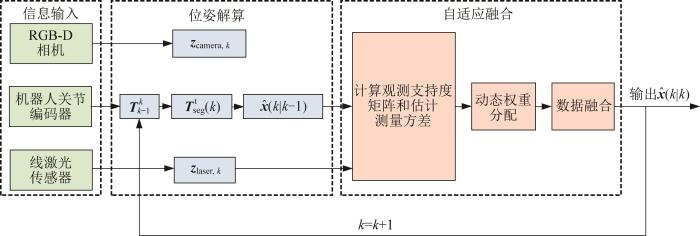
RGB-D相机与线激光传感器的融合定位框架如图5所示。首先，将2种传感器测得的位姿经坐标转换统一到同一基准坐标系下；然后，利用IAWF算法计算各传感器的权重，以自适应完成传感器的加权融合。与经典的卡尔曼滤波（Kalman filtering, KF）算法需要建立准确的系统动态方程不同^[16]，本文所提出的多传感器自适应加权融合策略仅需关注管片在相邻2个时刻的位姿变化。

设从k-1时刻至k时刻管片在末端执行器坐标系{t}中的齐次变换矩阵为Tk-1k，根据位姿转换关系，可得：

式中：Tsegt(k-1)、Tsegt(k)分别为k-1时刻和k时刻下管片坐标系{seg}相对于末端执行器坐标系{t}的齐次变换矩阵；Ttb(k-1)、Ttb(k)分别为k-1时刻和k时刻下末端执行器坐标系{t}相对于拼装机器人基坐标系{b}的齐次变换矩阵，可根据机器人关节编码器数据和机器人正运动学模型进行求解。

设x^(k-1|k-1)为上一时刻的管片位姿融合结果，在给定当前时刻机器人各关节转动角度的条件下，根据式(39)和式(40)，可由x^k-1|k-1预测当前时刻的管片位姿x^k|k-1。设RGB-D相机和线激光测量系统在当前时刻测得的管片位姿分别为zcamera,k和zlaser,k，同时将预测位姿x^(k|k-1)作为第3种传感器的观测值。然后，构建zcamera,k、zlaser,k和x^k|k-1的观测支持度矩阵，并分别计算三者的测量方差估计值。基于观测支持度矩阵和测量方差估计值，利用式(33)分别计算zcamera,k、zlaser,k和x^k|k-1对应的权重W₁k、W₂k和W₃k。最后，通过式(34)将三者进行融合，得到当前时刻的位姿融合结果x^k|k，即：

通过自适应调整权重，将线激光测量系统与RGB-D相机的位姿测量结果进行加权融合，以抑制管片拼装过程中的动态测量误差，从而提高管片拼装位姿检测的鲁棒性和精度。

为验证IAWF算法对RGB-D相机和线激光测量系统的位姿测量结果进行融合的有效性，开展位姿检测仿真实验。假设测量目标的初始位置p(0)=[000]T，其初始姿态用四元数表示为q(0)=[1000]T；测量目标作匀速运动，其速度 v =[0.010 0.020 0.015]^T m/s，角速度 ω =[0.01 0.02 0.03]^T rad/s；传感器的采样频率均为20 Hz。

通过仿真比较了60 s内单独使用RGB-D相机、线激光测量系统的目标位姿检测结果与基于IAWF、KF算法的目标位姿融合结果。为验证传感器异常情况下融合算法的鲁棒性，在第30秒时增大线激光测量噪声的协方差。RGB-D相机、线激光测量系统的测量噪声和过程噪声的协方差矩阵如表1所示。

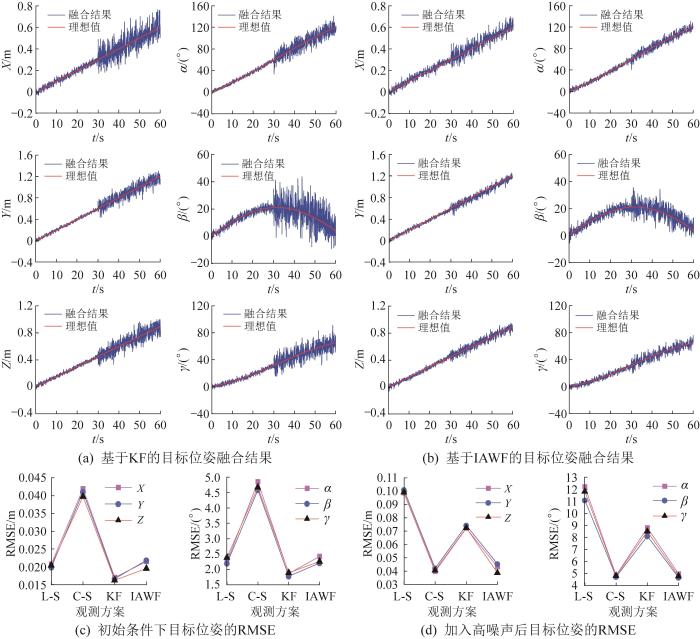
图6所示为基于不同融合算法的目标位姿对比及测量误差分析。图中：X、Y、Z为目标位置，α、β、γ为目标姿态（分别为绕X、Y、Z轴的旋转角），用欧拉角表示；L-S、C-S分别表示单独使用线激光测量系统和RGB-D相机。由图6可知，在0—30 s时间段内，基于IAWF算法的目标位姿融合结果的波动程度及均方根误差（root mean square error, RMSE）均小于基于KF算法的；IAWF算法融合得到的位姿精度高于单独使用RGB-D相机的测量结果，接近更高精度的线激光测量结果。在30—60 s时间段内，线激光测量噪声的协方差矩阵发生变化，测量方差增大，其测量精度低于RGB-D相机；基于IAWF算法的目标位姿融合结果的波动程度较小，位姿精度接近高精度的RGB-D相机测量结果。

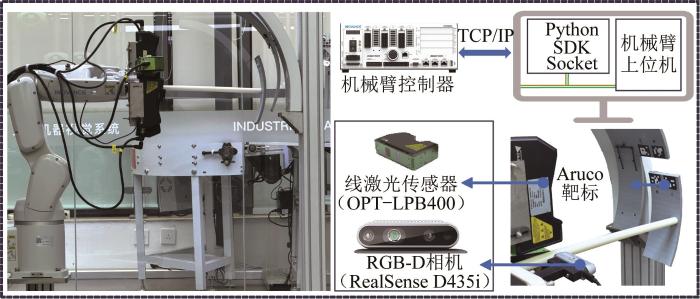
为了验证本文所提出的IAWF算法在盾构管片自动拼装定位中的有效性和精度，搭建了管片拼装实验平台与位姿检测系统，如图7所示。其中，六自由度机械臂可实现管片位姿的调整；线激光传感器的型号为OPT-LPB400，RGB-D相机的型号为Intel RealSense D435i，工控机CPU（central processing unit，中央处理器）的型号为Intel Core i5-13600K。位姿检测系统的平均检测频率可达20 Hz，能够实现管片的实时高精度定位。

在进行管片自动拼装实验前，先通过人工调整待拼装管片与已拼装管片之间的相对位姿，使得两者的错台和间隙最小化。随后，记录此时机械臂末端执行器相对于基坐标系的六维位姿，作为管片拼装的目标基准位姿。该基准位姿 (X, Y, Z, α, β, γ) = (531.262 mm, 235.873 mm, 702.975 mm, -101.461°, -43.865°, -79.271°)。

在每次拼装过程中，沿预定拼装路径选取60个关键点。每当机械臂末端执行器到达一个点位时，采集该点处线激光测量系统与RGB-D相机的测量数据，并计算管片的目标拼装位姿。同时，利用IAWF算法对2种传感器的感知结果进行融合，并将融合后的位姿作为当前点位的目标拼装位姿。

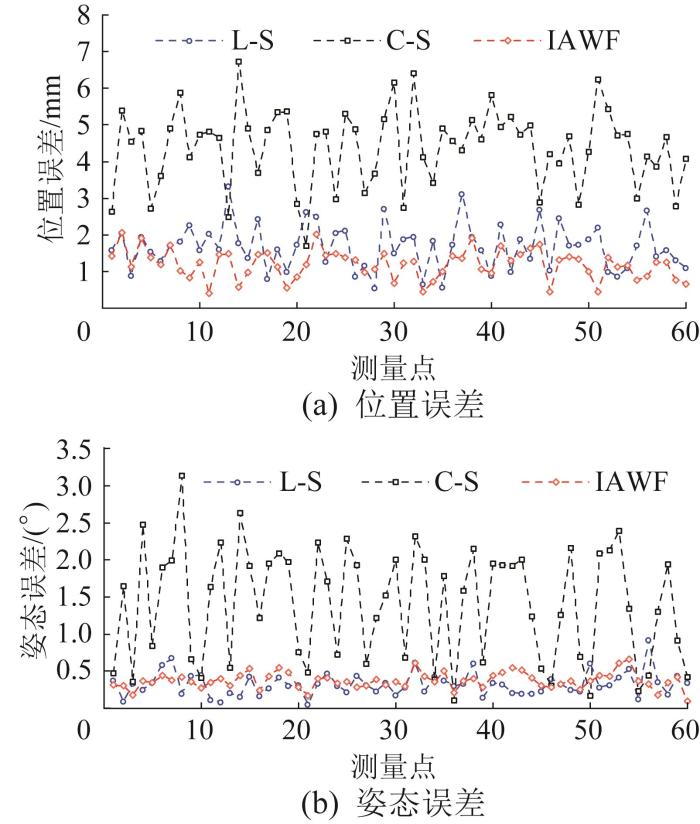
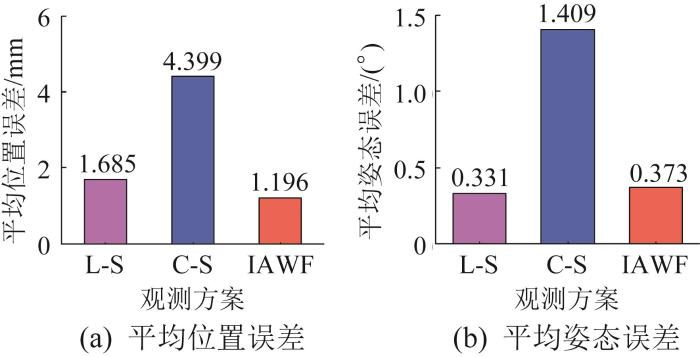
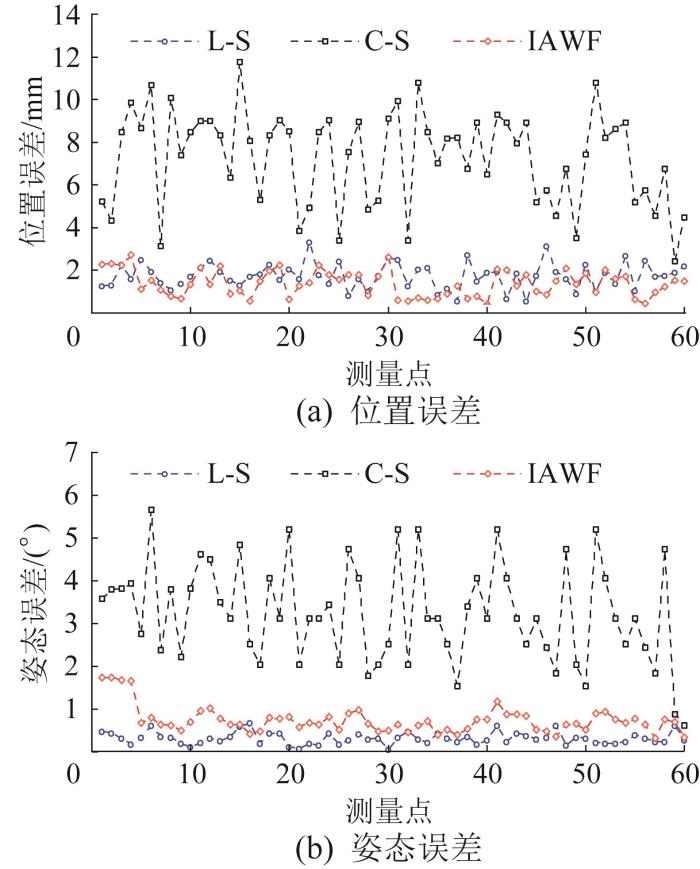
拼装实验在无干扰场景下进行，实验条件为室内光照均匀、环境稳定的正常工况，且所用管片边缘无缺损。在管片拼装过程中，使用线激光测量系统与RGB-D相机单独定位以及融合定位的误差如图8所示。结果表明，RGB-D相机测得的位姿误差波动较大，整体误差高于线激光测量系统单独定位与融合定位结果。相比之下，融合后的位姿误差波动幅度较小，接近线激光测量精度，验证了IAWF算法对相机定位性能的显著提升。正常工况下管片拼装的平均定位误差如图9所示。从平均误差来看，融合后的平均位置误差和平均姿态误差分别为1.196 mm与0.373°，与线激光测量结果接近；相较于RGB-D相机，平均位置误差与平均姿态误差分别下降了72.8%和73.5%。这一结果进一步证明了本文融合方法在提升定位精度方面的显著优势。

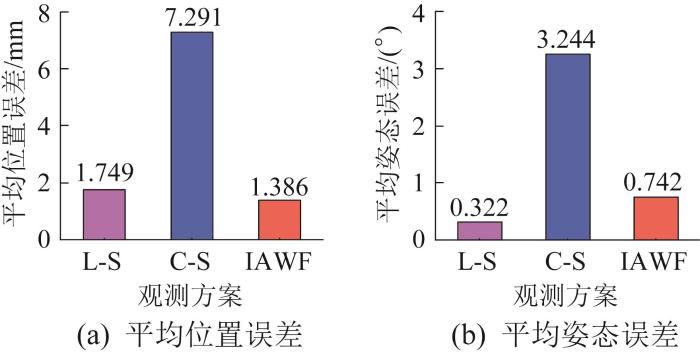
为验证低光照条件下的融合定位精度，在光照不足的室内环境中选用无缺损管片进行自动拼装实验。实验所测得的管片拼装定位误差曲线如图10所示。与光照条件良好的正常工况相比，RGB-D相机测得的位姿误差整体增大。这主要是因为光照不足导致靶标图像质量下降，影响了识别与定位精度。然而，利用IAWF算法将RGB-D相机测量数据与线激光测量数据融合后，定位误差的变化幅度较小，整体性能与单独使用线激光测量系统相当，表明融合方法在弱光条件下依然能保持较高的稳定性。低光照工况下管片拼装的平均定位误差如图11所示。结果显示：在光照不足的室内环境下，RGB-D相机测得的平均位置误差为7.291 mm，平均姿态误差为3.244°，较光照良好条件下分别增大了2.892 mm与1.835°。相比之下，融合后的平均位置误差与平均姿态误差分别为1.386 mm与0.742°，相比于光照良好条件下略有增大，增大量分别为0.190 mm和0.369°。与低光照条件下单独使用RGB-D相机定位相比，融合定位方式使得平均位置误差和平均姿态误差分别降低了81.0%与77.1%。

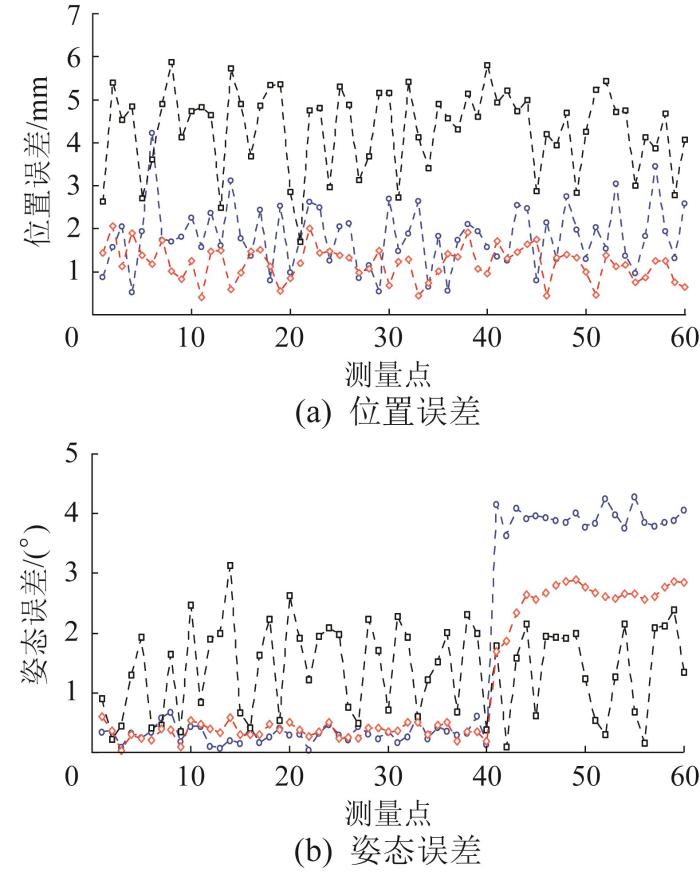
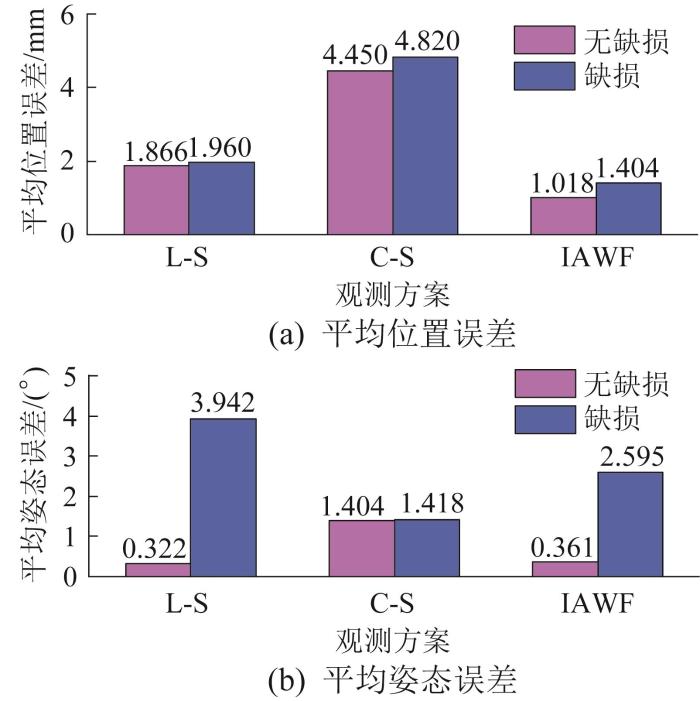
为验证IWAF算法在线激光测量系统受干扰条件下的融合定位性能，采用边缘存在缺口的管片，以模拟线激光测量数据异常场景。在测量过程中设若干点位，其中前40个点位照射管片的无缺损区域，第41个及其后的点位照射缺损区域，实现干扰条件的渐变模拟。边缘缺损管片拼装定位误差曲线如图12所示，对应的平均定位误差如图13所示。结果表明，在管片边缘缺损区域，线激光测量系统的定位精度明显下降。对于缺损区域，若仅依赖线激光测量数据，则平均位置误差显著增大。然而，通过IWAF算法将线激光测量系统与RGB-D相机的测量结果融合后，平均位置误差降低了28.4%，平均姿态误差降低了34.2%。结果表明，IWAF算法在线激光测量数据异常的情况下仍具备良好的鲁棒性。

融合定位实验验证了所提出的IWAF算法可有效提升管片位姿检测系统的抗干扰能力。为验证使用该方法后管片的拼装精度，在管片边缘破损、线激光测量数据异常的工况下，通过改变管片的初始位姿进行10次管片拼装实验，并同步测量拼装完成后管片间的错台和间隙。管片拼装误差如表2所示。结果表明，错台与间隙的最大值分别为4.8 mm和4.6 mm，满足5 mm的实际工程要求。

本文针对盾构管片自动拼装定位问题，通过融合线激光传感器和RGB-D相机的优势，结合IAWF算法实现了对管片拼装位姿的高精度和高鲁棒性检测。正常光照、光照不足和管片边缘破损三种不同工况下的实验结果表明，所提出的融合定位方法能够有效应对复杂环境对单一传感器性能的影响。在正常光照条件下，融合后的平均位置误差和平均姿态误差分别为1.196 mm与0.373°，接近线激光传感器的高精度测量结果；在低光照条件下，尽管RGB-D相机的测量误差增大，但融合后的定位误差仍保持较低水平，平均位置误差与平均姿态误差分别为1.386 mm与0.742°，显示出良好的抗干扰能力；在管片边缘破损、线激光测量数据异常的工况下，IAWF算法通过动态调整不同传感器的权重，有效降低了定位误差，平均位置误差和平均姿态误差分别降低了28.4%和34.2%，相较于单一传感器测量方法显著降低。管片拼装的最大错台和最大间隙分别为4.8 mm和4.6 mm，均满足实际工程要求。综上所述，IAWF算法在传感器异常或环境条件变化时均能保持稳定的融合效果，有效提升了位姿检测系统的整体可靠性。研究结果为盾构管片自动化拼装提供了理论支持与技术路径，为复杂地质条件下隧道施工的智能化发展奠定了基础。

本文链接：https：//www.zjujournals.com/gcsjxb/CN/10.3785/j.issn.1006-754X.2025.05.132