基于概率-区间混合模型的六足机器人运动稳定性优化设计方法

doi:10.3785/j.issn.1006-754X.2024.04.129

基于概率-区间混合模型的六足机器人运动稳定性优化设计方法

刘鑫^,^,, 李飞虎

长沙理工大学汽车与机械工程学院，湖南长沙 410114

Optimization design method for kinematic stability of hexapod robot based on probability-interval hybrid model

LIU Xin^,^,, LI Feihu

College of Automotive and Mechanical Engineering, Changsha University of Science and Technology, Changsha 410114, China

收稿日期: 2024-03-29 修回日期: 2024-04-22

基金资助:

国家自然科学基金资助项目.  52275235
湖南省杰出青年科学基金资助项目.  2021JJ10040
湖南省研究生科研创新项目.  CX20220900

First author contact: LIU X, LI F H. Optimization design method for kinematic stability of hexapod robot based on probability-interval hybrid model[J]. Chinese Journal of Engineering Design, 2024, 31(5): 585-591.

Received: 2024-03-29 Revised: 2024-04-22

作者简介 About authors

刘　鑫（1981—），男，教授，博士，从事机械结构可靠性优化设计研究，E-mail:lxym810205@163.com,http://orcid.org/0000-0003-4766-3517 , E-mail：lxym810205@163.com

摘要

针对中枢模式发生器（central pattern generator，CPG）模型的不确定性参数对六足机器人运动稳定性的影响，提出了一种基于概率-区间混合模型的六足机器人运动稳定性优化设计方法。首先，建立了六足机器人数值模型，并基于Matsuoka 和 Kimura模型建立了六足机器人CPG模型；其次，通过概率-区间混合模型来描述CPG模型的不确定性变量，并建立了六足机器人运动稳定性优化数学模型；再次，采用Karush-Kuhn-Tucker（KKT）最优化条件和基于最大熵原理的二次四阶矩方法对六足机器人运动稳定性优化设计问题进行解耦，将三层嵌套优化设计问题转化为单层优化设计问题，实现对优化问题的高效求解；最后，基于径向基函数建立六足机器人运动稳定性优化近似模型，并利用遗传算法求解最优设计解。结果表明，采用所提出的方法能够高效求解CPG模型的最优参数，提高了六足机器人的运动稳定性。因此，该方法在机器人运动控制领域具有较高的应用价值。

关键词： 六足机器人 ; 运动稳定性 ; 概率模型 ; 区间模型 ; 解耦策略

Abstract

Considering the influence of the uncertain parameters of central pattern generator (CPG) model on the kinematic stability of hexapod robot, an optimization design method for the kinematic stability of hexapod robot based on a probability-interval hybrid model was proposed. Firstly, the numerical model of the hexapod robot was established, and the CPG model of the hexapod robot was established based on the Matsuoka and Kimura models. Secondly, the uncertainty variables of the CPG model were described by the probability-interval hybrid model, and the kinematic stability optimization mathematical model of the hexapod robot was also constructed. Then, Karush-Kuhn-Tucker (KKT) optimization condition and the second order fourth moment method based on the maximum entropy principle were used to decouple the kinematic stability optimization design problem of the hexapod robot, and the three-level nested optimization design problem was transformed into a single-level optimization design problem, which realized the efficient solution of the optimization problem. Finally, the kinematic stability approximate model of hexapod robot was established based on radial basis function, and the optimal design solution was obtained by genetic algorithm. The results showed that the proposed method could effectively solve the optimal parameters of the CPG model and improve the kinematic stability of the hexapod robot. Therefore, this method has high application value in the field of robot motion control.

Keywords： hexapod robot ; kinematic stability ; probability model ; interval model ; decoupling strategy

PDF (2009KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

刘鑫, 李飞虎. 基于概率-区间混合模型的六足机器人运动稳定性优化设计方法[J]. 工程设计学报, 2024, 31(5): 585-591 doi:10.3785/j.issn.1006-754X.2024.04.129

LIU Xin, LI Feihu. Optimization design method for kinematic stability of hexapod robot based on probability-interval hybrid model[J]. Chinese Journal of Engineering Design, 2024, 31(5): 585-591 doi:10.3785/j.issn.1006-754X.2024.04.129

本文链接：https://www.zjujournals.com/gcsjxb/CN/10.3785/j.issn.1006-754X.2024.04.129

在机器人姿态控制过程中，腿部关节的旋转角度直接影响着机器人的运动稳定性与安全性^[1]。特别在六足机器人具有冗余自由度的情况下，对其腿部关节旋转角度的有效控制成为提升机器人运动稳定性的关键一环^[2]。六足机器人的腿部连杆之间装有旋转电机，作为机器人的旋转关节^[3]，并通过中枢模式发生器（central pattern generator, CPG）模型控制该关节电机的转动^[4-5]。因此，CPG模型的可靠性直接影响着六足机器人的运动稳定性与安全性。大量研表明，可靠的CPG模型能够最大限度地提升六足机器人的运动稳定性^[6]。

在现有六足机器人的运动控制中，通常将CPG模型中神经元细胞之间的相互抑制系数、神经元振荡器的适应系数以及CPG模型参数作为确定性参数来考虑，忽略了其不确定性对机器人运动稳定性的影响^[7]，导致CPG模型的节律周期信号响应与期望波形之间存在较大差异，致使机器人的控制失效，其运动稳定性难以保障。因此，需要研究一种针对CPG模型不确定性参数的优化设计方法，以提高机器人的运动稳定性，有效控制机器人姿态^[8]。

目前，大多数学者在研究不确定性参数对系统可靠性的影响时，倾向于采用概率模型来描述不确定性变量^[9]，并形成了相应的优化设计方法。然而，当缺乏足够的不确定性变量的数据样本时，就无法准确地建立相应的概率模型，导致概率模型无法准确地描述不确定性变量的信息^[10]。而区间模型不需要精确的概率分布^[11]，只需要确定其上下限，因此在一定程度上避免了概率模型的局限性。在自由度冗余、控制过程复杂的六足机器人的优化设计中，须考虑多种不同类型的设计参数，以控制机器人的运动稳定性。因此，本文采用概率-区间混合模型来描述六足机器人不确定性变量信息，并对机器人的运动稳定性进行优化设计。基于概率-区间混合模型的六足机器人运动稳定性的优化设计，本质上是一个三层嵌套的优化问题。如果采用传统的优化方法进行求解，则计算效率低下，计算成本较高。此外，计算高维、强非线性的数值模型往往会产生计算量过大和求解失败等问题。因此，本文采用Karush-Kuhn-Tucker（KKT）最优化条件^[12]和最大熵原理，提出了一种解耦策略，将三层嵌套的优化设计问题转化为单层嵌套的优化设计问题，以提高求解最优设计问题的效率。

综上所述，本文提出了一种基于概率-区间混合模型的六足机器人运动稳定性优化设计方法。首先，建立了六足机器人的运动控制模型和CPG模型；其次，针对六足机器人运动稳定性的优化设计问题，采用KKT最优化条件和最大熵原理进行解耦，将三层嵌套优化问题转化为单层优化问题；最后，基于径向基函数建立六足机器人运动稳定性近似优化问题，并且利用遗传算法进行高效求解。

1 六足机器人运动控制模型的建立

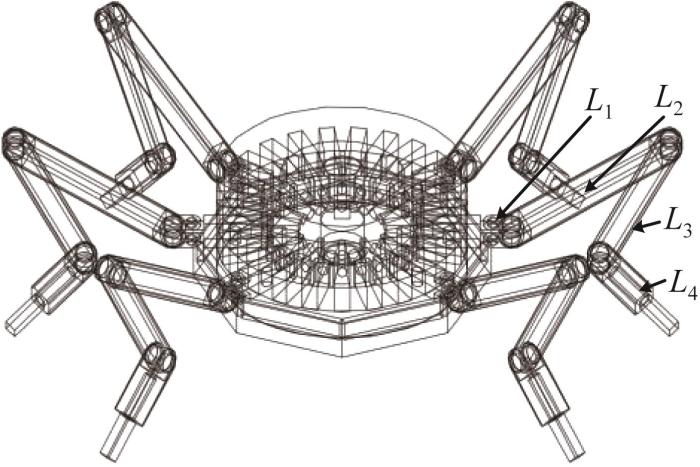
在六足机器人姿态控制过程中，机器人利用腿部关节的旋转来调整自身的运动姿态，并保持运动稳定性^[13]。作者利用工业建模软件构建了六足机器人的数值模型和运动仿真环境^[14]，为机器人的姿态控制研究提供依据。六足机器人的结构模型如图1所示。其主要由机器人躯体、运动足以及腿部旋转关节等部件构成^[15]，其中：机器人躯体与6个运动足按六边形的形式相互连接；腿部关节采用内膝肘式配置方式，腿部关节之间连杆的长度分别为L₁、L₂、L₃和L₄。其结构参数如表1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 六足机器人结构模型

Fig.1 Structure model of hexapod robot

表1 六足机器人结构尺寸

Table 1 Dimensions of hexapod robot structure

结构尺寸	数值
机身尺寸/ mm×mm×mm	11 003×7 724×328
L₁/ mm	30
L₂/ mm	291
L₃/ mm	222
L₄/ mm	167.5

新窗口打开| 下载CSV

在传统的六足机器人姿态控制研究中，通常对机器人腿部结构进行建模，并采用逆运动学方法计算其腿部关节的旋转角度^[16]。采用传统的方法控制六足机器人的运动稳定性存在着不少问题，如机器人建模的复杂性问题、逆运动学求解的不唯一性问题以及在复杂多变的工况下六足机器人的6个运动足与腿部旋转关节之间的协调性问题。

为了提高六足机器人的运动稳定性，本文基于Matsuoka和Kimura模型^[17]，构建了一种CPG模型，通过CPG模型的节律周期信号响应来控制六足机器人腿部关节的旋转。

CPG模型表示为：

\{\begin{array}{l} T_{r} μ_{f, i}^{'} + μ_{f, i} = b v_{f, i} + a y_{e, i} + c \\ T_{r} v_{f, i}^{'} + v_{f, i}^{'} = y_{f, i} \\ T_{r} μ_{e, i}^{'} + μ_{e, i} = b v_{e, i} + a y_{e, i} + c \\ T_{r} v_{e, i}^{'} + v_{e, i}^{'} = y_{e, i} \\ y_{f, e, i} = g (μ_{f, e, i}) = μ_{f, i} - μ_{e, i} (i = 1, \dots, n) \\ g (μ) = m a x (μ, 0) \end{array}

式中：T_r为节律信号的上升时间， $μ$ 为机器人腿部关节的节律信号， $v$ 为机器人腿部关节的角度，y_i 为神经元振荡器节律信号的输出， $a$ 为神经元细胞之间的相互抑制系数， $b$ 为神经元振荡器适应系数， $c$ 为恒定的激励输入， $g (u)$ 为门槛函数；下标f表示屈肌神经元，e表示伸肌神经元， $i$ 表示第 $i$ 个神经元振荡器。

采用CPG模型控制六足机器人腿部关节转动时，如果将CPG模型的不确定性参数当作确定性参数来考虑，会导致CPG模型的节律周期信号响应不稳定，且与期望的节律周期信号响应有较大差异，致使六足机器人的运动稳定性难以得到保障。因此，为了使CPG模型输出稳定、连续、平滑且具有相位关系的周期节律信号，需要研究一种针对CPG模型不确定性参数的优化设计方法。

2 六足机器人运动稳定性优化数学模型的建立

为了确保六足机器人的运动稳定性，将机器人质心位移作为机器人稳定系统的优化目标；考虑到CPG模型输出的周期节律信号的稳定、连续、平滑的特性与模型不确定性参数中的抑制系数a和适应系数b的设置有关，因此将其作为设计变量 $X$ ，分别对应X₁和X₂；同时，考虑到机器人腿部各关节旋转角度的相位关系与CPG模型中初值矩阵参数的设置有关，因此将CPG模型中初值矩阵参数分别作为概率变量和区间变量；此外，将机器人腿部关节输出角度差的可靠性指标和机器人运动速度的可靠性指标值作为约束条件。因此，得到六足机器人运动稳定性优化数学模型：

\{\begin{array}{l} m i n f_{w} (X, μ_{P}, μ_{Q}) \\ s . t . β_{1} [g_{J} (X, P, Q) = 1 - J (X, P, Q) \geq 0] \geq β_{t, 1} \\ β_{2} [g_{S} (X, P, Q) = S (X, P, Q) - 0.2 \geq 0] \geq β_{t, 2} \\ X = (X_{1} X_{2})^{T} \\ - 4 \leq X_{1} \leq - 2.8, - 15 \leq X_{2} \leq - 8 \\ P \sim N (μ_{P}, σ_{P}), Q = [0.005, 0.015] \end{array}

式中： $f_{w}$ 为机器人质心位移； $β_{1}$ 和 $β_{2}$ 为可靠性指标值； $g_{J}$ 为机器人腿部关节输出角度差约束的极限状态功能函数， $g_{S}$ 为机器人运动速度约束的极限状态功能函数；J和S分别为机器人腿部关节角度差函数和速度函数；P为概率变量，Q为区间变量； $β_{t, 1}$ 和 $β_{t, 2}$ 为约束函数的可靠性指标预设阈值，初始设定 $β_{t, 1}$ = $β_{t, 2}$ =3； $N (μ_{P}, σ_{P})$ 为概率变量P的均值和标准差。

式(2)所示的优化数学模型涉及内外层嵌套的可靠性优化^[18]，即：在外层，是对六足机器人质心位移可靠性指标求解的单层优化；在内层，由于极限状态功能函数中同时存在概率变量和区间变量，求解可靠性指标是双层优化设计问题。因而，六足机器人运动稳定性优化设计问题是内外三层嵌套的，如果采用传统的优化方法求解，效率低且时间成本较高，无法满足优化设计的要求^[19]。因此，需要采取一种解耦策略，高效求解六足机器人运动稳定性优化设计问题。

3 六足机器人运动稳定性优化问题的求解

3.1　优化问题的解耦方法

由于 $β_{1}$ 和 $β_{2}$ 的求解方法相同，本文以求解 $β_{1}$ 为例进行说明。

在六足机器人运动稳定性优化设计问题中， $β_{1}$ 可通过式(3)求解^[20]：

\{\begin{array}{l} β_{1} = \underset{U}{m i n} ‖U‖ \\ s . t . \underset{Q \in Ω_{Q}}{m i n} G_{J} (X, U, Q) = 0 \end{array}

(3)

式中：U为随机变量， $G_{J} (X, U, Q)$ 为极限状态功能函数， $Ω_{Q}$ 为区间变量Q的集合。

由式(3)可知， $β_{1}$ 的求解是双层相互嵌套的优化设计问题，即：利用式(4)求解外层可靠性指标β_L，利用式(5)求解内层极限状态功能函数 $G_{J} (X, U, Q^{*}) = 0$ 。

\{\begin{array}{l} β_{L} = \underset{U}{m i n} ‖U‖ \\ s . t . G_{J} (X, U, Q^{*}) = 0 \end{array}

(4)

\{\begin{array}{l} G_{J} (X, U, Q^{*}) = \underset{Q \in Ω_{Q}}{m i n} G_{J} (X, U, Q) = 0 \\ 0.005 \leq Q \leq 0.015 \end{array}

(5)

为了将求解外层可靠性指标和内层极限状态函数的双层优化设计问题转化为单层优化设计问题，本文采用KKT最优化条件，使Q服从均匀分布u(0.005, 0.015)，则 $g_{J} (X, P, Q)$ 极限状态功能函数可以表示为：

g_{J} (X, P, u) = 1 - J (X, P, u)

(6)

因此，将式(6)和(3)合并来求解可靠性指标，可表示为：

\{\begin{array}{l} β_{1} = \underset{U, V}{m i n} \sqrt[]{{‖U‖}^{2} + {‖V‖}^{2}} \\ s . t . G_{J}^{'} (X, U, V) = 0 \end{array}

(7)

式中：V为随机变量u转换成标准正态下的变量， $G_{J}^{'} (X, U, V)$ 为 $g_{J} (X, P, u)$ 转换成标准正态下的极限状态功能函数。

如式(7)所示，将求解可靠性指标的双层嵌套优化设计问题转换为仅具有概率模型的单层优化设计问题。

式(6)中极限状态功能函数 $g_{J} (X, P, u)$ 中的P和u都为概率变量，因此本文基于最大熵原理^[21]，利用求积分的方法求出式(6)中极限状态功能函数的最大失效概率 $p_{J, f}$ ，进而求解可靠性指标 $β_{1}$ ，以最大程度地提高可靠性指标的求解效率。

首先，将 $g_{J} (X, P, u)$ 标准化为：

y_{1} = \frac{g_{J} - μ_{g_{_{J}}}}{σ_{g_{_{J}}}}

(8)

式中： $μ_{g_{_{J}}}$ 为 $g_{J} (X, P, u)$ 的期望， $σ_{g_{_{J}}}$ 为 $g_{J} (X, P, u)$ 的标准差。

其次，计算y₁的前4阶矩 $v_{(j), y_{1}}^{}$ (j=0, 1, …, 4)，表示为：

E [y_{(j), 1}] = v_{(j), y_{1}}

(9)

其中：

\begin{matrix} v_{(0), y_{1}} = 1 \\ v_{(1), y_{1}} = 0 \\ v_{(2), y_{1}} = 1 \\ v_{(3), y_{1}} = \frac{μ_{(3), g_{_{J}} (X, P, u)}}{σ_{(3), g_{_{J}} (X, P, u)}} \\ v_{(4), y_{1}} = \frac{μ_{(4), g_{_{J}} (X, P, u)}}{σ_{(4), g_{_{J}} (X, P, u)}} \end{matrix}

最后，建立求解 $p_{J, f}^{}$ 的积分方程，如式(10)所示。

\begin{array}{l} p_{J, f} = P r [g_{J} (X, P, u) \leq 0] = P r (y_{1} \leq \frac{μ_{g_{_{J}}}}{σ_{g_{_{J}}}}) = \\ \int_{- \infty}^{\frac{μ_{g_{_{J}}}}{σ_{g_{_{J}}}}} e x p (- \sum_{k = 0}^{4} a_{k 1} y_{k, 1}) d y_{1} \end{array}

(10)

式中： $P r (•)$ 为相对应的极限状态功能函数 $g_{J} (X, P, u)$ 的概率函数，待定系数 $a_{k 1}$ (k=0, 1, …, 4)可通过式(11)可求得。

\int_{- \infty}^{+ \infty} y_{(j), 1} e x p (- \sum_{k = 0}^{4} a_{k 1} y_{k, 1}) d y_{j} = v_{(j), y_{1}}

(11)

式中：y_k_{, 1}为极限状态函数的k阶矩。

求得 $p_{J, f}^{}$ 后，则：

β_{1} = - Φ^{- 1} (p_{J, f})

(12)

式中： $Φ^{- 1} (\cdot)$ 为在标准正态分布函数下逆累积分布的逆函数。

本文采用KKT最优化条件，并基于最大熵原理，对六足机器人的运动稳定性优化设计问题进行解耦处理，从而将三层嵌套化设计问题转化为单层优化设计问题，并采用积分方法进行高效求解。

同理，可求得 $β_{2}$ ，则式(2)可表示为：

\{\begin{array}{l} m i n f_{w} (X, μ_{P}, μ_{Q}) \\ s . t . \int_{- \infty}^{\frac{μ_{g_{_{J}}}}{σ_{g_{_{J}}}}} e x p (- \sum_{k = 0}^{4} a_{k 1} y_{k, 1}) d y_{1} \leq Φ (- β_{t, 1}) \\ \int_{- \infty}^{\frac{μ_{g_{_{s}}}}{σ_{g_{_{s}}}}} e x p (- \sum_{k = 0}^{4} a_{k 2} y_{k, 2}) d y_{2} \leq Φ (- β_{t, 2}) \\ X = {(X_{1} X_{2})}^{T} \\ - 4 \leq X_{1} \leq - 2.8, - 15 \leq X_{2} \leq - 8 \\ P \sim N (μ_{P}, σ_{P}), Q = [0.005, 0.015] \end{array}

(13)

本文通过解耦策略，将六足机器人运动稳定性优化设计问题中的可靠性指标三层嵌套问题解耦成单层求解问题，有效提高了计算效率。

3.2　近似优化模型的建立

在六足机器人运动稳定性优化设计中，目标函数和极限状态功能函数无法通过显性函数表达式表示出来。由于目标函数和极限状态功能函数具备隐函数特征，本文首先采用拉丁超立方设计（latin hypercube design，LHD）方法^[22]，均匀采集初始实验样本点；然后，利用径向基函数（radial basis function, RBF）^[23]构建六足机器人运动稳定性优化的近似模型。因此，将六足机器人运动稳定性优化的数学模型转化为：

\{\begin{array}{l} m i n {\tilde{f}}_{w} (X, μ_{P}, μ_{Q}) \\ s . t . \int_{- \infty}^{\frac{μ_{{\tilde{g}}_{_{J}}}}{σ_{{\tilde{g}}_{_{J}}}}} e x p (- \sum_{k = 0}^{4} a_{k 1} {\tilde{y}}_{k, 1}^{}) d y_{1} \leq Φ (- β_{t, 1}^{}) \\ \int_{- \infty}^{\frac{μ_{{\tilde{g}}_{_{s}}}}{σ_{{\tilde{g}}_{_{s}}}}} e x p (- \sum_{k = 0}^{4} a_{k 2} {\tilde{y}}_{k, 2}^{}) d y_{2} \leq Φ (- β_{t, 2}^{}) \\ X = {(X_{1} X_{2})}^{T} \\ - 4 \leq X_{1} \leq - 2.8, - 15 \leq X_{2} \leq - 8 \\ P \sim N (μ_{P}, σ_{P}), Q = [0.005, 0.015] \end{array}

(14)

3.3　优化设计过程

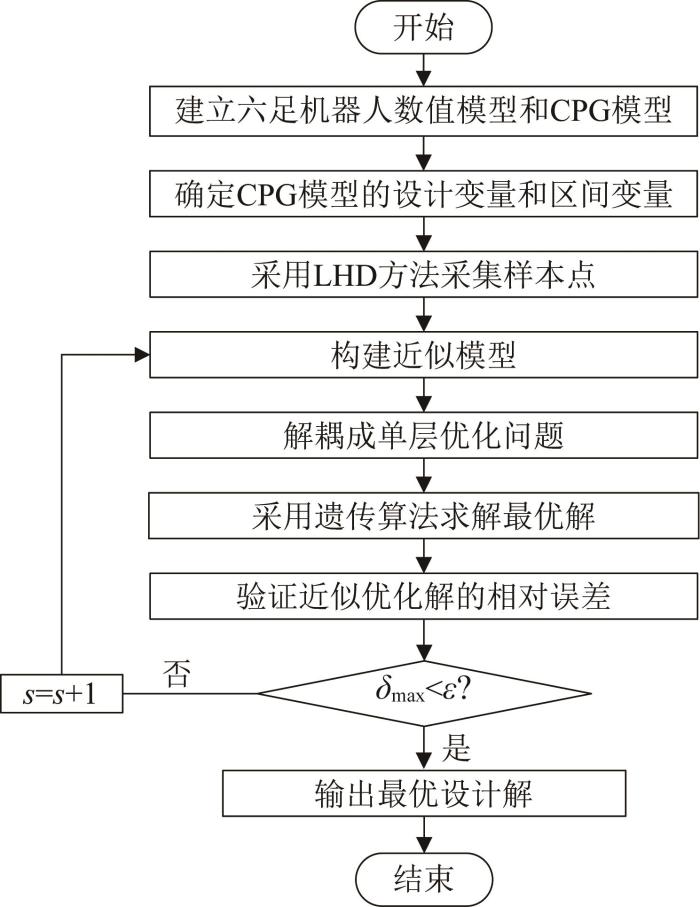
六足机器人运动稳定性优化设计的方法如图2所示，其具体流程如下。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 六足机器人运动稳定性优化设计方法

Fig.2 Optimization design method for kinematic stability of hexapod robot

Step 1：建立六足机器人数值模型，并基于Matsuoka和Kimura模型建立CPG模型。

Step 2：基于六足机器人CPG模型，确定设计变量 $X = {(X_{1} X_{2})}^{T}$ ，得出六足机器人质心位移。

Step 3：针对优化参数的随机变量，采用LHD方法均匀采样，设置初始循环次数s，允许误差ε<10%。

Step 4：利用采集的样本点计算出响应值，并基于RBF构建目标函数和极限状态功能函数的近似模型。

Step 5：采用KKT最优化条件和基于最大熵原理的二次四阶矩方法，对六足机器人运动稳定性优化设计问题中的可靠性指标进行解耦。

Step 6：基于遗传算法对六足机器人运动稳定性优化近似模型进行求解。

Step 7：计算解得的最优设计解 $f_{w}$ 与仿真值 ${\tilde{f}}_{w}$ 的最大相对误差 $δ_{m a x}$ ， $δ_{m a x} = m a x \{|(f_{w} - {\tilde{f}}_{w}) / f_{w}|\}$ 。如果 $δ_{m a x} < ε$ ，说明模型符合精度要求；否则，返回Step 4，直至模型满足精度要求。

4 六足机器人运动稳定性优化设计方法的应用

将本文提出的优化方法应用于六足机器人运动稳定性设计中。首先，基于概率-区间混合模型来描述CPG模型中的不确定性变量；其次，采用LHD方法均匀采集60个初始样本点，并通过六足机器人的运动仿真获得 ${\tilde{f}}_{w}$ 值；再次，利用RBF构建六足机器人运动稳定性优化的近似模型；最后，利用遗传算法求解最优设计解。其中，设定可靠性指标阈值为3，并要求ε<10%。因此，当目标函数值f_w=3.507 3 mm收敛时，求得优化设计解 X =(-3.999 996 606 -13.06 400 305)^T。

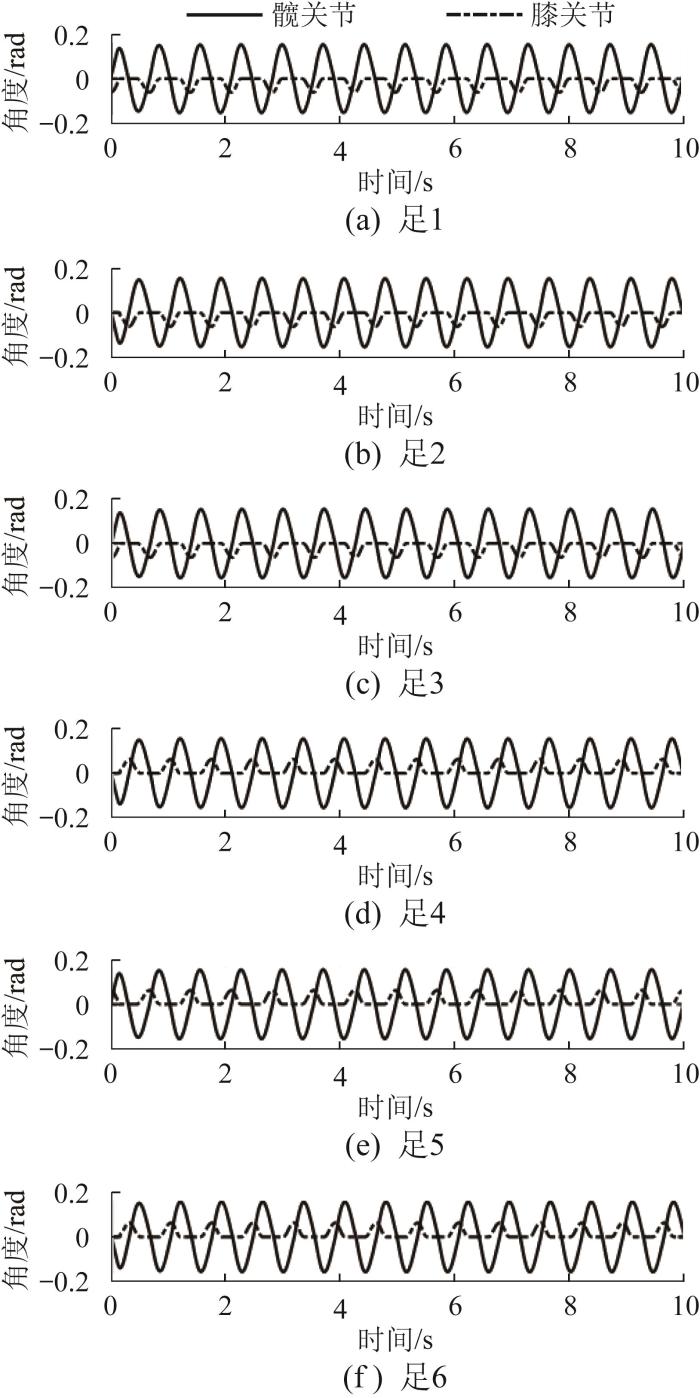
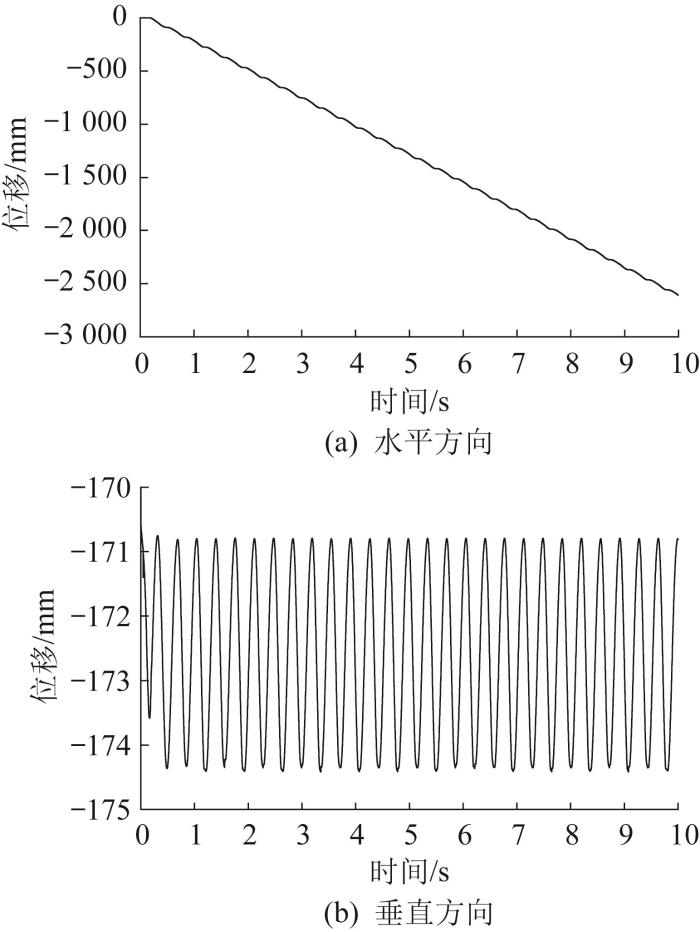
根据求出的优化设计解，再次进行六足机器人运动仿真。机器人节律周期信号如图3所示，其质心位移变化曲线如图4所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 六足机器人节律周期信号

Fig.3 Rhythm cycle signal of hexapod robot

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 六足机器人质心位移变化曲线

Fig.4 Displacement change curve of center of mass of hexapod robot

由图3可知：六足机器人的节律周期信号稳定且连续，并且6个运动足的信号之间具有相互对应的相位关系。可见采用CPG模型能有效控制六足机器人稳定行走。

由图4可知：在10 s内六足机器人沿水平方向匀速前进，其平均速度为0.269 m/s，移动了2 609 mm；其质心振动非常平稳，振幅为3.6 mm，与目标函数响应值的相对误差为2.5%，小于10%。

通过分析表明，所构建的近似模型具有较高的精度，且各项设定的指标值均满足约束条件的阈值，满足了六足机器人运动稳定性优化设计的要求。

5 结论

1）本文建立了六足机器人数值模型、运动控制模型，并搭建了机器人仿真模型。通过CPG模型的节律周期信号响应来控制机器人腿部关节的旋转，探究六足机器人的运动稳定性。

2）针对CPG模型中不确定性参数对六足机器人运动姿态的影响，本文提出了六足机器人运动稳定性优化设计方法。采用KKT最优化条件和最大熵原理，将三层优化设计问题转化成单层优化设计问题；同时，结合RBF建立近似模型，并运用遗传算法求解出最优设计解，极大地提高了求解效率。通过分析表明，该方法能有效求解六足机器人的最佳设计参数，提高机器人的运动稳定性，因此在机器人运动控制领域具有较高的应用价值。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[13]

CAO

， NIU

S J

， WANG

， et al.

Structural design and simulation of assistant leg based on ADAMS

［J］. Chinese Journal of Engineering Design， 2009， 16（5）： 340-343.