基于改进滑模控制的悬臂式掘进机轨迹跟踪技术

doi:10.3785/j.issn.1006-754X.2024.03.219

基于改进滑模控制的悬臂式掘进机轨迹跟踪技术

张旭辉^,^,¹^,², 李语阳¹, 杨文娟¹^,², 张超¹, 郑西利¹, 麻兵¹

1.西安科技大学机械工程学院，陕西西安 710054

2.陕西省矿山机电装备智能检测与控制重点实验室，陕西西安 710054

Trajectory tracking technology for boom-type roadheader based on improved sliding mode control

ZHANG Xuhui^,^,¹^,², LI Yuyang¹, YANG Wenjuan¹^,², ZHANG Chao¹, ZHENG Xili¹, MA Bing¹

1.College of Mechanical Engineering, Xi'an University of Science and Technology, Xi'an 710054, China

2.Shaanxi Key Laboratory of Intelligent Detection and Control for Mining Electromechanical Equipment, Xi'an 710054, China

收稿日期: 2023-11-28 修回日期: 2024-01-17

基金资助:

国家自然科学基金资助项目.  52104166
陕西省自然科学基础研究计划陕煤联合基金项目.  2021JLM-03
中国博士后科学基金面上项目.  2022MD723826
陕西省重点研发计划项目.  2023-YBGY-063

Received: 2023-11-28 Revised: 2024-01-17

作者简介 About authors

张旭辉（1972—），男，陕西凤翔人，教授，博士生导师，博士，从事煤矿机电设备智能检测与控制研究，E-mail:zhangxh@xust.edu.cn，https://orcid.org/0000-0002-5216-1362 , E-mail：zhangxh@xust.edu.cn

摘要

针对传统滑模控制在悬臂式掘进机轨迹跟踪中存在全局收敛速度慢、抖振显著等不足，提出了一种基于新型趋近律的改进滑模控制方法。通过在传统指数趋近律基础上引入掘进机机身的横向偏差、航向角偏差以及幂次趋近项，实现了掘进机轨迹偏差的快速收敛以及抖振的削弱；同时，采用边界层法进一步抑制抖振，解决了趋近律中符号函数乘积项易引起抖振的问题。分析了新型趋近律的存在性、可达性以及稳定性，并推导了干扰稳态误差的区间。考虑掘进机的不确定扰动，对传统滑模控制与改进滑模控制方法进行了仿真对比。结果表明，改进滑模控制的控制精度、收敛速度及抗干扰能力均优于传统滑模控制。最后，通过搭建实验平台测试了掘进机轨迹跟踪控制系统的性能，验证了改进滑模控制方法的可行性和有效性。研究结果可为煤矿井下恶劣环境中采掘装备的智能控制提供重要参考。

关键词： 悬臂式掘进机 ; 新型趋近律 ; 轨迹跟踪 ; 滑模控制

Abstract

Aiming at the shortcomings of traditional sliding mode control in trajectory tracking of boom-type roadheader, such as slow global convergence and significant chattering, an improved sliding mode control method based on novel reaching law is proposed. By introducing lateral deviation and heading angle deviation of the roadheader body and adding power reaching term to the traditional exponential reaching law, the rapid convergence of trajectory deviation and chattering reduction for the roadheader were achieved. At the same time, the boundary layer method was employed to further suppress chattering, which addressed the problem of chattering easily caused by the product term of sign functions in the reaching law. The existence, reachability and stability of the novel reaching law were analyzed, and the interval of disturbance steady-state error was derived. Considering the uncertain disturbance of the roadheader, the simulation comparison was conducted between traditional sliding mode control method and improved sliding mode control method. The results indicated that the control accuracy, convergence speed and anti-interference ability of the improved sliding mode control were superior to the traditional sliding mode control. Finally, an experimental platform was set up to test the performance of the roadheader trajectory tracking control system, which verified the feasibility and effectiveness of the improved sliding mode control method. The research results can provide important reference for the intelligent control of mining equipment in the harsh environment of underground coal mine.

Keywords： boom-type roadheader ; novel reaching law ; trajectory tracking ; sliding mode control

PDF (2355KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

张旭辉, 李语阳, 杨文娟, 张超, 郑西利, 麻兵. 基于改进滑模控制的悬臂式掘进机轨迹跟踪技术[J]. 工程设计学报, 2024, 31(4): 491-501 doi:10.3785/j.issn.1006-754X.2024.03.219

ZHANG Xuhui, LI Yuyang, YANG Wenjuan, ZHANG Chao, ZHENG Xili, MA Bing. Trajectory tracking technology for boom-type roadheader based on improved sliding mode control[J]. Chinese Journal of Engineering Design, 2024, 31(4): 491-501 doi:10.3785/j.issn.1006-754X.2024.03.219

本文链接：https://www.zjujournals.com/gcsjxb/CN/10.3785/j.issn.1006-754X.2024.03.219

悬臂式掘进机在煤矿掘进工作面建设中占据重要地位^[1]，尤其在硬岩掘进方面具有独特优势。在用于煤矿巷道成形时，需要控制悬臂式掘进机的机身和截割臂以实现多自由运动，从而获得矩形、拱形、梯形等不同截面的巷道。目前，悬臂式掘进机的智能化程度较低，主要依靠操作人员手动控制。由于煤矿井下的低照度、高粉尘环境，操作人员的视线易受粉尘干扰，从而无法准确判断掘进机机身位置，导致在自动截割前机身偏离巷道规划中心线，极易造成截割面超挖、欠挖以及潜在的安全隐患^[2]。悬臂式掘进机机身的轨迹跟踪控制是实现煤矿巷道智能化成形的技术难题。

现阶段，常见的轨迹跟踪算法大多适用于移动机器人、无人驾驶车辆等，而针对悬臂式掘进机的研究主要集中在精确定位、智能截割等方面^[3]。悬臂式掘进机机身的运动类似于履带式移动机器人^[4-6]。在移动机器人轨迹跟踪方面，潘天宇等^[7]提出了一种基于改进等速趋近律的滑模轨迹跟踪方法，该方法有效地提高了移动机器人对不同转弯半径的跟踪能力。姜立标等^[8]提出了基于趋近律自适应调整的滑模控制轨迹跟踪算法，实现了智能车辆对期望轨迹的快速平稳跟踪。李昆鹏等^[9]采用人工场法并引入位姿偏差，实现了轮式移动机器人的自适应轨迹跟踪。Kanayama等^[10]提出了一种经典的移动机器人轨迹跟踪控制器，该控制器的结构简单且具有较强的自适应性。Sun等^[11]设计了适用于移动机器人的局部渐进稳定控制器，并给出了全局有界的轨迹跟踪控制策略，该控制方法简单且有效。匡文龙等^[12]设计了一种结合Lyapunov方法和反演滑模技术的轨迹跟踪控制器，有效提高了农用履带机器人轨迹偏差的收敛速度。王明明等^[13]提出了一种基于多幂次趋近律的滑模控制方法，并将其应用于移动机器人的轨迹跟踪，结果表明，该控制方法具有响应快速、鲁棒性强等优点。上述文献主要针对运动环境相对简单的地面移动机器人，但由于煤矿巷道底板地质条件多变，悬臂式掘进机的行走轨迹会受到多种因素干扰，难以保证行驶平稳性，增加了运动控制的难度^[14-15]。为解决上述问题，Qu等^[16]提出了一种将BP（back propagation，反向传播）神经网络与状态估计相结合的悬臂式掘进机行走轨迹跟踪控制策略，实现了控制律的动态优化并提高了控制算法的鲁棒性。韩庆珏等^[17]针对深海履带车，基于路径偏差模型设计了轨迹跟踪控制策略，并通过仿真验证了其控制效果。然而，上述文献大多并未验证外部扰动对轨迹跟踪稳定性的影响，因此并不能完全满足煤矿井下悬臂式掘进机的实际控制需求。

考虑到滑模控制具有对参数变化不敏感、对外部干扰具有高鲁棒性以及响应迅速等优点^[18]，本文提出了一种基于新型趋近律的改进滑模控制方法，用于悬臂式掘进机的轨迹跟踪和纠偏控制。通过在传统指数趋近律中引入掘进机机身的横向偏差与航向角偏差以及增加幂次趋近项的方式，设计了新型趋近律，并采用边界层法解决符号函数乘积项所引起的抖振问题，从而在加快轨迹偏差收敛速度的同时削弱抖振。最后，对新型趋近律进行理论分析，并通过控制仿真和轨迹跟踪实验来验证改进滑模控制方法的轨迹跟踪效果。

1 悬臂式掘进机轨迹跟踪问题描述

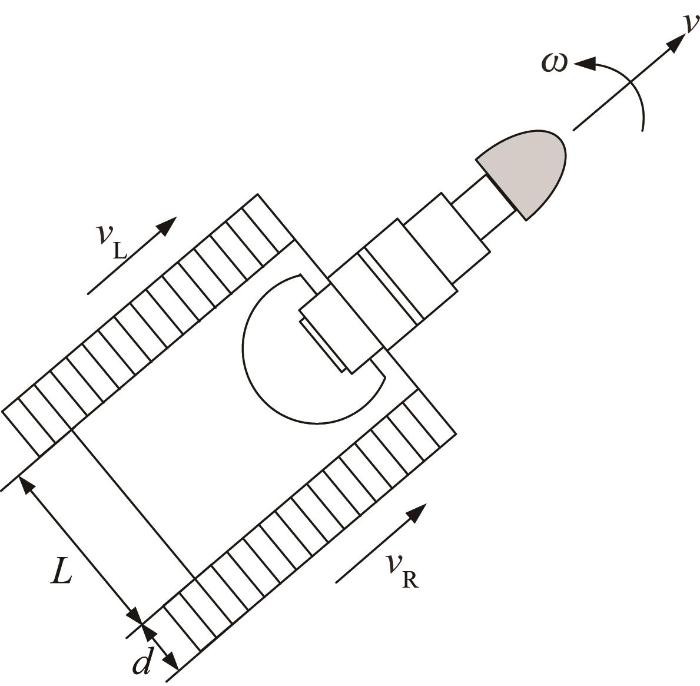
悬臂式掘进机为典型的履带式移动机器人，其行走装置由液压马达驱动的左右2条履带构成，依靠差速运动来实现机身的直行和转弯。悬臂式掘进机的几何模型如图1所示。图中： $v$ 为掘进机机身的前进线速度， $ω$ 为掘进机机身的转向角速度，v_L为左侧履带的运行速度，v_R为右侧履带的运行速度， $L$ 为掘进机机身宽度， $d$ 为单侧履带的宽度。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 悬臂式掘进机几何模型

Fig.1 Geometric model of boom-type roadheader

根据图1，悬臂式掘进机机身速度与左右两侧履带运行速度之间的关系可表示为：

{(v, ω)}^{T} = C^{- 1} (v_{L}, v_{R})^{T}

其中：

C = [\begin{matrix} 1 & - \frac{L + d}{4} \\ 1 & \frac{L + d}{4} \end{matrix}]

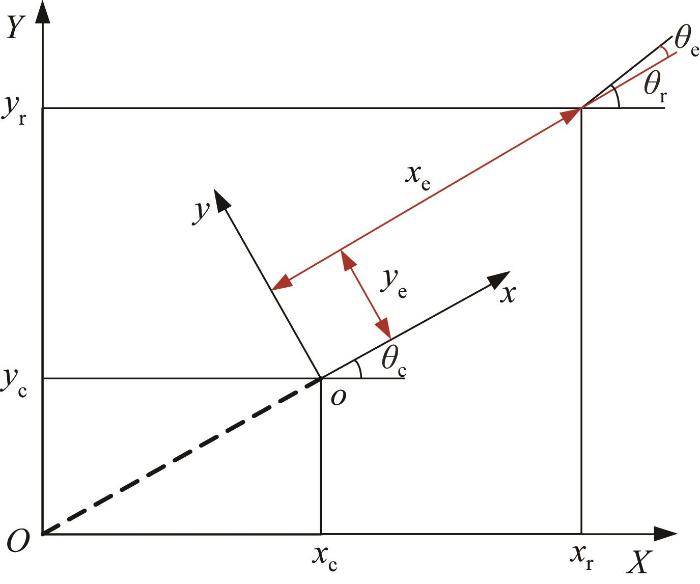
悬臂式掘进机的轨迹跟踪偏差模型如图2所示。图中：O-XY为全局坐标系，掘进机在坐标系O-XY下的位姿可由向量 $p_{c} = (x_{c}, y_{c}, θ_{c})^{T}$ 确定，对应的实际速度 $q_{c} = (v_{c}, ω_{c})^{T}$ ，其中 $(x_{c}, y_{c})$ 为掘进机机身质心在坐标系O-XY下的位置坐标， $θ_{c}$ 为机身前进方向与X轴的夹角，规定当掘进机逆时针转向X轴时， $θ_{c} > 0 °$ ；掘进机在坐标系O-XY下的期望位姿由向量 $p_{r} = (x_{r}, y_{r}, θ_{r})^{T}$ 描述，对应的期望速度 $q_{r} = (v_{r}, ω_{r})^{T}$ 。o-xy为局部坐标系，其原点o为掘进机质心，跟随掘进机一起运动。掘进机在坐标系o-xy下的位姿偏差由向量 e_p $= (x_{e}, y_{e}, θ_{e})^{T}$ 描述，其中 $x_{e}$ 、 $y_{e}$ 、 $θ_{e}$ 分别为坐标系o-xy下掘进机的横向、纵向和航向角偏差。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 悬臂式掘进机轨迹跟踪偏差模型

Fig.2 Trajectory tracking deviation model for boom-type roadheader

根据图2所示的几何关系，可得悬臂式掘进机的运动学模型：

\{\begin{array}{l} {\dot{x}}_{c} = v_{c} c o s θ_{c} \\ {\dot{y}}_{c} = v_{c} s i n θ_{c} \\ {\dot{θ}}_{c} = ω_{c} \end{array}

将式(2)改写为矩阵形式，可表示为：

{\dot{p}}_{c} = [\begin{array}{l} {\dot{x}}_{c} \\ {\dot{y}}_{c} \\ {\dot{θ}}_{c} \end{array}] = [\begin{array}{l} c o s θ_{c} \\ s i n θ_{c} \\ 0 \end{array} \begin{matrix}  \end{matrix} \begin{array}{l} 0 \\ 0 \\ 1 \end{array}] [\begin{array}{l} v_{c} \\ ω_{c} \end{array}]

在任意给定的初始误差下，悬臂式掘进机从当前位姿 $p_{c} = (x_{c}, y_{c}, θ_{c})^{T}$ 对目标轨迹中的期望位姿 $p_{r} = (x_{r}, y_{r}, θ_{r})^{T}$ 进行跟踪时，要实时计算其当前位姿与期望位姿的偏差，以确定控制输入来实现位姿误差纠偏。定义全局坐标系下掘进机的位姿偏差 E_p $= p_{r}$ - $p_{c}$ ，通过变换矩阵 T_e可将全局坐标系下的位姿偏差 E_p转换为局部坐标系下的位姿偏差 e_p，从而建立局部坐标下的轨迹跟踪位姿偏差模型。位姿偏差变换方程可表示为：

e_{p} = [\begin{array}{l} x_{e} \\ y_{e} \\ θ_{e} \end{array}] = T_{e} E_{p} = [\begin{array}{l} c o s θ_{c} \\ - s i n θ_{c} \\ 0 \end{array} \begin{matrix}  \end{matrix} \begin{matrix} s i n θ_{c} \\ c o s θ_{c} \\ 0 \end{matrix} \begin{matrix}  \end{matrix} \begin{array}{l} 0 \\ 0 \\ 1 \end{array}] [\begin{array}{l} x_{r} - x_{c} \\ y_{r} - y_{c} \\ θ_{r} - θ_{c} \end{array}]

对式(4)进行微分，可进一步得到位姿偏差微分方程：

{\dot{e}}_{p} = [\begin{array}{l} {\dot{x}}_{e} \\ {\dot{y}}_{e} \\ {\dot{θ}}_{e} \end{array}] = [\begin{array}{l} ω_{c} y_{e} - v_{c} + v_{r} c o s θ_{e} \\ - ω_{c} x_{e} + v_{r} s i n θ_{e} \\ ω_{r} - ω_{c} \end{array}]

结合式(2)及式(4)，可推导得到：

\{\begin{array}{l} {\dot{x}}_{e} = ({\dot{x}}_{r} - {\dot{x}}_{c}) c o s θ_{c} + (x_{r} - x_{c}) (- s i n θ_{c}) ω_{c} + \\ ({\dot{y}}_{r} - {\dot{y}}_{c}) s i n θ_{c} + (y_{r} - y_{c}) (c o s θ_{c}) ω_{c} = \\ ω_{c} y_{e} - v_{c} + v_{r} c o s θ_{e} \\ {\dot{y}}_{e} = - ({\dot{x}}_{r} - {\dot{x}}_{c}) s i n θ_{c} - (x_{r} - x_{c}) (c o s θ_{c}) ω_{c} + \\ ({\dot{y}}_{r} - {\dot{y}}_{c}) c o s θ_{c} - (y_{r} - y_{c}) (s i n θ_{c}) ω_{c} = \\ - ω_{c} x_{e} + v_{r} s i n θ_{e} \\ {\dot{θ}}_{e} = {\dot{θ}}_{r} - {\dot{θ}}_{c} = ω_{r} - ω_{c} \end{array}

通过上述分析可知，悬臂式掘进机的轨迹跟踪问题即为寻找有界输入——机身控制速度 u $= {(v, ω)}^{T}$ ，使得任意初始误差下的位姿偏差 e_p均可收敛到0，即 $\underset{t \to \infty}{l i m} ‖(x_{e}, y_{e}, θ_{e})^{T}‖ = 0$ 。

2 悬臂式掘进机轨迹跟踪控制器设计

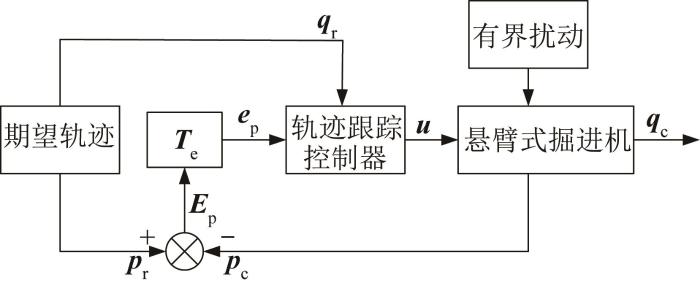
由于悬臂式掘进机机身运动受限，采用2个控制输入来减小3个方向上的跟踪误差；另外，掘进机易受巷道环境等因素干扰，导致其机身轨迹偏离预设路线。滑模控制是一类特殊的非线性控制方法，无须获取被控对象的精确模型，且对外加不确定扰动不敏感，其可根据系统实时状态（如轨迹偏差），以跃变的控制方式迫使系统轨迹按设计好的“滑动模态”运动。为了实现更为有效的轨迹跟踪，本文设计了一种基于改进滑模控制的悬臂式掘进机轨迹跟踪控制器，其控制过程如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 悬臂式掘进机轨迹跟踪控制框图

Fig.3 Trajectory tracking control block diagram of boom-type roadheader

悬臂式掘进机轨迹跟踪控制系统的全局输入为期望位姿 p_r和期望速度 q_r，全局输出为掘进机当前时刻的位姿 p_c。首先，基于期望位姿 p_r和当前位姿 p_c，利用式(4)计算得到当前的位姿偏差 e_p。随后，轨迹跟踪控制器基于输入的位姿偏差 e_p和期望速度 q_r实时计算得到掘进机的控制速度 $u = {(v, ω)}^{T}$ 。最后，控制器输出的控制速度 u 下发至掘进机执行机构，从而得到掘进机当前的实际速度 q_c。由于掘进机在煤矿井下工作时不可避免地会受到内部与外部的干扰，因此其实际速度 q_c与控制速度 u 并不完全相等。为简化问题，本文假设 q_c= u，则可通过控制掘进机履带速度差来不断调整机身位姿，以使位姿偏差趋于0。

2.1　滑模切换函数设计

反步（back-stepping）法又称反演法，其是一种用于设计不确定非线性系统控制器的系统化方法，可将控制律的设计与Lyapunov理论相结合，从而将复杂的高阶系统拆分为低阶子系统。基于此，本文采用反步法来设计滑模控制的切换函数。

引理1 对于任意 $x \in R$ 且 $|x| < \infty$ ，存在 $ϕ (x) = x s i n (a r c t a n x) \geq 0$ ，有且仅当 $x = 0$ 时等号成立^[19]。

根据上述引理，基于反步法设计滑模切换函数，具体步骤如下。

当 $x_{e} = 0$ 时，Lyapunov函数 $V_{y} = \frac{1}{2} y_{e}^{2}$ 。假设 $θ_{e} = - a r c t a n (v_{r} y_{e})$ ，则有：

\begin{array}{l} {\dot{V}}_{y} = y_{e} {\dot{y}}_{e} = y_{e} (- ω x_{e} + v_{r} s i n θ_{e}) = \\ - ω x_{e} y_{e} - v_{r} y_{e} s i n [a r c t a n (v_{r} y_{e})] \end{array}

(7)

由引理1可知， $v_{r} y_{e} s i n [a r c t a n (v_{r} y_{e})] \geq 0$ （有且仅当 $v_{r} y_{e} = 0$ 时，等号成立），则有 ${\dot{V}}_{y} \leq 0$ 。因此可以得出：若 $x_{e}$ 收敛至0且 $θ_{e}$ 收敛至 $- a r c t a n (v_{r} y_{e})$ ，则系统状态 $y_{e}$ 收敛至0。

根据上述结论，本文改进滑模控制的切换函数可设计为：

s = [\begin{array}{l} s_{1} \\ s_{2} \end{array}] = [\begin{array}{l} x_{e} \\ θ_{e} + a r c t a n (v_{r} y_{e}) \end{array}]

(8)

由Lyapunov稳定性判定可知，所设计的滑模切换函数满足系统稳定的条件。通过设计悬臂式掘进机轨迹跟踪滑模控制器，使得 $s_{i} \to 0$ $(i = 1, 2)$ ，即可实现 $x_{e}$ 收敛至0且θ_e收敛至 $- a r c t a n (v_{r} y_{e})$ ，进而实现y_e收敛至0。由于期望线速度v_r不为0，因此当y_e收敛至0时，θ_e收敛至0，进而可实现悬臂式掘进机在轨迹跟踪过程中的偏差收敛。

2.2　新型趋近律设计

滑模运动可分为趋近过程和滑动模态两个阶段，而趋近过程即为滑模切换函数 $s \to 0$ 的过程。高为炳^[20]提出了基于趋近律的滑模控制设计方法，有效缩短了趋近过程所需的时间并削弱了系统抖振，极大改善了趋近运动的实时动态性能^[21]。指数趋近律是一种典型的趋近律，当系统初始状态远离滑模面（即 $|s|$ 的值较大）时，其能够使系统状态以较大的趋近速度趋近滑模面。但由于自身结构缺陷，指数趋近律的切换区域为带状，使得系统状态最终不会稳定在平衡原点处，而是在平衡原点附近的切换带内不定地切换。本文在传统指数趋近律的基础上，提出了一种新型趋近律：

\dot{s} = - k_{1} {|s|}^{α} s g n (s) - k_{2} |x| s g n (s) - k_{3} s

(9)

式中： $x$ 为系统状态变量，满足 $\underset{t \to \infty}{l i m} |x| = 0$ ； $α$ 、k₁、k₂、k₃为增益系数，满足 $0 < α < 1$ ，k₁>0，k₂>0，k₃>0。

新型趋近律在传统指数趋近律的基础上引入了状态变量 $|x|$ 作为等速趋近项的增益并增加了一个幂次趋近项，可有效地削弱系统抖振，实现趋近效果的动态改善，进一步提高了趋近速度。根据系统状态条件的不同，滑模切换函数s从初始状态运动至滑模面 $s = 0$ 的过程可分为2个阶段：1）当 $|s| > 1$ ，即系统状态远离滑模面时，新型趋近律中的第1项和第3项起主要作用；2）当 $|s| < 1$ ，即系统状态接近于滑模面时，新型趋近律中的第2项起主要作用，此时第1项和第3项接近于0，有效抑制了接近滑模面时的初始系统抖振。此时，在滑模控制律的作用下，系统状态变量x进入滑模面并不断向平衡原点移动， $k_{2} |x| s g n (s)$ 项逐渐减小，故穿越滑模面的幅值也逐渐减小并最终稳定于平衡原点处，这会使造成抖振现象的等速趋近项系数变为0，即消除了系统稳定后的抖振现象。新型趋近律不仅保留了指数趋近律和幂次趋近律的优点，保证了在不同阶段实现快速收敛，而且能够动态适应系统状态变量和滑模切换函数的变化，从而获得更好的控制性能。综上，新型趋近律的总体性能优于传统指数趋近律。

定理1　系统可在新型趋近律的作用下于有限时间内到达滑模面。

取Lyapunov函数 $V = 1 / 2 s^{2}$ ，证明新型趋近律的可达性。对上述Lyapunov函数求导，可得：

\begin{array}{l} \dot{V} = s \dot{s} = s (- k_{1} {|s|}^{α} s g n (s) - k_{2} |x| s g n (s) - k_{3} s) = \\ - (k_{1} {|s|}^{α + 1} + k_{2} |x| |s| + k_{3} s^{2}) \leq 0 \end{array}

(10)

由式(10)可知，有且仅当 $s = 0$ 时， $\dot{V} = s \dot{s} = 0$ 。综上可知，新型趋近律满足滑模面可达性，即存在系统滑动模态。

2.3　新型趋近律稳态误差界分析

由于煤矿巷道环境复杂，悬臂式掘进机在运行时易受到不确定干扰，从而导致机身轨迹偏离预定路线。在系统存在不确定性以及外加干扰的情况下，新型趋近律能够使系统于有限时间内收敛至平衡原点附近的一个邻域内，将该区域称为稳态误差区间。为了证明上述结论，定义系统出现有界干扰 $d (t)$ 后的趋近律 $\dot{s}$ 如下：

\dot{s} = - k_{1} {|s|}^{α} s g n (s) - k_{2} |x| s g n (s) - k_{3} s + d (t)

(11)

引理2　令 $x \in D \subset R^{n}$ ， $\dot{x} = f (x)$ ， $f : R^{n} \to R^{n}$ 为定义在平衡原点邻域 $D$ 内的连续函数，假设存在连续函数 $V$ 满足下列条件^[22]：

1） $V$ 是正定的；

2） $\dot{V}$ 除平衡原点外是负定的；

3）存在实数 $ε > 0$ 、 $λ \in (0,1)$ 以及邻域 $N \subset D$ ，使得 $\dot{V} + ε V^{λ} \leq 0$ ；

则函数 $\dot{x} = f (x)$ 关于平衡原点可在有限时间内收敛。

定理2　对于存在不确定外界扰动的趋近律，假设 $|d (t)| \leq δ$ ， $δ > 0$ 为常数，则 $s$ 和 $\dot{s}$ 可在有限时间内收敛至以下区域：

|s| \leq m i n \{{(δ / k_{1})}^{1 / α}, δ / k_{3}\}

(12)

|\dot{s}| \leq m i n \{{δ, k_{1} (δ / k_{3})}^{α}\} + m i n \{k_{3} {(δ / k_{1})}^{1 / α}, δ\} + δ

(13)

为证明上述定理，取Lyapunov函数 $V = 1 / 2 s^{2}$ ，并对其求导：

\begin{array}{l} \dot{V} = s \dot{s} = - k_{1} {|s|}^{α + 1} - k_{2} |x| |s| - k_{3} s^{2} + s d (t) \leq \\ - k_{1} {|s|}^{α + 1} - k_{2} |x| |s| - k_{3} {|s|}^{2} + |d (t)| |s| \leq \\ - k_{1} {|s|}^{α + 1} - k_{2} |x| |s| - k_{3} {|s|}^{2} + δ |s| \end{array}

(14)

式(14)可变形为：

\dot{V} + k_{2} |x| |s| \leq - k_{1} {|s|}^{α + 1} - k_{3} {|s|}^{2} + δ |s|

(15)

若不等式 $k_{1} {|s|}^{α} + k_{3} |s| \geq δ$ 成立，则有：

\dot{V} + \sqrt[]{2} k_{2} |x| V^{1 / 2} \leq 0

(16)

由引理2可得，若满足 $k_{1} {|s|}^{α} \geq δ$ 或 $k_{3} |s| \geq δ$ ，则式(16)成立，即系统可在有限时间内收敛，对应区域分别为：

|s| = {(δ / k_{1})}^{1 / α}

(17)

|s| = {(δ / k_{1})}^{1 / α}

(18)

综上，系统可在有限时间内收敛到以下区域：

|s| \leq m i n \{{(δ / k_{1})}^{1 / α}, δ / k_{3}\}

(19)

将式(19)代入式(11)，可得：

\begin{array}{l} |\dot{s}| = k_{1} {|s|}^{α} + k_{2} |x| + k_{3} |s| + |d (t)| \leq \\ k_{1} m i n {\{{(δ / k_{1})}^{1 / α}, δ / k_{3}\}}^{α} + k_{2} |x| + \\ k_{3} m i n \{{(δ / k_{1})}^{1 / α}, δ / k_{3}\} + δ = \\ m i n \{{δ, k_{1} (δ / k_{3})}^{α}\} + k_{2} |x| + \\ m i n \{k_{3} {(δ / k_{1})}^{1 / α}, δ\} + δ \end{array}

(20)

鉴于在平衡原点附近 $|x| \to 0$ ，则有：

|\dot{s}| \leq m i n \{{δ, k_{1} (δ / k_{3})}^{α}\} + m i n \{k_{3} {(δ / k_{1})}^{1 / α}, δ\} + δ

2.4　滑模控制器设计

为进一步减弱系统抖振，采用边界层法，即引入光滑连续的饱和函数 $s a t (\cdot)$ 取代趋近律中的符号函数 $s g n (\cdot)$ 。该方法设计了一个边界层，在边界层外采用切换控制，即正常的滑模控制；在边界层内将切换项连续化，即采用连续状态的线性化反馈控制，通过动态切换状态来减小控制过程中滑模面附近的抖振。引入的光滑连续饱和函数sat $(s)$ 表示为：

s a t (s) = \{\begin{array}{l} 1, \\ k s, \\ - 1, \end{array} \begin{matrix}  \end{matrix} \begin{matrix}  \end{matrix} \begin{matrix} s > Δ \\ |s| \leq Δ \\ s < - Δ \end{matrix}

(21)

其中：

k = \frac{1}{Δ}

式中： $Δ$ 为边界层厚度， $Δ > 0$ ，可根据实际情况选取适当的值。

引入光滑连续饱和函数后的趋近律可表示为：

\dot{s} = - k_{1} {|s|}^{α} s a t (s) - k_{2} |x| s a t (s) - k_{3} s

(22)

令 $ξ = a r c t a n (v_{r} y_{e})$ ，联立式(8)、式(21)和式(22)，可得：

\begin{array}{l} \dot{s} = [\begin{array}{l} {\dot{s}}_{1} \\ {\dot{s}}_{2} \end{array}] = [\begin{array}{l} {\dot{x}}_{e} \\ {\dot{θ}}_{e} + \frac{\partial ξ}{\partial v_{r}} {\dot{v}}_{r} + \frac{\partial ξ}{\partial y_{e}} {\dot{y}}_{e} \end{array}] = \\ [\begin{array}{l} ω y_{e} - v + v_{r} c o s θ_{e} \\ ω_{r} - ω + \frac{\partial ξ}{\partial v_{r}} {\dot{v}}_{r} + \frac{\partial ξ}{\partial y_{e}} (- ω x_{e} + v_{r} s i n θ_{e}) \end{array}] = \\ [\begin{array}{l} - k_{11} {|s_{1}|}^{α_{1}} s a t (s_{1}) - k_{12} |x_{e}| s a t (s_{1}) - k_{13} s_{1} \\ - k_{21} {|s_{2}|}^{α_{2}} s a t (s_{2}) - k_{22} |θ_{e}| s a t (s_{2}) - k_{23} s_{2} \end{array}] \end{array}

(23)

对于式(23)中系统状态变量的选取，主要结合滑模切换函数的设计来确定。对于趋近律 ${\dot{s}}_{1}$ ，状态变量取 $x_{e}$ 可实现横向偏差较大时的快速趋近以及横向偏差较小时的缓慢趋近，从而解决传统等速趋近项增益固定的问题，实现趋近速率与系统状态变量的变化相关联，进而避免因系统轨迹在接近滑模面时速度过大而导致系统抖振增大。对于趋近律 ${\dot{s}}_{2}$ ，通过分析位姿偏差微分方程可知，由于非完整约束，纵向偏差y_e不受直接控制，航向角偏差θ_e对轨迹偏差的控制精度有显著影响，同时由滑模切换函数可知，若θ_e收敛至0，则y_e必然收敛至0。因此，对于趋近律 ${\dot{s}}_{2}$ ，状态变量取θ_e，当系统状态进入滑动模态后，切换增益随状态变量θ_e的变化而动态调节，可有效抑制切换抖振。

对式(23)进行整理，可得基于新型趋近律的滑模控制律为：

u = [\begin{array}{l} v \\ ω \end{array}] = [\begin{array}{l} ω y_{e} + v_{r} c o s θ_{e} + k_{11} {|s_{1}|}^{α_{1}} s a t (s_{1}) + k_{12} |x_{e}| s a t (s_{1}) + k_{13} s_{1} \\ \frac{ω_{r} + \frac{\partial ξ}{\partial v_{r}} {\dot{v}}_{r} + \frac{\partial ξ}{\partial y_{e}} (v_{r} s i n θ_{e}) + k_{21} {|s_{2}|}^{α_{2}} s a t (s_{2}) + k_{22} |θ_{e}| s a t (s_{2}) + k_{23} s_{2}}{1 + \frac{\partial ξ}{\partial y_{e}} x_{e}} \end{array}]

(24)

其中：

\frac{\partial ξ}{\partial v_{r}} = \frac{y_{e}}{1 + (v_{r} y_{e})^{2}}

\frac{\partial ξ}{\partial y_{e}} = \frac{v_{r}}{1 + (v_{r} y_{e})^{2}}

3 悬臂式掘进机轨迹跟踪仿真分析

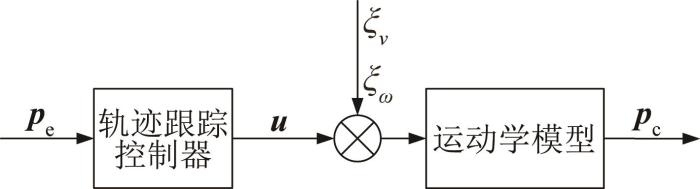
为了验证本文基于新型趋近律的改进滑模控制方法的响应特性和鲁棒性，将改进滑模控制方法与文献[23]中基于指数趋近律的传统滑模控制方法进行仿真对比分析。利用MATLAB/Simulink软件开展悬臂式掘进机轨迹跟踪控制仿真，仿真结构如图4所示。鉴于在任意给定的初始位姿下，起始位置与期望位置之间仅包括直线路径和圆弧路径^[24]，故本文将分别针对直线轨迹和圆弧轨迹进行轨迹跟踪仿真分析。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 悬臂式掘进机轨迹跟踪仿真结构

Fig.4 Trajectory tracking simulation structure of boom-type roadheader

考虑到悬臂式掘进机在煤矿巷道中行进时会受到各类不确定扰动，例如地质条件变化、履带打滑以及液压驱动系统存在执行误差等，因此在仿真中通过对控制系统的输出量施加不确定干扰来模拟突变工况，从而验证滑模控制方法的鲁棒性。本文改进滑模控制律中增益参数的选取如表1所示。

表1 悬臂式掘进机轨迹跟踪仿真控制参数

Table 1 Control parameters for trajectory tracking simulation of boom-type roadheader

参数	数值	参数	数值
$Δ$ t^①/s	0.001	k₁₂	5
$Δ$	0.01	k₁₃	3
α₁	0.03	k₂₁	7
α₂	0.03	k₂₂	5
k₁₁	7	k₂₃	3

① $Δ$ t为采样步长。

新窗口打开| 下载CSV

3.1　直线轨迹跟踪

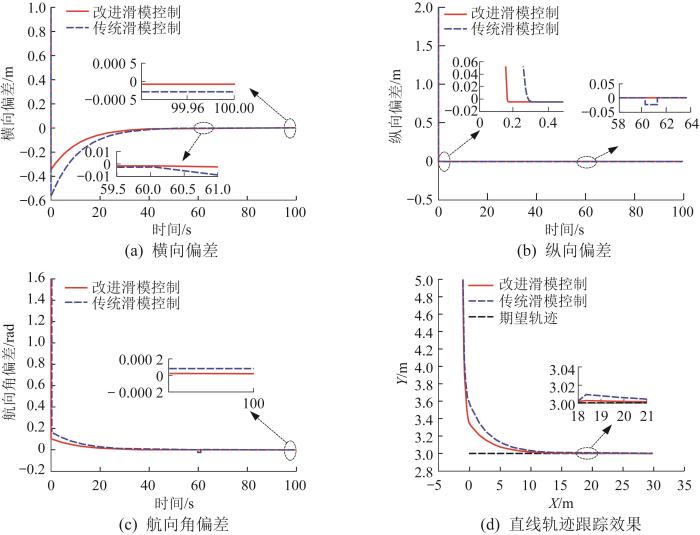
直线轨迹跟踪是轨迹跟踪问题中最基本的跟踪形式之一，通过直线轨迹跟踪仿真可验证控制方法的快速性和稳定性。本文选取的悬臂式掘进机直线期望轨迹为 $y_{r} = 3$ m、 $x_{r} = 0.3 t$ （t为仿真时间）的水平直线。设掘进机的初始位姿为（-1 m，5 m，-π/2），期望线速度 $v_{r} = 0.3 m / s$ ，期望角速度 $ω_{r} = 0 r a d / s$ ；仿真时间t=100 s，并在t=60 s处加入扰动幅值不大于2的脉冲干扰。不同滑模控制方法下掘进机的直线轨迹跟踪仿真结果如图5所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 悬臂式掘进机直线轨迹跟踪仿真结果对比

Fig.5 Comparison of simulation results of linear trajectory tracking of boom-type roadheader

图5所示仿真结果表明，悬臂式掘进机在2种滑模控制方法的调控下均能快速跟踪直线期望轨迹。由于本文新型趋近律引入了系统状态变量 $x_{e}$ 和 $θ_{e}$ ，其对轨迹偏差的消除和抖振抑制有较为显著的效果，因此在初始偏差相同的情况下，改进滑模控制的轨迹偏差收敛速度相较于传统滑模控制更快，使得系统进入稳态所需的时间缩短了5.6 s。

由图5(a)可知，2种滑模控制方法均出现了抖振现象，但由于本文新型趋近律在到达滑模面时的趋近速度减慢，而指数趋近律在接近滑模面时仍保持较大的趋近速度，使得系统状态穿越滑模面后仍朝负向运动，故指数趋近律的负向最大偏差值大于本文新型趋近律的，表明新型趋近律降低了系统在接近滑模面时的抖振频率，有效地抑制了抖振。由图5(a)和图5(c)可知，当仿真结束时，改进滑模控制下掘进机的横向偏差和航向角偏差较传统滑模控制下的小。此外，从图5(d)中可以看出，当出现随机干扰时，改进滑模控制下掘进机的轨迹波动幅值小且调整速度更快，进一步验证了改进滑模控制抑制系统抖振的有效性；传统滑模控制下掘进机的轨迹波动幅值虽也较小，但需要行驶较长距离才能使轨迹偏差收敛。相比之下，本文改进滑模控制方法的性能更优，适用于工况环境复杂且存在较多未知干扰的掘进机轨迹跟踪控制。

3.2　圆弧轨迹跟踪

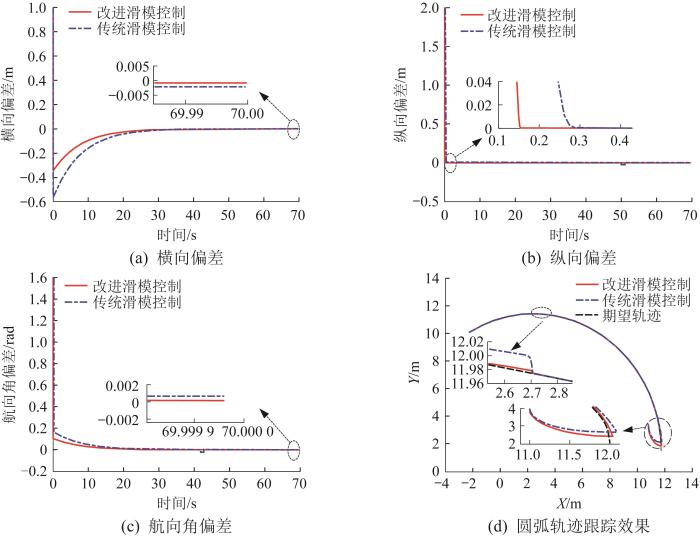
圆弧轨迹跟踪是一种典型的轨迹跟踪方式，可验证掘进机航向角实时变化时控制方法的性能。在本文中，圆弧期望轨迹设置为 $x_{r} = 2 + 10 c o s 0.03 t$ ， $y_{r} = 2 + 10 s i n 0.03 t$ ， $θ_{r} = 0.03 t$ 。悬臂式掘进机的初始位姿设为(11 m，4 m，- $π$ /2)，期望线速度 $v_{r} = 0.3 m / s$ ，期望角速度 $ω_{r} = 0.03 r a d / s$ ；仿真时间t=70 s，在t=50 s处加入扰动幅值不大于2的脉冲干扰。不同滑模控制方法下掘进机的圆弧轨迹跟踪仿真结果如图6所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 悬臂式掘进机圆弧轨迹跟踪仿真结果对比

Fig.6 Comparison of simulation results of circular arc trajectory tracking of boom-type roadheader

由图6仿真结果可以得出，在初始偏差相同的情况下，2种滑模控制方法均可以实现圆弧轨迹的快速跟踪，但本文改进滑模控制无论是在响应速度还是在抖振抑制方面均表现出较好的控制性能，且能够保持较高的跟踪精度。由图6(a)可知，改进滑模控制方法需要31.7 s将横向偏差缩小至0.02 m，而在相同初始偏差下，传统滑模控制方法需要37.3 s。此外，图6(a)所示的横向偏差变化曲线同样验证了改进滑模控制的抖振抑制效果优于传统滑模控制，在改进滑模控制下，最大负向偏差为0.34 m，而在传统滑模控制下，最大负向偏差为0.56 m。由图6(b)可知，改进滑模控制方法可以更快地将纵向偏差收敛于0 m，且无明显抖振现象。由图6(c)可知，在相同初始偏差下，改进滑模控制方法将航向角偏差减小至0.02 rad仅需43.8 s，而传统滑模控制方法需要49.5 s。结合图6(a)和图6(c)可知，在仿真结束时，改进滑模控制下掘进机的横向偏差以及航向角偏差均小于传统滑模控制下的。从图6(d)中可以看出，在出现随机干扰时，改进滑模控制下掘进机的轨迹波动幅值较小，进一步验证了该控制方法更具鲁棒性。

4 悬臂式掘进机轨迹跟踪实验研究

4.1　实验平台搭建

为了进一步验证本文改进滑模控制方法的有效性和可行性，采用电机驱动的履带式煤矿救援机器人替代悬臂式掘进机，开展轨迹跟踪实验验证。考虑到掘进机的理想行走轨迹为煤矿巷道的中心线，且通常在掘进作业前由地质部门设定，因此在本文实验中以楼道环境模拟煤矿巷道。轨迹跟踪实验平台由硬件和软件两部分组成。硬件部分由内置DSP控制器的履带式机器人、计算机、MG045捷联惯导、360°棱镜和XI-1001Q数字全站仪等构成，如图7所示。其中，XI-1001Q数字全站仪的定位精度小于等于0.01 m，MG045捷联惯导的姿态精度小于等于0.01 (º)/h；加速度精度小于等于 $5 \times 10^{- 5} g$ ，航向保持精度小于等于0.01 (º)/h。将XI-1001Q数字全站仪的测量模式设置为跟踪模式，并将MG045捷联惯导和棱镜放置在一起，完成初始对准后动态获取履带式机器人的位姿信息。计算机用于接收处理位置和航向角信息，并把测得的数据解算后作为轨迹跟踪控制器的输入，通过位姿偏差计算得到控制指令再下发至DSP控制器。DSP控制器根据控制指令通过逆运动学解算得到左右电机的期望速度，并通过内置的PID（proportional integral derivative，比例-积分-微分）控制完成电机的转动控制，使得机器人按要求运动。基于MATLAB和Unity3D软件开发上位机软件平台，以实现远程控制。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 履带式机器人轨迹跟踪实验平台

Fig.7 Trajectory tracking experimental platform for tracked robot

由于大多数情况下巷道中心线都是直线，因此实验以图7中楼道中线为期望轨迹，设定楼道中线起点为坐标系原点，期望轨迹为 $Y$ 轴，机器人起始位置设为（x_c, y_c）=（-0.3 m, 0 m），初始航向角θ_c=π/2，轨迹跟踪控制参数与表1中控制参数相同。设置期望轨迹如式(25)所示，实验开始前履带式机器人与期望轨迹间无初始航向角偏差，纵向初始偏差为0 m，仅存在0.3 m的初始横向偏差。

\{\begin{array}{l} x_{r} = 0 \\ y_{r} = 0.2 t \\ θ_{r} = \frac{π}{2} \end{array}

(25)

4.2　实验结果与分析

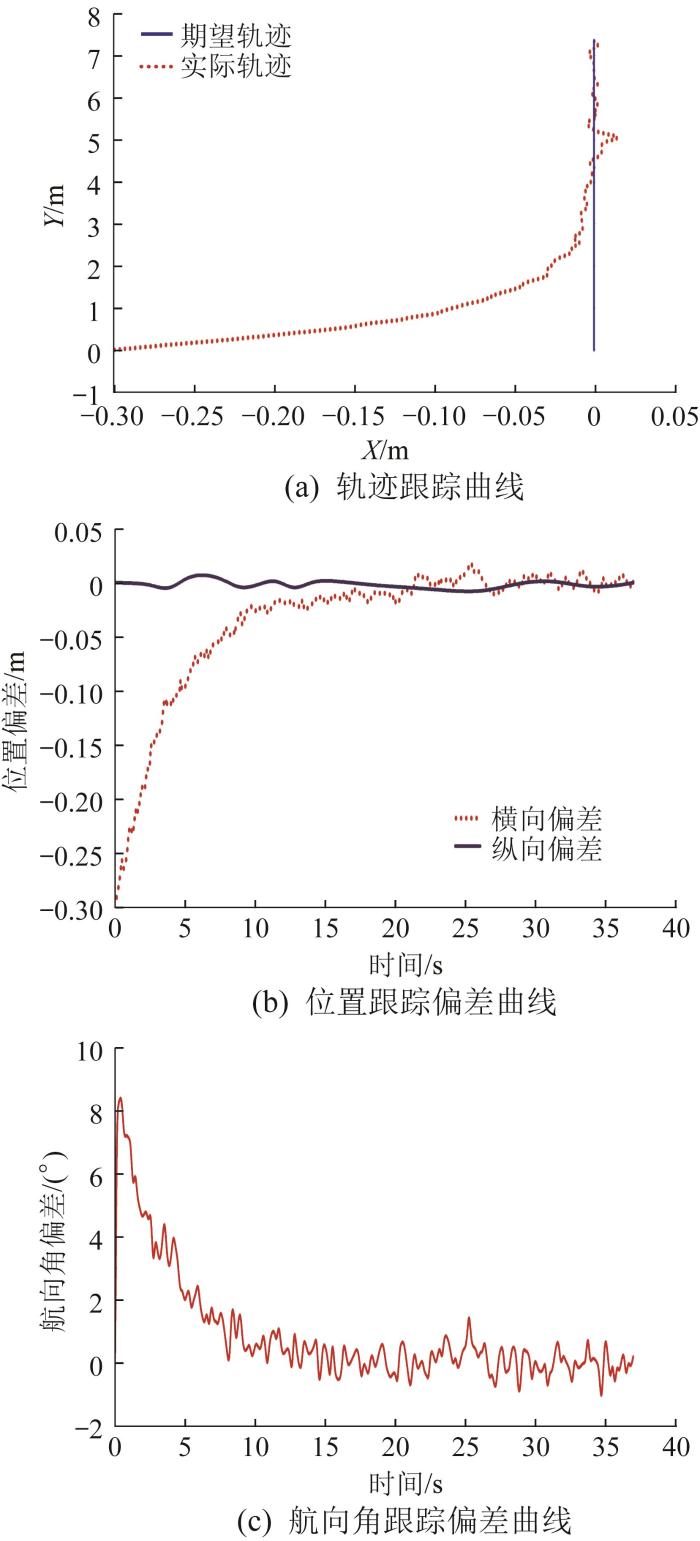
履带式机器人的轨迹跟踪实验结果如图8所示（为方便表示，此处航向角偏差未换算为弧度制）。从图8中可以看出，机器人自跟踪开始后，能够迅速调整方向跟踪期望轨迹，在26 s后实际轨迹与期望轨迹基本吻合，轨迹偏差趋于稳定。由图8(a)可知，在起始位置以及到达期望轨迹的航向角调整阶段，机器人轨迹的曲率变化较为明显，即出现了轻微的抖振现象，其余阶段机器人的轨迹均较为平滑，表明本文改进滑模控制方法对抑制抖振具有一定的效果。从图8(b)和图8(c)中可以看出，由于存在初始横向偏差，机器人在运动起始时的转向幅度较大，通过调整航向角实现了对期望轨迹的跟踪。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 履带式机器人轨迹跟踪实验结果

Fig.8 Experimental results of trajectory tracking of tracked robot

表2所示为实验过程中记录的部分机器人位姿偏差。由表2和图8(b)可知，在整个轨迹跟踪过程中，机器人未明显超前或落后于期望轨迹，纵向偏差较为稳定，最大偏差保持在0.010 m内；对于横向偏差，自机器人运动开始逐渐缩小至0 m，随后在调整航向角时发生波动，最大偏差为0.018 m，但在26 s后横向偏差基本保持在0 m附近波动。由表2和图8(c)可知，除运动起始时机器人的航向角偏差变化较大外，航向角偏差随着机器人运动逐渐收敛于0°附近，稳定运行时航向角偏差小于2°。实验结果表明，本文改进滑模控制方法在轨迹跟踪方面具有良好的控制性能及稳定性，进一步验证了该控制方法的可行性。由于实验条件限制，在煤矿巷道复杂环境下开展验证实验将是后续研究的主要工作。

表2 履带式机器人轨迹跟踪实验的部分数据

Table 2 Partial data of trajectory tracking experiment of tracked robot

时间/s	横向偏差/m	纵向偏差/m	航向角偏差/（°）
0	-0.300	0	0
5	-0.091	0.006	2.16
20	-0.016	-0.004	-0.16
25	0.018	-0.007	1.85
37	0.003	0.001	0.21

新窗口打开| 下载CSV

5 结论

针对悬臂式掘进机的轨迹跟踪问题，提出了一种基于新型趋近律的改进滑模控制方法，从而提高了掘进机轨迹跟踪过程中的轨迹偏差收敛速度及控制精度。通过理论分析以及仿真和实验验证，得出如下结论：

1）基于悬臂式掘进机的运动学模型分析了其位姿偏差微分方程，提出了基于位姿偏差的轨迹跟踪控制模型；并采用反步法设计了滑模控制切换函数，实现了轨迹跟踪过程中偏差的快速收敛。

2）相较于指数趋近律，所提出的新型趋近律不仅能够缩短趋近过程和削弱系统抖振，而且可进一步提高控制精度，进而提升了滑模控制的性能。同时，针对趋近律中符号函数乘积项所引起的抖振，采用边界层法来进行抑制。

3）考虑到被控系统受不确定性和外部干扰的影响，通过理论分析和控制仿真验证了在出现外部干扰时新型趋近律能够使被控系统在有限时间内收敛至平衡原点。仿真对比结果表明，本文改进滑模控制方法具有较强的鲁棒性，能够控制悬臂式掘进机机身更快地跟踪期望轨迹，且进入稳态后位置偏差小于0.02 m，验证了该控制方法的有效性和稳定性。实验结果表明，改进滑模控制方法能够将履带式机器人的轨迹跟踪误差控制在较小范围内，且能保证机器人稳定运行时的轨迹波动范围满足实际应用要求。

随着煤矿智能化的进一步推进，本文所提出的基于改进滑模控制的轨迹跟踪技术可为实现悬臂式掘进机的自主定向掘进作业提供一定的借鉴。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

王国法，刘峰，孟祥军，等.

煤矿智能化（初级阶段）研究与实践

［J］.煤炭科学技术，2019，47（8）：1-36.