一种柔性采摘机械臂的运动学分析与仿真

doi:10.3785/j.issn.1006-754X.2024.03.135

一种柔性采摘机械臂的运动学分析与仿真

张伟涛^,^,, 赵栋杰^,^,, 王禄, 包新棉, 黄保赛

聊城大学机械与汽车工程学院，山东聊城 252059

Kinematics analysis and simulation of a flexible picking robot arm

ZHANG Weitao^,^,, ZHAO Dongjie^,^,, WANG Lu, BAO Xinmian, HUANG Baosai

School of Mechanical & Automotive Engineering, Liaocheng University, Liaocheng 252059, China

通讯作者: 赵栋杰（1977—），男，山东聊城人，副教授，博士，从事机器人技术与应用研究，E-mail: zhaodongjie@lcu.edu.cn，https://orcid.org/0000-0002-4918-8708

收稿日期: 2023-03-23 修回日期: 2023-06-28

基金资助:

山东省重点研发计划资助项目. 2017NC212010
山东省高校科研计划项目. J18KB009

Received: 2023-03-23 Revised: 2023-06-28

作者简介 About authors

张伟涛（1997—），男，山东枣庄人，硕士生，从事柔性机器人技术研究，E-mail:1256587669@qq.com，https://orcid.org/0009-0008-6818-0753 , E-mail：1256587669@qq.com

摘要

针对刚性机械臂在果蔬采摘作业中的不足，设计了一种结构简单、运动灵活的柔性采摘机械臂。首先，基于等圆弧假设建立了柔性采摘机械臂的运动学模型，对其进行了从关节空间到操作空间和从驱动空间到关节空间的正、逆运动学分析以及各柔性关节之间的解耦分析。然后，利用MATLAB软件对柔性采摘机械臂的运动学模型进行了数值计算，同时利用ADAMS软件建立柔性采摘机械臂的虚拟样机模型，选用与理论分析相同的工况开展运动学仿真，验证了理论分析结果的准确性。仿真结果表明，该柔性采摘机械臂可实现灵活、协调运动。研究结果可为后续柔性机械臂的运动控制提供依据。

关键词： 柔性采摘机械臂 ; 运动学模型 ; 仿真分析

Abstract

Aiming at the shortcomings of rigid robot arm in fruit and vegetable picking, a flexible picking robot arm with simple structure and flexible movement was designed. Firstly, the kinematics model of the flexible picking robot arm was established based on the equal arc hypothesis, and the forward and inverse kinematics analysis from joint space to operation space and from driving space to joint space was carried out, as well as the decoupling analysis between the flexible joints. Then, the kinematics models of the flexible picking robot arm were numerically calculated by using MATLAB software, and the virtual prototype model of the flexible picking robot arm was established by ADAMS software. The kinematics simulation was carried out under the same working conditions as the theoretical analysis, and the accuracy of the theoretical analysis results was verified. The simulation results showed that the flexible picking robot arm could move flexibly and coordinatedly. The research results can provide a basis for the subsequent motion control of flexible robot arms.

Keywords： flexible picking robot arm ; kinematics model ; simulation analysis

PDF (1904KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

张伟涛, 赵栋杰, 王禄, 包新棉, 黄保赛. 一种柔性采摘机械臂的运动学分析与仿真[J]. 工程设计学报, 2024, 31(2): 230-237 doi:10.3785/j.issn.1006-754X.2024.03.135

ZHANG Weitao, ZHAO Dongjie, WANG Lu, BAO Xinmian, HUANG Baosai. Kinematics analysis and simulation of a flexible picking robot arm[J]. Chinese Journal of Engineering Design, 2024, 31(2): 230-237 doi:10.3785/j.issn.1006-754X.2024.03.135

采摘作业是林果生产的重要环节，但传统的人工采摘方式需要投入大量劳动力。随着劳动力成本的增加和科学技术的发展，采摘机器人的应用将成为采摘行业的必然选择^[1]。采摘机械臂是采摘机器人的重要组件，其性能直接影响采摘作业的效率与成功率。目前，采摘机械臂大多为笛卡尔型或关节型工业机械臂^[2-4]，这类刚性机械臂通常存在体积大、灵活性不足和成本高等缺陷，且不适用于果实密集、作业空间狭窄等场景。相比之下，柔性机械臂结构简单，运动灵活，适应性强，尺寸、质量较小，且具有较高的外负载能力（不低于50 N），更适用于采摘作业环境^[5]。

近年来，国内外学者针对柔性机械臂在勘探、医疗、救援和航空航天等领域的应用开展了研究。Webster等^[6]研制了一种由3段横截面直径依次减小的弹性圆管组成的柔性机器人，其具有6个空间弯曲自由度。Mcmahan等^[7-8]研制了一种基于3根绳索驱动和内部气压控制的超冗余柔性机器人以及一种仿章鱼触手的连续型机器人。Zhang等^[9]搭建了基于形状记忆合金（shape memory alloy, SMA）驱动的具有4个关节的模块化柔性机械臂，并根据SMA的特点设计了自反馈控制系统，实现了该柔性机械臂的自主控制。Simaan^[10]研究了一种由超弹性中心骨架和沿骨架轴向均布的支撑圆盘组成的绳驱柔性机器人，可用于咽喉手术。胡海燕等^[11-13]对自主研制的线驱动连续型机器人进行了运动学分析与仿真，并在此基础上进一步设计了一种具有多关节段的连续型结肠镜机器人，可用于结肠前段和中段疾病的检查。但是，柔性机械臂在农业领域的应用研究鲜有报道。

为此，笔者设计了一种适用于果蔬采摘作业的柔性机械臂，并基于等圆弧假设对其进行运动学分析。然后，利用MATLAB软件对柔性采摘机械臂的运动学正、逆解进行数值计算，同时利用ADAMS软件构建该机械臂的虚拟样机模型并开展运动学仿真分析，以验证理论分析结果的准确性。

1 柔性采摘机械臂结构设计

本文提出的基于人机协作的果蔬采摘机器人设计方案如图1所示。该机器人主要由运动底盘、柔性采摘机械臂和收集装置三部分组成，其中柔性采摘机械臂的顶端装有柔性手爪。当机器人进行采摘作业时，先控制运动底盘到达作业位置处，再控制柔性采摘机械臂将柔性手爪移送至目标果实处并控制柔性手爪完成采摘作业，最后控制柔性采摘机械臂将果实送入收集装置。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 果蔬采摘机器人结构

Fig.1 Structure of fruit and vegetable picking robot

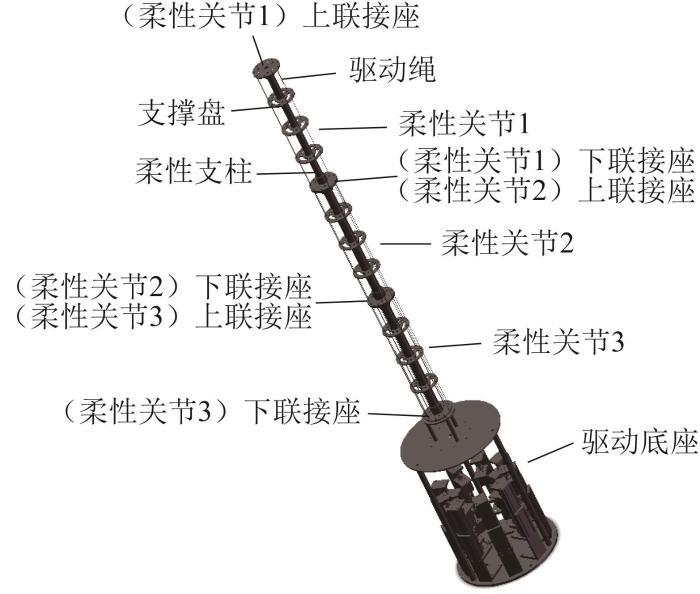
如图2所示，柔性采摘机械臂主要由驱动底座和柔性臂组成。其中：驱动底座内部周向均布9个直线模组；柔性臂是一个直径为98 mm、高1 500 mm的圆柱体，由3个结构相同的柔性关节串联而成，各柔性关节均具有1个弯曲自由度和1个旋转自由度。柔性关节由柔性支柱、上下联接座、驱动绳以及均布在上下联接座之间的3个支撑盘组成。柔性支柱由直径为20 mm的拉簧和套在拉簧外侧的硅胶管组成，拉簧作为中心骨架，可使柔性支柱具有超弹性；上下联接座和支撑盘均固定在柔性支柱上，各联接座和支撑盘的圆周上均布9个相对的绳孔；各柔性关节的3根驱动绳间隔120º均匀分布，其上端固定在上联接座的绳孔上，中部穿过支撑盘、下联接座上对应的绳孔，下端固定在对应直线模组的滑座上；3个柔性关节的驱动绳交错布置，以实现柔性臂的六自由度运动。该结构方案可有效减小柔性臂的体积与质量，使其具有快速响应能力。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 柔性采摘机械臂结构

Fig.2 Structure of flexible picking robot arm

2 柔性采摘机械臂运动学分析

运动学建模与分析是实现机械臂运动控制的基础。对于传统的刚性机械臂，通常采用D-H法对其进行运动学分析^[14-16]，但柔性采摘机械臂的中心骨架为弹性体，其运动与变形较为复杂，难以用D-H法实现运动学建模与分析。为此，提出了一种基于等圆弧假设的柔性采摘机械臂运动学建模与分析方法。

柔性采摘机械臂由钢丝绳驱动，属于间接驱动，其驱动空间与操作空间不一致，故在对其进行运动学分析时，需要考虑关节空间到操作空间的映射关系以及驱动空间到关节空间的映射关系。柔性采摘机械臂的3种空间之间的映射关系如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 柔性采摘机械臂的空间映射关系

Fig.3 Spatial mapping relation of flexible picking robot arm

2.1　关节空间与操作空间的映射关系

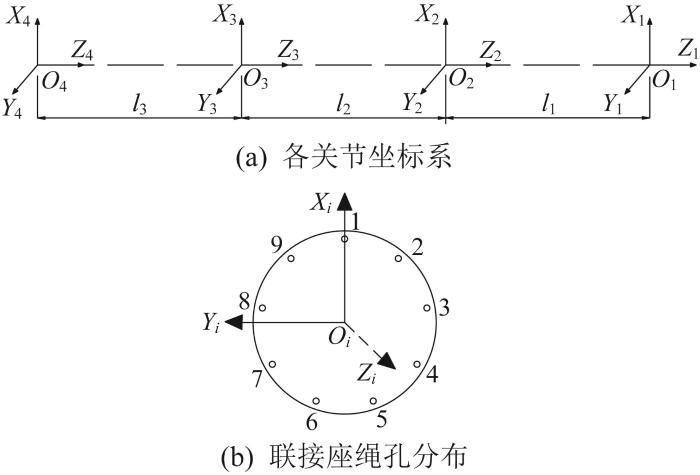
为方便研究柔性采摘机械臂各柔性关节之间的运动学关系，在其柔性臂底端和各柔性关节顶端建立坐标系，如图4(a)所示。其中：O₄-X₄Y₄Z₄表示设在柔性臂底端的基坐标系，O_i -X_iY_iZ_i （i=1, 2, 3）表示设在柔性关节i顶端的关节坐标系。规定各坐标系的原点为各联接座的圆心，Z轴沿联接座法线方向，X轴指向联接座绳孔1的圆心，Y轴按右手定则确定。柔性臂各关节坐标系及联接座绳孔分布如图4所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 柔性臂关节坐标系及联接座绳孔分布示意

Fig.4 Schematic diagram of coordinate system of flexible arm and distribution of rope holes of connecting seat

2.1.1　关节空间—操作空间的正运动学分析

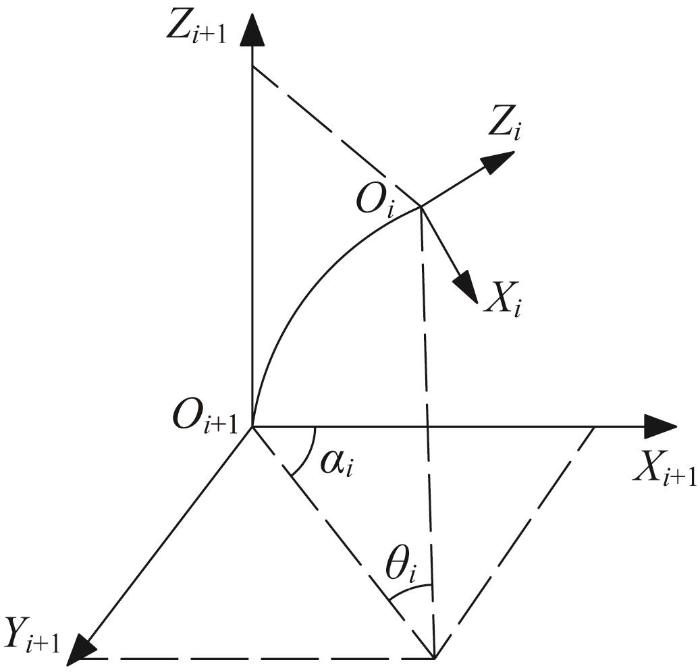
由上文分析可知，各柔性关节均具有2个自由度，其运动可分解为前一个坐标系O_i -X_iY_iZ_i 相对于后一个坐标系O_i₊₁-X_i₊₁Y_i₊₁Z_i₊₁的弯曲运动，以及弯曲平面绕Z_i₊₁轴的旋转运动。如图5所示，弯曲运动和旋转运动对应的臂形角分别为θ_i 和α_i，其中θ_i 表示柔性关节i在弯曲平面内的圆心角，即弯曲角；α_i 表示柔性关节i的弯曲平面相对于后一个坐标系中Z_i₊₁轴的旋转角。故整个柔性采摘机械臂的臂形由6个臂形角决定。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 柔性关节运动示意

Fig.5 Schematic diagram of flexible joint motion

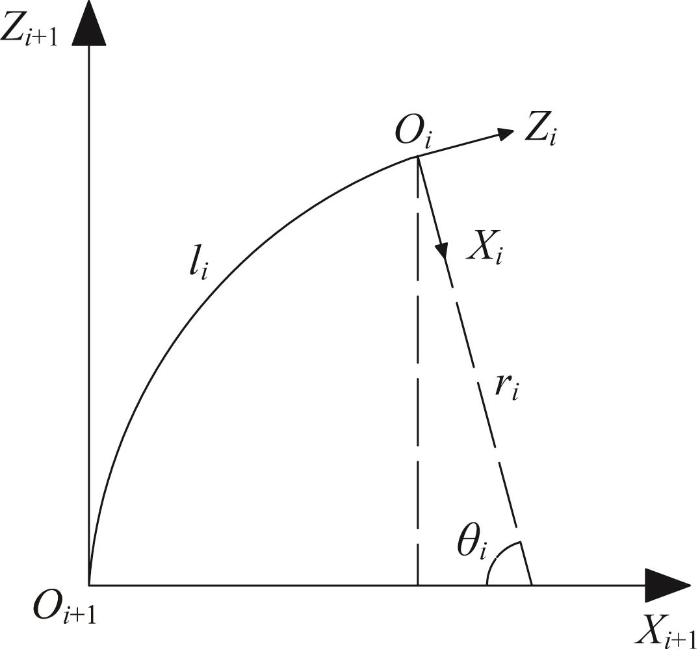
柔性关节的弯曲运动如图6所示。由图6可知，原点O_i 在坐标系O_i₊₁-X_i₊₁Y_i₊₁Z_i₊₁中的X、Z向坐标可表示为：

x_{O_{i}}^{O_{i + 1}} = \frac{l_{i}}{θ_{i}} (1 - c θ_{i})

(1)

z_{O_{i}}^{O_{i + 1}} = \frac{l_{i}}{θ_{i}} s θ_{i}

(2)

式中：s表示sin，c表示cos，下文同；l_i 表示柔性关节i的长度。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 柔性关节弯曲运动示意

Fig.6 Schematic diagram of flexible joint bending motion

由此可得，柔性关节弯曲运动对应的齐次变换矩阵 $_{i}^{i + 1} T_{b e n d}$ 为：

_{i}^{i + 1} T_{b e n d} = [\begin{matrix} c θ_{i} & 0 & s θ_{i} & x_{O_{i}}^{O_{i + 1}} \\ 0 & 1 & 0 & 0 \\ - s θ_{i} & 0 & c θ_{i} & z_{O_{i}}^{O_{i + 1}} \\ 0 & 0 & 0 & 1 \end{matrix}]

(3)

同理，柔性关节旋转运动对应的齐次变换矩阵 $_{i}^{i + 1} T_{r o t a t e}$ 为：

{}_{i}^{i + 1} T_{r o t a t e} = [\begin{matrix} c α_{i} & - s α_{i} & 0 & 0 \\ s α_{i} & c α_{i} & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]

(4)

联立式(3)和式(4)，可得坐标系O_i -X_iY_iZ_i 相对于坐标系O_i₊₁-X_i₊₁Y_i₊₁Z_i₊₁的齐次变换矩阵 ${}_{i}^{i + 1} T$ ，为：

\begin{array}{l} {}_{i}^{i + 1} T_{} = {}_{i}^{i + 1}T T_{r o t a t e} {}_{i}^{i + 1}T T_{b e n d} = \\ \begin{matrix}  \end{matrix} \begin{matrix}  \end{matrix} \begin{matrix}  \end{matrix} [\begin{matrix} n_{x} & - s α_{i} & o_{x} & p_{x} \\ n_{y} & c α_{i} & o_{y} & p_{y} \\ n_{z} & 0 & o_{z} & p_{z} \\ 0 & 0 & 0 & 1 \end{matrix}] \end{array}

(5)

其中：

[\begin{matrix} n_{x} \\ n_{y} \\ n_{z} \end{matrix}] = [\begin{matrix} c θ_{i} c α_{i} \\ c θ_{i} s α_{i} \\ - s θ_{i} \end{matrix}]

[\begin{matrix} o_{x} \\ o_{y} \\ o_{z} \end{matrix}] = [\begin{matrix} s θ_{i} c α_{i} \\ s θ_{i} s α_{i} \\ c θ_{i} \end{matrix}]

[\begin{matrix} p_{x} \\ p_{y} \\ p_{z} \end{matrix}] = [\begin{matrix} \frac{l_{i}}{θ_{i}} (1 - c θ_{i}) c α_{i} \\ \frac{l_{i}}{θ_{i}} (1 - c θ_{i}) s α_{i} \\ \frac{l_{i}}{θ_{i}} s θ_{i} \end{matrix}]

综上，坐标系O₁-X₁Y₁Z₁与基坐标系O₄-X₄Y₄Z₄之间的齐次变换矩阵 ${}_{1}^{4} T$ 为：

{}_{1}^{4} T = {}_{3}^{4}T {}_{2}^{3}T {}_{1}^{2}T

(6)

2.1.2　关节空间—操作空间的逆运动学分析

逆运动学分析是根据已知的柔性采摘机械臂末端位姿，利用式(6)求解相应的臂形角。逆运动学求解过程涉及由超越方程组成的方程组，很难求得解析解，因此本文采用粒子群优化（particle swarm optimization, PSO）算法来计算数值解，并利用MATLAB软件编程求解。

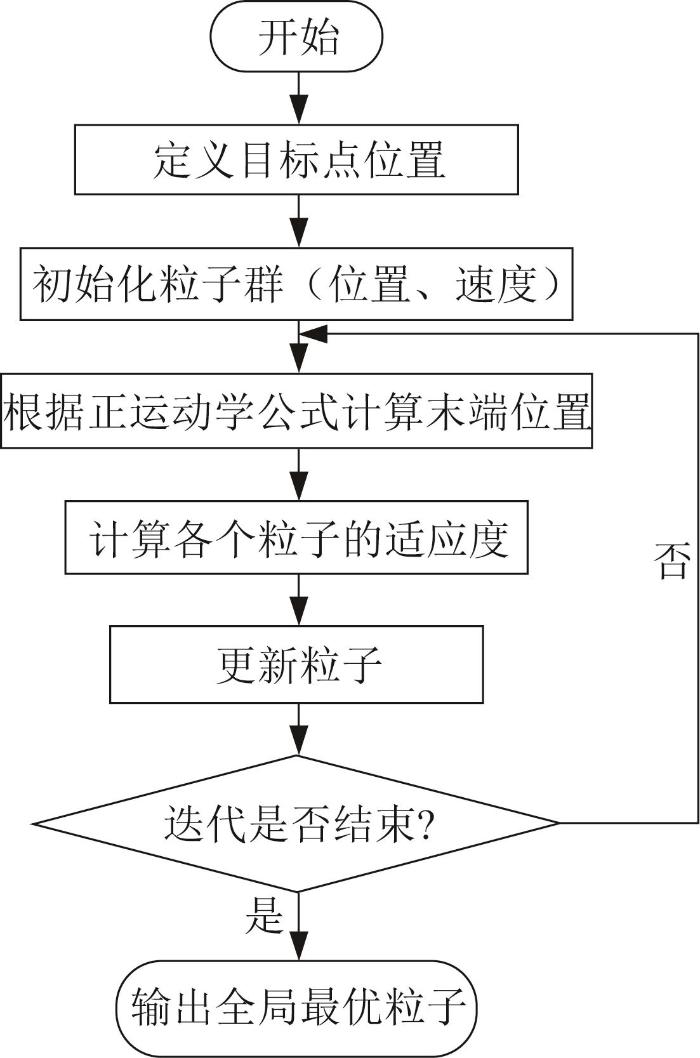
PSO算法^[17-19]是近年来发展起来的一种仿生优化算法，其从随机解出发，通过追随当前搜索到的最优值来寻找全局最优解，并利用适应度来评价解的品质。PSO算法具有精度高、收敛快和操作简单等优点，被广泛应用于不同领域。基于PSO的柔性采摘机械臂逆运动学分析流程如图7所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 基于PSO的柔性采摘机械臂逆运动学分析流程

Fig.7 Inverse kinematics analysis process of flexible picking robot arm based on PSO

根据图7所示流程和式(6)，利用MATLAB软件编写PSO程序并进行求解。设随机粒子种群大小M=40，迭代次数T=500，学习因子C₁=C₂=1.496 2，惯性权重w=0.7，并定义5个目标点。柔性采摘机械臂的逆运动学求解结果如表1所示。

表1 柔性采摘机械臂的逆运动学求解结果 (rad)

Table 1 Solution results of inverse kinematics for flexible picking robot arm

目标点/mm	α₁	θ₁	α₂	θ₂	α₃	θ₃
(130, 100, 1 460)	2.77	0.29	-3.14	0.79	5.43	-0.79
(140, 200, 1 360)	6.29	-0.59	-2.89	-1.24	-3.64	-0.11
(150, 300, 1 260)	5.93	-0.83	-2.79	-1.54	-1.19	0.22
(160, 400, 1 160)	5.04	0.62	-0.33	-1.59	2.86	0.13
(170, 500, 1 000)	-4.39	-0.53	-0.48	1.59	-5.92	0.63

新窗口打开| 下载CSV

2.2　关节空间与驱动空间的映射关系

通过改变驱动绳长度可实现柔性采摘机械臂的臂形变化，故其驱动空间到关节空间的映射关系即为驱动绳长度与臂形角之间的映射关系。

2.2.1　关节空间—驱动空间的正运动学分析

在利用等圆弧假设对柔性采摘机械臂进行运动学分析时，假设机械臂运动时各柔性关节的柔性支柱均为等曲率圆弧，并将每个柔性关节分为4个相同的柔性单元（相邻联接座与支撑盘以及相邻支撑盘之间部分）。下文以柔性关节3为例进行分析，其柔性支柱的弯曲角为θ₃，则各柔性单元的柔性支柱的弯曲角为θ₃/4，旋转角为α₃。

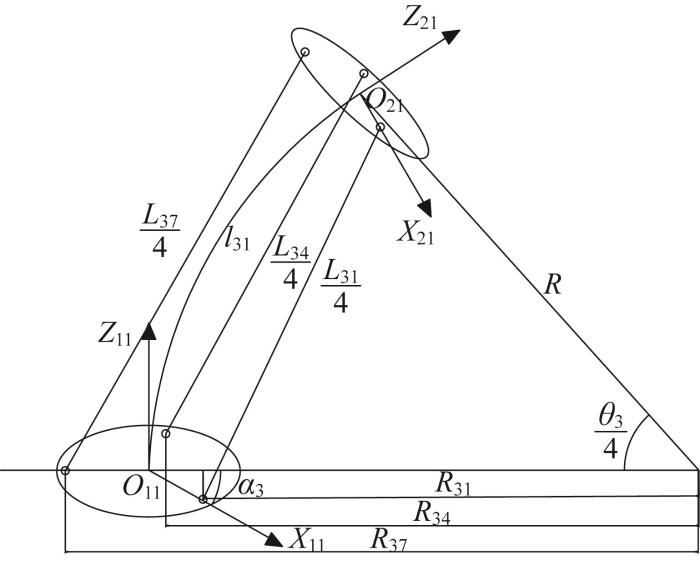
在柔性采摘机械臂弯曲过程中，各柔性单元的驱动绳近似为直线段。如图8所示，弧O₁₁O₂₁表示柔性关节3中某一柔性单元对应的柔性支柱，O₁₁为固定端，O₂₁为自由端；α₃表示弧O₁₁O₂₁所在平面相对于Z₁₁轴的旋转角，θ₃/4表示弧O₁₁O₂₁对应的圆心角；l₃₁和R分别表示弧O₁₁O₂₁的长度和曲率半径，L₃_n /4和R₃_n （n=1, 4, 7）分别表示各段驱动绳的长度以及绳孔n与弧心之间的径向距离。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 柔性单元结构示意

Fig.8 Schematic diagram of flexible unit structure

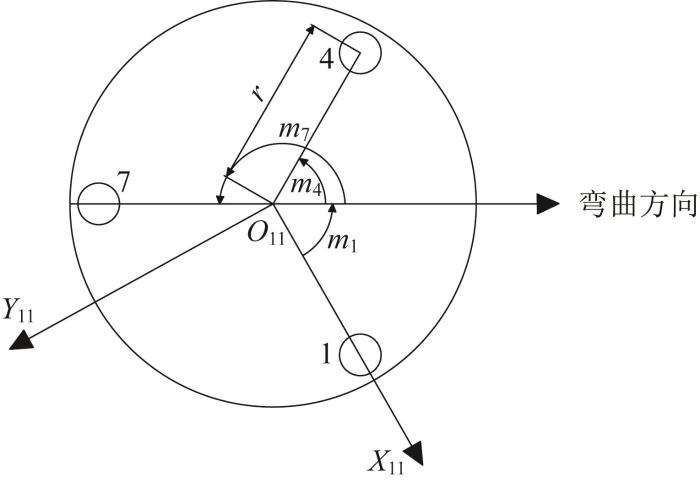
图9所示为柔性关节3中某一柔性单元的固定端截面。图中：m_n (n=1, 4, 7）表示绳孔n与固定端O₁₁之间连线与柔性支柱弯曲方向的夹角，r表示绳孔到固定端O₁₁的距离。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 柔性单元固定端截面示意

Fig.9 Schematic diagram of flexible unit fixed end section

结合图8和图9，可知：

R_{3 n} = R - r c m_{n} = \frac{4 l_{31}}{θ_{3}} - r c m_{n}

(7)

其中：

\{\begin{array}{l} m_{1} = - α_{3} \\ m_{4} = \frac{2}{3} π - α_{3} \\ m_{7} = \frac{4}{3} π - α_{3} \end{array}

此外，根据图9，还可得：

{(\frac{L_{3 n}}{4})}^{2} = 2 R_{3 n}^{2} - 2 R_{3 n}^{2} c (\frac{θ_{3}}{4})

(8)

联立式(7)和式(8)，可得：

\begin{array}{l} L_{3 n} = 4 \sqrt[]{2 R_{3 n}^{2} [1 - c (\frac{θ_{3}}{4})]} = \\ \begin{matrix}  \end{matrix} \begin{matrix}  \end{matrix} 4 \sqrt[]{2 {(\frac{4 l_{31}}{θ_{3}} - r c m_{n})}^{2} [1 - c (\frac{θ_{3}}{4})]} \end{array}

(9)

2.2.2　关节空间—驱动空间的逆运动学分析

利用式(9)计算得到柔性关节3的弯曲角θ₃：

\begin{array}{l} θ_{3} = \frac{4 (L_{31} - L_{34}) l_{31}}{L_{31} r c (2 π / 3 - α_{3}) - L_{34} r c α_{3}} = \\ \begin{matrix}  \end{matrix} \frac{4 (L_{31} - L_{37}) l_{31}}{L_{31} r c (4 π / 3 - α_{3}) - L_{37} r c α_{3}} \end{array}

(10)

进而利用式(10)计算得到柔性关节3的旋转角α₃：

α_{3} = a r c t a n \frac{\sqrt[]{3} (L_{34} - L_{37})}{2 L_{31} - L_{34} - L_{37}}

(11)

2.3　解耦分析

柔性采摘机械臂的3个柔性关节以串联的方式安装在驱动底座上，仅柔性关节3直接与驱动底座相连，其驱动绳的长度变化量由臂形角决定，而柔性关节1，2的驱动绳的长度变化量不仅与其自身的臂形角有关，还会受到其下方柔性关节的臂形角的影响，即柔性关节1，2的驱动绳的长度变化量与其下方柔性关节存在耦合关系，需要进行解耦处理。

柔性关节2的驱动绳穿过柔性关节3的绳孔，该部分驱动绳会与柔性关节3发生同样的弯曲。因此，在计算柔性关节2驱动绳的长度变化量时，应叠加柔性关节3驱动绳的长度变化量。对于柔性关节1驱动绳的长度变化量，亦采用同样的方法处理。

通过分析得到，各柔性关节驱动绳长度变化量的解耦表达式为：

\{\begin{array}{l} Δ L_{3 n} = f (θ_{3}, α_{3 n}), n = 1, 4, 7 \\ Δ L_{2 n} = f (θ_{2}, α_{2 n}) + f (θ_{3}, α_{3 n}), n = 2, 5, 8 \\ Δ L_{1 n} = f (θ_{3}, α_{3 n}) + f (θ_{2}, α_{2 n}) + f (θ_{1}, α_{1 n}), n = 3, 6, 9 \end{array}

(12)

式中： $∆ L_{1 n}$ 、 $∆ L_{2 n}$ 和 $∆ L_{3 n}$ 分别表示柔性关节1，2，3的3根驱动绳的长度变化量， $α_{1 n}$ 、 $α_{2 n}$ 和 $α_{3 n}$ 分别表示3个柔性关节的绳孔n处的驱动绳所对应的旋转角。

3 仿真验证

利用MATLAB软件对上文构建的柔性采摘机械臂运动学模型进行数值计算。同时，为验证理论分析结果的准确性，在相同工况下，利用ADAMS软件构建柔性采摘机械臂的虚拟样机模型以开展运动学仿真分析，并与基于MATLAB的理论分析结果进行对比。

3.1　基于MATLAB的运动学理论分析结果

基于上文推导得到的柔性采摘机械臂的正运动学模型，使用MATLAB软件编程并进行数值计算，分别获得单关节（柔性关节3）运动和三关节联合运动时柔性采摘机械臂的末端位置及其各驱动绳的长度变化量随臂形角的变化曲线。

1）单关节运动情况。

设定柔性采摘机械臂初始时处于直立状态，该状态下臂形角及各驱动绳的长度变化量均为0，此时机械臂末端（即柔性关节3末端）坐标为[0，0，500] mm；令弯曲角θ₃的变化范围为[0, π/3]，旋转角α₃的变化范围为[0, π/3]，这2个臂形角均采用单调匀速递增的方式变化。

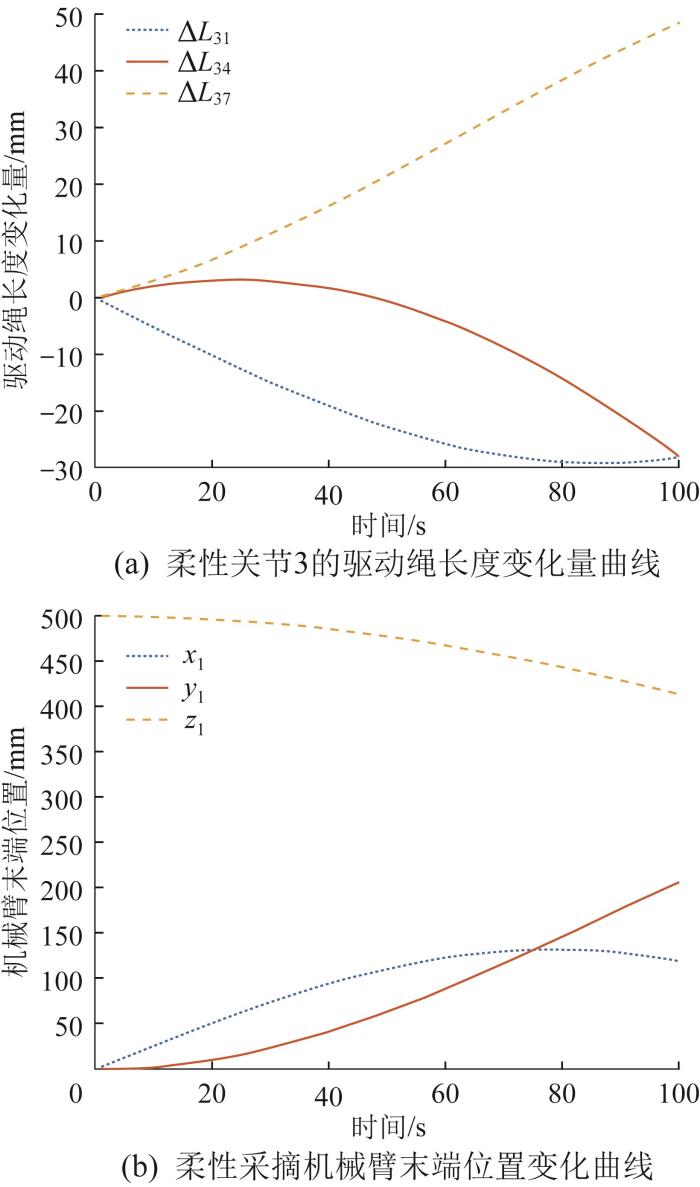
设柔性采摘机械臂的运动时间为100 s，基于MATLAB计算得到单关节运动时柔性关节3驱动绳的长度变化量以及柔性采摘机械臂末端位置（记为x₁、y₁、z₁）的变化曲线，结果如图10所示。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 单关节运动时柔性采摘机械臂的运动学分析结果

Fig.10 Kinematics analysis results of flexible picking robot arm under single joint motion

2）三关节联合运动情况。

同样设定柔性采摘机械臂初始时处于直立状态，其末端坐标为[0，0，1 500] mm。设定柔性关节3的弯曲角θ₃的变化范围为[0，π/6]，旋转角α₃=0；柔性关节2的弯曲角θ₂的变化范围为[0，π/6]，旋转角α₂=0；柔性关节1的弯曲角θ₁的变化范围为[0，π/6]，旋转角α₁的变化范围为[0，π/3]；各臂形角均采用单调匀速递增的方式变化。

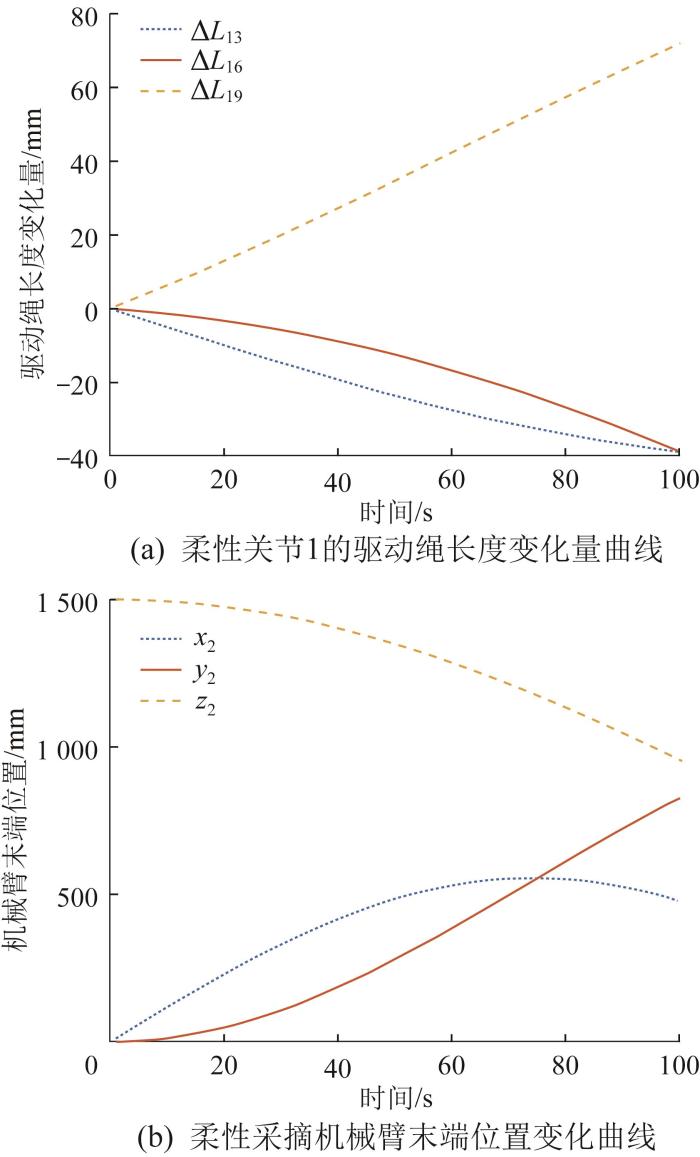
同样设定柔性采摘机械臂的运动时间为100 s，基于MATLAB计算得到三关节联合运动时柔性关节1驱动绳的长度变化量及柔性采摘机械臂末端位置（记为x₂、y₂、z₂）的变化曲线，结果如图11所示。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 三关节联合运动时柔性采摘机械臂的运动学分析结果

Fig.11 Kinematics analysis results of flexible picking robot arm under combined motion of three joints

3.2　基于ADAMS的运动学仿真分析

利用ADAMS软件建立柔性采摘机械臂的虚拟样机模型，选择与3.1节相同的工况，分析单关节运动、三关节联合运动这2种情况下柔性采摘机械臂末端位置随臂形角的变化规律，并与3.1节的理论分析结果进行对比。

柔性采摘机械臂虚拟样机模型的构建方法如下：对柔性采摘机械臂模型进行必要的结构简化后，将其另存为x_t格式并导入ADAMS软件；对导入的模型施加约束和驱动，并分别设置单关节运动与三关节联合运动情况下的仿真参数。所建立的柔性采摘机械臂虚拟样机模型如图12所示。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 柔性采摘机械臂虚拟样机模型

Fig.12 Virtual prototype model of flexible picking robot arm

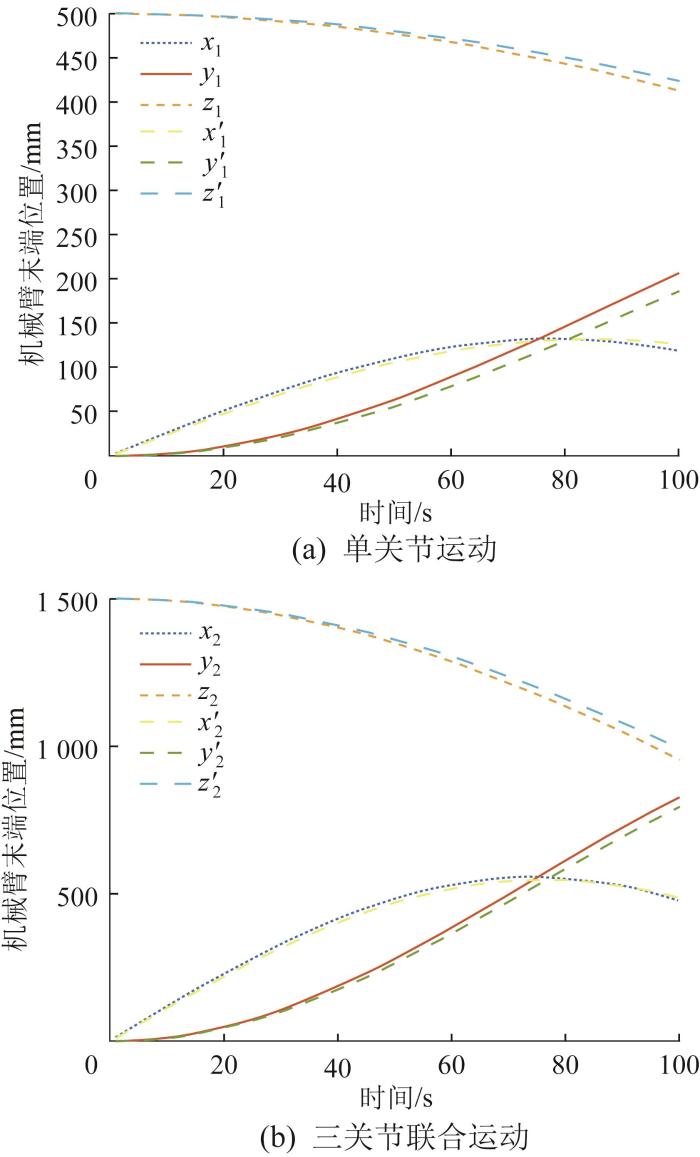
基于图12所示的柔性采摘机械臂虚拟样机模型，开展运动学仿真分析。分别提取2种运动情况下柔性采摘机械臂末端位置（ $x_{1}^{'}$ 、 $y_{1}^{'}$ 、 $z_{1}^{'}$ 和 $x_{2}^{'}$ 、 $y_{2}^{'}$ 、 $z_{2}^{'}$ ）的变化曲线，并与基于MATLAB的理论分析结果进行对比，如图13所示。由图13可知，在单关节运动和三关节联合运动情况下，柔性采摘机械臂末端位置的理论分析结果与仿真结果的相对误差均小于5%，由此验证了理论分析结果的准确性。此外，仿真结果表明，该柔性采摘机械臂的各柔性关节可协调运动，且运动过程平稳。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 不同运动情况下柔性采摘机械臂末端位置的变化曲线对比

Fig.13 Comparison of end position variation curves of flexible picking robot arm under different motion conditions

4 结论

1）针对刚性机械臂在果蔬采摘作业中的不足，提出了一种基于柔性机械臂的采摘机器人设计方案，并对柔性采摘机械臂进行了结构设计。

2）基于等圆弧假设建立了柔性采摘机械臂的运动学模型，并对其进行了从关节空间到操作空间及从驱动空间到关节空间的正、逆运动学分析。

3）利用MATLAB软件对柔性采摘机械臂的运动学模型进行了数值计算，并利用基于ADAMS的虚拟样机模型在相同工况下对该机械臂进行了运动学仿真分析，验证了理论分析结果的准确性。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

段洁利，陆华忠，王慰祖，等.

水果采收机械的现状与发展

［J］.广东农业科学，2012，39（16）：189-192. doi：10.3969/j.issn.1004-874X.2012.16.059

DOI:10.3969/j.issn.1004-874X.2012.16.059 [本文引用: 1]

DUAN

J L

， LU

H Z

， WANG

W Z

， et al.

Present situation and development of the fruit harvesting machinery

［J］. Guangdong Agricultural Sciences， 2012， 39（16）： 189-192.

DOI:10.3969/j.issn.1004-874X.2012.16.059 [本文引用: 1]

[2]

高国华，郑玉航，马帅，等.

黄瓜采摘机械臂运动学分析与样机试验

［J］.中国农机化学报，2017，38（7）：3-9.

[本文引用: 1]

GAO

G H

， ZHENG

Y H

， MA

， et al.

Kinematic analysis and prototype test of cucumber harvesting manipulator

［J］. Journal of Chinese Agricultural Mechanization， 2017， 38（7）： 3-9.

[本文引用: 1]

[3]

张文翔，张兵园，贡宇，等.

果蔬采摘机器人机械臂研究现状与展望

［J］.中国农机化学报，2022，43（9）：232-237，244.

ZHANG

W X

， ZHANG

B Y

， GONG

， et al.

Research status and prospect of fruit and vegetable picking robot manipulator

［J］. Journal of Chinese Agricultural Mechanization， 2022， 43（9）： 232-237， 244.

[4]

王丽丽，范晋伟，赵博，等.

果蔬采摘机械臂结构设计与性能测试

［J］.农业工程，2017，7（2）：107-113，23. doi：10.3969/j.issn.2095-1795.2017.02.028

DOI:10.3969/j.issn.2095-1795.2017.02.028 [本文引用: 1]

WANG

L L

， FAN

J W

， ZHAO

， et al.

Structural design and performance test of fruit and vegetable picking manipulator

［J］. Agricultural Engineering， 2017， 7（2）： 107-113， 23.

DOI:10.3969/j.issn.2095-1795.2017.02.028 [本文引用: 1]

[5]

赵云伟，耿德旭，刘晓敏，等.

气动柔性果蔬采摘机械手运动学分析与实验

［J］.农业机械学报，2019，50（8）：31-42. doi：10.6041/j.issn.1000-1298.2019.08.004

DOI:10.6041/j.issn.1000-1298.2019.08.004 [本文引用: 1]

ZHAO

Y W

， GENG

D X

， LIU

X M

， et al.

Kinematics analysis and experiment of pneumatic flexible fruit and vegetable picking manipulator

［J］. Transactions of the Chinese Society for Agricultural Machinery， 2019， 50（8）： 31-42.

DOI:10.6041/j.issn.1000-1298.2019.08.004 [本文引用: 1]

[6]

WEBSTER

R J

， ROMANO

J M

， COWAN

N J

Mechanics of precurved-tube continuum robots

［J］. IEEE Transactions on Robotics， 2008， 25（1）： 67-78.

[本文引用: 1]

[7]

MCMAHAN

， JONES

B A

， WALKER

I D

Design and implementation of a multi-section continuum robot： Air-Octor

［C］//IEEE/RSJ International Conference on Intelligent Robots and Systems. Edmonton， Aug. 2-6， 2005.

[本文引用: 1]

[8]

MCMAHAN

， CHITRAKARAN

， CSENCSITS

， et al.

Field trials and testing of the octarm continuum manipulator

［C］// Proceedings of the 2006 IEEE International Conference on Robotics and Automation. Orlando， May 15-19， 2006.

[本文引用: 1]

[9]

ZHANG

L F

， XU

， YANG

Research on soft manipulator actuated by shape memory alloy （SMA） springs

［C］//2017 IEEE International Conference on Real-time Computing and Robotics （RCAR）. Okinawa， Jul. 14-18， 2017.

[本文引用: 1]

[10]

SIMAAN

Snake-like units using flexible backbones and actuation redundancy for enhanced miniaturization

［C］//Proceedings of the 2005 IEEE International Conference on Robotics and Automation. Barcelona， Apr. 18-22， 2005.

[本文引用: 1]

[11]

胡海燕，王鹏飞，孙立宁，等.

线驱动连续型机器人的运动学分析与仿真

［J］.机械工程学报，2010，46（19）：1-8. doi：10.3901/jme.2010.19.001

DOI:10.3901/jme.2010.19.001 [本文引用: 1]

H Y

， WANG

P F

， SUN

L N

， et al.

Kinematic analysis and simulation for cable-driven continuum robot

［J］. Journal of Mechanical Engineering， 2010， 46（19）： 1-8.

DOI:10.3901/jme.2010.19.001 [本文引用: 1]

[12]

郭伟，肖滔，胡海燕，等.

一种连续型肠道机器人的通过性研究与仿真

［J］.机械与电子，2010，28（7）：63-67. doi：10.3969/j.issn.1001-2257.2010.07.019

DOI:10.3969/j.issn.1001-2257.2010.07.019

GUO

， XIAO

， HU

H Y

， et al.

Trafficability analysis and simulation for a continuum endoscope robot

［J］. Machinery and Electronics， 2010， 28（7）： 63-67.

DOI:10.3969/j.issn.1001-2257.2010.07.019

[13]

胡海燕，李伟达，李娟，等.

结肠镜机器人结构设计与通过性研究

［J］.哈尔滨工程大学学报，2013，34（2）：233-239. doi：10.3969/j.issn.1006-7043.201204049

DOI:10.3969/j.issn.1006-7043.201204049 [本文引用: 1]

H Y

， LI

W D

， LI

， et al.

Structure design and trafficability of colonoscopic robot

［J］. Journal of Harbin Engineering University， 2013， 34（2）： 233-239.

DOI:10.3969/j.issn.1006-7043.201204049 [本文引用: 1]

[14]

薛忠健

基于D-H法的锻造机器人运动学分析

［J］.机电工程技术，2020，49（11）：40-42，128. doi：10.3969/j.issn.1009-9492.2020.11.010

DOI:10.3969/j.issn.1009-9492.2020.11.010 [本文引用: 1]

XUE

Z J

Kinematic analysis of forging robot based on D-H method

［J］. Mechanical & Electrical Engineering Technology， 2020， 49（11）： 40-42， 128.

DOI:10.3969/j.issn.1009-9492.2020.11.010 [本文引用: 1]

[15]

刘守法，王晋鹏，李勇，等.

基于D-H法的5-DOF串并联机床运动学分析

［J］.制造技术与机床，2018（11）：110-115.

LIU

S F

， WANG

J P

， LI

， et al.

Kinematics analysis of 5-DOF series-parallel machine tool based on D-H method

［J］. Manufacturing Technology & Machine Tool， 2018（11）： 110-115.

[16]

方方闻怡，梁医，冯虎田.

基于D-H法的轨道摇臂摄影机器人运动学分析

［J］.机械设计与制造工程，2021，50（8）：15-20. doi：10.3969/j.issn.2095-509X.2021.08.003

DOI:10.3969/j.issn.2095-509X.2021.08.003 [本文引用: 1]

FANG

F W Y

， LIANG

， FENG

H T

Kinematics analysis of orbital rocker robot based on D-H method

［J］. Machine Design and Manufacturing Engineering， 2021， 50（8）： 15-20.

DOI:10.3969/j.issn.2095-509X.2021.08.003 [本文引用: 1]

[17]

白晓慧，何小娟，孙超利，等.

基于分层学习的改进PSO算法求解复杂优化问题

［J］.太原科技大学学报，2021，42（3）：169-174. doi：10.3969/j.issn.1673-2057.2021.03.001

DOI:10.3969/j.issn.1673-2057.2021.03.001 [本文引用: 1]

BAI

X H

， HE

X J

， SUN

C L

， et al.

Particle swarm optimization algorithm based on hierarchical learning for complex optimization problem

［J］. Journal of Taiyuan University of Science and Technology， 2021， 42（3）： 169-174.

DOI:10.3969/j.issn.1673-2057.2021.03.001 [本文引用: 1]

[18]

薛永生，吴立尧.

基于模拟退火的改进粒子群算法研究及应用

［J］.海军航空工程学院学报，2018，33（2）：248-252. doi：10.7682/j.issn.1673-1522.2018.02.012

DOI:10.7682/j.issn.1673-1522.2018.02.012

XUE

Y S

， WU

L Y

Research and application of improved PSO algorithm based on simulated annealing

［J］. Journal of Naval Aeronautical and Astronautical University， 2018， 33（2）： 248-252.

DOI:10.7682/j.issn.1673-1522.2018.02.012

[19]

周驰，高海兵，高亮，等.

粒子群优化算法

［J］.计算机应用研究，2003，20（12）：7-11. doi：10.3969/j.issn.1001-3695.2003.12.003

DOI:10.3969/j.issn.1001-3695.2003.12.003 [本文引用: 1]

ZHOU

， GAO

H B

， GAO

， et al.

Particle swarm optimization （PSO） algorithm

［J］. Application Research of Computers， 2003， 20（12）： 7-11.

DOI:10.3969/j.issn.1001-3695.2003.12.003 [本文引用: 1]

水果采收机械的现状与发展

2012

... 采摘作业是林果生产的重要环节，但传统的人工采摘方式需要投入大量劳动力.随着劳动力成本的增加和科学技术的发展，采摘机器人的应用将成为采摘行业的必然选择^[1].采摘机械臂是采摘机器人的重要组件，其性能直接影响采摘作业的效率与成功率.目前，采摘机械臂大多为笛卡尔型或关节型工业机械臂^[2-4]，这类刚性机械臂通常存在体积大、灵活性不足和成本高等缺陷，且不适用于果实密集、作业空间狭窄等场景.相比之下，柔性机械臂结构简单，运动灵活，适应性强，尺寸、质量较小，且具有较高的外负载能力（不低于50 N），更适用于采摘作业环境^[5]. ...

水果采收机械的现状与发展

2012

黄瓜采摘机械臂运动学分析与样机试验

2017

黄瓜采摘机械臂运动学分析与样机试验

2017

果蔬采摘机器人机械臂研究现状与展望

2022

果蔬采摘机器人机械臂研究现状与展望

2022

果蔬采摘机械臂结构设计与性能测试

2017

果蔬采摘机械臂结构设计与性能测试

2017

气动柔性果蔬采摘机械手运动学分析与实验

2019

气动柔性果蔬采摘机械手运动学分析与实验

2019

Mechanics of precurved-tube continuum robots

2008

... 近年来，国内外学者针对柔性机械臂在勘探、医疗、救援和航空航天等领域的应用开展了研究.Webster等^[6]研制了一种由3段横截面直径依次减小的弹性圆管组成的柔性机器人，其具有6个空间弯曲自由度.Mcmahan等^[7-8]研制了一种基于3根绳索驱动和内部气压控制的超冗余柔性机器人以及一种仿章鱼触手的连续型机器人.Zhang等^[9]搭建了基于形状记忆合金（shape memory alloy, SMA）驱动的具有4个关节的模块化柔性机械臂，并根据SMA的特点设计了自反馈控制系统，实现了该柔性机械臂的自主控制.Simaan^[10]研究了一种由超弹性中心骨架和沿骨架轴向均布的支撑圆盘组成的绳驱柔性机器人，可用于咽喉手术.胡海燕等^[11-13]对自主研制的线驱动连续型机器人进行了运动学分析与仿真，并在此基础上进一步设计了一种具有多关节段的连续型结肠镜机器人，可用于结肠前段和中段疾病的检查.但是，柔性机械臂在农业领域的应用研究鲜有报道. ...

Design and implementation of a multi-section continuum robot： Air-Octor

2005

Field trials and testing of the octarm continuum manipulator

2006

Research on soft manipulator actuated by shape memory alloy （SMA） springs

2017

Snake-like units using flexible backbones and actuation redundancy for enhanced miniaturization

2005

线驱动连续型机器人的运动学分析与仿真

2010

线驱动连续型机器人的运动学分析与仿真

2010

一种连续型肠道机器人的通过性研究与仿真

2010

一种连续型肠道机器人的通过性研究与仿真

2010

结肠镜机器人结构设计与通过性研究

2013

结肠镜机器人结构设计与通过性研究

2013

基于D-H法的锻造机器人运动学分析

2020

... 运动学建模与分析是实现机械臂运动控制的基础.对于传统的刚性机械臂，通常采用D-H法对其进行运动学分析^[14-16]，但柔性采摘机械臂的中心骨架为弹性体，其运动与变形较为复杂，难以用D-H法实现运动学建模与分析.为此，提出了一种基于等圆弧假设的柔性采摘机械臂运动学建模与分析方法. ...

基于D-H法的锻造机器人运动学分析

2020

基于D-H法的5-DOF串并联机床运动学分析

2018

基于D-H法的5-DOF串并联机床运动学分析

2018

基于D-H法的轨道摇臂摄影机器人运动学分析

2021

基于D-H法的轨道摇臂摄影机器人运动学分析

2021

基于分层学习的改进PSO算法求解复杂优化问题

2021

... PSO算法^[17-19]是近年来发展起来的一种仿生优化算法，其从随机解出发，通过追随当前搜索到的最优值来寻找全局最优解，并利用适应度来评价解的品质.PSO算法具有精度高、收敛快和操作简单等优点，被广泛应用于不同领域.基于PSO的柔性采摘机械臂逆运动学分析流程如图7所示. ...

基于分层学习的改进PSO算法求解复杂优化问题

2021

基于模拟退火的改进粒子群算法研究及应用

2018

基于模拟退火的改进粒子群算法研究及应用

2018

粒子群优化算法

2003

粒子群优化算法

2003

〈

〉