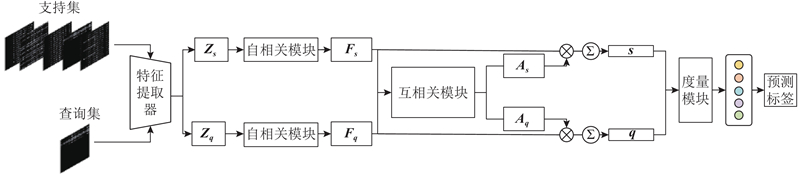
目前,大多数小样本学习是以情节学习范式对模型进行训练,一个情节或任务$ {T}_{i} $ N -way K -shot分类,表示每个任务中只有N 个可学习的类别,每个类别中有K 个样本. 每个情节或任务$ {T}_{i} $ $ {{{S}}}=\{{(x}_{\mathrm{1,1}},{c}_{\mathrm{1,1}}),({x}_{\mathrm{1,2}},{c}_{\mathrm{1,2}}),\cdots ,({x}_{N,K},{c}_{N,K})\} $ $ {Q}=\{{q}_{1},{q}_{2},\cdots ,{q}_{N\times M}\} $ $ {x}_{N,K} $ N 个类别的第K 个样本,$ {c}_{N,K}$ N 个类别的第K 个样本标签.
[1]
DAI B, WANG Y, YE C, et al A novel method for extracting time series information of deformation area of a single landslide based on improved U-Net neural network
[J]. Frontiers in Earth Science , 2021 , 9 : 785476
DOI:10.3389/feart.2021.785476
[本文引用: 1]
[2]
CHEN D, ZHANG F, ZHANG X Heterogeneous IoT intrusion detection based on fusion word embedding deep transfer learning
[J]. IEEE Transactions on Industrial Informatics , 2023 , 19 (8 ): 9183 - 9193
DOI:10.1109/TII.2022.3227640
[本文引用: 1]
[3]
HE M S, HUANG Y M, WANG X L, et al A lightweight and efficient IoT intrusion detection method based on feature grouping
[J]. IEEE Internet of Things Journal , 2024 , 11 (2 ): 2935 - 2949
DOI:10.1109/JIOT.2023.3294259
[本文引用: 1]
[4]
FINN C, ABBEEL P, LEVINE S. Model-agnostic meta-learning for fast adaptation of deep networks [C]//Proceedings of the International Conference on Machine Learning . New York: ACM, 2017: 1126-1135.
[本文引用: 1]
[6]
WANG Y, XU C, LIU C, et al. Instance credibility inference for few-shot learning [C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Seattle: IEEE, 2020: 12833–12842.
[本文引用: 1]
[7]
ZHAO L, LU J, XU Y, et al. Few-shot class-incremental learning via class-aware bilateral distillation [C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Vancouver: IEEE, 2023: 11838–11847.
[本文引用: 1]
[8]
LU C M, WANG X F, YANG A M, et al A few-shot-based model-agnostic meta-learning for intrusion detection in security of Internet of Things
[J]. IEEE Internet of Things Journal , 2023 , 10 (24 ): 21309 - 21321
DOI:10.1109/JIOT.2023.3283408
[本文引用: 7]
[9]
SHI Z X, XING M Y, ZHANG J, et al. Few-shot network intrusion detection based on model-agnostic meta-learning with L2F method [C]//Proceedings of the IEEE Wireless Communications and Networking Conference . Glasgow: IEEE, 2023: 1–6.
[本文引用: 3]
[10]
YAN Y, YANG Y, GU Y, et al. A few-shot intrusion detection model for the Internet of Things [C]//Proceedings of the 3rd International Conference on Electronic Information Engineering and Computer Science . Changchun: IEEE, 2024: 531–537.
[本文引用: 1]
[11]
DU L, GU Z Q, WANG Y, et al A few-shot class-incremental learning method for network intrusion detection
[J]. IEEE Transactions on Network and Service Management , 2024 , 21 (2 ): 2389 - 2401
DOI:10.1109/TNSM.2023.3332284
[本文引用: 2]
[12]
DI MONDA D, MONTIERI A, PERSICO V, et al Few-shot class-incremental learning for network intrusion detection systems
[J]. IEEE Open Journal of the Communications Society , 2024 , 5 : 6736 - 6757
DOI:10.1109/OJCOMS.2024.3481895
[本文引用: 1]
[13]
FINDER S E, AMOYAL R, TREISTER E, et al. Wavelet convolutions for large receptive fields [C]// Proceedings of the European Conference on Computer Vision . Madrid: Springer, 2024: 363–380.
[本文引用: 1]
[14]
KANG D, KWON H, MIN J, et al. Relational embedding for few-shot classification [C]//Proceedings of the IEEE/CVF International Conference on Computer Vision . Montreal: IEEE, 2021: 8802–8813.
[本文引用: 1]
[15]
HE K, ZHANG X, REN S, et al. Deep residual learning for image recognition [C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition . Las Vegas: IEEE, 2016: 770–778.
[本文引用: 2]
[16]
XU C, SHEN J, DU X A method of few-shot network intrusion detection based on meta-learning framework
[J]. IEEE Transactions on Information Forensics and Security , 2020 , 15 : 3540 - 3552
DOI:10.1109/TIFS.2020.2991876
[本文引用: 1]
[17]
YANG J C, LI H W, SHAO S, et al FS-IDS: a framework for intrusion detection based on few-shot learning
[J]. Computers and Security , 2022 , 122 : 102899
DOI:10.1016/j.cose.2022.102899
[本文引用: 1]
[18]
SNELL J, SWERSKY K, ZEMEL R S. Prototypical networks for few-shot learning [C]//Proceedings of the Neural Information Processing Systems . Long Beach: [s. n. ], 2017: 4080-4090.
[本文引用: 1]
[19]
SIMON C, KONIUSZ P, NOCK R, et al. Adaptive subspaces for few-shot learning [C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Seattle: IEEE, 2020: 4135–4144.
[本文引用: 1]
[20]
NETO E C P, DADKHAH S, FERREIRA R, et al CICIoT2023: a real-time dataset and benchmark for large-scale attacks in IoT environment
[J]. Sensors , 2023 , 23 (13 ): 5941
DOI:10.3390/s23135941
[本文引用: 1]
[21]
KORONIOTIS N, MOUSTAFA N, SITNIKOVA E, et al Towards the development of realistic botnet dataset in the Internet of Things for network forensic analytics: bot-IoT dataset
[J]. Future Generation Computer Systems , 2019 , 100 : 779 - 796
DOI:10.1016/j.future.2019.05.041
[本文引用: 1]
[22]
DRAPER-GIL G, LASHKARI A H, MAMUN M S I, et al. Characterization of encrypted and VPN traffic using time-related features [C]//Proceedings of the 2nd International Conference on Information Systems Security and Privacy . Portugal: SciTEPress, 2016: 407-414.
[本文引用: 1]
[23]
WANG Y, ZHANG Z, ZHAO K, et al A few-shot learning based method for industrial Internet intrusion detection
[J]. International Journal of Information Security , 2024 , 23 (5 ): 3241 - 3252
DOI:10.1007/s10207-024-00889-x
[本文引用: 3]
[24]
ZHAO R J, GUI G, XUE Z, et al A novel intrusion detection method based on lightweight neural network for internet of things
[J]. IEEE Internet of Things Journal , 2021 , 9 (12 ): 9960 - 9972
[本文引用: 2]
[25]
YAO W, ZHAO H, SHI H Privacy-preserving collaborative intrusion detection in edge of internet of things: a robust and efficient deep generative learning approach
[J]. IEEE Internet of Things Journal , 2023 , 11 (9 ): 15704 - 15722
[本文引用: 2]
A novel method for extracting time series information of deformation area of a single landslide based on improved U-Net neural network
1
2021
... 在物联网(IoT)领域中,由于攻击类型的多样性和复杂性,收集足够多的标注样本变得异常困难. 此外,IoT环境中的新型攻击和未知威胁不断涌现,传统的模型很难适应这种快速变化的威胁环境[1 -2 ] . 开发能够在小样本条件下有效检测未知类别攻击的IoT入侵检测模型变得至关重要[3 ] . ...
Heterogeneous IoT intrusion detection based on fusion word embedding deep transfer learning
1
2023
... 在物联网(IoT)领域中,由于攻击类型的多样性和复杂性,收集足够多的标注样本变得异常困难. 此外,IoT环境中的新型攻击和未知威胁不断涌现,传统的模型很难适应这种快速变化的威胁环境[1 -2 ] . 开发能够在小样本条件下有效检测未知类别攻击的IoT入侵检测模型变得至关重要[3 ] . ...
A lightweight and efficient IoT intrusion detection method based on feature grouping
1
2024
... 在物联网(IoT)领域中,由于攻击类型的多样性和复杂性,收集足够多的标注样本变得异常困难. 此外,IoT环境中的新型攻击和未知威胁不断涌现,传统的模型很难适应这种快速变化的威胁环境[1 -2 ] . 开发能够在小样本条件下有效检测未知类别攻击的IoT入侵检测模型变得至关重要[3 ] . ...
1
... 为了实现这一目标,研究者们正在探索多种方法来增强小样本物联网入侵检测模型的泛化能力. 这些方法包括元学习[4 ] 、迁移学习[5 ] 、数据增强[6 ] 和类增量学习[7 ] . Lu等[8 ] 提出基于与模型无关的元学习(model-agnostic meta-learning,MAML) 的元学习入侵检测方法,该方法有效解决了小样本学习样本不足的问题. Shi等[9 ] 提出基于MAML的方法,通过引入学会遗忘(learn to forget,L2F)衰减机制,解决了MAML强制共享初始化导致任务之间发生冲突,无法快速收敛到最优位置的问题. Yan等[10 ] 提出通过短时傅里叶变换将一维网络流量转换为图像的新型数据处理方法. Du等[11 ] 将小样本类增量学习应用到入侵检测系统中,提出分支融合策略的少样本类增量入侵检测系统. Di Monda等[12 ] 针对现有网络入侵检测系统(network intrusion detection system,NIDS)在面对新攻击时需要大量恶意流量样本和完全重新训练的局限性,提出能够快速适应新攻击并及时预测的NIDS. 本文提出新的小样本物联网入侵检测方法. 该方法融合了小波变换[13 ] 与关系嵌入[14 ] 技术,旨在解决物联网中未知类别的攻击. 通过引入小波变换构建特征提取网络:小波残差网络(wavelet transform residual network,WTRN). 该网络由小波变换网络和ResNet[15 ] 构成. WTRN显著提升了对可区分信息的捕捉能力,尤其在处理物联网中细微差异的攻击时,能够有效提取关键特征,为后续的检测任务提供精确的特征表示. 关系嵌入技术可以为入侵检测提供强大的分类器. 本文研究的主要创新点如下. ...
A comprehensive survey on transfer learning
1
2021
... 为了实现这一目标,研究者们正在探索多种方法来增强小样本物联网入侵检测模型的泛化能力. 这些方法包括元学习[4 ] 、迁移学习[5 ] 、数据增强[6 ] 和类增量学习[7 ] . Lu等[8 ] 提出基于与模型无关的元学习(model-agnostic meta-learning,MAML) 的元学习入侵检测方法,该方法有效解决了小样本学习样本不足的问题. Shi等[9 ] 提出基于MAML的方法,通过引入学会遗忘(learn to forget,L2F)衰减机制,解决了MAML强制共享初始化导致任务之间发生冲突,无法快速收敛到最优位置的问题. Yan等[10 ] 提出通过短时傅里叶变换将一维网络流量转换为图像的新型数据处理方法. Du等[11 ] 将小样本类增量学习应用到入侵检测系统中,提出分支融合策略的少样本类增量入侵检测系统. Di Monda等[12 ] 针对现有网络入侵检测系统(network intrusion detection system,NIDS)在面对新攻击时需要大量恶意流量样本和完全重新训练的局限性,提出能够快速适应新攻击并及时预测的NIDS. 本文提出新的小样本物联网入侵检测方法. 该方法融合了小波变换[13 ] 与关系嵌入[14 ] 技术,旨在解决物联网中未知类别的攻击. 通过引入小波变换构建特征提取网络:小波残差网络(wavelet transform residual network,WTRN). 该网络由小波变换网络和ResNet[15 ] 构成. WTRN显著提升了对可区分信息的捕捉能力,尤其在处理物联网中细微差异的攻击时,能够有效提取关键特征,为后续的检测任务提供精确的特征表示. 关系嵌入技术可以为入侵检测提供强大的分类器. 本文研究的主要创新点如下. ...
1
... 为了实现这一目标,研究者们正在探索多种方法来增强小样本物联网入侵检测模型的泛化能力. 这些方法包括元学习[4 ] 、迁移学习[5 ] 、数据增强[6 ] 和类增量学习[7 ] . Lu等[8 ] 提出基于与模型无关的元学习(model-agnostic meta-learning,MAML) 的元学习入侵检测方法,该方法有效解决了小样本学习样本不足的问题. Shi等[9 ] 提出基于MAML的方法,通过引入学会遗忘(learn to forget,L2F)衰减机制,解决了MAML强制共享初始化导致任务之间发生冲突,无法快速收敛到最优位置的问题. Yan等[10 ] 提出通过短时傅里叶变换将一维网络流量转换为图像的新型数据处理方法. Du等[11 ] 将小样本类增量学习应用到入侵检测系统中,提出分支融合策略的少样本类增量入侵检测系统. Di Monda等[12 ] 针对现有网络入侵检测系统(network intrusion detection system,NIDS)在面对新攻击时需要大量恶意流量样本和完全重新训练的局限性,提出能够快速适应新攻击并及时预测的NIDS. 本文提出新的小样本物联网入侵检测方法. 该方法融合了小波变换[13 ] 与关系嵌入[14 ] 技术,旨在解决物联网中未知类别的攻击. 通过引入小波变换构建特征提取网络:小波残差网络(wavelet transform residual network,WTRN). 该网络由小波变换网络和ResNet[15 ] 构成. WTRN显著提升了对可区分信息的捕捉能力,尤其在处理物联网中细微差异的攻击时,能够有效提取关键特征,为后续的检测任务提供精确的特征表示. 关系嵌入技术可以为入侵检测提供强大的分类器. 本文研究的主要创新点如下. ...
1
... 为了实现这一目标,研究者们正在探索多种方法来增强小样本物联网入侵检测模型的泛化能力. 这些方法包括元学习[4 ] 、迁移学习[5 ] 、数据增强[6 ] 和类增量学习[7 ] . Lu等[8 ] 提出基于与模型无关的元学习(model-agnostic meta-learning,MAML) 的元学习入侵检测方法,该方法有效解决了小样本学习样本不足的问题. Shi等[9 ] 提出基于MAML的方法,通过引入学会遗忘(learn to forget,L2F)衰减机制,解决了MAML强制共享初始化导致任务之间发生冲突,无法快速收敛到最优位置的问题. Yan等[10 ] 提出通过短时傅里叶变换将一维网络流量转换为图像的新型数据处理方法. Du等[11 ] 将小样本类增量学习应用到入侵检测系统中,提出分支融合策略的少样本类增量入侵检测系统. Di Monda等[12 ] 针对现有网络入侵检测系统(network intrusion detection system,NIDS)在面对新攻击时需要大量恶意流量样本和完全重新训练的局限性,提出能够快速适应新攻击并及时预测的NIDS. 本文提出新的小样本物联网入侵检测方法. 该方法融合了小波变换[13 ] 与关系嵌入[14 ] 技术,旨在解决物联网中未知类别的攻击. 通过引入小波变换构建特征提取网络:小波残差网络(wavelet transform residual network,WTRN). 该网络由小波变换网络和ResNet[15 ] 构成. WTRN显著提升了对可区分信息的捕捉能力,尤其在处理物联网中细微差异的攻击时,能够有效提取关键特征,为后续的检测任务提供精确的特征表示. 关系嵌入技术可以为入侵检测提供强大的分类器. 本文研究的主要创新点如下. ...
A few-shot-based model-agnostic meta-learning for intrusion detection in security of Internet of Things
7
2023
... 为了实现这一目标,研究者们正在探索多种方法来增强小样本物联网入侵检测模型的泛化能力. 这些方法包括元学习[4 ] 、迁移学习[5 ] 、数据增强[6 ] 和类增量学习[7 ] . Lu等[8 ] 提出基于与模型无关的元学习(model-agnostic meta-learning,MAML) 的元学习入侵检测方法,该方法有效解决了小样本学习样本不足的问题. Shi等[9 ] 提出基于MAML的方法,通过引入学会遗忘(learn to forget,L2F)衰减机制,解决了MAML强制共享初始化导致任务之间发生冲突,无法快速收敛到最优位置的问题. Yan等[10 ] 提出通过短时傅里叶变换将一维网络流量转换为图像的新型数据处理方法. Du等[11 ] 将小样本类增量学习应用到入侵检测系统中,提出分支融合策略的少样本类增量入侵检测系统. Di Monda等[12 ] 针对现有网络入侵检测系统(network intrusion detection system,NIDS)在面对新攻击时需要大量恶意流量样本和完全重新训练的局限性,提出能够快速适应新攻击并及时预测的NIDS. 本文提出新的小样本物联网入侵检测方法. 该方法融合了小波变换[13 ] 与关系嵌入[14 ] 技术,旨在解决物联网中未知类别的攻击. 通过引入小波变换构建特征提取网络:小波残差网络(wavelet transform residual network,WTRN). 该网络由小波变换网络和ResNet[15 ] 构成. WTRN显著提升了对可区分信息的捕捉能力,尤其在处理物联网中细微差异的攻击时,能够有效提取关键特征,为后续的检测任务提供精确的特征表示. 关系嵌入技术可以为入侵检测提供强大的分类器. 本文研究的主要创新点如下. ...
... 如表3 所示,从数据集、分类设置和准确率3个方面列举了其他研究人员的结果并比较. 其中,文献[8 ]与本文研究较类似,从数据集角度来看,Lu等[8 ] 对CSV中的样本进行处理,通过整理NSL-KDD、CICDDoS2019和CICIDS2017等5种数据集,构建适用于小样本物联网入侵检测的数据集,研究模型对未知类别样本检测的实验. 对PCAP中的样本进行处理,分别在CICIOT2023和BotIoT数据集上构建适用于小样本物联网入侵检测的数据集,并分别进行实验. 与文献[8 ]相同的是,最终都是将样本转换为更易处理的图像数据. 从小样本学习的技术路线来看,Lu等[8 -9 ] 遵循基于参数优化的元学习范式,Wang等[23 ] 与本研究基于度量学习框架. 从检测目标来看,Zhao等[24 -25 ] 使用基于深度学习的方法对已知类别攻击进行检测,本文方法主要针对未知类别攻击. 虽然对未知类别攻击的检测难度更高,但从结果来看,本文方法更优. ...
... [8 ]对CSV中的样本进行处理,通过整理NSL-KDD、CICDDoS2019和CICIDS2017等5种数据集,构建适用于小样本物联网入侵检测的数据集,研究模型对未知类别样本检测的实验. 对PCAP中的样本进行处理,分别在CICIOT2023和BotIoT数据集上构建适用于小样本物联网入侵检测的数据集,并分别进行实验. 与文献[8 ]相同的是,最终都是将样本转换为更易处理的图像数据. 从小样本学习的技术路线来看,Lu等[8 -9 ] 遵循基于参数优化的元学习范式,Wang等[23 ] 与本研究基于度量学习框架. 从检测目标来看,Zhao等[24 -25 ] 使用基于深度学习的方法对已知类别攻击进行检测,本文方法主要针对未知类别攻击. 虽然对未知类别攻击的检测难度更高,但从结果来看,本文方法更优. ...
... 对CSV中的样本进行处理,通过整理NSL-KDD、CICDDoS2019和CICIDS2017等5种数据集,构建适用于小样本物联网入侵检测的数据集,研究模型对未知类别样本检测的实验. 对PCAP中的样本进行处理,分别在CICIOT2023和BotIoT数据集上构建适用于小样本物联网入侵检测的数据集,并分别进行实验. 与文献[8 ]相同的是,最终都是将样本转换为更易处理的图像数据. 从小样本学习的技术路线来看,Lu等[8 -9 ] 遵循基于参数优化的元学习范式,Wang等[23 ] 与本研究基于度量学习框架. 从检测目标来看,Zhao等[24 -25 ] 使用基于深度学习的方法对已知类别攻击进行检测,本文方法主要针对未知类别攻击. 虽然对未知类别攻击的检测难度更高,但从结果来看,本文方法更优. ...
... [8 -9 ]遵循基于参数优化的元学习范式,Wang等[23 ] 与本研究基于度量学习框架. 从检测目标来看,Zhao等[24 -25 ] 使用基于深度学习的方法对已知类别攻击进行检测,本文方法主要针对未知类别攻击. 虽然对未知类别攻击的检测难度更高,但从结果来看,本文方法更优. ...
... Comparative analysis between proposed method and related works
Tab.3 方法 数据集 物联网数据集 实验设置 A c /%UTRS LNN[24 ] BotIoT Y N/A 96.15 0.0003 L2F+MAML[9 ] CICIDS2017 N 2-way 10-shot 94.66 10.00 MAML+CNN[8 ] FSIDSIOT Y 5-way 5-shot 89.64 28.91 MAML+CNN[8 ] FSIDSIOT Y 5-way 10-shot 92.19 18.16 IPN-IDS[23 ] CICIDS2017 N 5-way 5-shot 84.94 25.57 IPN-IDS [23 ] CICIDS2017 N 5-way 10-shot 86.35 15.21 CIDIOT[25 ] CICIOT2023 Y N/A 77.20 0.017 本文方法 CICIDS2017 N 5-way 5-shot 98.82 31.41 本文方法 CICIDS2017 N 5-way 10-shot 98.89 19.08 本文方法 BotIoT Y 5-way 5-shot 99.30 34.89 本文方法 BotIoT Y 5-way 10-shot 99.33 22.49 本文方法 CICIOT2023 Y 5-way 5-shot 93.50 29.91 本文方法 CICIOT2023 Y 5-way 10-shot 93.12 18.16
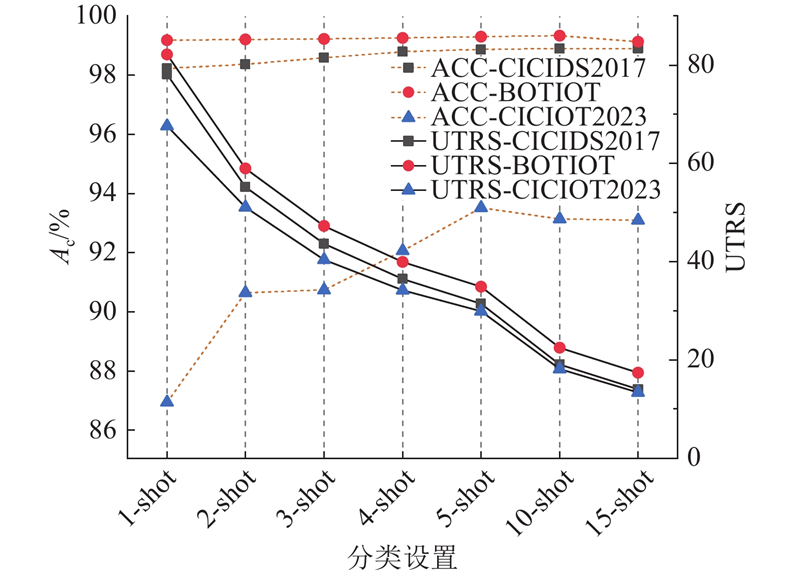
考虑现有的评估指标没有反映样本数量和未知攻击对检测准确率的影响,为了更好地评估基于相同数据集不同算法之间的差异,定义新的指标:未知威胁响应分数. ...
... [
8 ]
FSIDSIOT Y 5-way 10-shot 92.19 18.16 IPN-IDS[23 ] CICIDS2017 N 5-way 5-shot 84.94 25.57 IPN-IDS [23 ] CICIDS2017 N 5-way 10-shot 86.35 15.21 CIDIOT[25 ] CICIOT2023 Y N/A 77.20 0.017 本文方法 CICIDS2017 N 5-way 5-shot 98.82 31.41 本文方法 CICIDS2017 N 5-way 10-shot 98.89 19.08 本文方法 BotIoT Y 5-way 5-shot 99.30 34.89 本文方法 BotIoT Y 5-way 10-shot 99.33 22.49 本文方法 CICIOT2023 Y 5-way 5-shot 93.50 29.91 本文方法 CICIOT2023 Y 5-way 10-shot 93.12 18.16 考虑现有的评估指标没有反映样本数量和未知攻击对检测准确率的影响,为了更好地评估基于相同数据集不同算法之间的差异,定义新的指标:未知威胁响应分数. ...
3
... 为了实现这一目标,研究者们正在探索多种方法来增强小样本物联网入侵检测模型的泛化能力. 这些方法包括元学习[4 ] 、迁移学习[5 ] 、数据增强[6 ] 和类增量学习[7 ] . Lu等[8 ] 提出基于与模型无关的元学习(model-agnostic meta-learning,MAML) 的元学习入侵检测方法,该方法有效解决了小样本学习样本不足的问题. Shi等[9 ] 提出基于MAML的方法,通过引入学会遗忘(learn to forget,L2F)衰减机制,解决了MAML强制共享初始化导致任务之间发生冲突,无法快速收敛到最优位置的问题. Yan等[10 ] 提出通过短时傅里叶变换将一维网络流量转换为图像的新型数据处理方法. Du等[11 ] 将小样本类增量学习应用到入侵检测系统中,提出分支融合策略的少样本类增量入侵检测系统. Di Monda等[12 ] 针对现有网络入侵检测系统(network intrusion detection system,NIDS)在面对新攻击时需要大量恶意流量样本和完全重新训练的局限性,提出能够快速适应新攻击并及时预测的NIDS. 本文提出新的小样本物联网入侵检测方法. 该方法融合了小波变换[13 ] 与关系嵌入[14 ] 技术,旨在解决物联网中未知类别的攻击. 通过引入小波变换构建特征提取网络:小波残差网络(wavelet transform residual network,WTRN). 该网络由小波变换网络和ResNet[15 ] 构成. WTRN显著提升了对可区分信息的捕捉能力,尤其在处理物联网中细微差异的攻击时,能够有效提取关键特征,为后续的检测任务提供精确的特征表示. 关系嵌入技术可以为入侵检测提供强大的分类器. 本文研究的主要创新点如下. ...
... 如表3 所示,从数据集、分类设置和准确率3个方面列举了其他研究人员的结果并比较. 其中,文献[8 ]与本文研究较类似,从数据集角度来看,Lu等[8 ] 对CSV中的样本进行处理,通过整理NSL-KDD、CICDDoS2019和CICIDS2017等5种数据集,构建适用于小样本物联网入侵检测的数据集,研究模型对未知类别样本检测的实验. 对PCAP中的样本进行处理,分别在CICIOT2023和BotIoT数据集上构建适用于小样本物联网入侵检测的数据集,并分别进行实验. 与文献[8 ]相同的是,最终都是将样本转换为更易处理的图像数据. 从小样本学习的技术路线来看,Lu等[8 -9 ] 遵循基于参数优化的元学习范式,Wang等[23 ] 与本研究基于度量学习框架. 从检测目标来看,Zhao等[24 -25 ] 使用基于深度学习的方法对已知类别攻击进行检测,本文方法主要针对未知类别攻击. 虽然对未知类别攻击的检测难度更高,但从结果来看,本文方法更优. ...
... Comparative analysis between proposed method and related works
Tab.3 方法 数据集 物联网数据集 实验设置 A c /%UTRS LNN[24 ] BotIoT Y N/A 96.15 0.0003 L2F+MAML[9 ] CICIDS2017 N 2-way 10-shot 94.66 10.00 MAML+CNN[8 ] FSIDSIOT Y 5-way 5-shot 89.64 28.91 MAML+CNN[8 ] FSIDSIOT Y 5-way 10-shot 92.19 18.16 IPN-IDS[23 ] CICIDS2017 N 5-way 5-shot 84.94 25.57 IPN-IDS [23 ] CICIDS2017 N 5-way 10-shot 86.35 15.21 CIDIOT[25 ] CICIOT2023 Y N/A 77.20 0.017 本文方法 CICIDS2017 N 5-way 5-shot 98.82 31.41 本文方法 CICIDS2017 N 5-way 10-shot 98.89 19.08 本文方法 BotIoT Y 5-way 5-shot 99.30 34.89 本文方法 BotIoT Y 5-way 10-shot 99.33 22.49 本文方法 CICIOT2023 Y 5-way 5-shot 93.50 29.91 本文方法 CICIOT2023 Y 5-way 10-shot 93.12 18.16
考虑现有的评估指标没有反映样本数量和未知攻击对检测准确率的影响,为了更好地评估基于相同数据集不同算法之间的差异,定义新的指标:未知威胁响应分数. ...
1
... 为了实现这一目标,研究者们正在探索多种方法来增强小样本物联网入侵检测模型的泛化能力. 这些方法包括元学习[4 ] 、迁移学习[5 ] 、数据增强[6 ] 和类增量学习[7 ] . Lu等[8 ] 提出基于与模型无关的元学习(model-agnostic meta-learning,MAML) 的元学习入侵检测方法,该方法有效解决了小样本学习样本不足的问题. Shi等[9 ] 提出基于MAML的方法,通过引入学会遗忘(learn to forget,L2F)衰减机制,解决了MAML强制共享初始化导致任务之间发生冲突,无法快速收敛到最优位置的问题. Yan等[10 ] 提出通过短时傅里叶变换将一维网络流量转换为图像的新型数据处理方法. Du等[11 ] 将小样本类增量学习应用到入侵检测系统中,提出分支融合策略的少样本类增量入侵检测系统. Di Monda等[12 ] 针对现有网络入侵检测系统(network intrusion detection system,NIDS)在面对新攻击时需要大量恶意流量样本和完全重新训练的局限性,提出能够快速适应新攻击并及时预测的NIDS. 本文提出新的小样本物联网入侵检测方法. 该方法融合了小波变换[13 ] 与关系嵌入[14 ] 技术,旨在解决物联网中未知类别的攻击. 通过引入小波变换构建特征提取网络:小波残差网络(wavelet transform residual network,WTRN). 该网络由小波变换网络和ResNet[15 ] 构成. WTRN显著提升了对可区分信息的捕捉能力,尤其在处理物联网中细微差异的攻击时,能够有效提取关键特征,为后续的检测任务提供精确的特征表示. 关系嵌入技术可以为入侵检测提供强大的分类器. 本文研究的主要创新点如下. ...
A few-shot class-incremental learning method for network intrusion detection
2
2024
... 为了实现这一目标,研究者们正在探索多种方法来增强小样本物联网入侵检测模型的泛化能力. 这些方法包括元学习[4 ] 、迁移学习[5 ] 、数据增强[6 ] 和类增量学习[7 ] . Lu等[8 ] 提出基于与模型无关的元学习(model-agnostic meta-learning,MAML) 的元学习入侵检测方法,该方法有效解决了小样本学习样本不足的问题. Shi等[9 ] 提出基于MAML的方法,通过引入学会遗忘(learn to forget,L2F)衰减机制,解决了MAML强制共享初始化导致任务之间发生冲突,无法快速收敛到最优位置的问题. Yan等[10 ] 提出通过短时傅里叶变换将一维网络流量转换为图像的新型数据处理方法. Du等[11 ] 将小样本类增量学习应用到入侵检测系统中,提出分支融合策略的少样本类增量入侵检测系统. Di Monda等[12 ] 针对现有网络入侵检测系统(network intrusion detection system,NIDS)在面对新攻击时需要大量恶意流量样本和完全重新训练的局限性,提出能够快速适应新攻击并及时预测的NIDS. 本文提出新的小样本物联网入侵检测方法. 该方法融合了小波变换[13 ] 与关系嵌入[14 ] 技术,旨在解决物联网中未知类别的攻击. 通过引入小波变换构建特征提取网络:小波残差网络(wavelet transform residual network,WTRN). 该网络由小波变换网络和ResNet[15 ] 构成. WTRN显著提升了对可区分信息的捕捉能力,尤其在处理物联网中细微差异的攻击时,能够有效提取关键特征,为后续的检测任务提供精确的特征表示. 关系嵌入技术可以为入侵检测提供强大的分类器. 本文研究的主要创新点如下. ...
... 采用网络流量可视化[11 ,16 ] 的方法,将具有相同五元组(源IP、目的IP、源端口、目的端口、协议)的数据包视为一个数据流. 提取每个数据流的前16个数据包和每个数据包的前256字节作为一个样本. 每个字节的大小刚好对应0~255的灰度,可以形成16×256的矩阵. 经过矩阵变换,可以形成64×64大小的灰度图[17 ] . ...
Few-shot class-incremental learning for network intrusion detection systems
1
2024
... 为了实现这一目标,研究者们正在探索多种方法来增强小样本物联网入侵检测模型的泛化能力. 这些方法包括元学习[4 ] 、迁移学习[5 ] 、数据增强[6 ] 和类增量学习[7 ] . Lu等[8 ] 提出基于与模型无关的元学习(model-agnostic meta-learning,MAML) 的元学习入侵检测方法,该方法有效解决了小样本学习样本不足的问题. Shi等[9 ] 提出基于MAML的方法,通过引入学会遗忘(learn to forget,L2F)衰减机制,解决了MAML强制共享初始化导致任务之间发生冲突,无法快速收敛到最优位置的问题. Yan等[10 ] 提出通过短时傅里叶变换将一维网络流量转换为图像的新型数据处理方法. Du等[11 ] 将小样本类增量学习应用到入侵检测系统中,提出分支融合策略的少样本类增量入侵检测系统. Di Monda等[12 ] 针对现有网络入侵检测系统(network intrusion detection system,NIDS)在面对新攻击时需要大量恶意流量样本和完全重新训练的局限性,提出能够快速适应新攻击并及时预测的NIDS. 本文提出新的小样本物联网入侵检测方法. 该方法融合了小波变换[13 ] 与关系嵌入[14 ] 技术,旨在解决物联网中未知类别的攻击. 通过引入小波变换构建特征提取网络:小波残差网络(wavelet transform residual network,WTRN). 该网络由小波变换网络和ResNet[15 ] 构成. WTRN显著提升了对可区分信息的捕捉能力,尤其在处理物联网中细微差异的攻击时,能够有效提取关键特征,为后续的检测任务提供精确的特征表示. 关系嵌入技术可以为入侵检测提供强大的分类器. 本文研究的主要创新点如下. ...
1
... 为了实现这一目标,研究者们正在探索多种方法来增强小样本物联网入侵检测模型的泛化能力. 这些方法包括元学习[4 ] 、迁移学习[5 ] 、数据增强[6 ] 和类增量学习[7 ] . Lu等[8 ] 提出基于与模型无关的元学习(model-agnostic meta-learning,MAML) 的元学习入侵检测方法,该方法有效解决了小样本学习样本不足的问题. Shi等[9 ] 提出基于MAML的方法,通过引入学会遗忘(learn to forget,L2F)衰减机制,解决了MAML强制共享初始化导致任务之间发生冲突,无法快速收敛到最优位置的问题. Yan等[10 ] 提出通过短时傅里叶变换将一维网络流量转换为图像的新型数据处理方法. Du等[11 ] 将小样本类增量学习应用到入侵检测系统中,提出分支融合策略的少样本类增量入侵检测系统. Di Monda等[12 ] 针对现有网络入侵检测系统(network intrusion detection system,NIDS)在面对新攻击时需要大量恶意流量样本和完全重新训练的局限性,提出能够快速适应新攻击并及时预测的NIDS. 本文提出新的小样本物联网入侵检测方法. 该方法融合了小波变换[13 ] 与关系嵌入[14 ] 技术,旨在解决物联网中未知类别的攻击. 通过引入小波变换构建特征提取网络:小波残差网络(wavelet transform residual network,WTRN). 该网络由小波变换网络和ResNet[15 ] 构成. WTRN显著提升了对可区分信息的捕捉能力,尤其在处理物联网中细微差异的攻击时,能够有效提取关键特征,为后续的检测任务提供精确的特征表示. 关系嵌入技术可以为入侵检测提供强大的分类器. 本文研究的主要创新点如下. ...
1
... 为了实现这一目标,研究者们正在探索多种方法来增强小样本物联网入侵检测模型的泛化能力. 这些方法包括元学习[4 ] 、迁移学习[5 ] 、数据增强[6 ] 和类增量学习[7 ] . Lu等[8 ] 提出基于与模型无关的元学习(model-agnostic meta-learning,MAML) 的元学习入侵检测方法,该方法有效解决了小样本学习样本不足的问题. Shi等[9 ] 提出基于MAML的方法,通过引入学会遗忘(learn to forget,L2F)衰减机制,解决了MAML强制共享初始化导致任务之间发生冲突,无法快速收敛到最优位置的问题. Yan等[10 ] 提出通过短时傅里叶变换将一维网络流量转换为图像的新型数据处理方法. Du等[11 ] 将小样本类增量学习应用到入侵检测系统中,提出分支融合策略的少样本类增量入侵检测系统. Di Monda等[12 ] 针对现有网络入侵检测系统(network intrusion detection system,NIDS)在面对新攻击时需要大量恶意流量样本和完全重新训练的局限性,提出能够快速适应新攻击并及时预测的NIDS. 本文提出新的小样本物联网入侵检测方法. 该方法融合了小波变换[13 ] 与关系嵌入[14 ] 技术,旨在解决物联网中未知类别的攻击. 通过引入小波变换构建特征提取网络:小波残差网络(wavelet transform residual network,WTRN). 该网络由小波变换网络和ResNet[15 ] 构成. WTRN显著提升了对可区分信息的捕捉能力,尤其在处理物联网中细微差异的攻击时,能够有效提取关键特征,为后续的检测任务提供精确的特征表示. 关系嵌入技术可以为入侵检测提供强大的分类器. 本文研究的主要创新点如下. ...
2
... 为了实现这一目标,研究者们正在探索多种方法来增强小样本物联网入侵检测模型的泛化能力. 这些方法包括元学习[4 ] 、迁移学习[5 ] 、数据增强[6 ] 和类增量学习[7 ] . Lu等[8 ] 提出基于与模型无关的元学习(model-agnostic meta-learning,MAML) 的元学习入侵检测方法,该方法有效解决了小样本学习样本不足的问题. Shi等[9 ] 提出基于MAML的方法,通过引入学会遗忘(learn to forget,L2F)衰减机制,解决了MAML强制共享初始化导致任务之间发生冲突,无法快速收敛到最优位置的问题. Yan等[10 ] 提出通过短时傅里叶变换将一维网络流量转换为图像的新型数据处理方法. Du等[11 ] 将小样本类增量学习应用到入侵检测系统中,提出分支融合策略的少样本类增量入侵检测系统. Di Monda等[12 ] 针对现有网络入侵检测系统(network intrusion detection system,NIDS)在面对新攻击时需要大量恶意流量样本和完全重新训练的局限性,提出能够快速适应新攻击并及时预测的NIDS. 本文提出新的小样本物联网入侵检测方法. 该方法融合了小波变换[13 ] 与关系嵌入[14 ] 技术,旨在解决物联网中未知类别的攻击. 通过引入小波变换构建特征提取网络:小波残差网络(wavelet transform residual network,WTRN). 该网络由小波变换网络和ResNet[15 ] 构成. WTRN显著提升了对可区分信息的捕捉能力,尤其在处理物联网中细微差异的攻击时,能够有效提取关键特征,为后续的检测任务提供精确的特征表示. 关系嵌入技术可以为入侵检测提供强大的分类器. 本文研究的主要创新点如下. ...
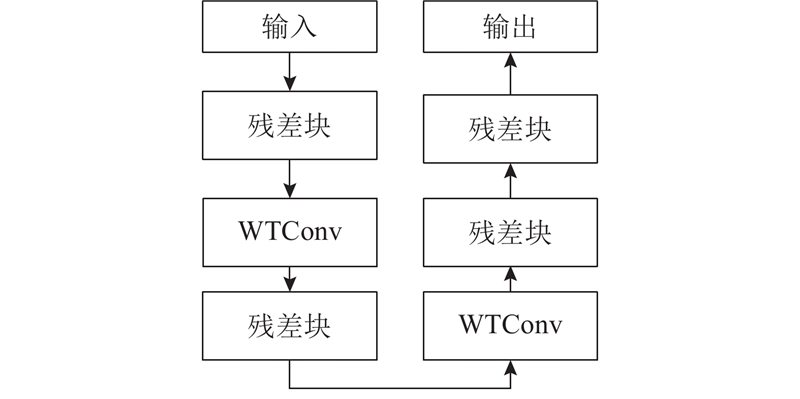
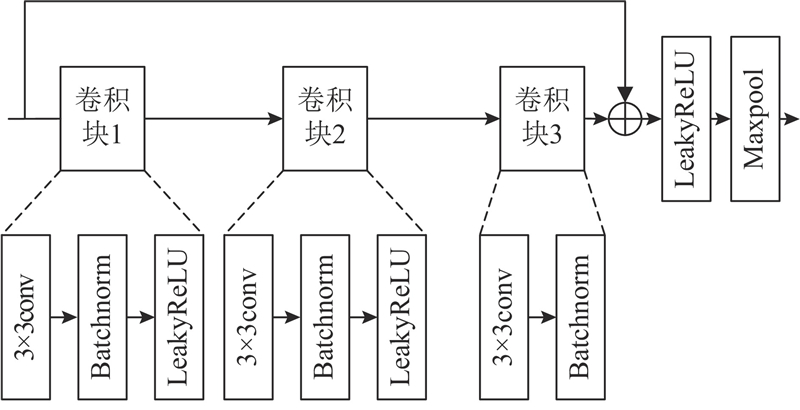
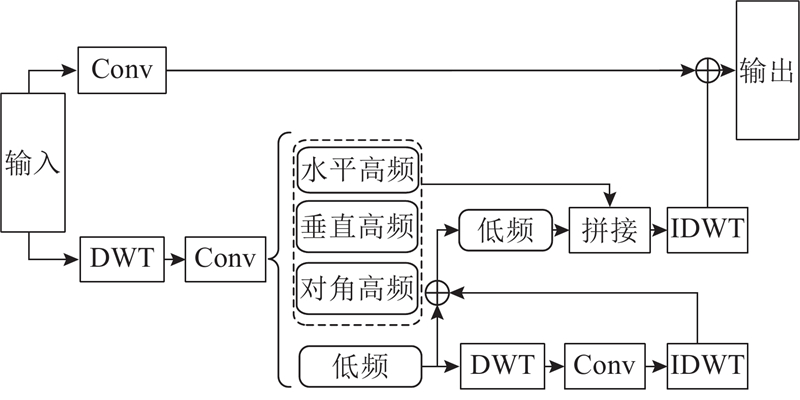
... 在过去的几年中,卷积神经网络(CNN)在计算机视觉领域中起着主导作用. He等[15 ] 提出诸多基于CNN的模型. 其中,ResNet的出现极大地影响了计算机视觉领域. 为了提高模型对网络流量全局信息的捕捉能力,在ResNet12的基础上,利用小波变换设计特征提取网络:WTRN. 该网络由残差块和WTConv组成. WTRN的结构如图2 所示. 接下来将详细介绍这2个组件. ...
A method of few-shot network intrusion detection based on meta-learning framework
1
2020
... 采用网络流量可视化[11 ,16 ] 的方法,将具有相同五元组(源IP、目的IP、源端口、目的端口、协议)的数据包视为一个数据流. 提取每个数据流的前16个数据包和每个数据包的前256字节作为一个样本. 每个字节的大小刚好对应0~255的灰度,可以形成16×256的矩阵. 经过矩阵变换,可以形成64×64大小的灰度图[17 ] . ...
FS-IDS: a framework for intrusion detection based on few-shot learning
1
2022
... 采用网络流量可视化[11 ,16 ] 的方法,将具有相同五元组(源IP、目的IP、源端口、目的端口、协议)的数据包视为一个数据流. 提取每个数据流的前16个数据包和每个数据包的前256字节作为一个样本. 每个字节的大小刚好对应0~255的灰度,可以形成16×256的矩阵. 经过矩阵变换,可以形成64×64大小的灰度图[17 ] . ...
1
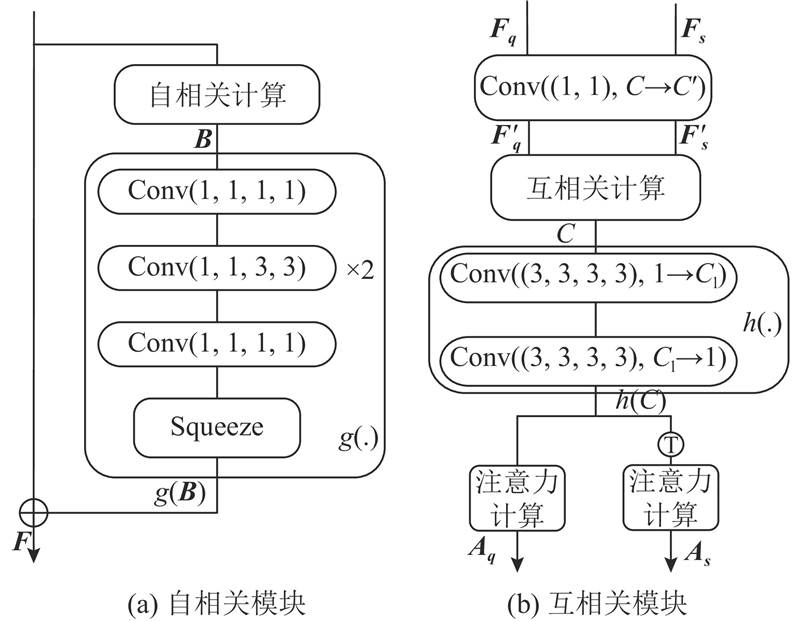
... 通过构造分类器来检测恶意流量. 提出基于关系嵌入的小样本物联网入侵检测方法,该方法采用基于度量[18 -19 ] 的学习策略,专门针对小样本学习场景来构建分类器. 度量学习的核心步骤通常包括提取样本的精确表示和通过度量函数进行分类. 采取同样的思想,设计度量框架,该度量框架专为网络流量分类量身定制. 通过计算样本的自相关表示和互相关表示,能够获得样本特征的精确表示,为后续的分类任务打下坚实基础. ...
1
... 通过构造分类器来检测恶意流量. 提出基于关系嵌入的小样本物联网入侵检测方法,该方法采用基于度量[18 -19 ] 的学习策略,专门针对小样本学习场景来构建分类器. 度量学习的核心步骤通常包括提取样本的精确表示和通过度量函数进行分类. 采取同样的思想,设计度量框架,该度量框架专为网络流量分类量身定制. 通过计算样本的自相关表示和互相关表示,能够获得样本特征的精确表示,为后续的分类任务打下坚实基础. ...
CICIoT2023: a real-time dataset and benchmark for large-scale attacks in IoT environment
1
2023
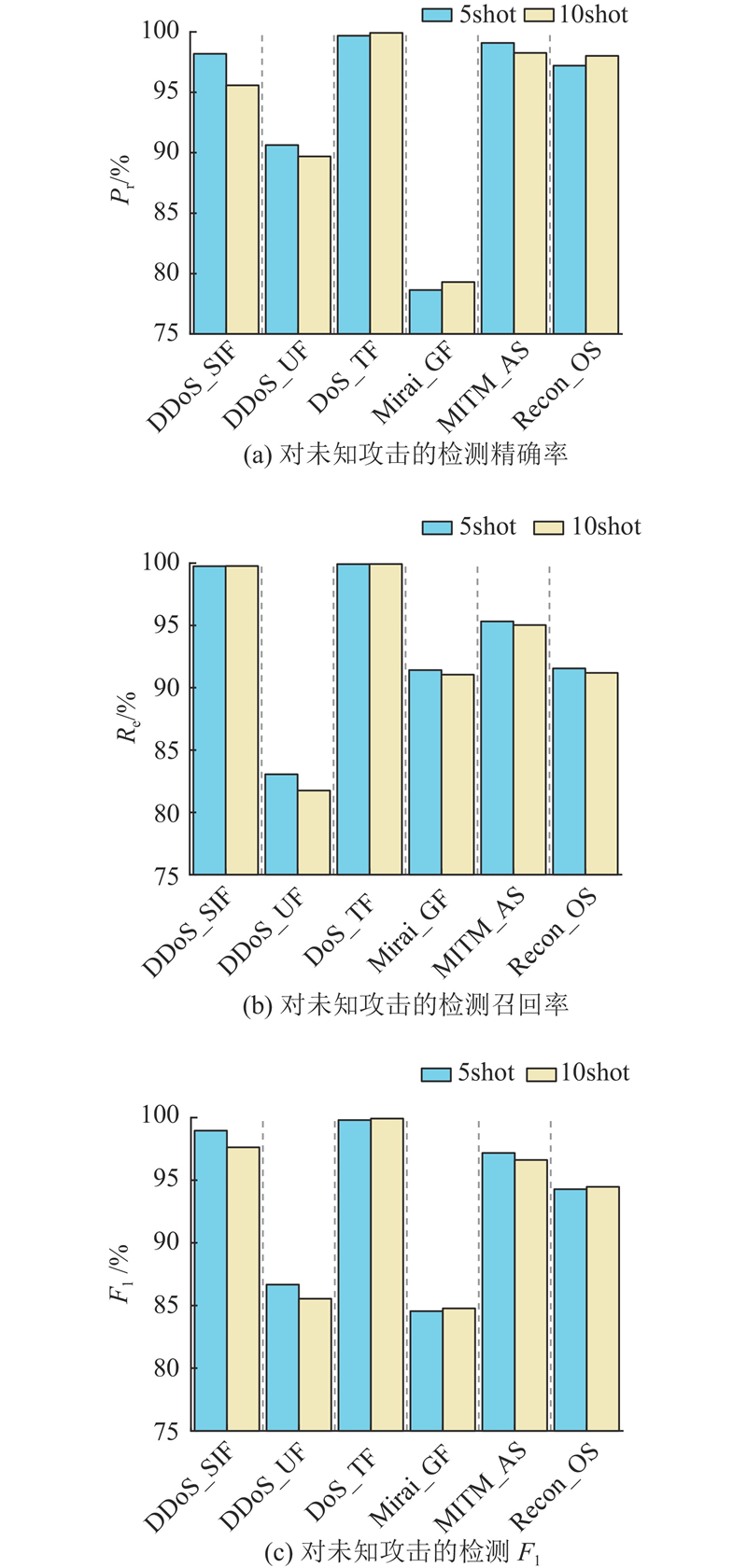
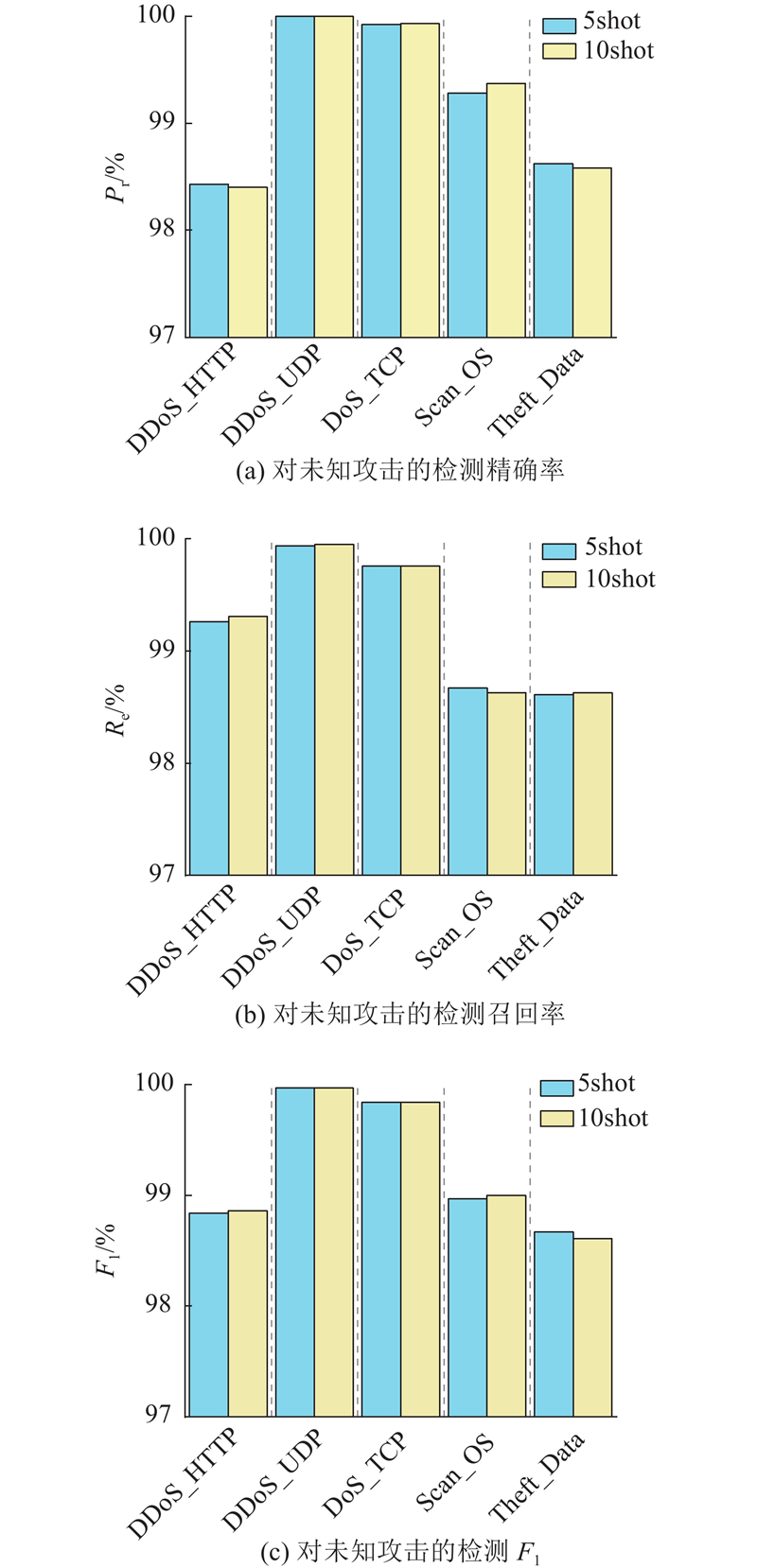
... 采用2个公开的数据集来评估本文模型,分别是来自加拿大网络安全研究所的CICIOT2023[20 ] 和来自新南威尔士大学的BotIoT[21 ] . ...
Towards the development of realistic botnet dataset in the Internet of Things for network forensic analytics: bot-IoT dataset
1
2019
... 采用2个公开的数据集来评估本文模型,分别是来自加拿大网络安全研究所的CICIOT2023[20 ] 和来自新南威尔士大学的BotIoT[21 ] . ...
1
... 为了能够更全面地与其他研究工作进行对比,在CICIDS2017[22 ] 数据集上开展对未知类别检测的实验. 选取CICIDS2017数据集中的5种攻击和良性流量作为实验对象. 为了满足5-way K-shot范式,每次选择一种攻击作为未知类别,对于每种设置,开展5组平行实验. 取5组实验的平均检测准确率作为最终的结果. ...
A few-shot learning based method for industrial Internet intrusion detection
3
2024
... 如表3 所示,从数据集、分类设置和准确率3个方面列举了其他研究人员的结果并比较. 其中,文献[8 ]与本文研究较类似,从数据集角度来看,Lu等[8 ] 对CSV中的样本进行处理,通过整理NSL-KDD、CICDDoS2019和CICIDS2017等5种数据集,构建适用于小样本物联网入侵检测的数据集,研究模型对未知类别样本检测的实验. 对PCAP中的样本进行处理,分别在CICIOT2023和BotIoT数据集上构建适用于小样本物联网入侵检测的数据集,并分别进行实验. 与文献[8 ]相同的是,最终都是将样本转换为更易处理的图像数据. 从小样本学习的技术路线来看,Lu等[8 -9 ] 遵循基于参数优化的元学习范式,Wang等[23 ] 与本研究基于度量学习框架. 从检测目标来看,Zhao等[24 -25 ] 使用基于深度学习的方法对已知类别攻击进行检测,本文方法主要针对未知类别攻击. 虽然对未知类别攻击的检测难度更高,但从结果来看,本文方法更优. ...
... Comparative analysis between proposed method and related works
Tab.3 方法 数据集 物联网数据集 实验设置 A c /%UTRS LNN[24 ] BotIoT Y N/A 96.15 0.0003 L2F+MAML[9 ] CICIDS2017 N 2-way 10-shot 94.66 10.00 MAML+CNN[8 ] FSIDSIOT Y 5-way 5-shot 89.64 28.91 MAML+CNN[8 ] FSIDSIOT Y 5-way 10-shot 92.19 18.16 IPN-IDS[23 ] CICIDS2017 N 5-way 5-shot 84.94 25.57 IPN-IDS [23 ] CICIDS2017 N 5-way 10-shot 86.35 15.21 CIDIOT[25 ] CICIOT2023 Y N/A 77.20 0.017 本文方法 CICIDS2017 N 5-way 5-shot 98.82 31.41 本文方法 CICIDS2017 N 5-way 10-shot 98.89 19.08 本文方法 BotIoT Y 5-way 5-shot 99.30 34.89 本文方法 BotIoT Y 5-way 10-shot 99.33 22.49 本文方法 CICIOT2023 Y 5-way 5-shot 93.50 29.91 本文方法 CICIOT2023 Y 5-way 10-shot 93.12 18.16
考虑现有的评估指标没有反映样本数量和未知攻击对检测准确率的影响,为了更好地评估基于相同数据集不同算法之间的差异,定义新的指标:未知威胁响应分数. ...
... [
23 ]
CICIDS2017 N 5-way 10-shot 86.35 15.21 CIDIOT[25 ] CICIOT2023 Y N/A 77.20 0.017 本文方法 CICIDS2017 N 5-way 5-shot 98.82 31.41 本文方法 CICIDS2017 N 5-way 10-shot 98.89 19.08 本文方法 BotIoT Y 5-way 5-shot 99.30 34.89 本文方法 BotIoT Y 5-way 10-shot 99.33 22.49 本文方法 CICIOT2023 Y 5-way 5-shot 93.50 29.91 本文方法 CICIOT2023 Y 5-way 10-shot 93.12 18.16 考虑现有的评估指标没有反映样本数量和未知攻击对检测准确率的影响,为了更好地评估基于相同数据集不同算法之间的差异,定义新的指标:未知威胁响应分数. ...
A novel intrusion detection method based on lightweight neural network for internet of things
2
2021
... 如表3 所示,从数据集、分类设置和准确率3个方面列举了其他研究人员的结果并比较. 其中,文献[8 ]与本文研究较类似,从数据集角度来看,Lu等[8 ] 对CSV中的样本进行处理,通过整理NSL-KDD、CICDDoS2019和CICIDS2017等5种数据集,构建适用于小样本物联网入侵检测的数据集,研究模型对未知类别样本检测的实验. 对PCAP中的样本进行处理,分别在CICIOT2023和BotIoT数据集上构建适用于小样本物联网入侵检测的数据集,并分别进行实验. 与文献[8 ]相同的是,最终都是将样本转换为更易处理的图像数据. 从小样本学习的技术路线来看,Lu等[8 -9 ] 遵循基于参数优化的元学习范式,Wang等[23 ] 与本研究基于度量学习框架. 从检测目标来看,Zhao等[24 -25 ] 使用基于深度学习的方法对已知类别攻击进行检测,本文方法主要针对未知类别攻击. 虽然对未知类别攻击的检测难度更高,但从结果来看,本文方法更优. ...
... Comparative analysis between proposed method and related works
Tab.3 方法 数据集 物联网数据集 实验设置 A c /%UTRS LNN[24 ] BotIoT Y N/A 96.15 0.0003 L2F+MAML[9 ] CICIDS2017 N 2-way 10-shot 94.66 10.00 MAML+CNN[8 ] FSIDSIOT Y 5-way 5-shot 89.64 28.91 MAML+CNN[8 ] FSIDSIOT Y 5-way 10-shot 92.19 18.16 IPN-IDS[23 ] CICIDS2017 N 5-way 5-shot 84.94 25.57 IPN-IDS [23 ] CICIDS2017 N 5-way 10-shot 86.35 15.21 CIDIOT[25 ] CICIOT2023 Y N/A 77.20 0.017 本文方法 CICIDS2017 N 5-way 5-shot 98.82 31.41 本文方法 CICIDS2017 N 5-way 10-shot 98.89 19.08 本文方法 BotIoT Y 5-way 5-shot 99.30 34.89 本文方法 BotIoT Y 5-way 10-shot 99.33 22.49 本文方法 CICIOT2023 Y 5-way 5-shot 93.50 29.91 本文方法 CICIOT2023 Y 5-way 10-shot 93.12 18.16
考虑现有的评估指标没有反映样本数量和未知攻击对检测准确率的影响,为了更好地评估基于相同数据集不同算法之间的差异,定义新的指标:未知威胁响应分数. ...
Privacy-preserving collaborative intrusion detection in edge of internet of things: a robust and efficient deep generative learning approach
2
2023
... 如表3 所示,从数据集、分类设置和准确率3个方面列举了其他研究人员的结果并比较. 其中,文献[8 ]与本文研究较类似,从数据集角度来看,Lu等[8 ] 对CSV中的样本进行处理,通过整理NSL-KDD、CICDDoS2019和CICIDS2017等5种数据集,构建适用于小样本物联网入侵检测的数据集,研究模型对未知类别样本检测的实验. 对PCAP中的样本进行处理,分别在CICIOT2023和BotIoT数据集上构建适用于小样本物联网入侵检测的数据集,并分别进行实验. 与文献[8 ]相同的是,最终都是将样本转换为更易处理的图像数据. 从小样本学习的技术路线来看,Lu等[8 -9 ] 遵循基于参数优化的元学习范式,Wang等[23 ] 与本研究基于度量学习框架. 从检测目标来看,Zhao等[24 -25 ] 使用基于深度学习的方法对已知类别攻击进行检测,本文方法主要针对未知类别攻击. 虽然对未知类别攻击的检测难度更高,但从结果来看,本文方法更优. ...
... Comparative analysis between proposed method and related works
Tab.3 方法 数据集 物联网数据集 实验设置 A c /%UTRS LNN[24 ] BotIoT Y N/A 96.15 0.0003 L2F+MAML[9 ] CICIDS2017 N 2-way 10-shot 94.66 10.00 MAML+CNN[8 ] FSIDSIOT Y 5-way 5-shot 89.64 28.91 MAML+CNN[8 ] FSIDSIOT Y 5-way 10-shot 92.19 18.16 IPN-IDS[23 ] CICIDS2017 N 5-way 5-shot 84.94 25.57 IPN-IDS [23 ] CICIDS2017 N 5-way 10-shot 86.35 15.21 CIDIOT[25 ] CICIOT2023 Y N/A 77.20 0.017 本文方法 CICIDS2017 N 5-way 5-shot 98.82 31.41 本文方法 CICIDS2017 N 5-way 10-shot 98.89 19.08 本文方法 BotIoT Y 5-way 5-shot 99.30 34.89 本文方法 BotIoT Y 5-way 10-shot 99.33 22.49 本文方法 CICIOT2023 Y 5-way 5-shot 93.50 29.91 本文方法 CICIOT2023 Y 5-way 10-shot 93.12 18.16
考虑现有的评估指标没有反映样本数量和未知攻击对检测准确率的影响,为了更好地评估基于相同数据集不同算法之间的差异,定义新的指标:未知威胁响应分数. ...