[1]
吴世娟. 崩塌落石对澜沧江跨越管道的影响及其防治研究 [D]. 成都: 西南石油大学, 2016.
[本文引用: 1]
WU Shijuan. Study on the impact of rockfalls on Lantsang crossing pipeline and their prevention measures [D]. Chengdu: Southwest Petroleum University, 2016.
[本文引用: 1]
[2]
王磊, 邓清禄, 杨辉建, 等 危岩体坠落冲击对输气管道影响的分析评价
[J]. 水文地质工程地质 , 2007 , 34 (5 ): 29 - 32
[本文引用: 1]
WANG Lei, DENG Qinglu, YANG Huijian, et al Evaluation on the safety of natural gas pipeline impacted by dangerous rock fall
[J]. Hydrogeology and Engineering Geology , 2007 , 34 (5 ): 29 - 32
[本文引用: 1]
[3]
张洪涛. 忠武输气管道地质灾害风险控制研究[D]. 青岛: 中国石油大学(华东), 2015.
[本文引用: 1]
ZHANG Hongtao. Risk control of the geological hazard for Zhongxian-Wuhan gas pipeline [D]. Qingdao: China University of Petroleum (East China), 2015.
[本文引用: 1]
[4]
王东源, 赵宇, 王成华 阳坝落石对输油管道的冲击分析
[J]. 自然灾害学报 , 2013 , 22 (3 ): 229 - 235
[本文引用: 1]
WANG Dongyuan, ZHAO Yu, WANG Chenghua Analysis of rockfall impact on buried oil pipeline at Yangba
[J]. Journal of Natural Disasters , 2013 , 22 (3 ): 229 - 235
[本文引用: 1]
[6]
JING H, DENG Q, HAO J, et al. Analysis and numerical simulation on dynamic response of buried pipeline caused by rock fall impaction [C]//Proceedings of the Volume 2: Pipeline Integrity Management . Calgary: ASME, 2012: 303-311.
[本文引用: 1]
[8]
DONG F, BIE X, TIAN J, et al Experimental and numerical study on the strain behavior of buried pipelines subjected to an impact load
[J]. Applied Sciences , 2019 , 9 (16 ): 3284
DOI:10.3390/app9163284
[本文引用: 2]
[9]
JIANG F, DONG S, ZHAO Y, et al Investigation on the deformation response of submarine pipelines subjected to impact loads by dropped objects
[J]. Ocean Engineering , 2019 , 194 : 106638
DOI:10.1016/j.oceaneng.2019.106638
[本文引用: 1]
[10]
TIAN J, ZHANG J, DONG F, et al Dynamic response of buried pipeline subject to impact loads using piezoceramic transducers
[J]. International Journal of Pressure Vessels and Piping , 2019 , 177 : 103984
DOI:10.1016/j.ijpvp.2019.103984
[本文引用: 1]
[11]
荆宏远. 落石冲击下浅埋管道动力学响应分析与模拟 [D]. 武汉: 中国地质大学, 2007.
[本文引用: 1]
JING Hongyuan. Analysis and numerical simulation on dynamic response of buried pipeline caused by rockfall impaction [D]. Wuhan: China University of Geosciences, 2007.
[本文引用: 1]
[12]
TAVAKOLI MEHRJARDI G, KARIMI M Numerical modeling of buried steel pipe subjected to impact load
[J]. Journal of Pipeline Systems Engineering and Practice , 2021 , 12 (4 ): 04021048
DOI:10.1061/(ASCE)PS.1949-1204.0000588
[本文引用: 2]
[13]
TAVAKOLI MEHRJARDI G, KAVANDI M, AMINI F, et al Large-scale experimental study of the response of steel buried pipe subjected to rockfall impacts
[J]. Journal of Pipeline Systems Engineering and Practice , 2024 , 15 (2 ): 04024011
DOI:10.1061/JPSEA2.PSENG-1572
[本文引用: 1]
[14]
朱治儒. 崩塌落石冲击埋地油气管道的模型试验及作用机理研究 [D]. 成都: 成都理工大学, 2021.
[本文引用: 2]
ZHU Zhiru. Model test and mechanism research of collapsing rocks impacting buried oil and gas pipelines [D]. Chengdu: Chengdu University of Technology, 2021.
[本文引用: 2]
[15]
王联伟. 几种在役管道典型地质灾害评价方法研究 [D]. 北京: 北京科技大学, 2015.
[本文引用: 1]
WANG Lianwei. Study on several typical geological disaster damage assessment method for in service pipelines [D]. Beijing: University of Science and Technology Beijing, 2015.
[本文引用: 1]
[16]
ZHANG J, LIANG Z, HAN C, et al Buckling behaviour analysis of a buried steel pipeline in rock stratum impacted by a rockfall
[J]. Engineering Failure Analysis , 2015 , 58 : 281 - 294
DOI:10.1016/j.engfailanal.2015.09.009
[本文引用: 1]
[17]
RAO P, WU Z, CUI J Analysis of deformation of adjacent buried pipeline under rockfall impact load
[J]. Geotechnical and Geological Engineering , 2022 , 40 (3 ): 1463 - 1474
DOI:10.1007/s10706-021-01975-w
[本文引用: 1]
[18]
熊健, 邓清禄, 张宏亮, 等 崩塌落石冲击荷载作用下埋地管道的安全评价
[J]. 安全与环境工程 , 2013 , 20 (1 ): 108 - 114
[本文引用: 1]
XIONG Jian, DENG Qinglu, ZHANG Hongliang, et al Safety assessment on the response of buried pipeline caused by rockfall impact load
[J]. Safety and Environmental Engineering , 2013 , 20 (1 ): 108 - 114
[本文引用: 1]
[19]
赵璐. 落石冲击作用下埋地输气管道的动力响应及极限分析 [D]. 成都: 西南石油大学, 2018.
[本文引用: 7]
ZHAO Lu. Dynamic response and limit analysis of buried gas pipeline under rockfall impact [D]. Chengdu: Southwest Petroleum University, 2018.
[本文引用: 7]
[21]
朱斌, 蒋楠, 贾永胜, 等 下穿燃气管道爆破振动效应现场试验研究
[J]. 岩石力学与工程学报 , 2019 , 38 (12 ): 2582 - 2592
[本文引用: 1]
ZHU Bin, JIANG Nan, JIA Yongsheng, et al Field experiment on blasting vibration effect of underpass gas pipelines
[J]. Chinese Journal of Rock Mechanics and Engineering , 2019 , 38 (12 ): 2582 - 2592
[本文引用: 1]
[22]
杨成. 建(构)筑物拆除塌落冲击作用下地铁隧道动力响应测试与仿真分析 [D]. 武汉: 江汉大学, 2023.
[本文引用: 1]
YANG Cheng. Dynamic response test and simulation analysis of subway tunnel under the impact of building (structure) demolition collapse [D]. Wuhan: Jianghan University, 2023.
[本文引用: 1]
[23]
WANG G L, QU S Y, HOU X M, et al. Preliminary study on vertical subsoil participating mass [J]. Advanced Materials Research , 2011, 199/200: 1429–1434.
[本文引用: 1]
[24]
American Lifelines Alliance. Guidelines for the design of buried steel pipe [R]. Reston: ASCE, 2001.
[本文引用: 1]
[25]
胡宗耀. 城区爆破振动影响下埋地HDPE排水管道振速安全阈值研究 [D]. 武汉: 中国地质大学(武汉), 2022.
[本文引用: 1]
HU Zongyao. Study on safety threshold of vibration velocity of buried HDPE drainage pipeline under the influence of blasting vibration in urban area [D]. Wuhan: China University of Geosciences, 2022.
[本文引用: 1]
[26]
张鹏, 安兆暾, 李虎 爆破塌落触地载荷下浅埋缺陷PE HD管道力学响应分析
[J]. 安全与环境学报 , 2023 , (6 ): 1844 - 1851
[本文引用: 1]
ZHANG Peng, AN Zhaotun, LI Hu Dynamic response of shallow-buried defect PE HD gas pipeline under touchdown load of blasting collapse
[J]. Journal of Safety and Environment , 2023 , (6 ): 1844 - 1851
[本文引用: 1]
[27]
董飞飞, 张东山, 田江平, 等 冲击载荷作用下埋地长输管道动力响应研究
[J]. 石油机械 , 2020 , 48 (1 ): 132 - 141
[本文引用: 6]
DONG Feifei, ZHANG Dongshan, TIAN Jiangping, et al Study on dynamic response of buried long distance pipeline under impact load
[J]. China Petroleum Machinery , 2020 , 48 (1 ): 132 - 141
[本文引用: 6]
[28]
张虎, 邵磊, 余成, 等 冲击荷载对埋地管道影响的试验与数值模拟研究
[J]. 地震工程与工程振动 , 2022 , 42 (3 ): 243 - 252
[本文引用: 6]
ZHANG Hu, SHAO Lei, YU Cheng, et al Experimental and numerical simulation study of impact loading on buried pipeline
[J]. Earthquake Engineering and Engineering Dynamics , 2022 , 42 (3 ): 243 - 252
[本文引用: 6]
[29]
YANKELEVSKY D Z, KARINSKI Y S, FELDGUN V R Re-examination of the shock wave’s peak pressure attenuation in soils
[J]. International Journal of Impact Engineering , 2011 , 38 (11 ): 864 - 881
DOI:10.1016/j.ijimpeng.2011.05.011
[本文引用: 1]
1
... 崩塌落石是山区常见的地质灾害之一,其携带的动能对基础设施和人民安全构成众多威胁. 我国西部山区的油气管网规模庞大,落石冲击管道事件时有发生[1 -2 ] ,轻则导致管道凹陷,重则引起油气泄露,导致灾难性的环境事故. 2005年4月,忠县-武汉顺溪段管道上方的混凝土盖板被崩塌落石砸穿,管道局部出现严重的内凹变形[3 ] . 2008年,汶川地震引起兰成渝管道康县段阳坝近1 000 m3 的崩塌,其中最大直径约为4 m、质量接近50 t的巨石将兰成渝管道接头砸开,造成柴油泄漏[4 ] . ...
1
... 崩塌落石是山区常见的地质灾害之一,其携带的动能对基础设施和人民安全构成众多威胁. 我国西部山区的油气管网规模庞大,落石冲击管道事件时有发生[1 -2 ] ,轻则导致管道凹陷,重则引起油气泄露,导致灾难性的环境事故. 2005年4月,忠县-武汉顺溪段管道上方的混凝土盖板被崩塌落石砸穿,管道局部出现严重的内凹变形[3 ] . 2008年,汶川地震引起兰成渝管道康县段阳坝近1 000 m3 的崩塌,其中最大直径约为4 m、质量接近50 t的巨石将兰成渝管道接头砸开,造成柴油泄漏[4 ] . ...
危岩体坠落冲击对输气管道影响的分析评价
1
2007
... 崩塌落石是山区常见的地质灾害之一,其携带的动能对基础设施和人民安全构成众多威胁. 我国西部山区的油气管网规模庞大,落石冲击管道事件时有发生[1 -2 ] ,轻则导致管道凹陷,重则引起油气泄露,导致灾难性的环境事故. 2005年4月,忠县-武汉顺溪段管道上方的混凝土盖板被崩塌落石砸穿,管道局部出现严重的内凹变形[3 ] . 2008年,汶川地震引起兰成渝管道康县段阳坝近1 000 m3 的崩塌,其中最大直径约为4 m、质量接近50 t的巨石将兰成渝管道接头砸开,造成柴油泄漏[4 ] . ...
危岩体坠落冲击对输气管道影响的分析评价
1
2007
... 崩塌落石是山区常见的地质灾害之一,其携带的动能对基础设施和人民安全构成众多威胁. 我国西部山区的油气管网规模庞大,落石冲击管道事件时有发生[1 -2 ] ,轻则导致管道凹陷,重则引起油气泄露,导致灾难性的环境事故. 2005年4月,忠县-武汉顺溪段管道上方的混凝土盖板被崩塌落石砸穿,管道局部出现严重的内凹变形[3 ] . 2008年,汶川地震引起兰成渝管道康县段阳坝近1 000 m3 的崩塌,其中最大直径约为4 m、质量接近50 t的巨石将兰成渝管道接头砸开,造成柴油泄漏[4 ] . ...
1
... 崩塌落石是山区常见的地质灾害之一,其携带的动能对基础设施和人民安全构成众多威胁. 我国西部山区的油气管网规模庞大,落石冲击管道事件时有发生[1 -2 ] ,轻则导致管道凹陷,重则引起油气泄露,导致灾难性的环境事故. 2005年4月,忠县-武汉顺溪段管道上方的混凝土盖板被崩塌落石砸穿,管道局部出现严重的内凹变形[3 ] . 2008年,汶川地震引起兰成渝管道康县段阳坝近1 000 m3 的崩塌,其中最大直径约为4 m、质量接近50 t的巨石将兰成渝管道接头砸开,造成柴油泄漏[4 ] . ...
1
... 崩塌落石是山区常见的地质灾害之一,其携带的动能对基础设施和人民安全构成众多威胁. 我国西部山区的油气管网规模庞大,落石冲击管道事件时有发生[1 -2 ] ,轻则导致管道凹陷,重则引起油气泄露,导致灾难性的环境事故. 2005年4月,忠县-武汉顺溪段管道上方的混凝土盖板被崩塌落石砸穿,管道局部出现严重的内凹变形[3 ] . 2008年,汶川地震引起兰成渝管道康县段阳坝近1 000 m3 的崩塌,其中最大直径约为4 m、质量接近50 t的巨石将兰成渝管道接头砸开,造成柴油泄漏[4 ] . ...
阳坝落石对输油管道的冲击分析
1
2013
... 崩塌落石是山区常见的地质灾害之一,其携带的动能对基础设施和人民安全构成众多威胁. 我国西部山区的油气管网规模庞大,落石冲击管道事件时有发生[1 -2 ] ,轻则导致管道凹陷,重则引起油气泄露,导致灾难性的环境事故. 2005年4月,忠县-武汉顺溪段管道上方的混凝土盖板被崩塌落石砸穿,管道局部出现严重的内凹变形[3 ] . 2008年,汶川地震引起兰成渝管道康县段阳坝近1 000 m3 的崩塌,其中最大直径约为4 m、质量接近50 t的巨石将兰成渝管道接头砸开,造成柴油泄漏[4 ] . ...
阳坝落石对输油管道的冲击分析
1
2013
... 崩塌落石是山区常见的地质灾害之一,其携带的动能对基础设施和人民安全构成众多威胁. 我国西部山区的油气管网规模庞大,落石冲击管道事件时有发生[1 -2 ] ,轻则导致管道凹陷,重则引起油气泄露,导致灾难性的环境事故. 2005年4月,忠县-武汉顺溪段管道上方的混凝土盖板被崩塌落石砸穿,管道局部出现严重的内凹变形[3 ] . 2008年,汶川地震引起兰成渝管道康县段阳坝近1 000 m3 的崩塌,其中最大直径约为4 m、质量接近50 t的巨石将兰成渝管道接头砸开,造成柴油泄漏[4 ] . ...
Loading of a gravel-buried steel pipe subjected to rockfall
1
2006
... 众多研究人员对落石冲击下的管道受力和变形开展了广泛的研究. Pichler等[5 -6 ] 采用有限元模拟,评估不同地表垫层厚度和不同落石冲击能条件下埋地钢管的受力情况. Liu等[7 ] 采用有限元方法,讨论管道-土壤相对刚度、管道埋深和冲击能对埋地管道应力分布的影响. Dong等[8 ] 开展落石冲击作用下埋地管道应变行为的缩尺实验和数值研究,从理论上推导了施加在土壤上的冲击载荷以及冲击载荷引起的埋地管道的应变. Jiang等[9 ] 通过缩尺实验和数值方法研究管道在掉落物体冲击载荷下的响应,开展广泛的参数研究,以调查各种因素的影响,包括掉落物体的速度、质量和形状、管道壁厚、混凝土涂层、内部压力和自由管道跨度长度. Tian等[10 ] 将嵌入式和表面黏结式压电陶瓷传感器用于冲击荷载下埋地管道的冲击力和加速度监测,通过缩尺模型试验探讨冲击能量、管道尺寸及管道埋深对管道动力响应的影响. 荆宏远[11 ] 分别从理论计算和数值仿真的角度,探讨落石冲击下管道的动力学响应,研究落石垂直冲击管道正上方时管体的极限承载力. Tavakoli Mehrjardi等[12 ] 使用有限元数值方法模拟埋地钢管在冲击荷载下的动力响应,评估管道埋深、落石高度、冲击区域大小和土壤阻尼等因素的影响. Tavakoli Mehrjardi等[13 ] 开展埋地钢管的落石冲击大尺度模型试验,研究落石的穿透深度、冲击力、管道圆周应变及管道竖向变形,以管道环向应力超过材料屈服应力作为管道失效的判别依据. 朱治儒等[14 -15 ] 设计落石冲击埋地钢管的足尺模型试验,针对不同的冲击高度,对管道应力及位移进行监测,研究不同高度落石冲击试验下埋地管道的力学响应. ...
1
... 众多研究人员对落石冲击下的管道受力和变形开展了广泛的研究. Pichler等[5 -6 ] 采用有限元模拟,评估不同地表垫层厚度和不同落石冲击能条件下埋地钢管的受力情况. Liu等[7 ] 采用有限元方法,讨论管道-土壤相对刚度、管道埋深和冲击能对埋地管道应力分布的影响. Dong等[8 ] 开展落石冲击作用下埋地管道应变行为的缩尺实验和数值研究,从理论上推导了施加在土壤上的冲击载荷以及冲击载荷引起的埋地管道的应变. Jiang等[9 ] 通过缩尺实验和数值方法研究管道在掉落物体冲击载荷下的响应,开展广泛的参数研究,以调查各种因素的影响,包括掉落物体的速度、质量和形状、管道壁厚、混凝土涂层、内部压力和自由管道跨度长度. Tian等[10 ] 将嵌入式和表面黏结式压电陶瓷传感器用于冲击荷载下埋地管道的冲击力和加速度监测,通过缩尺模型试验探讨冲击能量、管道尺寸及管道埋深对管道动力响应的影响. 荆宏远[11 ] 分别从理论计算和数值仿真的角度,探讨落石冲击下管道的动力学响应,研究落石垂直冲击管道正上方时管体的极限承载力. Tavakoli Mehrjardi等[12 ] 使用有限元数值方法模拟埋地钢管在冲击荷载下的动力响应,评估管道埋深、落石高度、冲击区域大小和土壤阻尼等因素的影响. Tavakoli Mehrjardi等[13 ] 开展埋地钢管的落石冲击大尺度模型试验,研究落石的穿透深度、冲击力、管道圆周应变及管道竖向变形,以管道环向应力超过材料屈服应力作为管道失效的判别依据. 朱治儒等[14 -15 ] 设计落石冲击埋地钢管的足尺模型试验,针对不同的冲击高度,对管道应力及位移进行监测,研究不同高度落石冲击试验下埋地管道的力学响应. ...
Modeling the behavior of natural gas pipeline impacted by falling objects
1
2014
... 众多研究人员对落石冲击下的管道受力和变形开展了广泛的研究. Pichler等[5 -6 ] 采用有限元模拟,评估不同地表垫层厚度和不同落石冲击能条件下埋地钢管的受力情况. Liu等[7 ] 采用有限元方法,讨论管道-土壤相对刚度、管道埋深和冲击能对埋地管道应力分布的影响. Dong等[8 ] 开展落石冲击作用下埋地管道应变行为的缩尺实验和数值研究,从理论上推导了施加在土壤上的冲击载荷以及冲击载荷引起的埋地管道的应变. Jiang等[9 ] 通过缩尺实验和数值方法研究管道在掉落物体冲击载荷下的响应,开展广泛的参数研究,以调查各种因素的影响,包括掉落物体的速度、质量和形状、管道壁厚、混凝土涂层、内部压力和自由管道跨度长度. Tian等[10 ] 将嵌入式和表面黏结式压电陶瓷传感器用于冲击荷载下埋地管道的冲击力和加速度监测,通过缩尺模型试验探讨冲击能量、管道尺寸及管道埋深对管道动力响应的影响. 荆宏远[11 ] 分别从理论计算和数值仿真的角度,探讨落石冲击下管道的动力学响应,研究落石垂直冲击管道正上方时管体的极限承载力. Tavakoli Mehrjardi等[12 ] 使用有限元数值方法模拟埋地钢管在冲击荷载下的动力响应,评估管道埋深、落石高度、冲击区域大小和土壤阻尼等因素的影响. Tavakoli Mehrjardi等[13 ] 开展埋地钢管的落石冲击大尺度模型试验,研究落石的穿透深度、冲击力、管道圆周应变及管道竖向变形,以管道环向应力超过材料屈服应力作为管道失效的判别依据. 朱治儒等[14 -15 ] 设计落石冲击埋地钢管的足尺模型试验,针对不同的冲击高度,对管道应力及位移进行监测,研究不同高度落石冲击试验下埋地管道的力学响应. ...
Experimental and numerical study on the strain behavior of buried pipelines subjected to an impact load
2
2019
... 众多研究人员对落石冲击下的管道受力和变形开展了广泛的研究. Pichler等[5 -6 ] 采用有限元模拟,评估不同地表垫层厚度和不同落石冲击能条件下埋地钢管的受力情况. Liu等[7 ] 采用有限元方法,讨论管道-土壤相对刚度、管道埋深和冲击能对埋地管道应力分布的影响. Dong等[8 ] 开展落石冲击作用下埋地管道应变行为的缩尺实验和数值研究,从理论上推导了施加在土壤上的冲击载荷以及冲击载荷引起的埋地管道的应变. Jiang等[9 ] 通过缩尺实验和数值方法研究管道在掉落物体冲击载荷下的响应,开展广泛的参数研究,以调查各种因素的影响,包括掉落物体的速度、质量和形状、管道壁厚、混凝土涂层、内部压力和自由管道跨度长度. Tian等[10 ] 将嵌入式和表面黏结式压电陶瓷传感器用于冲击荷载下埋地管道的冲击力和加速度监测,通过缩尺模型试验探讨冲击能量、管道尺寸及管道埋深对管道动力响应的影响. 荆宏远[11 ] 分别从理论计算和数值仿真的角度,探讨落石冲击下管道的动力学响应,研究落石垂直冲击管道正上方时管体的极限承载力. Tavakoli Mehrjardi等[12 ] 使用有限元数值方法模拟埋地钢管在冲击荷载下的动力响应,评估管道埋深、落石高度、冲击区域大小和土壤阻尼等因素的影响. Tavakoli Mehrjardi等[13 ] 开展埋地钢管的落石冲击大尺度模型试验,研究落石的穿透深度、冲击力、管道圆周应变及管道竖向变形,以管道环向应力超过材料屈服应力作为管道失效的判别依据. 朱治儒等[14 -15 ] 设计落石冲击埋地钢管的足尺模型试验,针对不同的冲击高度,对管道应力及位移进行监测,研究不同高度落石冲击试验下埋地管道的力学响应. ...
... 管道受落石正上方冲击时的环向应变[8 -12 ] 为 ...
Investigation on the deformation response of submarine pipelines subjected to impact loads by dropped objects
1
2019
... 众多研究人员对落石冲击下的管道受力和变形开展了广泛的研究. Pichler等[5 -6 ] 采用有限元模拟,评估不同地表垫层厚度和不同落石冲击能条件下埋地钢管的受力情况. Liu等[7 ] 采用有限元方法,讨论管道-土壤相对刚度、管道埋深和冲击能对埋地管道应力分布的影响. Dong等[8 ] 开展落石冲击作用下埋地管道应变行为的缩尺实验和数值研究,从理论上推导了施加在土壤上的冲击载荷以及冲击载荷引起的埋地管道的应变. Jiang等[9 ] 通过缩尺实验和数值方法研究管道在掉落物体冲击载荷下的响应,开展广泛的参数研究,以调查各种因素的影响,包括掉落物体的速度、质量和形状、管道壁厚、混凝土涂层、内部压力和自由管道跨度长度. Tian等[10 ] 将嵌入式和表面黏结式压电陶瓷传感器用于冲击荷载下埋地管道的冲击力和加速度监测,通过缩尺模型试验探讨冲击能量、管道尺寸及管道埋深对管道动力响应的影响. 荆宏远[11 ] 分别从理论计算和数值仿真的角度,探讨落石冲击下管道的动力学响应,研究落石垂直冲击管道正上方时管体的极限承载力. Tavakoli Mehrjardi等[12 ] 使用有限元数值方法模拟埋地钢管在冲击荷载下的动力响应,评估管道埋深、落石高度、冲击区域大小和土壤阻尼等因素的影响. Tavakoli Mehrjardi等[13 ] 开展埋地钢管的落石冲击大尺度模型试验,研究落石的穿透深度、冲击力、管道圆周应变及管道竖向变形,以管道环向应力超过材料屈服应力作为管道失效的判别依据. 朱治儒等[14 -15 ] 设计落石冲击埋地钢管的足尺模型试验,针对不同的冲击高度,对管道应力及位移进行监测,研究不同高度落石冲击试验下埋地管道的力学响应. ...
Dynamic response of buried pipeline subject to impact loads using piezoceramic transducers
1
2019
... 众多研究人员对落石冲击下的管道受力和变形开展了广泛的研究. Pichler等[5 -6 ] 采用有限元模拟,评估不同地表垫层厚度和不同落石冲击能条件下埋地钢管的受力情况. Liu等[7 ] 采用有限元方法,讨论管道-土壤相对刚度、管道埋深和冲击能对埋地管道应力分布的影响. Dong等[8 ] 开展落石冲击作用下埋地管道应变行为的缩尺实验和数值研究,从理论上推导了施加在土壤上的冲击载荷以及冲击载荷引起的埋地管道的应变. Jiang等[9 ] 通过缩尺实验和数值方法研究管道在掉落物体冲击载荷下的响应,开展广泛的参数研究,以调查各种因素的影响,包括掉落物体的速度、质量和形状、管道壁厚、混凝土涂层、内部压力和自由管道跨度长度. Tian等[10 ] 将嵌入式和表面黏结式压电陶瓷传感器用于冲击荷载下埋地管道的冲击力和加速度监测,通过缩尺模型试验探讨冲击能量、管道尺寸及管道埋深对管道动力响应的影响. 荆宏远[11 ] 分别从理论计算和数值仿真的角度,探讨落石冲击下管道的动力学响应,研究落石垂直冲击管道正上方时管体的极限承载力. Tavakoli Mehrjardi等[12 ] 使用有限元数值方法模拟埋地钢管在冲击荷载下的动力响应,评估管道埋深、落石高度、冲击区域大小和土壤阻尼等因素的影响. Tavakoli Mehrjardi等[13 ] 开展埋地钢管的落石冲击大尺度模型试验,研究落石的穿透深度、冲击力、管道圆周应变及管道竖向变形,以管道环向应力超过材料屈服应力作为管道失效的判别依据. 朱治儒等[14 -15 ] 设计落石冲击埋地钢管的足尺模型试验,针对不同的冲击高度,对管道应力及位移进行监测,研究不同高度落石冲击试验下埋地管道的力学响应. ...
1
... 众多研究人员对落石冲击下的管道受力和变形开展了广泛的研究. Pichler等[5 -6 ] 采用有限元模拟,评估不同地表垫层厚度和不同落石冲击能条件下埋地钢管的受力情况. Liu等[7 ] 采用有限元方法,讨论管道-土壤相对刚度、管道埋深和冲击能对埋地管道应力分布的影响. Dong等[8 ] 开展落石冲击作用下埋地管道应变行为的缩尺实验和数值研究,从理论上推导了施加在土壤上的冲击载荷以及冲击载荷引起的埋地管道的应变. Jiang等[9 ] 通过缩尺实验和数值方法研究管道在掉落物体冲击载荷下的响应,开展广泛的参数研究,以调查各种因素的影响,包括掉落物体的速度、质量和形状、管道壁厚、混凝土涂层、内部压力和自由管道跨度长度. Tian等[10 ] 将嵌入式和表面黏结式压电陶瓷传感器用于冲击荷载下埋地管道的冲击力和加速度监测,通过缩尺模型试验探讨冲击能量、管道尺寸及管道埋深对管道动力响应的影响. 荆宏远[11 ] 分别从理论计算和数值仿真的角度,探讨落石冲击下管道的动力学响应,研究落石垂直冲击管道正上方时管体的极限承载力. Tavakoli Mehrjardi等[12 ] 使用有限元数值方法模拟埋地钢管在冲击荷载下的动力响应,评估管道埋深、落石高度、冲击区域大小和土壤阻尼等因素的影响. Tavakoli Mehrjardi等[13 ] 开展埋地钢管的落石冲击大尺度模型试验,研究落石的穿透深度、冲击力、管道圆周应变及管道竖向变形,以管道环向应力超过材料屈服应力作为管道失效的判别依据. 朱治儒等[14 -15 ] 设计落石冲击埋地钢管的足尺模型试验,针对不同的冲击高度,对管道应力及位移进行监测,研究不同高度落石冲击试验下埋地管道的力学响应. ...
1
... 众多研究人员对落石冲击下的管道受力和变形开展了广泛的研究. Pichler等[5 -6 ] 采用有限元模拟,评估不同地表垫层厚度和不同落石冲击能条件下埋地钢管的受力情况. Liu等[7 ] 采用有限元方法,讨论管道-土壤相对刚度、管道埋深和冲击能对埋地管道应力分布的影响. Dong等[8 ] 开展落石冲击作用下埋地管道应变行为的缩尺实验和数值研究,从理论上推导了施加在土壤上的冲击载荷以及冲击载荷引起的埋地管道的应变. Jiang等[9 ] 通过缩尺实验和数值方法研究管道在掉落物体冲击载荷下的响应,开展广泛的参数研究,以调查各种因素的影响,包括掉落物体的速度、质量和形状、管道壁厚、混凝土涂层、内部压力和自由管道跨度长度. Tian等[10 ] 将嵌入式和表面黏结式压电陶瓷传感器用于冲击荷载下埋地管道的冲击力和加速度监测,通过缩尺模型试验探讨冲击能量、管道尺寸及管道埋深对管道动力响应的影响. 荆宏远[11 ] 分别从理论计算和数值仿真的角度,探讨落石冲击下管道的动力学响应,研究落石垂直冲击管道正上方时管体的极限承载力. Tavakoli Mehrjardi等[12 ] 使用有限元数值方法模拟埋地钢管在冲击荷载下的动力响应,评估管道埋深、落石高度、冲击区域大小和土壤阻尼等因素的影响. Tavakoli Mehrjardi等[13 ] 开展埋地钢管的落石冲击大尺度模型试验,研究落石的穿透深度、冲击力、管道圆周应变及管道竖向变形,以管道环向应力超过材料屈服应力作为管道失效的判别依据. 朱治儒等[14 -15 ] 设计落石冲击埋地钢管的足尺模型试验,针对不同的冲击高度,对管道应力及位移进行监测,研究不同高度落石冲击试验下埋地管道的力学响应. ...
Numerical modeling of buried steel pipe subjected to impact load
2
2021
... 众多研究人员对落石冲击下的管道受力和变形开展了广泛的研究. Pichler等[5 -6 ] 采用有限元模拟,评估不同地表垫层厚度和不同落石冲击能条件下埋地钢管的受力情况. Liu等[7 ] 采用有限元方法,讨论管道-土壤相对刚度、管道埋深和冲击能对埋地管道应力分布的影响. Dong等[8 ] 开展落石冲击作用下埋地管道应变行为的缩尺实验和数值研究,从理论上推导了施加在土壤上的冲击载荷以及冲击载荷引起的埋地管道的应变. Jiang等[9 ] 通过缩尺实验和数值方法研究管道在掉落物体冲击载荷下的响应,开展广泛的参数研究,以调查各种因素的影响,包括掉落物体的速度、质量和形状、管道壁厚、混凝土涂层、内部压力和自由管道跨度长度. Tian等[10 ] 将嵌入式和表面黏结式压电陶瓷传感器用于冲击荷载下埋地管道的冲击力和加速度监测,通过缩尺模型试验探讨冲击能量、管道尺寸及管道埋深对管道动力响应的影响. 荆宏远[11 ] 分别从理论计算和数值仿真的角度,探讨落石冲击下管道的动力学响应,研究落石垂直冲击管道正上方时管体的极限承载力. Tavakoli Mehrjardi等[12 ] 使用有限元数值方法模拟埋地钢管在冲击荷载下的动力响应,评估管道埋深、落石高度、冲击区域大小和土壤阻尼等因素的影响. Tavakoli Mehrjardi等[13 ] 开展埋地钢管的落石冲击大尺度模型试验,研究落石的穿透深度、冲击力、管道圆周应变及管道竖向变形,以管道环向应力超过材料屈服应力作为管道失效的判别依据. 朱治儒等[14 -15 ] 设计落石冲击埋地钢管的足尺模型试验,针对不同的冲击高度,对管道应力及位移进行监测,研究不同高度落石冲击试验下埋地管道的力学响应. ...
... 管道受落石正上方冲击时的环向应变[8 -12 ] 为 ...
Large-scale experimental study of the response of steel buried pipe subjected to rockfall impacts
1
2024
... 众多研究人员对落石冲击下的管道受力和变形开展了广泛的研究. Pichler等[5 -6 ] 采用有限元模拟,评估不同地表垫层厚度和不同落石冲击能条件下埋地钢管的受力情况. Liu等[7 ] 采用有限元方法,讨论管道-土壤相对刚度、管道埋深和冲击能对埋地管道应力分布的影响. Dong等[8 ] 开展落石冲击作用下埋地管道应变行为的缩尺实验和数值研究,从理论上推导了施加在土壤上的冲击载荷以及冲击载荷引起的埋地管道的应变. Jiang等[9 ] 通过缩尺实验和数值方法研究管道在掉落物体冲击载荷下的响应,开展广泛的参数研究,以调查各种因素的影响,包括掉落物体的速度、质量和形状、管道壁厚、混凝土涂层、内部压力和自由管道跨度长度. Tian等[10 ] 将嵌入式和表面黏结式压电陶瓷传感器用于冲击荷载下埋地管道的冲击力和加速度监测,通过缩尺模型试验探讨冲击能量、管道尺寸及管道埋深对管道动力响应的影响. 荆宏远[11 ] 分别从理论计算和数值仿真的角度,探讨落石冲击下管道的动力学响应,研究落石垂直冲击管道正上方时管体的极限承载力. Tavakoli Mehrjardi等[12 ] 使用有限元数值方法模拟埋地钢管在冲击荷载下的动力响应,评估管道埋深、落石高度、冲击区域大小和土壤阻尼等因素的影响. Tavakoli Mehrjardi等[13 ] 开展埋地钢管的落石冲击大尺度模型试验,研究落石的穿透深度、冲击力、管道圆周应变及管道竖向变形,以管道环向应力超过材料屈服应力作为管道失效的判别依据. 朱治儒等[14 -15 ] 设计落石冲击埋地钢管的足尺模型试验,针对不同的冲击高度,对管道应力及位移进行监测,研究不同高度落石冲击试验下埋地管道的力学响应. ...
2
... 众多研究人员对落石冲击下的管道受力和变形开展了广泛的研究. Pichler等[5 -6 ] 采用有限元模拟,评估不同地表垫层厚度和不同落石冲击能条件下埋地钢管的受力情况. Liu等[7 ] 采用有限元方法,讨论管道-土壤相对刚度、管道埋深和冲击能对埋地管道应力分布的影响. Dong等[8 ] 开展落石冲击作用下埋地管道应变行为的缩尺实验和数值研究,从理论上推导了施加在土壤上的冲击载荷以及冲击载荷引起的埋地管道的应变. Jiang等[9 ] 通过缩尺实验和数值方法研究管道在掉落物体冲击载荷下的响应,开展广泛的参数研究,以调查各种因素的影响,包括掉落物体的速度、质量和形状、管道壁厚、混凝土涂层、内部压力和自由管道跨度长度. Tian等[10 ] 将嵌入式和表面黏结式压电陶瓷传感器用于冲击荷载下埋地管道的冲击力和加速度监测,通过缩尺模型试验探讨冲击能量、管道尺寸及管道埋深对管道动力响应的影响. 荆宏远[11 ] 分别从理论计算和数值仿真的角度,探讨落石冲击下管道的动力学响应,研究落石垂直冲击管道正上方时管体的极限承载力. Tavakoli Mehrjardi等[12 ] 使用有限元数值方法模拟埋地钢管在冲击荷载下的动力响应,评估管道埋深、落石高度、冲击区域大小和土壤阻尼等因素的影响. Tavakoli Mehrjardi等[13 ] 开展埋地钢管的落石冲击大尺度模型试验,研究落石的穿透深度、冲击力、管道圆周应变及管道竖向变形,以管道环向应力超过材料屈服应力作为管道失效的判别依据. 朱治儒等[14 -15 ] 设计落石冲击埋地钢管的足尺模型试验,针对不同的冲击高度,对管道应力及位移进行监测,研究不同高度落石冲击试验下埋地管道的力学响应. ...
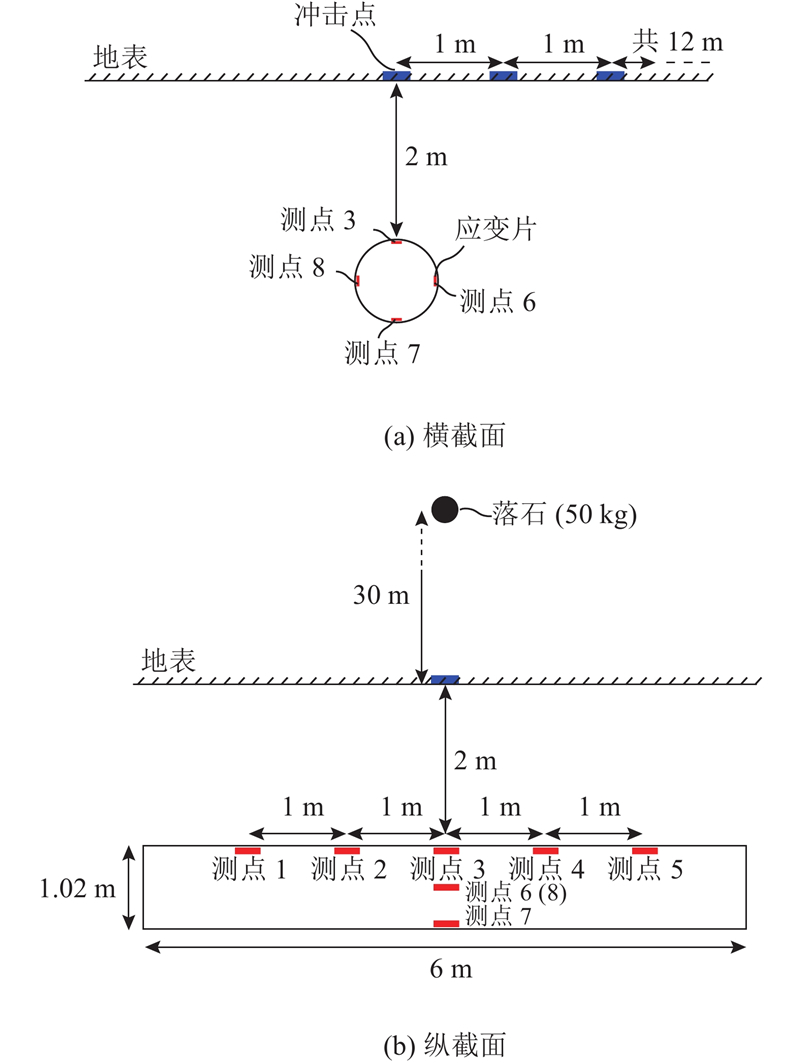
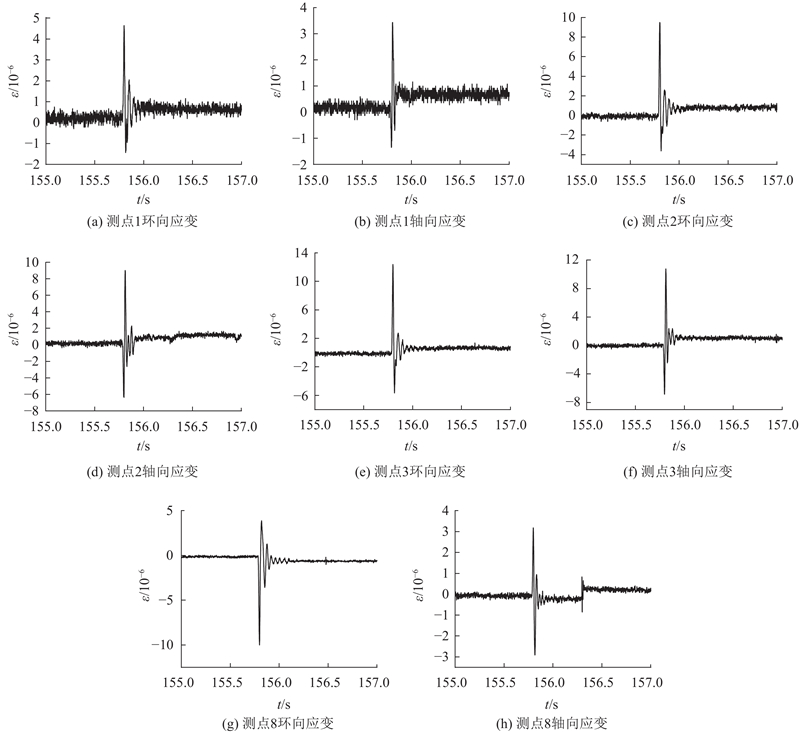
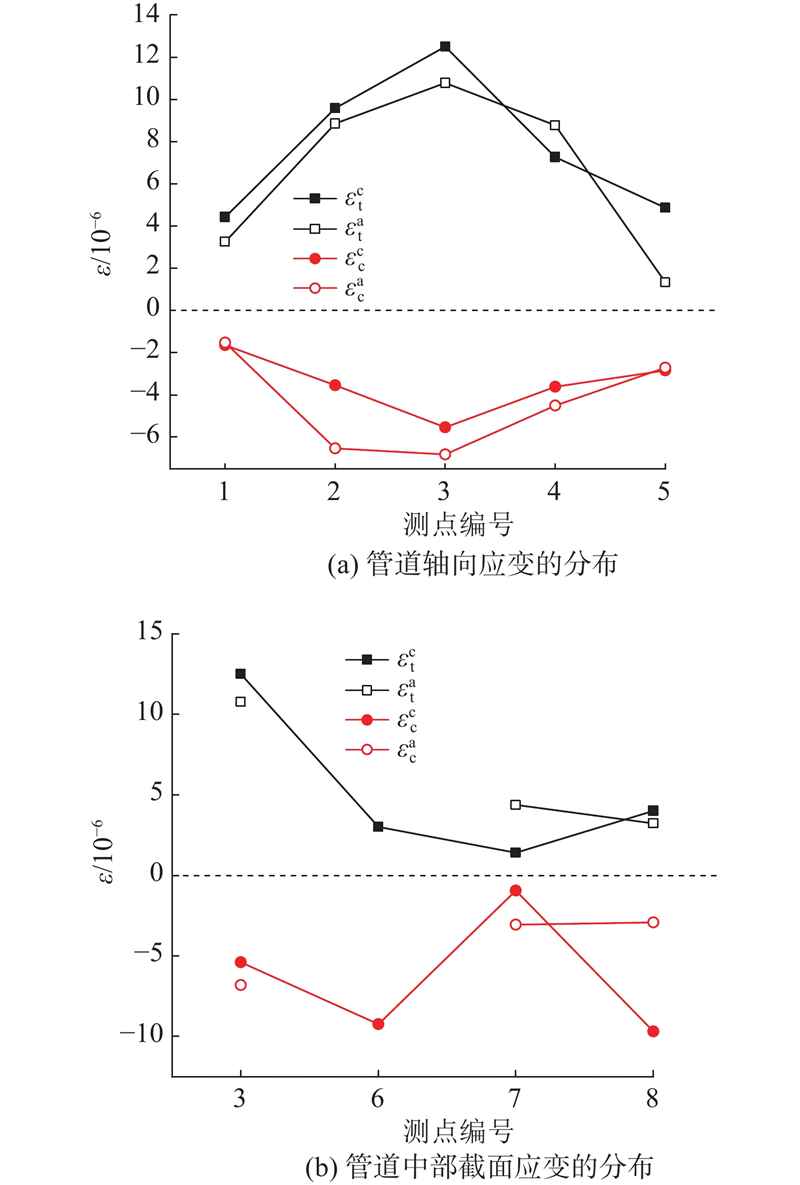
... 不考虑落石直接刺穿管壁的特殊情况,埋地油气管道在落石冲击下的失效模式主要为局部屈曲变形(椭圆化)[14 ] . 管道动态应变为本试验的主要监测项目,通过在管道内壁粘贴不同方向的应变片进行测量. 试验中所用的应变片为单轴50 mm,120 Ω型号的应变片,接1/4桥,经屏蔽线缆与DH8302动态信号采集仪相连,采样频率为2 kHz. 应变监测点共有8处,4处在管道中部截面沿环向分布,4处在管道顶部对称于中部截面沿轴向分布. 每处监测点分别布置环向应变片和轴向应变片共16个,具体如图1 所示. 对于采集到的应变时程曲线,利用低通滤波法去除高频噪声. 截止频率设为1 kHz,远大于一般埋地钢管的振动主频[21 -22 ] ,保留了有效信息. ...
2
... 众多研究人员对落石冲击下的管道受力和变形开展了广泛的研究. Pichler等[5 -6 ] 采用有限元模拟,评估不同地表垫层厚度和不同落石冲击能条件下埋地钢管的受力情况. Liu等[7 ] 采用有限元方法,讨论管道-土壤相对刚度、管道埋深和冲击能对埋地管道应力分布的影响. Dong等[8 ] 开展落石冲击作用下埋地管道应变行为的缩尺实验和数值研究,从理论上推导了施加在土壤上的冲击载荷以及冲击载荷引起的埋地管道的应变. Jiang等[9 ] 通过缩尺实验和数值方法研究管道在掉落物体冲击载荷下的响应,开展广泛的参数研究,以调查各种因素的影响,包括掉落物体的速度、质量和形状、管道壁厚、混凝土涂层、内部压力和自由管道跨度长度. Tian等[10 ] 将嵌入式和表面黏结式压电陶瓷传感器用于冲击荷载下埋地管道的冲击力和加速度监测,通过缩尺模型试验探讨冲击能量、管道尺寸及管道埋深对管道动力响应的影响. 荆宏远[11 ] 分别从理论计算和数值仿真的角度,探讨落石冲击下管道的动力学响应,研究落石垂直冲击管道正上方时管体的极限承载力. Tavakoli Mehrjardi等[12 ] 使用有限元数值方法模拟埋地钢管在冲击荷载下的动力响应,评估管道埋深、落石高度、冲击区域大小和土壤阻尼等因素的影响. Tavakoli Mehrjardi等[13 ] 开展埋地钢管的落石冲击大尺度模型试验,研究落石的穿透深度、冲击力、管道圆周应变及管道竖向变形,以管道环向应力超过材料屈服应力作为管道失效的判别依据. 朱治儒等[14 -15 ] 设计落石冲击埋地钢管的足尺模型试验,针对不同的冲击高度,对管道应力及位移进行监测,研究不同高度落石冲击试验下埋地管道的力学响应. ...
... 不考虑落石直接刺穿管壁的特殊情况,埋地油气管道在落石冲击下的失效模式主要为局部屈曲变形(椭圆化)[14 ] . 管道动态应变为本试验的主要监测项目,通过在管道内壁粘贴不同方向的应变片进行测量. 试验中所用的应变片为单轴50 mm,120 Ω型号的应变片,接1/4桥,经屏蔽线缆与DH8302动态信号采集仪相连,采样频率为2 kHz. 应变监测点共有8处,4处在管道中部截面沿环向分布,4处在管道顶部对称于中部截面沿轴向分布. 每处监测点分别布置环向应变片和轴向应变片共16个,具体如图1 所示. 对于采集到的应变时程曲线,利用低通滤波法去除高频噪声. 截止频率设为1 kHz,远大于一般埋地钢管的振动主频[21 -22 ] ,保留了有效信息. ...
1
... 众多研究人员对落石冲击下的管道受力和变形开展了广泛的研究. Pichler等[5 -6 ] 采用有限元模拟,评估不同地表垫层厚度和不同落石冲击能条件下埋地钢管的受力情况. Liu等[7 ] 采用有限元方法,讨论管道-土壤相对刚度、管道埋深和冲击能对埋地管道应力分布的影响. Dong等[8 ] 开展落石冲击作用下埋地管道应变行为的缩尺实验和数值研究,从理论上推导了施加在土壤上的冲击载荷以及冲击载荷引起的埋地管道的应变. Jiang等[9 ] 通过缩尺实验和数值方法研究管道在掉落物体冲击载荷下的响应,开展广泛的参数研究,以调查各种因素的影响,包括掉落物体的速度、质量和形状、管道壁厚、混凝土涂层、内部压力和自由管道跨度长度. Tian等[10 ] 将嵌入式和表面黏结式压电陶瓷传感器用于冲击荷载下埋地管道的冲击力和加速度监测,通过缩尺模型试验探讨冲击能量、管道尺寸及管道埋深对管道动力响应的影响. 荆宏远[11 ] 分别从理论计算和数值仿真的角度,探讨落石冲击下管道的动力学响应,研究落石垂直冲击管道正上方时管体的极限承载力. Tavakoli Mehrjardi等[12 ] 使用有限元数值方法模拟埋地钢管在冲击荷载下的动力响应,评估管道埋深、落石高度、冲击区域大小和土壤阻尼等因素的影响. Tavakoli Mehrjardi等[13 ] 开展埋地钢管的落石冲击大尺度模型试验,研究落石的穿透深度、冲击力、管道圆周应变及管道竖向变形,以管道环向应力超过材料屈服应力作为管道失效的判别依据. 朱治儒等[14 -15 ] 设计落石冲击埋地钢管的足尺模型试验,针对不同的冲击高度,对管道应力及位移进行监测,研究不同高度落石冲击试验下埋地管道的力学响应. ...
1
... 众多研究人员对落石冲击下的管道受力和变形开展了广泛的研究. Pichler等[5 -6 ] 采用有限元模拟,评估不同地表垫层厚度和不同落石冲击能条件下埋地钢管的受力情况. Liu等[7 ] 采用有限元方法,讨论管道-土壤相对刚度、管道埋深和冲击能对埋地管道应力分布的影响. Dong等[8 ] 开展落石冲击作用下埋地管道应变行为的缩尺实验和数值研究,从理论上推导了施加在土壤上的冲击载荷以及冲击载荷引起的埋地管道的应变. Jiang等[9 ] 通过缩尺实验和数值方法研究管道在掉落物体冲击载荷下的响应,开展广泛的参数研究,以调查各种因素的影响,包括掉落物体的速度、质量和形状、管道壁厚、混凝土涂层、内部压力和自由管道跨度长度. Tian等[10 ] 将嵌入式和表面黏结式压电陶瓷传感器用于冲击荷载下埋地管道的冲击力和加速度监测,通过缩尺模型试验探讨冲击能量、管道尺寸及管道埋深对管道动力响应的影响. 荆宏远[11 ] 分别从理论计算和数值仿真的角度,探讨落石冲击下管道的动力学响应,研究落石垂直冲击管道正上方时管体的极限承载力. Tavakoli Mehrjardi等[12 ] 使用有限元数值方法模拟埋地钢管在冲击荷载下的动力响应,评估管道埋深、落石高度、冲击区域大小和土壤阻尼等因素的影响. Tavakoli Mehrjardi等[13 ] 开展埋地钢管的落石冲击大尺度模型试验,研究落石的穿透深度、冲击力、管道圆周应变及管道竖向变形,以管道环向应力超过材料屈服应力作为管道失效的判别依据. 朱治儒等[14 -15 ] 设计落石冲击埋地钢管的足尺模型试验,针对不同的冲击高度,对管道应力及位移进行监测,研究不同高度落石冲击试验下埋地管道的力学响应. ...
Buckling behaviour analysis of a buried steel pipeline in rock stratum impacted by a rockfall
1
2015
... 落石冲击埋地钢管的研究多采用缩尺试验和有限元模拟方法,相应的足尺试验研究较少. 缩尺试验可能受到尺度效应的影响,而数值模拟方法有待足尺试验数据的进一步验证. 目前,研究人员已开展广泛的参数研究,但很少讨论管-石偏距这一变量,特别是考虑到一定的管-石偏距可能更符合实际情况. Zhang等[16 ] 模拟埋地管道受立方体落石冲击时的屈曲行为,讨论冲击速度、埋深、岩石高度和底面积以及管-石偏距对埋地管道应力和塑性应变的影响,研究结果显示,管道凹陷的长度和宽度随着管-石偏距的增大而减小. Rao等[17 ] 借助经验公式和理论推导,分析管径、壁厚、埋深、落石冲击速度和管-石偏距对埋地管道变形的影响规律,结果表明,当管-石偏距大于2 m时,管道的竖向位移随着偏距的增大而明显减小. 熊健等[18 ] 运用LS-DYNA显式动力学分析软件,建立崩塌落石冲击作用下埋地管道的三维有限元模型,研究落石规模、管道尺寸和埋深及管-石偏距等因素对埋地管道安全的影响规律,采用三次多项式拟合得到管顶应力与管-石偏距的关系,但这一关系仅适用于单一特定条件,普适性不足. 结果显示,当管-石偏距超过1.5 m时,管顶应力下降了一个数量级. 赵璐[19 ] 运用有限元软件,研究落石冲击作用下埋地输气管道的动力响应及管道临界失效准则,给出在特定的冲击速度和管道埋深条件下不同典型落石体积对应的管-石安全临界偏距. ...
Analysis of deformation of adjacent buried pipeline under rockfall impact load
1
2022
... 落石冲击埋地钢管的研究多采用缩尺试验和有限元模拟方法,相应的足尺试验研究较少. 缩尺试验可能受到尺度效应的影响,而数值模拟方法有待足尺试验数据的进一步验证. 目前,研究人员已开展广泛的参数研究,但很少讨论管-石偏距这一变量,特别是考虑到一定的管-石偏距可能更符合实际情况. Zhang等[16 ] 模拟埋地管道受立方体落石冲击时的屈曲行为,讨论冲击速度、埋深、岩石高度和底面积以及管-石偏距对埋地管道应力和塑性应变的影响,研究结果显示,管道凹陷的长度和宽度随着管-石偏距的增大而减小. Rao等[17 ] 借助经验公式和理论推导,分析管径、壁厚、埋深、落石冲击速度和管-石偏距对埋地管道变形的影响规律,结果表明,当管-石偏距大于2 m时,管道的竖向位移随着偏距的增大而明显减小. 熊健等[18 ] 运用LS-DYNA显式动力学分析软件,建立崩塌落石冲击作用下埋地管道的三维有限元模型,研究落石规模、管道尺寸和埋深及管-石偏距等因素对埋地管道安全的影响规律,采用三次多项式拟合得到管顶应力与管-石偏距的关系,但这一关系仅适用于单一特定条件,普适性不足. 结果显示,当管-石偏距超过1.5 m时,管顶应力下降了一个数量级. 赵璐[19 ] 运用有限元软件,研究落石冲击作用下埋地输气管道的动力响应及管道临界失效准则,给出在特定的冲击速度和管道埋深条件下不同典型落石体积对应的管-石安全临界偏距. ...
崩塌落石冲击荷载作用下埋地管道的安全评价
1
2013
... 落石冲击埋地钢管的研究多采用缩尺试验和有限元模拟方法,相应的足尺试验研究较少. 缩尺试验可能受到尺度效应的影响,而数值模拟方法有待足尺试验数据的进一步验证. 目前,研究人员已开展广泛的参数研究,但很少讨论管-石偏距这一变量,特别是考虑到一定的管-石偏距可能更符合实际情况. Zhang等[16 ] 模拟埋地管道受立方体落石冲击时的屈曲行为,讨论冲击速度、埋深、岩石高度和底面积以及管-石偏距对埋地管道应力和塑性应变的影响,研究结果显示,管道凹陷的长度和宽度随着管-石偏距的增大而减小. Rao等[17 ] 借助经验公式和理论推导,分析管径、壁厚、埋深、落石冲击速度和管-石偏距对埋地管道变形的影响规律,结果表明,当管-石偏距大于2 m时,管道的竖向位移随着偏距的增大而明显减小. 熊健等[18 ] 运用LS-DYNA显式动力学分析软件,建立崩塌落石冲击作用下埋地管道的三维有限元模型,研究落石规模、管道尺寸和埋深及管-石偏距等因素对埋地管道安全的影响规律,采用三次多项式拟合得到管顶应力与管-石偏距的关系,但这一关系仅适用于单一特定条件,普适性不足. 结果显示,当管-石偏距超过1.5 m时,管顶应力下降了一个数量级. 赵璐[19 ] 运用有限元软件,研究落石冲击作用下埋地输气管道的动力响应及管道临界失效准则,给出在特定的冲击速度和管道埋深条件下不同典型落石体积对应的管-石安全临界偏距. ...
崩塌落石冲击荷载作用下埋地管道的安全评价
1
2013
... 落石冲击埋地钢管的研究多采用缩尺试验和有限元模拟方法,相应的足尺试验研究较少. 缩尺试验可能受到尺度效应的影响,而数值模拟方法有待足尺试验数据的进一步验证. 目前,研究人员已开展广泛的参数研究,但很少讨论管-石偏距这一变量,特别是考虑到一定的管-石偏距可能更符合实际情况. Zhang等[16 ] 模拟埋地管道受立方体落石冲击时的屈曲行为,讨论冲击速度、埋深、岩石高度和底面积以及管-石偏距对埋地管道应力和塑性应变的影响,研究结果显示,管道凹陷的长度和宽度随着管-石偏距的增大而减小. Rao等[17 ] 借助经验公式和理论推导,分析管径、壁厚、埋深、落石冲击速度和管-石偏距对埋地管道变形的影响规律,结果表明,当管-石偏距大于2 m时,管道的竖向位移随着偏距的增大而明显减小. 熊健等[18 ] 运用LS-DYNA显式动力学分析软件,建立崩塌落石冲击作用下埋地管道的三维有限元模型,研究落石规模、管道尺寸和埋深及管-石偏距等因素对埋地管道安全的影响规律,采用三次多项式拟合得到管顶应力与管-石偏距的关系,但这一关系仅适用于单一特定条件,普适性不足. 结果显示,当管-石偏距超过1.5 m时,管顶应力下降了一个数量级. 赵璐[19 ] 运用有限元软件,研究落石冲击作用下埋地输气管道的动力响应及管道临界失效准则,给出在特定的冲击速度和管道埋深条件下不同典型落石体积对应的管-石安全临界偏距. ...
7
... 落石冲击埋地钢管的研究多采用缩尺试验和有限元模拟方法,相应的足尺试验研究较少. 缩尺试验可能受到尺度效应的影响,而数值模拟方法有待足尺试验数据的进一步验证. 目前,研究人员已开展广泛的参数研究,但很少讨论管-石偏距这一变量,特别是考虑到一定的管-石偏距可能更符合实际情况. Zhang等[16 ] 模拟埋地管道受立方体落石冲击时的屈曲行为,讨论冲击速度、埋深、岩石高度和底面积以及管-石偏距对埋地管道应力和塑性应变的影响,研究结果显示,管道凹陷的长度和宽度随着管-石偏距的增大而减小. Rao等[17 ] 借助经验公式和理论推导,分析管径、壁厚、埋深、落石冲击速度和管-石偏距对埋地管道变形的影响规律,结果表明,当管-石偏距大于2 m时,管道的竖向位移随着偏距的增大而明显减小. 熊健等[18 ] 运用LS-DYNA显式动力学分析软件,建立崩塌落石冲击作用下埋地管道的三维有限元模型,研究落石规模、管道尺寸和埋深及管-石偏距等因素对埋地管道安全的影响规律,采用三次多项式拟合得到管顶应力与管-石偏距的关系,但这一关系仅适用于单一特定条件,普适性不足. 结果显示,当管-石偏距超过1.5 m时,管顶应力下降了一个数量级. 赵璐[19 ] 运用有限元软件,研究落石冲击作用下埋地输气管道的动力响应及管道临界失效准则,给出在特定的冲击速度和管道埋深条件下不同典型落石体积对应的管-石安全临界偏距. ...
... 赵璐[19 ] 选取不同的管-石偏距,对落石(正方体和球体)冲击埋地输气管道进行有限元模拟计算,绘制了管道失效时的管-石临界偏距与落石动能之间的关系曲线,但未给出具体的表达式. 文献[19 ]中,管道管材为X80,直径为1.219 m,壁厚为0.015 3 m,埋深为0.8 m,内压为10 MPa,弹性模量为210 GPa,屈服强度为614 MPa. 将上述相关参数代入式(10),以落石质量和下落高度为横纵坐标,可得空间曲面,如图9 所示. 曲面上的任意点为相应落石质量和高度下的管-石临界偏距. 临界偏距与落石质量或下落高度呈上升速率逐渐变缓的正相关关系. 根据动能与重力势能的能量守恒关系,将文献[19 ]的落石动能转换为落石质量与下落高度,将对应的临界偏距绘制于图9 中. 从图9 可见,由式(10)表征的临界偏距与文献[19 ]的数值计算结果吻合良好. ...
... 选取不同的管-石偏距,对落石(正方体和球体)冲击埋地输气管道进行有限元模拟计算,绘制了管道失效时的管-石临界偏距与落石动能之间的关系曲线,但未给出具体的表达式. 文献[19 ]中,管道管材为X80,直径为1.219 m,壁厚为0.015 3 m,埋深为0.8 m,内压为10 MPa,弹性模量为210 GPa,屈服强度为614 MPa. 将上述相关参数代入式(10),以落石质量和下落高度为横纵坐标,可得空间曲面,如图9 所示. 曲面上的任意点为相应落石质量和高度下的管-石临界偏距. 临界偏距与落石质量或下落高度呈上升速率逐渐变缓的正相关关系. 根据动能与重力势能的能量守恒关系,将文献[19 ]的落石动能转换为落石质量与下落高度,将对应的临界偏距绘制于图9 中. 从图9 可见,由式(10)表征的临界偏距与文献[19 ]的数值计算结果吻合良好. ...
... 所示. 曲面上的任意点为相应落石质量和高度下的管-石临界偏距. 临界偏距与落石质量或下落高度呈上升速率逐渐变缓的正相关关系. 根据动能与重力势能的能量守恒关系,将文献[19 ]的落石动能转换为落石质量与下落高度,将对应的临界偏距绘制于图9 中. 从图9 可见,由式(10)表征的临界偏距与文献[19 ]的数值计算结果吻合良好. ...
... 可见,由式(10)表征的临界偏距与文献[19 ]的数值计算结果吻合良好. ...
... 文献[19 ]中所得管-石临界偏距与式(10)计算结果的对比 ...
... Comparison between critical pipe-rock offset distance in reference [19 ] and calculated result from equation (10) ...
7
... 落石冲击埋地钢管的研究多采用缩尺试验和有限元模拟方法,相应的足尺试验研究较少. 缩尺试验可能受到尺度效应的影响,而数值模拟方法有待足尺试验数据的进一步验证. 目前,研究人员已开展广泛的参数研究,但很少讨论管-石偏距这一变量,特别是考虑到一定的管-石偏距可能更符合实际情况. Zhang等[16 ] 模拟埋地管道受立方体落石冲击时的屈曲行为,讨论冲击速度、埋深、岩石高度和底面积以及管-石偏距对埋地管道应力和塑性应变的影响,研究结果显示,管道凹陷的长度和宽度随着管-石偏距的增大而减小. Rao等[17 ] 借助经验公式和理论推导,分析管径、壁厚、埋深、落石冲击速度和管-石偏距对埋地管道变形的影响规律,结果表明,当管-石偏距大于2 m时,管道的竖向位移随着偏距的增大而明显减小. 熊健等[18 ] 运用LS-DYNA显式动力学分析软件,建立崩塌落石冲击作用下埋地管道的三维有限元模型,研究落石规模、管道尺寸和埋深及管-石偏距等因素对埋地管道安全的影响规律,采用三次多项式拟合得到管顶应力与管-石偏距的关系,但这一关系仅适用于单一特定条件,普适性不足. 结果显示,当管-石偏距超过1.5 m时,管顶应力下降了一个数量级. 赵璐[19 ] 运用有限元软件,研究落石冲击作用下埋地输气管道的动力响应及管道临界失效准则,给出在特定的冲击速度和管道埋深条件下不同典型落石体积对应的管-石安全临界偏距. ...
... 赵璐[19 ] 选取不同的管-石偏距,对落石(正方体和球体)冲击埋地输气管道进行有限元模拟计算,绘制了管道失效时的管-石临界偏距与落石动能之间的关系曲线,但未给出具体的表达式. 文献[19 ]中,管道管材为X80,直径为1.219 m,壁厚为0.015 3 m,埋深为0.8 m,内压为10 MPa,弹性模量为210 GPa,屈服强度为614 MPa. 将上述相关参数代入式(10),以落石质量和下落高度为横纵坐标,可得空间曲面,如图9 所示. 曲面上的任意点为相应落石质量和高度下的管-石临界偏距. 临界偏距与落石质量或下落高度呈上升速率逐渐变缓的正相关关系. 根据动能与重力势能的能量守恒关系,将文献[19 ]的落石动能转换为落石质量与下落高度,将对应的临界偏距绘制于图9 中. 从图9 可见,由式(10)表征的临界偏距与文献[19 ]的数值计算结果吻合良好. ...
... 选取不同的管-石偏距,对落石(正方体和球体)冲击埋地输气管道进行有限元模拟计算,绘制了管道失效时的管-石临界偏距与落石动能之间的关系曲线,但未给出具体的表达式. 文献[19 ]中,管道管材为X80,直径为1.219 m,壁厚为0.015 3 m,埋深为0.8 m,内压为10 MPa,弹性模量为210 GPa,屈服强度为614 MPa. 将上述相关参数代入式(10),以落石质量和下落高度为横纵坐标,可得空间曲面,如图9 所示. 曲面上的任意点为相应落石质量和高度下的管-石临界偏距. 临界偏距与落石质量或下落高度呈上升速率逐渐变缓的正相关关系. 根据动能与重力势能的能量守恒关系,将文献[19 ]的落石动能转换为落石质量与下落高度,将对应的临界偏距绘制于图9 中. 从图9 可见,由式(10)表征的临界偏距与文献[19 ]的数值计算结果吻合良好. ...
... 所示. 曲面上的任意点为相应落石质量和高度下的管-石临界偏距. 临界偏距与落石质量或下落高度呈上升速率逐渐变缓的正相关关系. 根据动能与重力势能的能量守恒关系,将文献[19 ]的落石动能转换为落石质量与下落高度,将对应的临界偏距绘制于图9 中. 从图9 可见,由式(10)表征的临界偏距与文献[19 ]的数值计算结果吻合良好. ...
... 可见,由式(10)表征的临界偏距与文献[19 ]的数值计算结果吻合良好. ...
... 文献[19 ]中所得管-石临界偏距与式(10)计算结果的对比 ...
... Comparison between critical pipe-rock offset distance in reference [19 ] and calculated result from equation (10) ...
Experimental study on the maximum impact force by rock fall
2
2018
... 落石冲击埋地管道的足尺模型试验位于武汉市江汉大学野外试验场,场地平整开阔,长×宽为100 m×60 m,周围无既有建(构)筑物. 场地内为平整的黏性土层,经现场钻孔与土样检测,土壤天然密度约为1.84 g/cm3 ,弹性模量约为10 MPa,黏聚力为55 kPa,内摩擦角为15°,接近完全饱和. 结合试验场的实际条件,落石质量拟设为50 kg,从30 m高度自由落体冲击地面. 管-石偏距设为0~12 m. 试验未考虑落石形状、下落姿态及滚动旋转的影响. 为了工程应用的简便起见,在各类落石冲击力的经验或半经验计算公式中,上述因素的影响一般均忽略[20 ] . 在试验中,落石由普通硅酸盐水泥浇筑的球形混凝土球简化模拟. 采用汽车起重机将落石吊升至试验高度,待姿态稳定后,远程激活遥控式吊钩自动脱钩,使落石自由落体,冲击地面. 试验选用的钢管为双面埋弧焊螺旋管,钢号为Q235B,外径为1.02 m,壁厚为0.01 m,总长为6 m. 双面埋弧焊螺旋管被广泛应用于我国西气东输油气长输管道的工程中. 根据调研可知,西气东输管道一般埋深为1~ 4 m,因地形、地质和水文条件而变化. 综合成本和安全因素,试验钢管埋深取常见值2 m. 落石冲击点位于管道中部截面与地面的相交线上. 为了最大程度地减小多次实验对土层原状条件的影响,落石冲击试验由远及近依次进行. 管-石偏距是本试验主要关注的管道动态响应的影响因素. ...
... 当落石垂直冲击地面时,冲击力可由下式[20 ] 计算得到: ...
下穿燃气管道爆破振动效应现场试验研究
1
2019
... 不考虑落石直接刺穿管壁的特殊情况,埋地油气管道在落石冲击下的失效模式主要为局部屈曲变形(椭圆化)[14 ] . 管道动态应变为本试验的主要监测项目,通过在管道内壁粘贴不同方向的应变片进行测量. 试验中所用的应变片为单轴50 mm,120 Ω型号的应变片,接1/4桥,经屏蔽线缆与DH8302动态信号采集仪相连,采样频率为2 kHz. 应变监测点共有8处,4处在管道中部截面沿环向分布,4处在管道顶部对称于中部截面沿轴向分布. 每处监测点分别布置环向应变片和轴向应变片共16个,具体如图1 所示. 对于采集到的应变时程曲线,利用低通滤波法去除高频噪声. 截止频率设为1 kHz,远大于一般埋地钢管的振动主频[21 -22 ] ,保留了有效信息. ...
下穿燃气管道爆破振动效应现场试验研究
1
2019
... 不考虑落石直接刺穿管壁的特殊情况,埋地油气管道在落石冲击下的失效模式主要为局部屈曲变形(椭圆化)[14 ] . 管道动态应变为本试验的主要监测项目,通过在管道内壁粘贴不同方向的应变片进行测量. 试验中所用的应变片为单轴50 mm,120 Ω型号的应变片,接1/4桥,经屏蔽线缆与DH8302动态信号采集仪相连,采样频率为2 kHz. 应变监测点共有8处,4处在管道中部截面沿环向分布,4处在管道顶部对称于中部截面沿轴向分布. 每处监测点分别布置环向应变片和轴向应变片共16个,具体如图1 所示. 对于采集到的应变时程曲线,利用低通滤波法去除高频噪声. 截止频率设为1 kHz,远大于一般埋地钢管的振动主频[21 -22 ] ,保留了有效信息. ...
1
... 不考虑落石直接刺穿管壁的特殊情况,埋地油气管道在落石冲击下的失效模式主要为局部屈曲变形(椭圆化)[14 ] . 管道动态应变为本试验的主要监测项目,通过在管道内壁粘贴不同方向的应变片进行测量. 试验中所用的应变片为单轴50 mm,120 Ω型号的应变片,接1/4桥,经屏蔽线缆与DH8302动态信号采集仪相连,采样频率为2 kHz. 应变监测点共有8处,4处在管道中部截面沿环向分布,4处在管道顶部对称于中部截面沿轴向分布. 每处监测点分别布置环向应变片和轴向应变片共16个,具体如图1 所示. 对于采集到的应变时程曲线,利用低通滤波法去除高频噪声. 截止频率设为1 kHz,远大于一般埋地钢管的振动主频[21 -22 ] ,保留了有效信息. ...
1
... 不考虑落石直接刺穿管壁的特殊情况,埋地油气管道在落石冲击下的失效模式主要为局部屈曲变形(椭圆化)[14 ] . 管道动态应变为本试验的主要监测项目,通过在管道内壁粘贴不同方向的应变片进行测量. 试验中所用的应变片为单轴50 mm,120 Ω型号的应变片,接1/4桥,经屏蔽线缆与DH8302动态信号采集仪相连,采样频率为2 kHz. 应变监测点共有8处,4处在管道中部截面沿环向分布,4处在管道顶部对称于中部截面沿轴向分布. 每处监测点分别布置环向应变片和轴向应变片共16个,具体如图1 所示. 对于采集到的应变时程曲线,利用低通滤波法去除高频噪声. 截止频率设为1 kHz,远大于一般埋地钢管的振动主频[21 -22 ] ,保留了有效信息. ...
1
... 钢管受落石正上方冲击时的冲击荷载按下式[23 -24 ] 计算: ...
1
... 钢管受落石正上方冲击时的冲击荷载按下式[23 -24 ] 计算: ...
1
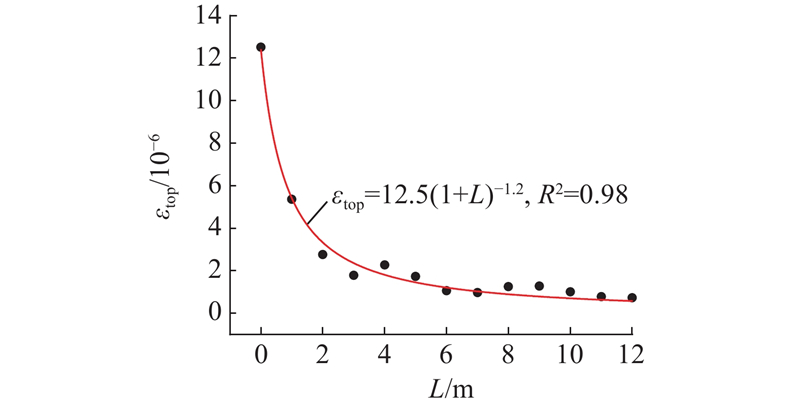
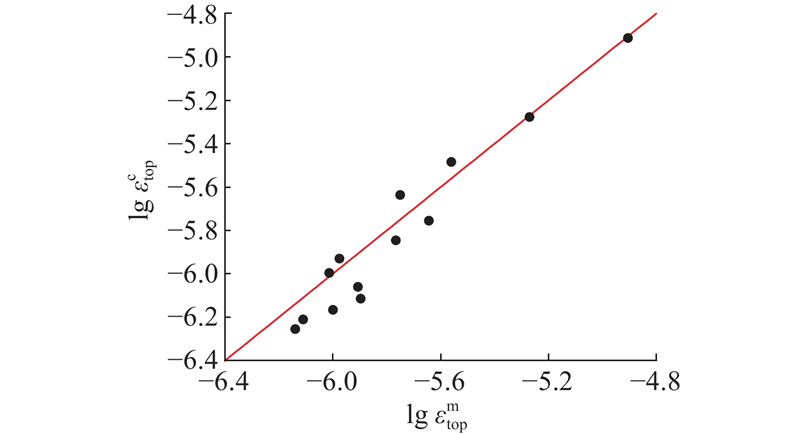
... 将本试验的相关参数代入式(7),计算得到$\varepsilon _{\mathrm{top}} $ L = 0−6 ,与实测应变(12.5 × 10−6 )的误差约为3%. 如图7 所示为不同管-石偏距下的管道顶部实测应变$ \varepsilon^{\mathrm{m}}_{{\mathrm{top}}} $ $\varepsilon _{\mathrm{top}}^{\mathrm{c}} $ [25 ] ;管道内压的增加会增大管线系统的整体刚度,减小冲击力作用下的弯曲变形,从而使附加荷载引起的管身应力不断减小[26 ] . 式(7)对应的空管无内压条件代表了最危险情况,从管道安全评估的角度而言,符合工程实践中偏保守的取值. ...
1
... 将本试验的相关参数代入式(7),计算得到$\varepsilon _{\mathrm{top}} $ L = 0−6 ,与实测应变(12.5 × 10−6 )的误差约为3%. 如图7 所示为不同管-石偏距下的管道顶部实测应变$ \varepsilon^{\mathrm{m}}_{{\mathrm{top}}} $ $\varepsilon _{\mathrm{top}}^{\mathrm{c}} $ [25 ] ;管道内压的增加会增大管线系统的整体刚度,减小冲击力作用下的弯曲变形,从而使附加荷载引起的管身应力不断减小[26 ] . 式(7)对应的空管无内压条件代表了最危险情况,从管道安全评估的角度而言,符合工程实践中偏保守的取值. ...
爆破塌落触地载荷下浅埋缺陷PE HD管道力学响应分析
1
2023
... 将本试验的相关参数代入式(7),计算得到$\varepsilon _{\mathrm{top}} $ L = 0−6 ,与实测应变(12.5 × 10−6 )的误差约为3%. 如图7 所示为不同管-石偏距下的管道顶部实测应变$ \varepsilon^{\mathrm{m}}_{{\mathrm{top}}} $ $\varepsilon _{\mathrm{top}}^{\mathrm{c}} $ [25 ] ;管道内压的增加会增大管线系统的整体刚度,减小冲击力作用下的弯曲变形,从而使附加荷载引起的管身应力不断减小[26 ] . 式(7)对应的空管无内压条件代表了最危险情况,从管道安全评估的角度而言,符合工程实践中偏保守的取值. ...
爆破塌落触地载荷下浅埋缺陷PE HD管道力学响应分析
1
2023
... 将本试验的相关参数代入式(7),计算得到$\varepsilon _{\mathrm{top}} $ L = 0−6 ,与实测应变(12.5 × 10−6 )的误差约为3%. 如图7 所示为不同管-石偏距下的管道顶部实测应变$ \varepsilon^{\mathrm{m}}_{{\mathrm{top}}} $ $\varepsilon _{\mathrm{top}}^{\mathrm{c}} $ [25 ] ;管道内压的增加会增大管线系统的整体刚度,减小冲击力作用下的弯曲变形,从而使附加荷载引起的管身应力不断减小[26 ] . 式(7)对应的空管无内压条件代表了最危险情况,从管道安全评估的角度而言,符合工程实践中偏保守的取值. ...
冲击载荷作用下埋地长输管道动力响应研究
6
2020
... 为了进一步验证式(7)的适用性,对比了研究人员既有室内试验数据[27 -28 ] 与式(7)的计算结果. 董飞飞等[27 ] 开展埋地管道的室内缩尺冲击试验:管道试件为Q235级镀锌钢管,外径和壁厚分别为0.114、0.002 5 m,埋深为0.6 m. 试验在尺寸为3 m×3 m×1.5 m的土箱中进行,土体为粉质黏土. 落石冲击荷载由落石冲击试验机进行模拟,设有4种落石高度(0.5、1.0、1.5、2.0 m)以及3种冲击偏移距离(0、0.75、1.5 m). 由于未给出具体的土体变形模量,考虑土体性质与本文接近,E s 取10 MPa,α 取1.2. 张虎等[28 ] 在同样的土箱中进行缩尺试验:外径为0.139 m,壁厚为0.002 5 m,长度为2.8 m的Q235级钢管,埋深为0.5 m,落石冲击高度为2.0 m,冲击偏移距离为0、0.3、0.6 m;土体为压实的细砂. 根据经验,E s 取30 MPa,α 取1.5、2.5、3.5进行比对. 将相关参数代入式(7)进行计算. ...
... [27 ]开展埋地管道的室内缩尺冲击试验:管道试件为Q235级镀锌钢管,外径和壁厚分别为0.114、0.002 5 m,埋深为0.6 m. 试验在尺寸为3 m×3 m×1.5 m的土箱中进行,土体为粉质黏土. 落石冲击荷载由落石冲击试验机进行模拟,设有4种落石高度(0.5、1.0、1.5、2.0 m)以及3种冲击偏移距离(0、0.75、1.5 m). 由于未给出具体的土体变形模量,考虑土体性质与本文接近,E s 取10 MPa,α 取1.2. 张虎等[28 ] 在同样的土箱中进行缩尺试验:外径为0.139 m,壁厚为0.002 5 m,长度为2.8 m的Q235级钢管,埋深为0.5 m,落石冲击高度为2.0 m,冲击偏移距离为0、0.3、0.6 m;土体为压实的细砂. 根据经验,E s 取30 MPa,α 取1.5、2.5、3.5进行比对. 将相关参数代入式(7)进行计算. ...
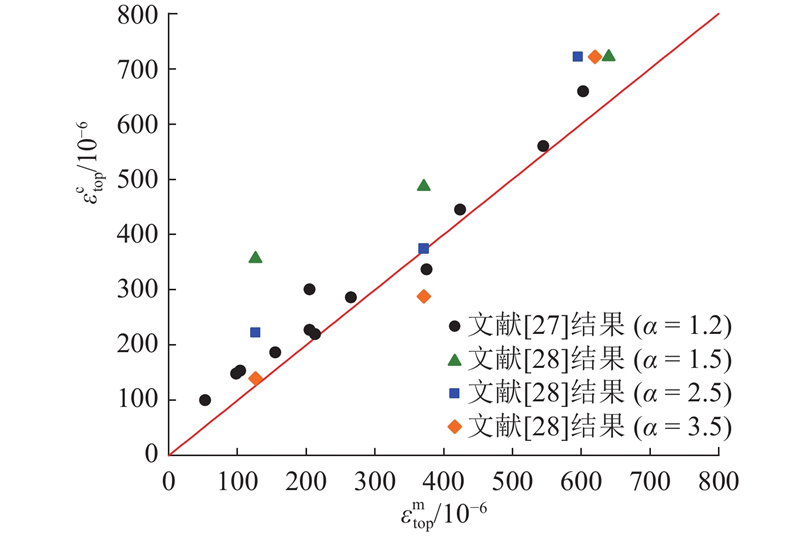
... 如图8 所示为试验数据与式(7)计算结果的对比情况. 可见,式(7)与文献[27 ]的缩尺试验结果具有良好的吻合度. 当α 取2.5~3.5时,式(7)可以较好地表征细砂土中的应变测试结果[28 ] 及其随管-石偏距的衰减趋势. 在相同条件下,α 越大,则管道顶部应变随管-石偏距的衰减程度越大,表明土壤对落石冲击应力波的耗散能力越强. 图8 表明,与粉质黏土相比,细砂具有更强的应力波耗散能力,这与爆炸应力波领域的相关研究[29 ] 相似,反映式(7)具有一定的广泛性. ...
... 文献[27 , 28 ]的室内试验结果与式(7)计算结果的对比 ...
... Comparison of measured strain from published indoor test[27 -28 ] and calculated strain from equation (7) ...
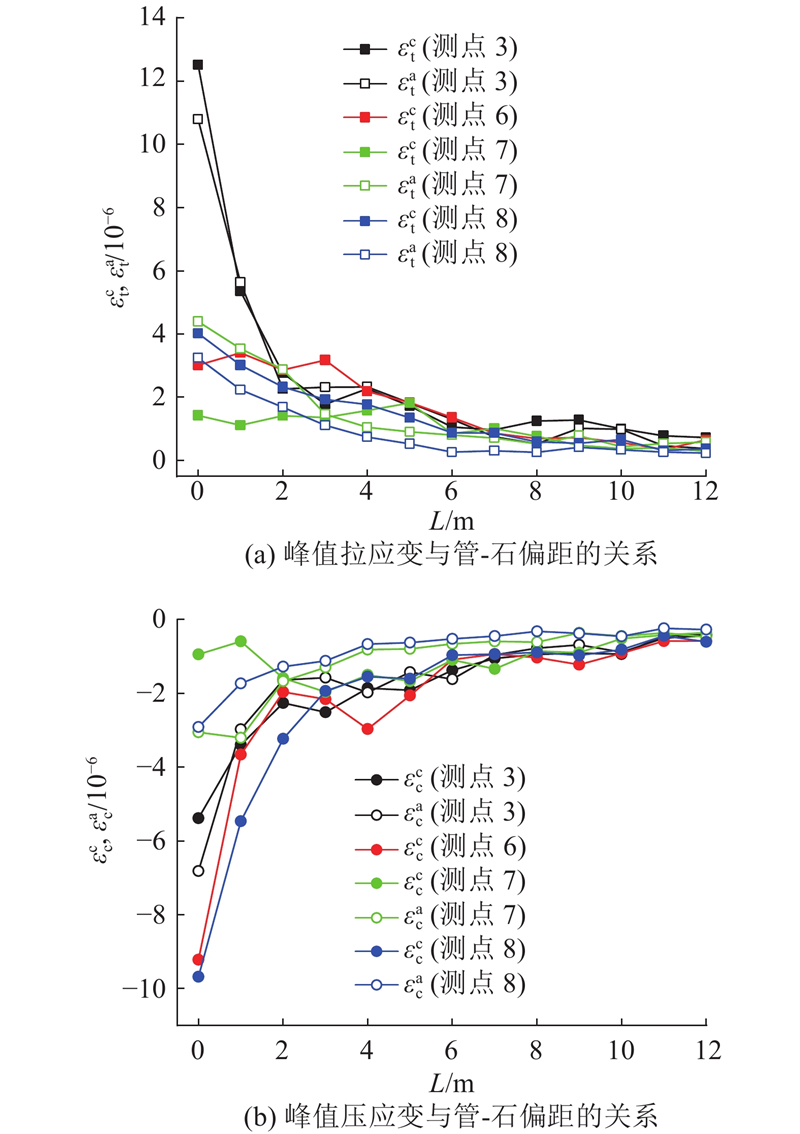
... (2) 管道顶部应变$\varepsilon _{\mathrm{top}} $ $\varepsilon _{\mathrm{top}} $ f (1+L )且指数为−α 的幂函数. α 越大表明土壤对落石冲击应力波的耗散能力越强,该幂函数关系与足尺模型试验结果和文献[27 , 28 ]的室内试验结果吻合良好. 在本文足尺模型试验的条件下,当L 从0 m增加至2 m时,$\varepsilon _{\mathrm{top}} $ −6 迅速降低至3×10−6 ,说明将管-石偏距控制在2 m是减小管道动力响应的有效措施. ...
冲击载荷作用下埋地长输管道动力响应研究
6
2020
... 为了进一步验证式(7)的适用性,对比了研究人员既有室内试验数据[27 -28 ] 与式(7)的计算结果. 董飞飞等[27 ] 开展埋地管道的室内缩尺冲击试验:管道试件为Q235级镀锌钢管,外径和壁厚分别为0.114、0.002 5 m,埋深为0.6 m. 试验在尺寸为3 m×3 m×1.5 m的土箱中进行,土体为粉质黏土. 落石冲击荷载由落石冲击试验机进行模拟,设有4种落石高度(0.5、1.0、1.5、2.0 m)以及3种冲击偏移距离(0、0.75、1.5 m). 由于未给出具体的土体变形模量,考虑土体性质与本文接近,E s 取10 MPa,α 取1.2. 张虎等[28 ] 在同样的土箱中进行缩尺试验:外径为0.139 m,壁厚为0.002 5 m,长度为2.8 m的Q235级钢管,埋深为0.5 m,落石冲击高度为2.0 m,冲击偏移距离为0、0.3、0.6 m;土体为压实的细砂. 根据经验,E s 取30 MPa,α 取1.5、2.5、3.5进行比对. 将相关参数代入式(7)进行计算. ...
... [27 ]开展埋地管道的室内缩尺冲击试验:管道试件为Q235级镀锌钢管,外径和壁厚分别为0.114、0.002 5 m,埋深为0.6 m. 试验在尺寸为3 m×3 m×1.5 m的土箱中进行,土体为粉质黏土. 落石冲击荷载由落石冲击试验机进行模拟,设有4种落石高度(0.5、1.0、1.5、2.0 m)以及3种冲击偏移距离(0、0.75、1.5 m). 由于未给出具体的土体变形模量,考虑土体性质与本文接近,E s 取10 MPa,α 取1.2. 张虎等[28 ] 在同样的土箱中进行缩尺试验:外径为0.139 m,壁厚为0.002 5 m,长度为2.8 m的Q235级钢管,埋深为0.5 m,落石冲击高度为2.0 m,冲击偏移距离为0、0.3、0.6 m;土体为压实的细砂. 根据经验,E s 取30 MPa,α 取1.5、2.5、3.5进行比对. 将相关参数代入式(7)进行计算. ...
... 如图8 所示为试验数据与式(7)计算结果的对比情况. 可见,式(7)与文献[27 ]的缩尺试验结果具有良好的吻合度. 当α 取2.5~3.5时,式(7)可以较好地表征细砂土中的应变测试结果[28 ] 及其随管-石偏距的衰减趋势. 在相同条件下,α 越大,则管道顶部应变随管-石偏距的衰减程度越大,表明土壤对落石冲击应力波的耗散能力越强. 图8 表明,与粉质黏土相比,细砂具有更强的应力波耗散能力,这与爆炸应力波领域的相关研究[29 ] 相似,反映式(7)具有一定的广泛性. ...
... 文献[27 , 28 ]的室内试验结果与式(7)计算结果的对比 ...
... Comparison of measured strain from published indoor test[27 -28 ] and calculated strain from equation (7) ...
... (2) 管道顶部应变$\varepsilon _{\mathrm{top}} $ $\varepsilon _{\mathrm{top}} $ f (1+L )且指数为−α 的幂函数. α 越大表明土壤对落石冲击应力波的耗散能力越强,该幂函数关系与足尺模型试验结果和文献[27 , 28 ]的室内试验结果吻合良好. 在本文足尺模型试验的条件下,当L 从0 m增加至2 m时,$\varepsilon _{\mathrm{top}} $ −6 迅速降低至3×10−6 ,说明将管-石偏距控制在2 m是减小管道动力响应的有效措施. ...
冲击荷载对埋地管道影响的试验与数值模拟研究
6
2022
... 为了进一步验证式(7)的适用性,对比了研究人员既有室内试验数据[27 -28 ] 与式(7)的计算结果. 董飞飞等[27 ] 开展埋地管道的室内缩尺冲击试验:管道试件为Q235级镀锌钢管,外径和壁厚分别为0.114、0.002 5 m,埋深为0.6 m. 试验在尺寸为3 m×3 m×1.5 m的土箱中进行,土体为粉质黏土. 落石冲击荷载由落石冲击试验机进行模拟,设有4种落石高度(0.5、1.0、1.5、2.0 m)以及3种冲击偏移距离(0、0.75、1.5 m). 由于未给出具体的土体变形模量,考虑土体性质与本文接近,E s 取10 MPa,α 取1.2. 张虎等[28 ] 在同样的土箱中进行缩尺试验:外径为0.139 m,壁厚为0.002 5 m,长度为2.8 m的Q235级钢管,埋深为0.5 m,落石冲击高度为2.0 m,冲击偏移距离为0、0.3、0.6 m;土体为压实的细砂. 根据经验,E s 取30 MPa,α 取1.5、2.5、3.5进行比对. 将相关参数代入式(7)进行计算. ...
... [28 ]在同样的土箱中进行缩尺试验:外径为0.139 m,壁厚为0.002 5 m,长度为2.8 m的Q235级钢管,埋深为0.5 m,落石冲击高度为2.0 m,冲击偏移距离为0、0.3、0.6 m;土体为压实的细砂. 根据经验,E s 取30 MPa,α 取1.5、2.5、3.5进行比对. 将相关参数代入式(7)进行计算. ...
... 如图8 所示为试验数据与式(7)计算结果的对比情况. 可见,式(7)与文献[27 ]的缩尺试验结果具有良好的吻合度. 当α 取2.5~3.5时,式(7)可以较好地表征细砂土中的应变测试结果[28 ] 及其随管-石偏距的衰减趋势. 在相同条件下,α 越大,则管道顶部应变随管-石偏距的衰减程度越大,表明土壤对落石冲击应力波的耗散能力越强. 图8 表明,与粉质黏土相比,细砂具有更强的应力波耗散能力,这与爆炸应力波领域的相关研究[29 ] 相似,反映式(7)具有一定的广泛性. ...
... 文献[27 , 28 ]的室内试验结果与式(7)计算结果的对比 ...
... Comparison of measured strain from published indoor test[27 -28 ] and calculated strain from equation (7) ...
... (2) 管道顶部应变$\varepsilon _{\mathrm{top}} $ $\varepsilon _{\mathrm{top}} $ f (1+L )且指数为−α 的幂函数. α 越大表明土壤对落石冲击应力波的耗散能力越强,该幂函数关系与足尺模型试验结果和文献[27 , 28 ]的室内试验结果吻合良好. 在本文足尺模型试验的条件下,当L 从0 m增加至2 m时,$\varepsilon _{\mathrm{top}} $ −6 迅速降低至3×10−6 ,说明将管-石偏距控制在2 m是减小管道动力响应的有效措施. ...
冲击荷载对埋地管道影响的试验与数值模拟研究
6
2022
... 为了进一步验证式(7)的适用性,对比了研究人员既有室内试验数据[27 -28 ] 与式(7)的计算结果. 董飞飞等[27 ] 开展埋地管道的室内缩尺冲击试验:管道试件为Q235级镀锌钢管,外径和壁厚分别为0.114、0.002 5 m,埋深为0.6 m. 试验在尺寸为3 m×3 m×1.5 m的土箱中进行,土体为粉质黏土. 落石冲击荷载由落石冲击试验机进行模拟,设有4种落石高度(0.5、1.0、1.5、2.0 m)以及3种冲击偏移距离(0、0.75、1.5 m). 由于未给出具体的土体变形模量,考虑土体性质与本文接近,E s 取10 MPa,α 取1.2. 张虎等[28 ] 在同样的土箱中进行缩尺试验:外径为0.139 m,壁厚为0.002 5 m,长度为2.8 m的Q235级钢管,埋深为0.5 m,落石冲击高度为2.0 m,冲击偏移距离为0、0.3、0.6 m;土体为压实的细砂. 根据经验,E s 取30 MPa,α 取1.5、2.5、3.5进行比对. 将相关参数代入式(7)进行计算. ...
... [28 ]在同样的土箱中进行缩尺试验:外径为0.139 m,壁厚为0.002 5 m,长度为2.8 m的Q235级钢管,埋深为0.5 m,落石冲击高度为2.0 m,冲击偏移距离为0、0.3、0.6 m;土体为压实的细砂. 根据经验,E s 取30 MPa,α 取1.5、2.5、3.5进行比对. 将相关参数代入式(7)进行计算. ...
... 如图8 所示为试验数据与式(7)计算结果的对比情况. 可见,式(7)与文献[27 ]的缩尺试验结果具有良好的吻合度. 当α 取2.5~3.5时,式(7)可以较好地表征细砂土中的应变测试结果[28 ] 及其随管-石偏距的衰减趋势. 在相同条件下,α 越大,则管道顶部应变随管-石偏距的衰减程度越大,表明土壤对落石冲击应力波的耗散能力越强. 图8 表明,与粉质黏土相比,细砂具有更强的应力波耗散能力,这与爆炸应力波领域的相关研究[29 ] 相似,反映式(7)具有一定的广泛性. ...
... 文献[27 , 28 ]的室内试验结果与式(7)计算结果的对比 ...
... Comparison of measured strain from published indoor test[27 -28 ] and calculated strain from equation (7) ...
... (2) 管道顶部应变$\varepsilon _{\mathrm{top}} $ $\varepsilon _{\mathrm{top}} $ f (1+L )且指数为−α 的幂函数. α 越大表明土壤对落石冲击应力波的耗散能力越强,该幂函数关系与足尺模型试验结果和文献[27 , 28 ]的室内试验结果吻合良好. 在本文足尺模型试验的条件下,当L 从0 m增加至2 m时,$\varepsilon _{\mathrm{top}} $ −6 迅速降低至3×10−6 ,说明将管-石偏距控制在2 m是减小管道动力响应的有效措施. ...
Re-examination of the shock wave’s peak pressure attenuation in soils
1
2011
... 如图8 所示为试验数据与式(7)计算结果的对比情况. 可见,式(7)与文献[27 ]的缩尺试验结果具有良好的吻合度. 当α 取2.5~3.5时,式(7)可以较好地表征细砂土中的应变测试结果[28 ] 及其随管-石偏距的衰减趋势. 在相同条件下,α 越大,则管道顶部应变随管-石偏距的衰减程度越大,表明土壤对落石冲击应力波的耗散能力越强. 图8 表明,与粉质黏土相比,细砂具有更强的应力波耗散能力,这与爆炸应力波领域的相关研究[29 ] 相似,反映式(7)具有一定的广泛性. ...