浙江大学学报(工学版)

浙江大学学报(工学版), 2026, 60(3): 495-503 doi: 10.3785/j.issn.1008-973X.2026.03.005

交通工程、土木工程

砂土地基中吸力桶基础的复合承载特性

陈政宇,, 张陈蓉,, 时振昊, 郝宸

1. 同济大学 地下建筑与工程系，上海 200092

2. 同济大学 岩土及地下工程教育部重点实验室，上海 200092

Combined bearing behavior of suction bucket foundation in sand

CHEN Zhengyu,, ZHANG Chenrong,, SHI Zhenhao, HAO Chen

1. Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China

2. Key Laboratory of Geotechnical and Underground Engineering of Ministry of Education, Tongji University, Shanghai 200092, China

通讯作者: 张陈蓉，女，副研究员，博士. orcid.org/0009-0005-6573-8123. E-mail：zcrong33@tongji.edu.cn

收稿日期: 2025-05-20  

基金资助: 国家自然科学基金资助项目（51779175）.

Received: 2025-05-20  

Fund supported: 国家自然科学基金资助项目（51779175）.

作者简介 About authors

陈政宇（2001—），男，硕士生，从事岩土工程的研究.orcid.org/0009-0001-9550-0897.E-mail：2232578@tongji.edu.cn , E-mail：2232578@tongji.edu.cn

摘要

针对砂土地基中海上风机吸力桶基础的复合承载问题开展研究. 采用状态相关砂土弹塑性模型，基于ABAQUS有限元软件UMAT子程序开展数值模拟. 通过土单元试验的模拟，验证了模型的合理性. 对砂土中吸力桶基础的承载特性进行模拟，将计算结果与遵循Mohr-Coulomb屈服准则理想弹塑性土体模型(MC模型)的计算结果进行对比，分析砂土中吸力桶基础复合加载下破坏包络面的区别. 结果表明，砂土状态相关的模型能够合理地反映吸力桶基础的承载特性，采用MC模型得到的吸力桶基础在二维及三维荷载空间的复合承载性能在大部分情况下更保守. 吸力桶基础在三维荷载组合作用下，在桶顶施加一定的竖向荷载有利于提高基础的水平-力矩复合承载力，但效果有限.

关键词： 砂土 ; 吸力桶基础 ; 状态相关模型 ; 砂土模型

Abstract

The combined bearing capacity of suction bucket foundations for offshore wind turbines in sandy soil was analyzed. A state-dependent elastoplastic model for sand was employed, and numerical simulations were conducted by using the UMAT subroutine in ABAQUS finite element software. The model’s validity was verified through simulations of soil element tests. Simulations were performed on the bearing behavior of suction bucket foundations in sandy soil. The computation results were compared with those obtained from an ideal elastic-plastic soil model following the Mohr-Coulomb yield criterion (MC model). Differences in the failure envelope surfaces under combined loading of the suction bucket foundation in sand were analyzed. Results show that the state-dependent sand model can reasonably reflect the bearing characteristics of the suction bucket foundation. The combined bearing capacity of the suction bucket foundation in two-dimensional and three-dimensional load spaces, which is obtained using the MC model, is generally more conservative in most cases. Applying a certain vertical load at the top of the bucket can improve the horizontal-moment composite bearing capacity of the foundation under three-dimensional combined loading, but the effect is limited.

Keywords： sand ; suction bucket foundation ; state-dependent model ; sand model

PDF (1619KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

陈政宇, 张陈蓉, 时振昊, 郝宸. 砂土地基中吸力桶基础的复合承载特性. 浙江大学学报(工学版)[J], 2026, 60(3): 495-503 doi:10.3785/j.issn.1008-973X.2026.03.005

CHEN Zhengyu, ZHANG Chenrong, SHI Zhenhao, HAO Chen. Combined bearing behavior of suction bucket foundation in sand. Journal of Zhejiang University(Engineering Science)[J], 2026, 60(3): 495-503 doi:10.3785/j.issn.1008-973X.2026.03.005

海上风电因风资源稳定且不占用陆地面积，已成为重要的清洁能源技术[1]. 在海上风电场向更深水域和复杂海床条件发展的过程中，稳定可靠的基础设计方案对保证风机上部结构的稳定性和寿命具有重要意义[2]. 在众多基础类型中，吸力桶基础因其具有施工便利性和回收方便的特点，近年来在海上风电场领域得到了广泛关注[3].

复合承载破坏包络面是揭示基础承载性能的重要手段[4]. 基础整体破坏时的竖向荷载V、水平荷载H和力矩荷载M各分量的组合值，在二维或三维荷载空间中形成包络面. 若设计承载力位于包络面内，则表示基础的承载力和整体稳定性满足要求；反之，则基础发生破坏[5]. Gourvenec等[6]通过试验和数值模拟研究桶形基础的复合承载特性，计算V-H、V-M和H-M荷载空间内的破坏包络面，揭示了荷载组合对基础稳定性的影响机制. 范庆来等[7-9]基于遵循Mohr-Coulomb屈服准则的理想弹塑性模型（MC模型），对砂土中基础的承载特性开展数值模拟分析，探讨内摩擦角对基础破坏包络面轨迹的影响. Zhang等[10]通过三维有限元模拟分析桩靴基础在复合荷载下的承载性能，给出包络面的解析表达式. 针对砂土地基最常用的土体模型是MC模型. Bolton[11]通过室内单元试验研究发现，砂土的摩擦角和剪胀角随着有效围压的增加而显著降低，即MC模型采用恒定的摩擦角和剪胀角，不能准确地反映砂土在加载过程中强度和剪胀性的变化. 为此，Manzari等[12-14]提出更合理的状态相关砂土模型，通过引入状态参数，综合考虑有效围压和相对密实度对砂土力学特性的影响. Fu等[15]将状态相关模型应用于砂土中基础的性能模拟，对基础在安装及服役期的变形和承载力进行预测.

尽管状态相关概念描述砂土的力学特性更合理，但将其用于砂土中吸力桶基础复合承载性能的评估较少. 本文引入状态相关砂土弹塑性模型，采用ABAQUS有限元软件及用户自定义材料子程序UMAT模拟吸力桶与土体的相互作用，得到砂土中吸力桶基础的复合承载包络面. 通过对Toyoura砂固结不排水静三轴试验的模拟，验证了状态相关砂土模型的正确性. 开展砂土中吸力桶基础的单向和复合加载承载特性研究，与基于MC模型的数值模拟结果进行对比，指出MC模型在模拟砂土中吸力桶的基础承载特性时，在绝大部分荷载组合下偏保守.

1. 状态相关砂土弹塑性模型及有限元验证

1.1. 模型介绍

1.1.1. 弹性性质

假设为各向同性弹性，切变模量Gt和体变模量Kt参考Dołżyk-Szypcio[16]提出的模型，具体如下：

$ {G_{\text{t}}} = G_{\text{e}}^{{\text{ref}}}\frac{{{{(2.97 - e)}^2}}}{{1+e}}\sqrt {p {p_{\text{a}}}} , $

$ {K_{\text{t}}} = {G_{\text{t}}}\frac{{2(1+v)}}{{3(1 - 2v)}} . $

式中：e为当前孔隙比，ν为泊松比，$ G_{\text{e}}^{{\text{ref}}} $为弹性切变模量的参考值，p为初始围压，pa为大气压力.

1.1.2. 砂土的状态相关性描述

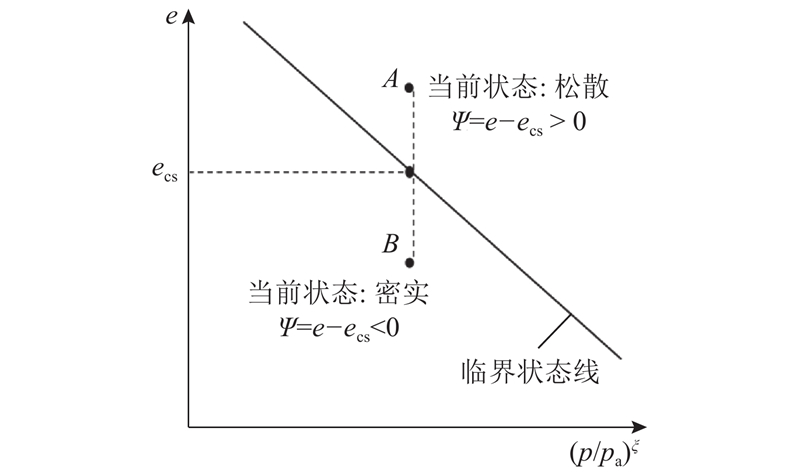
砂土的力学特性与其密实度及剪切过程中的平均有效应力相关[17]. 考虑砂土的状态相关性，引入Been等[18]提出的状态参数$ \psi $：

$ \psi = e - {e_{{\text{cs}}}} . $

式中：ecs为对应平均有效应力下的临界孔隙比. 参考文献[19]，可得e-p空间的临界状态线为

$ {e_{{\text{cs}}}} = {e_\Gamma } - \lambda {\left( {\frac{p}{{{p_{\text{a}}}}}} \right)^\xi } . $

式中：$ {e_\Gamma } $、$ \lambda $和$ \xi $为材料参数，$ {e_\Gamma } $为p = 0时的临界孔隙比，即临界状态线的截距. 如图1所示，当状态参数$ \psi > 0 $时，砂土处于松散状态，表现为剪缩性；当$ \psi < 0 $时，砂土处于密实状态，表现为剪胀性.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   临界状态线与状态参数

Fig.1   Critical state line and state parameter


1.1.3. 屈服准则和硬化定律

屈服面采用Pietruszczak等[20]提出的形式，如下所示：

$ F = q - g(\theta )pM_1 = 0 . $

式中：p为平均有效应力；q为广义偏应力；$ M_1 $为硬化变量；$ g(\theta ) $为$ \pi $平面上的边界面形状函数，参考文献[21]的椭圆插值函数，有

$ g(\theta ,c) = \frac{{4c'}}{{1+c'+(1 - c')\sin \;(3\theta) }} - \frac{{1+c' - (1 - c')\sin \;(3\theta) }}{2}. $

其中，$ c' = {M_{\text{e}}}/{M_{\text{c}}} $，$ {M_{\text{e}}} $和$ {M_{\text{c}}} $分别为三轴拉伸和压缩应力路径下土体达到临界状态时的应力比.

三轴压缩应力路径下，$ g = 1 $，由式(5)可得，此时$ M_1 = q/p = \eta $. 硬化变量M的演化与广义塑性切应变相关，服从如下硬化法则：

$ \frac{{\partial M_1}}{{\partial \varepsilon _{\mathrm{q}}^{\mathrm{p}}}} = - \frac{{h{G_{\text{t}}}}}{{M_1g(\theta )p}}({M_{\text{p}}} - M_1) . $

式中：$\varepsilon _{\mathrm{q}}^{\mathrm{p}}$为塑性切应变；$ {M_{\text{p}}} $为峰值应力比；$ h = {h_1} - {h_2}e $, 其中$ {h_1} $和$ {h_2} $为材料硬化参数.

$ {M_{\text{p}}} $与状态参数$ \psi $的关系如下：

$ {M_{\text{p}}} = {M_{\text{c}}}\exp\; ( - n\psi ) . $

式中：n为控制材料状态相关的参数.

由一致性条件可得，塑性模量为

$ {K_{\text{p}}} = - \frac{{\partial F}}{{\partial M_1}}\frac{{\partial M_1}}{{\partial \varepsilon _{\mathrm{q}}^{\mathrm{p}}}}\frac{{\partial Q}}{{\partial q}} = \frac{{h{G_{\text{t}}}}}{M_1}({M_{\text{p}}} - M_1) . $

1.1.4. 塑性流动法则

塑性势函数Q = 0，模型采用非相关联流动法则. 假定偏应变分量与边界面的偏应力分量一致，即偏应变满足相关联流动法则，可得

$ {\mathrm{d}}\varepsilon _{\mathrm{q}}^{\mathrm{p}} = {\mathrm{d}}\lambda \frac{{\partial Q}}{{\partial q}} . $

式中：

$ \left.\begin{gathered} \frac{{\partial Q}}{{\partial q}} = \frac{{\partial F}}{{\partial q}}, \\ \frac{{\partial Q}}{{\partial \theta }} = \frac{{\partial F}}{{\partial g(\theta )}}\frac{{\partial g(\theta )}}{{\partial \theta }} = - \frac{q}{{g(\theta )}}\frac{{\partial g(\theta )}}{{\partial \theta }}. \\ \end{gathered}\right\} $

剪胀系数D为塑性体应变增量$ {\mathrm{d}}\varepsilon _{\text{v}}^{\text{p}} $和塑性切应变增量$ {\mathrm{d}}\varepsilon _{\mathrm{q}}^{\mathrm{p}} $的比值，具体表达式如下：

$ D = \frac{{{d_0}}}{{{M_{\text{c}}}}}\left({M_{\text{d}}}g(\theta ) - \frac{q}{p}\right) = \frac{{{d_0}}}{{{M_{\text{c}}}}}g(\theta )({M_{\text{d}}} - M_1) . $

式中：$ {d_0} $为剪胀参数；$ {M_{\text{d}}} $为发生剪缩-剪胀相转换时的应力比，$ {M_{\text{d}}} $与状态参数$ \psi $的关系为

$ {M_{\text{d}}} = {M_{\text{c}}}\exp\; (m\psi ) . $

其中，m为控制材料剪胀性的参数.

1.2. 砂土模型的验证

基于有限元软件ABAQUS中自定义的材料子程序UMAT实现上述砂土模型，UMAT文件编译参考文献[22]. 设置状态变量数组STATEV，存储更新每一步与求解相关的状态变量数组.

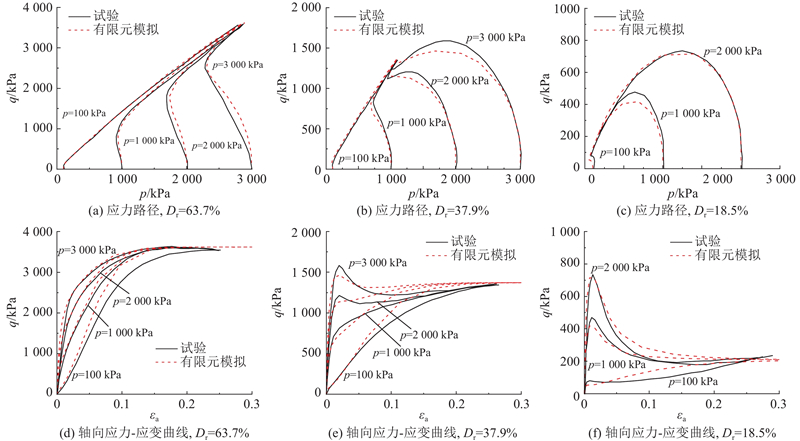
Verdugo等[23]开展Toyoura砂土固结不排水三轴剪切试验. 本文采用有限元方法对试验结果进行模拟，验证状态相关砂土弹塑性模型的合理性. 具体选取3种相对密实度Dr = 63.7%、37.9%、18.5%，分别对应中密砂I、中密砂II、松砂. 设置4种初始围压$ {\sigma _3} $，分别为100、1 000、2 000、3 000 kPa. 其中3 000 kPa的高围压仅针对中密砂I和中密砂II.

Toyoura砂状态的相关参数参考文献[24]，具体见表1. 其中，采用 m-103kg-kN-s计量单位，砂土的最大、最小孔隙比分别为0.977和0.597.

表 1   状态相关砂土模型的参数

Tab.1  Parameter of state-dependent sand model

参数数值参数数值
$ {G}_{{\mathrm{e}}}^{{\mathrm{ref}}} $/MPa125ξ0.7
v0.05d00.88
$ {M}_{{\mathrm{c}}} $1.25m3.5
$ {M}_{{\mathrm{e}}} $0.9375h13.15
$ {e}_{\Gamma} $0.934h23.05
λ0.019n1.1

新窗口打开| 下载CSV


如图2所示为有限元模拟与试验结果的对比. 其中，εa为轴向应变. 从图2可见，模拟结果再现了试验现象. 在相应的围压条件下，中密砂加载后平均有效应力先降低后升高，偏应力持续增长，对应较密实砂土先剪缩后剪胀的行为特征. 在相应的围压条件下，松砂的模拟结果显示平均有效应力持续降低，偏应力先达到峰值强度后下降，对应土体持续剪缩的行为特征. 从上述对比可见，状态相关砂土模型准确描述了砂土的峰值强度和临界状态应力，有限元数值模拟与试验结果的规律一致. 其中应力路径曲线的误差较小，而应力-应变曲线存在稍许偏差，原因可能是非测量模型参数的选取存在误差，且现有模型未考虑加载过程中可能的砂土颗粒破碎、应变局部化、静态液化等行为.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   不排水三轴试验结果的对比

Fig.2   Comparison of undrained triaxial test result


2. 砂土中吸力桶基础的承载特性分析

数值模拟中使用最广泛的砂土模型为遵循Mohr-Coulomb屈服准则的理想弹塑性模型（MC模型），采用摩擦角与剪胀角来反映砂土的强度和剪胀特性，摩擦角和剪胀角在整个加载过程中保持不变. 考虑到砂土颗粒材料的状态相关特性，随着加载的持续和有效围压的变化，摩擦角与剪胀角改变，即状态参数的改变会影响砂土的力学特性.

2.1. 数值分析模型

2.1.1. 基本设置

吸力桶基础的尺寸如下：直径为6 m，高为6 m，厚度为0.1 m. 为了提高计算效率，节约成本[25]，有限元建模为圆柱形，整体计算区域的半径为桶体直径的5倍，即直径为30 m，高为30 m. 将桶-土外部面面接触设置为有限滑移的硬接触，粗糙系数为0.4，允许法向脱离. 内部设置为Tie接触.

针对MC模型参数，童森杰等[26]基于状态相关模型，给出剪胀角$ {\theta _{\max }} $和峰值摩擦角$ {\varphi _{\mathrm{p}}} $与初始状态参数$ {\psi _0} $的拟合关系如下：

$ {\theta _{\max }} = - 70{\psi _0}, $

$ {\varphi _{\mathrm{p}}} = {\varphi _{\mathrm{c}}}+47.868{( - {\psi _0})^{1.4}}. $

式中：$ {\varphi _{\mathrm{c}}} $为砂土临界状态的摩擦角.

地基土为均质Toyoura砂土，均为排水条件且考虑Dr= 37.9%和63.7% 2种初始相对密实度的中密砂，根据状态相关的概念可知，强度沿深度非均质分布. 土体每6 m分为一层，共分为5层. MC模型参数分别见表2、3. 其中，E1~E5为弹性模量，φ1~φ5为摩擦角，θ1~θ5为剪胀角，下标1~5分别对应由上至下5个土层，c为黏聚力，e0为初始孔隙比，emin、emax分别为最小和最大孔隙比. 摩擦角与剪胀角考虑峰值状态，由式(14)、(15)计算得到；弹性模量由式(1)转化得到；不考虑密度的变化，因为该变量的变化对结果的影响不大.

表 2   MC砂土模型的参数(Dr = 37.9%)

Tab.2  Parameter of MC sand model (Dr = 37.9%)

弹性参数摩擦角剪胀角其他参数
E1 = 86.54 MPaφ1 = 32.38°θ1 = 5.13°φc = 31.15°
E2 = 117.60 MPaφ2 = 32.04°θ2 = 4.09°c = 0.1 kPa
E3 = 142.02 MPaφ3 = 31.78°θ3 = 3.19°e0 = 0.833
E4 = 162.82 MPaφ4 = 31.56°θ4 = 2.37°emin = 0.597
E5 = 181.24 MPaφ5 = 31.39°θ5 = 1.61°emax = 0.977
ν = 0.05———
ρ = 2.446———

新窗口打开| 下载CSV


表 3   MC砂土模型的参数(Dr = 63.7%)

Tab.3  Parameter of MC sand model (Dr = 63.7%)

弹性参数摩擦角剪胀角其他参数
E1 = 100.01 MPaφ1 = 35.20°θ1 = 11.99°φc = 31.15°
E2 = 135.90 MPaφ2 = 34.71°θ2 = 10.95°c = 0.1
E3 = 164.12 MPaφ3 = 34.31°θ3 = 10.05°e0 = 0.735
E4 = 188.15 MPaφ4 = 33.96°θ4 = 9.23°emin = 0.597
E5 = 209.45 MPaφ5 = 33.64°θ5 = 8.47°emax = 0.977
ν = 0.05———
ρ = 2.446———

新窗口打开| 下载CSV


数值模拟包括3个分析步骤，见图3. 其中，Nele为网格数量，V为竖向力，d为竖向位移. 第1步为地应力平衡，采用ODB导入法平衡土体初始应力状态. 第2步为接触设置. 第3步进行加载，采用位移加载法，在参考点处施加各向位移(d、h、θ). 计算网格采用C3D8R模型，网格加密前、后的吸力桶基础竖向加载荷载-位移曲线对比见图3(b)，误差仅为0.63%，可以认为网格密度设置不影响结果.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

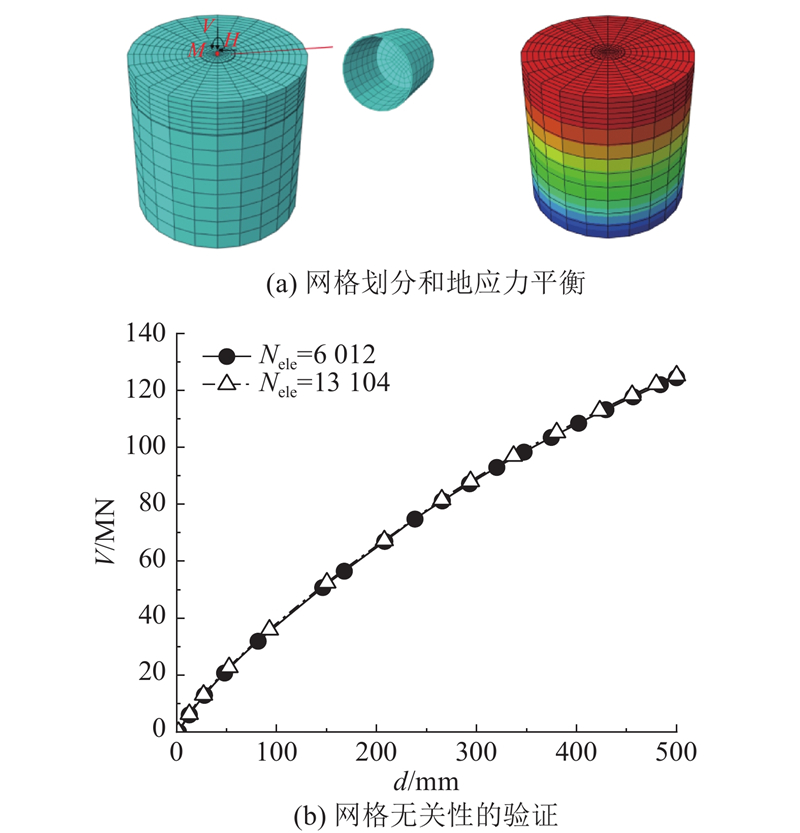
图 3   网格、地应力平衡与网格无关性的验证

Fig.3   Verification of mesh, geostress equilibrium and mesh independence


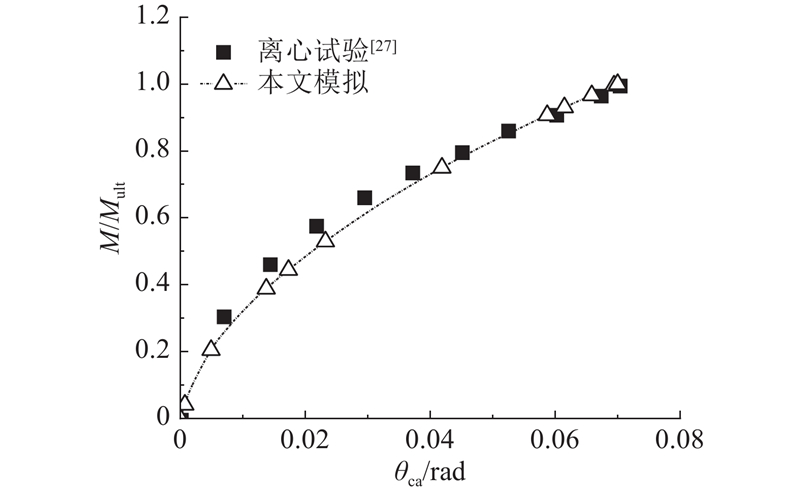
2.1.2. 数值模型验证

王欢[27]开展了砂土中吸力桶基础的水平受荷承载特性离心试验，砂土相对密实度为60%，离心加速度为100g，吸力桶基础采用铝合金制作，材料弹性模量为72 GPa，泊松比为0.3，基础尺寸如下：底面直径为150 mm、高为150 mm、厚度为4 mm. 如图4所示为利用本文模型模拟得到的砂土中吸力桶基础归一化力矩M/Mult-转角$\theta_{\mathrm{ca}} $曲线与离心试验结果的对比. 其中，M为弯矩，Mult为弯矩极限值. 从图4可见，两者较一致，表明本文砂土模型用于吸力桶基础荷载位移曲线有限元数值模拟的合理性.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   力矩-转角曲线的对比(Dr = 60%)

Fig.4   Comparison of moment-rotation curve (Dr = 60%)


2.1.3. 荷载位移曲线的对比分析

如图5所示为采用2种土体模型计算得到的单一荷载下吸力桶的荷载位移曲线对比图，单一荷载具体包括竖向荷载、水平荷载和力矩. 其中，y为水平位移. 从图5(a)可以看出，在加载初期，利用本文的状态相关砂土模型与MC模型得到的竖向荷载-位移曲线重合度较高. 在加载后期，采用MC模型得到的竖向荷载相对较小. 相对密实度较大的土体的荷载位移曲线位于上方，表明承载性能更优越.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   荷载-位移曲线的对比

Fig.5   Comparison of load-displacement curve


崔希君等[28]的研究表明，吸力桶在水平荷载与力矩作用下周边土体的破坏机制较相似. 从图6的水平加载应力$\sigma $云图可知，极限状态下土体的最不利受力处位于吸力桶前侧区域. 从图5(b)可知，当加载位移较小时，利用MC模型得到的水平荷载偏大. 该现象的原因可能是分层土体取该层中点处的摩擦角与剪胀角会高估该层土体强度，由此表现出更大的横向抗力，而加载位移较大时情况则相反，对应基础承载力的设计往往不够准确，易造成工程风险或材料浪费. 状态相关模型全面考虑砂土所受围压及相对密实度的变化，更精确地反映了吸力桶基础的承载特性. 对比图5(b)、(c)可知，在加载后期，无论是水平力位移曲线还是力矩转角曲线，MC砂土模型在相同位移下得到的吸力桶荷载都更小.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6   水平极限荷载下的应力云图(Dr = 37.9%)

Fig.6   Stress contour plot under ultimate horizontal loading (Dr = 37.9%)


2.2. 复合加载破坏包络面的对比分析
2.2.1. 承载力和包络面的确定方法

参考姜明涛[29]的切线相交法，从荷载位移曲线上获取吸力桶基础的承载力，取曲线起点和终点的2条切线的交点所对应的荷载q作为极限荷载qult，该荷载在荷载位移曲线上对应的位移s即为吸力桶基础承载破坏时的极限位移sult，具体见图7.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7   切线相交法

Fig.7   Tangent intersection method


参考王伟臣[30]采用的Probe加载法，联合位移加载法，每组荷载中控制加载的位移比不变，直至某一位移达到切线法确定的结构极限位移，找到不同荷载组合作用下二维荷载空间内的承载力控制点. 对相应荷载进行无量纲化处理，用平滑曲线相连，得到吸力桶基础的复合加载破坏包络线.

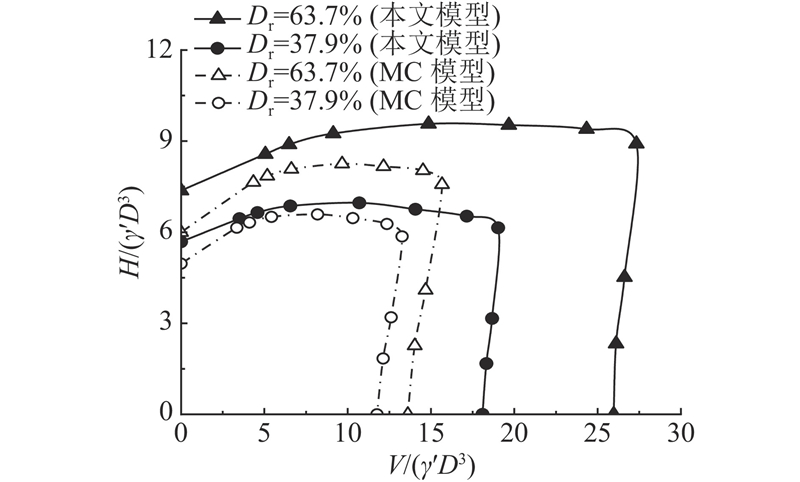
2.2.2. V-H包络面

如图8所示为通过数值计算得到的吸力桶基础V-H二维加载模式下无量纲化包络面的对比图. 其中，$\gamma^{\prime}$为土的重度，D为吸力桶直径，H为水平力. 从图8可见，在吸力桶基础上施加一定的竖向荷载，有利于吸力桶水平承载力的提高，当相对密实度较大时，吸力桶基础的V-H复合承载力更大. 利用状态相关砂土模型与MC模型得到的无量纲化水平极限荷载皆在V趋于极限时急剧下降，转为以竖向承载为主，在竖向位移达到极限状态时发生破坏. 当砂土采用MC模型模拟时，竖向荷载对水平承载力的提高作用更明显，利用MC模型得到的吸力桶V-H复合承载力较状态相关模型更保守.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8   V-H平面内无量纲化破坏包络线的对比

Fig.8   Comparison of normalized failure envelope in V-H loading space


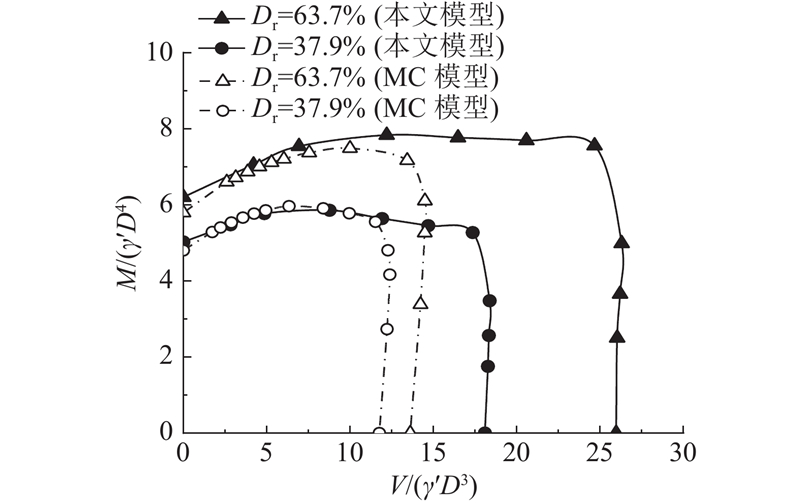
2.2.3. V-M包络面

如图9所示为通过数值计算得到的吸力桶基础V-M二维加载模式下无量纲化包络面的对比图. 可见，在吸力桶基础上施加一定的竖向荷载有利于力矩承载力的提高，当相对密实度较大时，吸力桶基础的V-M复合承载力更大. 利用状态相关砂土模型与MC砂土模型得到的无量纲化水平极限荷载都在V趋于极限时急剧下降，转为以竖向承载为主，在竖向位移达到极限状态时发生破坏. 仅当无量纲竖向荷载4<V/(γ'D3)＜9时，密实度为37.9%的砂土采用MC模型得到的极限力矩更大，表明竖向荷载对极限力矩的提高作用在使用MC模型时较状态相关模型更明显. 在其他V-M复合加载的情况下，MC模型较为保守.

图 9

新窗口打开| 下载原图ZIP| 生成PPT

图 9   V-M平面内无量纲化破坏包络线的对比

Fig.9   Comparison of normalized failure envelope in V-M loading space


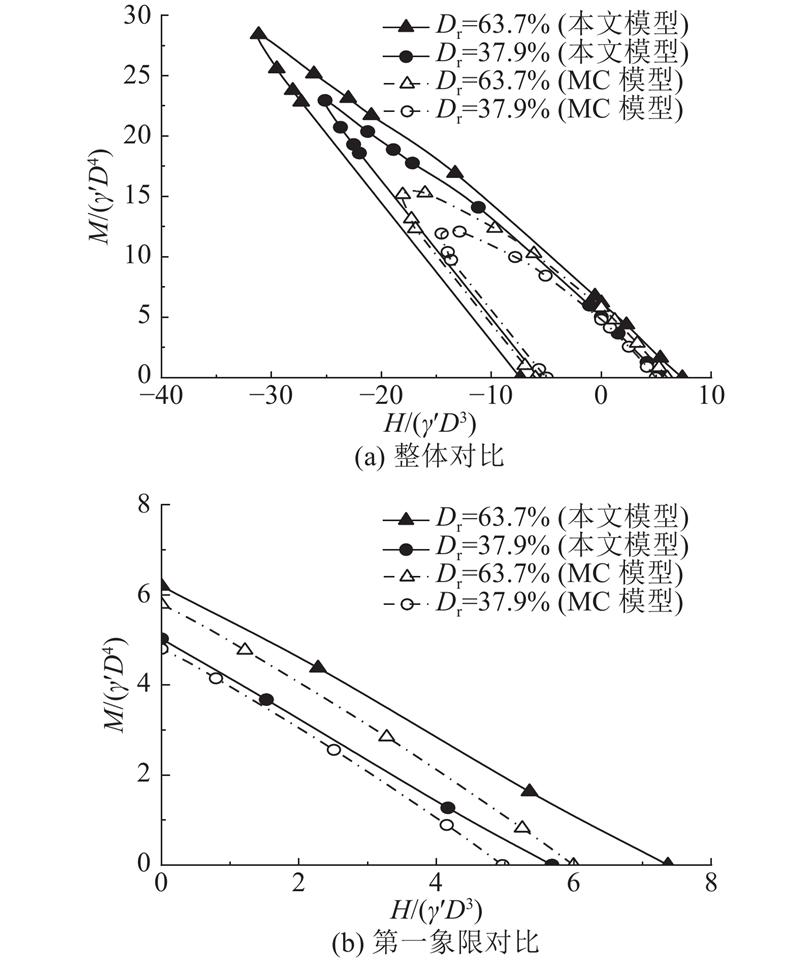
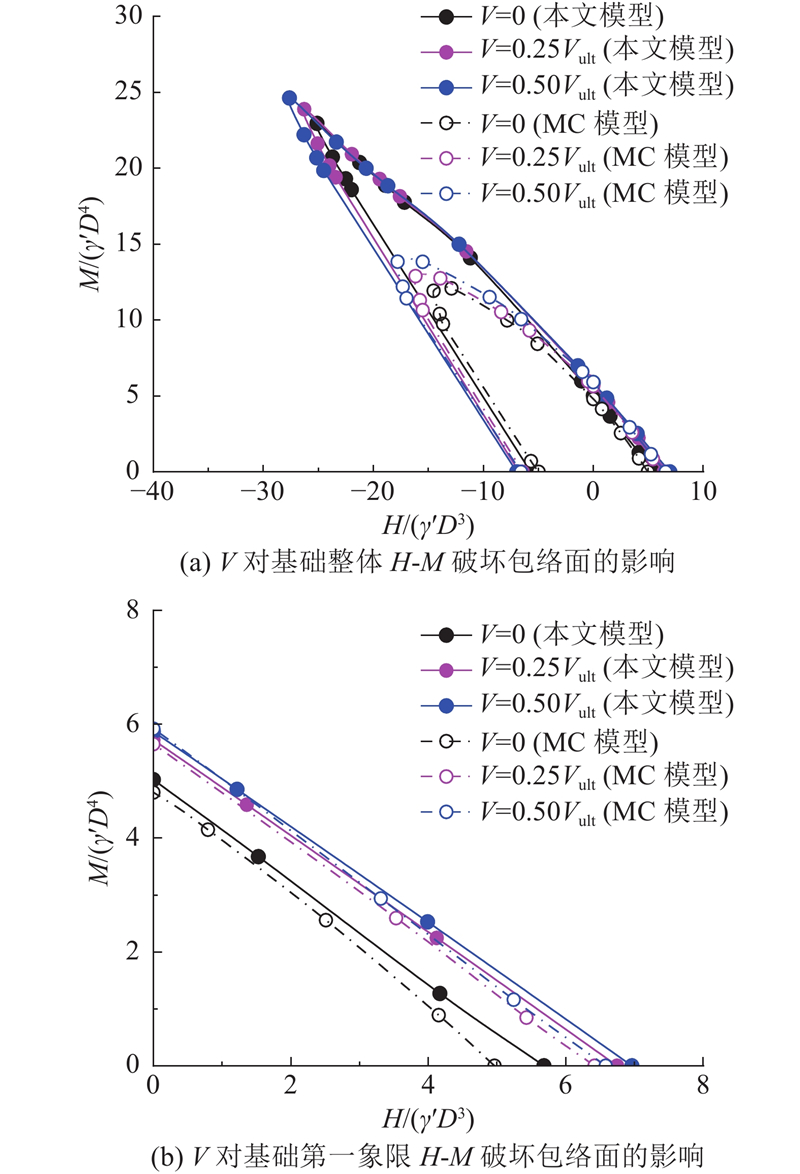
2.2.4. H-M包络面

如图10所示为通过数值计算得到的吸力桶基础H-M二维加载模式下无量纲化包络面的对比图. 从图10(a)可见，H-M二维荷载空间的破坏包络线具有较强的非对称性，这是由于水平荷载和力矩荷载存在耦合相关性. 整体而言，吸力桶基础在H-M空间内的复合承载性能较差，力矩荷载和水平荷载在第一象限相互增强，在第二象限相互抵消，该抵消作用使得吸力桶基础的H-M破坏包络线在第二象限能够延伸至很远.

图 10

新窗口打开| 下载原图ZIP| 生成PPT

图 10   H-M平面内无量纲化破坏包络线的对比

Fig.10   Comparison of normalized failure envelope in H-M loading space


对比2种相对密实度结果可知，当相对密实度较大时，吸力桶基础的H-M复合承载力更大. 对比2种砂土模型的效果可知，两者得到的H-M破坏包络线形状相似，使用MC模型的破坏包络面的范围明显更小，表明利用MC模型整体评价吸力桶的H-M复合承载性能更保守.

从图10(b)可见，吸力桶H-M复合加载最不利的荷载工况是水平荷载与力矩荷载同向，即H-M包络线第一象限的部分. 整体来看， 随着水平荷载的增大，吸力桶基础的极限力矩均大致呈线性降低，显示了力矩与水平荷载之间的强耦合相关性.

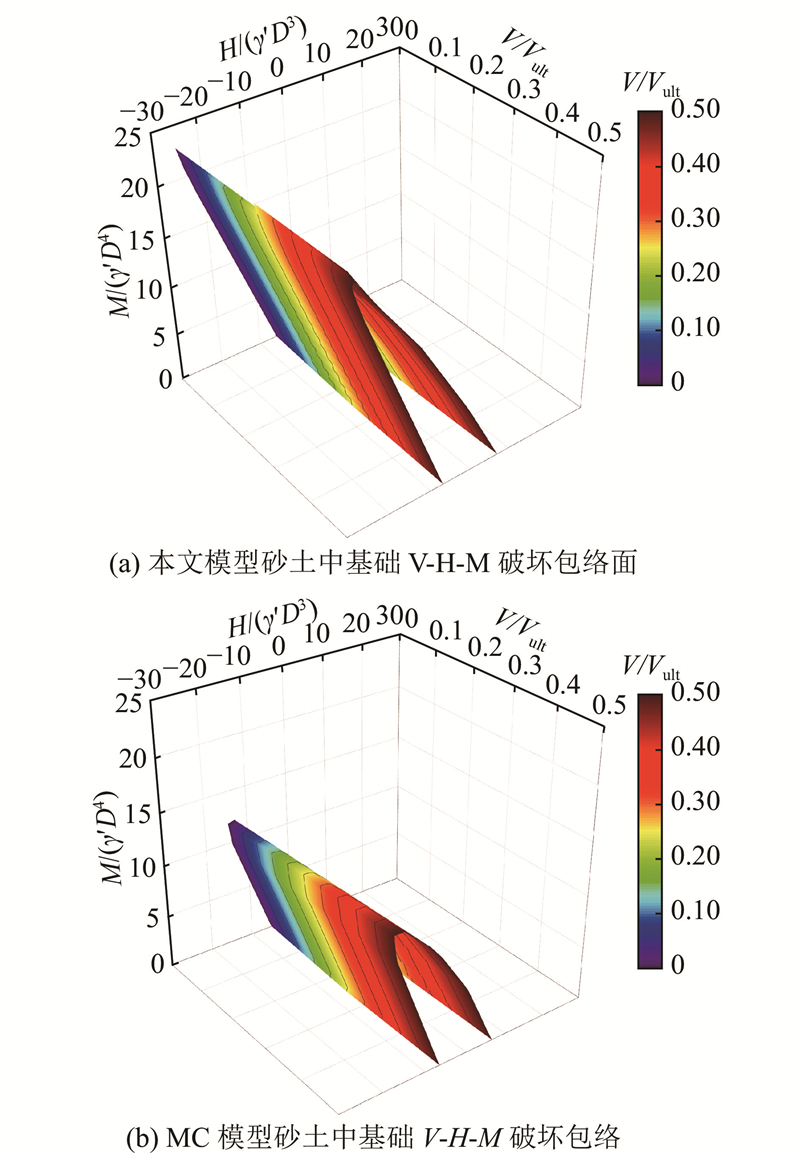
2.2.5. V-H-M包络面

以相对密实度为37.9%的砂土为例，研究在V-H-M共同作用下海上风机吸力桶基础的承载能力. 王伟臣[30]指出，在实际的海洋工程中，风机基础所受的竖向荷载为结构上部自重，一般不超过竖向承载力极限值Vult的一半. 将竖向荷载分量V/Vult = 0、0.25、0.5 3种情况下的基础H-M无量纲化包络面连成曲面，形成V-H-M破坏包络面，如图11、12所示. 从图11(a)、(b)可见，随着竖向荷载逐渐增大至0.5Vult，吸力桶基础的H-M破坏包络面均向外扩张，但变化幅度不大. 在图12(a)、(b)中体现为V-H-M三维包络面的开口随竖向荷载的增大而略微扩大，说明当V≤0.5Vult时，桶顶竖向荷载对基础H-M复合承载力有一定的增强作用，该作用随着竖向荷载的增大而略有提升，但幅度不大. 该变化趋势与崔希君等[28]的模拟结果相符. 对比2种砂土模型的效果可知，图11(b)显示，在V-H-M三者耦合作用下，当竖向荷载为0.5Vult且水平荷载很小时，采用MC模型得到的基础极限力矩较状态相关模型略大，其余加载情况下利用MC模型得到的H-M破坏包络面范围均较小，这与图9中V-M包络面的对比规律相符. 利用MC模型评价实际工程中吸力桶基础的V-H-M复合承载力，在绝大部分情况下偏于保守.

图 11

新窗口打开| 下载原图ZIP| 生成PPT

图 11   V对基础H-M破坏包络面的影响(V≤0.5Vult)

Fig.11   Influence of V on H-M failure envelope of foundation (V≤0.5Vult)


图 12

新窗口打开| 下载原图ZIP| 生成PPT

图 12   V-H-M荷载作用下吸力桶基础的破坏包络面(V≤0.5Vult)

Fig.12   Failure envelope of suction bucket foundation under V-H-M loading (V≤0.5Vult)


上述二维及三维荷载组合破坏包络面分析表明，本文采用状态相关砂土模型开展吸力桶基础承载特性的三维有限元数值模拟，相较于状态相关砂土模型，绝大部分情况下使用遵循Mohr-Coulomb屈服准则的理想弹塑性模型评价砂土中吸力桶的复合承载性能更保守.

3. 结　论

（1）采用砂土状态相关模型，通过引入状态参数，模拟砂土的强度和剪胀特性. 对Toyoura砂不排水剪切试验的模拟表明，本文的状态相关砂土模型能够表征加载过程中初始围压和相对密实度的影响，模拟剪切过程中的应力路径和应力-应变曲线.

（2）砂土中吸力桶基础在V-H、V-M复合加载模式下，施加一定的竖向荷载有利于提高水平和力矩承载力. 与状态相关砂土模型相比，仅在V-M加载模式下，当密实度为37.9%且无量纲竖向荷载4<V/(γ’D3)＜9时，砂土采用MC模型得到的极限力矩更大，其余情况下利用MC模型得到的吸力桶V-H与V-M复合承载力均较保守.

（3）砂土中吸力桶基础在H-M复合加载模式下，因水平荷载与力矩荷载存在耦合相关性，破坏包络面存在不对称性，具体为第一象限相互增强，第二象限相互抵消. 当使用MC模型和状态相关模型时，基础破坏包络线在第一象限内均大致呈线性降低. 使用MC模型评价吸力桶的H-M复合承载性能更保守.

（4）砂土中吸力桶基础在V-H-M复合加载模式下，当V＜0.5Vult时，桶顶竖向荷载对基础H-M复合承载力具有一定的增强作用，该作用随着竖向荷载的增大而略有提升，但幅度不大. 在V-H-M三者耦合作用下，相较于状态相关模型，采用MC模型得到的吸力桶基础V-H-M复合承载力在绝大部分情况下更偏于保守.

（5）当砂土采用状态相关模型和MC模型时，吸力桶的单向及复合承载力均随着密实度的增大而增大.

参考文献

许维凯

海上风电发展趋势分析与探讨

[J]. 资源节约与环保, 2023, (1): 140- 143

[本文引用: 1]

XU Weikai

Analysis and discussion on the development trend of offshore wind power

[J]. Resource Conservation and Environmental Protection, 2023, (1): 140- 143

[本文引用: 1]

毋晓妮, 廖倩, 李晔

海上风机吸力式桶形基础承载特性研究综述

[J]. 海洋技术学报, 2020, 39 (1): 91- 106

[本文引用: 1]

WU Xiaoni, LIAO Qian, LI Ye

Review on bearing characteristics of suction bucket foundations for offshore wind turbines

[J]. Journal of Ocean Technology, 2020, 39 (1): 91- 106

[本文引用: 1]

张东明, 陈守祥, 郑淼, 等

海上风机吸力桶基础的应用和技术分析

[J]. 中国水运(下半月), 2023, 23 (11): 133- 135

[本文引用: 1]

ZHANG Dongming, CHEN Shouxiang, ZHENG Miao, et al

Application and technical analysis of suction caisson foundations for offshore wind turbines

[J]. China Water Transport (Second Half), 2023, 23 (11): 133- 135

[本文引用: 1]

PARK J S, PARK D

Vertical bearing capacity of bucket foundation in sand overlying clay

[J]. Ocean Engineering, 2017, 134: 62- 76

DOI:10.1016/j.oceaneng.2017.02.015      [本文引用: 1]

范夏玲

海上风电吸力桩基础破坏包络面理论研究

[J]. 能源与环境, 2023, (6): 60- 62

[本文引用: 1]

FAN Xialing

Theoretical research on failure envelope surface of offshore wind power suction pile foundation

[J]. Energy and Environment, 2023, (6): 60- 62

[本文引用: 1]

GOURVENEC S, RANDOLPH M

Effect of strength non-homogeneity on the shape of failure envelopes for combined loading of strip and circular foundations on clay

[J]. Géotechnique, 2003, 53 (6): 575- 586

[本文引用: 1]

范庆来, 郑静, 武科

砂土地基上条形浅基础破坏包络面

[J]. 应用基础与工程科学学报, 2015, 23 (4): 773- 781

[本文引用: 1]

FAN Qinglai, ZHENG Jing, WU Ke

Failure envelope of strip shallow footings on sand

[J]. Journal of Basic Science and Engineering, 2015, 23 (4): 773- 781

[本文引用: 1]

汤振, 罗强, 贾虎

砂土地基条形浅基础在倾斜荷载下的破坏包络面

[J]. 人民长江, 2018, 49 (Suppl.2): 291- 293

TANG Zhen, LUO Qiang, JIA Hu

Failure envelope of strip shallow footings on sand under inclined load

[J]. Yangtze River, 2018, 49 (Suppl.2): 291- 293

张雨坤, 王冲冲, 李大勇, 等

砂土中裙式吸力基础复合承载特性数值模拟

[J]. 科学技术与工程, 2021, 21 (4): 1515- 1521

[本文引用: 1]

ZHANG Yukun, WANG Chongchong, LI Dayong, et al

Numerical simulation of bearing characteristics of modified suction caissons in sand under combined loads

[J]. Science Technology and Engineering, 2021, 21 (4): 1515- 1521

[本文引用: 1]

ZHANG Y, BIENEN B, CASSIDY M J, et al

The undrained bearing capacity of a spudcan foundation under combined loading in soft clay

[J]. Marine Structures, 2011, 24 (4): 459- 477

[本文引用: 1]

BOLTON M D

The strength and dilatancy of sands

[J]. Geotechnique, 1986, 36 (1): 65- 78

[本文引用: 1]

MANZARI M T, DAFALIAS Y F

A critical state two-surface plasticity model for sands

[J]. Géotechnique, 1997, 47 (2): 255- 272

[本文引用: 1]

YANG J, LUO X D

Exploring the relationship between critical state and particle shape for granular materials

[J]. Journal of the Mechanics and Physics of Solids, 2015, 84: 196- 213

DOI:10.1016/j.jmps.2015.08.001     

GUO N, ZHAO J

The signature of shear-induced anisotropy in granular media

[J]. Computers and Geotechnics, 2013, 47: 1- 15

DOI:10.1016/j.compgeo.2012.07.002      [本文引用: 1]

FU S, YANG Z X, ASCE M, et al

Large-deformation finite-element simulation

[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2023, 149 (6): 04023038

DOI:10.1061/JGGEFK.GTENG-10480      [本文引用: 1]

DOŁŻYK-SZYPCIO K. Stress-strain behaviour of Toyoura sand in undrained triaxial compression [C]// 7th International Symposium on Deformation Characteristics of Geomaterials. Glasgow: [s. n.], 2019: 15010.

[本文引用: 1]

王子珺, 赵伯明

砂土统一本构模型研究及其三维数值实现

[J]. 工程力学, 2021, 38 (10): 181- 187

[本文引用: 1]

WANG Zijun, ZHAO Boming

Research on unified constitutive model of sand and its three-dimensional numerical implementation

[J]. Engineering Mechanics, 2021, 38 (10): 181- 187

[本文引用: 1]

BEEN K, JEFFERIES M G

A state parameter for sands

[J]. Géotechnique, 1985, 35 (2): 99- 112

[本文引用: 1]

MANZANAL D, FERNÁNDEZ MERODO J A, PASTOR M

Generalized plasticity state parameter-based model for saturated and unsaturated soils. Part 1: saturated state

[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2011, 35 (12): 1347- 1362

DOI:10.1002/nag.961      [本文引用: 1]

PIETRUSZCZAK S, STOLLE D

Modeling of sand behavior under earthquake excitation

[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1987, 11: 221- 240

DOI:10.1002/nag.1610110302      [本文引用: 1]

陈洲泉, 黄茂松

砂土各向异性与非共轴特性的本构模拟

[J]. 岩土工程学报, 2018, 40 (2): 243- 251

[本文引用: 1]

CHEN Zhouquan, HUANG Maosong

Constitutive modeling of anisotropic and non-coaxial behaviors of sand

[J]. Journal of Geotechnical Engineering, 2018, 40 (2): 243- 251

[本文引用: 1]

SHI Z. Numerical modelling of cyclic degradation of natural clay [D]. Evanston: Northwestern University, 2016.

[本文引用: 1]

VERDUGO R, ISHIHARA K

The steady state of sands

[J]. Soils and Foundations, 1996, 36 (2): 81- 91

DOI:10.3208/sandf.36.2_81      [本文引用: 1]

LI X S, DAFALIAS Y F

Dilatancy for cohesionless soils

[J]. Géotechnique, 2000, 50 (4): 449- 460

[本文引用: 1]

张雁鹏. 海上风电四吸力筒导管架基础承载性能数值研究[D]. 大连: 大连海洋大学, 2024.

[本文引用: 1]

ZHANG Yanpeng. Numerical study on bearing performance of quadruple suction caisson jacket foundation for offshore wind turbines [D]. Dalian: Dalian Ocean University, 2024.

[本文引用: 1]

童森杰, 黄茂松, 时振昊, 等

基于初始状态参数的砂土峰值摩擦角和极限强度

[J]. 岩石力学与工程学报, 2022, 41 (2): 389- 398

[本文引用: 1]

TONG Senjie, HUANG Maosong, SHI Zhenhao, et al

Peak frictional angle and ultimate drainage strength of sand based on initial state parameter

[J]. Chinese Journal of Rock Mechanics and Engineering, 2022, 41 (2): 389- 398

[本文引用: 1]

王欢. 砂土海床大直径单桩基础和桶形基础水平受荷特性研究[D]. 杭州: 浙江大学, 2020.

[本文引用: 1]

WANG Huan. Study on lateral load-bearing behavior of large-diameter monopile and bucket foundations in sandy seabed [D]. Hangzhou: Zhejiang University, 2020.

[本文引用: 1]

崔希君, 史永晋, 魏羲, 等

复合加载模式下四筒导管架基础承载特性分析

[J]. 太阳能学报, 2024, 45 (6): 581- 588

[本文引用: 2]

CUI Xijun, SHI Yongjin, WEI Xi, et al

Analysis of bearing characteristics of four-bucket jacket foundation in combined loading mode

[J]. Acta Energiae Solaris Sinica, 2024, 45 (6): 581- 588

[本文引用: 2]

姜明涛. 砂土中海上风电机组四筒导管架基础承载特性研究[D]. 天津: 天津大学, 2019.

[本文引用: 1]

JIANG Mingtao. Study on bearing characteristics of four-bucket jacket foundation for offshore wind turbine in sand [D]. Tianjin: Tianjin University, 2019.

[本文引用: 1]

王伟臣. 吸力式三桶导管架基础在黏土中承载特性研究[D]. 天津: 天津大学, 2022.

[本文引用: 2]

WANG Weichen. Study on characteristics of geotechnical capacities for tripod suction buckets foundations in clay [D]. Tianjin: Tianjin University, 2022.

[本文引用: 2]

/

〈 〉